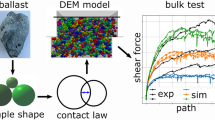
Abstract
In this paper we show DEM simulations of static and cyclic large triaxial tests on a sample of railway ballast. The sample is reconstructed from X-Ray tomography images of an untested laboratory sample, recovered by impregnation with an epoxy resin. Measurements of both shape and fabric are carried out; the sample shows a high anisotropy of particle orientations due to the preparation procedure and a high shape heterogeneity. A DEM model is then generated using clumps to model single particles, preserving the shape of each particle and the fabric of the sample. Results of static and cyclic simulations are shown and compared with previous simulations on numerically generated samples, showing the importance of an accurate representation of the whole range of particle shapes, as well as confirming the effect of particle anisotropy on the mechanical response.
Graphical Abstract

Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
The mechanical behaviour of coarse-grained soils such as sand and gravel is strongly affected by their discrete nature, and the Discrete Element Method (DEM) is often employed to study their behaviour and link their macroscopic response with microscopic (i.e., particle or contact level) quantities. Early DEM applications would often fail to reproduce all features of the mechanical behaviour of a soil because single particles were often modelled by simple spheres (in 3D), far from real particle shapes. More recently, efforts have been made in the direction of modelling real shapes, exploiting digital imaging technologies which allow for an accurate representation of the 3D morphology of a particle, as well as several modelling techniques that have been proposed to provide objects that hold some of the real particle shape features and that can be easily used in DEM [1,2,3,4].
If particles with irregular shapes are used, then their orientation in space can be defined. Particle orientation can be included, together with orientation of interparticle contacts, in the characterisation of fabric. Capturing the real fabric of a granular system may be as important as modelling their real shape, especially when the sample is expected to be highly anisotropic, e.g., as a consequence of loading history or sample preparation, as this can have a significant effect on the macroscopic mechanical response.
Recently, technologies such as X-Ray Computed Tomography (XRCT) have been used to provide a geometrical description of whole samples of soil, even allowing for complete laboratory tests to be carried out inside an X-Ray scanner to look inside the soil sample at different stages in a non-destructive manner (e.g., [5]). A complete geometrical representation of a sample holds information on the real shape of all particles, as well as on their orientation, and therefore can be used to build a digital twin of a real laboratory sample, and use it to simulate laboratory tests in DEM [6].
This approach is however limited by the dimensions of the sample and testing device that can be accommodated inside an X-Ray scanner. Railway ballast is often characterised in the laboratory as a soil, with classic triaxial tests; however, due to the large size of particles (usually ranging between 20 and 63 mm), samples need to be large enough to contain a sufficient number of particles such that the mechanical behaviour of the aggregate can be considered relevant and repeatable. This means that typical dimensions of ballast cylindrical samples can be as large as \(d=300 \text{m}\text{m}\) and \(h=450 \text{m}\text{m}\) or more [7,8,9]. These dimensions do not allow real-time, non-destructive imaging through XRCT, therefore alternative solutions for the recovery of undisturbed ballast samples should be used. These include the use of low viscosity resins or glues that are injected in the sample and cure until forming a solid mixture, with little or no disturbance to the position of particles. When X-Ray scans are taken, the lower density of such matrix compared to that of soil particles makes it possible to separate particles from the surrounding matrix, due to the different X-Ray attenuation coefficients of the two phases. Sample impregnation with epoxy resin, in particular, has been successfully employed for the preservation of ballast, both for laboratory cylindrical samples of scaled ballast [10] and for samples recovered directly from in-service railway tracks [11].
The richness of spatial information provided by XRCT is also associated with the variability of particle shapes. Without this information, it is usually not feasible to acquire a geometrical description for each particle, and DEM models often adopt a limited number of different shapes (e.g.: one [12], three [13], 100 [14]); this is generally considered sufficient to appreciate the effect of a realistic shape on the mechanical behaviour, especially in comparison with the basic case of simple spheres. This is particularly true for a rather angular material such as ballast for which some interlocking between particles can usually be achieved even with few different real shapes. Also, ballast is usually considered to be composed of rather blocky rock clasts, and this is often reflected in the choice of shapes to be employed [12,13,14]. However, some particles can have more flat or elongated geometries, and their presence can affect the fabric and relative density of a sample. More generally, when the aim is to replicate a real experiment, and eventually provide a numerical tool to complement and/or replace laboratory experiments, it is important to account for the whole range of real shapes.
In this paper, we briefly present an application of resin recovery of one large triaxial sample of ballast, prepared for the large triaxial apparatus in Nottingham [8] but not tested; we show measurements of shape and fabric; finally, we use the reconstructed geometry and an experimentally informed contact model to produce for the first time an “avatar” DEM model of a ballast laboratory sample, with real particle shape, fabric and contact mechanics, and carry out simulations of static and cyclic triaxial tests. These simulations will be compared with previous simulations in which particle shape (because of the limited number of shapes in use) and fabric could not be fully accounted for.
2 Reconstruction of a virtual ballast sample for DEM
2.1 Sample preparation
A ballast cylindrical sample with \(d = 300 \text{m}\text{m}\) and \(h = 450 \text{m}\text{m}\), that could be accommodated in the large triaxial device in use at the University of Nottingham [8], was prepared, following a standardised procedure of layered compaction, similar to that adopted by other researchers (e.g., [9, 14, 15]). The aggregate is poured inside a steel split mould in three steps, and at the end of each step the layer is vibro-compacted for 30 s with an overload of 20 kg on top of the layer. This procedure was found to consistently give a total mass of about 48–50 kg, corresponding to a voids ratio close to 0.700 considering the nominal dimensions of the sample and a particle density of 2650 kg/m3; in this specific case, a total mass of 48.7 kg was obtained. The value of particle density is a commonly used value for granite ballast such as the ballast from the Mount Sorrel quarry used here, and was confirmed by a test for particle density carried out on 20 large particles of the same material, following the procedure detailed in [16]. The sample thus prepared is enclosed laterally in a rubber membrane and vertically by two aluminium platens; the membrane is sealed at the two platens by means of O-rings and “jubilee” clips (Fig. 1a).
2.2 Resin recovery
After carrying out the described procedure, the sample is typically put under vacuum so that it can sustain itself when the mould is removed while being accommodated inside the triaxial cell. While in this case the sample was not being prepared for actual testing, vacuum was still applied through a hole in the top platen to facilitate the injection of resin. It is assumed that this operation has little or no impact on the sample fabric, particularly in comparison with the high anisotropy that the previous compaction phase is expected to have produced.
A dark, low viscosity epoxy resin (PX672H by Robnor Resinlab [17]) was then injected through a second hole in the top platen; after 24 h, the curing process had finished and the rubber membrane could be removed. The preserved sample is shown in Fig. 1b. The sample was then scanned in the µ-VIS X-Ray facility in Southampton [18], with a resolution of 1.09568 mm/pixel. The procedure for the identification of single particles included the application of a median filter and an adaptive segmentation technique [19], followed by a watershed algorithm to separate particles. The resulting stack of binarised images was subsequently processed to extract point clouds describing the surface of each individual particle. Further details on the scanning parameters, the procedure followed, and issues encountered will be described in a separate publication.
2.3 Sample reconstruction as a DEM model
Image processing of the acquired scans, including steps such as binarization and segmentation, finally provided a set of 657 individual particles, each described by a point cloud on their surface. With the given resolution, each particle was described by an average of ~ 10,000 points. A 3D triangulated mesh enclosing a volume was then reconstructed for each particle after estimating the normal vectors to the surface at each point of the cloud with the software MeshLab [20], to provide a reference geometrical description which could then be used to create a virtual model of each particle for the DEM simulations. The clump technique was chosen, specifically the “bubblepack” algorithm proposed by [21] and implemented in the commercial software [22]. Clumps are collections of overlapping spheres with no internal contacts. The parameters that need to be defined in order to build clumps from a surface description are the ratio ρ between the smallest and largest sphere of one clump, and the angle θ measuring the overlap between two neighbouring spheres and ranging between 0° (no overlap) and 180° (complete overlap); values of ρ = 0.3 and θ = 140° had been previously found to be a satisfactory compromise between shape accuracy and computational effort required [13], and were therefore replicated here, giving an average of 108 spheres per clump. A bounding cylinder with vertical axis passing through the centre of mass of the sample was fitted to measure its dimensions, giving a height of 460.2 mm and diameter of 293.8 mm (consistent with the mould’s internal diameter of 300 mm and the membrane thickness of 4 mm). An image of the final DEM sample made of clumps is shown in Fig. 2. Clumps had to be expanded slightly to compensate for volume loss due to some issues with particle reconstruction from the scan (e.g., volume loss around contacts where some voxels had to be removed to facilitate segmentation) and to the natural tendency of clumps to underestimate the reference particle’s volume, especially at corners and at cavities that are formed between neighbouring spheres. A total volume corresponding to a mass of 48.7 kg, as measured while preparing the sample, was targeted. This expansion was carried out very slowly while allowing clumps to displace and rotate, so that the sample’s fabric would be preserved while leaving the sample stress-free.
a Reconstructed sample. b DEM model of the reconstructed sample made of clumps with random colourisation, with the same view as in Fig. 1b. The sample is loaded axially by two blocks used to model the end platens. c Bonded spheres layer used to model the flexible lateral membrane
2.4 Particle size distribution
A Particle Size Distribution (PSD) was determined for the reconstructed clumps. First, a surface description of clumps was obtained as a 3D triangulated mesh, similar to the mesh describing the original particle shape. The methodology developed to obtain such a triangulation of the outer surface consists of creating a mesh for each sphere composing the clump and then performing a union operation applied to all spheres. A classic approach to define the size of an irregularly shaped particle is to use its equivalent diameter, i.e., the diameter of a sphere with the same volume as the particle. This is usually quite accurate if particles are mostly equidimensional (high compactness), as it gives results that are consistent with the standard sieving procedure carried out in the laboratory. This however becomes less accurate when the amount of flat and elongated particles is non-negligible, as might be the case for ballast: reproducing numerically the experimental procedure, where square apertures determine the size of a particle, with the equivalent diameter may overestimate the size. If a bounding box is defined, then its intermediate length is a more appropriate quantity to determine whether the particle will pass a certain sieve or not. In particular, to cover all possible orientations of a particle, one should consider several bounding boxes with different orientations and take the smallest of all intermediate dimensions I as the reference size. Other criteria (e.g., taking the bounding box with the smallest volume) may also overestimate the reference size (Fig. 3). Here, the different orientations are obtained by aligning one face of the box alternatively with each of the faces of the particle mesh’s convex hull [23].
Two bounding boxes obtained for one quite flat clump (C = 0.29, F = 0.62, E = 0.08). The blue box has the smallest intermediate length (\(I=55 \text{m}\text{m}\)), which should be used to calculate the PSD; the red box is the one with the smallest volume, and largely overestimates the size (\(I=73 \text{m}\text{m}\)).
The PSDs calculated with the two methods (equivalent diameter and minimum intermediate length) are shown in Fig. 4 and compared with the nominal experimental PSD. While the difference between the two methods is clear, and the intermediate length gives a better match with the experimental curve, both curves lie below the experimental one, which indicates that particles appear larger than they are. This is due to the bounding box being a convex approximation of the particle shape; because of this, for some concave particles that would pass through a certain sieve in the laboratory, their numerical counterpart may be found to be retained instead. Nevertheless the use of the bounding box seems better than the equivalent diameter in replicating the sieving process.
Particle Size Distribution after correcting the volume to reach the target mass, determined both with the classic equivalent diameter and with the alternative method based on the smallest intermediate length. The range defined in the guidelines is also shown [24]
3 Shape and fabric
3.1 Shape analysis
The resolution of the scan is sufficient to allow an accurate and reliable definition of the first scale of shape parameters (form); angularity (second) could also be determined but it still lacks a unique definition for 3D shapes, and form itself is considered sufficient to characterise shape for the purposes of this paper; roughness would need a higher resolution and anyway is not directly modelled when reproducing the real shape of particles (it is typically only accounted for through the interparticle friction—and here through normal stiffness as well, see Sect. 4.1—in the contact law).
In terms of form characterisation, several definitions are available, based on different parameters. Generally, the determination of 3 equivalent dimensions (major, intermediate and minor) is needed. As seen in Sect. 2.4, the oriented bounding box can provide this; for shape characterisation, the bounding box is usually defined as the one, among many bounding boxes, that minimises some quantity (e.g., volume or intermediate length). The obtained parameters, however, are not unique and depend on the chosen box. An alternative method makes use of the Surface Orientation Tensor (SOT) [25], that provides a more objective definition exploiting the whole particle surface description: it is a particle-based tensor using the dyadic product of the outwards normal to each facet of the triangulated surface weighted by the facet area. The ratios of the three eigenvalues of this tensor (\({f}_{1}\ge {f}_{2}\ge {f}_{3}\)) can provide a measure of compactness \(C\), flakiness \(F\) and elongation \(E\), which are the classic parameters that can be used to describe the “form” of a particle. These are defined respectively as \(C={f}_{3}/{f}_{1}\), \(F={(f}_{1}-{f}_{2})/{f}_{1}\) and \(E={(f}_{2}-{f}_{3})/{f}_{1}.\) These parameters sum up to 1 and can therefore be shown graphically in a triangular map (i.e., ternary plot, Fig. 5), where values for the 657 particles reconstructed from the scan are compared with values for the 3 shapes used to numerically generate similar ballast triaxial samples in previous simulations [13].
Ternary plot of form indices compactness, flakiness and elongation determined for each particle from the eigenvalues of the particle’s Surface Orientation Tensor as described by [25]. Grey dots represent all particles extracted from the scan; the three black crosses correspond to the three shapes used in previous simulations [13]. Grid lines are drawn with the same colour as the axis they refer to
It is clear from this ternary plot that the 657 ballast particles extracted from the scan are characterised by a significant shape heterogeneity; average values are 0.36 for compactness, 0.44 for flakiness and 0.18 for elongation, but in general a wide range of different shapes can be observed, including some very flaky or elongated particles. Often, in previous DEM simulations of ballast, blocky and compact particles had been chosen (e.g., [12, 13]), and flat and elongated shapes had been intentionally discarded [14]. Regulations for railway ballast such as [24] propose alternative indices to describe the overall form of a sample, such as a flakiness index, a shape index and a particle length index that are proposed in [26, 27] and tables are provided in [24] to categorise the aggregate accordingly. The laboratory procedure to calculate these indices was replicated numerically; Table 1 shows the indices determined for the sample reconstructed from the scan and for the sample in [13]. Each individual particle in the samples is analysed, and the final index returns a global measure of shape for the whole samples. Here, the shape of original particles (reconstructed from scans) was used; if clumps were used instead, the result would have been essentially unchanged as they reproduce well the form of original particles with the resolution adopted. Based on the categorisation proposed in [24], the values for the scanned sample fall in the group with lowest flakiness (FI ≤ 15) and the second groups with smallest shape index (SI ≤ 20) and particle length (PL ≤ 6). It means that this specific shape distribution is not characterised by extreme flakiness or elongation, but it is rather a commonly heterogeneous distribution of shapes.
3.2 Fabric analysis
While the resolution of the scan was not sufficient to retrieve accurate information on contact-based quantities (position, area and orientation of contacts), particle orientation could be easily determined and analysed, by defining a vector \(\overrightarrow{l}\) as the eigenvector corresponding to the smallest eigenvalue of the inertia tensor of the particle. A fabric tensor based on particle orientations \(\overrightarrow{{l}^{p}}\) was calculated as \({G}_{ij}=\frac{1}{{N}_{p}}\sum _{p=1}^{{N}_{p}}\overrightarrow{{l}^{p}}\otimes \overrightarrow{{l}^{p}}\), where Np is the number of particles. The diagonal components of three local fabric tensors and the global one are given in Table 2, with z as the axial (vertical) direction and the two horizontal x and y axes orthonormal with z. A scalar representing particle anisotropy is also calculated as the norm \(F=\sqrt{\mathbf{F}:\mathbf{F}}\) of the anisotropy fabric tensor \(\mathbf{F}=3\mathbf{G}-\mathbf{I}\). A perfectly isotropic sample would have \({G}_{xx}={G}_{yy}={G}_{zz}=0.333\) and \(F=0\). The prevalence of x and y (horizontal) components compared to z (vertical) components is a clear sign that particles are mostly oriented along (or close to) the horizontal plane, as an effect of compaction during sample preparation.
The change of particle fabric over the height of the sample was also analysed. The sample was divided in three equal layers and each particle was assigned to one of those based on the position of its centre of mass; fabric tensors were then calculated for each of the three layers. It might be expected that layered compaction generates a non-uniform fabric over the height of the sample, as the lower layers receive more compaction energy [15]; however, this is not the case for the sample that was scanned, which looks quite homogeneous (Table 2).
Particle fabric was also compared with that of the numerically generated sample used in [13]. In that case, the laboratory procedure for sample preparation had not been replicated, and particles had been instead generated with random positions and orientations and a smaller volume, and then slowly expanded until reaching the target voids ratio in a stress-free configuration. This procedure gives a rather isotropic sample in terms of particle orientations, as shown in Table 3. Then, the laboratory procedure was also replicated numerically on the same sample, to assess its effect on anisotropy. The sample generated isotropically was dispersed over a cylinder extending beyond the top platen of the actual sample, mixed and then left to settle under gravity in three steps, with a dynamic compaction at the end of each step performed by applying a cyclic force to the top platen. Particle fabric for this compacted sample is also shown in Table 3. While this operation slightly increases the anisotropy of the sample (\(F\) from 0.064 to 0.111), it is clear that the level of anisotropy of the laboratory sample (0.404) cannot be achieved with the numerically generated sample despite replicating the preparation technique. This is strongly related to the shape distribution: a heterogeneous distribution including also flat and elongated particles is clearly more prone to be arranged in a more anisotropic configuration, as those are the particles that have a more defined orientation and are more likely to align in a certain plane, looking for more stable configurations depending on the external condition applied. Compact particles, on the other hand, have a less clear orientation, and, when forced to rotate by the loading applied, they tend to assume more random orientations. A sufficiently heterogeneous shape distribution therefore allows a higher particle anisotropy, with all the consequences for the mechanical behaviour which will be analysed in the following sections.
Finally, to assess the amount of anisotropy with respect to field ballast, particle orientations were compared with measurements carried out by [11] on samples retrieved directly from the track. The distribution of particle orientations, expressed here as the angle ψmaj between the orientation \(\overrightarrow{l}\) and the horizontal plane, is drawn in Fig. 6 for the laboratory sample, showing a particle anisotropy comparable with that observed in operational tracks after about 30 years of service [11].
Probability of particle orientations of the laboratory sample reconstructed from XRCT scan, compared with equivalent data for two different ballast samples retrieved in the field [11]. The isotropic case (horizontal dashed line at 20%) is also shown for reference
3.3 Relative density
In addition to particle shape and orientation, another physical quantity affecting the mechanical behaviour is relative density \({D}_{R}\), defined as a function of the actual voids ratio \({e}_{0}\) and the minimum and maximum voids ratio (\({e}_{min}\) and \({e}_{max}\)) that can be obtained for that sample:
The two samples analysed here (sample reconstructed from scan and numerically generated sample) have the same total mass (48.7 kg); for the numerical sample, this corresponds to a voids ratio e0 = 0.733, whereas the scanned sample has slightly different dimensions, and therefore its voids ratio is comparable but slightly smaller (e0 = 0.685). Their different shape (and size) distributions however can lead to a different relative density, which is a more appropriate parameter to describe the influence of density on the mechanical response.
To estimate the smallest voids ratio \({e}_{min}\) for each of the two DEM samples, the three-step compaction procedure described in Sect. 3.2 was replicated with a fictitious µ = 0 between particles. While not realistic, using a low or null interparticle friction is a common choice in DEM to obtain very dense states (e.g., [14], [28]), and it can be acceptable in this case where the only purpose is to have an estimate of \({e}_{min}\) allowing to compare two different samples. To determine \({e}_{max}\), particles were redistributed in a taller cylinder and left to deposit under gravity with a more realistic interparticle friction \(\mu =0.7\) [29], until equilibrium was achieved. Values of relative density DR are reported in Table 4, showing a markedly higher initial density for the scanned sample. The effect of relative density on the macroscopic behaviour is generally observed in the dilation rate, as will be shown in the following sections.
4 DEM simulations
4.1 Model description and loading conditions
To re-cap, two different numerical samples were analysed. One is reconstructed from XRCT scans of the laboratory sample, as described in Sect. 2; this will be referred to as “scanned sample” in the following sections. The second sample is a numerically generated sample made of 747 clumps using only 3 different particle shapes, already used in [13]. Two different configurations were generated with the latter sample: one obtained by simply expanding clumps, which will be referred to as “3-shape sample, isotropic”; a second one obtained by replicating the experimental procedure of compaction, as described in Sect. 3.2, referred to as “3-shape sample, compacted”. On this set of three initial samples, DEM simulations of static and cyclic triaxial tests were carried out, using the commercial software PFC3D [22]. Apart from the different samples, the other parameters of the DEM model are the same in all simulations. A flexible membrane consisting of 12,600 monodisperse bonded spheres (each with 5.4 mm radius) was modelled, as described in [13]. The two end platens were modelled by rigid blocks with the same size and density as those used in the large triaxial device in [8]. A confining pressure of 60 kPa was used, which is a common value for railway ballast testing. Interparticle friction was set to 0.7, based on experiments [29], whereas a low coefficient (0.1) was assigned to contacts with platens, which are typically lubricated in the experiments that are modelled here; a non-zero value was still needed to avoid excessive sliding of the whole sample along the platen during shearing. No friction was assumed between the ballast and the lateral rubber membrane. An elasto-plastic contact law for rough surfaces was employed for contacts between ballast particles, as described in detail in [30], based on experiments by Altuhafi et al. carried out with the same interparticle device used in [29]; the law defines a dependency of contact normal stiffness on surface properties such as the fractal dimension Df and root mean square height h, which were obtained from fitting of experimental data, as well as on material parameters E and ν, for which typical values for granite ballast, as the material used in these experiments, were employed [31]. A simple linear contact model with an arbitrary stiffness \({k}_{n}={k}_{s}=3\times {10}^{6} N/m\) was used for ballast-platen contacts. Cundall’s local damping was used, with the typical value of 0.7 for the damping coefficient \(\alpha\). The main parameters of the model are summarised in Table 5. Sample dimensions were slightly different between the two samples: the 3-shape samples have the nominal dimensions of the triaxial cell (d=300 mm; h=450 mm), while the scanned and reconstructed sample has the dimensions measured from the scan as shown in Sect. 2.3.
Gravity was included to account for the sample and platen self-weights, with an acceleration of 9.81 m/s2; these contributions are not negligible and should not be discarded considering the relatively low confining pressure of tests on ballast and the large size of the sample. While for the compacted 3-shape sample gravity was already active during the previous compaction phase, for the scanned sample and 3-shape isotropic sample it was activated after sample generation, and the sample was left to settle under its own (and the top plate) weight; this process introduced some contact anisotropy into the 3-shape isotropic sample (Table 6). Contact anisotropy was calculated with the same definition of fabric tensor and fabric anisotropy in Sect. 3.2, using normal vectors at contacts as the vector \(\overrightarrow{l}\) to build the fabric tensor. Isotropic confinement was then carried out by slowly increasing the confining pressure until the target value of 60 kPa, and then keeping it constant while waiting for equilibrium. Contact anisotropy decreases during isotropic confinement, but some anisotropy remains (Table 6), both because the confining pressure is probably too low to erase the memory of the initial contact anisotropy and because the sample and platen self-weights can induce a little loading anisotropy.
In the next sections, results from both static and cyclic triaxial test simulations are reported; components and invariants of the stress tensor are determined directly from contact forces with the classic homogenisation equation \({\sigma }_{ij}=\frac{1}{V}\sum _{{N}_{c}}{f}_{i}{l}_{j}\) [32], where contact quantities \(\overrightarrow{f}\) (contact force) and \(\overrightarrow{l}\) (branch vector connecting the centroids of the two bodies in contact) are summed over all contacts \({N}_{c}\) lying inside volume \(V\).
4.2 Static triaxial tests
Confined samples were subjected to static triaxial tests by imposing a constant velocity of \(1 \text{m}\text{m}/\text{s}\) to the bottom platen, while keeping the top one fixed, only allowing this top platen to rotate about its centre of mass, similarly to what happens in the large triaxial device. These triaxial simulations reproduce similar laboratory tests carried out in the large triaxial device described in [8]; those tests had to be stopped at an axial strain \({\epsilon }_{a}=12\%\), due to the sample expanding radially and reaching the inner cell used for volume measurements. At that point, ballast samples are typically still undergoing large dilation and are far from critical state. Other triaxial tests on scaled ballast [33] and regular size ballast [7] reached respectively \({\epsilon }_{a}=16\%\) and \(20\%\) but still showed some residual volumetric deformation. In these simulations, it was attempted to reach larger strains (\({\epsilon }_{a}=25\%\)); accurate volume measurements were achieved by continuously calculating the volume enclosed by the flexible membrane.
Figure 7 shows the macroscopic response of three triaxial DEM simulations with \({\sigma }_{3}=60 \text{k}\text{P}\text{a}\). The effect of compaction on the 3-shape sample is negligible and limited only to the initial stiffness; the response is then very similar to that of the isotropic sample, as the two samples share the same particle shape and size distribution, as well as the same initial density. The sample reconstructed from the scan has a very different behaviour, with a much higher dilation rate and a higher peak stress (\({\phi }_{max}=54^\circ\) compared to \(42^\circ\) for both 3-shape samples). Stress ratio at critical state is also larger for the reconstructed sample, with \({\phi }_{max}\sim39^\circ\) (closer to values typically expected for angular gravels), while for the two 3-shape samples it drops down to \(\sim33^\circ\). While the higher dilation can be explained by the different initial relative density (Table 4), and is linked with the larger difference between peak and critical state strength according to [34], the larger critical state strength results from the different shape distributions. The beneficial influence of particle flakiness and elongation on the critical state strength is consistent with results obtained by [35] from DEM simulations of both ellipsoids and angular shapes.
It is clear from Fig. 7 that different samples with different shape distributions and relative densities can have very different mechanical behaviours. In addition to this, the relatively small number of particles composing the sample, which is however typical of these laboratory tests on ballast, is also a possible source of large variability in the mechanical response. Due to this, the purpose of this work was not directly to match the experimental data of a single test or set of tests; to do so, it would be necessary to replicate the same fabric of the reference experimental test, i.e., ideally having non-destructive scans of a sample during testing, but this is not feasible due to the large dimensions of the sample and cell, that cannot be accommodated inside an X-Ray facility. Nevertheless, it is still interesting to compare DEM simulations of different samples with a real laboratory test that was carried out with \({\sigma }_{3}=60 \text{k}\text{P}\text{a}\) (Fig. 7), although the laboratory test was stopped at \({\epsilon }_{a}=12\%\). It can be observed that none of the samples used for simulations can give a satisfactory fit of the experimental data: the numerically generated 3-shape samples show a similar volumetric behaviour, but their peak strength is slightly lower, and stress drops earlier and more significantly, whereas a clear peak cannot be easily detected for experimental data, possibly suggesting that strength will not drop as much while approaching critical state; the scanned sample shows a higher dilation and consequently a higher peak stress; the critical state is evident for this sample when the sample has finished changing in volume and gives an estimate of the final critical state for the laboratory-tested experimental sample.
To better understand the effect of shape distribution on the mechanical behaviour, a micromechanical analysis, including the evolution of particle and contact fabric and showing how different particle shapes can affect the distribution of contacts, can be helpful. The initial values of particle anisotropy for the three samples after generation were previously shown in Table 3; at the start of axial loading, i.e., just after isotropic confinement, particle anisotropy has essentially not changed much (Fig. 8), showing that confinement at these low pressures cannot erase the previous loading history (and in particular the effect of compaction). The evolution during the test confirms that the amount of particle anisotropy of the scanned sample cannot be achieved with the numerical sample made of 3 compact shapes, even after the sample has undergone large deviatoric strains. This is related to the larger amount of flaky and elongated particles in the scanned sample, that can easily become aligned along the horizontal plane already during the preparation phase, also facilitating interlocking between particles during shearing. This larger particle anisotropy also affects contact anisotropy in turn: the several flaky and elongated particles aligned horizontally are more likely to build contacts along the vertical direction, as they offer larger surface areas in that direction. This effect can be quantified with the Surface Orientation Tensor [25]: typically used to determine form parameters (as in Sect. 3.1), this also gives information on the direction in which contacts are more likely to be created, which can be determined as the first eigenvector of the tensor. Figure 9 shows a histogram of the angle \(\beta\) between the horizontal plane and the SOT’s first eigenvector (i.e., corresponding to the maximum eigenvalue) for all clumps in the three samples at the end of confinement; for the scanned sample, the vertical direction (values close to 1) is clearly the preferential direction for contact creation, whereas the other two samples show more random and isotropic behaviours. This is consistent with the initially higher contact anisotropy for the scanned sample (Table 6); contact anisotropy remains higher for the whole duration of the simulation (Fig. 10), similar to the evolution of particle anisotropy.
Probability of the orientation of the first eigenvector (i.e., corresponding to the maximum eigenvalue) of the Surface Orientation Tensor [25] for all particles of different samples at the end of confinement
Flaky and elongated particles, as they deviate from rounded shapes, increase their resistance to rotation; the suppression of this mechanism induces an increase in interparticle sliding, which is a more energy-demanding mechanism [35] and is therefore reflected in a higher critical state stress ratio. A good measure of the increased resistance to rotation due to shape is provided by a mechanics-based shape index \({\alpha }_{c}\) proposed by [36]. This parameter, defined at points of contact between particles, measures the angle between the normal vector to the surface of a particle at the contact point and the branch vector connecting the contact point with the particle’s centre of mass; this is related to the additional contribution to the particle’s rotational resistance that a normal contact force generating a moment with respect to the centre of mass can offer. While for a sphere \({\alpha }_{c}=0^\circ\), and for compact shapes \({\alpha }_{c}\) is relatively small, more irregular particles can offer larger values of \({\alpha }_{c}\), and therefore higher rotational resistance, as shown by their probability distribution in Fig. 11. This explains the difference in critical state stress ratio observed in Fig. 7.
4.3 Cyclic triaxial tests
Cyclic triaxial tests were carried out by applying a sinusoidal axial force to the bottom platen; the magnitude of this force ranges between a lower \({F}_{min}\) that is the sum of the bottom platen’s own weight and the magnitude of all contact forces acting on the bottom platen at the end of confinement, and a higher \({F}_{max}={F}_{min}+\varDelta F\) where \(\varDelta F\) is the product of the platen’s cross sectional area with the deviatoric stress applied \({q}_{max}=180 \text{k}\text{P}\text{a}\). The frequency of the applied loading affects the strain rate applied; in order to limit this, and avoid unwanted inertial effects, this was kept lower in the first few cycles, when the sample is softer and a given increment of deviatoric stress would cause a larger strain rate, and then gradually increased. The frequency was 1 Hz for the first cycle, 3 Hz for cycles 2–4, 5 Hz for cycles 5–19 and then fixed at 10 Hz; with these values, the quasi-static condition \(I<{10}^{-3}\) was observed, with \(I\) as the inertial number defined in [37] as a function of strain rate, sample properties and loading conditions.
Figure 12 shows the accumulated axial strain at the end of each cycle for the three samples. While it is still impractical for DEM simulations of cyclic loading to achieve the number of cycles of typical experiments (e.g., 106 as in [8]), the number of cycles performed (> 2000) is still considered sufficient for a meaningful analysis of the data, both for a comparison of the three samples and for a comparison with experimental data. Both 3-shape samples are much softer than the reconstructed scanned sample; they accumulate a large amount of axial deformation in the first 50–100 cycles and then become slightly stiffer, although still retaining a higher deformation rate than the scanned sample for the whole test. The scanned sample has deformations that are of the same order as those obtained experimentally by [8] for the same loading conditions. Again, the larger particle and contact anisotropy can be deemed to be responsible for the much stiffer response. Their evolution is shown in Figs. 13 and 14 respectively. Particle anisotropy remains stable for the scanned sample, for which it was already high at the start due to the effect of sample preparation; it grows slightly for the 3-shape samples but, as in the static tests, it remains far from the anisotropy of the reconstructed scanned sample. Contact anisotropy shows a small decrease in the first ~ 50 cycles, as more horizontal contacts are formed while the number of vertical contacts remains stable, and then stabilises for the rest of the simulation for all three samples. Once more, the anisotropy in the reconstructed scanned sample remains much higher than the anisotropy in the 3-shape samples, consistently with the higher particle anisotropy and with the higher axial stiffness observed in Fig. 12.
5 Conclusion
By injecting epoxy resin in an untested laboratory large triaxial sample of railway ballast, it was possible to preserve the sample, and subsequent XRCT scan allowed for measurements of particle shape and fabric. These showed a rather heterogeneous distribution of particle shapes, including quite flaky and elongated ones, and a high anisotropy from the start, comparable with that of field ballast after 30 years of service, purely due to the effect of compaction. A DEM model of the reconstructed sample was built, holding the real particle shape and fabric, with clumps employed to model single particles. Numerically generated samples were also considered for comparison; these comprised only three, rather compact (equidimensional) shapes, with no flaky and elongated clumps. This was found to affect the fabric of the sample: lower particle and contact anisotropy could be achieved in this case, compared to the scanned sample which did contain flaky and elongated shapes.
The effect of this on the mechanical behaviour was highlighted through DEM simulations of both static and cyclic triaxial tests. Static triaxial loading showed a higher critical state strength for the reconstructed (scanned) sample, which can be explained with reference to the more irregular form of particles, that can offer a larger rotational resistance, as confirmed by a micromechanical analysis. The higher dilation rate observed for the scanned sample is related to the higher relative density at the start of the test. Cyclic loading simulations also showed a significant improvement of the performance for the scanned sample, for which the larger initial anisotropy resulted in lower accumulated axial strains compared to the numerical (3-shape) samples.
While capturing the correct particle shape and fabric can be in general useful when simulating the mechanical behaviour of coarse-grained soils, it becomes essential for gravelly soils like ballast, for which samples are made of relatively few particles, and a high variability of shapes is observed. Simply modelling real shape is not enough if the range of shapes used is limited and if the fabric is not reproduced correctly.
These results also give further insight on the properties of ballast to be used for laboratory tests, as well as in the field. Current regulations do not define limits concerning the shape of particles employed. While it can be argued that flaky and elongated particles might be more prone to breakage, it is shown here that even a relatively low percentage by mass of such shapes, as in the sample considered here, can significantly improve the ballast’s performance, with potential benefits in terms of track stability (reduction of differential settlements and of required maintenance interventions).
Several future perspectives remain open to follow this work. To improve the quality of sample reconstruction, limit some issues with particle segmentation and acquire information on contacts, future work will focus on increasing the resolution of the scan. Furthermore, work will focus on impregnating a laboratory sample after reaching a critical state and scanning to compare the fabric at a critical state with the work presented here. This work will also provide a whole new set of particle shapes, that could be used to artificially reconstruct a sample in untested conditions and carry out full simulations on it as a realistic avatar ballast.
With real particle shape and fabric (from XRCT scans) and contact mechanics (advanced contact law determined from interparticle tests), it is expected that the DEM model could not just complement, but eventually replace laboratory tests on ballast. In the future, more experimental tests will be required in order to provide a validation of the model, including tests reaching critical state, as well as more simulations on samples with different shape distributions.
Data Availability
Data will be made available on request.
References
Ferellec, J.F., McDowell, G.R.: Modelling realistic shape and particle inertia in DEM. Geotechnique. 60(3), 227–232 (2010)
Deiros Quintanilla, I., Voivret, C., Combe, G., Emeriault, F.: Quantifying degradation of railway ballast using numerical simulations of micro-deval test and in-situ conditions. Procedia Eng. 143(Ictg), 1016–1023 (2016)
Stasiak, M., Combe, G., Desrues, J., Richefeu, V., Villard, P., Armand, G.: Experimental investigation of mode I fracture for brittle tube-shaped particles. EPJ Web Conf. Powders grains. 07015, 4–7 (2017)
Kawamoto, R., Andò, E., Viggiani, G., Andrade, J.E.: Level set discrete element method for three-dimensional computations with triaxial case study. J. Mech. Phys. Solids. 91, 1–13 (2016)
Andò, E., Hall, S.A., Viggiani, G., Desrues, J.: Experimental micromechanics: grain-scale observation of sand deformation. Géotechnique Lett 2(3), 107–112 (2012)
Kawamoto, R., Andò, E., Viggiani, G., Andrade, J.E.: All you need is shape: predicting shear banding in sand with LS-DEM. J. Mech. Phys. Solids 111, 375–392 (2018)
Indraratna, B., Ionescu, D., Christie, H.D.: Shear behavior of railway ballast based on large-scale triaxial tests. J. Geotech. Geoenviron. Eng. 124(5), 439–449 (1998)
Aursudkij, B., McDowell, G.R., Collop, A.C.: Cyclic loading of railway ballast under triaxial conditions and in a railway test facility. Granul. Matter. 11(6), 391–401 (2009)
Mishra, D., Kazmee, H., Tutumluer, E., Pforr, J., Read, D., Gehringe, E.: Characterization of railroad ballast behavior under repeated loading. Transp. Res. Rec. 2374, 169–179 (2013)
Le Pen, L., Harkness, J., Zervos, A., Powrie, W.: The influence of membranes on tests of coarse-grained materials at low cell pressures. Geomech. Micro Macro Proc. TC105 ISSMGE Int. Symp. IS Cambridge 1, 449–454 (2015)
Le Pen, L., Ahmed, S., Zervos, A., Harkness, J., Powrie, W.: Resin recovery and the use of computed tomography for quantitative image analysis of railway ballast. Civil Comp Proc 104, 1–14 (2014)
de Bono, J., Li, H., McDowell, G.R.: A new abrasive wear model for railway ballast. Soils Found. 60(3), 714–721 (2020)
Tolomeo, M., McDowell, G.R.: Modelling real particle shape in DEM: a comparison of two methods with application to railway ballast. Int. J. Rock. Mech. Min. Sci 159, 105221 (2022)
Zhang, J., Wang, X., Yin, Z.Y., Liang, Z.: DEM modeling of large-scale triaxial test of rock clasts considering realistic particle shapes and flexible membrane boundary. Eng. Geol. 279(October), 105871 (2020)
Suiker, A.S.J., Selig, E.T., Frenkel, R.: Static and cyclic triaxial testing of ballast and subballast. J. Geotech. Geoenviron. Eng 131(6), 771–782 (2005)
BS EN 1097-6: 2013. Tests for mechanical and physical properties of aggregates. British Standards Institution (2013)
Robnor Resinlab:. [Online]. Available: https://robnor-resinlab.com/
µ-VIS X-ray Imaging Centre:. [Online]. Available: https://www.southampton.ac.uk/muvis
Madhusudhan, B.N.M., Sahoo, S.K., Alvarez-Borges, F., Ahmed, S., North, L.J., Best, A.I.: Gas bubble dynamics during methane hydrate formation and its influence on geophysical properties of sediment using high-resolution synchrotron imaging and rock physics modeling. Front. Earth Sci. 10(June), 1–12 (2022)
Cignoni, P., Callieri, M., Corsini, M., Dellepiane, M., Ganovelli, F., Ranzuglia, G.: MeshLab: an open-source mesh processing tool. In: Sixth Eurographics Italian Chapter Conference, pp. 129–136. (2008)
Taghavi, R.: Automatic clump generation based on mid-surface. In: The 2nd International FLAC/DEM Symposium June, pp. 791–797. (2011)
PFC — Particle Flow Code: Ver. 7.0. Itasca Consulting Group, Inc., Minneapolis: Itasca, (2021)
Johannes Korsawe: Minimal Bounding Box (2022). https://www.mathworks.com/matlabcentral/fileexchange/18264-minimal-bounding-box), MATLAB Central File Exchange. Retrieved April 23, 2020.
BS: EN 13450: 2013. Aggregates for railway ballast. British Standards Institution (2013)
Orosz, Ã., Angelidakis, V., Bagi, K.: Surface orientation tensor to predict preferred contact orientation and characterise the form of individual particles. Powder Technol. no. 394, 312–325 (2021)
BS EN 933-3: 2012. Tests for geometrical properties of aggregates. Part 3: determination of particle shape — Flakiness index. British Standards Institution (2012)
BS EN 933-4: 2008. Tests for geometrical properties of aggregates Part 4: determination of particle shape — shape index. British Standards Institution (2008)
Macaro, G., Utili, S., Martin, C.M.: DEM analyses of pipe-soil interaction for offshore pipelines on sand Geomech. Micro Macro October, 595–600 (2015)
Wong, C.P.Y., Coop, M.R.: Development of inter-particle friction in a railway ballast. Geotech. Lett. no. 10(4), 535–541 (2020)
Tolomeo, M., McDowell, G.R.: Implementation of real contact behaviour in the DEM modelling of triaxial tests on railway ballast. Powder Technol. 412( October):118021 (2022)
Afrouz, A.A.: Practical Handbook of Rock Mass Classification Systems and Modes of Ground Failure. CRC Press, Boca Raton (1992)
Christoffersen, J., Mehrabadi, M.M., Nemat-Nasser, S.: A micromechanical description of granular material behavior. J. Appl. Mech 48(2), 339 (1981)
Harkness, J., Zervos, A., Le Pen, L., Aingaran, S., Powrie, W.: Discrete element simulation of railway ballast: modelling cell pressure effects in triaxial tests. Granul. Matter 18(3), 65 (2016)
Bolton, M.D.: The strength and dilatancy of sands. Géotechnique 36(1), 65–78 (1986)
Harkness, J., Zervos, A.: Some effects of particle shape on the mechanical behaviour of granular materials In: DEM8, pp. 1–11 (2019)
Kawamoto, R., Andrade, J.E., Matsushima, T.: A 3-D mechanics-based particle shape index for granular materials. Mech. Res. Commun. no. 92, 67–73 (2018)
Midi, G.: On dense granular flows. Eur. Phys. J. E. no. 14(4), 341–365 (2004)
Acknowledgements
This work was supported by the Engineering and Physical Sciences Research Council [grant number EP/S026460/1] in collaboration with Professor M. R. Coop and Dr. B. A. Baudet at University College London and Dr. A. Zervos at University of Southampton. The authors would like to thank Dr. A. Zervos and Dr. B. N. Madhusudhan for providing the data from the X-Ray scan.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tolomeo, M., McDowell, G.R. DEM study of an “avatar” railway ballast with real particle shape, fabric and contact mechanics. Granular Matter 25, 32 (2023). https://doi.org/10.1007/s10035-023-01322-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10035-023-01322-1