Abstract
Increasing seepage flow causes soil particles to migrate, i.e., from local piping to complete fluidization, resulting in reduced effectives stress and degraded shear stiffness of the soil foundation. This process has received considerable attention in the past years, however, majority of them concentrate on macro-aspects such as the internal erosion and soil deformation, while there is a lack of fundamental studies addressing the energy transport at micro-scale of fluid-soil systems during soil approaching fluidization. In this regard, the current study presents an assessment of the energy evolution in soil fluidization based on the discrete element method (DEM) coupled with computation fluid dynamics (CFD). In this paper, an upward seepage flow of fluid is modelled by CFD based on the modified Navier–Stokes equations, while soil particles are governed by DEM with their mutual interactions being computed through fluid-particle force models. The energy transformation from the potential state to kinetic forms during fluid flowing is discussed with respect to numerical (CFD-DEM) results and the energy conservation concepts. The results show that majority of the potential energy induced by fluid flows has lost due to frictional mechanisms, while only a small amount of energy is needed to cause the soil to fluidize completely. The contribution of rotational and translational components to the total kinetic energy of particles, and their changing roles during soil fluidization is also presented. The effect of boundary condition on the energy transformation and fluidization of soil is also investigated and discussed.
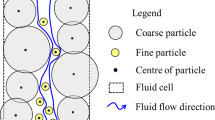
Graphical abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Soil foundations (natural subgrade) often experience increasing seepage flow along the depth beneath transport embankments and dam infrastructure. The internal flow under increasing differential hydraulic gradients can cause soil particles to migrate, e.g., internal erosion and fluidization, where the failure mode is mainly governed by soil characteristics and loading state [1,2,3,4,5]. When the fluid flow continues to increase and exceeds a threshold level, the soil faces a critical state, in which the void ratio rapidly increases, and this is accompanied with substantial degradation in the micro-structure and the shear strength. In this state, soil particles can float and behave like a fluid with complete loss in bearing capacity and shear strength. Recent site investigations [6, 7] across the heavy haul rail network in Australia have shown that a subgrade soft soil can fluidize and migrate upwards under an increasing hydraulic gradient, i.e., mud pumping, resulting in extensive fouling of the overlying granular layers including capping and ballast, thus an inevitably deteriorated track performance. Figure 1 shows an example of subgrade soil fluidization, causing mud flow over the track surface. While considerable effort has been made to understand the potential mechanisms and establish preventive solutions for this problem in the past years, failure induced by internal erosion and fluidization of the subgrade has still been commonly reported worldwide, leading to substantial maintenance costs and adverse rail incidents [7,8,9,10].
Modelling the migration of soil particles under seepage flow has received considerable attention in the past years [1, 11,12,13]. Conventional approaches based on mathematical derivations and continuum-based numerical methods (e.g., finite element method FEM) can be used to estimate the amount of particles washed-out and the corresponding changes in hydraulic conductivity of fluid-soil systems [4, 14, 15]. However, these methods cannot provide quantitative information of particle interactions and localised system behaviour. This is why numerical methods such as the discrete element method (DEM) coupled with computational fluid dynamics (CFD) have emerged as an effective approach to advance our understanding of soil-fluid interaction behaviour at the micro-scale. In this coupled method, DEM is used to describe the individual behaviour of soil particles considering their mutual interactions, while CFD is used to simulate the fluid response. The interaction between solid and fluid phases is carried out and their parameters are updated over time. It is noteworthy that there are different computational methods included in the general term CFD, for example, resolved or fine meshing techniques such as the Lattice Boltzmann Method (LBM) as well as unresolved or coarse meshing techniques such as the averaged Navier–Stokes (NS) theories. Recent years have seen an expanding effort in the coupled CFD-DEM approach to improve the model accuracy as well as extending its application in wider contexts [16,17,18,19,20].
The use of energy-based concepts to clarify the mechanism of geotechnical failures has been adopted more commonly in recent developments. For instance, various analytical and experimental studies have captured the energy dissipation trends quantified through cyclic loops to explain the occurrence of plastic strain accumulation and failure of geomaterials under cyclic loading [21,22,23]. In this regard, DEM has shown its outstanding advantages as it enables the dynamic behaviour of soil particles to be estimated in detail. It has been successfully employed to estimate the required kinetic energy to trigger geotechnical failures such as internal erosion, rock falls and slope instability [18, 24, 25]. Therefore, using DEM coupled with CFD is a rigorous approach to improve our understanding of how the energy of a soil-fluid system evolves during soil fluidization considering different micro-factors such as particle contacts and migration.
In the current study, the coupled CFD-DEM computation is used to investigate the energy transformation of a saturated soil subjected to increasing seepage flow. As past studies mainly focused on macro-aspects of soil and fluid, the major contribution of the current study is the use of micro-quantities such as detailed particle migration and localized fluid variables obtained from the numerical simulations to compute the energy transport while soil is fluidizing. Understanding this mechanism would be crucial to advance our knowledge of using energy concepts to explain soil failure such as the internal erosion and fluidization as being addressed in the current study. The DEM incorporated into LIGGGHTS codes is employed to simulate the subgrade soil [18, 24, 26], while the CFD based on the modified NS theories (i.e., OpenFOAM) is used to model the fluid [26] as elaborated below.
2 Theoretical background
2.1 Discrete element method
The discrete element method (DEM) [27] incorporating the influence of fluid on particles in a fluid-particle system can be described through the follow governing equations:
where Upi and ωpi are the translational and angular velocities of particle i, respectively while mi is the mass of solid particle; \({\varvec{F}}_{c,ij}\) and \({\varvec{M}}_{c,ij}\) are the contact force and torque acting on particle i by particle j (or walls); \(n_{i}^{c}\) denotes the number of total contacts of particle i; t is the time; \({\varvec{F}}_{g,i}\) is the gravitational force; Ii is the inertia moment of particle i. The rolling resistance is described through the rolling friction torque \({\varvec{M}}_{r,ij}\). Influence of seepage flow on the behaviour of particle i is reflected through the total hydraulic force \({\varvec{F}}_{f,i}\) which will be detailed later in this paper. The subscripts p and f denote particle and fluid, respectively.
The laboratory results of the sandy soil, which will be presented in the coming sections of this paper, were used to validate the numerical analysis, so the nonlinear Hertz-Mindlin contact model which has been successfully employed for granular soils in the past [19, 28, 29] was adopted. Two major components, i.e., the tangential \({\varvec{F}}_{ct}\) and normal \({\varvec{F}}_{cn}\) contact forces of this model are computed based on the contact stiffness given by [28, 29]:
where \(k_{cn}\) and \(k_{ct}\) are the normal and tangential contact stiffness, respectively; \(\delta_{n}\) is the overlap of two particles i and j in contact;\(R^{*}\), \(E^{*}\) and \(G^{*}\) are the effective radius, Young’s and shear modulus. The subscripts cn and ct denote the normal and tangential components of the contact. Detailed calculation of these parameters can be found elsewhere [29].
The current study used the directional constant torque model to simulate the rolling resistance as follows [30,31,32]:
where \({\varvec{M}}_{r}\) and \(\mu_{r}\) are the rolling torque and friction coefficients while \({\varvec{\omega}}_{{{\varvec{rel}}}}\) is the relative angular velocity between two particles in contact. As the soil was modelled under low confining pressure (i.e., no compression load) and subjected to small level of hydraulic gradient i (i.e., i < 2.5), a small rolling friction coefficient μr = 0.1 was used. Indeed, Govani et al. [31] compared the results from numerical simulations (DEM and CFD-DEM coupling) for the angle of repose and spout-fluid bed of granular materials with experimental data while varying rolling friction coefficient. They concluded that the numerical results were most reasonable when the rolling friction coefficient varied from 0.1 to 0.125. The current study hence adopted the value for this parameter of 0.1 with respect to the coarse and relatively rounded sand (i.e., the average sphericity of particles captured through Micro-CT scanning was around 0.75) under low confinement used in the experiment.
2.2 Computational fluid dynamics based on Navier–Stokes theories
The authors have employed the modified Navier–Stokes (NS) equations where the effect of solid soil particles on the fluid flow is considered as follows:
where n is the overall porosity in the computed domain while \(\rho_{f} , _{f} ,{\varvec{U}}_{f}\) and p are the density, viscous stress, velocity and pressure of fluid, respectively; I is the identity tensor; g is the gravitational acceleration; \({\varvec{f}}_{p}\) is the mean volumetric particle–fluid interaction force which represents the effect of solid particles on the fluid phase.
The finite volume method (FVM) was used to solve the NS equations, so that the fluid domain was discretised into a finite number of cells where the governing equations were solved locally using the averaged fluid velocity and pressure. Each fluid cell contained a number of soil particles which, on the other hand, would change the momentum of fluid phase. The averaged fluid variables at each fluid cell were used to compute fluid forces acting on solid particles. The mean volumetric particle–fluid interaction force \({\varvec{f}}_{p}\) in a fluid cell is calculated by:
where \(n_{p}\) is the number of particles in the cell with a volume \(V_{c}\); \({\varvec{F}}_{fi}\) is the total hydraulic force induced by fluid acting on particle i. The contribution of each particle to \({\varvec{f}}_{p}\) is weighted by the factor \(\varpi_{i}\) which is defined as the ratio between the volume of particle i occupied in the fluid cell to its total volume. In other words, \(\varpi_{i}\) varies from 0 to 1 depending on the portion that particle i is occupied by the fluid cell. The divided void fraction technique [26, 30] that is capable of dividing the particle into a number of smaller parts was adopted. In this technique, a solid particle was divided into different portions which were then used to compute the solid and void fractions of the fluid cell, depending on whether or not those portions were occupied by the cell.
2.3 Hydraulic forces acting on particles due to fluid flowing
When fluid flows through a porous particulate medium, it would result in certain hydraulic forces acting on particles. According to Zhou et al. [17], the total fluid-particle interaction force \({\varvec{F}}_{f}\) can include the drag force, the pressure gradient force, the viscous force, and other unsteady forces such as the virtual mass, the Basset and the lift forces. Considering a small hydraulic gradient i.e., i < 2.5 as used in the current simulation, the drag, pressure gradient and viscous forces would be predominant over other unsteady forces. Therefore, only 3 major components of \({\varvec{F}}_{f}\) are considered as follows:
where \({\varvec{F}}_{d}\) is the drag force, \({\varvec{F}}_{\nabla p}\) is the pressure gradient force and \({\varvec{F}}_{\nabla \cdot \tau }\) is the viscous force. The drag force \({\varvec{F}}_{d}\) is generated by the variation of the point stress tensor in the fluid when it is flowing through the particle, whereas \({\varvec{F}}_{\nabla p}\) and \({\varvec{F}}_{\nabla \cdot \tau }\) are induced due to the macroscopic stress variation, i.e., varying fluid stress tensor over different fluid cells [17, 33].
The drag force, which is one of the major components of the total fluid-particle interaction force, mainly depends on the fluid-particle relative velocity, the drag coefficient, and the size of particle. Basically, there are a number of methods to estimate this force such as Ergun [34], Wen and Yu [35], and Di Felice [36]. By comparing these models, Kafui et al. [33] indicated that Di Felice method can better capture the smooth transition of drag force with varying porosity. Therefore, the method based on Di Felice approach was adopted in the current simulation as follows:
where \(C_{d}\) is the drag coefficient, \(D_{p}\) is the diameter of the particle, and \(C_{d}\) is then computed with respect to the Reynolds number \(Re_{p}\) by:
where the particle Reynolds number \(Re_{p}\) is determined as:
where \(\mu_{f}\) is the fluid viscosity. In this calculation, the difference (\({\varvec{U}}_{f} - {\varvec{U}}_{p}\)) represents the relative velocity between fluid and particle. The larger the fluid-particle relative velocity, the larger the drag force. Also, Eq. (12) shows that the porosity function \(n_{f}^{ - }\) represents the presence of other particles in the cell in relation to the power factor χ which can be estimated by [33, 36]:
The pressure gradient force is generated when there is a difference in fluid pressure over a surface, i.e., \(\nabla p\) including buoyant and external components [17]. The computation of this force acting on soil particle can be given by:
The viscous force is normally induced when there is a difference in deviator (shear) stress over the fluid flow space, which can be described as [17]:
2.4 Energy transformation of fluid-particle system subjected to fluidization
A fluid can only flow through a porous soil medium when there is a hydraulic potential energy, which is defined by the hydraulic gradient i between the inlet and outlet of the flow. The transformation of energy in this fluid-soil system can generally be described through energy conservation as follows [37]:
where Ein is the total energy inserted into the system through the fluid flow; Eout is the total energy at the outlet of the system; Ework is the total energy to get work done in the system; and Eloss denotes the dissipation or loss of energy while fluid is flowing through and interacts with the soil.
For a porous soil subjected to a fluid flow, the work done can be considered as any change in the soil induced by the fluid flow such as the migration of soil particles associated with soil erosion and deformation. The energy loss Eloss can be induced by the interactions between fluid–fluid and fluid–solid elements (e.g., walls and particles interactions), the interactions, e.g., sliding and rolling over each other of solid particles, the elastic energy storage of the soil-fluid system and by thermal dissipation. Of these factors, the energy dissipation induced by solid particle contacts is governed through the contact models and parameters (e.g., friction coefficients) used in DEM, while the energy loss Eloss due to the interactions of fluid depends mainly on the fluid viscosity, the contact surface between fluid and solid elements and the fluid-particle interaction force models being used. For example, when the drag force is large enough, it can make soil particles migrate and fluid velocity change locally around the particles, resulting in variation in the kinetic energy (computed based on velocity of individual elements) of the system. Fluid can change its flow velocity significantly due to interaction with solid particles (i.e., through solving the modified Navier–Stokes equations Eqs. (6) and (7) incorporating fluid–solid interaction terms), thereby affecting the energy dissipation.
The internal (i.e., molecular and atomic motion) and the thermal aspects are not included here with respect to the current laboratory testing as described later. The net potential energy \(E_{p,fnet}\), which is the difference between the inlet Ein and outlet Eout components, can be computed for a unit volume of flow (volumetric potential energy of fluid) as follows:
where i is the hydraulic gradient over the flow length L. The hydraulic gradient i can be either constant or time-dependent, i.e., i(t). For the incremental form of i, the total input \(E_{p,fnet}\) across different stages can be rewritten by:
where ik denotes the value of i at stage k. Indeed, this potential energy varies with the difference in water head between the inlet and outlet of the fluid-particle domain. Therefore, by measuring the head of water at different depths, one can determine the potential energy of fluid acting on the system.
The potential energy that the fluid flow inserts into the system can be transformed into 3 major components, i.e., (1) the kinetic energy of particles \(E_{k,p}\); (2) the kinetic energy of fluid \(E_{k,f}\); (3) and the energy loss or dissipation due to friction \(E_{loss}\). Given the same amount of input energy, the larger the energy loss, the lesser the kinetic energy to be transferred, and therefore, the less the soil migration. The loss of energy heavily depends on the properties of materials such as the shape and size of particles, the surface texture and the porous features (e.g., the porosity and tortuosity). In addition, the viscosity of fluid that affects how it resists flowing can cause a loss to the total potential energy in the system. For a normal soil foundation such as subgrade and capping materials under rail track where the viscosity of the underground water rarely changes, the energy loss in the system will mainly be governed by the soil and the foundation properties. For example, the particle size distribution of subgrade soil and the use of filter layer (e.g., capping) can significantly affect the retention capacity and the loss of fluid flow. Soil with wider gradation can have larger seepage flow accompanied with higher potential of internal erosion, thus the larger the kinetic energy being transferred to soil particles. The kinetic energy \(E_{k,p}\) of a particle moving with a translational velocity Up and angularity velocity \({\varvec{\omega}}_{p}\) is computed as follows:
where mp and Ip are the mass and the moment of inertia of particles.
In DEM, the velocity components of particles are computed and updated in every time step, enabling the kinetic energy of particles to be computed in detail. Given a fluid flow Qf = Uf,s × Af, where Uf,s is the superficial flow velocity and Af is the cross-sectional area of the flow during a time Δt, the total kinetic energy induced by all particles migrating in the fluid-particle system is then computed by:
where nm is the total number of particles which are moving (rotating and/or displacing) under the fluid flow. The total kinetic energy \(\sum E_{k,p}\) of the particles can vary significantly with time, depending on the evolution of flow and particle migration. Therefore, the term \(\sum E_{k,p}\) should be considered in the entire process, i.e., until the flow becomes stable with no more particle migration. In the meantime, the kinetic energy of fluid in the simulated system is estimated by:
where \(V_{f}\) is the actual flow volume of fluid throughout the simulated system, while the term \(\frac{1}{2}\rho_{f} U_{f}^{2}\) is the fluid energy per a unit flow volume.
Soil is generally non-uniform in its porous features, so the seepage fluid velocity will vary at different locations within the soil depending on the porosity, resulting in different kinetic energy of fluid distributed over the flow domain. As the current study uses the average fluid variables in coarse meshing CFD, the total kinetic energy of fluid in the entire system can be computed by summarizing the kinetic energy in individual fluid cells as follows:
where \(U_{fj}\) and \(V_{fj}\) are the averaged fluid velocity and the fluid volume in cell j, while nfc is the total number of fluid cells. It is noteworthy that the above computation is different from the method based on the superficial flow velocity that does not include the loss of energy by internal flow friction. In this study, because the hydraulic gradient i increased over time, the fluid energy in the entire process was calculated with respect to the actual volume of fluid flow at a certain value of i during Δt. The corresponding kinetic energy of the solid elements was then calculated and combined with the fluid component to obtain the total kinetic energy of the system.
3 Experimental observation on soil fluidization under increasing seepage
An experiment was carried out to examine the response of granular soil to increasing seepage flow (Fig. 2). In this test, coarse sand with particle size from about 0.57 to 1.8 mm was used. The soil was poured into a 62 mm diameter cell and light compaction was applied at different layers to ensure the uniformity of the test specimen. The mass and volume of the soil filled into the cell were recorded so that the dry density and porosity could be computed accordingly. An upward flow was induced through soil specimen from the bottom. The constant-head water tank was used to control the input hydraulic gradient (i.e., the potential energy of fluid) while manometers were used to measure water heads along the specimen height. The water flow was gently triggered at small levels of hydraulic gradient. The height of water tank was then increased gradually while the response of the test specimen was observed. Soil deformation and fluidization were estimated through image processing on the video captured during the test.
Figure 3a shows how heave and fluidization of the soil specimen were captured during the test. It is apparent that increasing seepage flow caused soil particles to move upwards, making the specimen surface rise, i.e., heave formation. When this development reached a critical state, the soil lost its resistance to the fluid flow, resulting in a full collapse of the soil fabric accompanied with a swift increase in the hydraulic conductivity (Fig. 3b), thus causing fluidization. For example, the total heave in the soil specimen (porosity n = 0.38) at i = 1.0 and 1.16 (before the complete fluidization) was approximately 3.6 and 7.1 mm, respectively. As shown in Fig. 3b, the discharge velocity swiftly increases at the critical value of hydraulic gradient (i = 1.2), and this can be attributed to soil expansion, hence increasing porosity. This experiment showed that while macro-response of soil such as the deformation and hydraulic conductivity could be captured well using a conventional testing approach, the evolution in micro-features of the soil specimen such as the migration of individual particles, changes in localized porosity (i.e., due to the non-uniform response of soil at different layers and regions) and particle contacts could not be properly quantified or understood. It is also noteworthy that the failure of soil observed in the current experiment might share the same mechanism with the conventional phenomenon, i.e., sand “boiling” where the effective stress of soil drops to zero under seepage flow. While past studies of sand “boiling” mainly focused on macroscale and continuum perspectives [3, 4, 38], the current study aims to address microscale evolutions and the associated energy transformation of soil. This was why the term “fluidization”, which has been used widely to emphasize the transformation of solid materials to fluid-like state [33, 36, 39], was adopted in the current study.
4 Numerical model setup
4.1 Representative soil specimen in DEM
Soil specimen was first established in DEM before it was coupled with CFD. The number of particles in DEM was estimated based on the particle size distribution (PSD) of the coarse sand used in experimentation (Fig. 2). Specifically, the quantity of particles at each size was calculated based on their mass ratio in the assembly. For simplicity in computation, a representative volume of soil was created in DEM to minimize the computational cost. The width of this specimen was 16 mm, which was around 9 times larger than the largest soil particles, thus eliminating the boundary effects. The PSD built in DEM was compared with the real PSD of the soil to ensure there was no significant deviation between the two PSD curves (Fig. 2b). The periodic boundary which ensures a continuous particle interaction was used, which aimed to present the soil region at the middle of the cell without interaction with the cell walls. In order to achieve the desired porosity (i.e., experimental value n = 0.38), the friction coefficients were adjusted during assembling, for example, reducing this parameter would result in a more compacted specimen and the vice versa. The friction coefficients were then reset to the desired value during the coupling with CFD.
Numerical parameters such as Young’s modulus (E), friction coefficients (fr) and Poisson’s number (ν) were assumed with respect to previous DEM studies on sandy soils [1, 11, 19, 29]. Specifically, E = 8 × 103 kPa, fr = 0.5 and ν = 0.3 were adopted for fluid-particle coupling simulations. The density of soil particle assembly was 2650 kg/m3 with respect to the laboratory specimen. Several previous studies [11, 19, 40] indicate that appropriate assumption of these parameters would not influence significantly the numerical results in DEM modelling, especially for loose to medium granular soils without confinement and external loading. Indeed, the Young’s modulus is often scaled down in DEM investigations to reduce the computational effort and cost without significant effect on the results [11, 40].
It is noteworthy that soil under different confinement states can behave differently under increasing seepage flow [41, 42]. The larger confining pressure means the larger effective stress acting on soil particles, resulting in higher resistance to fluidization. Increasing confining pressures also leads to smaller porosity (i.e., denser particles and smaller constriction size) that would result in larger retention of the soil matrix, thus less soil migration. These effects can be very complex as they can significantly change with the magnitude and direction (i.e., the anisotropy) of the effective stress induced by confinement. For simplicity and consistency with laboratory testing, the current numerical investigation did not examine in detail the effect of confining pressure (i.e., soil compressed only by the body weight of material).
4.2 Coupling DEM with CFD to model fluid flow through the soil specimen
The current CFD used the finite volume method to solve the modified NS equations (Eqs. 6, 7) in each fluid cell locally, which meant the fluid domain including the soil region was divided into a number of cells. In this method, the fluid cells are normally suggested to be about 2 to 5 times bigger than the largest particles in DEM, since the averaged fluid variables are used to compute the fluid-particle interaction forces. The size of fluid cells was 4 mm which was approximately 2.2 times larger than the largest soil particles (Dp = 1.8 mm). Extended paths were added at the inlet (bottom) and outlet (top) of the DEM specimen to ensure computational stability and a fully developed condition of flow, especially at soil boundaries. These meshing criteria were used consistently over different specimens and hydraulic gradients.
The seepage flow was generated at the inlet of the fluid domain (Fig. 4a) by controlling the hydraulic pressure. The hydraulic gradient i was computed using the drop in hydraulic pressure and the length that the fluid travelled through the particulate domain (i.e., the thickness of the soil specimen). A slip boundary condition was used to eliminate flow friction on the cell walls. The input pressure was increased gradually while a zero-pressure was applied at the outlet to mimic the overflow condition at the soil surface in the experiment. The flow pressure was only increased when none of the soil particles migrated significantly (i.e., the largest velocity of particles < 6 × 10–6 m/s) and the discharge velocity became stable, i.e., unchanged output velocity (i.e., fully dissipated flow energy, see Fig. 4b). Deionised water (density of 1000 kg/m3; dynamic viscosity (μf) of 10.04 × 10–4 Pa.s) was used with respect to laboratory testing. The fluid velocity and pressure were computed at each input pressure across different fluid cells, thus enabling changes in fluid behaviour to be captured over time considering the effect of solid phase.
5 Numerical results and discussion
5.1 Development of soil fluidization under increasing hydraulic gradient
5.1.1 Response of soil particles
Figure 5 shows how particles travel upwards at different levels of i under periodic boundary condition, causing the soil surface to rise (i.e., heave formation). In fact, there is insignificant migration of particles when i is small and the hydraulic forces are less than the body weight of solid particles, however, when i > 1, the particles begin to displace considerably. The results show that the soil surface has displaced 5.1% compared to the initial specimen height when i = 1.26, which agrees well with the experimental data, i.e., 4.5% at i = 1.0 (Fig. 3). It is noteworthy that the numerical simulation focused on the representative region at the middle of the cell without wall-soil friction, which could be a factor causing this difference. Accompanied with the heave development is the degradation in soil contact network as shown in Fig. 5b. At the initial stage, the majority of strong contacts (red lines) are located at lower layers due to the gravitational effect, however, when i = 1.26, these strong contacts disappear with the increasing hydraulic forces. As soil begins to fluidize, the contact network is apparently broken as highlighted in Fig. 5b. It is important to note that the size of the simulated soil element had insignificant effect on the predicted hydraulic curve (e.g., the critical value ic) and soil degradation process because these parameters were normalized over the depth of the specimen. For example, i was computed as the ratio between the applied flow pressure and the length, while the degradation of particle contacts depends on the ratio between the hydraulic forces and the effective stress.
The displacement of soil particles also meant increasing the soil porosity. Figure 6 shows that porosity of the soil specimen only increases slightly when i < 1.47, however, it swiftly jumps when the soil begins to fluidize, i.e., soil particles are floating and migrating rapidly under hydraulic forces. The coordination number (CN) which represents the number of contacts per particle in the soil specimen decreases gradually with increasing i before it drops sharply at the critical value of i. In fact, the value of CN decreases from around 9.4 to only 4.1 when i exceeds 1.47. These quantitative changes further attest to the degradation in contact network that was observed earlier. It is noteworthy that the current numerical investigation used a highly uniform soil (i.e., coarse sand), so internal erosion (e.g., piping) was not significant while heave formation was the major failure mechanism. Widening the particle size distribution would result in more internal erosion with complex evolutions of micro-scale parameters in the fluid-soil system [1, 43].
5.1.2 Hydraulic behaviour
Figure 7 shows the predicted hydraulic conductivity in comparison with the current and past experimental results. The experimental data from Fleshman and Rice [4], where Ottawa sand (Grade 20–30) was used for laboratory test on soil fluidization, is adopted for the current evaluation. The Ottawa sand has relatively similar range of particle size to the current soil (coarse sand) as shown in Fig. 2b. The results show that the predicted hydraulic behaviour matches well the experimental data. Indeed, the difference in the predicted and measured values can be considered insignificant for permeability of geomaterials which normally varies in a wide range (e.g., in the order of 10–2 to 10–5 for sandy soils) [15, 44]. Also, the permeability results are often found sensitive to the equipment calibration and measurement procedure, which usually change across different experimental tests.
The predicted discharge velocity swiftly increases at i = 1.47 indicating the critical state at which the soil begins to expand substantially. This is attributed to those changes in the soil fabric and porosity as shown earlier in Figs. 5 and 6 where porosity of the soil increases abruptly at the same level of i, resulting in a rapid increase in hydraulic conductivity. The predicted critical value of i based on the current CFD-DEM coupling is larger than the measured value (i = 1.16), which was probably because of the averaged variables of fluid in coarse meshing system used to solve Navier–Stokes equations, resulting in inaccurate hydraulic forces acting on particles. As the soil used in the current study was highly uniform in particle size and porous features, changing mesh size of CFD would not affect significantly the averaged fluid variables in the cells. Despite this limitation, the current numerical results have captured well the corresponding behaviours of various soil parameters such as the porosity, contact network, heave formation and hydraulic conductivity when soil is approaching fluidization subjected to increasing seepage flow.
5.2 Energy transformation during soil fluidization
5.2.1 Transformation of flow energy from the potential to kinetic forms
Increasing hydraulic gradient i means the larger potential energy \(E_{p,f}\) of fluid flows being applied on the fluid-soil system, resulting in greater kinetic energy to be transferred to fluid and soil elements. Figure 8 shows how this transformation occurs in the soil-fluid system over increasing i. In this analysis, the energy components were computed with respect to the discharged volume obtained during the simulation time; for example, the potential energy of fluid was computed based on the potential energy per a unit volume of discharged water (Eqs. 17, 18), and the actual volume of water which went through the soil during each step of i. The results show that increasing potential energy of fluid results in rising kinetic components of fluid and solid elements. The total kinetic energy of the system is significant smaller than the total input energy \(E_{p,f}\), which is because of the energy loss of fluid while going through the soil. Although the energy loss accounts for about 50 to 60% of the total energy inserted into the system when i < ic, however, it is important to note this loss can vary significantly with soil properties such as the porous and particle shape characteristics. As i approaches and exceeds the critical level ic, the energy loss becomes smaller, and the total kinetic energy tends to be closer to the total energy \(E_{p,f}\). This indicates that when soil is fluidizing, soil particles loosen and behave like a fluid while compromising their resistance to the fluid flow, which in turn increases the kinetic energy. The results also reveal that most potential flow energy is transferred to the kinetic energy of fluid, whereas the kinetic energy of particles \(E_{k,p}\) only accounts for a very small part (see Fig. 9). Indeed, \(E_{k,p}\) only becomes significant when particles begin to migrate, i.e., at the fluidization state where most soil particles move upward rapidly. This increasing \(E_{k,p}\) also explains why the total kinetic energy in the system becomes almost identical to the total potential energy at the fluidization state.
5.2.2 Kinetic energy evolution of soil particles
The contribution of translational and rotational components to the total kinetic energy of particles in the system is represented in Fig. 9. The results show that when i < 0.84, any change in the fluid potential energy does not affect much the kinetic energy transferred to the solid particles. During this period, the kinetic energy of particles \(E_{k,p}\) including both translational and rotational parts is very small (< 3 × 10–11 J), because the soil particles are almost static subjected to the small level of i. It is important to note that although soil particles do not move significantly, the computational results show a certain small degree of \(E_{k,p}\) due to the fluid-soil interactions plus the computational errors (i.e., the residual errors in approximation method at each numerical step). When i ≥ 0.84, there are increasing waves of kinetic energy corresponding to different incremental steps of i. The kinetic energy drops after reaching the peak because particles stabilized themselves at each new level of i as shown earlier in Fig. 4. When the soil begins to fluidize at i > 1.47, there is a big jump in both rotational and translational kinetic energy, i.e., approximately 104 to 106 times larger compared to earlier (stable) stages. Interestingly, the translational component becomes predominant over the rotational part during soil fluidization, albeit they are relatively the same at earlier periods. For example, the translational \(E_{k,p}\) exceeds 10–5 J, whereas the rotational \(E_{k,p}\) reaches only about 2 × 10–7 J at the fluidizing state. This is because at this state, the hydraulic forces including mainly the drag and pressure gradient components as considered in the current study are very large that make soil particles move vertically rather than spinning, resulting in predominant translational behaviour of the particles during fluidization.
Figure 10 represents the contributions that different size particles have made to the total kinetic energy of particles in the system. The results show that the rotational \(E_{k,p}\) changes significantly with different particle sizes when i < ic. Specifically, the larger the diameter, the smaller the rotational \(E_{k,p}\). On the other hand, there is insignificant difference in the translational \(E_{k,p}\) across different size particles during stable stages. Indeed, at several peaks of translational \(E_{k,p}\) where i increases to a new level, smaller particles (diameter from 0.6 to 0.7 mm) tend to displace more, resulting in larger magnitudes of translational \(E_{k,p}\). However, this difference is still marginal compared to that in the rotational components (Fig. 10a). The difference between the rotational and translational kinetic energies is probably because the small particles such as those with diameter from 0.6 to 0.8 mm have less contact with the surrounding particles, thus experiencing less restriction to rotating when subjected to fluid flow, given the low confinement and rolling friction as considered in the current study (Fig. 10c). In contrast, the small particles could not migrate due to the confinement from surrounding larger particles when i is small, resulting in a relatively identical level of translational kinetic energy across different size particles. It is interesting that the effects of particle size become less important when soil is fluidizing, which is not surprising, because, all particles regardless of their size behave similarly within a fluid domain, i.e., being washed out and floating during fluidization.
5.2.3 Influence of boundary condition to the loss of energy
In order to understand how the boundary condition can affect the energy transformation, an additional case using fixed boundary, i.e., stiff wall-soil particle contact was investigated. This wall-soil contact aimed to present the soil regions which were adjacent to the cell walls. In this simulation, soil and fluid properties were remained unchanged from the periodic boundary (i.e., soil-soil particle contact discussed earlier), while the friction coefficient of 0.5 for wall-soil contact was similar to that of the soil-soil boundary case to assess the effect of boundary type. In Fig. 11, the results show significant differences in the evolution of particulate kinetic energy. For example, at an early stage (i < 0.63), both rotational and translation components of \(E_{k,p}\) are much smaller compared to the soil-soil boundary case, which indicates how well the confining walls have restricted particles from movement when i is small. Furthermore, there is no difference between the rotational and translational \(E_{k,p}\) of particles during this time, which is different from the periodic boundary, where the rotational part takes the major role. The wall-soil contact also causes the fluidization to occur apparently later, i.e., after 3 s at i > 1.89 compared to approximately 2.2 s at i > 1.47 in the periodic soil-soil boundary. This is also understandable, because in the wall-soil contact, soil particles will move continually along the wall, giving more contacts and friction compared to the soil-soil boundary on which particles will contact each other individually during a short time. These results indicate that the soil located near to the cell walls require much more fluid potential energy to trigger fluidization due to the larger energy loss attributed to friction. Despite these differences, the largest magnitude of \(E_{k,p}\) that particles can reach just before and after fluidization is identical in both cases. Furthermore, the translational component always makes the predominant contribution to the total kinetic energy of particles during fluidization, regardless of the boundary condition.
The current numerical simulations remained several limitations that require greater efforts in the future study. First, spherical particles were used in the current model, whereas the actual shapes of granular particles are angular, resulting in certain deviation in the predicted outcomes. Recent DEM and CFD-DEM coupling studies [45,46,47] have shown significant efforts in modelling real shape of particles, including fluidization and migration of granular materials, however, the remaining complex issues with the contact and fluid-particle interaction behaviours of non-spherical particles still require mammoth improvements. Second, the microscale aspects that the particle size distribution (PSD) and surface textures can affect soil fluidization were not considered. Different gradations and surface roughness of grains can have significant effects on particle migration as they affect the retention capacity of soils.
6 Conclusion
This study used a coupled CFD-DEM approach to investigate the microscale transformation of energy during soil fluidization under increasing seepage flow. The macro-behaviour such as the hydraulic conductivity and the soil deformation predicted by the numerical method was validated with experimental data, while the micro-variables such as the porosity, particle migration and the degree of contact were used to understand the energy evolution inside the system. Salient conclusions can be drawn as follows:
-
The coupled CFD-DEM method showed acceptable predictions of soil response to increasing hydraulic gradient. The predicted hydraulic conductivity was close to the measured value (i.e., 0.0068 m/s), while the predicted heave formation matched the experimental observations well.
-
Increasing upward seepage flow caused the soil particles to expand, resulting in a degraded contact network and an increasing void ratio. The average contact number per particle dropped from 9.4 to only 4.1 when soil fluidized at the critical hydraulic gradient. The abrupt increase in porosity associated with soil fabric collapse was found to be the reason for the rapid increase in hydraulic conductivity when the soil began to fluidize.
-
Increasing hydraulic gradient caused the potential energy of fluid to increase, thus more kinetic energy to be transferred to soil elements. The study indicated that 50 to 60% of the total potential energy by fluid inserted into the soil was lost due to fluid-particle interactions, while only a very small percentage of this energy (< 1%) was transferred to the kinetic energy of the soil particles assembly.
-
The kinetic energy of particles evolved from the predominantly rotational to the overwhelmingly translational behaviour when the soil specimen approached fluidization under increasing seepage flow. As the hydraulic forces acting on particles increased rapidly at the fluidizing state, soil particles were pulled upwards with the flow, causing a swift increase in translational kinetic energy.
-
The frictional contacts that soil particles made with stiff walls of the cell significantly affected the kinetic energy evolution of particles. The numerical results showed that soil particles near to the walls had received much smaller kinetic energy transferred from fluid compared to those soil particles which were farther from the cell walls (i.e., the middle of the cell with soil-soil contact boundary). Furthermore, a greater level of potential energy from the fluid, for example at i > 1.89, was required to trigger soil fluidization when the soil was located near to the walls.
Abbreviations
- c :
-
(Subscript/superscript) denotes contact
- f :
-
(Subscript) denotes fluid
- p :
-
(Subscript) denotes particle
- \({\varvec{f}}_{p}\) :
-
Mean volumetric particle–fluid interaction force
- f r :
-
Sliding friction coefficient
- \({\varvec{g}}\) :
-
Gravitational acceleration
- i :
-
Hydraulic gradient
- k :
-
Stiffness
- m :
-
Mass of particles
- n :
-
Porosity
- p :
-
Pressure
- t :
-
Time
- C d :
-
Drag coefficient
- \(D\) :
-
Diameter of particle
- \(E\) :
-
Young’s modulus
- \(E_{in}\) :
-
Total energy at the inlet (input energy)
- \(E_{out}\) :
-
Total energy at the outlet (output energy)
- \(E_{loss}\) :
-
Dissipation or loss of energy
- E work :
-
Total energy to get work done
- \(E_{p}\) :
-
Potential energy
- \(E_{k}\) :
-
Kinetic energy
- \({\varvec{F}}_{c}\) :
-
Contact force
- \({\varvec{F}}_{d}\) :
-
Drag force
- \({\varvec{F}}_{\nabla p}\) :
-
Pressure gradient force
- \({\varvec{F}}_{\nabla \cdot \tau }\) :
-
Viscous force
- \({\varvec{F}}_{g}\) :
-
Gravitational force
- \({\varvec{F}}_{f}\) :
-
Total hydraulic force
- \(G\) :
-
Shear modulus
- \({\varvec{M}}_{c}\) :
-
Torque induced by particle contact
- \({\varvec{M}}_{r}\) :
-
Torque induced by rolling friction
- R :
-
Radius of particle
- Re:
-
Particle Reynolds number
- U :
-
Translational velocity
- V :
-
Volume
- V c :
-
Volume of fluid cell
- V p :
-
Volume of particle
- \(\delta_{n}\) :
-
Overlap of two particles in contact
- μ f :
-
Dynamic viscosity
- \(\mu_{r}\) :
-
Rolling friction coefficient
- ν :
-
Poisson’s number
- ρ :
-
Density of material
- τ :
-
Viscous stress
- χ :
-
Power factor
- ω :
-
Angular velocity
References
Nguyen, T.T., Indraratna, B.: A coupled CFD-DEM approach to examine the hydraulic critical state of soil under increasing hydraulic gradient. ASCE Int. J. Geomech. 20(9), 04020138 (2020). https://doi.org/10.1061/(ASCE)GM.1943-5622.0001782
Xiao, M., Shwiyhat, N.: Experimental investigation of the effects of suffusion on physical and geomechanic characteristics of sandy soils. Geotech. Test. J. 35(6), 890–900 (2012)
Skempton, A.W., Brogan, J.M.: Experiments on piping in sandy gravels. Geotechnique 44(3), 449–460 (1994)
Fleshman, M.S., Rice, J.D.: Laboratory modeling of the mechanisms of piping erosion initiation. J. Geotech. Geoenviron. Eng. 140(6), 04014017 (2014)
Ke, L., Takahashi, A.: Experimental investigations on suffusion characteristics and its mechanical consequences on saturated cohesionless soil. Soils Found. 54(4), 713–730 (2014). https://doi.org/10.1016/j.sandf.2014.06.024
Nguyen, T.T., Indraratna, B.: Rail track degradation under mud pumping evaluated through site and laboratory investigations. Int. J. Rail Transp. (2021). https://doi.org/10.1080/23248378.2021.1878947
Nguyen, T.T., Indraratna, B., Kelly, R., Phan, N.M., Haryono, F.: Mud pumping under railtracks: mechanisms. Assess. Solut. Aust. Geomech. J. 54(4), 59–80 (2019)
Hudson, A., Watson, G., Le Pen, L., Powrie, W.: Remediation of mud pumping on a ballasted railway track. Procedia Eng. 143, 1043–1050 (2016). https://doi.org/10.1016/j.proeng.2016.06.103
Huang, J., Su, Q., Wang, W., Phong, P.D., Liu, K.: Field investigation and full-scale model testing of mud pumping and its effect on the dynamic properties of the slab track–subgrade interface. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 233(8), 802–816 (2019). https://doi.org/10.1177/0954409718810262
Duong, T.V., Cui, Y.-J., Tang, A.M., Dupla, J.-C., Canou, J., Calon, N., Robinet, A.: Investigating the mud pumping and interlayer creation phenomena in railway sub-structure. Eng. Geol. 171, 45–58 (2014). https://doi.org/10.1016/j.enggeo.2013.12.016
Tao, H., Tao, J.: Quantitative analysis of piping erosion micro-mechanisms with coupled CFD and DEM method. Acta Geotech. 12(3), 573–592 (2017). https://doi.org/10.1007/s11440-016-0516-y
Indraratna, B., Phan, N.M., Nguyen, T.T., Huang, J.: Simulating subgrade soil fluidization using LBM-DEM coupling. Int. J. Geomech. 21(5), 04021039 (2021). https://doi.org/10.1061/(ASCE)GM.1943-5622.0001997
Wang, X., Huang, B., Tang, Y., Hu, T., Ling, D.: Microscopic mechanism and analytical modeling of seepage-induced erosion in bimodal soils. Comput. Geotech. 141, 104527 (2022). https://doi.org/10.1016/j.compgeo.2021.104527
Nguyen, V.T., Rujikiatkamjorn, C., Indraratna, B.: Analytical solutions for filtration process based on constriction size concept. J. Geotech. Geoenviron. Eng. 139(7), 1049–1061 (2013). https://doi.org/10.1061/(asce)gt.1943-5606.0000848
Nguyen, T.T., Indraratna, B.: The role of particle shape on hydraulic conductivity of granular soils captured through Kozeny–Carman approach. Géotech. Lett. 10(3), 398–403 (2020). https://doi.org/10.1680/jgele.20.00032
He, X., Xu, H., Li, W., Sheng, D.: An improved VOF-DEM model for soil-water interaction with particle size scaling. Comput. Geotech. 128, 103818 (2020). https://doi.org/10.1016/j.compgeo.2020.103818
Zhou, Z.Y., Kuang, S.B., Chu, K.W., Yu, A.B.: Discrete particle simulation of particle–fluid flow: model formulations and their applicability. J. Fluid Mech. 661, 482–510 (2010). https://doi.org/10.1017/S002211201000306X
Shan, T., Zhao, J.: A coupled CFD-DEM analysis of granular flow impacting on a water reservoir. Acta Mech. 225(8), 2449–2470 (2014). https://doi.org/10.1007/s00707-014-1119-z
Shamy, U.E., Zheghal, M.: Coupled continuum-discrete model for saturated granular soils. J. Eng. Mech. 131(4), 413–426 (2005)
Nguyen, N.H.T.: Collapse of partially and fully submerged granular column generating impulse waves: an empirical law of maximum wave amplitude based on coupled multiphase fluid–particle modeling results. Phys. Fluids 34(1), 013310 (2022). https://doi.org/10.1063/5.0076755
Nguyen, T.T., Indraratna, B., Singh, M.: Dynamic parameters of subgrade soils prone to mud pumping considering the influence of kaolin content and the cyclic stress ratio. Transp. Geotech. 29, 100581 (2021). https://doi.org/10.1016/j.trgeo.2021.100581
Vucetic, M., Dobry, R.: Effect of soil plasticity on cyclic response. J. Geotech. Eng. 117(1), 89–107 (1991). https://doi.org/10.1061/(ASCE)0733-9410(1991)117:1(89)
Sun, J.I., Golesorkhi, R., Seed, H.B.: Dynamic moduli and damping ratios for cohesive soils. Earthquake Engineering Research Center, College of Engineering, University of California at Berkeley (1988)
Nguyen, T.T., Indraratna, B.: The energy transformation of internal erosion based on fluid-particle coupling. Comput. Geotech. 121, 103475 (2020). https://doi.org/10.1016/j.compgeo.2020.103475
Le, V.T., Marot, D., Rochim, A., Bendahmane, F., Nguyen, H.H.: Suffusion susceptibility investigation by energy-based method and statistical analysis. Can. Geotech. J. 55(1), 57–68 (2017). https://doi.org/10.1139/cgj-2017-0024
Kloss, C., Goniva, C., Hager, A., Amberger, S., Pirker, S.: Models, algorithms and validation for opensource dem and cfdem. Prog. Comput. Fluid Dyn. Int. J. 12(2), 140–152 (2012)
Cundall, P.A., Strack, O.D.L.: A discrete numerical model for granular assemblies. Géotechnique 29, 47–65 (1979)
Gao, Y., Wang, Y.H.: Experimental and DEM examinations of K0 in sand under different loading conditions. J. Geotech. Geoenviron. Eng. 140(5), 04014012 (2014). https://doi.org/10.1061/(ASCE)GT.1943-5606.0001095
Li, Y., Xu, Y., Thornton, C.: A comparison of discrete element simulations and experiments for ‘sandpiles’ composed of spherical particles. Powder Technol. 160(3), 219–228 (2005). https://doi.org/10.1016/j.powtec.2005.09.002
Nguyen, T.T., Indraratna, B.: Experimental and numerical investigations into hydraulic behaviour of coir fibre drain. Can. Geotech. J. 54(1), 75–87 (2017). https://doi.org/10.1139/cgj-2016-0182
Goniva, C., Kloss, C., Deen, N.G., Kuipers, J.A.M., Pirker, S.: Influence of rolling friction on single spout fluidized bed simulation. Particuology 10(5), 582–591 (2012). https://doi.org/10.1016/j.partic.2012.05.002
Zhou, Y.C., Wright, B.D., Yang, R.Y., Xu, B.H., Yu, A.B.: Rolling friction in the dynamic simulation of sandpile formation. Physica A 269(2), 536–553 (1999). https://doi.org/10.1016/S0378-4371(99)00183-1
Kafui, K.D., Thornton, C., Adams, M.J.: Discrete particle-continuum fluid modelling of gas–solid fluidised beds. Chem. Eng. Sci. 57(13), 2395–2410 (2002)
Ergun, S.: Fluid flow through packed columns. Chem. Eng. Prog. 48(2), 89–94 (1952)
Wen, C.Y., Yu, Y.H.: Mechanics of fluidization. Chem. Eng. Prog. Symp. Ser. 162, 100–111 (1966)
Di Felice, R.: The voidage function for fluid-particle interaction systems. Int. J. Multiph. Flow 20(1), 153–159 (1994). https://doi.org/10.1016/0301-9322(94)90011-6
Massey, B., Ward-Smith, J.: Mechanics of Fluids, 8th edn. Taylor & Francis, New York (2006)
Terzaghi, K.: Theoretical Soil Mechanics. John Wiley & Sons Inc., London (1943)
Nguyen, T.T., Indraratna, B., Leroueil, S.: Localized behaviour of fluidized subgrade soil subjected to cyclic loading. Can. Geotech. J. (2022). https://doi.org/10.1139/cgj-2021-0550
Tsuji, Y., Kawaguchi, T., Tanaka, T.: Discrete particle simulation of 2-dimensional fluidized-bed. Powder Technol. 77, 79–87 (1993)
Sato, M., Kuwano, R.: Effects of internal erosion on mechanical properties evaluated by triaxial compression tests. Jpn. Geotech. Soc. Spec. Publ. 2(29), 1056–1059 (2016). https://doi.org/10.3208/jgssp.JPN-127
Chang, D., Zhang, L.: A stress-controlled erosion apparatus for studying internal erosion in soils. Geotech. Test. J. 34(6), 579–589 (2011). https://doi.org/10.1520/gtj103889
Kawano, K., Shire, T., O’Sullivan, C.: Coupled particle-fluid simulations of the initiation of suffusion. Soils Found. 58(4), 972–985 (2018). https://doi.org/10.1016/j.sandf.2018.05.008
Trani, L.D.O., Indraratna, B.: The use of particle size distribution by surface area method in predicting the saturated hydraulic conductivity of graded granular soils. Géotechnique 60(12), 957–962 (2010). https://doi.org/10.1680/geot.9.T.014
Zhong, W., Yu, A., Liu, X., Tong, Z., Zhang, H.: DEM/CFD-DEM modelling of non-spherical particulate systems: theoretical developments and applications. Powder Technol. 302, 108–152 (2016). https://doi.org/10.1016/j.powtec.2016.07.010
Wang, S., Shen, Y.: Super-quadric CFD-DEM simulation of chip-like particles flow in a fluidized bed. Chem. Eng. Sci. 251, 117431 (2022). https://doi.org/10.1016/j.ces.2022.117431
Wang, X., Yin, Z.-Y., Su, D., Wu, X., Zhao, J.: A novel approach of random packing generation of complex-shaped 3D particles with controllable sizes and shapes. Acta Geotech. 17(2), 355–376 (2022). https://doi.org/10.1007/s11440-021-01155-3
Acknowledgements
This research was supported by the Australian Government through the Australian Research Council’s Linkage Projects funding scheme (Project LP160101254) and the ARC Industrial Transformation Training Centre for Advanced Technologies in Rail Track Infrastructure (ITTC-Rail). The financial and technical support from industry, namely SMEC, Tetra Tech Coffey, ACRI and Sydney Trains is acknowledged.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is a part of the topical collection: Energy transport and dissipation in granular systems.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nguyen, T.T., Indraratna, B. Fluidization of soil under increasing seepage flow: an energy perspective through CFD-DEM coupling. Granular Matter 24, 80 (2022). https://doi.org/10.1007/s10035-022-01242-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10035-022-01242-6