DEM simulations of agglomerates impact breakage using Timoshenko beam bond model

Abstract

Attrition and breakage of agglomerates are prevalent during production and handling processes in many industries. Therefore, it is highly desirable to be able to model and analyse the agglomerate breakage process under various loading conditions. The ensemble strength and breakage patterns of agglomerates are still not well understood despite a significant amount of research being carried out. In this study, three-dimensional discrete element method (DEM) simulation of the impact breakage behaviour of agglomerates were performed using a Timoshenko beam bond model which considers axial, shear, twisting and bending behaviours on the bonds. An advantage of the Timoshenko beam bond model is the pertinent parameters of the bond contact have clear physical meaning and therefore could be determined through corresponding experimental characterisations. The mechanical properties of the bonds in this study were firstly calibrated using experimental measurements. The validation of the Timoshenko beam bond model was then undertaken by direct comparisons between the numerical simulation and experimental results of impact tests. It was shown that the time evolution of the agglomerate breakage process obtained from simulation had good agreement with experimental observations. Numerical results indicate that most of the damage happens at the early stage of the impact and a cone shape fracture zone is formed quickly inside the agglomerate where strong compressive stresses are concentrated. It is found that the exterior of the fracture zone is surrounded by an arch shape tensile stress which dominates the fracture propagation.

1 Introduction

The production and handling of agglomerates are of significant importance for a wide range of industries such as mineral, chemical, agricultural and pharmaceutical industries [1]. Since agglomerates are formed from smaller constituent particles, attrition and breakage can occur during processing or transport. Therefore, understanding agglomerate’s mechanical behaviour is of great importance for optimisation of relevant industrial processes [2, 3]. A variety of work has been conducted to study the breakage patterns of agglomerates [4,5,6,7,8,9]. Compression and impact loading experiments are usually carried out to explore the strength and breakage patterns of agglomerates [10, 11]. Nevertheless, it is prohibitively difficult to experimentally measure the dynamic propagation of cracks inside an agglomerate because the failure usually happens rapidly and in a small region. Numerical simulations can alternatively provide new insights into these processes since simulations are not hindered by length scale or time scale. Particularly, Discrete Element Method (DEM) has been found to be a powerful tool for understanding these processes because of its capability for realistic representation of the agglomerates and for obtaining quantitative information on the microscopic particle scale [6, 12, 13].

In general, DEM models used in the open literature for studying the breakage of agglomerate can be classified into two kinds of contact models between constituent particles, namely, cohesive contact models and bonded contact models. The cohesive contact model assumes that the constituent particles of the agglomerates are attracted together through cohesive force, which is suitable to study weak and ductile agglomerates. Ning et al. [14] carried out both experiments and DEM simulations to investigate the impact breakage of lactose agglomerates. The agglomerates consisted of primary particles held together through weak surface forces and were relatively easy to break. The simulated agglomerate samples consisted of 2000 poly-disperse primary particles and the average coordination number of primary particles was around 5.4. The JKR model [15] was used to calculate the normal contact with adhesion. Both experimental and simulation results indicated that the failure mode of the week agglomerate was ductile. Significant deformation was visible in the impact region and the development of a clear crack plane was not found during impact. The breakage pattern was found to be caused by local structural re-arrangement due to particle sliding. Thornton [13] performed numerical simulations of agglomerate impact breakage using DEM with an auto-adhesive contact model [16]. The averaged damage of the constituent particles or damage ratio was defined as the ratio of number of broken bonds and total initial bonds, which was used to represent the degree of impact breakage in DEM simulations. A range of impact velocities had been examined and the corresponding evolutions of damage ratio were analysed in their studies. The observed breakage patterns of agglomerates were divided into three types, namely rebound, fracture and shattering, which were significantly dependent on the magnitude of impact velocity. Fracture was reserved for breakage patterns in which clear fracture planes (cracks) were visible. Shattering can be viewed as a further evolution of fracture, in which large daughter fragments were broken into small clusters of primary particles under higher impact velocities [17]. Tong et al. [18] numerically studied the effect of impact velocity and impact angle on the breakage process of a loose agglomerate. The agglomerate was bonded together through van der Waals forces of fine particles. It was observed that the agglomerates experienced a large plastic deformation before disintegrating. A clear shear zone during the impact was observed from the velocity field inside the agglomerates. The impact energies in normal and tangential directions were analysed and an impact angle at 45º was shown to give a maximum breakage performance for a given velocity. The JKR-type cohesive model is suitable for modelling ductile agglomerates but less applicable for brittle agglomerates. Subero [19] concluded that the difference between self-adhesive bonding and bonding by means of a binder is a shortcoming of the comparisons between experiments and DEM simulation with a cohesive model. The numerical agglomerates simulated by JKR-type model always fail through localised disintegration. This is different from the experimental observation of the impact breakage of brittle agglomerates bonded by a binder. Note that agglomerates made from wet granulation processes are usually bonded by a binder and are prevalent in many industries such as chemical, food and pharmaceuticals [20].

Besides the cohesive contact model, the bonded contact model uses beam elements or a set of elastic springs to link the centres of particles in a bonded contact, which could be applied to study hard and brittle materials [21, 22]. Carmona et al. [23] studied the detailed development of the fragmentation processes of brittle agglomerates using a three-dimensional DEM bond model. They stated that the two-dimensional simulations cannot reproduce the meridional fracture planes found in experiments. The agglomerate consisted of approximately 22,000 particles that were interconnected by approximately 136,000 Euler–Bernoulli beam-truss elements. The failure rule of the bond takes into account breaking due to stretching and bending of a beam. With this model, the time evolution of the fragmentation process and the involved stress fields were directly accessed and analysed. Khanal et al. [24] used the parallel bond model in PFC2D to investigate the effect of aggregate shape on the fragmentation of particle composites. Different compositions were formed representing different proportions of sand and aggregate particles. Five different aggregate shapes (circular, triangular, quadrilateral, pentagonal and hexagonal) were studied. It was found that particle shape had a remarkable influence on the fragmentation behaviour of the specimen, especially at low impact velocities. Le Bouteiller and Naaim [25] used the bond model in PFC2D to study the breakage of agglomerates under normal impact and shear loading. Under impact loading, the damage ratio was found to depend on the ratio of the incident kinetic energy to the bonding energy. Under shear loading, the damage ratio was related to the ratio of the work of friction to the bonding energy. However, all of the above simulation results were not rigorously compared with experimental results because the size and other mechanical properties of constituent particles of the agglomerates were different to those of the experiments.

As the agglomerates studied in this paper are formed by small particles joined together through liquid binder or cement material, the cohesive contact model is not an optimum option to study the impact breakage process. Cohesive contact models generally assumes that a cohesive force between particles exists continuously if two particles are within a certain distance. A bonded contact model is more appropriate where the breakage of a bond is irreversible and the damage is permanent in reality. Recently, a new bonded contact model based on the Timoshenko beam theory which considers axial, shear, twisting and bending behaviours has been developed [26]. The bond model was verified by both bending and dynamics response of a simply supported beam. In addition, the predictions of the loading response of a concrete cylinder by the bond model have shown to be consistent with the Eurocode equation. Further applications of the model to more complicated processes such as impact loading of cementitious materials and loading of fibre reinforced polymers bonded to concrete have also been demonstrated [27, 28].

In this study, the suitability of the Timoshenko beam bond model (TBBM) for studying the impact breakage process of binder-bonded agglomerates will be investigated. The parameters of the bonded contact model are based on the experimental measurements of binder mechanical strengths. The focus is thus placed on whether the realistic temporal and spatial evolution of the macroscopic failure mechanism observed in experiments can be reproduced based on the dynamic behaviour of the bonds modelled at the microscopic scale. The layout of this study is organized as follows: in the model section, the characteristics of the Timoshenko beam bond model and its implementation are discussed. The calibration of the bond parameters and the validation of the agglomerates under normal impact experiments are presented in the results and discussions section. The breakage process will then be analysed and main conclusions will be summarised.

2 Timoshenko beam bond model

The bonded contact model developed at the University of Edinburgh [26, 27] is used to model the breakage process of agglomerates in this study. In this model, the constituent spheres can interact with each other either through a bonded or non-bonded contact, but not both at the same time. Both contact types can resist compressive and shear forces, but a bonded contact can also resist tensile forces as well as bending and twisting moments, as described below. Note that this is different from the parallel-bond model in PFC code in which the bonded contact can act in parallel with the non-bonded contact when there is a bond between two particles [22]. The definition of bond contact points, torsion stiffness and shear stiffness between parallel bond model and Timoshenko beam bond model are different. A comparative assessment of the performance of beam bending simulations using different bond models has been recently carried out [29]. Further information about the contact model including time step selection, bond initialisation, and failure criteria can be found in the Appendix.

2.1 Non-bonded contact calculation

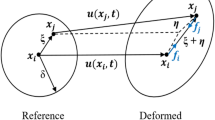
For the non-bonded contact, the Hertz-Mindlin model is adopted as shown in Fig. 1. The normal force calculation is based on the Hertzian contact theory and tangential force is based on Mindlin-Deresiewicz’s work [30]. Both normal and tangential forces have damping components where the damping coefficient is related to the coefficient of restitution [31

$${\mathbf{F}}_{n} = {\mathbf{F}}_{ns} + {\mathbf{F}}_{nd},$$

(1)

$${\mathbf{F}}_{ns} = \frac{4}{3}E^{*} \sqrt {R^{*} } {{\varvec{\updelta}}}_{n}^{1.5},$$

(2)

$${\mathbf{F}}_{nd} = - 2\sqrt{\frac{5}{6}} \eta_{n} \sqrt {S_{n} m^{*} } {\mathbf{u}}_{n,r},$$

(3)

where ${{\varvec{\updelta}}}_{n}$ is the normal overlap, E* is the equivalent Young’s modulus, R* is the equivalent radius, $\eta_{n}$ is the damping ratio, S_n is the normal stiffness, ${\mathbf{u}}_{n,r}$ is the normal component of relative velocity and m* is the equivalent mass.

Fig. 1

Spring-dashpot model for non-bonded contact

Likewise, the tangential force is calculated as the sum of the tangential spring force and damping force given as follows,

$${\mathbf{F}}_{t} = {\mathbf{F}}_{ts} + {\mathbf{F}}_{td},$$

(4)

$${\mathbf{F}}_{ts} { = } - S_{t} {{\varvec{\updelta}}}_{t} ,$$

(5)

$${{\varvec{\updelta}}}_{t} = \left\{ \begin{gathered} \int_{{t_{c} }}^{t} {{\mathbf{u}}_{t,r} dt{\text{ if }}\left| {\mathbf{F}} \right|_{t} \le \mu_{f} \left| {{\mathbf{F}}_{n} } \right|} \hfill \\ \mu_{f} \left| {{\mathbf{F}}_{n} } \right|{\mathbf{t}}_{ab} /k_{t} {\text{ if }}\left| {\mathbf{F}} \right|_{t} > \mu_{f} \left| {{\mathbf{F}}_{n} } \right| \hfill \\ \end{gathered} \right.$$

(6)

$${\mathbf{F}}_{td} = - 2\sqrt{\frac{5}{6}} \eta_{t} \sqrt {S_{t} m^{*} } {\mathbf{u}}_{t,r},$$

(7)

where ${{\varvec{\updelta}}}_{t}$ is the tangential overlap and ${\mathbf{u}}_{t,r}$ is the tangential component of relative velocity. $S_{t}$ is the tangential stiffness. The tangential force is limited by the Coulomb law of friction (i.e.${\mathbf{F}}_{{t,{\text{ limit}}}} = - \mu_{s} \left\| {{\mathbf{F}}_{n} } \right\|{\mathbf{t}}_{ab}$) where $\mu_{s}$ is the static friction coefficient, ${\mathbf{t}}_{ab}$ is the tangential unit vector. The damping ratios in normal and tangential directions are the same and shown in Table 1.

Table 1 Definition of the non-bonded contact parameters

The rolling friction is implemented as the contact independent directional constant torque mode [32, 33].

$$\tau_{i} = - \mu_{r} F_{n} r_{i} \omega_{i}$$

(8)

where $\mu_{r}$ is the rolling friction coefficient, $r_{i}$ is the distance from the centre of mass of the particle to the contact point, $\omega_{i}$ is the unit angular velocity of the particle at the contact point. Table 1 summarizes the definitions of the non-bonded contact parameters.

2.2 Bonded contact calculation

For a bonded contact, a virtual beam element is considered to exist between the particles bonding them together. Each bond is assumed to be a cylinder which connects the centre of the corresponding particles as shown in Fig. 2. Therefore, the length of the bond is equal to the distance between two particle centres which can be calculated as follows,

$$L_{B} = \left\| {{\mathbf{r}}_{b} - {\mathbf{r}}_{a} } \right\|$$

(9)

where ${\mathbf{r}}_{a}$ and ${\mathbf{r}}_{b}$ are the positions of the particles a and b respectively. The radius of the bond is defined as follows,

$$R_{B} = \lambda \cdot \min \left( {R_{a} ,R_{b} } \right)$$

(10)

where R_a and R_b are the radii of particles a and b respectively. The numerical parameter $\lambda$, termed the bond radius multiplier, is a constant that is used to adjust the ratio of the bond radius to the particle radius.

Fig. 2

Schematic of a single bond connecting two particles

One characteristic of a bonded contact is that it not only resists compressive and shear forces, but also resists tensile forces, bending moment and twisting moments. Each bond is subjected to internal forces and moments caused by the displacements and rotations of the particles it connects. As the bonds are assumed to behave like beams, the internal forces and moments can be determined through beam theory. The Timoshenko beam theory is used here to describe the response of a thick beam under varying loading actions [34]. As shown in Fig. 3, the forces and moments are calculated based on the local coordinate system of the bond. The x axis of this local coordinate system is defined by the centroidal axis of the bond which runs between the centres of the bonded particles. The other two local axes lie normal to each other as well as the centroidal axis of the bond. It should be observed that the directions of the positive bending moments in the local yx and zx planes are different if the sign convention is adopted in Fig. 3. A transformation matrix is constructed to transform the vectors in global coordinate to the local coordinate [26].

Fig. 3

The forces and moments acting on two ends of a bond

The forces and moments acting on the bond can be broken down as follows: axial forces $F_{\alpha x}$ and $F_{\beta x}$; shear forces $F_{\alpha y}$, $F_{\alpha z}$, $F_{\beta y}$ and $F_{\beta z}$; twisting moments $M_{\alpha x}$ and $M_{\beta x}$; bending moments $M_{\alpha y}$, $M_{\alpha z}$, $M_{\beta y}$ and $M_{\beta z}$. The relationship between the forces (and moments) and translational (rotational) displacements of a bond can be determined using the Timoshenko beam theory. At each time step, the incremental forces (and moments) are calculated and then added to the running total of previous time step to get the updated values of present forces (and moments). That is,

$${\mathbf{F}}^{t} = {\mathbf{F}}^{t - 1} + \Delta {\mathbf{F}}$$

(11)

$${\mathbf{M}}^{t} = {\mathbf{M}}^{t - 1} + \Delta {\mathbf{M}}$$

(12)

The calculations of the incremental forces and moments are listed in Table 2 where E_B is the bond Young’s Modulus, L_B is the bond length and A_B is the bond cross-sectional area, I_B is the moment of inertia of the cross-sectional area about the neutral axis of the beam, $\Phi_{s}$ is the Timoshenko shear coefficient for a circular cross-section, $\upsilon_{B}$ is the Poisson’s ratio. The relevant parameters can be calculated as follows,

$$A_{B} = \pi R_{B}^{2}$$

(13)

$$I_{B} = \pi R_{B}^{4} /4$$

(14)

$$\Phi = \frac{{20R_{B}^{2} \left( {1 + \upsilon_{B} } \right)}}{{3L_{B}^{2} }}$$

(15)

Table 2 Incremental forces and moments calculations

It can be seen from Table 2 that the incremental axial forces depend only on the corresponding relative translational displacements in the local x axis. Based on the equation of equilibrium in the local x axis, the incremental axial forces at each end are equal and opposite. The incremental shear forces depend on not only the corresponding relative translational displacements but also the rotational displacements. The twisting moments at the two sides of the beam are equal and opposite and only depend on the corresponding relative rotational displacements about the x-axis. The bending moments depend on both the rotational displacements and the relative translational displacements. The bending moments are balanced with the remaining shear forces and the equations of moment equilibrium can be written as,

$$M_{\beta z} + M_{\alpha z} - F_{\alpha y} L_{B} = 0$$

(16)

$$M_{\beta y} + M_{\alpha y} + F_{\alpha z} L_{B} = 0$$

(17)

Calibration of DEM bond model parameters is very important to achieve a predictive simulation. The parameters required by the TBBM model can be classified into three groups, i.e. the packing characteristics of the assembly, the non-bonded contact parameters and the bonded contact parameters. Since the primary aim of this study is to investigate if the TBBM model could predict the breakage phenomena of an agglomerate under impact, it is of great interest to compare the simulation results with experiments that include measurements on the bond model parameters. Subero et al. [35] presented a technique that was able to fabricate agglomerates with controlled porosity as well as different inter-particle bond strengths. Normal impact testing of these agglomerates was further carried out and high speed video was used to record the impact process [36]. These experiments provide an excellent benchmark to validate the present bonded DEM model. The experimental results will be directly used to compare with the simulation results in this study. The experimental agglomerates are made of glass ballotini with bisphenol-based epoxy resin binder. The packing of the agglomerate studied here replicates the macro void-free agglomerate referred to in their paper [36], which means that there are no artificial large voids inside each agglomerate. The properties of constituent particles are taken from reported values for glass beads [37, 38]. A summary of the properties of the constituent particles (glass ballotini) is given in Table 3. An advantage of the TBBM model is that the associated properties of the bond contacts have clear physical meaning. Therefore, the properties of the experimental binder could be used to calibrate the bond contact parameters. The bond radius multiplier is estimated based on the scanner electron micrographs of the experimental agglomerate. The coefficient of variation of the bond strengths is approximated using the variations observed in the tensile tests of the inter-particle bond. Note that the length of the bond in TBBM is always the distance that connects the centres of two bonded particles which is different from the experimental solid bond. This is an assumption of TBBM since TBBM’s original intention is to be used as a meso-model to simulate cementitious materials. A cylindrical shape of the beam is assumed to mimic the experimental bonds in this work. The compressive and shear strengths of the binder were not measured in the reported experiments and are estimated based on other published experimental findings [39]. Delenne [39] conducted a couple of compression and tension loading tests to examine the failure behaviour of an epoxy resin binder. Their experimental results showed that the failure strength in compression is considerably larger than that in tension and they assumed no failure in compression. This was adopted in this study by setting the compressive strength to be over 10 times larger than the tensile strength. The Poisson’s ratio of the epoxy resin binder is set to 0.4 based on the experimental results of Bardella [40]. The sensitivity analyses of the shear strengths and coefficient of variation of bond strengths on the impact damage of the agglomerate were also carried out and provided in the Appendix.

Table 3 Summary of the Non-bonded contact parameters

3 Results and discussions

3.1 Calibration of Young’s modulus

Since the impact velocity studied here is quite small, the constituent glass particles are assumed to be rigid and will not be damaged or broken. The agglomerates are made up of glass particles and epoxy resin binder. Therefore, the mechanical properties of the binder have a major impact on the overall breakage pattern of the agglomerates under impact. The Young’s modulus of the binder is a significant factor that would influence the global elasticity of the agglomerates. A higher Young’s modulus of the binder would increase the stiffness of the agglomerates and result in a more brittle failure mode. In contrast, an agglomerate would be allowed to have more deformations during impact if it is made up of a lower Young’s modulus binder. The Young’s modulus of the experimental binder was measured in a tensile test which consists of a sample of binder material held between two grips and subjected to one-dimensional tension [19]. The average Young’s modulus determined from the stress strain experimental curve was 3GPa. In DEM simulation, a similar procedure was carried out. The length of the bond in the DEM simulation is 12.5 mm and the radius of the bond is 0.67 mm. As shown in Fig. 4b, two particles were bonded together in the beginning of a simulation. The particles at each end were restrained in a box. The boxes were then displaced at a speed of 0.03 m/s and the stress on the bond was recorded during loading. The loading results are presented in Fig. 5 where the experiment and simulation results have good agreement.

Fig. 4

a Experimental setup of tensile test of binder [18], and b simulation setup in DEM

Fig. 5

Calibration of bond stiffness using a tensile test

3.2 Calibration of tensile strength

Most of the experiments and simulation results in the literature suggest that agglomerates typically break through the failure at the inter-particle contacts and the majority of the failures are tensile failures [39, 41, 42]. It is thus most important to calibrate the bond’s tensile strength characteristics. Quasi-static tensile tests were performed to measure the inter-particle bond tensile strength [19]. Two purpose-built grips with a spherical cavity shape were used to hold a doublet formed by two glass beads with binder in-between at the contact. In DEM simulations, a similar setup was made as shown in Fig. 6. A bond is formed between the two particles at the start of the simulation. The loading rate in the simulation is set to 0.25 mm/min. The averaged tensile strength was estimated to be 23 MPa and the fracture surface was observed to be circular plate. When two particles experience tensile force, the bond between them can break due to two different forms of contact separation. The contact can either fail internally in the bulk of the binder or at the interface between the glass particles and the binder. The tensile strength measurement in this test is considered to cover both effects. A coefficient of variance 0.1 of the tensile strength is included in the bond contact model to take into account of the material heterogeneity.

Fig. 6

a Experimental setups of the doublet pull-off test. b simulation setups of the doublet pull-off test

3.3 Preparation of the agglomerate

An agglomerate is made up of an assembly of primary particles stuck together with binders. The packing structure, such as void size and its distribution, will have an impact on the macroscopic mechanical strength of the agglomerate. Subero [35] developed an agglomeration technique to produce well-defined bond properties and void distribution in a laboratory. The constituent primary particles were spherical glass ballotini within a narrow particle size range of 1.4–1.7 mm. The constituent particles were held together with a bisphenol-based epoxy resin binder. The glass particles were first mixed in a planetary mixer with a small amount of binder and then poured into a 30 mm spherical mould. The agglomerate had a mean mass of 21.076 g with an estimated porosity of 0.43. The final agglomerate product was reported to be a porous structure where the binder formed solid bridges after curing while the interstices between particles remained void [36]. Detailed description of the preparation of the experimental agglomerates can be found elsewhere [19, 35].

In this study, an attempt is made to reproduce the whole agglomerate structure numerically. The collective particle rearrangement technique developed by Labra et al. [43] is used here to produce the agglomerates at the required porosity. A spherical specimen with 30 mm in diameter is first constructed and meshed using the GID software [44]. The mesh generation allows the use of boundary conditions to assign the particles close to the selected surfaces. The generation process starts by randomly inserting particles into the meshed spherical mould until the porosity reaches approximately 20%. The particles are randomly generated to a truncated Gaussian size distribution with a mean diameter of 1.5 mm and a standard deviation of 0.05 mm. An iterative process is then carried out to rearrange the particles based on the branch vectors and overlaps of the surrounding particles until a local equilibrium is reached. Particles with overlaps greater than a predefined limit are removed. The packing procedure continues until the porosity matches a predefined target while the magnitude of the maximum overlap is continuously minimised until an acceptable level is reached.

The initial particle assembly generated in this study is shown in Fig. 7 and the corresponding constituent particle size distribution is shown in Fig. 8. A total of 4104 constituent spheres were generated with the minimum and maximum diameter set to 1.4 mm and 1.7 mm, respectively. The porosity of the numerically generated agglomerate is 0.43 which matches that of the experimental agglomerate. The contact radius multiplier is set at 1.2 times the particle physical radius. Upon bonding of the agglomerate, a total of 17,414 bonds are formed, which means that there is an average of 8.5 bonds per particle initially. The characteristics of the numerical agglomerate are summarised in Table 4.

Fig. 7

Initial agglomerate and bond layouts. a Layout of initial agglomerate without bonds. b Layout of the initial bond network. c Front view of a right diametrical clip of the agglomerate with bonds. d Scanner electron micrographs of experimental agglomerate fragment [34]

Fig. 8

Constituent particle size distribution of the agglomerate

Table 4 Characteristics of the numerical agglomerate

3.4 Validation against normal impact experiment

The summary of the non-bonded contact parameters, characteristic of the agglomerate and the bonded contact parameters are listed in Tables 3, 4 and 5 respectively. Initially, the agglomerate is close to the target plane but does not touch it. The agglomerate (all the constituent particles) is then assigned a vertical velocity of −4 m/s. The simulation time is reset to zero when the agglomerate first makes contact with the target plane in order to be consistent with the frame sequence of the experimental video recordings.

Table 5 Summary of the bonded contact parameters

Figure 9 shows the comparison of the simulation results with the experimental high speed digital video recordings. The colour scale of the simulation results indicates the amount damage undergone by each constituent particle which is defined by the proportion of bonded contacts that have failed for the particle from its initial state. This means that a particle’s damage ratio varies from zero when the number of bonds connected to that particle remain the same as the initial bond time, to a damage ratio of unity when all existing bonds have been broken. As it can be seen in Fig. 9, the computed overall breakage evolution with time is in good agreement with the experimental observations, including the generation of the debris. No oblique crack or fragmentation are noted and only localized damage is observed in this case, i.e. most of the damage of the agglomerate are restricted to the area adjacent to the impact zone.

Fig. 9

Comparison of simulation with the high-speed digital video recording of an agglomerate under normal impact against a rigid target: t = 0 corresponds to the first contact between the agglomerate and the target. a DEM simulations. b Experiments

The general failure mode of the agglomerate in this case could be recognized as semi-brittle [45] since an obvious plastic deformation zone is formed soon after the agglomerate contacts with the target plane. Figure 10 shows the deformation evolution of the fracture zone in the agglomerate. Particle damage smaller than 0.1 is shown as less opaque in order to clearly visualise the distribution of particle damage. It can be observed that a cone shape deformation zone is quickly formed after the particles in the bottom of the agglomerate are in contact with the target plane. The damage starts from the region of contact with plane where maximum stress exists but does not diametrically propagate through the agglomerate. Therefore, no further fracture planes are developed. This is confirmed in Fig. 11 where a diametrical clip is shown in the centre of the agglomerate. While the agglomerate is still moving toward the plane, the area of the flattened circular contact region becomes larger over time. The shape of the deformation zone is thus changing, which is caused by the local structural re-arrangement due to the sliding between constituent primary particles. The particles inside this cone shape deformation zone are totally damaged (damage equal to unity). The total volume of the deformation zone does not seem to grow too much, but the debris starts to detach from deformation zone and splashes out after 0.44 ms.

Fig. 10

Evolution of the deformation zone of the agglomerate under normal impact. Particle damage smaller than 0.1 are shown as less opaque

Fig. 11

Side view (a) and front view (b,c,d) of a slice of the agglomerate at different time instants

The final breakage product of the agglomerate under impact can be separated into a largest survived cluster and accompanying fine debris [46]. Figure 12 presents a comparison between the experimental and the numerical largest survived cluster. Both experimental and numerical largest survived clusters show an irregular surface roughly parallel to the target plane. The experimental observations indicate that the particles are very loose on this new surface and can detach easily during handling, which is qualitatively consistent with the damage distribution of constituent particles in the numerical simulation. Figure 12d shows a front view of the cone shape fracture zone obtained in the simulation. Note that this cone shape of fracture zone is also similar to the so-called Hertzian ring cracking which is typically found in the experiments of low impact velocity regime of solid particles such as soda-lime glass [47, 48].

Fig. 12

Front view of the largest survived cluster after impact. a Experimental survived cluster. b Particle damage distribution of simulated agglomerate. c Simulated survived cluster with particle damage below 0.1. d Simulated fracture zone with particle damage over 0.1

Figure 13 shows the time evolution of several averaged quantities of the constituent particles, namely, the damage ratio, kinetic energy, rotational kinetic energy, vertical and transversal velocities. The averaged particle vertical position is also plotted to indicate the approximate centre of mass of the agglomerate. Initially, the impact energy is high while the contact area between the agglomerate and plane is small due to the spherical nature of the agglomerate shape, so the damage ratio does not grow very fast. As the agglomerate continues to move downward the contact area is increasing, resulting in a rapid increase of the damage ratio. This can be confirmed through Fig. 14 where the change of damage ratio is shown along with displacement of the agglomerate. A catastrophic breakage of the bonds occurs near the contact plane at the early stage of the impact as indicated in Figs. 13a and 15. Meanwhile, this phase is associated with a sharp decrease of the total kinetic energy as shown in Fig. 13b. The dissipated kinetic energy in the vertical direction is partially transferred to rotational energy and transversal kinetic energy of the damaged particles, as indicated in Fig. 13c and d. Since the damaged fragments are no longer bonded to the agglomerate, the additional rotational kinetic energy and transversal kinetic energy thus enable them to escape from the fracture zone. It is interesting to note that the total rotational kinetic energy goes down for a short period and increases again to reach the peak. This may be because the fragments get jammed inside the agglomerate at first, leading to a decrease of the rotational kinetic energy, but become free to rotate after they escape. As the kinetic energy of the agglomerate drops, the damage rate also drops while the total amount of damage continues to increase. At this stage, most of the damage happens around the boundary of the fracture zone as can be seen in Fig. 15. The final positions of the broken bonds and their break time are recorded and provided in Fig. 16 where the broken bonds are coloured and their thickness are scaled with their breakage time. It shows that most of the broken bonds are concentrated upon the cone shape fracture zone at the early time of impact and then the damage gets spread to the peripheries until the impact process ends.

Fig. 13

Time evolution of the averaged damage (a), kinetic energy (b), rotational kinetic energy (c), vertical and horizontal velocities of particles (d)

Fig. 14

Damage rate with the displacement curve

Fig. 15

Time evolution of the bond network (Intact bond: blue beams; broken bond: red beams). Incremental damages within each time interval are shown

Fig. 16

Spatiotemporal distribution of the broken bonds. a Front view. b Bottom view. The bond thickness is scaled by the broken time

The time evolution of the number of broken bonds resulting from tension and shear is shown in Fig. 17. No bond is predicted to fail through compression during the simulation. Tension failure is the dominant failure mechanism that accounts for the majority of broken bonds, which is also in line with the experimental studies [11, 39]. The tension failure in fracture zone is also termed Mode I fracture in many studies on failure pattern of rock and concrete [49]. Figure 18 shows the time evolution of stress distribution on the unbroken bonds. The number of bonds that reached 80% of max tensile strength sharply increases after the agglomerate impacts the plate and arrives at the peak around 0.26 ms. Later, the number decreases as the impact energy dissipates. The trend of the number of bonds that reached 80% of max shear strength is similar while its total number is less than the number of strong tensile stress. It is interesting to note that there are still some unbroken bonds that reached 80% of their max strength even when the kinetic energy of the agglomerate was completely dissipated. This indicates that the impact has caused a permanent change of the agglomerate which also shows the potential of using the current bond model to study the fatigue problem of agglomerate under repeated impacts. Figure 19 shows the bond force rose diagram in which the contact orientation versus the intensities of the compressive, tensile and shear forces on the bonds are presented. The elevation angle is 0° when the bond orientation is parallel to the contact plane and 90° or 270° when the bond orientation is perpendicular to the contact plane. It can be seen that the distribution of compressive forces on the bond has a clear inclination. The maximum compressive forces on the bond are located around 90° or 270° and minimum compressive forces are at around 0°. The maximum of the tensile forces is located at the horizontal bonds but some of the vertical bonds also carry a large tensile force. The shear force network does not have a strong inclination. The maximum shear force is located at around 260°. On the other hand, Fig. 19 implies that the intensity of the shear force network is significantly smaller than the tensile force network.

Fig. 17

Time evolution of the number of failed bonds

Fig. 18

a Time evolution of the number of bonds reaching 80% of max tensile strength. b Time evolution of the number of bonds reaching 80% of max shear strength

Fig. 19

Force rose diagram of the bonds (t = 0.26 ms)

Figure 20 shows the coarse-graining damage and maximum principal stress distributions of the agglomerate at different time instants. The coarse-graining fields are calculated using the Particle Analytics® software which transforms the discrete particle-based data to bulk continuum field information [50]. The stress is calculated based on the contact forces acting on the particles, i.e. bonded contact force is used when the bond is intact and non-bonded contact force is used when there is no bond. The coarse-graining length scale is chosen as 1.5 times the particle diameter following on previous work of Weinhart et al. [51]. There is no special treatment of the near-wall region in the current coarse-graining analysis. The stresses are correct at boundaries because the particle and wall interaction force is included in the coarse-graining analysis. A right diametrical clip has applied on the agglomerates to better show the inside fields. It can be seen from the Fig. 20b that both compressive stress (in blue colour) and tensile stress (in red colour) are generated inside the agglomerate when it impacts the plane. At the early of the impact, the strong compressive stress region is covered by a strong tensile stress region that is approximate an arch shape. The compressive stresses are centred at the fracture zone while tensile stresses are located around the fracture zone boundary. As the tensile wave propagates toward the top of the agglomerate, the bonds at the tensile stress region break. As a result, the fracture zone expands. On the other hand, the intensity of the tensile stress decreases because it disperses to the upper expansion zones and the dissipation of the total kinetic energy of the agglomerate as impact time goes on.

Fig. 20

Coarse-graining damage and maximum principal stress distributions of the agglomerate at different time instants. A right diametrical clip was applied to the agglomerates to better show the inside fields. a Coarse-graining damage contour plot. b Coarse-graining maximum principal stress contour plot (Blue is compressive stress and red is tensile stress)

4 Conclusion and outlook

In this work, the recently developed Timoshenko beam bond model was used to simulate the breakage process of agglomerates under normal impact with a target plane. The axial force, shear force, twisting moment and bending moment acting on the bonds are calculated and updated until the failure criteria are met based on the Timoshenko beam theory. The breakage of a bond is a one-off event and a broken bond is removed permanently. One attractive characteristic of the model is that the bond contact associated parameters have clear physical meaning. Experimental measurements of the binder have been directly used to characterize the mechanical properties of the bonds. The Young’s modulus of the bonds was calibrated through tension tests and the tensile strength of the bonds was calibrated through inter-particle pull-off tests. In addition, the number of constituent particles and the packing structure of the simulated agglomerate were also carefully generated to match the experimental agglomerate. Finally, the validation against normal impact experiment of the agglomerate was carried out. Comparison between the numerical simulation and experimental records of the evolution of the agglomerate breakage process showed good agreement. Moreover, the superiority of the Timoshenko beam bond model over the experimental technique is that detailed information of the force, stress and damage on the constituent particles of the agglomerate could be directly accessed after the simulations.

Numerical results show that the majority of damage occurs quickly as the agglomerate comes into contact with the plane and tensile failures are dominated. At the early time of the impact process, a cone shape of fracture zone is formed along with large compressive stress exerted by the wall and an arch shape tensile stress region is generated around the boundary of the fracture zone which has a dominant effect on the fracture propagation. The total kinetic energy of the agglomerate decreases sharply due to the broken bonds, which leads to the decrease of the intensity of tensile stress waves. As most of the kinetic energy drops and the total damage of particles increases gradually. Meanwhile, the agglomerate continues to approach the target plane along with the deformation of the fracture zone. When the agglomerate has dissipated most of its kinetic energy, the process reaches a final stable period with no further obvious damages.

DEM can provide a full history of the fracture mechanics and detailed insight of agglomerate breakage under impacts after elaborating experimental calibration and validation. In future endeavours, DEM could be used for model driven design of the agglomerate handing and processing processes. Note that there are many different kinds of agglomerates in pharmaceuticals and other industries. Depending on the agglomeration mechanisms, different models other than the TBBM model of this work may be required. For example, JKR cohesive model could be used for the agglomerate bonded by the self-adhesive mechanism. A generic practice with a model driven design framework [52] was proposed recently where various stages of verification, characterisation, calibration and validation to facilitate Quality by Design for product quality and design space is guided by multiscale particulate modelling.

Appendix

1.1 Time step selection

A reasonable selection of the computational time step is crucial for achieving a stable and accurate simulation using the Timoshenko beam bond model (TBBM). Since both bonded contacts and non-bonded contacts are considered in the simulation, the critical computational time step should be determined based on the lower value of these two type of contacts. For non-bonded contacts, the critical time step is determined using the Rayleigh time step. For bonded contacts, the critical time step is calculated based on an approximate solution of a single degree of freedom in a mass spring system [53]. Ten percent of the critical time step is usually considered to be safe to ensure a stable explicit integration of the simulation and is adopted here. The aforementioned formulas of the time step calculation are given as follows [26, 27],

$$\Delta t_{crit} = \min \left( {\Delta t_{crit,R} , \, \Delta t_{crit,B} } \right)$$

(18)

$$\Delta t_{crit,R} = \frac{{\pi R_{p,\min } \sqrt {\rho_{p} /G_{p} } }}{{\left( {0.1631\nu_{p} + 0.8766} \right)}}$$

(19)

$$\Delta t_{crit,B} = 2\sqrt {\frac{{m_{p,\min } }}{{K_{b,\max } }}} = \sqrt {\frac{{16\pi \rho_{p,\min } }}{{3K_{b,\max } }}\left( {\frac{{L_{B,\min } K_{1,\min } }}{{\pi \lambda E_{B} }}} \right)^{1.5} }$$

(20)

$$\Delta t \le 0.1\Delta t_{crit}$$

(21)

where $L_{B,\min }$ is the minimum bond length,$K_{1,\min }$ is the value of the minimum stiffness coefficient in the axial force calculation, $K_{b,\max }$ is the largest bond stiffness coefficient in the forces and moments calculation equations, which is usually the maximum stiffness coefficient in the axial force calculation. All these relevant parameters could be obtained after the bond initialisation process. A sensitive study of the time step has been carried out with 20% percent, ten percent and six percent of the critical time step. The effect of the selected numerical time steps on the prediction of the average damage ratio of the agglomerate under impact is shown in Fig. 

Fig. 21

Effect of the numerical time step on the prediction of average damage ratio of the agglomerate under impact

21. It is confirmed that 10% of the critical time step seems enough in this case while the results from 20% percent of the critical time step slightly over-predicted the average damage ratio compared with results from 6% of the critical time step.

1.2 Bond initialisation

A predefined time step is used to create bonds between particles of specified types. The creating of bonds in this work is a one-off procedure triggered at the beginning of a simulation. If two particles’ contact radii overlap, they will be bonded together. The contact radius of a particle is usually set to be equal or larger than the physical radius, which is used to extend the bond contact search radius for each particle and can be seen to represent a finite cementation thickness. As a result, particles which are not in physical contact can still be bonded together. Note that the contact radius is only used in the bond initialisation process and bond force calculations, while the physical radius is still adopted in all other computations including the non-bonded contact force calculations. The contact radius used in this study is 1.2 times the particle physical radius, which is recommended as the default value in the thesis of Brown (2014). Once a bond has been created, it is assigned a compressive stress strength $\sigma_{C}$, a tensile stress strength $\sigma_{T}$ and a shear stress strength $\sigma_{S}$. These strengths define the maximum stresses that the bond can withstand before failure. The strengths of a bond are defined from a predefined normal distribution bounded by zero and twice of the mean strength. The bond strengths are assigned as follows,

$$\sigma_{C} = S_{C} \cdot \left( {\left( {\varsigma_{C} \cdot N} \right) + 1} \right)$$

(22)

$$\sigma_{T} = S_{T} \cdot \left( {\left( {\varsigma_{T} \cdot N} \right) + 1} \right)$$

(23)

$$\sigma_{S} = S_{S} \cdot \left( {\left( {\varsigma_{S} \cdot N} \right) + 1} \right)$$

(24)

where $N$ is a random number drawn from a standard normal distribution; $S_{C}$,$S_{T}$, $S_{S}$ is the mean bond compressive, tensile and shear strength, respectively; $\varsigma_{C}$,$\varsigma_{T}$, $\varsigma_{S}$ is the coefficient of variation (CoV) of the compressive, tensile and shear strength, respectively. Note that a larger value of CoV will correspond to a more heterogeneous material property.

1.3 Failure criteria of bonds

When two particles are bonded together, the compressive, tensile and shear stress on the bond are calculated every time step. The bonds are assumed to behave in an elastic and brittle manner. A bond will fail if one of the maximum stresses exceeds the corresponding failure criterion. In this study, the tensile stress is considered positive and compressive stress is negative. The maximum compressive and tensile stresses in a bond occur at the outermost fibres of the bond. Based on the beam theory, the maximum compressive and tensile stress can be determined through a summation of contributions from axial forces and bending moments, which is calculated as follows,

$$\sigma_{C,\max } = \max \left[ {0, - \min \left( {\frac{{F_{ix} }}{{A_{B} }} \pm \frac{{R_{B} \sqrt {M_{iy}^{2} + M_{iz}^{2} } }}{{I_{B} }}} \right)} \right] \, i = \alpha ,\beta$$

(25)

$$\sigma_{T,\max } = \max \left[ {0,{\text{ max}}\left( {\frac{{F_{ix} }}{{A_{B} }} \pm \frac{{R_{B} \sqrt {M_{iy}^{2} + M_{iz}^{2} } }}{{I_{B} }}} \right)} \right] \, i = \alpha ,\beta$$

(26)

The shear stresses are calculated through a summation of contributions from shear forces and twisting moments. Since the shear force and twisting moment at the two ends of the bond are equal and opposite, the maximum shear stress can be determined at either end. The shear forces are uniform over the cross section while the torsion stress is greatest at the outermost fibre. Therefore, the maximum shear stress can be calculated as,

$$\sigma_{S,\max } = \frac{{\left| {M_{\alpha x} } \right|R_{B} }}{{2I_{B} }} + \frac{{R_{B} \sqrt {F_{\alpha y}^{2} + F_{\alpha z}^{2} } }}{{3A_{B} }}$$

(27)

If all the calculated stresses are smaller than the corresponding strength, i.e. failure criteria are not met, then forces (moments) opposite of the internal forces (moments) are applied to the two particles to act as restoring forces (moments) to resist the translational and rotational displacements. Once a bond has failed, the bonded contact will be removed permanently.

1.4 Model characteristics

The TBBM model has been implemented in the commercial software EDEM® (2.7 onwards) (Edinburgh, UK) through the use of EDEM’s API (Application Programming Interface) functionality [54]. A series of benchmark cases have been carried out to ensure that the mathematical descriptions in the programmed code match the theories and expectations. The verification cases including static loading of a simply support beam, free vibration of a simply supported beam and thin rectangular planes under various loading conditions have been performed [26]. The predictions from the Timoshenko beam bond model and the classical solutions have been found to be in very good agreement (< 1%).

It is worth addressing the similarity and differences between the forces and moments calculation of the TBBM model and other bonded contact models. Among them, the parallel bond model in PFC3D is a popular model that is used in the simulations of rock fracturing processes [22, 55]. In the parallel bond model, a set of elastic springs with constant normal and shear stiffness is used to transmit the force between two bonded particles. The moment induced by particle rotation is resisted by a set of elastic springs uniformly distributed over the bond cross section. Basically, the calculations of axial forces and twisting moments are the same for these two models. However, the shear stiffness for calculating the shear forces is different between parallel bond model and Timoshenko beam bond model. The calculation of bending moments is also different where the parallel bond model considers the contributions caused by the relative rotational displacements of particles, whereas the Timoshenko beam bond model calculated the moments based on the beam theory.

Euler–Bernoulli beam theory has also been used in some bonded contact models [23, 41]. Since the bond radii between particles in DEM are generally comparable in magnitude with bond lengths, these bonds behave like thick beams. One advantage of the Timoshenko beam theory is that it takes into account shear deformation, making it suitable for describing the behaviour of thick beams. As shown in Fig. 22, the Euler–Bernoulli beam theory assumes the cross sections perpendicular to the neutral axis of the beam to remain both plane and perpendicular after deflection [56]. Whilst this assumption is known to be acceptable for slender beams, for stocky beams such as those concerned in the great majority of DEM of bonded materials including the present study, the shear deformation can be significant and thus should not be neglected. The Timoshenko beam theory includes the effect of shear deformation, which is therefore more appropriate here.

Fig. 22

Projection view of beam deformation under bending moment in Timoshenko and Euler-Bernouli models

1.5 Effects of shear strength

The shear strength of the experimental epoxy resin binder studied in this work is not provided by Subero [35]. Delenne [39] shows that the yield load for shearing loading path is around 60% of the yield load for tensile loading path for an epoxy resin binder. Figure 23 presents the effect of shear strength on the simulated damage ratio evolution of the agglomerate under normal impact against a rigid wall. The tensile strength was set to be 23 MPa and three shear strengths (10 MPa, 20 MPa and 30 MPa) were studied. It can be seen that the damage of the agglomerate slightly decreases as the increase of shear strength. This is because fewer bonds fail in shear mode when the shear strength becomes larger. Since the number of bonds that fails in shear mode is much smaller than the number of bonds that fails in tensile mode, the overall damage pattern is not altered as shown in Fig. 24. It is noted that the experimental study of Delenne [39] shows that the yield force of the material subjected simultaneously to a combined tension/shearing or compression/shearing loadings will be different from the yield force under a pure loading path. Hence, further works would be needed to investigate the effects of a varying shear strength model or a more elaborated failure criterion on the simulations of the agglomerate damage processes.

Fig. 23

Effect of the shear strengths on the prediction of average damage ratio of the agglomerate under normal impact against a rigid wall

Fig. 24

Damage of the simulated agglomerate at 3.8 ms. a Shear strength = 10 MPa. b Shear strength = 30 MPa

1.6 Effects of coefficient of variation of bond strengths

In general, a larger value of the coefficients of variation means that a wider distribution of the bond strengths within the agglomerate. Figure 25 shows the effects of coefficient of variation of bond strengths on the simulated damage ratio evolution of the agglomerate under normal impact against a rigid wall. The coefficients of variation of compressive, tensile and shear strengths are assumed to be the same here. It can be seen that the predicted damage ratio of the agglomerate slightly increases as the value of the coefficient of variation increases from 0 to 0.1. The predicted damage ratio significantly increases as the value of the coefficient of variation increases from 0 to 0.5. Figure 26 shows that many damages were also found at locations beyond the bottom part of the agglomerates when the coefficient of variation is 0.5. This is because the agglomerate becomes more heterogeneous when the coefficient of variation becomes larger. The impact force transmits into the whole agglomerate during the impact processes causing the breakage of the weak bonds within the agglomerate.

Fig. 25

Effect of the coefficient of variation of bond strengths on the prediction of average damage ratio of the agglomerate

Fig. 26

Damage of the simulated agglomerate at 3.8 ms. a Coefficient of variation of bond strength is 0. b Coefficient of variation of bond strength is 0.5