1 Introduction

In recent decades, a new class of materials whose properties can be changed by certain external physical fields has been developed; those materials are known as smart structures. Although scientists and researchers have been dealing with them for some time now, their applications in everyday life remain limited. Commercialization is hindered mainly by economic factors and by the complexity of the auxiliary equipment necessary to control the properties of such structures. Another major problem in classic intelligent materials is the need to use physical fields of very high densities, such as magnetism or temperature, to change their properties, which makes them difficult to control and unsafe to use. Nonetheless, some smart materials have been commercialized in, for example, the defence [26, 29], aviation [7, 17] and automotive industries [10].

An alternative smart material that partially eliminates the above-mentioned problems is Vacuum Packed Particles (VPP) [5, 12, 22, 41]. VPP structures are composed of polymer granular media inside a plastomer coating, whose mechanical properties can be controlled by a physical phenomenon known as the jamming phase transition. Granular media can be soft and flowing like a dense liquid if they are loosely combined, but become rigid as a firm solid when they are vacuum packed. Since they are built of simple polymer granules, they are extremely cheap, even 1000 times less expensive than magnetoreological fluid [36]. Additionally, a simple vacuum pump is used to control the material’s mechanical properties, which significantly reduces the price and increases safety of use. Another huge advantage of VPP over classic smart materials is the energy density needed to control changes in their properties; it is 10 times lower than for MR fluid and almost 60 times lower than for hot glue [14].

The benefit of the jamming mechanism was first noticed in medical applications, when vacuum mattresses began to replace rigid spine boards [25]. Apart from that, VPP are used in medicine as endoscopes or ortheses [8, 34]. At present, the most popular field of VPP applications is robotics, where one example is a robot gripper that can handle all sorts of objects [1, 2, 12, 18] or an aerospace structure used as a switchable stiffness morphing element [11]. In the field of mechanical engineering, the most important application of jammed granular systems is in the damping of vibrations [37]. VPP seem to be competitive towards the most popular and widely commercialized magnetorheological fluids (MRF) and devices that work on the basis thereof [13, 32, 43]. In [33, 41] the authors proved that vibrations of beam-like elements can be efficiently attenuated by VPP. Placing a beam in a sleeve filled with granular media and controlling the level of the vacuum within it proved to be an efficient strategy for the semi-active damping of vibrations. Other papers [39, 40] have proved that VPP can be adapted in linear damping absorbers that are similar to MR dampers.

VPP show potential for other commercial applications, such as active collision energy absorbers [19, 27, 31, 42], but the main problem is that prototyping has overtaken basic research and modeling. It can be stated with great certainty that, without defined material properties and the proper modeling methodology, it is not possible to design and build a real engineering facility of high quality. To date, research has mainly focused on the influence of underpressure on the static and dynamic behavior of the material [3, 33]. The effects of underpressure a under uniaxial stress state was investigated in paper [37] whereas in papers [9, 11] the behaviour of VPP under a bending test was shown. In paper [24] research on adhesive control by means of the granular jamming mechanism is presented, while work [6] shows the influence of grain type on the macroscopic behaviour of VPP. Interesting results are provided in paper [21], where the authors investigated the influence of the outer shell on the behaviour of VPP. The aforementioned works involved static tests for both hard [38] and soft [28] particles. In work [3] a dynamic test of a beam made of VPP was conducted and modeled, while in papers [4, 5] the results of research on the damping properties of VPP under dynamic loading were shown.

If according to work [14] VPP will be treated as a separate group of material, subgroup of soil but with possibility to control, there is insufficient information on the effects of high strain rate and temperature on the behaviour of this composite. In the literature one can find studies on extremely high speeds [30, 35] or high temperatures [15] for triaxial tests of soil materials, which mechanical behavior is similar to VPP [33]. Nevertheless, such research results were not reported for VPP composite, which mechanical strength and susceptibility to control needs to be evaluated for potential applications in soft robotics.

Additionally, there are shortcomings in the modeling and a lack of a proper constitutive model which could be easily integrated into the finite element code and thus allow engineers to model and analyze objects using VPP.

To overcome the above-mentioned deficiencies, the aim of this paper is to investigate the influence of strain rate and temperature on the mechanical properties of VPP, and to preliminary develop a constitutive equation that can describe the behavior of the material under the impact of strain, strain rate, temperature, and underpressure.

2 Experimental research

In the first part of the paper, the results of the experimental research on strain rate and temperature under different stress state are shown. Tests were performed under different pressure conditions inside the sample, which made it possible to determine the basic mechanical parameters of the material as a function of underpressure, strain rate or temperature.

2.1 Material and methods

The VPP specimens used in this study consisted of two rigid discs and a space filled with granules encapsulated by an elastomer coating. The diameter of the sample was 51 mm and its full length 140 mm, where the VPP space was equal to 100 mm. A photograph of a sample and a description of its dimensions are presented in Fig. 1. All of the samples were filled to a packing fractions of 57% (it was measured and calculated with a assumption of material density \(1450 \frac{\hbox {kg}}{\hbox {m}^3}\)), with ball-shaped granular particles having a diameter of about 3 mm made of plastic POM MT24u01 with a Young modulus of 2900 MPa.The outer shell was made of polyethylene with a thickness of 0.15 mm and a Young modulus of 10 MPa. The outer shell was initially pre-folded to reduce the effect of load carrying capability.

Fig. 1
figure 1

VPP cylindrical specimen

Full size image

Before each test, the sample was placed in a mold specially prepared for the purpose of filling the sample to the proper shape. The grains were poured in randomly, and in the next stage the largest reproducible packing ratio, controlled by the precise weighing of the sample, was achieved. In Fig. 1 the typical sample of the VPP is presented. Next, a partial vacuum was applied, and only then was the sample placed in the testing machine jaws. After each test, the sample was removed from the jaws, the vacuum was removed, the grains were reorganized and the sample was placed again in the mould. Additionally, each of these tests was carried out on three independent samples of the VPP material, which made it possible to prove that the observed phenomena were physical, not random.

In order to examine the impact of strain rate on the response of the VPP, compressive and tensile tests were performed using a horizontal test stand equipped with an MTS actuator equipped with a DIC ARAMIS system, as shown in Fig. 2.

Fig. 2
figure 2

Test stand

Full size image
Fig. 3
figure 3

Testing machine with temperature chamber

Full size image

Five different underpressure values were used: 0.01 MPa, 0.03 MPa, 0.05 MPa, 0.07 MPa, and 0.09 MPa and five strain rate values: (\(0.033{\frac{1}{\hbox {s}}}\) \(0.5{\frac{1}{\hbox {s}}}\), \(2.0{\frac{1}{\hbox {s}}}\), \(3.0{\frac{1}{\hbox {s}}}\) \(4.5{\frac{1}{\hbox {s}}}\)), separately for the tension and compression stress states at a temperature of \(25\,^{\circ }\hbox {C}\). To perform the statistical processing and to check the repeatability of the results, each test was repeated three times.

To examine the influence of temperature, the tension and compression tests were performed at temperatures of \(25\,^{\circ }\hbox {C}\), \(40\,^{\circ }\hbox {C}\), \(55\,^{\circ }\hbox {C}\), \(75\,^{\circ }\hbox {C}\). Those tests were performed on an INSTRON 8802 testing machine equipped with an INSTRON 3119-108 temperature chamber (Fig. 3) in which the temperature could be accurately controlled. The experiments were performed for different underpressure values: (0.01 MPa, 0.05 MPa, 0.05 MPa, 0.07 MPa 0.09 MPa) and at a strain rate of \(0.033\frac{1}{\hbox {s}}\). Each test was repeated three times. Generally, all the results revealed little scatter in the recorded experimental data (lower than 2%). An exception was the result for a vacuum pressure equal to 0.01 MPa, where the difference was higher than 15%. At such a low underpressure conditions, VPP are quite unpredictable, which was also confirmed in previous works of the authors [36]. The results obtained for the lowest partial vacuum values should be treated as qualitative.

Fig. 4
figure 4

Strain in y direction (tension/compression) recorded by ARAMIS system

Full size image

Due to the difficulty of measuring the strain by an optical method in the thermal chamber, this was done by registering the displacement of the jaws of the testing machine and then converting these values into engineering strain. In order to be able to make any comparison of the research on the influence of strain rate and strain temperature, the strain in both experiments was determined analogously. The deformation was registered in the ARAMIS system to check whether the adopted assumption was not burdened with too much error. The registered uniform distribution of deformations in the y direction, which is parallel to the tension/compression direction, shown in Fig. 4, proves that the assumptions made with the engineering strain calculation were correct.

2.2 Experimental results

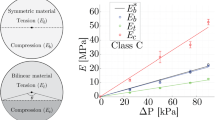
Figure 5 shows the stress–strain curves for different underpressure values for compression and tension at a strain rate of \(0.033{\frac{1}{\hbox {s}}}\). For tension and compression, the curves have a similar shape and reach higher values with increasing negative pressure. The values of the yield point and maximum stress (identified as \(\sigma _{0.035}\)) for compression and tension change approximately linearly with increasing negative pressure, shown in Fig. 6. The yield strength values in the underpressure range of 0.01–0.09 MPa change by about 250%, and the maximum stresses by 90%, which shows the great potential for control offered by VPP. In Fig. 6, it can also be seen that the material has different compressive and tensile properties, as the maximum difference in the yield point is 600%, while the maximum stress is 280%.

Analyzing the stress–strain curves in Fig. 7, it can be concluded that for both low (left) and high (right) values of negative pressure, strain rate hardening occurs.

Fig. 5
figure 5

Stress–Strain curve for compression (left) and tension (right)

Full size image
Fig. 6
figure 6

Yield stress (left) and \(\sigma _{0.035}\) (right) as a function of underpressure

Full size image
Fig. 7
figure 7

Stress–strain curve for underpressure 0.01 MPa (left) and 0.09 MPa (right)

Full size image
Fig. 8
figure 8

YS (left) and \(\sigma _{0.035}\) (right) as a function of strain rate

Full size image

Figure 8 shows the influence of strain rate on the YS and \(\sigma _{0.035}\). It can be seen that the characteristics of the changes in the yield point as a function of strain rate, which are strongly nonlinear, are very similar for each negative pressure value. The values of YS and \(\sigma _{0.035}\) change significantly at a strain rate range of \(0{-}2\frac{1}{\hbox {s}}\), while above it is almost constant. A similar relationship exists for \(\sigma _{0.035}\). It can be observed that these parameters change by about 26% in the strain rate range of \(0{-}2\frac{1}{\hbox {s}}\), but only 3% in the range of \(2{-}4.5\frac{1}{\hbox {s}}\), showing a certain saturation.

The effect of temperature on the stress–strain relationship is shown in Fig. 9. For both low (left) and high (right) values of negative pressure, a temperature softening occurs.

Fig. 9
figure 9

Stress–strain curve for underpressure 0.01 MPa (left) and 0.09 MPa (right)

Full size image
Fig. 10
figure 10

YS (left) and \(\sigma _{0.035}\) (right) in function of temperature

Full size image

The effect of temperature on YS and \(\sigma _{0.035}\) is shown in Fig. 10. It can be seen that the characteristics of the changes in the yield point as a function of temperature are almost linear within the tested temperature range for each negative pressure value. For the lowest underpressure value, it changes by approx 40%, and for the highest by about 30%. A similar trend can be observed for \(\sigma _{0.035}\), where the characteristics are also almost linear and the change varies in a range of 30–50%. To find a correlation between VPP and the particle material, the normalized value of YS, and the Young modulus of the particle, based on the manufacturer’s data, are presented in Fig. 11. These values were normalized to their reference value at a temperature equal to \(25\,^{\circ }\hbox {C}\). Generally, this is a quasi-linear relationship for both parameters, where the slope is slightly different. The YS slope was equal to − 0.006 whereas the YM was − 0.0082, a difference of about 26%.

Fig. 11
figure 11

Norm values of Yield Stress (VPP) and Young modulus of granular parent material

Full size image

3 Modelling

As was shown in the last section, the investigated structure features an elasto–plastic (Fig. 5) with strain rate hardening (Fig. 7) and temperature softening (Fig. 9). Additionally, the underpressure parameter affects the plasticization and hardening of the material (Fig. 5). Previous work has shown that such materials display isotropic behaviour [36], therefore it was decided to describe the VPP using the Huber-von Mises-Hencky rule [20]. The yield function describing the plasticity of the material is defined by , which incorporates different behaviours of the material for the tension and compression stress states (compare Fig. 6). It was assumed that the material has a different plasticity function radius depending on the sign of the first stress tensor invariant, as described by Eq. 2.

$$\begin{aligned} \phi = \frac{1}{2}{s_{ij}}{s_{ij}}-\frac{{\sigma _{y+/-}(\epsilon , \dot{\epsilon }, T, p)}^2}{3} \le 0 \end{aligned}$$
(1)
$$\begin{aligned} \sigma _{y+/-}(\epsilon , \dot{\epsilon }, T, p)= \left\{ \begin{array}{ll} \sigma _{y+}(\epsilon , \dot{\epsilon }, T, p) &{} \text {if}\; I_{\sigma }= tr\sigma =\sigma _{kk}>0 \\ \sigma _{y-}(\epsilon , \dot{\epsilon }, T, p) &{} \text {if}\; I_{\sigma }= tr\sigma =\sigma _{kk}<0\\ \end{array} \right. \end{aligned}$$
(2)

where \(\phi\), plasticity function; \(s_{ij}\), deviatoric components of stress tensor; \(\sigma _{y+/-}(\epsilon , \dot{\epsilon }, T, p)\), radius of plasticity function; \(\epsilon\), strain; \(\dot{\epsilon }\), strain rate; T, temperature; p, underpressure; \(I_{\sigma }\), first invariant of stress tensor.

Since the function must be \(\epsilon , \dot{\epsilon }, T, p\) parameter dependent, it was decided to modify the the Johnson–Cook (JC) [23], which already contains 3 of the 4 above parameters.

3.1 Johnson–Cook model

The basic form of the JC model can be expressed by Eq. 3, a fully empirical model describing the evolution of yield surface depending on strain, strain rate and temperature.

$$\begin{aligned} \sigma _{y+/-}(\epsilon , \dot{\epsilon }, T)=(A+{B}{\epsilon }^n)\left(1+Cln\left( \frac{\dot{\epsilon }}{\dot{\epsilon }_0}\right) \right)\left(1-\left( {\frac{T-T_R}{T_m-T_R}}\right) ^m\right) \end{aligned}$$
(3)

where A, Yield Stress for reference strain rate \(\dot{\epsilon }_0\) and temperature \(T_R\); B, n, strain hardening parameters; C, dynamic hardening coefficient; m, material constant associated with temperature softening; \(T_R\), \(\dot{\epsilon }_0\), reference temperature and strain rate; \(T_m\), reference melt temperature.

In order to conduct an appropriate modeling process, it is necessary to define the material’s melting temperature, as well as the reference strain rate and temperature, which in this work were assumed to be \(175\,^{\circ }\hbox {C}\), \(0.033\frac{1}{\hbox {s}}\) and \(25\,^{\circ }\hbox {C}\) respectively. The model has five independent material constants (A, B, n, C, m); three of them refer to the strain hardening effect (A, B, n), C controls the effect of strain rate, and m describes the impact of temperature. In the next subsection, the method of identifying the model parameters based on the experimental results is presented.

3.2 Parameter identification procedure

The model identification process was performed using LMFIT (Non-Linear Least-Squares Minimalization and Curve-Fitting for Python). The source code was written in the PYTHON programming language. The library made it possible to identify the JC model parameters based on various optimization methods. In this paper, the Levenberg-Marquardt method was used [16]. Identification was performed based on the engineering stress—engineering strain curve, since, for such a small value of strain, the differences are negligible. On the other hand, it should be remembered that in the case of a higher deformation value, this should be done for a true stress-true strain curve. The identification procedures were performed separately for selected undepressure values of 0.01 MPa, 0.05 MPa and 0.09 MPa. The procedure was repeated for the compression and tension states. For the brevity of the paper, an example of parameter identification procedure for an underpressure of 0.05 MPa and the compression state is presented.

The first parameter in Eq. 3 was assumed to be yield stress (YS). The strain hardening parameters B and n were identified based on the data obtained from the experiments for a strain rate of \(0.033\frac{1}{\hbox {s}}\) and a temperature of \(25\,^{\circ }\hbox {C}\). Since the value of the strain rate was equal to the reference value \(\dot{\epsilon }_0\), the whole parenthesis was 0 regardless of parameter C. A similar procedure can be applied to the third part of the equation. When T is equal to \(T_R\) this part equals 1 without affecting the value of parameter m. Figure 12 shows a comparison of the simulation and the experimental results for the identified B and n parameters.

Fig. 12
figure 12

Comparison of model and experimental results after identification of parameters B and n (\(SR=0.033\frac{1}{\hbox {s}}\), \(T=25\,^{\circ }\hbox {C}\) \(p=0.05\,\hbox {MPa}\))

Full size image

Secondly, parameter C, describing dynamic hardening, was identified. The procedure was carried out for the data obtained from the experiments at a strain rate of \(4.5\frac{1}{\hbox {s}}\). In this case, the parameters A, B and n were adapted as those previously identified, and the current strain rate was \(\dot{\epsilon }\) as \(4.5 \frac{1}{\hbox {s}}\). Parameter \(\dot{\epsilon }_0\) was assumed to be \(0.033 \frac{1}{\hbox {s}}\). Since the temperature in this test was \(25^o C\), which is equal to the reference temperature, the second part of the equation was again equal to 1, irrespective of the value of m. Figure 13 shows the good fit of the simulation-experiment after A, B, n, and C parameter identification.

Fig. 13
figure 13

Comparison of model and experimental results after identification of parameter C (\(SR=4.5\frac{1}{\hbox {s}}\), \(T=25\,^{\circ }\hbox {C}\) \(p=0.05\,\hbox {MPa}\))

Full size image

The last parameter m was identified based on the results of the tests at \(75\,^{\circ }\hbox {C}\) and \(0.03\frac{1}{\hbox {s}}\). Parameters A, B, n and C were adopted as those previously identified, but the current temperature T was assumed to be \(75^o C\) and the strain rate \(0.033 \frac{1}{\hbox {s}}\). The verification of this procedure is depicted in Fig. 14.

Fig. 14
figure 14

Comparison of model and experimental results after identification of parameter m (\(SR=0.033\frac{1}{\hbox {s}}\), \(T=75\,^{\circ }\hbox {C}\), \(p=0.05\,\hbox {MPa}\))

Full size image

The described procedure was repeated analogously for other underpressure values for both compression and tension. The values of all the parameters identified are presented in Table 1.

Table 1 Parameters of JC model
Full size table

3.3 Model modification: JC-p model

Based on the results obtained during the identification process, a modification of the Johnson–Cook model was proposed, which incorporates the effect of internal underpressure on the radius of the Huber- von Mises-Hencky plasticity surface [20]. The expanded Johnson–Cook law, hereinafter referred to as the JC-p model, can be described by the Eq. 4:

$$\begin{aligned} \sigma (\epsilon , \dot{\epsilon }, T, p)=({\alpha }+{\beta }{p}+({\Psi }+{\gamma }{p}){\epsilon }^{\Upsilon -{\chi }{p}})\left(1+({\Xi -{\mu }p})ln\left( \frac{\dot{\epsilon }}{\dot{\epsilon }_0}\right) \right)\left(1-\left( {\frac{T-T_R}{T_m-T_R}}\right) ^{ {\eta }p^\psi }\right) \end{aligned}$$
(4)

where \(\alpha , \beta , \Psi , \gamma , \Upsilon , \chi , \Xi , \mu , \eta , \psi\), material constants.

In this form, the model has ten constants, which were identified using the LFMIT library, separately for the tension and compression stress states. The identification procedure was performed analogously to those described in the previous section. In the first step, the parameters \(\alpha , \beta\) were identified based on the results of YS as a function of underpressure. Then \(\Psi , \gamma , \Upsilon , \chi\) were found based on the results of parameters B and n. Finally parameters \(\Xi , \mu , \eta , \psi\) were identified based on parameters C and m.

The results of the material parameters, calculated separately for tension and compression, are presented in Table 2. The model described by Eqs. 3 and 4 is suitable for description of the material behavior beyond yielding. The behavior before yielding is not included in the model.

Table 2 Material constants
Full size table

3.4 Validation and analysis

To verify the JC-p model’s correctness and reliability, a validation procedure was conducted. The model was verified for various values of strain rate, temperature and underpressure to check whether there was good correlation across the whole range of parameters. A comparison of the simulation and experimental results is presented for a few such trials. In Figs. 15, 16 and 17 the continuous red line marks the model results , while the discontinuous lines (blue circle, black triangle and green circle markers) show the experimental results. Figure 15 shows a comparison of the experimental and simulation results for the compression and tension stress states at a temperature of \(25\,^{\circ }\hbox {C}\) and a strain rate of \(2.0\frac{1}{\hbox {s}}\). The figure shows the comparison for three values of underpressure: 0.01 MPa, 0.05 MPa and 0.09 MPa.

Fig. 15
figure 15

Comparison of the experimental data with JC-p model for strain rate \(2.0\frac{1}{\hbox {s}}\) and temperature \(25\,^{\circ }\hbox {C}\) for compression (left) and tension (right)

Full size image

Figure 16 shows results for temperature \(25\,^{\circ }\hbox {C}\) and strain rates of \(4.5\frac{1}{\hbox {s}}\). In this case the comparison was made also for three values of underpressure.

Fig. 16
figure 16

Comparison of experimental data with JC-p model for strain rate \(4.5\frac{1}{\hbox {s}}\) and temperature \(25\,^{\circ }\hbox {C}\) for compression (left) and tension (right)

Full size image

Figure 17 shows the results under a strain rate of \(0.033\frac{1}{\hbox {s}}\) and at a temperature of \(55\,^{\circ }\hbox {C}\).

Fig. 17
figure 17

Comparison of experimental data with JC-p model for strain rate \(0.033\frac{1}{\hbox {s}}\) and temperature \(55\,^{\circ }\hbox {C}\) for compression (left) and tension (right)

Full size image

After validating the model and obtaining a good correlation, an analysis was performed of the impact of the strain rate in a range of \(0.033\frac{1}{\hbox {s}}{-}4.5\frac{1}{\hbox {s}}\) . Figure 18 shows the continuous characteristic of the YS (left) and \(\sigma _{0.035}\) (right) as a function of strain rate for three values of underpressure: 0.01 MPa, 0.05 MPa and 0.09 MPa.

Fig. 18
figure 18

YS (left) and \(\sigma _{0.035}\) (right) as a function of strain rate

Full size image

The graph shows that the greatest parameter hardening occurred at lower strain rates values (\(0.033{-}2\frac{1}{\hbox {s}}\)).

To explain this effect more precisely, the parameter of Strain Rate Sensitivity (SRS) was calculated, defined as 5. This equation provides an analytical solution for the proposed constitutive model (Eq. 6).

$$\begin{aligned} SRS(\epsilon , \dot{\epsilon }, T, p)=\frac{\partial \sigma (\epsilon , \dot{\epsilon }, T, p)}{\partial \dot{\epsilon }}\mid {_{\epsilon , T,p}}\end{aligned}$$
(5)
$$\begin{aligned} SRS(\epsilon , \dot{\epsilon }, T, p)=({\alpha }+{\beta }{p}+({\Psi }+{\gamma }{p}){\epsilon }^{\Upsilon -{\chi }{p}})\left({\frac{\Xi -{\mu }p}{\dot{\epsilon }_0}}\right)\left( \frac{1}{\dot{\epsilon }}\right) )\left(1-\left( {\frac{T-T_R}{T_m-T_R}}\right) ^{ {\eta }p^\psi }\right)\mid {_{\epsilon , T, p}} \end{aligned}$$
(6)

The SRS parameters were calculated for two values of strain equal to 0.002 (designated later as \(SRS_{0.002}\)) and 0.035 (designated later as \(SRS_{0.035}\)), for three values of underpressure (0.01 MPa, 0.05 MPa, 0.09 MPa) at a constant temperature of \(25\,^{\circ }\hbox {C}\). The results are shown in Fig. 19. Analyzing both figures, it can be seen that the SRS parameter for each value of underpressure is saturated for both strain cases (0.002 and 0.035). The greatest change occurs in the range \(0{-}1 \frac{1}{\hbox {s}}\) and tends to zero for strain rates higher than \(2 \frac{1}{\hbox {s}}\).

Fig. 19
figure 19

\(SRS_{YS}\) (left) and \(SRS_{0.035}\) (right) in function of strain rate

Full size image

4 Conclusions

In this paper, experimental and modeling research on VPP was performed, and it was confirmed that, even for higher strain rates and at various temperatures, the properties of VPP can be controled by the underpressure, and the investigated structures can be counted among the group of smart materials. At a vacuum pressure range of 0.01–0.09 MPa, the Yield Strength changes by about 250%, and the maximum stress by 90% (see Fig. 6), which is similar to the values presented in papers [36, 37]. Additionally, the material has different tension and compression properties, i.e. the difference between YS is almost 600%. The investigated material is also strain rate-dependent across the whole range of the vacuum. The values of the YS and \(\sigma _{0.035}\) change strongly nonlinearly as a function of strain rate (compare Fig. 8). The values of this parameter change dynamically over a strain range of \(0{-}2\frac{1}{\hbox {s}}\), while above the latter value remains almost constant. At the highest vacuum pressure, in the tested strain rate range the strengthening of the material is equal to about 27% for YS, and almost 35% for \(\sigma _{0.035}\), which is a value comparable to other smart materials, e.g. shape memory polymers [15]. VPP feature temperature softening behaviour for both low and high values of underpressure. The parameters YS and \(\sigma _{0.035}\), display an almost linear characteristic as a function of temperature (see Fig. 10). The change in the parameter value in a temperature range of \(25\,^{\circ }\hbox {C}\)–\(75\,^{\circ }\hbox {C}\) is about 40%. An initial attempt was made to compare the VPP temperature softening with respect to the granulates’ parent material (POM MT24u01). A decrease in the value of the VPP Yield Stress compared with the change in stiffness (Young modulus) of POM MT24u01 was made. Based on the results shown in Fig. 11, a correlation can be found; both characteristics are quasi-linear, but the slope value is slightly different. This is probably due to the fact that for VPP other additional phenomena have a strong impact on the global properties (e.i. the outer shell, friction, the surface roughness of a single grain). Nevertheless, it could be a really interesting problem for future work to look more precisely for the above-mentioned correlation in order to determine in detail what the relationship is between VPP and different granulate materials in terms of temperature behaviour.

The collected empirical data permitted a deep understanding of the material’s behavior under different strains, strain rates, temperatures and underpressures. Based on these results, it was possible to formulate a preliminary constitutive equation describing the material’s behavior \(\sigma (\epsilon , \dot{\epsilon }, T, p)\). The proposed model is an extension of the Johnson–Cook model, enriched by underpressure parameters, which were identified on the basis of the experimental tests and were followed up by a validation procedure. A close correlation was obtained for higher values of strain rate, i.e. \(2,0 \frac{1}{\hbox {s}}\), regardless of the vacuum value and stress state (see Fig. 15). The difference was lower for the compression state, whereas for the tension tests and higher temperatures (mainly in the tensile probes and at lower underpressures), the model is less reliable. Nevertheless, when the lowest value of vacuum pressure (Fig. 17) is omitted, the model is within 12% if the measurements, which is acceptable, especially if account is taken of the contrast between the complexity of the structure and the simplicity of the model.

Based on the research presented here, it can be concluded that:

  • The material displays hardening with increasing strain rate and softening with increasing temperature over the whole range of vacuum pressures applied.

  • A constitutive equation suitable to describe the material’s behavior as a function of strain, strain rate, temperature and underpressure \(\sigma (\epsilon , \dot{\epsilon }, T, p)\) is presented; the equation makes it possible to obtain a close correlation between simulation and experiment. A process that makes progress towards implementing a constitutive modeling of jammed granular materials in commercial finite element codes was presented.

  • In future work, it would be worth investigating temperature and strain rate effects beyond those ranges already tested, and additionally, to find what the relationship is between granulates’ parent materials and macroscopic VPP behaviour.