Damping prediction of particle dampers for structures under forced vibration using effective fields

Abstract

Particle damping is a promising damping technique for a variety of technical applications. However, their non-linear behavior and multitude of influence parameters, hinder currently its wide practical use. So far, most researchers focus either on determining the energy dissipation inside the damper or on the overall damping behavior when coupled to a structure. Indeed, currently almost no knowledge exchange between both approaches occurs. Here, a bridge is build to combine both techniques for systems under forced vibrations by coupling the energy dissipation field and effective particle mass field of a particle damper with a reduced model of a vibrating structure. Thus, the overall damping of the structure is estimated very quickly. This combination of both techniques is essential for an overall efficient dimensioning process and also provides a deeper understanding of the dynamical processes. The accuracy of the proposed coupling method is demonstrated via a simple application example. Hereby, the energy dissipation and effective mass of the particle damper are analyzed for a large excitation range first using a shaker setup. The particle damper exhibits multiple areas of different efficiency. The underlying structure is modeled using FEM and modal reduction techniques. By coupling both parts it is shown that multiple eigenmodes of the structure are highly damped using the particle damper. The damping prediction using the developed coupling procedure is validated via experiments of the overall structure with particle damper.

1 Introduction

Passive and active damping techniques exist to increase damping in a vibrating structure. While active damping techniques require feedback, passive damping techniques do not, making them often very robust and economically. A promising passive damping technique to reduce vibrations is the use of particle dampers. Containers attached to the vibrating structure are filled with granular material. By structural vibrations, momentum is transferred to the granular material which interacts with each other. As a result, energy is dissipated by impacts and frictional phenomena between the particles.

Particle dampers are a derivative of classical impact dampers and extend their good properties. Particle dampers are passive damping devices and are robust against harsh environmental conditions [15, 21]. In many cases they add only little mass to the overall system [6] and can be applied to a wide frequency range [3]. In contrast to impact damper, they lead to lower force peaks and a reduced sound transmission [7].

Despite their huge potential to damp undesired vibrations, particle dampers are so far rarely used for industrial applications. The major reason for this is that there exists no general and simple design guideline which is due to their highly non-linear behavior and the variety of influence parameters. To study particle dampers, two major approaches have been used in the past.

In the first approach, the energy dissipation and effective particle mass, also called effective fields, inside an isolated damper are directly analyzed for a given excitation range and amplitude range [4, 13, 16, 24] using the Discrete Element Method (DEM) or experimental shaker setups. In this way, statements about the amount of energy dissipation and thus the damper’s efficiency can be made. Additionally, experimental or numerical parameter studies on different influence parameters [13] can be performed, giving deeper insights into the micromechanic non-linear energy dissipation effects. Based on this, first design rules can be derived. However, these studies are often limited to a small excitation range. Also, no direct statements on the damping behavior of the overall structure with particle damper are drawn.

In the second approach, the particle dampers are attached to a vibrating structure and the overall damping is determined, which is often performed experimentally [5, 14, 20, 22]. In addition, the influence of the damper on the system eigenfrequencies can be analyzed. Also, numerical studies of this second approach are possible. Thereby, a model of the structure is coupled with a particle damper model. For the particle damper either computational expensive Discrete Element models are used [12] or very simplified models such as a single particle [8] or a particle chain [9] models. However, both experimental and numerical studies on the overall structure might be extremely time-consuming.

For an efficient overall dimensioning process it is essential to close the gap between both approaches. Only in this way, it is possible to transfer knowledge between the approaches, gain a deeper understanding of the processes, and shorten finally the overall design process. To do so, Trigui [23] coupled the energy dissipation field of a particle damper with a full Finite Element model of a plate to calculate the overall damping using the frequency response function obtained from time integration. A good agreement between experiments and numerical results is reported, but the investigated excitation range is small and a coupling with a full Finite Element model can still be very time-consuming. Thus, this approach is not suited for fast analysis of the damping behavior of arbitrarily large and complex structures.

In this paper, the effective fields of a particle damper are coupled to modaly reduced Finite Element models. At first, the effective fields of the particle damper are obtained for a large excitation range, in our case experimentally using a shaker setup. The Finite Element model is reduced in size via modal reduction techniques. Then, the effective fields of the particle damper are coupled with the reduced model. The overall damping of the structure is predicted by the analytical solution of the reduced model, i.e. the particular solution of the differential equation. Thus, no time integration needs to be performed, making it very time efficient. In addition, the reduction of the eigenfrequencies of the structure, due to the coupled particle mass, is obtained. The proposed coupling procedure is validated by comparison to experimental results for a particle damped beam structure. Different influence parameters like excitation force and particle damper position are analyzed.

The paper is organized in the following way: In Sect. 2, the energy dissipation and effective mass of a single particle damper, i.e., the effective fields, are determined. Therefore, the experimental shaker setup and the evaluation methods are introduced. The obtained results in form of effective fields are discussed. In the following Sect. 3, the underlying structure, i.e., an elastic beam with free-free boundary condition, is introduced. In Sect. 4, the coupling procedure of the effective fields to a reduced model of the beam is presented. The results of the coupling procedure are compared to corresponding experiments in Sect. 5. Finally, the conclusion is given in Sect. 6.

2 Effective fields of single particle damper

To analyze the energy dissipation and effective particle mass of a particle damper, it is investigated isolated from the underlying structure. Thus, insights are made independently of the structure used later and can be applied to other systems. The particle damper is subjected to a defined horizontal vibration using a rheonomic constraint, e.g., it follows the given movement perfectly. Thereby, the energy dissipation and effective particle mass for a given excitation frequency range and excitation amplitude range are obtained. The effective particle mass describes how much the mass of the particles is coupled to the container movement. The particle container movement is given as $x_\mathrm{{c}} = X \sin (\varOmega t)$, with the amplitude X and angular frequency $\varOmega = 2 \pi f$. The corresponding container velocity and acceleration follow as $\dot{x}_\mathrm{{c}} = X \varOmega \cos (\varOmega t) = \dot{X}\cos (\varOmega t)$ and $\ddot{x}_\mathrm{{c}} = -X \varOmega ^2 \sin (\varOmega t) = -\ddot{X}\sin (\varOmega t)$. Often, the dimensionless excitation intensity $\varGamma = \ddot{X}/g$ is used, with g as gravity constant.

These investigations can be performed numerically using DEM [13] or experimentally as done in this paper. Only for small particle numbers, DEM simulations are somewhat quickly possible and enable easy parameter studies. For large particle numbers, this is very time consuming. Also, if not validated experimentally uncertainties about their accuracy remain. Experimental investigations are also often time consuming but lead to accurate results without significant uncertainties. In contrast to DEM simulations, no dependency on the particle number exists. Thus, even fine powders can be analyzed experimentally.

2.1 Experimental setup

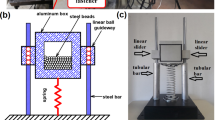
For the analysis of the effective fields, a corresponding testbed is set up [10, 11] and shown in Fig. 1.

Fig. 1

Schematic representation (left) and picture (right) of testbed for determination of effective fields of particle damper

The particle container is a aluminum cylinder with an inner radius of 2 cm and an adjustable length of $5 \pm 0.5$~ cm. To realize the adjustable length, the container and the cap of the container are equipped with a fine thread. This adjustable length of the cylinder will be used later to set up the clearance h between particle bed and container cap very precisely, see also Fig. 1-left. The mass of the container is $m_\mathrm{{con}} = 200\,\mathrm{g}$. To realize the rheonomic constraint of the container movement, the container is excited by a controlled harmonic force via a shaker perpendicular to gravity. The excitation force is controlled in such a way that the frequency and acceleration magnitude of the container stays constant. The force sensor, the accelerometers, and the control system are from Brüel & Kjaer. Two accelerometers are used. The first for the controller and the second to trigger the measurement. While the container is excited by the LDS V455 shaker, its acceleration is controlled via the LDS Comet system. Due to the impacting particles on the container walls, the acceleration signal is very noisy. In order to use this acceleration signal in the control of the excitation, this accelerometer is additionally equipped with a mechanical low-pass filter. It consists of a plastic tube which is designed in a way that its eigenfrequency is at 2.5 kHz. Hence, single particle impacts on the container walls are filtered efficiently, as their contact frequency is normally significantly above 5 kHz. Simultaneously, frequencies up to the excitation range of 1 kHz are only little influenced.

The velocity of the particle container is measured via the laser vibrometer (LV) PSV-500 from Polytec. The data acquisition of the velocity and force signals are accomplished by the Front-End of the PSV-500 with a sampling frequency of 40 kHz. The second accelerometer, seen in Fig. 1, is not equipped with a filter as it is only used for triggering the measurement.

The feasible measurement range of the experimental setup is between excitation frequencies of 40 Hz to 1 kHz and between excitation amplitudes of $0.8 \le \varGamma \le 40$. The measurement range is divided into a logarithmic grid of 420 points. Hence, 28 frequencies and 15 acceleration values are used and each combination is measured for a duration of 5 s.

For the later experiment the particle container is filled with 350 g of steel powder with a radius of 200–400 µm. The container cap is used to adjust a clearance h of 1 mm between powder bed and cap, see also Fig. 1.

2.2 Complex power

The effective fields of particle dampers are determined by the complex power method [26]. Via the measured velocity and measured excitation force of the particle container, the complex power (P) is determined as

$$\begin{aligned} P = \frac{1}{2} F^{*} \bar{V}^{*}. \end{aligned}$$

(1)

Hereby, $F^{*}$ denotes the fast Fourier transform (FFT) of the driving force signal at driving frequency and $\bar{V}^{*}$ the conjugate FFT of the velocity signal at driving frequency. The dissipated energy per radian $E_\mathrm{{diss}}$ and per cycle $\widetilde{E}_\mathrm{{diss}}$ follow from the complex power to

$$\begin{aligned} E_\mathrm{{diss}}&= \frac{1}{\varOmega } \text {Real}(P), \end{aligned}$$

(2)

$$\begin{aligned} \widetilde{E}_\mathrm{{diss}}&= 2 \pi E_\mathrm{{diss}}. \end{aligned}$$

(3)

To enable a judgment about the damper’s efficiency the reduced loss factor $\eta ^*$ is used [9, 13]. The reduced loss factor is calculated by a scaling of the dissipated energy Eq. 2 with the kinetic energy of the particle system using the mass of the particle bed $m_\mathrm{{bed}}$, i.e., the mass of all particles, to

$$\begin{aligned} \eta ^* = \frac{E_\mathrm{{diss}}}{\frac{1}{2} m_\mathrm{{bed}} |V^{*}|^2}. \end{aligned}$$

(4)

Another important quantity, the effective moving mass $M_\mathrm{{eff}}$, is determined by dividing the FFT of the excitation signal $F^{*}$ by the FFT of the acceleration signal $A^{*}$ to

$$\begin{aligned} M_\mathrm{{eff}} = \frac{F^{*}}{A^{*}} = \frac{F^{*}}{\mathrm{i} \varOmega V^{*}}, \end{aligned}$$

(5)

with i being the imaginary unit. By the effective moving mass and the known container mass $m_\mathrm{{con}}$, the effective particle mass $m_\mathrm{{eff}}$ can be obtained by $m_\mathrm{{eff}} = |M_\mathrm{{eff}} - m_\mathrm{{con}}|$ [18]. The effective particle mass describes how much mass of the particle bed is “felt” by the container, i.e., how much the mass of the granular matter is coupled to the container movement. Connecting the particle damper to a structure, this effective particle mass will lead to a reduction of the structure’s eigenfrequency.

2.3 Effective fields

Next, the experimental results using the setup presented in Sect. 2.1 are analyzed. The obtained energy dissipation field, i.e., the reduced loss factor, is shown in Fig. 2. The marks red filled circle, red filled triangle, red filled square indicate the equilibrium points of the particle damper coupled to a structure, discussed later in Sect. 5. For a better visibility reduced loss factor values above one are marked in yellow.

Fig. 2

Energy dissipation field: Reduced loss factor of 350 g steel powder inside cylindrical particle container. Red filled circle, red filled triangle, red filled square: Equilibrium points obtained from structure coupling (colour figure online)

In the plot, two regions can be observed showing high reduced loss factor values $\eta ^* \ge 1$. The first region is at excitation frequencies between 100 Hz and 200 Hz and high acceleration intensities $\varGamma > 10$. In this regime, the particle motion can be characterized as bouncing bed, see [13]. The particle bed moves together as a quasi single body and collides inelastically with the container walls. Bannerman [1] and Sack [17] derived a formula for this regime. They obtain that the particle damper works most efficient for a given clearance h of the particle damper, see Fig. 1, at a constant container stroke of

$$\begin{aligned} X_\mathrm{{opt}} = \frac{h}{\pi }. \end{aligned}$$

(6)

Applying this formula to our system one obtains $X_\mathrm{{opt}} =$~ 318 µm. This container stroke is indicated in Fig. 2 and is in great agreement with the experimentally obtained high reduced loss factor values. Using from [1, 17] the prediction for the energy dissipation per cycle at the optimal container stroke, one obtains the maximum reduced loss factor for this motion mode to be

$$\begin{aligned} \eta _\mathrm{{max}}^* = \frac{4 m_\mathrm{{bed}} \dot{X}^2}{\pi m_\mathrm{{bed}} \dot{X}^2} = \frac{4}{\pi } \approx 1.27. \end{aligned}$$

(7)

Indeed, only for very high acceleration intensities $\varGamma > 20$ reduced loss factor values close to the theoretical one are obtained. The reason for this discrepancy might be due to gravity. Bannerman [1] and Sack [17] derived and proved their formula under the condition of microgravity, i.e., $g \approx$ 0 m/${\mathrm{s}^2}$. If gravity is present, additional effects in horizontal direction like friction and rolling of particles might occur, having a significant influence if the excitation intensity is not high enough. Also, air resistance might play a role, as here much smaller particles are used as in [1, 17]. Another important property of the bouncing bed mode can be observed at very high acceleration intensities $\varGamma > 20$. The energy dissipation of this mode is sensitive to the container stroke. Starting from the high reduced loss factor values, one observes only a little decrease of the reduced loss factor to higher container strokes, see Fig. 2 ($X > X_\mathrm{{opt}}$). For lower container strokes as the optimal one ($X < X_\mathrm{{opt}}$), a high decrease of the reduced loss factor can be seen. In this area, the particle bed begins to scatter and no regular movement is visible anymore [1, 17]. This is not the case for medium acceleration intensities $4< \varGamma < 13$. Here, the loss factor is insensitive to the container stroke but not as high reduced loss factor values are achieved.

The second regime of high reduced loss factor values up to $\eta ^* = 1.8$ is at high excitation frequencies $400\,\mathrm{Hz}< f < 800\,\mathrm{Hz}$ and low to medium excitation intensities $\varGamma < 5$. It is shown in [13] using Discrete Element simulations that for bigger particles as used here the system is in a state of global fluidization in this regime. Although not as high reduced loss factor values in [13] for this regime are obtained. A similar state is assumed here, but with additional influence parameters. For instance, friction between the particles or air resistance could have a bigger effect, however, it is hard to judge from experiments.

In the area of medium acceleration intensities $\varGamma \approx 5$ and medium excitation frequencies $100\,\mathrm{Hz}< f < 500\,\mathrm{Hz}$, medium reduced loss factor values are obtained $0.5< \eta ^* < 1$. This regime connects the two areas of high reduced loss factor values. Still, this regime is classified for bigger particles as global fluidization [13]. In all other regimes, rather low reduced loss factor values are achieved $\eta ^* < 0.5$. These regimes might be classified as solid-like state, local fluidization, or decoupled [13, 27].

Note, in Fig. 2 the reduced loss factor is shown. It is coupled via Eq. 4 to the dissipated energy. Considering a fixed frequency the reduced loss factor might reduce to higher excitation intensities. This does not imply that the dissipated energy is decreasing, see Eq. 4. On the contrary, the dissipated energy is still monotonically increasing for this setting. Only very few exceptions occur on the whole measurement range.

For the later use of the particle damper connected to an underlying structure, an operation in the areas of high reduced loss factor values should be aimed. This depends on the characteristics of the particle damper as well as on the dynamics of the underlying structure. Using knowledge of previous studies [13] the characteristics of particle dampers can be influenced in a targeted manner, e.g., by the clearance, particle density, or container shape. However, in this paper, the accuracy of the coupling procedure is of most interest and not an efficient design of the particle damper to match the dynamics of the underlying structure.

The ratio of the effective particle mass to the mass of the particle bed is shown in Fig. 3. Values much smaller as one mean that the mass of the particle bed is only weakly coupled to the container movement and influence later only little the dynamics of the structure. Values of one and higher indicate a strong mass coupling instead.

Fig. 3

Effective mass field: Ratio of effective particle mass to mass of the particle bed of 350 g steel powder inside cylindrical particle container. Red filled circle, red filled triangle, red filled square: Equilibrium points obtained from structure coupling (colour figure online)

For excitation frequencies up to $f < 175$ Hz and all excitation intensities the mass ratio is high with values of $0.8< \frac{m_\mathrm{{eff}}}{m_\mathrm{{bed}}} < 1.2$. The reduced loss factor ranges from very low to very high values for this area. For excitation frequencies $f > 175$ Hz and high acceleration intensities $\varGamma > 10$ the mass ratio is very low. In this area, the reduced loss factor is also low and might be characterized by a decoupling of the particle bed from the container [13]. For excitation frequencies $f > 175$ Hz and low excitation intensities $\varGamma < 2.5$ very high mass ratio values up to two are obtained. The corresponding reduced loss factor is also high in this regime. Thus, a high reduced loss factor causes the mass ratio to be high, but vice versa is not necessarily true. This can be explained as only if the particles interact a lot with the container a lot of energy can possibly dissipate. Thus, the effective mass is high, but the dissipated energy might not be high. For instance, this would be the case for a very tight particle packing. On the other hand, if the particles have only little interaction with the container walls, the energy dissipation and effective mass are low.

It should be noted that here only one specific parameter combination is used for the particle damper. Changing these might have an significant influence on the effective fields. Here, these parameters were chosen on knowledge of previous studies, see [13]. However, an optimization of the particle damper itself is above the scope of this paper.

3 Testing structure and experimental setup

In the next step, the particle container is coupled to an underlying structure. The previous experimentally determined effective fields are used to predict the overall damping of the system and the influence of the effective particle mass on the eigenfrequencies of the vibrating structure. This coupling will provide a useful tool to evaluate quickly the efficiency of a particle damper on a structure, facilitating easier particle damper design.

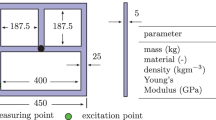
As an application example, a beam-like structure is used. A picture and a schematic representation of the beam and testbed are shown in Fig. 4. As mentioned, the experiments are only used for validation purposes.

Fig. 4

Schematic representation (top) and picture (bottom) of the testbed to determine the overall damping behavior of the particle damper

The testbed consists of the flexible beam with a hollow profile supported by three soft cables, thus free-free boundary conditions can be assumed. The beam parameters are listed in Table 1. The total weight of the 1.8 m long beam and its mountings is 6.6 kg including the empty particle container. The particle mass of 350 g is thus about 5 % of the total system mass.

Table 1 Parameters of the beam

The beam is exited in the transverse direction with a variable force by a shaker at its free end at $x = 5$ cm. A sine sweep excitation is used with frequencies between 15 and 600 Hz in 300 s. Thus, for this slow frequency change, a stationary state of the system can be assumed for every instant of time. The measurement is windowed using a hanning window. The windows are combined using a peak hold algorithm. The sampling frequency is 12.8 kHz. The shaker and its power amplifier are from Brüel & Kjaer, namely the Modal Exciter Type 4824 and Power Amplifier Type 2719. As only the input current to the shaker is controlled and not the input force, 1 kg of additional weight is placed at the excitation position. This reduces the values of the shape functions at the excitation point and thus the force distortion. The excitation force is measured by the force transducer 8230-001 by Brüel & Kjaer and the velocity profile of the beam is measured by the laser vibrometer PSV-500 from Polytec and analyzed with the software BK Connect.

The particle container can be placed at any desired position on the beam. For the investigated analysis in this paper, the container is placed at first at the free, not excited end at $x = 1.765$ m, as shown in Fig. 4. Later on, the position of the particle damper is varied.

4 Damping prediction using effective fields

To predict in the design process the overall damping of the system with the particle damper coupled to it, an accurate model of the structure is necessary. Thus, the beam is modeled using the Finite Element Method (FEM) [25]. It is discretized with 90 Euler-Bernoulli beam elements. The support, the force sensor and its mounting, and the particle container are included as point masses. A free–free support is chosen as the boundary condition. Setting up the equation of motion leads to a system of the form

$$\begin{aligned} {\varvec{M}}\ddot{{\varvec{z}}}+ {\varvec{K}}{\varvec{z}}&= {\varvec{f}}. \end{aligned}$$

(8)

With ${\varvec{z}}\in \mathbb {R}^{n}$ being the $n-$nodal displacements and ${\varvec{f}}\in \mathbb {R}^{n}$ being the vector of applied forces. Here, the applied forces consist of the shaker excitation and the forces by the particle damper. The matrices ${\varvec{M}}\in \mathbb {R}^{n \times n}$ and ${\varvec{K}}\in \mathbb {R}^{n \times n}$ are the mass and stiffness matrices, respectively.

To reduce the FEM model in size a modal reduction is performed. This is done by transforming Eq. 8 to modal coordinates ${\varvec{q}}\in \mathbb {R}^{m}$ and neglecting certain modes such that $m < n$. Thus the computational cost can be reduced significantly and allow also the efficient use of more complex structures. By solving the eigenvalue problem $({\varvec{K}}- \omega _k^2 {\varvec{M}}) \bar{{\varvec{\phi }}}^{(k)} = \mathbf{0}$ the reduced model can be stated as

$$\begin{aligned} {\varvec{E}}\ddot{{\varvec{q}}}+ {\varvec{D}}\dot{{\varvec{q}}}+ {\varvec{\varOmega }}{\varvec{q}}&= {\varvec{\varPhi }}^\mathrm{{T}} {\varvec{f}}, \end{aligned}$$

(9)

$$\begin{aligned} y(x)&= {\varvec{\varPhi }}(x) {\varvec{q}}. \end{aligned}$$

(10)

Hereby, six modes are included in the reduction. These are the two rigid body modes (translation in $y-$direction, rotation around vertical axis) and the first four elastic bending modes. The matrix ${\varvec{E}}$ denotes the identity matrix. The structural damping, i.e., without particle damper, is included in Eq. 9 using Rayleigh damping and results in ${\varvec{D}}= \alpha {\varvec{E}}+ \beta {\varvec{\varOmega }}$ with $\alpha$ and $\beta$ based on experimental results, see [12]. The matrix ${\varvec{\varOmega }}$ contains the the squared eigenfrequencies $\omega _k^2$ of the system on its diagonal and ${\varvec{\varPhi }}= [{\varvec{\phi }}^{(1)}, {\varvec{\phi }}^{(2)}, \ldots ,{\varvec{\phi }}^{(m)}]$ contains corresponding the mass normalized shape functions ${\varvec{\phi }}^{(k)}$. The Eq. 10 describes the output displacement y(x) at position x of the beam.

In the following, the damping of each mode excited in its eigenfrequency is predicted. Since Eq. 9 is a decoupled differential equation, a single mode is considered now. This is justified, as the deformation of the beam is dominated by the mode excited in its eigenfrequency. The vector of applied forces ${\varvec{f}}$ is replaced by the shaker excitation $F \cos (\varOmega t)$, with F being the force amplitude and $\varOmega$ the angular frequency, and the forces introduced by the particle damper. The particle damper forces consist of the additional inertia term due to the effective particle mass $m_\mathrm{{eff}}$ and the damping forces due to the energy dissipation expressed as effective viscous damping $d_\mathrm{{eff}}$, see also Fig. 4. Thus, one obtains for the $k-$th mode

$$\begin{aligned}&\ddot{q}_k + D_k \dot{q}_k + \omega _k^2 q_k = \phi _\mathrm{{sh}}^{(k)} F \cos (\varOmega t) - \nonumber \\&\quad \phi _\mathrm{{pd}}^{(k)} \left( m_\mathrm{{eff}} (\varOmega ,\varGamma ) \ddot{y}_\mathrm{{pd}} + d_\mathrm{{eff}} (\varOmega ,\varGamma ) \dot{y}_\mathrm{{pd}} \right) . \end{aligned}$$

(11)

Hereby, $\phi _\mathrm{{sh}}^{(k)}$ denotes the shape function value of the $k-$th eigenmode at the shaker excitation position and $\phi _\mathrm{{pd}}^{(k)}$ at the particle damper position, respectively. The particle damper state is described by $y_\mathrm{{pd}} = \phi _\mathrm{{pd}}^{(k)} q_k$. Inserting the derivatives of this relationship into Eq. 11 and rewriting it, one obtains

$$\begin{aligned}&\underbrace{\left( 1 + \phi _\mathrm{{pd}}^{(k)^2} m_\mathrm{{eff}} (\varOmega ,\varGamma ) \right) }_{m} \ddot{q}_k + \underbrace{\left( D_k + \phi _\mathrm{{pd}}^{(k)^2} d_\mathrm{{eff}} (\varOmega ,\varGamma ) \right) }_{d} \dot{q}_k \nonumber \\&\quad + \underbrace{\omega _k^2}_{k} q_k =\underbrace{\phi _\mathrm{{sh}}^{(k)} F}_{R} \cos (\varOmega t). \end{aligned}$$

(12)

Equation (12) can thus also be written as

$$\begin{aligned} m \ddot{q}_k + d \dot{q}_k + k q_k = R \cos (\varOmega t). \end{aligned}$$

(13)

To solve Eq. 13 the effective particle mass and the effective viscous damping are needed. For excitation of constant frequency and force amplitude, the system will reach a stationary state, after the transients vanish. The elastic coordinate and thus the particle damper is then vibrating with the excitation frequency $\varOmega$. The effective particle mass can thus directly be determined from Fig. 3 as $m_\mathrm{{eff}} = m_\mathrm{{eff}} (\varOmega , \varGamma )$. The effective viscous damping coefficient in a stationary state is calculated by the dissipated energy per cycle and the excitation conditions [19]. The effective viscous damping coefficient follows to

$$\begin{aligned} d_\mathrm{{eff}} = \frac{\widetilde{E}_\mathrm{{diss}}(\varOmega , \varGamma )}{\pi \varOmega X^2}, \end{aligned}$$

(14)

with X being the vibration amplitude of the particle damper. The dissipated energy per cycle $\widetilde{E}_\mathrm{{diss}}$ is obtained from Fig. 2 using Eq. 4.

The effective eigenfrequency, i.e., the undamped eigenfrequency of the system influenced by the particle mass, follows to

$$\begin{aligned} \omega _{k,\mathrm {eff}} = \sqrt{\frac{k}{m}} = \omega _k \sqrt{\frac{1}{1 + \phi _\mathrm{{pd}}^{(k)^2} m_\mathrm{{eff}}}}. \end{aligned}$$

(15)

The elastic coordinate will have its maximum amplitude at an excitation frequency of $\varOmega = \omega _{k,\mathrm {eff}} \sqrt{1-2\zeta _k^2}$, with $\zeta _k$ being the damping ratio [19]. For $\zeta _k<< 1$ it follows $\varOmega \approx \omega _{k,\mathrm {eff}}$. Using the analytical solution of Eq. 13, i.e., $q_k = Q_k \cos (\varOmega t - \psi)$, under the condition of a stationary state and an excitation in the effective eigenfrequency of the undamped system, i.e., $\varOmega = \omega _{k,\mathrm {eff}}$, the amplitude of the elastic coordinate $Q_k$ and the damping ratio $\zeta _k$ follow to

$$\begin{aligned} \zeta _k&= \frac{d}{2 m \omega _{k,\mathrm {eff}}}, \end{aligned}$$

(16)

$$\begin{aligned} Q_k&= \frac{R}{2 m \zeta _k \omega _{k,\mathrm {eff}}^2}. \end{aligned}$$

(17)

Finally, the vibration amplitude of the particle damper results in $X = \phi _\mathrm{{pd}}^{(k)} Q_k$ and its dimensionless acceleration in $\varGamma = \phi _\mathrm{{pd}}^{(k)} \ddot{Q}_k / g$. As Eq. 14–Eq. 17 are depending on each other via the effective fields, a fixed point iteration scheme is used to solve these equations, see Fig. 5. Since the effective fields are determined at discrete excitation frequencies and amplitudes, a linear interpolation is performed to obtain interim values. For vibration amplitudes above the measurement range, linear extrapolation is used. In the performed studies, the iteration scheme converges in general in five to ten iterations. Only if the equilibrium point has a vibration intensity above the measurement range, the maximum iteration counter of 100 is reached.

Fig. 5

Iteration scheme to find equilibrium state of structure coupled to particle damper

The system reaches a stationary state if the input energy is equal to the dissipated energy. While the input energy is increasing linearly with the vibration intensity, the energy dissipation of a perfect viscous damper with a constant coefficient is increasing quadratic. Thus, only one unique equilibrium point exists, see Fig. 6a. For particle dampers instead, the viscous damping coefficient is not constant. Thus, the question arises if two or more equilibrium points are possible. Multiple equilibrium points only exist if the dissipated energy falls below the input energy after the first equilibrium point is reached, as indicated in Fig. 6b. Then, the vibration amplitude would increase until the next equilibrium is reached. For particle dampers, a constant viscous damper coefficient $d_\mathrm{{eff}}$ is equivalent to a constant reduced loss factor, see Eqs. 4 and 14, if the excitation frequency is not changing. From Eqs. 4 and 14 it follows that a second equilibrium point is only possible, if the reduced loss factor is sharply decreasing to higher excitation intensities. This is only rarely the case for the utilized damper, see Fig. 2. Thus, it is not expected that multiple equilibrium points exist for this system.

Fig. 6

Input energy and dissipation energy progression for a constant viscous damper coefficient (a) and for multiple equilibrium points (b)

Although the above procedure applies to arbitrary large structures, some inaccuracies might occur. It is assumed that the shape functions of the underlying structure are unaffected by the additional particle mass. If the additional particle mass is getting to high a noticeable reduction of the shape function value at the particle damper position will be seen. This results in a reduced container acceleration and thus in a reduced energy dissipation and damping ratio. Alternatively, the shape functions could be recalculated in every iteration of the fixed point scheme. Though, this can be very time consuming for large structures. Also, it is assumed that the particle container is performing a perfect translational movement. An additional rotation of the particle container is not represented. Last, a unique solution of the fixed point iteration scheme is assumed, i.e., there exists only one point where the input energy is equal to the dissipated energy. If this is not the case, only one equilibrium point is found.

Using a fully coupled FEM–DEM simulation one could reduce the above mentioned inaccuracies. Still, some inaccuracies remain [12] and much higher simulation times are necessary. The accuracy and speed of simulation of such fine powder as used here are also questionable. Thus, the presented damping calculation does not seek for an exact calculation. Rather, a first good qualitative approximation of the damping shall be accomplished, giving an engineer a first design tool at an already early state of the design process.

4.1 Valuation of efficiency

The damping prediction scheme, shown in Fig. 5, is used to predict the damping of the structure coupled to the particle damper. However, no information is gained if the particle damper works efficient related to the used particle mass. Here, it is assumed that the particle damper can be considered as efficient if its reduced loss factor is above one, i.e., if the dissipated energy per cycle of the damper is $\widetilde{E}_\mathrm{{diss}} \ge \pi m_\mathrm{{bed}} \dot{X}^2$. Using this assumption, one can calculated the damping ratio of the structure one would obtain under this requirement. Inserting $\widetilde{E}_\mathrm{{diss}} = \pi m_\mathrm{{bed}} \dot{X}^2$ into Eq. 16 and neglecting the structural damping, i.e., $D_k = 0$, one can solve for the resulting damping ratio. As the effective mass of the particle damper is not known, it is approximated by $m_\mathrm{{eff}} \approx m_\mathrm{{bed}}$. This is justified, as a high reduced loss factor also results in a high effective mass, as seen from Figs. 2 and 3. This results in the damping ratio of the whole system under the condition that the particle damper exhibits a reduced loss factor of one, to

$$\begin{aligned} \zeta _{k,\eta _1^*} = \frac{\phi _\mathrm{{pd}}^{(k)^2} d_\mathrm{{eff}}}{2 m \omega _{k,\mathrm {eff}}} = \frac{\phi _\mathrm{{pd}}^{(k)^2} m_\mathrm{{bed}}}{2 \left( 1 + \phi _\mathrm{{pd}}^{(k)^2} m_\mathrm{{eff}} \right) } \approx \frac{\phi _\mathrm{{pd}}^{(k)^2} m_\mathrm{{bed}}}{2 \left( 1 + \phi _\mathrm{{pd}}^{(k)^2} m_\mathrm{{bed}} \right) }. \end{aligned}$$

(18)

Thus, one can judge the efficiency of the particle damper just by comparing the experimental measured damping ratio to this theoretical value. This formula could also be used for quick testing of possible mounting points of the particle damper. Changing the mounting points means to change $\phi _\mathrm{{pd}}^{(k)}$.

5 Results and comparison of damping prediction

Next, experiments on the structure with added particle damper are performed. Thus, the damping ratio of the structure is determined. This damping ratio is then compared to the analytical approach, described in Sect. 4 and shown in Fig. 5. For this, the effective fields of the pure particle damper, see Figs. 2 and 3, are coupled to a modal reduced model of the structure, e.g., Eq. 9. As mentioned before, the effective fields of the pure particle damper can be determined experimentally using a shaker setup as done here and shown in Fig. 1, or numerically using DEM [13]. The later approach makes the whole coupling approach independent of experiments.

At first, the numerical model of the beam is validated, e.g., Eq. 9. Thus, the numerically obtained eigenfrequencies of the system without filled particle damper, and the corresponding frequency response function (FRF) are compared to measurements. The output node for the FRF is at the particle container position. As the velocity of the node is measured, the FRF’s mobility is plotted. For the excited frequency range four eigenmodes are determined between 51.7 Hz and 513 Hz. The results are shown in Table 2 and Fig. 7.

Table 2 Eigenfrequencies of undamped system

Fig. 7

Frequency response function of undamped system

The eigenfrequencies fit very well. The biggest difference occurs for the fourth mode, i.e., at 513 Hz, with a difference of 4.1 %. A good agreement is also observed within the FRF. All modes are well recognizable and only slightly damped, thus the additional damping by the particle damper will be observed easily. The resulting four flexible shape functions obtained by the modal reduction are shown in Fig. 8.

Fig. 8

Mode shapes of beam. The black dashed lines indicate the position of the shaker (left) and the initial particle damper position (right)

Especially, at the particle damper position of $x = 1.765$ m, high shape function amplitudes are achieved. This is important, as the resulting higher container acceleration normally also leads to a higher energy dissipation of the particle damper. At the shaker excitation position of $x = 4$ cm, comparable low shape function amplitudes are observed. This reduces the force distortion, as mentioned before.

As the reduced FEM model of the system is verified, it is now coupled with the effective fields of the particle damper as described in Sect. 4. The beam is excited with a current of 1 A which equals a force amplitude of about 26 N. The obtained damping ratios are shown in Fig. 9. The legend entry “undamped” corresponds to the experimentally obtained damping without particles, while the entry “experiment” the actual measured damping by the particle damper denotes. The damping prediction by the iterative scheme, see Fig. 5, is labeled with “iterative”. The solution of Eq. 18 is denoted by $\zeta _{k,\eta _1^*}$ and describes the damping in case of a reduced loss factor of one. The last entry “full FEM” describes the coupling results obtained by a transient FEM beam model coupled with the effective fields as proposed in [23]. In addition, in Figs. 2 and 3 the equilibrium points of the particle damper are marked by red filled circle, obtained by solving the iterative scheme. Furthermore, in Table 3 the reduction of the eigenfrequencies is listed, which occurs due to the particle mass coupling.

Fig. 9

Damping ratios of system with $F = 26\,\mathrm{N}$

Table 3 Relative reduction of eigenfrequencies of undamped to damped system

The damping of the first eigenmode is only a little bit increased compared to the undamped cased. Although the damping is six times higher, the absolute value is still small. Its value is only a fraction of $\zeta _{1,\eta _1^*}$ and thus far away from being considered as efficient. In Figs. 2 and 3 no equilibrium points are marked, as the resulting acceleration of the particle container is outside the measurement range. The damping prediction by the iterative scheme is still good, as outside the measurement range linear interpolated values are taken. Although the dissipated energy is low, the effective particle mass is high. Using Eq. 15 and the measured reduced eigenfrequency it follows to $m_\mathrm{{eff}} = 0.85m_\mathrm{{bed}}$. As result, the eigenfrequency reduces about 4.6 %. Similar, this reduction of the eigenfrequency is approximated numerically with 3.7 %.

The second and third modes show a very similar damping behavior. The relative and absolute damping values compared to the undamped case are greatly increased. Damping ratios up to 1.8 % are achieved in the experiments. The damping prediction by the iterative scheme is about 35 % off and could thus be considered as acceptable for qualitative assessment. The equilibrium points of Figs. 2 and 3 lie in the measurement range. The experimental damping values reach about 50 % of $\zeta _{k,\eta _1^*}$. Thus, the damping might already be considered as close to efficient. The reduction of the eigenfrequencies differ with 1.3 % and 0.8 %. Thus, these are only roughly approximated.

The fourth mode shows the strongest damping with 2 %. The damping ratio is slightly above $\zeta _{4,\eta _1^*}$ and thus the damper can be considered as very efficient. The damping prediction by the iterative scheme is 28 % higher. The equilibrium point in Fig. 2 is in the area of the highest reduced loss factor values. The eigenfrequency reduces 5.7 % and thus the most of all modes. The calculation of the effective eigenfrequency by Eq. 15 is a little bit off with a difference of 2 % to the experimental result.

Overall, a first good approximation of the damping values and effective eigenfrequencies is accomplished. The evaluation of the iterative scheme is done within seconds and no need for computational inefficient FEM-DEM simulations are necessary. It is shown that it is possible to damp with a single damper multiple different eigenfrequencies at an almost constant efficient level. Damping ratios up to 2 % are achieved with a particle mass of 5 % of the systems mass. To check in the next step the robustness of the approach, the excitation force amplitude is varied. In Fig. 10 the damping values for $F = 13\,\mathrm{N}$ and $F = 52\,\mathrm{N}$ are shown. In Figs. 2 and 3 the equilibrium points are marked for $F = 13\,\mathrm{N}$ (red filled triangle) and $F = 52\,\mathrm{N}$ (red filled square). For all modes and excitations, except for one case, a first good approximation of the damping ratio is achieved again using the iterative scheme. Especially, for the lower excitation level, see Fig. 10a, high damping ratios up to 2.5 % are obtained. For the higher excitation, see Fig. 10b, the damping ratios are reducing with values of about 1 %. This is reasonable as the equilibrium points in Fig. 2 for the higher excitation lie in areas of low reduced loss factor values. This can especially be observed for mode three and four.

Fig. 10

Damping ratios of system for different excitation intensities for the experiment (blue filled rectangle) and iterative scheme (red filled rectangle) (colour figure online)

For the second mode at high excitation level, a very high damping ratio is calculated by the iterative scheme, although in the experiment a small value is measured. As seen in Fig. 2, the particle damper shows a high reduced loss factor for the second mode on a large excitation range. Thus, inaccuracies by calculating the vibration intensity of the particle container are probably not the reason for the damping discrepancies. However, the calculated equilibrium point reaches the state of bouncing bed. The particle container performs an additional rotation, due to the form of the shape function of the beam, see Fig. 8. This is not represented by the damper model. In the experiments, used for derivation of the damper model a pure linear motion exists. Thus, it is assumed that this effect destroys the bouncing bed motion mode, as will be proven later. This results in much lower energy dissipation and thus in reduced damping in the real system.

Besides the iterative scheme, a coupling of the effective fields with a full FEM model of the beam is implemented. This is similar to the approach of Trigui [23]. Likewise, to the experiments, a sine sweep excitation is used. The beam’s equation of motion Eq. 8 is integrated using ode15s of Matlab. The modal parameters are extracted from the resulting FRF with the function modalfit using the Least-Squares Complex Exponential Method [2]. The results are shown additionally in Fig. 9 and labeled with “full FEM”. Much higher simulation times, hours instead of seconds, are necessary for obtaining these results. The resulting effective eigenfrequencies and damping ratios are a little bit closer to the experimental measurements compared to the iterative scheme. However, the results are very sensitive to different simulation parameters like sweep rate, interpolation method for effective fields, or modal extraction settings. Thus, great care has to be taken, choosing these parameters. This also shows the computational advantage of the presented iterative scheme and the negligible influence due to the changing shape functions of the reduced model as uncertainties of the full FEM approach almost outweigh these.

5.1 Influence of particle damper position

As the rotation of the particle container seems to have a big influence on the damping, it is analyzed next what happens if no container rotation occurs. Thus, the particle damper is placed for every eigenmode at a corresponding extrema of the shape function with zero slope, i.e., at $x = 0.9$ m for eigenmode one and three, see Fig. 8. The so determined damping ratios are shown in Fig. 11 for excitations of $F = 13\,\mathrm{N}$, 26 N, and 52 N, respectively.

Fig. 11

Damping ratios of system with particle damper placed at extrema of the shape function with zero slope for different excitation intensities for experiment (blue filled rectangle) and iterative scheme (red filled rectangle) (colour figure online)

From Fig. 11, two major aspects can be seen. First, the differences between experimental results and damping prediction by the iteration scheme are reasonably small for almost every excitation case and eigenmode. Except for mode three and four of the high excitation case, see Fig. 11c, the damping approximation can be considered as good. This is reasonable, as the particle damper performs only a translational movement as supposed in the iterative scheme. Even the second eigenmode is greatly damped at high excitation force amplitudes, see Fig. 11c compared to Fig. 10b. This also proves the above assumption that the additional container rotation destroys the bouncing bed motion mode.

Second, even higher damping ratios are achieved compared to the first particle damper position, see Figs. 9 and 10. This can be explained by the fact that the particle damper is now mounted directly at an extremum of the corresponding shape functions. At the position before, lower shape function values were realized. Note, the particle damper was mounted before at $x = 1.765$ m and not at the very end of the beam, which is due to the mounting plate. In this area the shape functions are showing a high gradient, resulting in lower shape function values as for the extrema with zero slope. On the other hand, if the particle damper is placed at the extrema with zero slope, the other shape functions might exhibit a node or a very low value at this position. This leads to extremely low damping ratios for these eigenmodes.

As consequence, the position of the particle damper has to be chosen carefully here but also for real applications. It depends on a variety of parameters. The magnitude of the shape function plays an important role. A higher value leads normally to higher damping. Placing the particle damper at a position where multiple shape functions have a high value, enables the efficient damping of multiple eigenmodes. Though, additional rotation of the particle container might reduce the energy dissipation significant. Also, the damping prediction by the iterative scheme gets worse since it does not include rotation. This trade-off has to be done for every application individually. As particle dampers are rather simple devices, also a placement of multiple units at different locations should be considered. This is still part of ongoing research.

6 Conclusion

To analyze particle dampers two major approaches exist. Either the energy dissipation inside the particle damper is analyzed directly or the particle damper is coupled to a structure and the overall damping ratio is determined. In this paper, an approach is presented to couple both methods. The approach is computational very efficient, yields first qualitative damping ratios, and allows the calculation of the reduction of eigenfrequencies due to the temporary coupled particle mass.

At first, the energy dissipation of the particle damper is analyzed for a wide excitation frequency range and intensity range using the complex power method. By calculating the reduced loss factor a judgment about the damper’s efficiency is possible. Also, the effective particle mass is achieved. It describes how much mass of the particles is felt by the underlying structure. In general, this evaluation on the damper level can be performed numerically or experimentally. Here, the experimental approach was taken. Second, the damper is coupled to a test structure. The structure is modeled using the Finite Element Method and reduced in size via modal reduction. This allows the easy inclusion of different complex bodies. To predict the overall damping the effective fields of the damper, i.e., the energy dissipation and effective particle mass fields, are coupled to the reduced model yielding an iterative process which can be evaluated quickly. Thus, a first approximation of the damping ratio is obtained. This method is verified experimentally.

Based on these coupled models various investigations have been conducted to show its qualitative accuracy and efficiency. While a perfect quantitative fit is not obtained, so gives the qualitative results useful guidelines during the particle damper design process. The position of the particle damper plays an important role. Placing the particle damper at an extremum with zero slope of the shape function a good agreement between damping prediction and the experimental result is achieved. By placing the damper at a position where the shape function exhibits an additional rotation, the damping prediction is still acceptable. Although, in some cases this greatly reduces the energy dissipation of the damper, i.e., for the bouncing bed motion mode. Even multiple eigenmodes can be damped efficiently if the particle damper is placed at a position, where these modes have a high shape function value.