1 Introduction

The macroscopic mechanical behaviour of granular media materials is related to the microscopic characteristics of particle contact. The constitutive law for rolling resistance has a significant influence on the behaviour of granular systems simulated using the discrete element method. Bardet and Huang [1] are probably the first to introduce rotational constraints into the discrete element model. They observed that the simulation results without contact couple between the particles are outside the range of theoretical values. They consider that the contact couple may play an important role. They also demonstrated that the internal friction angle of the particle system increases when the particle rolling is fixed. Morgan [2] introduced rotational damping into a discrete element model to simulate a fault gouge. The results were close to laboratory estimates. Sakaguchi et al. [3] introduced the concept of “rolling friction” into the discrete element model and studied the plugging of granular flow in the silo discharge through experiments and numerical simulations. They observed that an arch formed by circular disks was unstable in the DEM model without rolling friction. The DEM model with rolling friction that was introduced effectively formed arches, which was observed in the physical experiment. Iwashita and Oda [4] observed large voids and high rotational gradients in a shear band experiment. However, the numerical simulation without considering rolling resistance between particles could not obtain a similar result. They determined the rolling resistance as the cause for arching. Furthermore, the rolling resistance facilitates the formation of large voids in physical experiments. To obtain numerical results close to the experimental results, they introduced rolling resistance to the conventional discrete element method and proposed a modified discrete element method (MDEM). The rolling resistance model is composed of elastic rotational springs, a rotational dash pot, a no-tensile joint, and a rotational slider. Using this model, they successfully predicted the dilatancy behaviour of the shear band, which is similar to the experimental results for natural soil. The rolling stiffness was assumed to be proportional to the contact normal force in Iwashita and Oda [4]. However, it was subsequently modified to be proportional to both contact normal force and overlap width of the contacting particles [5]. Many researchers have proposed a series of rolling resistance models inspired by Iwashita and Oda’s work [6,7,8,9,11]. Jiang et al. [12] observed that most of the rolling resistance parameters in MDEM need to be determined by trial and error. Based on a theoretical analysis, they proposed a new definition of pure sliding and pure rolling, and introduced a “shape parameter \(\delta\)” in the rolling resistance model. It is a dimensionless parameter that is equal to the ratio of the width of the particle contact surface to its radius. MDEM is an effective method for establishing a contact constitutive model to describe the resistance behaviour between particles.

Although the rolling resistance discrete element contact constitutive model is being continuously improved by researchers, is difficult to determine the constitutive model parameters of rolling resistance. A good experimental method to identify a significant number of parameters is unavailable. There are two reasons for this. One is that many factors influence rolling resistance, and the mechanism of rolling resistance is not clear. At present, the more widely accepted theory is that rolling resistance is affected by micro-slip on the contact surface, elastic hysteresis of the material, particle irregular shape, and contact surface adhesion [13]. The other reason is that the rolling resistance is significantly smaller than the other resistances, and it is generally accompanied by sliding resistance during the rolling process. It is difficult to experimentally determine the mechanical behaviour under pure rolling resistance. Therefore, most of the rolling resistance parameters in the DEM model are determined by trial and error.

We observed a phenomenon wherein circular particles swung back and forth in the process of free rolling. It was close to the pure rolling state, and the main restoring force was rolling resistance. An optical experimental platform with a laser displacement sensor for detecting marginal rolling of particles was designed. The time-history curves of the rolling angular displacement of cylindrical samples of various sizes were obtained using this experimental platform. The cylindrical samples were made of rubber and aluminum. A method for identifying the constitutive parameters, rotational stiffness, and rotational damping coefficients in the MDEM model is proposed based on the mechanical theory of the rolling motion of particles and the experimental results. We applied the identified parameters to the MDEM model to simulate the experimental process. The results were consistent with the experimental phenomena.

2 Parameters of rolling resistance in MDEM

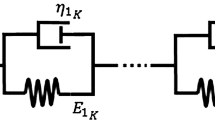
The constitutive model of contact particles in the MDEM (Fig. 1) can be divided into three components, which are in the normal, tangential, and rolling directions. The normal contact model is composed of normal springs, dashpots, and no-tension joints. The springs are used to provide an elastic restoring force, and the dashpots are used to provide viscous resistance. The contact model in the tangential and rolling directions is similar to the model in the normal direction. All these have springs that reflect elastic behaviour and dashpots that provide viscous resistance. In addition, the model in the tangential direction has a slider that reflects the resistance caused by sliding friction. The model in the rolling direction has a rotational slider that reflects the resistance caused by the rolling friction. Jun Ai et al. [13] compared the simulation results of different rolling resistance models and observed that the MDEM model is applicable to most discrete element simulation problems.

In the MDEM, the contact rolling resistance can be described as

$$\begin{aligned} M=\text{min}(K_{r}\cdot \theta +c_{r}\cdot {\dot{\theta }}, \mu _{r}\cdot F_{n}) \end{aligned}$$
(1)

where \(K_{r}\) is the rolling stiffness coefficient, \(c_{r}\) is the rolling damping coefficient, and \(\mu _{r}\) is the critical rolling coefficient.

\(\mu _{r}\) expresses the critical state wherein the particles can roll forward continuously. It can be determined conveniently by physical tests. However, it is highly difficult to determine \(K_{r}\) and \(c_{r}\) directly by experiment. \(K_{r}\) is generally determined from the tangential and normal stiffness by multiplying these with a proportionality coefficient [14]. Although the tangential and normal stiffness can be measured conveniently by physical experiments, the proportional coefficient is determined by trial and error. Certain experimental methods for detecting rolling resistance directly have been studied [15–18]. The rolling resistance is determined mainly based on the principle of energy conservation and the theory of static equilibrium. However, in these experimental methods, the rolling behaviour of particles is affected by rolling resistance as well as by other resistances that need to be considered. To measure the rolling resistance accurately using an experimental method, a rolling state involving only rolling resistance should be determined. We observed that a free rolling particle swung back and forth before it stopped. This is close to the pure rolling state, in which other resistances can be omitted. We suppose that the rolling resistance can be determined accurately from the swing curve of a rolling particle, and the curve can be measured using an experimental system.

3 Experimental design and method to identify parameters

3.1 Optical experimental system

A schematic of the rolling experiment of cylindrical samples is shown in Fig. 2a. An optical experimental device for detecting micro-displacements was developed. The displacement was measured by the following process: A cylindrical sample was placed on an optical experimental platform. Several contact points were selected at different locations on the circular surface of the cylindrical sample. The position of each contact point was adjusted to ensure that the sample was within the measurement range of the laser displacement sensor. We switched on the power of the experimental device, and the laser displacement sensor started to work. The laser spot position was set on the measuring point of the sample. The cylindrical sample was loaded with a marginal shock by the air impactor to swing back and forth. Meanwhile, a date acquisition terminal was used to obtain the position information of the cylindrical sample. When the entire data acquisition was completed, the displacement curve of the measured sample could be obtained by the data acquisition terminal. Next, a series of experiments were carried out in different cylindrical sample zones with various diameters, as shown in Fig. 2b and c. The displacement curves were obtained for analysis in each back and forth swing process.

3.2 Particle swing and parameter identification method

The experimental phenomenon is as follows. When circular particles cannot roll forward, these swing back and forth before stopping. The amplitude of the swing decreases gradually to zero. The back and forth swing process of particles is affected by the elastic restoring force. The swing frequency is reflected only by the rolling stiffness and rotational inertia of the particles. Because the rotational inertia can be measured conveniently, \(K_{r}\) can be determined by the swing frequency. The attenuation of the amplitude reflects the energy dissipation during the rolling process, and \(c_{r}\) can be determined by the attenuation of the amplitude of the swing curve. Therefore, \(K_{r}\) and \(c_{r}\) can be identified directly by detecting the swing displacement curve before the particle stops. Meanwhile, the influence of other resistance components on the measurement of rolling resistance parameters can be eliminated.

Because the displacement of the particle swing is highly marginal before it stops, we adopted a laser displacement sensor with high precision to measure the marginal displacement. An optical experimental device for detecting micro-displacements was established to measure the swing displacement time history data of the circular particles. The swing displacement frequency and attenuation information were obtained using an optical experimental device. Thereby, the parameters of the rolling resistance model were identified.

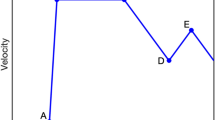
After impact loading, the circular particles attain a state of free rolling in the horizontal direction. The rolling process of a particle before it stops has two phases (Fig. 3a). In the first phase, it rolls forward and gradually slows down owing to the resistance. In the second phase, it cannot continue rolling forward and swings back and forth before it stops. The time-history curve of swing (Fig. 3b) could be obtained using an optical experimental device. This phenomenon was experimentally observed in this study. This back and forth swing is similar to an elastic restoring force, which can be produced only by the elastic rolling resistance. The rolling resistance of the particles can be expressed as

$$\begin{aligned} M=K_{r}\cdot \theta +c_{r}\cdot {\dot{\theta }} \end{aligned}$$
(2)

In the back and forth swing process of the circular particle, the horizontal direction of motion is considered as the x-direction, and the rotational direction of motion is considered as the z-direction. The equilibrium equations for the x- and z-directions can be expressed as Eqs.(3) and (4):

$$\begin{aligned}&\sum F_{x}=0: m\cdot \ddot{x}+c_{s}\cdot {\dot{x}}+K_{s}\cdot x=0 \end{aligned}$$
(3)
$$\begin{aligned}&\sum M_{z}=0: J\cdot \ddot{\theta }+c_{r}\cdot \dot{\theta }+K_{r}\cdot \theta =0 \end{aligned}$$
(4)

When there is no tangential deformation or relative sliding on the contact surface, the tangential damping coefficient \(c_{s}=0\), and the tangential stiffness coefficient \(k_{s}=0\). The transverse displacement x can be expressed as \(x=\theta \cdot R\). The equilibrium equation for the free rolling of particles on a horizontal surface can be expressed as Eqs. (5) and (6).

$$\begin{aligned}&\sum F_{x}\cdot R+\sum M_{z}=0 \end{aligned}$$
(5)
$$\begin{aligned}&(m\cdot R^{2}+J)\cdot \ddot{\theta }+c_{r}\cdot \dot{\theta }+K_{r}\cdot \theta =0 \end{aligned}$$
(6)

If the rotational inertia of a circular particle to the center is J , the equivalent rotational inertia \(I_{g}\) of the particle in the state of the horizontal back and forth swing can be expressed as Eq.(7). Thus, the equilibrium in Eq. (6) can be expressed using Eq. (8). In addition, the solution of Eq.(8) can be expressed as Eq. (9):

$$\begin{aligned}&I_{g}=m\cdot R^2+J \end{aligned}$$
(7)
$$\begin{aligned}&I_{g}\cdot \ddot{\theta }+c_{r}\cdot \dot{\theta }+K_{r}\cdot \theta =0 \end{aligned}$$
(8)
$$\begin{aligned}&\theta =e^{-\xi \omega t}\text{asin}(\omega _{r}t+\varphi ) \end{aligned}$$
(9)

The free vibration curve of the low damping system (Eq. (9)) was used to fit the swing curve of the cylindrical sample. According to Eq. (10), \(K_{r}\) can be obtained by measuring the period T and frequency \(\omega\) of the curve. c\(_{r}\) can be obtained using Eq. (11) and the attenuation change in the curve:

$$\begin{aligned}&\omega =\sqrt{\frac{K_{r}}{I_{g}}} \end{aligned}$$
(10)
$$\begin{aligned}&c_{r}=2I_{g}\omega \xi \end{aligned}$$
(11)

3.3 Experimental data processing

For the swing curve that is obtained (Fig. 3b), the position of the cylindrical sample when it is completely stationary is set as the origin. The angular displacement curve is transformed using the transverse displacement curve according to the radius of the sample. The adjusted swing curve is shown by the blue curve in Fig. 4.

The free vibration curve of the low-damping system was used to fit the swing curve of the cylindrical sample. The fitted curve (fitted with Eq. (12)) is indicated by the red dashed line in Fig. 4. This figure shows that the red fitted curve is in good agreement with the blue swing curve. Therefore, the swing curve of the cylindrical sample can be processed as a low-damping vibration curve:

$$\begin{aligned} \theta =e^{-0.479t}\times 0.174\text{sin}(7.565t+0.716) \end{aligned}$$
(12)

The rotational inertia I\(_{g}\) of the cylindrical sample can be obtained using Eq. (7). The equivalent rolling stiffness of the cylindrical sample in the swing process can be obtained using Eq. (10) as

$$\begin{aligned} K_{r}=\omega ^2 I_{g}=2.492\times 10^{-2}({\mathrm{N}\cdot \mathrm{m/rad}}) \end{aligned}$$
(13)

The damping coefficient is:

$$\begin{aligned} c_{r}=2I_{g}\omega \xi =4.153\times 10^{-4}({\mathrm{N}\cdot \mathrm{m}\cdot \mathrm{s/rad}}) \end{aligned}$$
(14)

The parameters \(K_{r}\) and \(c_{r}\) at different positions were obtained by processing the swing curves at other positions. A series of cylindrical samples with different diameters and materials was tested using the designed optical experimental system. The rolling resistance parameters were identified using this method.

Figures 5 and 6 show that the rolling resistance parameters of the cylindrical samples are related to their geometric size and elastic modulus E of the material. The elastic modulus of rubber samples \(E_{rub}\) is \(6.1\times 10^{6}\)Pa and that of the aluminum sample \(E_{al}\) is \(6.9\times 10^{10}\)Pa. For cylindrical sample of identical material, \(K_{r}\) and \(c_{r}\) increase with an increase in the diameter d. As shown in Fig. 7, where \(K_{r}\) is quadratic relation of d, which is consistent with the expression in reference [13]. \(c_{r}\) increases linearly with d. Similarly, for cylindrical samples of equal diameter, \(K_{r}\) and \(c_{r}\) increase with the increase in E. According to Eqs. (10) and (11) and experimental data, \(\frac{\omega _{rub}^{2}}{\textit{E}_{rub}} > \frac{\omega _{al}^{2}}{\textit{E}_{al}}\), \(\frac{\omega _{rub}}{\textit{E}_{rub}} > \frac{\omega _{al}}{\textit{E}_{al}}\). Therefore, \(K_{r}\) and \(c_{r}\) increase nonlinearity with E. Poisson’s ratio \(\mu\) has little effect on the measured rolling resistance parameters. The identified parameters \(K_{r}\) and \(c_{r}\) display a certain degree of dispersion caused by measurement errors and uncertain factors in the experiment. Their average values are expressed as \(\overline{K_{r}}\) and \(\overline{c_{r}}\), the standard deviation are \(S_{Kr}\) and \(S_{cr}\).

For the rubber samples, when the diameter d is 80mm, 100mm, 120mm, \(\overline{K_{r}}\) is 0.053(N · m/rad), 0.077(N· m/rad), and 0.211(N·m/rad), \(S_{Kr}\) is 0.021({N·m/rad), 0.022(N·m/rad), and 0.029(N·m/rad). \(\overline{c_{r}}\) is \(8.674\times 10^{-4}(\mathrm{N}\cdot \mathrm{m}\cdot \mathrm{s}/\mathrm{rad})\), \(2.669\times 10^{-3}(\mathrm{N}\cdot \mathrm{m}\cdot \mathrm{s/rad})\), and \(4.559\times 10^{-3}(\mathrm{N}\cdot \mathrm{m}\cdot \mathrm{s/rad})\), \(S_{cr}\) is \(1.627\times 10^{-4}(\mathrm{N}\cdot \mathrm{m}\cdot \mathrm{s/rad})\), \(4.427\times 10^{-3}(\mathrm{N}\cdot \mathrm{m}\cdot \mathrm{s/rad})\), and \(5.572\times 10^{-3}(\mathrm{N}\cdot \mathrm{m}\cdot \mathrm{s/rad})\). For the aluminum samples, when the diameter d is 80 mm, \(\overline{K_{r}}\) is \(1.107(\mathrm{N}\cdot \mathrm{m/rad})\), \(S_{Kr}\) is \(0.641(\mathrm{N}\cdot \mathrm{m/rad})\). \(\overline{c_{r}}\) is \(1.899\times 10^{-3}(\mathrm{N}\cdot \mathrm{m}\cdot \mathrm{s/rad})\), \(S_{cr}\) is \(6.808\times 10^{-4}(\mathrm{N}\cdot \mathrm{m}\cdot \mathrm{s/rad})\).

3.4 Verification of rolling stiffness coefficient \(K_{r}\)

When the angular displacement of the cylindrical sample attains its maximum, the angular velocity is zero. The point of the maximum angular displacement is set as the feature point of the test curve, as shown in Fig. 8. According to Eq. (2), the rolling resistance of the four feature points can be expressed by Eq. (15):

$$\begin{aligned} M_{1}=K_{r}\cdot \theta \end{aligned}$$
(15)

The resistance moment of a cylindrical sample in motion can be expressed by Eq. (16):

$$\begin{aligned} M_{2}=I_{g}\cdot \alpha \end{aligned}$$
(16)

where \(I_{g}\) represents the rotational inertia and \(\alpha\) represents the angular acceleration during the swing process. The rolling stiffness parameter \(K_{r}\) that is identified can be verified by comparing the differences between the two calculation methods in Eqs. (15) and (16).

As shown in Fig. 8, the feature point A in the test curve is considered as an example. The curve near the peak point is polynomially fitted with Eq. (17). The second-order derivative in Eq. (18) can be obtained by fitting Eq. (17).

$$\begin{aligned}&\theta =0.256t^3-4.042t^2+20.493t-33.714 \end{aligned}$$
(17)
$$\begin{aligned}&\theta ^{\prime \prime }=1.536t-8.084 \end{aligned}$$
(18)

The angular acceleration \(\alpha\) for the feature point A is calculated according to the horizontal coordinate and Eq. (18). The rolling resistance moment is calculated according to Eqs. (15) and (16), respectively. \(K_{r}\) is verified by comparing the values of the resistance moment obtained by the two methods. The verification results of \(K_{r}\) are presented in Table 1.

Table 1 shows that there is a certain difference between the resistance moment calculated using Eq. (15) (\(M_{1})\) and and that calculated using Eq. (16) (\(M_{2}\) ). The average relative difference \(\beta\) is calculated as \({\overline{\beta }}\)=11.7%. Thus, the relative difference between the two methods is marginal and satisfactory. It is feasible to calculate the rolling resistance using \(K_{r}\), which was identified by the dynamic experiment. In conclusion, the parameter \(K_{r}\) identified by the dynamic test can be used to establish a rolling resistance model.

4 Verification of rolling resistance model parameters by discrete element simulation

The \(K_{r}\) and \(c_{r}\) in the rolling process of the circular particles were identified by the dynamic test. Then, we substituted the identified parameters into the DEM with Eq. (1). As shown in Fig. 9a, the rolling process of a circular particle is simulated using the discrete element method. In this simulation, the diameter d of the particle is 80 mm, and its elastic modulus E is \(6.1\times 10^{6}\mathrm{Pa}\). The calculated swing curve is shown as the green curve in Fig. 9b.

The rolling resistance parameters identified by the dynamic test method were substituted into the discrete element model.Fig. 9b shows that the particle simulation motion curve is in good agreement with the test curve. Therefore, the rolling resistance parameters identified by the method proposed in this paper are applicable to the DEM simulation of particle material motion.

5 Summary and conclusions

To establish a discrete element model of particle rolling resistance, a high-precision experimental device for measuring micro-displacement was developed, and a method to identify the rolling resistance parameters of particles was studied. The main conclusions of this study are summarised as follows:

(1) We observed that a free rolling particle would swing back and forth before it stops. This is because of the elastic rolling resistance. The parameters of the rolling resistance model in the DEM can be determined by this experimental phenomenon.

(2) An optical experimental platform was developed that can be used to measure the time-history curve of particle swing. In addition, we propose a method to identify the rolling stiffness \(K_{r}\) and rolling damping parameter \(c_{r}\) based on the time-history curve.

(3) The results of the DEM simulation were in good agreement with the experimental results. The rolling resistance parameters identified by the method proposed in this study are applicable to DEM simulations.

Table 1 Verification results for rolling stiffness parameter \(K_{r}\)
Full size table
Fig. 1
figure 1

Constitutive model of particle contact in DEM

Full size image
Fig. 2
figure 2

Schematic diagram of experimental device layout: a experimental device; b rubber cylindrical samples; caluminum cylindrical samples

Full size image
Fig. 3
figure 3

Swing state of a circular particle before it stops rolling: a swing in rolling process; b swing transverse displacement curve

Full size image
Fig. 4
figure 4

Test curve and fitted curve of angular displacement

Full size image
Fig. 5
figure 5

Determination of rolling resistance parameters of rubber cylindrical sample with different diameters (mm): a rolling stiffness coefficient K\(_{r}\); b damping coefficient c\(_{r}\)

Full size image
Fig. 6
figure 6

Identification of rolling resistance parameters of different materials with identical diameter \((\textit{d}=80 \mathrm{mm}\)): a rolling stiffness coefficient \(K_{r}\); b damping coefficient \(c_{r}\)

Full size image
Fig. 7
figure 7

Rolling resistance coefficient variating with diameter d: a The variation of \(K_{r}\) with d; b The variation of \(c_{r}\) with d

Full size image
Fig. 8
figure 8

Verification of rolling stiffness coefficient \(K_{r}\) at feature points of angular displacement curve

Full size image
Fig. 9
figure 9

Verification of rolling process of a single circular particle by discrete element simulation: a simulation of single particle rolling process by discrete element method; b comparison between the calculation results of discrete element and the test curve. (parameters identified \(K_{r}=2.492\times 10^{-2}({\mathrm{N}\cdot \mathrm{m/rad}})\), \(c_{r}=4.153\times 10^{-4}({\mathrm{N}\cdot \mathrm{m}\cdot \mathrm{s/rad}})\))

Full size image