Meso-scale analyses of size effect in brittle materials using DEM

Abstract

The paper describes numerical meso-scale results of a size effect on strength, brittleness and fracture in brittle materials like concrete. The discrete element method (DEM) was used to simulate the size effect during quasi-static splitting tension with the experimental-based meso-structure. The two-dimensional (2D) calculations were carried out on concrete cylindrical specimens with two diameters wherein two different failure modes occurred (quasi-brittle and very brittle with the snap-back instability). Concrete was modelled as a random heterogeneous 4-phase material composed of aggregate particles, cement matrix, interfacial transitional zones and macro-voids, based on x-ray micro-CT-images of the real concrete meso-structure. Attention was paid to the effect of the different specimen diameter on both the strength, brittleness and fracture pattern. Each internal energy component was analyzed in the fracture process zone and beyond it, and compared for the different post-peak behaviour of concrete. The evolutions of the number of broken contacts, coordination number, crack displacements and normal contact forces were also shown. Of specific interest was the fracture initiation and formation of two different failure modes. Next, the 2D DEM results of a size effect for 4 different specimen diameters were directly compared with corresponding experiments from the research literature. The experimental size effect was realistically reproduced in numerical calculations, i.e. the concrete strength and ductility decreased with increasing concrete specimen diameter. The calculated decreasing strength approached an asymptote with increasing cylindrical specimen diameter within the considered specimen size range.

1 Introduction

The size effect is a fundamental phenomenon in brittle materials like concrete. It denotes that both the: (1) nominal structural strength (corresponding to the maximal load value reached in the loading process) and (2) material ductility (ratio between the energy consumed during the loading process before and after the load–deflection peak) always decrease with increasing structural size [1,2,3]. These two deformation process properties are of major importance for the assessment of the member safety and its interaction with adjacent structural members. Brittle members exhibit a transition from quasi-brittle response in the post-critical phase for small size members to the snap-back response (a catastrophic drop in strength related to a positive slope in a load–displacement softening branch) for large size members [4,5,6]. The size effect is an important practical result of a fracture phenomenon. Usually, the size effect has been specified for geometrically similar structures, differing only by the value of the size factor [3]. In the case of reinforced concrete, the size effect solely occurs if the failure takes place in concrete and the reinforcement yielding is excluded when a high reinforcement ratio is assumed.

Two mechanical size effects are important in brittle materials under loading: energetic (or deterministic) and statistical (or stochastic) one [1,2,3, 7, 8]. The deterministic size effect is caused by the formation of a region of intense strain localization with a certain volume (micro-crack region-called also fracture process zone FPZ) that always precedes discrete macro-cracks. The strain localization zone size is not negligible relative to the cross-section dimensions and is large enough to cause significant stress redistribution in the structure, i.e. the energy absorption in localization failure zones and energy release in remaining unloading regions. The value of energy absorption in localized failure zones is similar but the energy release grows with increasing member size (both normalized by the specimen size) that causes the decrease of the nominal strength for larger members; that is sensitive to the ratio between the size of strain localization zones and the specimen size. Thus it cannot be appropriately estimated in laboratory tests since it is different for various specimen sizes (the size of localized zones cannot be experimentally scaled). The post-peak behaviour depends upon the ratio between the energy absorption increment and energy release increment. The global snap-back instability is typical for large and slender structures, low fracture toughness and high tensile strength [9,10,11]. A statistical (stochastic) effect is caused by the spatial variability/randomness of the local material strength and occurs in concrete structures of a positive geometry [3, 12]. The first statistical theory has been introduced by Weibull [13] (called also the weakest link theory) which postulates that a structure fails when its strength is exceeded in the weakest spot (when the stress redistribution is not considered). A combination of the energetic theory with the Weibull statistical theory provides the general energetic-statistical theory for geometrically similar structures [8]. The deterministic size effect is important for moderate size structures. The Weibull statistical size effect is usually smaller and significantly increases as an asymptotic limit for very large size structures.

The main aim of our research works is to describe a quasi-static size effect in plain concrete with a realistic mechanical model during different failure mechanisms. The current paper numerically analyzes a quasi-static size effect in concrete at the meso-level in splitting tension tests during two different failure mechanisms: (1) quasi-brittle and (2) very brittle with a snap-back instability. The discrete element method (DEM) was employed to better understand the global size effect (expressed by strength and brittleness) and related failure mode change with respect to fracture. The focus was on the initiation and formation of local fractures at the aggregate level during two different failure mechanisms. The advantage of the discrete meso-scale approach is that it is able to directly simulate a heterogeneous meso-structure of materials. Thus it may be used for a detailed study of mechanisms of the initiation, growth and propagation of both micro-cracks and discrete macro-cracks that greatly control the macroscopic concrete behaviour [14,15,16,17]. It may also be used for a better calibration of continuous models for concrete with respect to the e.g. characteristic length of micro-structure, crack opening width, formation instant of a discrete macro-crack, effective elastic and inelastic parameters, damage evolution rule, fracture toughness and micro- and macro-cracking. Our experimental and theoretical investigation results on the coupled deterministic-statistical size effect in concrete and RC concrete at the macro-level were described in [4,5,6, 11, 18].

In the current paper, the damage growth and size effect in concrete cylinders of two diameters (D = 0.05 m and D = 0.15 m) were theoretically analysed for plane stress conditions. The 2D numerical results for D = 0.15 m were verified by the own laboratory experiments (wherein a snap-back instability occurred) with respect to the stress-displacement curve, shape and width of FPZ and macro-crack [14]. The concrete geometry at the meso-level was incorporated into DEM for D = 0.15 m from real concrete specimens with 3D x-ray micro-tomography images with a very high-resolution [14] using advanced tomography system Skyscan 1173 of the new generation [19]. The combined DEM/micro-CT-scan model emerged as a powerful tool to realistically capture concrete fracture under splitting tension [14] (2D analyses), bending [15, 16] (2D and 3D analyses) and uniaxial compression [17] (2D and 3D analyses). Therefore the DEM results for D = 0.15 m constitute a suitable reference for evaluating the performance of other specimen diameters. In DEM analyses, the smaller concrete specimen with the diameter of D = 0.05 m was intentionally cut out from the larger specimen to avoid a statistical size effect.

The innovative points of the present paper are the following:

• 1. Size effect investigations in concrete specimens during 2D quasi-static splitting tension [14] with the experiment-based meso-structure of concrete using a reliable 4-phase DEM concrete model.

• 2. Mesoscopic analyses of all energy components at a different stress-displacement stage with the dissipated and released portions, referred to the fracture process zone and the remaining unloading specimen region during quasi-brittle and very brittle failure.

• 3. Analyses of local fractures with respect to concrete strength and brittleness, based on the evolution of broken normal contacts, coordination number, compressive and tensile contact forces and macro-crack displacements.

The DEM calculation results for the larger cylindrical specimen (D = 0.15 m) were directly compared with our corresponding experiment with respect to the stress–strain evolution, a shape of FPZ and macro-crack and width of FPZ. In addition, the DEM simulation results of a size effect for 4 different concrete cylindrical specimen diameters (74–290 mm) were compared with the corresponding experimental results (Sect. 8).

Commonly, the deterministic size effect investigations in concrete have been performed at the macro-level by using different enhanced constitutive models for concrete, equipped with a characteristic material length (e.g. integral-type non-local models), crack band and cohesive crack approaches. Note that in contrast to DEM, continuum mechanics solutions do not consider cracking from the beginning of deformation, the damage rules have usually a priori assumed sigmoid shape and they are switched on in the softening regime only. Moreover, the heterogeneity of material properties (like stiffness, strength, fracture energy) is reflected in a homogenized sense only. The only link to the meso-structure is the presence of a characteristic length in enhanced continuum laws with softening. The characteristic length is usually chosen as a too large value as compared to experimental results (to speed up the calculations). The realistic curved cracks cannot be obtained without taking the material meso-structure into account. DEM was also used to reproduce damage in concrete by other researchers [20,21,22,23,24]. The splitting test for concrete was simulated within continuum mechanics [25,26,27,28,29,30] and discrete mechanics using DEM [31,32,33]. A simplified geometric meso-structure was however assumed in DEM calculations [31,32,33]. The size effect was found to increase with growing heterogeneity intensity [32].

The paper is organized as follows. After the introduction (Sect. 1), a short description of splitting tensile tests with respect to the size effect was addressed in Sect. 2. Next, the discrete element method (DEM) for concrete was described in Sect. 3. The DEM input data were presented in Sect. 4. The 2D DEM results of the size effect with respect to the strength, post-peak and fracture behaviour were discussed for two concrete specimens with the different diameter in Sects. 5–7. The DEM results were next compared with the corresponding experimental splitting tensile tests in Sect. 8. The final conclusions were stated in Sect. 9.

2 Size effect in split cylinder experiments of plain concrete

The splitting tensile tests (also known as the Brazilian tests) are the most popular laboratory tests on brittle materials for determination of its uniaxial tensile strength, owing to compressive loading and specimen shape simplicity. In this test, a distributed compressive traction along the length of concrete cylinder is applied, inducing a tensile stress in the transverse direction to loading and a compressive stress concentrated in a zone near the load application and support. The size effect on the plain concrete strength during splitting tensile tests on cylindrical specimens was investigated by several researchers [34,35,36,37,38]. They mainly focused on the tensile strength variation with the varying cylindrical specimen diameter D. The specimen diameter varied from 2 cm [37] up to almost 3 m [36]. To help the comparison of results for specimens of different sizes, it is useful to transform the loading force P into the nominal stress as σ = 2P/(πDL) according to the elastic solution by Timoshenko [39] (L-specimen length). The experimental results of Fig. 1 show a clear size effect in concrete, i.e. reduction of the maximum splitting tensile stress with increasing specimen diameter D, wherein P_max denotes the maximum vertical splitting force along the specimen length L except of 2 experimental results by Carmona et al. [34] for small specimens and by Hasegawa et al. [36] for large specimens. In the experiments [34], the smallest two specimens were the weakest and in the experiments [36], the strength was the same for the largest 4 specimens. Other splitting tensile tests exhibited the effect of the loading plate curvature, specimen width and length on the tensile strength. As the loading plate width b decreased, the maximum tensile stress slightly decreased [40]. The normalized specimen length L/D should be larger than L/D > 2 to get similar experimental results. Wei and Chau [41] and Kourkoulis et al. [42, 43] showed that the tensile strength became higher with increasing loading plate contact area. The most advisable testing conditions for an effective and robust characterization of the splitting tensile strength of concrete were discussed in [44].

Fig. 1

Relationship between maximum tensile stress σ = 2P_max/(πDL) and specimen diameter D (in logarithmic scale) in splitting tensile tests on plain concrete from laboratory experiments: a Bažant et al. [37], b Hasegawa et al. [36], c Carmona et al. [34], d Kadlecek et al. [38] and e and f Torrent [35] (continuous lines are trend lines) (P_max maximum vertical splitting force, D specimen diameter, L cylindrical specimen length)

3 Formulation of discrete element method (DEM) for concrete

The DEM calculations were performed with the three-dimensional spherical discrete element code YADE, that was developed at the University of Grenoble [45, 46]. DEM considers a material as consisting of particles interacting with each other through a contact law and Newton’s 2nd law via an explicit time-stepping scheme. Outstanding advantages of DEM include its ability to explicitly handle the modelling of particle-scale properties including size and shape which play an important role in the concrete fracture behaviour [45, 47, 48]. The disadvantage is a huge computational cost. The DEM model was successfully used for describing the behaviour of granular materials by taking shear localization into account [49,50,51,52]. It demonstrated also its usefulness for both local and global fracture simulations in concrete [14,15,16,17]. Our DEM calculations for concrete evidently exhibited that it was of major importance to take into account both the shape and place of aggregate particles, specimen macro-porosity and strength and number of interfacial transitional zones (ITZs) for a realistic reproduction of discrete macro-cracks [14,15,16]. ITZs due to a porous structure acted as an attractor for macro-cracks (created by bridging interfacial micro-cracks) and thus controlled both the concrete strength and brittleness [14,15,16].

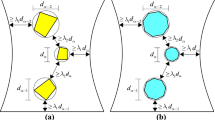
The 3D spherical discrete element method takes advantage of the so-called soft-particle approach (i.e. the model allows for particle deformation that is modelled as an overlap of particles). A linear normal contact model under compression was used. The interaction force vector representing the action between two spherical discrete elements in contact was decomposed into the normal and tangential components. A cohesive bond was assumed at the grain contacts exhibiting brittle failure under the critical normal tensile load. The tensile failure initiated contact separation and the shear cohesion failure initiated contact slip and sliding obeying the Coulomb friction law under normal compression. The linear elastic response was assumed before reaching the fracture condition. The contact forces were linked to the displacements through the normal and tangential stiffness moduli K_n and K_s (Fig. 2a–c) [45]

$$ \vec{F}_{n} = K_{n} U\vec{N}\;\;{\text{and}}\;\;\vec{F}_{s} = \vec{F}_{s,prev} + K_{s} \Delta \vec{X}_{s} , $$

(1)

where U is the overlap between elements, $\vec{N}$ denotes the unit normal vector at the contact point, $\vec{X}_{s}$ is the increment of the relative tangential displacement and $\vec{F}_{s,prev}$ is the tangential force from the previous iteration. The normal and tangential stiffness moduli K_n and K_s were computed as the functions of the modulus of elasticity E_c and Poisson’s ratio υ_c of the grains contact and two contacting grain radii R_A and R_B (to find the tangential stiffness K_s) [45]

Fig. 2

Mechanical response of DEM: a tangential contact model, b normal contact model, c loading and unloading path in tangential contact model and d modified Mohr–Coulomb model [45, 46]

$$ K_{n} = E_{c} \frac{{2R_{A} R_{B} }}{{R_{A} + R_{B} }}\;\;{\text{and}}\;\;K_{s} =_{c} E_{c} \frac{{2R_{A} R_{B} }}{{R_{A} + R_{B} }}. $$

(2)

If two grains in contact had the same size (R_A = R_B = R), the numerical stiffness was equal to K_n = E_cR and K_s = υ_cE_cR (thus K_s/K_n = υ_c). The contact forces $\vec{F}_{s}$ and $\vec{F}_{n}$ in the limit states were assumed to satisfy the Coulomb condition for the cohesive failure and frictional sliding states (Fig. 2d)

$$ \left\| {\vec{F}_{s} } \right\| - F_{max}^{s} - \left\| {\vec{F}_{n} } \right\| \times \tan \mu \le 0\quad ({\text{before}}\;{\text{contact}}\;{\text{breakage}}) $$

(3)

and

$$ \left\| {\vec{F}_{s} } \right\| - \left\| {\vec{F}_{n} } \right\| \times \tan \mu \le 0\quad \left( {{\text{after}}\;{\text{contact}}\;{\text{breakage}}} \right), $$

(4)

where μ denotes the inter-particle friction angle. Moreover, if any contact between grains after failure re-appeared, the cohesion between them was not taken into account (Eq. 3). A crack was considered as open if cohesive forces between grains (Eqs. 3 and 4) disappeared after reaching the critical threshold. The motion of fragments (mass-spring systems with cohesion) was similar to the rigid body motion. A choice of a very simple constitutive law was intended to capture on average various contact possibilities in a real concrete. The critical cohesive $F_{max}^{s}$ and tensile forces $F_{min}^{n}$ were assumed as a function of the cohesive stress C (maximum shear stress at the pressure equal to zero), tensile normal stress T and element radius R [45, 53]

$$ F_{max}^{s} = CR^{2} \;\;{\text{and}}\;\;F_{min}^{n} = TR^{2} . $$

(5)

For two elements in contact, the smaller values of C, T and R were used. A local non-viscous damping scheme was applied [54] to dissipate excessive kinetic energy in a discrete system. The damping parameter α_d was introduced to diminish the forces acting on the spheres

$$ \vec{F}_{damped}^{k} = \vec{F}^{k} - \alpha_{d} \cdot sgn\left( {\vec{v}_{p}^{k} } \right)\left| {\vec{F}^{k} } \right|, $$

(6)

where $\vec{F}^{k}$ and $\vec{v}_{p}^{k}$ are the kth-components of the residual force F and translational particle velocity v_p, respectively. A positive damping coefficient α_d was assumed smaller than 1 [sgn(•) to keep the sign of the kth component of velocity]. The equation could be separately applied to each kth component of the 3D vector x, y and z. Note that material softening was not assumed in the DEM model. The structural softening in calculations is solely due to fracture.

The five main local material parameters were needed for our discrete simulations: E_c, υ_c, μ, C and T. In addition, the values of the particle radius R, particle mass density ρ and damping parameters α_d were required. In general, the DEM material constants are calibrated with the aid of laboratory test results on concrete (e.g. uniaxial tension, uniaxial compression, simple shear, biaxial compression) due to the current data lack on mechanical properties of mortar specimens with the different initial porosity. The calibration process consists in running test simulations on a given assembly of discrete elements simulating concrete with the same material constants to reproduce the experimental mechanical behaviour [14, 16].

4 DEM input data

The section describes the input data assumed for 2D DEM calculations of a concrete splitting test. The 3D simulations are obviously more realistic than the 2D ones with respect to the fracture pattern [16, 17], however, the 2D analyses may be also useful as a means for studying several different relationships [15]. The differences between 2D and 3D DEM simulations for fractured concrete were found to be minimal at the peak load [16]. Thus the 2D results at the peak are equal to the 3D results. Those differences increased with growing post-peak deformation when assuming the same material parameters [16]. However, when the 2D DEM model is properly calibrated for concrete based on simple laboratory tests (uniaxial compression, uniaxial tension, shear, biaxial compression), it may be also used for obtaining realistic results of fracture and a post-peak stress–strain response [15]. In addition, the 2D analyses significantly cut the computation time of DEM simulations. Besides, the splitting laboratory test is usually identified as a typical 2D boundary value problem, i.e. the effect of the specimen length on the crack geometry is assumed to be negligible.

The concrete specimen was described in DEM computations as a four-phase material, composed of aggregate, cement matrix, interfacial transitional zones (ITZs) and macro-voids with the same location, shape and content of aggregates and macro-voids as in the experiment [14]. In the experiments, the minimum aggregate diameter was d_a(min) = 2 mm, maximum aggregate diameter was d_a(max) = 12 mm and mean aggregate diameter d_a(50) = 5 mm. The aggregate volumetric content was 47.8%. The total particle volumetric content (sand and aggregate) in concrete was 75%. The volume of all voids was p = 3.2% and the volume of voids with the diameter d_p < 1 mm was p = 1.6% based on micro-CT. The experimental width of ITZs was 20–50 μm. The experimental porosity of ITZs changed between 25% (at aggregates) down to 1.6% (cement matrix), based on the image binarization technique. The 3D x-ray micro-tomography images with a very high-resolution [19] were employed to give the necessary information for the geometric statistical characterization of aggregate and macro-void distributions in the specimens [14]. In 2D calculations, the specimen length L included one row of aggregate and mortar particles. In order to construct the real aggregate shape (2 mm ≤ d_a ≤ 12 mm) in 2D calculations based on images of the polished specimen surface [14], the clusters composed of spheres with the diameter of d = 1.0 mm connected to each other as rigid bodies were used. Based on experiments, all aggregate grains with the diameter in the range of 2 mm ≤ d_a ≤ 12 mm included ITZs. ITZs were simulated for the sake of simplicity as contacts between aggregate and cement matrix grains and thus they had not the physical width in contrast to experiments. The cement matrix was modelled however by spheres with the diameter range 0.35 mm ≤ d_cm < 2.0 mm without ITZs. The specimen preparation process consisted of two stages. Initially, aggregate particles and clusters simulating macro-voids were created. Later smaller particles were added until the final specimen was filled in 98.4% by particles in order to realistically model the experimental concrete micro-porosity of 1.6% (the micro-pores were assumed as the pores with the diameter d_p < 1 mm) [14]. Next, all contact forces due to the particle penetration U were deleted. In order to take the starting configuration into account, the initial overlap was subtracted in each calculation step when determining the normal forces ($\vec{F}_{n} = K_{n} \left( {U_{n} - U_{0} } \right)\vec{N}$, where U_o-the initial overlap and U_n—the overlap in the calculation n-steps). The grain size distribution curve was the same as in the experiment (with $d_{cm}^{min}$ = 0.35 mm). The macro-voids (d_p ≥ 1 mm) were modelled as empty regions with a real shape and place (after the cement matrix was created, the particles at the place of macro-voids were removed). The initial stresses in concrete due to shrinkage were not considered since the experimental specimens were carefully prepared. The specimen was cut out from a concrete block after the seventh day. The concrete block was covered with a plastic sheet during the initial curing period to avoid the surface evaporation and autogenous shrinkage. The specimen was next kept for 28 days in water.

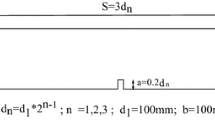
The following parameters of the cohesion and tensile strength were used in all DEM analyses of tensile splitting independently of the specimen diameter: cement matrix (E_c,cm = 15 GPa, C_cm = 140 MPa and T_cm = 25 MPa) and ITZs (E_c,ITZ = 12 GPa, C_ITZ = 112 MPa and T_ITZ = 20 MPa). ITZs were obviously the weakest phases. The ratio E_c,ITZ/E_c,cm = 0.8 was chosen based on the experiments by Xiao et al. [55]. The remaining ratios were also assumed as 0.8: C_ITZ/C_cm = 0.8 and T_ITZ/T_cm = 0.8 (Sect. 5) due to the lack of experimental results. Note that there were no any contacts between aggregate grains with d_a > 2 mm. The remaining parameters were constant for all phases and regions: υ_c = 0.2 (Poisson’s ratio of grain contact), μ = 18^o (inter-particle friction angle) [51], α_d = 0.08 (damping parameter) and ρ = 2.6 g/cm³ (mass density). The prescribed damping parameter α_d and velocity did not affect the results during bending [15]. In the case of α_d < 0.08, the too excessive kinetic energy was always created during fracture. The effect of the α_d-value on global results for α_d ≥ 0.08 became insignificant. The calculated mean nominal inertial number I for the maximum vertical load (that quantifies the significance of dynamic effects) was < 10⁻⁴ that always corresponded to a quasi-static regime. The detailed calibration procedure was described in [14] based on preliminary uniaxial compression tests. The material constants were assumed to produce in DEM simulations the same strength, elastic modulus and Poisson’s ratio of concrete as in uniaxial compression laboratory experiments. Using those material parameters, a very good agreement was achieved between numerical and experimental results for splitting with D = 0.15 m with respect to stress-displacement curve and fracture geometry (Fig. 3) [14]. The calculated global Young’s modulus E was about 3 times higher than E_c in Eq. (2). The calculated global Poisson’s ratio ν was 0.21 and was about equal to ν_c in Eq. (2). In order to avoid the effect of boundaries, a very rigid circular rod was used in simulations at the top and bottom of the specimen to transfer the load to the specimen. It was created by a single sphere with the 10-times higher stiffness than concrete. The deformation was induced by prescribing the vertical top displacement in such a way that the changes of a crack mouth opening displacement (CMOD) were about linear in time (as in experiments) [14]. CMOD was calculated as a horizontal displacement at the specimen mid-height between the mid-points of two regions with the area of A = 5×15 mm². These mid-points were at the distance of 40 mm as in the experiment. The 2D concrete specimen with D = 0.15 m included in total about 20,000 spheres. The time step was t = 10⁻⁸ s. For size effect simulations, the concrete specimen with the 3 times smaller diameter (D = 0.05 m) was artificially constructed by cutting it out from the specimen D = 0.15 m (Fig. 4) in order to entirely eliminate a statistical effect in concrete. This smaller concrete specimen included totally 2500 spheres. The deformation was induced by prescribing the vertical displacement at the specimen top. In addition, one DEM simulation was performed with the cut-out specimen of the diameter of D = 0.05 m with the reduced (about 3-times) minimum sphere diameter in the cement matrix of $d_{cm}^{min}$ = 0.10 mm instead of $d_{cm}^{min}$ = 0.35 mm.

Fig. 3

Calculated DEM results against experimental data in concrete specimen of diameter D = 0.15 m: A evolution of splitting tensile stress, σ = 2P/(πDL), against normalized vertical punch displacement v/D (curve ‘a’—experiment, curve ‘b’—DEM) and B fractured specimens (a) experiment, (b) calculated fracture based on displacements, crack displacements were magnified by factor 1000) [14] (colour figure online)

Fig. 4

Numerical construction of smaller 2D concrete specimen from larger specimen for DEM calculations (a D = 0.15 m and b D = 0.05 m)

The effect of the different ratios of T_ITZ/T_cm and C_ITZ/C_cm, different intergranular friction angle μ in ITZs and different minimum particle diameter in the cement matrix $d_{cm}^{min}$ was comprehensively discussed in [14, 15]. The calculations [14] showed that if $d_{cm}^{min}$ was small enough (e.g. $d_{cm}^{min}$ = 0.35 mm), its effect might be neglected in concrete specimens composed of a sufficiently large number of discrete elements.

5 Macroscopic DEM results: stress-displacement diagrams and fracture geometry

Figure 5 presents the DEM results of the evolution of the tensile splitting stress σ = 2P/(πDL) versus the normalized vertical piston displacement v/D for two different specimen diameters D: D = 0.05 m and D = 0.15 m. The numerical test for D = 0.05 m was carried out by prescribing the vertical displacement v. The calculated maximum tensile splitting stress with D = 0.15 m, σ_max = 2P_max/(πDL) = 3.0 MPa for v/D = 0.30% (v = 0.46 mm), was solely by 2% too low as compared to the experiment (Fig. 3A, [14]) and the calculated residual tensile stress was almost the same. The calculated rate of softening was also fairly consistent with the experiment. The results of Fig. 5 indicate a clear size effect on both the strength and brittleness. The calculated maximum tensile splitting stress σ_max was higher by about 17% (3.5 MPa against 3.0 MPa) and normalized vertical piston displacement v/D corresponding to the maximum tensile splitting stress was higher by about 20% (v/D = 0.36 against v/D = 0.30) for the smaller specimen diameter D = 0.05 m as compared to the larger specimen D = 0.15 m. The specimen with the smaller diameter D indicated a quasi-brittle failure mode and the specimen with the higher diameter D indicated a very brittle failure mode with the snap-back instability [14]. The smaller minimum sphere diameter, $d_{cm}^{min}$ = 0.1 mm, did not affect the peak stress, however, it slightly increased the concrete ductility due to the relatively small number of particles in the entire concrete specimen of D = 0.05 m (Fig. 5b).

Fig. 5

DEM results: evolution of nominal tensile splitting stress σ = 2P/(πDL) against normalized vertical piston displacement v/D for two different specimen diameters D and minimum particle diameters $d_{cm}^{min}$: a D = 0.05 m with $d_{cm}^{min}$ = 0.35 mm, b D = 0.05 m with $d_{cm}^{min}$= 0.10 mm and c D = 0.15 m with $d_{cm}^{min}$ = 0.35 mm [14]

Figure 6 displays the calculated fractured specimens wherein the localized zone (fracture process zone) is marked in cyan. The calculated macro-crack geometry was similar in both concrete specimens (Fig. 6). The calculated macro-crack shape for D = 0.15 m was also very similar to the experimental one (Fig. 3B). However, it was more curved than in experiments and followed sometimes the opposite edges of aggregates. A too big crack curvature in calculations was mainly that the experimental macro-crack also propagated through some weak aggregates (Fig. 3Ba) [14]. The large aggregate grain at the specimen bottom crushed in the experiment in contrast to DEM outcomes (our model has not included grain crushing yet). In DEM simulations, the broken contacts first occurred always in ITZs at corners of aggregate particles wherein tensile forces were the largest. Then they developed in ITZs along aggregate edges as in the experiment. Afterwards, they connected with each other in the cement matrix by bridging and created a discrete macro crack in the vertical central zone (similarly as in the experiment). Finally, the concrete specimen was divided at the failure into two halves. A localized zone (marked in cyan in Fig. 6) appeared in the specimen mid-height for P = 0.8P_max (D = 0.15 m) as in the experiment [14]. Its calculated width was w_lz = 3.9 mm based on the displacement jump (i.e. 0.33 × $d_{a}^{max}$ and 0.8 × d_(a)50) [14]. It was slightly larger than the experimental value obtained by the DIC technique (w_lz = 3.4 mm) [14]. The calculated width of the localized zone was the same for D = 0.05 m.

Fig. 6

Calculated fracture in concrete specimen for residual splitting tensile stress of σ = 1.5 MPa for 2 different specimen diameters: a D = 0.15 m and b D = 0.05 m black colour indicates aggregates, grey colour represents cement matrix, white colour shows macro-pores, cyan colour denotes area of FPZ and broken contacts, and blue colour shows supports (displacements were magnified by factor 100) (colour figure online)

6 Energy balance in process of cohesive failure and tensile contact separation

6.1 Non-fractured state (without normal contact breakage)

In a discrete undamaged concrete system there exist initially 2 main internal energies: elastic and dissipated energy. In addition, the numerical dissipation and kinetic energy also take place due to an application of DEM. The elastic internal energy stored at existing contacts N between aggregate grains E_e, expressed in terms of work of the elastic contact tangential forces F_s on the elastic tangential displacements S_c and the elastic contact normal forces F_n on the elastic penetration depths U (Fig. 2a, b) was

$$ E_{e} = \sum\limits_{1}^{N} {\left( {\frac{{\left| {F_{s} } \right|^{2} }}{{2K_{s} }} + \frac{{\left| {F_{n} } \right|^{2} }}{{2K_{n} }}} \right)} . $$

(7)

When the tangential force between grains reached the value of $F_{s}^{max}$ (Fig. 2a), the dissipated energy D_p, expressed in terms of work of the tangential (shear) forces on the conjugate sliding displacements S_l (Fig. 2a), was determined as (with F_μ = F_n × tanμ)

$$ D_{p} = D_{p'prev} + \Delta D_{p} \;\;{\text{with}}\;\;D_{p} = \mathop \sum \limits_{i}^{N} F_{\mu } S_{l} . $$

(8)

The dissipated energy was calculated incrementally at each time step and summed for the time period of the contact of two respective particles. The kinetic energy E_k of grains was caused by their translation and rotation (m—the particle mass, I—the moment of inertia of a particle, v_p—the particle translational velocity and ω_p—the particle rotational velocity)

$$ E_{k} = \mathop \sum \limits_{1}^{N} \left( {\frac{1}{2}mv_{p}^{2} + \frac{1}{2}I\dot{\omega }_{p}^{2} } \right). $$

(9)

In addition, the numerical dissipation D_n, expressed in terms of work of dampened normal and tangential forces (Eq. 6) on the conjugate normal and tangential displacements U and S_l (Fig. 2a, b) was specified as

$$ D_{n} = D_{n'prev} + D_{n} \;\;{\text{with}}\;\;D_{n} = \mathop \sum \limits_{i}^{N} (F_{damped}^{i} U\left( {S_{l} } \right)). $$

(10)

The cohesion contact failure energy release E_s was (Fig. 2a)

$$ E_{s} = \frac{1}{2}\left( {\frac{{\left( {F_{s}^{\hbox{max} } } \right)^{2} }}{{K_{s} }} - \frac{{\left( {F_{\mu } } \right)^{2} }}{{K_{s} }}} \right). $$

(11)

In general, the total accumulated energy was in the non-fractured specimen

$$ E_{{\left( {unfract} \right)}} = E_{e} + E_{k} + D_{p} + D_{n} + E_{s} . $$

(12)

It was equal to the external boundary work W expended on the particle assembly by the external vertical splitting force P on the vertical specimen top displacement v ($W = W_{prev} + \sum Pdv$).

6.2 Fractured state (with normal contact breakage)

When the particle normal contacts started to break during deformation, the broken normal springs were immediately removed from the DEM system (together with the tangential springs). Thus, the existing up to this moment internal elastic energy of removed (broken) contacts (shear and tensile contact energy) had to be added to the total internal energy. The total removed contact failure energy E_rc (composed of the shear E_s and tensile E_t contact failure energy) was equal to (Fig. 2a, b)

$$ E_{rc} = E_{s} + E_{t} = \frac{1}{2}\frac{{\left( {F_{s} } \right)^{2} }}{{K_{s} }} + \frac{1}{2}\frac{{\left( {F_{n}^{min} } \right)^{2} }}{{K_{n} }}, $$

(13)

where F_s is the actual elastic tangential force.

In general, the total accumulated energy E for the fractured specimen was thus equal to

$$ E_{{\left( {fract} \right)}} = E_{e} + E_{k} + D_{n} + E_{rc} = W. $$

(14)

6.3 Energy evolution in entire specimen

Figure 7 shows the evolution of all calculated energies, normalized by 0.25πD², against the normalized vertical piston displacement v/D in two concrete specimens D = 0.05 m and D = 0.15 m. The strain increment after the peak load was the same in both cases (Δv/D = 0.05%).

Fig. 7

Evolution of components of normalized energy E(W)/(0.25πD²) in 2D concrete specimen versus normalized vertical piston displacement v/D based on DEM ($d_{cm}^{min}$= 0.35 mm) for 2 different specimen diameters D = 0.05 m (D50) and D = 0.15 m (D150) within range of E/(0.25πD²) = 0–1.6 kNm/m² and E/(0.25πD²) = 0–0.1 kNm/m² (W external work, E total internal work, E_e(n) normal elastic energy, E_e(s) tangential elastic energy, D_p plastic dissipation, E_k kinetic energy, D_n numerical damping and E_rc energy of removed contacts)

The evolution of the elastic internal energy E_e in a normal and tangential direction was like the evolution of the mobilized specimen strength (expressed by the splitting tensile stress in Fig. 5). The elastic internal energy E_e was obviously higher than the plastic damping D_p due to cohesion. The elastic energy part due to the tangential force action E_e(s) was obviously smaller than that due to the normal force action E_e(n) in view of the lack of plastic damping in a normal direction. The kinetic energy E_k was insignificant due to both a quasi-static numerical test and numerical damping.

For the normalized vertical top displacement v/D = 0.35% corresponding to the peak load for D = 0.05 m, the normalized elastic internal energy was equal to $E_{e}^{n}$ = 96% (normal energy-70%, tangential energy-26%, n-‘normalized’), normalized plastic dissipation was $D_{p}^{n}$ ≈ 0.0%, normalized energy of removed contacts was equal to $E_{rc}^{n}$ = 0.5%, normalized kinetic energy was equal to $E_{k}^{n}$ ≈ 0% and normalized numerical damping was equal to $D_{n}^{n}$ = 3.5% with respect to the total normalized energy (Fig. 7). For v/D = 0.4 mm corresponding to the test end (Fig. 5), the normalized elastic internal energy was $E_{e}^{n}$ = 45%, normalized plastic dissipation was $D_{p}^{n}$ ≈ 0%, normalized energy of removed contacts was $E_{rc}^{n}$ = 4%, normalized kinetic energy was $E_{k}^{n}$ ≈ 0% and normalized numerical damping was $D_{n}^{n}$ = 51% with respect to the total normalized energy (Fig. 7). The energy of removed contacts started to gradually increase for v/D = 0.2%. For v/D ≥ 0.33%, its growth was pronounced.

In the case of D = 0.15 m, for the normalized vertical top displacement v/D = 0.30% corresponding to the peak load, the normalized elastic internal energy was equal to $E_{e}^{n}$ = 73% (normal energy-54%, tangential energy-19%), normalized plastic dissipation was $D_{p}^{n}$ ≈ 0.0%, normalized energy of removed contacts was equal to $E_{rc}^{n}$ = 2%, normalized kinetic energy was equal to $E_{k}^{n}$ ≈ 0% and normalized numerical damping was equal to $D_{n}^{n}$ = 25% with respect to the total normalized energy (Fig. 7). At the test end (v/D = 0.25%, Fig. 5), the normalized elastic internal energy was 64%, normalized plastic dissipation was $D_{p}^{n}$ ≈ 0%, normalized energy of removed contacts was equal to $E_{rc}^{n}$ = 3%, normalized kinetic energy was $E_{k}^{n}$ ≈ 0% and normalized numerical damping was $D_{n}^{n}$ = 33% with respect to the total normalized energy (Fig. 7). Due to the snap-back instability, the total internal energy reduced by 25%, the elastic normal internal elastic energy reduced by 50% and the elastic tangential internal energy reduced by 30%. In turn, the plastic dissipation, numerical damping and elastic energy from removed contacts increased on average by the factor 2. The energy of removed contacts started to gradually increase for v/D = 0.1%. It started to strongly grow for v/D ≥ 0.28%.

The total normalized internal energy was higher by 10% at the peak load (1.35 kN/m against 1.25 kN/m) and by 70% at the failure (1.6 kN/m against 0.95 kN/m) in the smaller specimen D = 0.05 m (Fig. 7a) as the result of both the higher vertical force P_max and ductility (Fig. 5). The contribution of the total normalized elastic energy with respect to the total normalized energy was higher for D = 0.05 m before the peak (97% versus 73%), and for D = 0.15 m at the failure (54% versus 45%) due to fracture (see Sect. 5). The total normalized elastic energy $E_{e}^{n}$ was thus higher by 40% at the peak load and smaller by 10% at the failure in the smaller concrete specimen of D = 0.05 m due to a different fracture intensity in both the concrete specimens (see Sect. 7.1). The stronger contribution of the total normalized elastic energy at the peak connected with smaller fracture intensity caused the higher strength of the small concrete specimen. The contribution of the numerical damping D_n was inverse, i.e. higher for D = 0.15 m before the peak load and for D = 0.05 m after the peak load. The normalized energy of removed contacts was slightly higher for D = 0.15 m before the peak load and for D = 0.05 m after the peak load. The removed tensile contact failure energy E_t was much higher than the removed shear contact failure energy E_s (Eq. 13).

6.4 Energy evolution in fractured and unloading specimen region

Figure 8 shows the split of normalized energies into two divided regions in concrete specimens D = 0.05 m and D = 0.15 m: (a) fractured region 4 mm wide (marked in cyan in Fig. 6) and (b) elastic region beyond the fractured region.

Fig. 8

Evolution of components of normalized energy E(W)/(0.25πD²) in concrete specimen with diameter of D = 0.05 m (D50) and D = 0.15 m (D150) versus normalized vertical piston displacement v/D using DEM for fractured region (a) and remaining unloaded region (b) and total elastic energy E_e (c) (W external work, E total internal work, E_e(n) normal elastic energy, E_e(s) tangential elastic energy, D_p plastic dissipation, E_k kinetic energy, D_n numerical damping and E_rc energy of removed contacts)

For the smaller specimen (D = 0.05 m), the total normalized internal (absorbed) energy E_absⁿ in the fractured zone was higher than the total normalized internal (released) energy E_relⁿ in the remaining unloaded region by the factor of 1.5 at the peak load and by the factor of 2.4 at the failure (Fig. 8A, B). For the larger specimen (D = 0.15 m), the total normalized internal (absorbed) energy E_absⁿ in the fractured zone was, however, smaller than the total normalized internal (released) energy E_relⁿ in the remaining region by the factor of 1.2 at the peak load and larger by the factor 1.2 at the failure.

The maximum total normalized internal energy absorbed in the fractured region was higher for D = 0.05 m (than for D = 0.15 m) by the factor 1.3 for the peak load and by the factor 2.4 at the failure (Fig. 8a, b). The maximum total normalized internal energy released in the region beyond the fracture zone was higher for D = 0.15 m (than for D = 0.05 m) by the factor 1.3 for the peak load (that contributed to the size effect on strength) and smaller by the factor 1.25% at the failure. The normalized numerical damping was obviously higher in the fractured region and was smaller for D = 0.15 m before the peak load and smaller for D = 0.05 m after the peak load. The energy of removed contacts was negligible beyond the main fractured region for both the specimens.

In the case of D = 0.05 m, the increment of the total normalized internal energy after the peak load absorbed in the fractured zone ΔE_absⁿ was by far higher than the increment of the total normalized internal energy after the peak load released in the remaining unloaded region ΔE_relⁿ (ΔE_absⁿ > ΔE_relⁿ) (Fig. 8) that caused a global quasi-brittle behaviour in the post-peak region of the small concrete specimen (Fig. 5). For D = 0.15 m, the increment of the total normalized internal energy after the peak load absorbed in the fractured zone ΔE_absⁿ was smaller than the increment of the total normalized internal energy after the peak load released in the remaining region ΔE_relⁿ (ΔE_absⁿ< ΔE_relⁿ) (Fig. 8) that contributed to a global very brittle behaviour with the snap-back instability in the post-peak regime (Fig. 5). The same tendency occurred for the total normalized elastic energy amounts after the peak load (Fig. 8c).

7 DEM results at meso-scale level

7.1 Evolution of broken normal contacts

The evolution of broken normal contacts can be helpful for determining more realistic damage evolution laws for concretes. Figure 9 demonstrates the evolution of the number of broken normal contacts for two concrete specimens D = 0.05 m and D = 0.15 m during deformation. The distribution of broken normal contacts up to the peak (Fig. 10a) and between the peak and failure (Fig. 10b) is depicted in Fig. 10 for two different specimen diameters D.

Fig. 9

2D DEM results: evolution of broken normal contacts n against normalized vertical displacement v/D in for two specimen diameters D = 0.05 m (D50) and D = 0.15 m (D150)

Fig. 10

DEM results: evolution of broken normal contacts for two different specimen diameters D: D = 0.05 m and D = 0.15 m and two different states: a before peak load and b after peak load (red marks—broken contacts up between peak load and failure, specimens are not properly scaled) (colour figure online)

The number of broken contacts obviously increased during deformation in particular after the peak load (Fig. 9). The total number of broken contacts was n = 350 (D = 0.05 m) and n = 1200 (D = 0.15 m) in the considered range of v/D. With respect to the specimen diameter, the total normalized number of broken contacts was slightly higher for D = 0.15 m, i.e. n/D = 8’000 1/m versus n/D = 7’000 1/m for D = 0.05 m. The relatively more contacts (by 50%) were broken before the peak load for D = 0.15 m (900/1200 = 0.75) than for D = 0.05 m (175/350 = 0.50) and after the peak load up to the failure for D = 0.05 m (175/350 = 0.50) than for D = 0.15 m (300/1200 = 0.33) (Figs. 10 and 11). Thus the contact damage rate was thus higher for D = 0.15 m before the peak load and for D = 0.05 m after the peak load. The numerical damping (closely related to the number of damaged contacts) was, therefore, higher for D = 0.05 m after the peak (Fig. 7).

Fig. 11

2D DEM results: evolution of coordination number N versus normalized vertical displacement v/D for two different specimen diameters: D = 0.05 m (D50) and D = 0.15 m (D150)

The continuous micro-cracking process already started from v/D = 0.17 for D = 0.05 m and from v/D = 0.10 for D = 0.15 m (Fig. 9) with a moderate intensity (Fig. 9). Later micro-cracking process became more intense in the smaller specimen of D = 0.05 m slightly before the peak load for P = 0.9P_max (v/D = 0.34) and in the larger specimen of D = 0.15 m more early before the peak load for P = 0.8P_max (v/D = 0.25) (similarly as in the experiment based on displacement measurements on the concrete surface using the DIC technique [14]). The contact damage intensity might be divided into two linear regimes for D = 0.05 m: before P = 0.9P_max (moderate intensity) and after P = 0.9 P_max (large intensity). For D = 0.15 m, it might be divided into three linear regimes: before P = 0.8P_max (small intensity), between P = 0.8P_max and P_max (large intensity) and after P_max (again moderate intensity). The results of the damage contact evolution are in agreement with the evolution of the energy of removed contacts (Fig. 7). The total number of broken normal contacts in ITZs: n = 60 for D = 0.05 m (n/D = 1200) and n = 220 for D = 0.15 m (n/D = 1450) was about 5 times smaller than in the cement matrix (n = 300/1000) (Fig. 9). Nearly 15%/70% (cement matrix) and 33%/80% (ITZs) of damaged normal contacts were broken before the peak load for D = 0.05 m/D = 0.15 m. The rate of the normal contact damage was always smaller in ITZs than in the cement matrix.

Figure 10 confirms that for the larger concrete specimen of D = 0.15 m much more contacts (relatively to the total cross-section area) were broken up to the peak and less relative contacts were broken in the softening region as compared to the specimen with D = 0.05 m (Fig. 10). At the peak, a macro-crack already developed for D = 0.15 m with the height of about 0.5D. For the smaller specimen, there existed solely many micro-cracks in the specimen - a macro-crack did not evolve at the peak. The snap-back behaviour occurred in the specimen of D = 0.15 m in the post-peak regime since this specimen was already strongly fractured at the peak load and a smaller  %-number of local contacts was needed to fully damage the specimen.

7.2 Evolution of coordination number

The evolution of the coordination number (average number of contacts per particle) N for two specimens D = 0.05 m and D = 0.15 m is demonstrated in Fig. 11. It was related to the evolution of broken normal contacts (Sect. 7.1).

The coordination number was always slightly smaller for D = 0.15 m due to a higher number of particles in the specimen (Fig. 11). It decreased during deformation due to fracture. Up to the peak load, the coordination number decreased from N = 4.9 down to N = 4.8 for D = 0.05 m and from N = 4.8 down to N = 4.68 for D = 0.15 m (the reduction rate was higher for D = 0.15 m). From the peak load to the test end, the coordination number reduced from N = 4.8 down to N = 4.6 for D = 0.05 m and from N = 4.68 down to N = 4.63 for D = 0.15 m (the reduction rate was higher for D = 0.05 m due to more intense fracture, Fig. 11).

7.3 Evolution of inter-particle contact forces

When subjected to the external load, the granular materials develops heterogeneous force networks to transmit stress at boundaries through inter-particle contacts [56, 57]. Thus the inter-particle contact force transmission in materials is essential for mesoscopic modelling of constitutive behaviour. The distribution of tensile forces is e.g. of particular relevance to the stress intensity factor which controls the initiation and propagation of cracks. The cracking process may be earlier predicted based on force transmission [57].

Figure 12 demonstrates the distribution of inter-particle normal contact forces F_n for two different specimen diameters D. The normal contact forces were split into the compressive (Fig. 12a) and tensile forces (Fig. 12b) and were shown for the peak load (Fig. 13) and at the failure (Fig. 12). The red/blue lines denote the forces in the assembly that are higher than 50% of F_max for the given specimen (so-called the strong contact forces) and the green lines denote the forces lower than 50% of F_max (so-called the weak contact forces).

Fig. 12

2D DEM results: distribution of inter-particle normal contact forces for two different specimen diameters D = 0.05 m (D50) and D = 0.15 m (D150): a compressive forces and b tensile forces (forces are shown up to the peak load for v/D = 0.36%/0.30% and after peak load for v/D = 0.40%/0.25%, red and blue colour—forces above mean value, green colour—forces below mean value) (colour figure online)

Fig. 13

DEM results: evolution of crack displacement versus normalized vertical displacement v/D in macro-crack in central specimen region (normal displacement ω and shear displacement δ for two different specimen diameters: D = 0.05 m (D50) and D = 0.15 m (D150)

The force transmission within particulate bodies was realized via co-existing strong and weak contacts which formed the corresponding strong and weak force networks [56]. The external vertical splitting force P was transmitted mainly via a network of strong compressive contact forces that formed clear force chains parallel to P (red lines in Fig. 12). Initially, the large vertical compressive normal contact forces were created in the specimen mid-region (Fig. 12). The tensile normal forces were located in a perpendicular (horizontal) direction. In the boundary regions compression obviously dominated over tension. Before the peak of the vertical force, the compression and tensile forces increased. Later, some single tensile forces started to break due to the contact damage. When a vertical macro-crack already crossed the specimen, the contact force networks appeared to be sparse and some tensile forces became located mainly along the specimen circumference caused by compression of two separated specimen’s halves. The mean width of the region with strong compressive normal contact forces was relatively larger for the peak load with D = 0.05 m (by 40%) due to its higher strength (Fig. 12). The  %-contribution of strong compressive/tensile normal contact forces was 31%/31% (peak load) and 26%/23% (failure load) for D = 0.15 m and was 38%/35% (peak load) and 17%/17% (failure) for D = 0.05 m, respectively. Thus, the %-number of strong compressive normal contact forces was higher at the peak load for the smaller specimen (38% against 31%) due to its higher strength. The %-number of strong tensile normal contact forces was also higher at the peak load for the smaller specimen (35% against 31%) due to a smaller cracking intensity. The large changes in the %-contribution of all contact forces in the post-peak regime solely occurred for D = 0.05 m due to a strong micro-cracking process (Fig. 10). These changes were hardly distinguishable for D = 0.15 m since the specimen was subjected to a strong fracture process before the peak load.

7.4 Evolution of crack displacements

Figure 13 presents the evolution of the average normal and shear displacement along the main central macro-crack exactly at the mid-height for two different specimen diameters: D = 0.05 m and D = 0.15 m.

The maximum compressive/tensile contact forces were: 32/7 N at the peak load and 19/6 N at the failure for D = 0.05 m and 38/9 N at the peak load and 31/8 N at the failure for D = 0.15 m. The failure had a clear tensile type. i.e. the normal crack displacement always dominated over the tangential crack displacement. The crack displacements evidently increased after the peak load. The normal crack displacement was slightly higher at the peak load for D = 0.15 m (0.20 μm versus 0.15 μm) and at the failure for D = 0.05 m (0.70 μm versus 0.60 μm versus). The tangential crack displacement was 5-7 times smaller than the normal one (Fig. 13).

8 Size effect: comparison of DEM predictions and experimental data

The numerical results were compared with the comprehensive splitting tensile tests performed by Carmona et al. [34] (Fig. 1). In the experiments, the force-CMOD curves were listed only. The laboratory tests were carried out on cylindrical concrete specimens with the diameter of D = 74 mm, 100 mm, 150 mm and 290 mm (the uniaxial compressive strength was 60 MPa). The weight proportion of the cement, crushed gravel (with the diameter d = 5–12 mm), gravel-sand (d = 0–5 mm), micro-silica and water in concrete was 1:1.93:1.93:0.1:0.33. The authors in [34] measured the vertical splitting force P against CMOD that was measured at the specimen mid-height between two symmetric points at the distance of 65 mm. The width of the loading/supporting plates was scaled with the specimen diameter.

Concrete was described in DEM computations as a three-phase material composed of aggregate, cement matrix and interfacial transitional zones (ITZs). The exact meso-structure of concrete used in experiments could not be reproduced in simulations due to the data lack. All particles were spherical and randomly distributed in specimens. The macro-void were neglected. The total grain volume was 75% as for normal concretes. The minimum mortar sphere diameter was $d_{cm}^{{\min} }$  =  0.1 mm. The content of grains was the following: d = 0.1–0.125 (20%), d = 0.125–2 mm (30%) and d = 2–12 mm (50%). All aggregate grains with the diameter of 2 mm ≤ d_a≤ 12 mm included ITZs. The cement matrix was modelled with spheres of the diameter 0.1 mm ≤ d_cm< 2 mm without ITZs. The width of the loading/supporting plate was b = 12.3 mm (D = 74 mm), b = 16.7 mm (D = 100 mm), b = 25 mm (D = 150 mm) and b = 48.3 mm (D = 290 mm) (as in the experiments). It was modelled by clusters composed of stiff spheres [14].

The following parameters of the cohesion and tensile strengths were mainly used in all DEM analyses: cement matrix (E_c,cm = 11 GPa, C_cm = 140 MPa and T_cm = 40 MPa) and ITZs (E_c,ITZ = 8.8 GPa, C_ITZ = 112 MPa and T_ITZ = 36 MPa). With those material constants, the uniaxial compressive strength was about 60 MPa as in the experiments. The ratios E_c,ITZ/E_c,cm, C_ITZ/C_cm and T_ITZ/T_cm were again chosen 0.8. The remaining parameters were the same as in Sect. 2: υ_c = 0.2, μ = 18^o, α_d = 0.08 and ρ = 2.6 g/cm³. The 2D concrete specimens included in total about 10,000, 19,000, 46,000 and 173,000 spheres for the specimen diameter of D = 74, 100, 150 and 290 mm, respectively. The crack opening CMOD was measured between two spheres in the specimen’s mid-height at the distance of 65 mm in a horizontal direction (as in the experiment).

The DEM results are compared with the experimental ones in Fig. 14 with respect to the vertical force evolution P against CMOD. The experimental and numerical results are in satisfactory agreement (Figs. 14 and 15). For two largest specimens (D = 150 mm and D = 290 mm), the peak vertical force P_max was lower by 10% than in the experiment and for two smallest specimens (D = 74 mm and D = 100 mm), the force P_max was higher by 15% and 25%. For a better accuracy, the real meso-structure of concrete specimens had to be faithfully reproduced in DEM.

Fig. 14

Vertical force P against crack mouth opening displacement (CMOD) from experiments by Carmona et al. [34] (red lines) as compared to DEM (black lines) for different specimen diameters (D = 74 mm (D74), D = 100 mm (D100), D = 150 mm (D150) and D = 290 mm (D290)) (colour figure online)

Fig. 15

Size effect in concrete during splitting tension from DEM simulations versus experiments [34]: a nominal strength σ versus specimen diameter D and b softening curve inclination to horizontal α versus specimen diameter D

Figure 15 describes the numerical size effect due to the specimen strength σ and specimen brittleness, expressed by the inclination α of the initial softening curve (α = f(CMOD/D)) to the horizontal in the counter-clockwise direction versus the experimental outcomes. The splitting strength increased with decreasing specimen diameter as a result of the fracture process zone with a non-homogeneous horizontal normal stress along the vertical direction [14]. Thus a size effect took place since the vertical macro-crack did not occur at the same time along the entire specimen diameter (Sect. 7.1, [58]). The material heterogeneity slightly augments the size effect [32]. The concrete brittleness also decreased with decreasing specimen diameter. The calculated concrete tensile strength changed by 16% between D = 74 mm and D = 100 mm, by 3% between D = 100 mm and D = 150 mm and by and 2.5% between D = 150 mm and D = 290 mm. The strength reached an asymptote with the large values of D [3]. The trends of the calculated varying σ versus D and α versus D were similar to the experimental ones except for two of the smallest specimens. The too low tensile strength in experiments for the smallest specimens was probably caused by boundary effects due to concrete drying. Note that other experimental outcomes in Fig. 1 did not show this unusual behaviour.

The deformed concrete specimens are shown in Fig. 16. For all concrete specimens, one almost vertical macro-crack appeared in the specimen’s central region. The macro-crack was strongly non-uniform (in particular under the loading plate and above the supporting plate) and possessed several small branches. Directly under the loading plate, a stiff wedge with two inclined cracks occurred (as in the experiments).

Fig. 16

Crack patterns from DEM in deformed concrete specimens: a D = 74 mm, b D = 100 mm, c D = 150 mm and d D = 290 mm for CMOD = 50 μm (displacements were magnified)

The numerical simulations of a size effect on splitting tension within enhanced continuum mechanics is the subject of ongoing research. The numerical predictions will be directly compared with the DEM results.

9 Summary and conclusions

The following conclusions may be offered based on 2D DEM calculations on the size effect during concrete splitting tensile tests by taking the experiment-based material heterogeneity into account in the meso-level geometry:

• The experimental size effect was realistically reproduced in calculations at the aggregate level, i.e. the concrete strength and ductility decreased with increasing concrete specimen diameter. The calculated decreasing strength approached an asymptote with increasing cylindrical specimen diameter within the considered specimen diameter range.

• The continuous micro-cracking process started in the central vertical region at a very early deformation stage, i.e. far before the peak load. It consisted of two/three intensity regimes depending upon the specimen size. Initially, it evolved with the moderate intensity before the peak load for both the specimens and later with the pronounced intensity for the smaller specimen or with the pronounced and following moderate intensity for the larger specimen. The pronounced micro-cracking process mainly started in the smaller specimen slightly before the peak load and in the larger specimen clearly before the peak load.

• The snap-back behaviour occurred after the peak load in the larger specimen since the specimen was already strongly fractured and relatively fewer contacts were needed in the post-peak regime to fully damage the specimen in contrast to the smaller specimen. The specimen failure had a clear tensile type. i.e. the normal crack displacement always dominated strongly over the tangential crack displacement. At the peak, a clear macro-crack already developed in the larger specimen with the height equal to the half of the specimen diameter. For the smaller specimen, there existed many micro-cracks at the peak load. The width of FPZ was about 1/3 of the maximum aggregate diameter.

• The higher strength of the smaller specimen was caused by the contribution of the normalized elastic energy that was greatly higher at the peak load than for the larger specimen due to the much lower fracture process intensity, expressed by a lower relative number of broken contacts with respect to the specimen diameter. The greatest total normalized internal energy absorbed in the fractured region was higher at the peak load by 30% in the smaller specimen. The greatest total normalized internal energy released in the region beyond the fracture zone was higher at the peak load by 30% for the larger specimen.

• The load was carried in the specimens by strong compressive normal contact forces. The  %-number of strong compressive/tensile normal contact forces was higher at the peak load for the smaller specimen due to its higher strength and low fracture intensity. After the peak, their drop was by far higher for the smaller specimen due to the high fracture intensity.