Heat transfer rates in sheared beds of inertial particles at high Biot numbers

Thomas Forgber; Bhageshvar Mohan; Christoph Kloss; Stefan Radl

doi:10.1007/s10035-016-0695-0

Granular Matter

February 2017, 19:14 | Cite as

Heat transfer rates in sheared beds of inertial particles at high Biot numbers

Authors
Authors and affiliations

Thomas Forgber
Bhageshvar Mohan
Christoph Kloss
Stefan Radl

Open Access

Original Paper

First Online: 17 January 2017

1.2k Downloads
4 Citations

Abstract

We investigate heat conduction rates through the contact network of sheared granular materials that consist of particles with a density much larger than that of the ambient fluid. The tool ParScale, a finite difference solver for intra-particle transport processes, is coupled to the discrete element method solver LIGGGHTS to carry out the simulations. Heat transfer to the surrounding fluid is considered via a fixed heat transfer coefficient. We identify a combination of Biot and Peclet number as the key non-dimensional influence parameter to describe the non-dimensional heat flux through the particle bed and provide an analytical solution to calculate mean particle temperature profiles. Simulations over a wide range of particle volume fractions, Biot and Peclet numbers are then performed in order to develop a continuum model for the heat flux. We show that for Biot numbers below $10^{-3}$ our results agree with a simple model based on a uniform particle temperature. However, for Biot numbers above a certain threshold, the conductive heat flux decreases substantially depending on the flow situation, and temperature gradients within the particle should be considered in order to correctly predict the heat transfer rate to the surrounding fluid.

Keywords

Sheared particle bed Thermal fluxes Discrete element method ParScale Heat transfer

List of symbols

Latin characters

a, b: Fitting constants for regime map
a: Thermal diffusivity ($\text {m}^2 \, \text {s}^{-1}$)
A: Cross sectional area ($\text {m}^2$)
Bi: Biot number
c: Integration constant
$c_\mathrm{p}$: Heat capacity ($\text {J}\, \text {kg}^{-1} \, \text {K}^{-1}$)
C: Number of contacts
d: Diameter (m)
e: Coefficient of restitution
Fo: Fourier number
$\mathbf{f}$: Force on particle ($\text {N} $)
$g^{*}$: Dimensionless bed morphology parameter
h: Spatial index
H: Height of simulation domain (m)
I: Moment of inertia ($\text {kg} \, \text {m}^2$)
I: Inertia number
k: Spring stiffness ($ \text {N} \,\text {m}^{-1} $)
m: Mass (kg)
n: Number of particles
p: Pressure normalized with density ($\text {m}^2 \, \text {s}^{-2}$)
Pe: Peclet number
Pr: Prandt number
q: Heat flux ($ \text {W} \,\text {m}^{-2} $)
Q: Heat exchange rate (W)
r: Particle radius ($ \text {m} $)
Re: Reynolds number
U: Perimeter (m)
$\mathbf{u}$: Fluid velocity ($\text {m} \, \text {s}^{-1}$)
t: Time (s)
T: Temperature ($ \text {K} $)
$\mathbf{v}$: Particle velocity ($\text {m} \, \text {s}^{-1}$)
V: Domain volume ($\text {m}^3$)
Y: Young’s modulus ($\text {N} \, \text {m}^{-2}$)
$\mathbf{x} $: Particle position ($ \text {m} $)

Greek characters

$\alpha $: Heat transfer coefficient ($\text {W}\, \text {m}^{-2} \, \text {K}^{-1}$)
$\delta $: Overlap distance during a particleparticle contact ($\text {m}$)
$\dot{\gamma } $: Dimensionless shear rate
$\gamma $: Shear rate ($\text {s}^{-1}$)
$\mu $: Friction coefficient
$\mu $: Dynamic viscosity (Pa s)
$\eta $: Viscous damping coefficient ($\text {N} \, \text {s} \, \text {m}^{-1} $)
$\varvec{\omega }$: Eigen frequency of damped harmonic oscillator ($\text {rad} \,\text {s}^{-1}$)
$\theta $: Temperature difference (K)
$\phi $: Particle volume fraction
$\epsilon $: Overlap area in case of particle-particle contact
${\varPi }$: Dimensionless length characterizing convective heat transport
$\lambda $: Thermal conductivity ($\text {W}\, \text {m}^{-1} \, \text {K}^{-1}$)
$\rho $: Density ($\text {kg}\,\text {m}^{-3}$)
$\tau $: Thermal number

Superscripts

conv: Convection
cond: Conductive
drift: Drift value
n: Normal direction
t: Tangential direction
trans: Transferred
x, y, z: Direction

Subscripts

0: Initial state
avg: Average value
bot: Bottom
c: Critical value
char: Characteristic value
co: Contact points in system
cyl: Cylinder
drift: Drift value
eff: Effective value
f: Fluid
i, j: Particle index
inert: Inertial
int: Intermediate
p: Particle
QS: Quasi-static
top: Top
s: Summation
vol: Volumetric value
x, y, z: Directions

1 Introduction

The reliable prediction of local temperatures in reactors for, e.g., $\text {CO}_2$ absorption, or biomass combustion is a research field of high interest. In these reactors particles undergo thermal or chemical transformation processes such as heating, drying, gasification, combustion, or reduction. The parallel sequence of these phenomena is still not fully understood [1, 2], and often highly dependand on the local temperature gradient inside the particle [3]. When using materials with a low heat conductivity, these gradients become extremely important in order to predict, e.g., reaction fronts. These fronts may lead to a significant change of the particle properties. Also, the surrounding flow field is typically also affected.

In addition, an accurate understanding of heat flow through static (or slowly moving) granular materials is needed in various heat treatment processes, e.g., for clayed soils, or thermal granular compaction. These systems have been investigated in detail by Smart et al. [4], Shi et al. [5], or Vargas et al. [6]. Also, a hotly debated question is the heating of brittle rocks in fault gouges during earthquakes in the field of geophysics, for instance as discussed in Rice [7]. The rising temperature in these systems has a significant effect on the overall behaviour since it leads to a pressurization of the fluid, and might cause fluidization [7, 8]. In the field of siliceous materials it is well known that rising temperatures even lead to grain melting as shown by Otsuki et al. [9]. A temperature rise in such particle beds can be seen even without any kind of external heat source, but just through the dissipation of mechanical energy, and the inability of a layer of particles to transfer heat to the environment [10].

Many researchers (e.g., [11, 12]) aimed towards the development of a rheological model in the context of a continuum description of granular materials. The study of Chialvo et al. [11] can be seen as a breakthrough in these studies, since different stress regimes (and the associated transitions between these regimes) for granular flow were quantitatively described for the first time. Mohan et al. [13] showed the existence of different regimes in the context of conductive and convective liquid transport in a sheared particle bed. In this latter work similarities between the transport of thermal energy and liquid adhering to the surface of the particles have been already discussed. Thereby, a dimensionless shear rate and a Peclet number were identified as the key dimensionless parameters. Unfortunately, the work of Mohan et al. [13] relied on the assumption of zero heat flux to the ambient fluid, critically limiting the applicability of their conclusions. Recently, Morris et al. [14] made a step towards more efficient simulations by introducing correction terms that account for the artificial softening of the particles in order to correctly calculate the conductive thermal flux.

The above mentioned previous work relied on the discrete element method (DEM), and mostly focussed on the rheological behaviour of granular matter. In case heat transfer was studied, typically a rather rudimentary approach for the local particle temperature distribution was adopted. Thus, often a spatially homogeneous particle temperature (i.e., no intra-particle temperature gradient) is considered. A good example for such an approach is the work of Tsory et al. [15]. Also, heat transfer to the ambient fluid is often not accounted for. For example, Rognon et al. [16, 17] did not even attempt to model the transferred heat from the particle to the ambient fluid (e.g., air), in line with the assumptions of Mohan et al. [13]. A more advanced study was perfromed by Shi et al. [5], who performed a thermally coupled CFD-DEM simulation in a rotary kiln under conduction-dominated flow conditions. Unfortunately, they used strongly simplified models for the fluid and solid phase. Most important, they also neglected intra-particle property profiles, which clearly limits the predictive capabilities of their model.

In related fields, Batchelor and O’Brien [18] obtained results for the effective conductivity of the granular material in the case of non-flowing uniform spherical particles embedded in a non-flowing matrix material. Thus, particles and the surrounding matrix were not allowed to move, and hence their analytical solution is rather limited. Shimizu [19] carried out thermal simulation using an Euler-Lagrange approach. He relied on a “thermal pipe network” to represent heat conduction due to particle-particle interactions, and failed to resolve intra-particle temperature gradients. Cheng et al. [20] were able to model the effective conductivity of a non-moving packing by performing simulations that take (i) conduction through the solid particles, (ii) conduction through the contact area between contacting particles, and (iii) the conduction via the ambient (but stagnant) fluid into account.

Only some research groups include more refined models for the temperature distribution inside individual particles. Relevant studies include the work of Feng et al. [21, 22] or Oschmann et al. [23]. The former propose a so-called discrete thermal element model (DTEM), which can be readily integrated with the DEM. Unfortunately, also this previous work made strong simplifications, e.g., by neglecting direct heat transfer in the contact zones, or by relying on a pipe-network structure to compute thermal fluxes. The model of Oschmann et al. can be seen as the ultimate model for heat conduction within a particle bed: they discretize each particle with ca. 20,000 computational nodes, and are hence able to predict the full three-dimensional temperature distribution within each single particle. Clearly, such an approach is computationally very demanding. This critically limits the size of the particle bed to be studied. Consequently, the number of parameter variations considered in the work of Oschmann et al. is too small to draw more general conclusions.

In summary, there is still very little quantitative knowledge about the thermal behaviour of particle beds that consist of particles with a non-uniform temperature distribution. This is especially true for beds that are sheared, and for which convective heat transport (i.e., transport due to individual particle motion) might be the dominating transport mechanism. Clearly, a thorough understanding of the relative rates of (i) the transferred heat to the ambient fluid, (ii) the convective heat transport, and (iii) the heat that is transported via conduction is still missing in literature.

When introducing thermal fluxes in the context of the granular flow simulations considered in our present contribution, it is important to consider the exact meaning of their definition. Critically, the term “convective flux” is fundamentally different from its meaning in classical continuum models: convective fluxes in the context of the present work are caused by random motion of individual particles. This is in contrast to the convective transport of thermal energy due to macroscopic (i.e., particle-average) motion: this “macroscopic” convective transport can be modeled with relative ease in continuum models [24]. Hence, this mode of thermal transport is not discussed in the present work. Another term is the transferred heat to the ambient fluid: in our present contribution this refers to the heat exchanged between the fluid and individual particles. At this point we reference the reader to our presentation in Sect. 2.4 which provides a more holistic view of all relevant thermal fluxes. Most important, these fluxes are the main output of our simulations, and can be subsequently used in continuum models to describe thermal transport in granular materials and fluid-particle systems. Unfortunately, rigorous closures for these fluxes are still missing in literature, currently limiting the application of continuum models to engineering problems. In this study, we focus on suspensions characterized by a large Stokes number ($St= 2/9 \, \rho _\mathrm{p} \mathbf{u} d_\mathrm{p}/ \mu _\mathrm{f}$) which are relevant for a number of practical applications involving gas-particle suspensions [25].

It is our goal to improve this situation by coupling DEM-based simulations to a tool that is capable of resolving intra-particle temperature profiles: our tool ParScale (see [26, 27]) allows us to efficiently solve a one-dimensional heat conduction equation within each particle. This enables us to provide answers to questions related to the occurence of situations in which intra-particle temperature profiles are significant. Clearly, this is of utmost importance for the correct selection of an appropriate simulation model for a certain fluid-particle heat transport problem. Specifically, we analyse the relevance of intra-particle temperature gradients by probing an adequate space of dimensionless parameters, most important the Biot and Peclet number. This allows us to identify critical dimensionless system parameters for which heat conduction inside the particle becomes limiting. Most important, the use of dimensionless parameters allows us to draw conclusions that are applicable to a wider range of real-world applications compared to previous work. Specifically, our contribution is meant to extend the work of Rognon et al. [16] to (i) a wider range of volume fractions, (ii) to fluid-particle systems with heat transfer to the ambient fluid, and (iii) includes the temperature distribution inside the particles. Same as Mohan et al. [13] we attempt to collapse the predicted conductive flux into one curve. This is done to lay the foundation for the development of a unified continuum model for predicting thermal transport in high-Biot number fluid-particle suspensions.

We note in passing that including heat transfer to the ambient fluid requires the specification of a heat transfer coefficient (details will be discussed in Sect. 2.4), or its dimensionless counterpart the Nusselt Number. Ranz and Marshall [28] developed one of the first Nusselt number correlations for thermal transfer between spheres and ambient fluid. Clearly their correlation is not applicable in dense particle flow which we focus on in the current manuscript. Gunn [29] proposed a still widely-used correlation for the Nusselt number in the porosity range of 0.35–1.0 for various Reynolds numbers. Thus, using Gunn’s results it is straight forward to estimate the heat transfer rate, and consequently also the Biot number, in any given fluid-particle flow systems.

Our paper is structured as follows: in Sect. 2 we describe the simulation method, including the governing equations for the DEM and the intra-particle heat transport model. Furthermore, we provide details about the coupling sequence between LIGGGTHS and ParScale. Section 3 summarizes our theoretical analysis of transport of thermal energy in a sheared particle bed. Section 3.2 considers effects due to heat conduction with the particles, and Sect. 3.3 aims on presenting results for limiting cases in order to better interpret our numerical data in Sect. 4. These subsections hence constitute the first part of our results. The second part of our results is placed in Sect. 4 where the sheared particle simulation setup is described in detail, including the effect of all relevant dimensionless numbers. Section 5 views our results in light of previous findings, and comments on possible future applications of ParScale. A consistent list summarizing the nomenclature used, including all quantities of secondary importance which are not mentioned after their first appearance in the paper, is available in “List of symbols”.

2 Simulation method

An overview of all relevant transport equations used in our simulations is provided in Table 1. Also, we have summarized the corresponding unknown simulation variables in Table 2. Note that some of the equations are discussed in more detail in the next Section. We want to emphasize that we solve the transport equations for the fluid only in Sect. 3.2, while in all other parts of our contribution we consider (i) the fluid to be held at a fixed temperature, and consider (ii) a fixed particle-fluid heat transfer coefficient. Also, as implied by our title, we consider inertial particles, i.e., particle motion is not affected by fluid motion. This is done to avoid the large computational effort needed to resolve local fluid flow and temperature, which would make our study unaffordable considering our current computational resources.

Table 1

Covering equations for particle flow (Newtons equation of motion), particle flow (Continuity equation, Navier-Stokes equation, scalar transport for e.g., temperature) and equations regarding internal thermal transport in spherical coordinates in one-dimensional form

Reference system	Equation
Particle flow	$\dfrac{d\, \mathbf{x}_\mathrm{i}}{d \, t} = \mathbf{v}_\mathrm{i} $
	$m \, \dfrac{d \, \mathbf{v}_\mathrm{i}}{d \, t} = \sum \limits _\mathrm{j} (\mathbf{f}\,^\mathrm{t}_\mathrm{ij} + \mathbf{f}\,^\mathrm{n}_\mathrm{ij}) $
	$I_\mathrm{i} \, \dfrac{d \, \varvec{\omega }_\mathrm{i}}{d\, t} = \sum \limits _\mathrm{j} \mathbf{f}\,^\mathrm{t}_\mathrm{ij} \times \mathbf{r}_\mathrm{ij}$
Fluid flow	$ \varvec{\nabla } \cdot \mathbf{u} = 0$
	$\dfrac{ \partial \, \mathbf{u}}{\partial \, t} + \varvec{\nabla } \cdot \left( \mathbf{u} \mathbf{u} \right) = -\varvec{\nabla }p+ Re^{-1} \nabla ^2{\mathbf{u}} $
	$\dfrac{ \partial \, \theta }{\partial \, t} +\varvec{\nabla } \cdot \left( \mathbf{u} \theta \right) = Pe^{-1} \nabla ^2{\theta }$
Internal thermal transport	$\dfrac{\partial T}{\partial t} = a \cdot \left( \dfrac{\partial ^2 T}{\partial r^2} + \dfrac{2}{r} \, \dfrac{\partial T}{\partial r} \right) $

Table 2

List of unknown simulation quantities

Reference system	Unknown quantities
Particle flow	Particle positions $\mathbf{x}_\mathrm{i}$
	Particle velocities $\mathbf{v}_\mathrm{i}$
	Angular velocity $\varvec{\omega }_\mathrm{i}$
Fluid flow	Fluid velocities $\mathbf{u}$
	Pressure p
	Scalar quantity $\theta $ e.g., temperature
Internal thermal transport	Particle temperature T

2.1 Particle flow model

The open-source software package LIGGGHTS [13, 30] is a well established discrete element method-based tool and was used in combination with a spring-dashpot model [30] in the present work. Note that we do not solve any transport equations for the fluid, but consider (i) the fluid to be held at a fixed temperature, and consider (ii) a fixed particle-fluid heat transfer coefficient. Specifically, the following contact force models in the tangential (i.e., $\mathbf{f}\,^\mathrm{t}_\mathrm{i,j}$) and normal direction (i.e., $\mathbf{f}\,^\mathrm{n}_\mathrm{i,j}$) were applied:

$$\begin{aligned}&\mathbf{f}\,^\mathrm{t}_\mathrm{i,j} = - k^\mathrm{t} \, \mathbf{u}^\mathrm{t}_\mathrm{ij} - \eta ^\mathrm{t} \mathbf{v}^\mathrm{t}_\mathrm{ij} \end{aligned}$$

(1)

$$\begin{aligned}&\mathbf{f}\,^\mathrm{n}_\mathrm{i,j} = k^\mathrm{n} \, \delta _\mathrm{ij} \mathbf{n}_\mathrm{ij} - \eta ^\mathrm{n} \, \mathbf{v}^\mathrm{n}_\mathrm{ij} \end{aligned}$$

(2)

with:

$$\begin{aligned} \delta _\mathrm{ij} = r_\mathrm{i} + r_\mathrm{j} - \mid \mathbf{r}'_\mathrm{i} - \mathbf{r}'_\mathrm{j} \mid . \end{aligned}$$

(3)

Thereby $\delta _\mathrm{ij}$ indicates the normal overlap, which is positive in case of overlapping particles. Below we summarize the most important quantities that are relevant for the interpretation of our work. For the meaning of other symbols we refer to the Nomenclature. The characteristic contact time $t_\mathrm{co}$ of the above linear spring-dashpot model is defined as:

$$\begin{aligned} t_\mathrm{co} = \pi /\omega \end{aligned}$$

(4)

with

$$\begin{aligned} \omega = \sqrt{(k/m_\mathrm{eff}- \eta ^2) / (4 \, m_\mathrm{eff}^2)}. \end{aligned}$$

(5)

This contact time $t_\mathrm{co}$ limits the time step $\bigtriangleup \, t$ for the integration of Newtons equation of motion. The coefficient of restitution $e_\mathrm{n}$ is defined as

$$\begin{aligned} e = \text {exp} \left( \dfrac{- \pi \eta }{m_\mathrm{eff} \, \sqrt{(k/m_\mathrm{eff}- \eta ^2) / (4 \, m_\mathrm{eff}^2)}} \right) \end{aligned}$$

(6)

and was adjusted to 0.9. In our simulations, the spring stiffness and damping coefficient in the normal and tangential direction are set equal. In order to obtain a certain restitution coefficient, and a certain dimensionless shear rate $\gamma ^{*}$, we adjust $\eta $ and k. For more information on the used parameter ranges and routines to calculate, e.g., the effective Young’s modulus, we refer the interested reader to Sect. 1 and “Appendix”.

2.2 Transport within a particle

In order to calculate intra-particle properties, a tool called ParScale (short for Particle Scale) [31] was developed. It is capable of resolving individual property profiles (e.g., that of the temperature, or a dissolved chemical species) inside a particle. Specifically, ParScale relies on the so-called Method of Lines (MoL) as outlined in the next paragraph. The resulting system of equations is solved by an already established multi-step solver called CVODE. This enables ParScale to perform flexible and stable simulations, even in case of fast changing environmental conditions, or (numerically) stiff systems that are typical for non-isothermal reactive porous particles.

The next sections outline the governing equations, provide more detailed information on the solution procedure, and give an overview of the parallel coupling strategy.

2.2.1 Governing equations

In this paper only heat conduction inside non-porous particles is taken into account. Note, the current development state of ParScale already allows the treatment of mass transfer, multiple chemical reactions, as well as phase change phenomena (e.g., evaporation) taking place inside porous particles. However, these phenomena are not accounted for in our present study.

The basic approach of the MoL is to (i) discretize the transport equation related to all intra-particle properties in space, and (ii) then integrate the discretized equations in time. At this stage, a one-dimensional spatial discretization in a radial coordinate system centered at the particle position has been employed. Therefore, every particle is spatially split in a fixed number of grid points. At each of these points, the differential heat balance in spherical coordinates is solved (see Eq. 8). We want to amplify that the thermal boundary condition of the heat transfer equation solved in ParScale is a combination of the transferred heat flux to the surrounding $q^\mathrm{trans}$ and the per-particle heat conduction rate (which is calculated by summing over all particle-particle contact points, similar to what is done in Eq. 10). Since we are only tracking solid, non-porous particles, we can assume for the particles’ mean heat conductivity $\lambda _\mathrm{p} = const.$ After introducing the thermal diffusivity a, the differential heat balances reads:

$$\begin{aligned}&a = \dfrac{\lambda _\mathrm{p}}{\rho \, c_\mathrm{p}} \end{aligned}$$

(7)

$$\begin{aligned}&\dfrac{\partial T}{\partial t} = a \cdot \left( \dfrac{\partial ^2 T}{\partial r^2} + \dfrac{2}{r} \, \dfrac{\partial T}{\partial r} \right) \end{aligned}$$

(8)

For discretisation in physical space, a second order central differencing scheme is used. A verification case, i.e., the convective cooling of a sphere, was used to ensure a correct implementation of the discretization schemata, and the integration of ParScale with the solver CVODE. For details of the differencing scheme, as well as results of the verification studies, the reader is referred to “Appendix” and Sect. 1.

2.3 Code architecture and parallel coupling strategy

ParScale is developed in a C++ environment, relies on a hierarchical class structure, and is packaged in a library that can be easily integrated with other particle-based simulation tools. Most important, ParScale is equipped with well-structured data containers for the easy transfer of particle information during a parallel simulation run. Note, that data containers are separated from an external particle simulator, in order to ensure a maximum level of compatibility with different simulators and parallelization strategies. In summary, ParScale is scalable, flexible, and can be adapted to the users needs by the simple addition of user-defined classes. ParScale is currently hosted on a public Github repository [31], together with detailed installation instructions and a comprehensive user documentation. ParScale has two different run modes: (i) a stand-alone mode, and (ii) a coupling mode in which ParScale acts as a slave to an external DEM or CFD-DEM simulator. At the current development state ParScale features coupling to LIGGGHTS, as well as CFDEMcoupling. Example cases placed in the public repository demonstrate the usage of ParScale, contain several verification cases to prove the correct implementation, and provide some post-processing and plotting routines. Since ParScale is combined with the open-source solver LIGGGHTS in the current work, an overview of a single time step of a coupled LIGGGHTS-ParScale simulation is shown in Fig. 1. At the beginning of every time step LIGGGHTS is running as the master program. It solves for the particle movement (i.e., all DEM-based calculations) and hands over surface temperatures, actual heat transfer coefficients, and fluxes due to an eventual conductive heat transfer between contacting particles. Some other coupling options are available, e.g., setting a specific environment temperature for each particle, which is used in the present contribution. Furthermore, it is possible to reset the whole particle temperature to a constant value. After all calculations of LIGGGHTS are completed, ParScale initializes from the last know time step and reacts to changes due to the coupling of the particle motion solver. Specifically, it updates the surface temperature, calculates source terms (e.g., due to reactions or phase change phenomena), and pushes these particle properties back to LIGGGHTS for the next time step. For visualisation and post-processing purposes, additional information (e.g., core, or the volume-averaged temperature, as well as conductive, or convective heat fluxes) can be exchanged with LIGGGHTS.

Fig. 1
Coupling between LIGGGHTS and ParScale for one time step including required coupling parameters and additional coupling options

2.4 Thermal fluxes

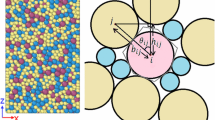
The definition of thermal fluxes is taken from the work of Mohan et al. [13] and a simplified example assemble including a description of coordinates can be found in Fig. 7. Physically seen, the convective flux (Eq. 9) is defined as the redistribution of thermal energy of the particles due to its macroscopic movement inside the simulation domain. In the contrary, the conductive thermal flux (Eq. 10) accounts for the heat exchanged between two particles in case of a collision. Drawing back to classical thermodynamics, the transferred heat flux (Eq. 11) describes the exchange of thermal energy between fluid and particle. This transferred amount of heat is mainly a function of the heat transfer coefficient $\alpha $ and the temperature difference between particle and ambient fluid. Note that $\mathbf {q}^\mathrm{cond}$ is defined for particles with equal physical properties regarding thermal conductivity and is calculated for the sum of all contacts in the domain with the volume V.

$$\begin{aligned} \mathbf {q}^\mathrm{conv}= & {} \dfrac{1}{V} \sum \limits _\mathrm{i} \, m_\mathrm{eff,i} \, c_\mathrm{p,i} \, T_\mathrm{vol,avg,i} \, \mathbf {v}_\mathrm{i} \end{aligned}$$

(9)

$$\begin{aligned} \mathbf {q}^\mathrm{cond}= & {} \dfrac{1}{V} \sum \limits _\mathrm{co} \, 2 \, \lambda _\mathrm{p} \, A_\mathrm{co}^{1/2} \, (T_\mathrm{i} - T_\mathrm{j}) \, \mathbf {r}_\mathrm{ij} \end{aligned}$$

(10)

$$\begin{aligned} q^\mathrm{trans}_\mathrm{i}= & {} \alpha \, (T_\mathrm{i} - T_\mathrm{f,i}) \end{aligned}$$

(11)

The conditional claim of a fully periodic, sheared bed with Lees-Edwards boundary conditions is that the domain-averaged particle velocity equals zero. When considering the sheared particle ensemble used in our work (see Sect. 4), it is important to note that we consider three different “thermal” regions as shown in Fig. 7 in Sect. 4. Most important, we only consider the center region (i.e., region B in Fig. 7) to calculate the fluxes. In such a case one has to correct the calculation of the convective flux as discussed in the next paragraph. Even though the above conditional claim related to the domain-averged particle velocity is fulfilled for the full box, this does not apply for our center region in which the thermal calculations are performed. Since we fix the temperature of the particles located inside the top and bottom region to enforce a predefined temperature gradient, the number of particles in these regions fluctuates over time. Also, dividing the domain into three regions causes a temporal fluctuation of the number (as well as the average speed) of the particles in each region. Thus, we see a drift convective flux due to the average macroscopic movement of the particles in the center region, which is characterized by the velocity $v_\mathrm{y,drift}$.

$$\begin{aligned} q^\mathrm{y,conv} = \dfrac{1}{V} \sum \limits _\mathrm{i} \, m_\mathrm{eff,i} \, c_\mathrm{p,i} \, T_\mathrm{vol,avg,i} \, (v^\mathrm{y}_\mathrm{i} + v^\mathrm{y}_\mathrm{drift,i}) \end{aligned}$$

(12)

or explicitly calculated

$$\begin{aligned} q^\mathrm{y,drift} = \dfrac{1}{V} \, v^\mathrm{y}_\mathrm{drift} \, \sum \limits _\mathrm{i} \, m_\mathrm{eff} \, c_\mathrm{p} \, T_\mathrm{vol,avg,i} \end{aligned}$$

(13)

As mentioned above, the number of particles in our center region is not fixed and can change due to the deformation of the box. Consequently, we need to weight our already corrected convective flux with the number of particles in the region when computing a time-average flux:

$$\begin{aligned} \mathbf {q}^\mathrm{conv} = \dfrac{\mathbf {q}^\mathrm{conv,i} \, n_\mathrm{p,i}}{1/i \, \sum \limits _\mathrm{i} \, n_\mathrm{p,i}} \end{aligned}$$

(14)

For the reference flux we choose the conductive flux in case our computational domain is completely filled with solid material. Thus, the reference heat flux is calculated as:

$$\begin{aligned} q_\mathrm{s} = - \lambda _\mathrm{p} \, \dfrac{\partial T}{\partial y} \end{aligned}$$

(15)

where $\partial T / \partial y$ is the temperature gradient in the gradient direction of the shear flow.

3 Theoretical analysis

3.1 Dimensional analysis

The key dimensionless flow parameters, i.e., the coefficient of restitution, the friction coefficient, the dimensionless stresses, the particle volume fraction, and the dimensionless shear rate have been well documented by Chialvo et al. [11], and Mohan et al. [13]. In agreement with Chialvo et al. [11] we define a scaled shear rate as

$$\begin{aligned} \dot{\gamma } = \gamma \, d^{3/2}_\mathrm{p} / \sqrt{k_\mathrm{n}/\rho _\mathrm{p}}. \end{aligned}$$

(16)

According to the experiments by Nordstrom et al. [32], and recent simulations [10, 33, 34], simple expressions that correlate the above defined dimensionless quantities can be found. Specifically, the scaled stress-shear rate data can be collapsed into curves by appropriately adjusting the critical volume fraction ($\phi _\mathrm{c}$), as well as a set of exponents as shown below. This scaling will be an inspiration for the re-scaling of the conductive heat flux in the present contribution (see Sect. 4). Thus, of key relevance are the three resulting stress regimes (here illustrated by the pressure), which are characterized by the following expressions:

$$\begin{aligned}&p_\mathrm{inert} \sim |\phi - \phi _\mathrm{c}|^{-2} \end{aligned}$$

(17)

$$\begin{aligned}&p_\mathrm{QS} \sim |\phi - \phi _\mathrm{c}|^{2/3} \end{aligned}$$

(18)

$$\begin{aligned}&p_\mathrm{int} \sim |\phi - \phi _\mathrm{c}|^{0}. \end{aligned}$$

(19)

Previous work only considered the conductive and convective heat transport rate in a sheared, but uncooled, particle bed (see, e.g., [17]). As pointed out by Mohan et al. [13], the Peclet number is the most influential parameter for heat transport in granular materials and reads:

$$\begin{aligned} Pe = \dfrac{(d_\mathrm{p}/2)^2}{\lambda _\mathrm{p}/(\rho _\mathrm{c} \, c_\mathrm{p})} \, \gamma \end{aligned}$$

(20)

Clearly, Pe characterizes the relative rates of convective and conductive heat transport within the particles in the absence of heat transfer to the ambient fluid. In the present work, however, we consider exactly this heat transfer rate to the ambient fluid, which is characterized by the heat transfer coefficient $\alpha $. Therefore, we must introduce a new dimensionless quantity, which we choose to be the Biot number defined as:

$$\begin{aligned} Bi = \dfrac{\alpha \, d_\mathrm{p}}{\lambda _\mathrm{p}} \end{aligned}$$

(21)

The Biot number can be interpreted as the ratio of (i) the intra-particle and (ii) the external resistance to heat transport. Thus, for high Biot numbers we expect intra-particle temperature profiles to be significant. We will see that also the Peclet number affects intra-particle temperature profiles, since conductive transport between particles (caused by particle-particle collisions) leads to a heat up of the outer shell of the particles.

As an alternative to the Peclet number, one could define a dimensionless convective heat transport rate by using the transferred heat flux (to the ambient fluid) as the reference, i.e.,

$$\begin{aligned} {\varPi }= \dfrac{Pe}{Bi} = \dfrac{\rho _\mathrm{p} \, c_\mathrm{p} \, d_\mathrm{p} \, \gamma }{\alpha } \end{aligned}$$

(22)

${\varPi }$ can be interpreted as a scaled length over which convective transport is able to balance the cooling (or heating) caused by the ambient fluid. This dimensionless number is useful in situations in which one wants to probe the effect of the the particles’ heat conductivity on the results: for fixed values of ${\varPi }$ one can illustrate the effect of heat conduction within the particles by varying the Biot number. Note, that for fixed Pe a variation of Bi does not lead to such a transparent illustration, since also Pe is a function of the particles’ heat conductivity, and both dimensionless numbers are zero in the limit of infinitely fast heat conduction within the particles. Since ${\varPi }$ is proportional to Pe and Bi, it is straight forward to interpret our results also in light of this new dimensionless quantity. We have already attempted this in most parts of the present contribution.

3.2 Effect of heat conduction within the particle

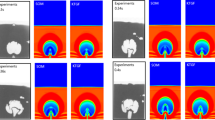
The goal of this Section is to theoretically investigate the cooling of a sphere under different conditions, and justify the assumption of spherical symmetry made in the current work. As pointed out by Schmidt et al. [35], as well as Oschmann et al. [23], the computational cost for a fully resolved particle is enormous: calculation time and data storage increase by a factor of about 1000 when using three-dimensionally resolved simulations. Fortunately, a one-dimensional discretization (as followed in the current work) is often an excellent approximation (in case of a sphere) when considering heat exchange in a certain Reynolds number range (see Nikrityuk et al. [36]). To support this finding, we study the transient cooling of a sphere, and consider different Reynolds numbers. We then compare the temperature change over the radius with the data provided by Nikrityuk et al. [36]. The latter performed a fully three-dimensional simulation, including a resolved flow and temperature profile simulation in the fluid surrounding the particle. For the simulation details we refer to Nikrityuk et al. [36]. We have summarized the key dimensionless parameters in the caption of Fig. 2.

Fig. 2
Comparison of the volume-averaged temperature profiles derived from the DNS data of Nikrityuk et al. [36], and a 1-D simulation performed with ParScale for $Re = 1, Bi \approx 0.365; Re = 10, Bi \approx 0.532; Re=50, Bi \approx 1.065$, $\lambda _\mathrm{p} / \lambda _\mathrm{f} = 7$

Table 3

Boundary conditions used for the cooled sphere simulations

Field/patch	Quantity	Type/value
Inlet	Velocity	Fixed value, to realize Re
	Pressure	Zero gradient
	Temperature	Fixed value $\theta = 0$
Outlet	Velocity	Zero gradient
	Pressure	Fixed value, 0
	Temperature	Zero gradient
Lateral walls	Velocity	Slip
	Pressure	Zero gradient
	Temperature	Zero gradient
Sphere surface	Velocity	No slip
	Pressure	Zero gradient
	Temperature	identical flux fluid and particle domain

In general, an excellent agreement between the DNS data and simulations performed with ParScale over a wide range of dimensionless times, i.e., Fo numbers, can be observed. This is especially true for large Re numbers, where only marginal differences between DNS data and predictions by ParScale are observed. As already pointed out by Nikrityuk et al. [36], the maximum difference between a fully three-dimensional simulation and a one-dimensional simulation is between 2$\%$ and $\approx 5\%$. To support this finding, we investigated conjugate heat transfer associated with the flow around a single sphere under significant internal heat transport limitation (see Fig. 3 for details). We listed all boundary conditions in Table 3 and governing equations in Table 1. As can be seen, the temperature profiles inside the particles approach spherical symmetry for higher Reynolds numbers. The reason for this behaviour is that the the temperature distribution in the ambient fluid becomes more uniform, since the rate of convective heat transport in the fluid increases with increasing Reynolds number. At low Reynolds numbers (see panel a of Fig. 3) a certain temperature gradient in the fluid in the main flow direction is observed. This temperature gradient leads to a shift of the maximum intra-particle temperature towards the rear stagnation point, causing a significant temperature gradient in the azimuthal direction. Fortunately, most industrial applications are concerned with improving external transport limitations, and hence operate at Reynolds numbers larger than unity. Also, a closer inspection of the global temperature difference in the left panel of Fig. 3 indicates a temperature fluctuation of about 0.17 dimensionless units. This is because $Bi<1$, i.e., the external heat exchange rate is typically much smaller than the heat conduction rate in the particle in case of low Reynolds number flows. In summary, the results in Figs. 2 and 3 support our assumption of a spherically-symmetric temperature profile within particles for most gas-particle systems. Of course, this statement only holds for flows involving single spherical particles, and cannot be easily generalized to non-spherical particles, or dense particle ensembles. Thus, we currently cannot provide a rigorous justification for spherical symmetry in dense granular flows where particle-particle heat conduction occurs. Fortunately, this mode of thermal transport (i.e., heat conduction through the contact areas) is typically small: an analysis of the amount of heat exchanged due to conduction (denoted as $\mathbf {Q}^\mathrm{cond}$) and transfer to the surrounding fluid (i.e., $Q^\mathrm{trans}$) on a per particle basis helps to support this argument. Specifically, one finds that the ratio of these heat exchange rates is (based on the expressions for the heat fluxes introduced in Eqs. (10) and (11):

$$\begin{aligned} \dfrac{\mathbf {Q}^\mathrm{cond}}{Q^\mathrm{trans}} = \dfrac{1}{Bi} \, \dfrac{2 \epsilon }{\pi } \, \dfrac{\langle \bigtriangleup T_\mathrm{co} \rangle }{T_\mathrm{i} - T_\mathrm{f,i}} \end{aligned}$$

(23)

Fig. 3
Temperature distribution in the fluid and in the particle when cooling a single sphere initially having the temperature $\theta _\mathrm{init}$ = 1, at Pr = 4.3 and $\lambda _\mathrm{p} / \lambda _\mathrm{f} = 1.37$—internal limitation problem; flow vertically downwards; white lines are temperature iso-contours in the fluid; a $Re_\mathrm{p}$ = 1, Fo = 2.6, $Bi \approx 0.15$; b $Re_\mathrm{p}$ = 100, Fo = 0.17, $Bi \approx 7.65$

Here we have introduced $\epsilon $ as a parameter that characterizes a typical overlap area, which is typically much smaller than unity. Also, we have denoted with $\langle \bigtriangleup T_\mathrm{co} \rangle $ a mean temperature difference of the contacting particles. If we now accept that the term $\langle \bigtriangleup T_\mathrm{co} \rangle / T_\mathrm{i} - T_\mathrm{f,i}$ is of order unity, we find

$$\begin{aligned} \dfrac{\mathbf {Q}^\mathrm{cond}}{Q^\mathrm{trans}} = \dfrac{\epsilon }{Bi}. \end{aligned}$$

(24)

Thus, the relative importance of the conductive heat flux decreases with increasing Biot number. It is now obvious that the heat exchange rate due to particle-particle contacts will not impact the shape of intra-particle temperature profiles, since the latter are significant only for $Bi>1$. Thus, one can readily transfer the findings related to intra-particle temperature profiles in a single particle to a cooled bed of particles in case one considers Biot numbers of order unity or larger.

3.3 Analytical solution for heat conduction in a cooled particle bed

In the following we present an analytical approach to calculate the temperature distribution in a sheared bed with a constant ambient fluid temperature $T_\mathrm{f}$, and study the limiting cases with respect to the Biot number. To the best of our knowledge no analytical solution for the mean temperature profile in a cooled bed of moving particles exists. To approach this issue, we first calculate the mean particle temperature distribution inside a static bed of cooled particles. Therefore, we use the particle heat conductivity $\lambda _\mathrm{p}$, as well as simple geometrical factors that describe the morphology of the particle bed. Specifically, we assume that the bed has an average effective cross-sectional area A, and an average effective cross-sectional perimeter U (see Fig. 4 that also illustrates their local counterparts). We note that the calculation of the effective area and perimeter cannot be done by taking a simple arithmetic mean of their local counterparts. This is due the fact that in the governing equation for heat conduction in the fin (discussed in the next paragraph) the cross-sectional area A comes into play in a non-linear fashion. Consequently, A will be also impacted by the average particle-particle contact area, which depends on $\phi _\mathrm{p}$, and hence the applied stress. Fortunately, in what follows it is not necessary to provide an expression for the effective cross-sectional area and perimeter. We will see that considering these effective quantities is sufficient to explain the qualitative features of the mean particle temperature distribution.

Fig. 4
Schematic illustration of the cooled fin approach (*left panel*) for computing the mean particle temperature based on an effective cross-sectional area A and perimeter U. Similar to the sheared *box* setup we assume $T_\mathrm{f} = (T_\mathrm{top} + T_\mathrm{bot})/2$. The right panel illustrates the corresponding local perimeter $U(y^{*})$ and the local cross sectional area $A(y^{*})$

In case we accept the above simplification, we can reduce the problem of heat conduction inside a static bed to the problem of heat transport in and around a convectively-cooled fin (see Fig. 4, left panel). The steady-state solution of this classical heat transport problem is straightforward, and relies on the following differential heat balance:

$$\begin{aligned} \lambda _\mathrm{p} \, \dfrac{\text {d}^2 T}{\text {d}y^2} - \dfrac{\alpha \, U}{A} (T-T_\mathrm{f}) = 0 \end{aligned}$$

(25)

Note that the above expression only considers thermal transport through the particles, and hence avoids complexities arising due to, e.g., heat conduction via the ambient fluid as mentioned in Kuipers et al. [24]. We feel that such complexities should be incorporated by a separate model for thermal transport in the surrounding fluid, and hence can be added in the future.

Normalization of the above heat balance equation by introducing

$$\begin{aligned}&y^{*} =\dfrac{y}{d_\mathrm{p}} \end{aligned}$$

(26)

$$\begin{aligned}&\theta = T - T_\mathrm{f} \end{aligned}$$

(27)

$$\begin{aligned}&\text {d} \theta = \text {d} T \end{aligned}$$

(28)

$$\begin{aligned}&\text {d}^2 \theta = \text {d}^2 T \end{aligned}$$

(29)

leads to

$$\begin{aligned} \dfrac{\text {d}^2 \theta }{\text {d}y^{*\,2}} = \underbrace{\dfrac{d_\mathrm{p} \, \alpha }{\lambda _\mathrm{p}}}_\mathrm{Bi} \, \underbrace{\dfrac{d_\mathrm{p} \, U}{A}}_{\mathrm{g}^{*} (Pe, \phi _\mathrm{p},\dot{\gamma })} \, \theta \end{aligned}$$

(30)

The first term on the right hand side of the above equation is equal to the Biot number. The second term, i.e., ($g^{*}$), represents a dimensionless metric for the bed morphology. The latter fluctuates in case the bed of particles is sheared (see our discussion below). However, it is reasonable to assume that this is irrelevant for the steady-state solution to a first approximation.

We next consider thermal transport in a sheared bed. Clearly, the rate of heat transport through the bed will be increased due to the motion of particles in such a case. This will not change the structure of the above differential equation as long as we assume that particle motion in the gradient direction leads to a diffusive transport of thermal energy. In other words, we assume that the additional heat flux caused by particle motion linearly scales with the temperature gradient. Consequently, only the magnitude of the heat conductivity will change, and one could simply introduce an effective heat conductivity of the sheared particle bed, i.e., $\lambda _\mathrm{eff}$ in Eq. 30. This effective heat conductivity will be some function of $\phi _\mathrm{p}$, $\dot{\gamma }$ and the particle parameters. Naturally, one would express $\lambda _\mathrm{eff} / \lambda _\mathrm{p}$ as some function of the Peclet number, the particle concentration and the dimensionless shear rate. Hence, one can easily split off the particles’ heat conductivity from $\lambda _\mathrm{eff}$ and remain the general structure of Eq. 30. Thus, we simply lump the effect of particle flow, i.e., the convective heat transport due to random particle motion, and the consequent change of A into the (unknown) function $g^{*}(Pe, \phi _\mathrm{p}, \dot{\gamma })$. Clearly, $g^{*}$ will decrease with increasing shear rate and increasing Peclet number (i.e., softer particles moving faster), since the effective heat conductivity and the area available for conduction will increase with increasing speed of shearing (or increasing particle softness). While $g^{*}$ lumps a large number of phyical effects, we have not attempted to decouple these effects in the present contribution. This is done since such a decoupling is not essential to understand the qualitative features of the particle temperature profiles discussed in the next paragraphs. Also, we note in passing that in the following, we have set $T_\mathrm{f}$ to be constant as indicated in Fig. 4.

We now use the following Ansatz for the solution of the temperature profile:

$$\begin{aligned} \theta = c_\mathrm{1 e^\mathrm{(Bi \, g^{*})y^{*}}} + c_\mathrm{2 e^{-(\mathrm Bi \, g^{*})y^{*}}} \end{aligned}$$

(31)

with the boundary conditions

$$\begin{aligned}&(1)&\, \, \, \, \text {for} \, y^{*}= 0: \theta = \theta _\mathrm{0} = T_\mathrm{bot} - T_\mathrm{f} \end{aligned}$$

(32)

$$\begin{aligned}&(2)&\, \, \, \, \text {for} \, y^{*}= H / d_\mathrm{p} = H^{*}: \theta = \theta _\mathrm{H} = T_\mathrm{top} - T_\mathrm{f} \end{aligned}$$

(33)

This leads us to the following constants:

$$\begin{aligned} c_\mathrm{1}= & {} \theta _\mathrm{0} - \dfrac{\theta _\mathrm{0} \, e^\mathrm{(Bi \, g^{*})H^{*}} - \theta _\mathrm{H}}{e^\mathrm{(Bi \, g^{*})H^{*}} - e^{-\mathrm (Bi \, g^{*})H^{*}}} \end{aligned}$$

(34)

$$\begin{aligned} c_\mathrm{2}= & {} \dfrac{\theta _\mathrm{0}\, e^\mathrm{(Bi \, g^{*})H^{*}} - \theta _\mathrm{H}}{e^\mathrm{(Bi \, g^{*})H^{*}} - e^{-(\mathrm Bi \, g^{*})H^{*}}}. \end{aligned}$$

(35)

Combining these constants with Eq. (31) one obtains the following mean particle temperature distribution:

$$\begin{aligned} \theta= & {} \left( \theta _\mathrm{0} - \dfrac{\theta _\mathrm{0}\, e^\mathrm{(Bi \, g^{*})H^{*}} - \theta _\mathrm{H}}{e^\mathrm{(Bi \, g^{*})H^{*}} - e^{-(\mathrm Bi \, g^{*})H^{*}}} \right) e^\mathrm{(Bi \, g^{*})y^{*}}\nonumber \\&+ \left( \dfrac{\theta _\mathrm{0}\, e^\mathrm{(Bi \, g^{*})H^{*}} - \theta _\mathrm{H}}{e^\mathrm{(Bi \, g^{*})H^{*}} - e^{-(\mathrm Bi \, g^{*})H^{*}}} \right) \text {e}^{-(\mathrm Bi \, g^{*})y^{*}} \end{aligned}$$

(36)

This equation does not allow us to explicitly calculate the effect of the shear rate on the resulting temperature profile. However, it provides us with an analytical solution to study certain limiting cases, namely sheared beds under the influence of high and low thermal heat exchange rates to the ambient fluid. Also, this analytical solution allows us to draw qualitative conclusions on the effect of the particle shear rate as mentioned above: faster shearing (i.e., increasing ${\varPi }$ or Pe) will lead to a more uniform temperature profile, since convective heat transport (due to random particle motion) becomes the dominating mode of thermal transport compared to heat transfer to the ambient fluid.

We note in passing that after calculating the temperature gradient from the above temperature profile, as well as integrating over the bed height, the mean heat flux based on the above analytical solution bed can be calculated as:

$$\begin{aligned} \dfrac{\partial \theta }{\partial y^{*} } = \theta '= & {} \left( \theta _\mathrm{0} - \dfrac{\theta _\mathrm{0}\, e^\mathrm{(Bi \, g^{*})H^{*}} - \theta _\mathrm{H}}{e^{(\mathrm Bi \, g^{*})H^{*}} - e^{-\mathrm (Bi \, g^{*})H^{*}}} \right) \, (\mathrm Bi \, g^{*}) \, e^\mathrm{(Bi \, g^{*})y^{*}} \nonumber \\&- \left( \dfrac{\theta _\mathrm{0}\, e^\mathrm{(Bi \, g^{*})H^{*}} - \theta _\mathrm{H}}{e^\mathrm{(Bi \, g^{*})H^{*}} - e^\mathrm{-(Bi \, g^{*})H^{*}}} \right) \, (\mathrm Bi \, g^{*}) \, e^{-(\mathrm Bi \, g^{*})y^{*}}\end{aligned}$$

(37)

$$\begin{aligned} \overline{q^\mathrm{y,analyt}}^{*}= & {} \frac{\lambda _\mathrm{eff} }{\lambda _\mathrm{p}} \end{aligned}$$

(38)

This heat flux has been normalized with the reference flux (i.e., $q_\mathrm{s}$), and requires the knowledge of $\lambda _\mathrm{eff}/ \lambda _\mathrm{p}$ or, alternatively, $g^{*}$. Unfortunately, the latter quantities are unknown, and hence must be modelled (e.g., via models for the conductive and convective fluxes developed in the present contribution). In the following we study certain limiting cases, and only compare the qualitative features of the temperature profiles inside the sheared bed between the simulation and the above analytical solution. Note, that $g^{*}$ has been adjusted in the following such that the difference between analytical solution and simulation data is a minimum. Thus, the following comparison is only helpful to judge whether the shape of the temperature profiles can be predicted. Models for the effective heat flux (due to conduction and convection) are proposed in Sect. 4, which can be used to compute the effective heat conductivity in a straight forward manner.

3.3.1 Small Biot number limit

The first limiting case we study is a sheared bed without any heat transfer to the ambient fluid. This is in line with the work of Rognon et al. [16] and Mohan et al. [13]. Therefore, it is clear that for a steady-state situation the temperature profile is linear, as seen in Fig. 5. A very good agreement can be observed from the above figure. Volume-averaged and surface temperature are collapsing in one point since the Biot number is small (and in the limit of thermally insulated particles, i.e., no heat exchange with the ambient fluid, $Bi=0$). Due to the low Biot number the solution is independent of the fluid temperature, the dimensionless shear rate and the volume fraction. Unfortunately, this solution does not lead to a deeper understanding of the total fluxes inside the bed and the relative contributions of convective and conductive transport rates. Thus, in the following we study a set of dimensionless parameters for which the temperature distribution is mainly governed by the heat transferred to the ambient fluid, and hence might help us to better understand the associated heat fluxes.

Fig. 5
Temperature profile for $\dot{\gamma } = 10^{-3}, \phi _\mathrm{p} = 0.64$. a $Pe = 0.01$, $Bi = 10^{-4}$, $g^{*}= 1500$, $T_\mathrm{f} = (T_\mathrm{top} + T_\mathrm{bot})/2$

3.3.2 High Biot number limit

The second limiting case is a sheared bed which is strongly cooled by the ambient fluid, i.e., heat transfer to the ambient fluid is fast. It is obvious that in this limiting case the temperature of the ambient fluid is of key importance. Also, we expect that for ${\varPi }$ approaching zero (at finite Bi) the convective and conductive flux will vanish, since the particle temperature approaches the fluid temperature. To illustrate this, we study high Biot number flows to highlight the mean particle temperature profiles in a sheared particle bed. For the shown set of dimensionless parameters a clear difference to Fig. 5 can be observed. The heat transfer to the ambient fluid leads to a fast relaxation of the bed temperature to the fluid temperature. Also, for even higher Biot numbers we observe a steeper gradient near the top and bottom of the bed (data not shown). This is explained by the corresponding decrease of ${\varPi }=Pe/Bi$, i.e., the dimensionless distance over which convective heat transport outbalances heat transfer to the ambient fluid decreases. In contrast, this gradient decreases with increasing Peclet number: fast shearing in combination with a low thermal conductivity of the particles smoothens out temperature gradients.

Fig. 6
Temperature profile for $\dot{\gamma } = 10^{-3}, \phi _\mathrm{p} = 0.64$. a $Pe = 100$, $Bi = 2$, $g^{*}= 0.5$, $T_\mathrm{f} = (T_\mathrm{top} + T_\mathrm{bot})/2$

Another key observation is that in case of low ${\varPi }$-number flows, the temperature gradient (and hence the thermal fluxes through the particle bed) is no longer constant over the simulation domain. Consequently, the size of the considered domain may affect the predicted mean thermal fluxes in that domain. Hence, in what follows it is essential to consider the size of the simulation domain for a correct interpretation of the results. Specifically, we now explore a wider range of dimensionless parameters to establish a more quantitative understanding of thermal fluxes through sheared particle beds (Fig. 6).

4 Simple shear flow

We now investigate the thermal behaviour of a sheared particle bed under different flow and thermal conditions. By applying Lees-Edwards boundary condition to a fully periodic box driven by a homogeneous shear flow, a combination of LIGGGHTS and ParScale can be used to study various influence parameters. The dimensions of the box are chosen to be $H/d_\mathrm{p}$ = 15 with a wide range of particle volume fractions ($\phi _\mathrm{p}$ = 0.30–0.64) studied. The z-direction serves as the spanwise direction, whereas in x-direction the homogeneous shear flow is driven. In y-direction we apply a temperature gradient by fixing the temperatures in the top and bottom layer. Figure 7 summarizes this setup in the $y-x$ plane, in which region A and C are the hot and cold region, respectively. In region B the temperature of the particles is allowed to evolve freely. Consequently we do not take the top and bottom layer into account during our post processing procedures, and just analyse thermal transport in the center region, i.e., region B. In order to study the transferred heat to the ambient fluid (note that [13, 16] considered particles in vacuum, i.e., perfectly insulated), the fluid temperature is set equal to the average of the top and bottom temperature. Note, that the number of particles, as well as their mean velocity is not constant in the center region, a fact that needs to be accounted for in the analysis. Wide ranges of various parameters and their influence on the thermal fluxes (corresponding to [13, 16]) are studied in what follows. An overview of these ranges is given in Table 4.

Fig. 7
Sheared bed assemblies considering three thermal regions A, B and C. The main flow direction is x as indicated by the *dashed arrows*, y denotes the gradient direction, and z indicates the spanwise direction

Table 4

Dimensionless input parameters for the sheared box simulations

Parameter	Min. value	Max. value
$\phi _\mathrm{p}$	0.3	0.64
$\dot{\gamma }$	$10^{-4}$	$10^{-1}$
Pe	$10^{-2}$	$10^{2}$
Bi	$10^{-5}$	25
$\mu $	0.1	Fixed
e	0.9	Fixed
$T_\mathrm{f}$	$(T_\mathrm{top}+T_\mathrm{bot})/2$	Fixed

Fig. 8
Typical result before the statistical steady state for $\phi _\mathrm{p} = 0.64$, $\dot{\gamma } = 10^{-3}$, a $Pe = 0.01$, $Bi = 10^{-5}$, b $Pe = 0.01$, $Bi = 25$, c $Pe = 100$, $Bi = 10^{-5}$, d $Pe = 100$, $Bi = 25$

These parameter ranges in Table 4 are chosen according to realistic scenarios involving solids particles in a gas. Relevant industrial applications for the high Biot number are, for example, thermally thick biomass particles (Mehrabian et al. [37]). The volume fraction covers more dilute flows ($\phi _\mathrm{p} = 0.3$), but also includes the densest packing possible under the assumption of mono-disperse spheres ($\phi _\mathrm{p} = 0.64$). Dimensionless shear rate and Peclet number relate to Rognon et al. [16] and account for soft and hard spheres and particle movement that can typically be found in earthquakes, landslides and general granular lubrication, respectively. Biot numbers up to $Bi = 25$ are typical for granular flows involving highly porous particles with low heat conductivity (e.g., wood, or polymeric materials), a typical size of $d_\mathrm{p} \sim $5–10 mm, and a Reynolds number of $Re = 100$ or higher.

In our simulations all particles are initialized with a uniform temperature, are forced to the temperatures in the top and bottom layer, and are sheared according to a predefined set of dimensionless parameters. After a certain shear deformation, the flow has converged into a statistical quasi-steady state, in which convective and conductive fluxes through the bed (i.e., region B) can be averaged and compared. Figure 8 shows typical results at such a state. In order to visualize the variety of flow situations, Fig. 8 summarizes results for certain limiting cases. Specifically, Fig. 8a shows the lowest Peclet and Biot number studied (compare Table 4). Figure 8b shows results for a flow that is dominated by the transferred flux to the ambient fluid, whereas Fig. 8c, d show results for the highest Peclet number studied and the extrema in the Biot number. As can be seen, a non-trivial distribution of particle temperatures develops in the simulation domain, depending on the combination of Peclet and Biot number. Interestingly, intra-particle temperature gradients appear for the situations characterized by a high Peclet number (see Fig. 8c, d). As expected, these gradients are most significant for the combination of a high Pe and Bi.

We next study the influence of the particle stiffness (i.e., the dimensionless shear rate) on conductive fluxes in the sheared bed over a wide range of Biot and Pelcet numbers. This analysis is motivated by the regimes observed for the evolution of the stresses in granular materials.

4.1 Effect of particle stiffness on conductive fluxes

Due to the large difference of the conductive flux depending on the particle concentration, Fig. 9 only depicts the influence of the particle stiffness for high particle loadings. Namely we study (a) $\phi _\mathrm{p}$ = 0.58 and (b) $\phi _\mathrm{p}$ = 0.64 for a Peclet number of 0.01. Thereby, higher dimensionless shear rates $\dot{\gamma }$ indicate softer particles (compare Eq. 16). Note, for lower particle concentrations the conductive flux dramatically decreases, and hence is of no significance for the practical application.

As seen on the left side of the figure, the dimensionless conductive heat flux drops to $10^{-5}$ (low Biot limit) and $10^{-9}$ (high Biot limit) for situations involving very stiff particles, i.e., at $\dot{\gamma } = 10^{-4}$. With increasing dimensionless shear rate the dimensionless conductive heat flux increases with a constant slope of two in double logarithmic space. This is observed over a wide range of Biot numbers. Thus, the transferred heat to the environment has no influence on this scaling law. Only at the highest studied shear rate this is not true any more, since the flow approaches an intermediate regime of heat conduction, similar to the one observed for stresses in sheared granular matter. This trend can also be observed for smaller particle volume fractions (data not shown), with the only difference that conductive fluxes are generally much smaller in such a flow.

In the intermediate regime the contribution of the conductive heat flux reaches a noticeable value. Most important, this is also the case for intermediate Biot numbers which are relevant for some industrial applications (i.e., $Bi \approx 1$). In contrast, the contribution for higher Biot numbers remains in the negligible range (e.g., for $Bi = 10$, the conductive flux is only 1 / 1000 of the reference flux). Investigating a higher particle volume fraction (i.e., $\phi _\mathrm{p} = 0.64$, see Fig. 9 (panel b)), the dimensionless conductive heat flux is not affected by the dimensionless shear rate anymore, and can be assumed to be constant for every shear rate. The results for the higher volume fraction and the dimensionless value are in agreement with Rognon et al. [16], even though their study was limited to one volume fraction. In our present work the flow reached the quasi-static regime where the ratio of contact forces and stiffness, which can be interpreted as a mean particle-particle overlap, does not change when changing the particles stiffness. Thus, the widely accepted fact [11] that for dense quasi-static granular (i) the dimensional contact stress scales linearly with the particles stiffness, and (ii) that the normalized stress is independent of the (dimensionless) shear rate in fixed volume simulations is of crucial importance: since contact stress and contact force are directly proportional, this also means that a typical inter-particle (contact) force scales linearly with the particles stiffness. Hence, the ratio of contact forces and stiffness, which can be interpreted as a mean particle-particle overlap, does not change when changing the particles stiffness in a fixed volume quasi-static flow. Since particle-particle conductive heat flux is affected by the overlapping area between particles, one would also expect that for dense granular flow in the quasi-static regime the conductive heat flux is not affected by the particles stiffness. Exactly this is what we observe in panel b of Fig. 9.

Fig. 10
Influence of the Peclet number and dimensionless shear rate on the dimensionless convective flux. a $\phi _\mathrm{p}$ = 0.54, b $\phi _\mathrm{p}$ = 0.62

Fig. 11
Influence of the Peclet number and dimensionless shear rate on the dimensionless convective flux for a variety of particle volume fractions a $\dot{\gamma } = 10^{-1}$, b $\dot{\gamma } = 10^{-2}$

Again, as already seen in Fig. 9 (panel a), the conductive flux near a shear rate of $\dot{\gamma } = 10^{-1}$ has an exceptional character also for the very dense regime: a slight increase of the conductive heat flux can be observed, indicating the shift to the intermediate regime. After evaluating the influence of a variety of Biot numbers and particle stiffness on the conductive flux, we will now investigate their effect on the convective fluxes as defined in Eq. (12).

4.2 Effect of the Peclet number and shear rate on convective fluxes

A number of research groups already made an attempt to model the convective heat flux in sheared beds. Mohan et al. [13] investigated the convective transport in combination with wet particles including liquid bridge formation, but never studied the influence on the resulting thermal flux. Rognon et al. [16] investigated the scaling of the convective heat flux in the gradient direction, and found that $q^\mathrm{conv,y} \approx 10^{-2} \, q_\mathrm{s} \, \tau $. The thermal number $\tau $ introduced by Rognon et al. scales linearly with the Peclet number defined in our contribution. Specifically, by assuming that the stress scales with $k_\mathrm{n}/d_\mathrm{p}$, we find from a comparison with Rognon et al.’s paper that $\tau = \sim \dot{\gamma } Pe$. Most important, since Rognon et al. [16] found that the particle stiffness has very little influence on the thermal transport rate for high Peclet numbers, $\tau $ and Pe are expected to be directly proportional and not affected by $\dot{\gamma }$. The previous work of Rognon et al. showed a regime map where the convective flux exceeds the conductive flux for $\tau \ge \approx 20$. We extend this previous analysis of Rognon et al. [16] to a variety of particle volume fractions, and have summarized our results in Fig. 10. For the moment we focus on a low Biot number in order to be consistent with Rognon et al. [16]. Both particle volume fractions considered in the present work show similar values for the dimensionless convective heat flux, indicating that random particle motion is only mildly influenced by the particle concentration in our simulations. For high particle concentrations (i.e., flow in the quasi-static regime, see Fig. 10b) our results are in good agreement with Rognon et al. [16]. This is true for both the slope with respect to the Peclet number, as well as the range of values. However, Rognon et al. [16] presented results in which an increase of the inertial number (i.e., $I \sim \dot{\gamma }$) does not necessarily cause an increase in the convective flux. This was reported to be especially the case at high Peclet numbers. We find that this is not always the case for somewhat lower particle concentrations: the dimensionless convective heat flux derived from our simulations indicated a significantly different, i.e., 1.5 times larger heat flux when increasing $\dot{\gamma }$ from $10^{-4}$ to $10^{-1}$. In other words: our results indicate that softer particles clearly lead to higher convective fluxes in dilute flows characterized by a low Peclet number.

We now have a closer look at the dependency of the convective fluxes near the critical particle concentration, i.e., the jamming point. Specifically, we consider the convective heat flux for the same particle stiffness (equal $\dot{\gamma }$) over a wide range of particle volume fractions. Figure 11a summarizes our findings for comparably stiff particles, specifically, we observe a minimum for the convective flux at $\phi _\mathrm{p} \approx 0.58$. We can only speculate on the origin of this minimum, which is clearly a result of the dependency of the particles’ random motion on the particle concentration. A tentative explanation is that below the critical volume fraction the velocity in Eq. (9) is the leading term. For $\phi _\mathrm{p > 0.58}$ the internal energy of the particles ($m_\mathrm{eff} \, c_\mathrm{p} \, T_\mathrm{vol,avg}$) is increasing, simply because more particles fit into a certain volume. However, the convective flux increases by approximately one order of magnitude in case we increase the particle volume fraction by just 5 percent. Hence, our simple explanation cannot fully describe such a strong increase in the thermal transport rate.

We finally note that according to Chialvo et al. [11] the critical particle volume fraction for transition to the quasi-static regime (in the context of granular rheology) is system dependant, and mainly influenced by the inter-particle friction coefficient. Specifically, this previous study identified a minimum critical volume fraction for $\mu = 1.0$ of ($\phi _\mathrm{c = 0.581}$), and a maximum for $\mu = 0.0$ at ($\phi _\mathrm{c} = 0.636$). Thus, when applying the results of our study, one needs to consider the inter-particle friction coefficient used in our present contribution.

Next, we consider the effect of the Biot number on the conductive fluxes.

4.3 Impact of the Biot number on conductive fluxes

Figure 12 depicts the influence of the Biot number on the conductive flux over a wide range of particle volume fractions. Thereby we focus on the highest and smallest studied Peclet number in order to gain some understanding how the speed of shearing affects the heat fluxes. As can be seen, the dimensionless conductive heat flux is constant for very low Biot numbers, and monotonically decreases with increasing Biot number (there are some fluctuations for $Pe=100$, situations involving stiff particles, and comparably dilute particle beds. Conductive fluxes are very small for these systems, and hence not of primary interest). This trend is also seen for other Peclet numbers and dimensionless shear rates (data not shown). Most important, the point at which the the Biot number influences the conductive heat flux shows a minor dependence on the particle volume fraction $\phi _\mathrm{p}$ and shear rate $\dot{\gamma }$. For $Pe = 0.01$ this point is $Bi \approx 10^{-2}$, while for $Pe = 100$ this point is located at $Bi \approx 1$. As seen before the scattering of conductive fluxes is inversely proportional to the dimensionless shear rate: higher dimensionless shear rates lead to less scattering (compare Fig. 12a, b). A major dependency of the dimensionless conductive heat flux on the Peclet number is observed, especially for high Bi. According to Eq. (20), at the same dimensionless shear rate and cooling rate (i.e., fixed $\alpha $), an increase in the particles’ thermal conductivity results in a lower Peclet number. However, in such a scenario the Biot number would also decrease inversely proportional to the heat conductivity. Thus, it is instructive to plot the conductive heat flux as a function of ${\varPi }^{-1}$, since then the particles’ heat conductivity does not influence ${\varPi }$. Figure 13 illustrates these data, where we can now easily identify the effect of intra-particulate heat transfer: for a fixed value of ${\varPi }$ and a fixed dimensionless shear rate, a decrease in Pe reflects an increase of the particles’ heat conductivity, and hence smaller intra-particle temperature gradients.

Fig. 12
Influence of the Biot number on the conductive flux over a wide range of particle volume fractions. a Pe = 0.01, $\dot{\gamma } = 10^{-2}$, b Pe = 0.01, $\dot{\gamma } = 10^{-4}$, c Pe = 100, $\dot{\gamma } = 10^{-2}$, d Pe = 100, $\dot{\gamma } = 10^{-4}$, e Pe = 1, $\dot{\gamma } = 10^{-2}$, f Pe = 1, $\dot{\gamma } = 10^{-4}$

If we now consider the data for $\dot{\gamma } = 10^{-2}$ in Fig. 13 (panel a), we observe that the conductive heat flux decreases upon an increase of the Peclet number (i.e., increasing intra-particle temperature gradients). Thus, the surface temperature for the case of $Pe =100$ is closer to that of the ambient fluid, leading to a suppressed heat conduction. Surprisingly, this effect is less pronounced for stiff particles, i.e., $\dot{\gamma } = 10^{-4}$. The conductive heat transfer rate for such stiff and rapidly cooled particles is, however, small, and hence of no technological relevance. Considering a more dense particle bed (i.e., the data shown in Fig. 13, panel b), we see similar trends, illustrating the importance to account for intra-particle temperature gradients in situations in which dense particle beds are rapidly cooled or slowly sheared (i.e., ${\varPi }$ is small). Interestingly, in particle beds undergoing fast shearing (characterized by large values for ${\varPi }$), the effect of intra-particle temperature gradients is rather small for $\phi = 0.58$. However, as illustrated in Fig. 13, panel b, for $\phi = 0.64$ and stiff particles, an increase of the Biot number (for ${\varPi }=const$) results in a large drop of the conductive flux. We have not systematically explored the origin of this effect. We speculate that it is due to the drop of the surface temperature in high Bi-number flows that greatly affects the conductive flux through the bed. After evaluating the influence of the Biot number, we now look more closely on the influence of the Peclet number in dense packed beds for a fixed Bi number. This is to illustrate the important effect of the speed of shearing on the conductive heat flux, which has been identified in the previous paragraph.

4.4 Effect of the Peclet number on conductive flux at several Biot numbers

In Fig. 14 we plot the dimensionless conductive heat flux over various Peclet numbers with different dimensionless shear rates and Biot numbers ranging from $10^{-5}$ to 25. As mentioned before, a higher Peclet number reflects a fast shearing of the particle bed. From Fig. 14 (panel a to d) we see that a change in the Peclet number has very little influence on the conductive heat flux for situations characterized by low Biot numbers (e.g., $Bi \le 0.1)$. This is in good agreement with Rognon et al. [16], and simply indicates that cooling caused by the ambient fluid is irrelevant since particles are quickly dispersed. In contrast, the dimensionless heat flux for higher Biot numbers strongly depends on the Peclet number: in some cases (e.g., Fig. 14, panel a, $Bi = 25$) we observe changes up to three orders of magnitude in the conductive heat flux. In other flow situations (Fig. 14b–d) the enhancement of the conductive heat flux is only seen for relatively high Peclet numbers. In summary, in dense particulate flows that are characterized by a larger Peclet number, a smaller difference of the conductive heat transfer rate is observed upon a change of the Biot number. The physical argument is, that in these quickly sheared beds heat is re-distributed by random particle motion, and hence intra-particle temperature gradients are of secondary importance.

Fig. 15
Influence of the Pelect number on the interial and quasi-static regime for a $Bi = 10^{-4}$, as well as b $Bi = 2$

As mentioned before, Rognon et al. [16] showed the existence of a general scaling law for the heat flux in sheared beds, and Mohan et al. [13] adapted and extended this to the flux of liquid adhering to the particles. We next make an attempt to establish a regime map that also accounts for the cooling by the ambient fluid.

4.5 Regimes of conductive heat transport

As demonstrated by Mohan et al. [13], a regime map for the conductive fluxes can be constructed by appropriate re-scaling of the dimensionless shear rate and fluxes. The idea is to perform simulations for a variety of particle concentrations (in our case $\phi $ was varied between 0.50 and 0.64), and then hope for a collapse of the data after the re-scaling operation. We also follow such and idea in the present contribution, and use for the re-scaling operation the exponents $a = 1/3, b = 7/5$ and $\phi _\mathrm{c} = 0.613$ as shown in the axis labels of Fig. 15. Most important, in addition to the particle concentration, we have also varied the Peclet and Biot number in our study. A collapse of the regimes for this variation in the thermal parameters would indicate that the (normalized) conductive flux is only a function of the flow parameters of the system (i.e., $\dot{\gamma }$ and $\phi $). We now probe if this is truly the case.

First, we investigate the influence of the Peclet number on the inertial and quasi-static regime at fixed Biot numbers. Figure 15 (panel a) reveals the dependency of the re-scaled fluxed on the Peclet number for a slow rate of cooling, i.e., $Bi=10^{-4}$. Our data indicates a reasonable agreement of the re-scaled data for all studied Peclet numbers (note that we studied $Pe = 0.01$ in most detail). Since we focus on particle volume fractions with $\phi _\mathrm{p} \ge 0.50$, all three flow regimes known from granular rheology can be identified: (i) an interial regime characterized by a quadratic increase of the conductive flux with the shear rate, (ii) a quasi-static regime where fluxes are independent of the shear rate, and (iii) an intermediate regime that is only relevant for very soft particles. Most important, our data is also in good agreement with the previous work of Mohan et al. [13]. Clearly, this is due to the small amount of heat transferred to the ambient fluid: in Fig. 15 (panel a) we considered a very small Biot number, and large values for ${\varPi }$ ranging from $10^2$ to $10^6$. The latter hints to the fact that the rate of cooling is small compared to convective heat transport, i.e., the redistribution of thermal energy due to particle motion in our simulation domain is fast.

As one might anticipate, a different behaviour will develop at higher Biot numbers, i.e., in case particles are rapidly cooled by the ambient fluid. Specifically, at a Biot number of $Bi = 2$, and as shown in Fig. 15 (panel b), we observe that the Peclet number has a critical effect on the conductive heat flux. First, considering the data for $Pe = 100$ (i.e., ${\varPi }= 50$) we observe that conductive heat fluxes are still of comparable magnitude to that observed for $Bi=10^{-4}$. Also, the three regimes can be identified, all with the same scaling with respect to the shear rate. The physical interpretation is that the redistribution of thermal energy is still fast compared to the cooling rate as indicated by the large value for ${\varPi }$. Thus, particles cannot cool down significantly while they move through the shear flow in our simulations. Consequently, the Biot number (characterizing the intra-particle temperature distribution) has little effect for large Peclet number flows as long ${\varPi }$ is large. This is due to the fact that the overall cooling of the particles is small, and hence intra-particle temperature gradients are (relative to the temperature gradient applied to the simulation domain) also small.

Most important, the situation changes as we decrease the Peclet number: for $Pe = 1$ (i.e., ${\varPi }= 0.5$) we already see a substantial decrease of the conductive heat flux, and with decreasing Pe (and hence ${\varPi }\ll 1$) thermal transport due to conduction is increasingly suppressed. Also, the slope of the curve characterizing the normalized conductive heat flux in the inertial regime appears to gradually increase with decreasing ${\varPi }$. However, this increase is rather small. We do not attempt to speculate on the physical origin of this finding due to the lack of more data that can support our arguments.

The physical interpretation of the observed decrease of the conductive heat flux for intermediate and small Pe numbers is that a layer of “equilibrated” particles forms: these particles have a temperature close to that of the ambient fluid. Consequently, this layer of equilibrated particles chokes off the conductive heat flux through the simulation box, since heat is primarily transferred to the ambient fluid. Clearly, this layer becomes thicker (and the layer in which particles still having an appreciable temperature gradient becomes thinner) when decreasing ${\varPi }$. As already discussed in our theoretical analysis presented in Sect. 3.3, the size of the simulation domain is important in these situations: clearly, the size of the simulation domain determines the relative thickness of the layer containing equilibrated particles, and hence affects the computed (domain-averaged) heat fluxes.

5 Conclusions

We investigated the heat transfer through a sheared bed of inertial particles that is cooled with a fixed rate by an ambient fluid. Also, we presented the newly developed library ParScale which we coupled to the well established DEM solver LIGGHHTS. This library, which models intra-particle transport processes, was used to resolve radial temperature profiles within every single particle. This enabled us to model the effect of the transferred heat flux (to the ambient fluid) on intra-particle temperature profiles. Hence, we accounted for the competition of heat transferred to the surrounding fluid, and the rate of heat conduction within the particles.

Next, we presented a simple analytical solution for the temperature profile in a sheared bed, and proved the consistency of this solution with our simulation data. Our solution is applicable over a wide range of flow situations, and requires the specification of only one additional system-dependent parameter if applied to simple shear flow.

Furthermore, we showed that our approach to discretize the particle in only one spatial direction (i.e., radially) is in good agreement with data obtained from direct numerical simulations (DNS) that utilize a full three-dimensional discretiztion. Specifically, our simulations indicate that the difference between DNS data, and the data obtained from a one-dimensional discretization is decreasing with rising Reynolds numbers. Also, the ratio of the thermal conductivities of the particle and the surrounding fluid is of a certain significance. Often, intra-particle temperature gradients are of industrial relevance only in high Reynolds number flows (i.e., large particles), and less important in case fluid-particle relative motion is slow (i.e., small Reynolds numbers). This suggests that our approach that relies on ParScale is an affordable, yet accurate way to account for intra-particle temperature gradients.

We then studied thermal transport rates for granular flows characterized by a low Biot number (i.e., slow heat transfer to the surrounding fluid), and found good agreement with literature data that considered particles in vacuum. Also, we extended the analysis by studying a wide range of particle volume fractions. Most important, in situations characterized by a small dimensionless shear rate we found that the convective flux shows a global minimum at the critical particle volume fraction. This finding coincides with the well known maximum in the fluctuations of the (normalized) pressure at the critical state. For softer particles (i.e., flows characterized by a large dimensionless shear rate) this minimum vanishes. The convective heat flux is then nearly unaffected by the particle concentration.

Subsequently, we focused on higher Biot numbers, and studied the influence of the Biot and Peclet number on the conductive heat flux through a sheared particle bed. We found that the conductive heat flux remains almost constant for relevant Biot numbers (i.e., speeds of cooling) at high Peclet numbers. For dense flows only a weak dependency is seen with respect to the particle stiffness, whereas for more dilute flows the conductive heat flux drops by more than one order of magnitude in case the particle stiffness is increased. This clearly hints to different regimes of heat conduction in dense and dilute beds, in analogy to the three stress regimes that are well accepted in granular rheology.

In order to make one step towards a unified model to predict thermal transport through sheared particle beds, we made an attempt to collapse the scaled conductive heat fluxes. We find that for some of the investigated flow situations the conductive heat fluxes can be collapsed into a single curve. This is a strong indication that a unified regime map that characterizes the mode of heat conduction in a cooled bed of particles can be constructed. Specifically, we showed that for high Peclet and small Biot numbers (i.e., large values for the parameter ${\varPi }$) the map characterizing the conductive heat flux is nearly independent of the Biot number. Thus, our data can be used to make reliable predictions of conductive heat transfer rates for these situations. In contrast, for small Peclet and high Biot numbers still challenges remain to close our model. Clearly, in order to create a rigorous regime map that allows a precise calculation of conductive, convective and transferred heat transfer rates, a deeper analysis of the data presented in this study is necessary. Most important, such an analysis has to account for the (normalized) size of the simulation domain. This is due to the nature of particle cooling in a granular shear flow, which leads to a non-uniform temperature gradient. We expect that the newly introduced parameter ${\varPi }$, as well as the newly derived expression for the local temperature gradient (see Sect. 3.3), will be inspiration for future work that may account for these effects.

The work of Morris et al. [14] discussed the effect of stiffness on the results, and provides a stiffness correction. Similarly, our results could be used to propose such a stiffness correction. Indeed, and as outlined in Morris et al. [14], developing such a correction for dense granular flows remains a delicate task.

Our study certainly has some limitations: especially in dense flows of soft particles, our approach to model the transferred heat flux should be extended by accounting for the surface area of the particle that is covered due to particle deformation during a collision. For example, this could be done using well established expressions for the particle-particle contact area, or (in more extreme situations with respect to particle concentration and softness) once could adopt a Monte Carlo area integration method. Such a method is already implemented in LIGGGHTS. Another important assumption of the present analysis was that the ambient fluid is kept at a fixed temperature. This assumption is valid as long as the heat transferred to the fluid is quickly removed, e.g., convection in the ambient fluid is sufficiently strong. Specifically, this means that the spatial fluid temperature variation is small over a characteristic distance (i.e., a few particle diameters), which is the case for high fluid Peclet numbers, and depends on the particle concentration (Munichi et al. [38]). This assumption of fast convective transport holds for most applications involving comparably large (i.e., mm-sized) particles suspended in a gas. However, future thoughts may extend our present work to applications that are characterized by extreme temperature gradients, i.e., systems involving smaller particles and low fluid Peclet numbers (i.e., slow fluid-particle relative motion). Also, since we fixed the ambient fluid temperature and the heat transfer coefficient, both quantities must be provided from a supplementary fluid model (e.g., that used in Kuipers et al. [24]). This exceeded the current study, however, can be implemented in a straight forward manner. Future considerations could then establish an even more rigorous understanding of thermal transport in flowing granular matter and the ambient fluid encountered in a number of engineering applications.

Notes

Acknowledgements

Open access funding provided by Graz University of Technology. We acknowledge the support by the European Commission through FP7 Grant agreement no. 604656, project ’NanoSim’. We thank ’NAWI Graz’ for providing access to dcluster.tugraz.at.

Compliance with ethical standards

Conflict of interest

The authors declare that they have no conflict of interest.

Appendix

Appendix 1: DEM parameters and calculation routines

The normal spring stiffness and the coefficient of restitution were set by adjusting the effective Young’s modulus $Y_\mathrm{eff}$ and the damping coefficient $\eta $. Thus, the following equations were applied:

$$\begin{aligned}&k = \dfrac{16}{15} \sqrt{r_\mathrm{eff}} \, Y_\mathrm{eff} \, \left( \dfrac{15 \, m_\mathrm{eff} \, v^2_\mathrm{char}}{16 \, \sqrt{r_\mathrm{eff}} \, Y_\mathrm{eff}}\right) ^{1/5}, \end{aligned}$$

(39)

$$\begin{aligned}&Y_\mathrm{eff} =\left[ \dfrac{(\gamma / \gamma ^{*})^2 d_\mathrm{p^3} \rho _\mathrm{p}}{(16/15)^{4/5} (r_\mathrm{eff})^{2/5} (m_\mathrm{eff})^{1/5} (v_\mathrm{char})^{2/5}}\right] ^{5/4}, and \end{aligned}$$

(40)

$$\begin{aligned}&\eta = \sqrt{\dfrac{4\, m_\mathrm{eff} \, k}{1 + \left( \frac{\pi }{\text {ln}(e)}\right) }} \end{aligned}$$

(41)

Note that the characteristic impact velocity $v_\mathrm{char}$ drops out of Eq. (39) after inserting Eq. (40) and therefore is irrelevant for the subsequent dimensional analysis. Table 5 outlines the adjusted parameter in order to obtain the dimensionless shear rate $\dot{\gamma }$.

Table 5

Adjusted DEM parameters

$\dot{\gamma }$	$Y_\mathrm{eff}$	$\bigtriangleup t$
$10^{-1}$	$1.32 \,\times 10^{3}$	$2.50 \,\times 10^{-3}$
$10^{-2}$	$4.18 \,\times 10^{5}$	$2.50 \,\times 10^{-4}$
$10^{-3}$	$1.32 \,\times 10^{8}$	$2.50 \,\times 10^{-5}$
$10^{-4}$	$4.18 \,\times 10^{10}$	$2.50 \,\times 10^{-6}$

Appendix 2: CDS scheme

For discretisation in physical space a second order accurate scheme (i.e., a central differences scheme) is used for the first and second derivative:

$$\begin{aligned}&\dfrac{\partial T}{\partial r} = \dfrac{T_\mathrm{h+1} - T_\mathrm{h-1}}{2 \, \bigtriangleup r} + O(\bigtriangleup r^2) \end{aligned}$$

(42)

$$\begin{aligned}&\dfrac{\partial ^2 T}{\partial r^2} = \dfrac{T_\mathrm{h+1} + T_\mathrm{h-1} - 2 T_\mathrm{h}}{\bigtriangleup r^2} + O(\bigtriangleup r^2) \end{aligned}$$

(43)

Appendix 3: Verification case—cooling of a sphere

The verification case considers a situation in which a spherical particle, initialized with the uniform temperature $T_\mathrm{0}$, is cooled by an ambient fluid with temperature $T_\mathrm{f}$. Table 6 summarizes the parameters of this case. Figure 16 illustrates the comparison between the numerical solution by ParScale and the analytical solution provided by [39] for a number of time coordinates. A very good agreement can be found over all investigated times and spatial coordinates with an average relative error of $10^{-5}$.

Table 6

Parameters for the verification case ’cooling of a sphere’

$c_\mathrm{p}$	300	(J$\,\text {m}^{-3}\,$K)
$\rho $	1000	(kg$\, \text {m}^{-3}$)
$\lambda _\mathrm{p}$	1	(W$\, \text {m}^{-1} \,\text {K}^{-1}$)
$\alpha $	100	(W$\, \text {m}^{-2} \,\text {K}^{-1}$)
$r_\mathrm{p}$	$5\cdot 10^{-3}$	(m)
$T_\mathrm{0}$	800	(K)
$T_\mathrm{f}$	300	(K)
$t_\mathrm{1},t_\mathrm{2},t_\mathrm{3},t_\mathrm{4}$	2,5,8,10	(s)

Fig. 16
Numerical (*symbols*) and analytical results (*lines*) for the temperature distribution in a sphere cooled by convection at $t_\mathrm{1}$ = 2 s, $t_\mathrm{2}$ = 5 s, $t_\mathrm{3}$ = 8 s, and $t_\mathrm{4}$ = 10 s

References

1.
Ding, Y.L., Forster, R.N., Seville, J.P.K., Parker, D.J.: Some aspects of heat transfer in rolling mode rotating drums operated at low to medium temperatures. Powder Technol. 121(2–3), 168–181 (2001)CrossRefGoogle Scholar
2.
Rickelt, S., Sudbrock, F., Wirtz, S., Scherer, V.: Coupled DEM/CFD simulation of heat transfer in a generic grate system agitated by bars. Powder Technol. 249, 360–372 (2013)CrossRefGoogle Scholar
3.
Peters, B.: Thermal Conversion of Solid Fuels (Developments in Heat Transfer). WIT Press, Ashurst (2002)Google Scholar
4.
Smart, A., Ottino, J.M.: Granular matter and networks: three related examples. Soft Matter 4(11), 2125 (2008)ADSCrossRefGoogle Scholar
5.
Shi, D., Vargas, W.L., McCarthy, J.J.: Heat transfer in rotary kilns with interstitial gases. Chem. Eng. Sci. 63(18), 4506–4516 (2008)CrossRefGoogle Scholar
6.
Vargas, W.L., McCarthy, J.J.: Heat conduction in granular materials. AIChE J. 47(5), 1052–1059 (2001)CrossRefGoogle Scholar
7.
Rice, J.R.: Heating and weakening of faults during earthquake slip. J. Geophys. Res. Solid Earth 111(5), 1–29 (2006)Google Scholar
8.
Sulem, J., Lazar, P., Vardoulakis, I.: Thermo-poro-mechanical properties of clayey gouge and application to rapid fault shearing. Int. J. Numer. Anal. Methods Geomech. 31(3), 523–540 (2007)CrossRefzbMATHGoogle Scholar
9.
Otsuki, K.: Fluidization and melting of fault gouge during seismic slip: Identification in the Nojima fault zone and implications for focal earthquake mechanisms. J. Geophys. Res. 108(B4) (2003). doi: 10.1029/2001JB001711
10.
Alonso-Marroquín, F., Vardoulakis, I., Herrmann, H.J., Weatherley, D., Mora, P.: Effect of rolling on dissipation in fault gouges. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 74(3), 1–10 (2006)CrossRefGoogle Scholar
11.
Chialvo, S., Sun, J., Sundaresan, S.: Bridging the rheology of granular flows in three regimes. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 85(2), 1–8 (2012)CrossRefGoogle Scholar
12.
Luding, S.: Introduction to discrete element methods basics of contact force models and how to perform the micro-macro transition to continuum theory. Eur. J. Environ. Civil Eng. 12, 785–826 (2008)CrossRefGoogle Scholar
13.
Mohan, B., Kloss, C., Khinast, J., Radl, S.: Regimes of liquid transport through sheared beds of inertial smooth particles. Powder Technol. 264, 377–395 (2014)CrossRefGoogle Scholar
14.
Morris, A.B., Americas, S.: Development of soft-sphere contact models for thermal heat conduction in granular flows. AIChE J. 02(00), 1–10 (2016)Google Scholar
15.
Tsory, T., Ben-Jacob, N., Brosh, T., Levy, A.: Thermal DEM-CFD modeling and simulation of heat transfer through packed bed. Powder Technol. 244, 52–60 (2013)CrossRefGoogle Scholar
16.
Rognon, P., Einav, I., Bonivin, J., Miller, T.: A scaling law for heat conductivity in sheared granular materials. EPL (Europhys. Lett.) 89(5), 1–6 (2010)CrossRefGoogle Scholar
17.
Rognon, P., Einav, I.: Thermal transients and convective particle motion in dense granular materials. Phys. Rev. Lett. 105, 1–4 (2010)CrossRefGoogle Scholar
18.
Batchelor, G.K., O’Brien, R.W.: Thermal or electrical conduction through a granular material. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 355(1682), 313–333 (1977)Google Scholar
19.
Shimizu, Y.: Three-dimensional simulation using fixed coarse-grid thermal-fluid scheme and conduction heat transfer scheme in distinct element method. Powder Technol. 165(3), 140–152 (2006)CrossRefGoogle Scholar
20.
Cheng, G.J., Yu, A.B., Zulli, P.: Evaluation of effective thermal conductivity from the structure of a packed bed. Chem. Eng. Sci. 54, 4199–4209 (1999)CrossRefGoogle Scholar
21.
Feng, Y.T., Han, K., Owen, D.R.J.: Discrete thermal element modelling of heat conduction in particle systems: pipe-network model and transient analysis. Powder Technol. 193(3), 248–256 (2009)CrossRefGoogle Scholar
22.
Feng, Y.T., Han, K., Li, C.F., Owen, D.R.J.: Discrete thermal element modelling of heat conduction in particle systems: basic formulations. J. Comput. Phys. 227(10), 5072–5089 (2008)ADSCrossRefzbMATHGoogle Scholar
23.
Oschmann, T., Schiemann, M., Kruggel-Emden, H.: Development and verification of a resolved 3D inner particle heat transfer model for the discrete element method (DEM). Powder Technol. 291, 392–407 (2015)CrossRefGoogle Scholar
24.
Kuipers, J.A.M., Prins, W., Van Swaaij, W.P.M.: Numerical calculation of wall-to-bed heat-transfer coefficients in gas-fluidized beds. AIChE J. 38(7), 1079–1091 (1992)CrossRefGoogle Scholar
25.
Yin, X., Sundaresan, S.: Fluid-particle drag in low-reynolds-number polydisperse gassolid suspensions. AIChE J. 55(6), 1352–1368 (2009)CrossRefGoogle Scholar
26.
Radl, S., Forgber, T., Aigner, A., Kloss, C.: ParScale—an open-source library for the simulation of intra-particle heat and mass transport processes in coupled simulations. In: IV International Conference on Particle-based Methods Fundamentals and Applications (PARTICLES 2015), pp. 46–55 (2015)Google Scholar
27.
Forgber, T., Tolchard, J.R., Zaabout, A., Dahl, P.I., Radl, S.: Optimal particle parameters for CLC and CLR processes—predictions by intra-particle transport models and experimental validation. In: IV International Conference on Particle-Based Methods Fundamentals and Applications (PARTICLES 2015), pp. 101–111 (2015)Google Scholar
28.
Ranz, W., Marshal, W.I.: Evaporation from drops. Chem. Eng. Prog. 48, 141–146 (1952)Google Scholar
29.
Gunn, D.J.: Transfer of heat or mass to particles in fixed and fluidised beds. Int. J. Heat Mass Transf. 21(4), 467–476 (1978)CrossRefGoogle Scholar
30.
Kloss, C., Goniva, C., Hager, A., Amberger, S., Pirker, S.: Models, algorithms and validation for opensource DEM and CFD-DEM. Prog. Comput. Fluid Dyn. 12, 140–152 (2012)MathSciNetCrossRefGoogle Scholar
31.
https://github.com/CFDEMproject/ParScale-PUBLIC (2015)
32.
Nordstrom, K.N., Verneuil, E., Arratia, P.E., Basu, a, Zhang, Z., Yodh, aG, Gollub, J.P., Durian, D.J.: Microfluidic rheology of soft colloids above and below jamming. Phys. Rev. Lett. 105(17), 1–4 (2010)Google Scholar
33.
Hatano, T.: Scaling properties of granular rheology near the jamming transition. J. Phys. Soc. Jpn. 77(12), 18–21 (2008)CrossRefGoogle Scholar
34.
Otsuki, M., Hayakawa, H.: Critical behaviors of sheared frictionless granular materials near the jamming transition. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 80(1), 5–10 (2009)Google Scholar
35.
Schmidt, R., Nikrityuk, P.: Numerical simulation of the transient temperature distribution inside moving particles. Can. J. Chem. Eng. 90, 246–262 (2012)CrossRefGoogle Scholar
36.
Nikrityuk, P., Meyer, B.: Gasification Processes: Modeling and Simulation, 1 edn. Wiley (2014)Google Scholar
37.
Mehrabian, R., Zahirovic, S., Scharler, R., Obernberger, I., Kleditzsch, Sn, Wirtz, S., Scherer, V., Lu, H., Baxter, L.L.: A CFD model for thermal conversion of thermally thick biomass particles. Fuel Process. Technol. 95, 96–108 (2012)CrossRefGoogle Scholar
38.
Municchi, F., Radl, S.: Consistent closures for Euler-Lagrange models of bi-disperse gas-particle suspensions derived from particle-resolved direct numerical simulations. submitted to: International Journal of Heat and Mass Transfer (2016)Google Scholar
39.
Crank, J.: The Mathematics of Diffusion, 2nd edn. Clarendon Press, Oxford (1975)zbMATHGoogle Scholar

Copyright information

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

Thomas Forgber
- 1
Email authorView author's OrcID profile
Bhageshvar Mohan
- 1
Christoph Kloss
- 2
Stefan Radl
- 1

1.Institute of Process- and Particle EngineeringGrazAustria
2.DCS Computing GmbHLinzAustria

Reference system	Equation
Particle flow	\(\dfrac{d\, \mathbf{x}_\mathrm{i}}{d \, t} = \mathbf{v}_\mathrm{i} \)
	\(m \, \dfrac{d \, \mathbf{v}_\mathrm{i}}{d \, t} = \sum \limits _\mathrm{j} (\mathbf{f}\,^\mathrm{t}_\mathrm{ij} + \mathbf{f}\,^\mathrm{n}_\mathrm{ij}) \)
	\(I_\mathrm{i} \, \dfrac{d \, \varvec{\omega }_\mathrm{i}}{d\, t} = \sum \limits _\mathrm{j} \mathbf{f}\,^\mathrm{t}_\mathrm{ij} \times \mathbf{r}_\mathrm{ij}\)
Fluid flow	\( \varvec{\nabla } \cdot \mathbf{u} = 0\)
	\(\dfrac{ \partial \, \mathbf{u}}{\partial \, t} + \varvec{\nabla } \cdot \left( \mathbf{u} \mathbf{u} \right) = -\varvec{\nabla }p+ Re^{-1} \nabla ^2{\mathbf{u}} \)
	\(\dfrac{ \partial \, \theta }{\partial \, t} +\varvec{\nabla } \cdot \left( \mathbf{u} \theta \right) = Pe^{-1} \nabla ^2{\theta }\)
Internal thermal transport	\(\dfrac{\partial T}{\partial t} = a \cdot \left( \dfrac{\partial ^2 T}{\partial r^2} + \dfrac{2}{r} \, \dfrac{\partial T}{\partial r} \right) \)

\(\dot{\gamma }\)	\(Y_\mathrm{eff}\)	\(\bigtriangleup t\)
\(10^{-1}\)	\(1.32 \,\times 10^{3}\)	\(2.50 \,\times 10^{-3}\)
\(10^{-2}\)	\(4.18 \,\times 10^{5}\)	\(2.50 \,\times 10^{-4}\)
\(10^{-3}\)	\(1.32 \,\times 10^{8}\)	\(2.50 \,\times 10^{-5}\)
\(10^{-4}\)	\(4.18 \,\times 10^{10}\)	\(2.50 \,\times 10^{-6}\)

\(c_\mathrm{p}\)	300	(J\(\,\text {m}^{-3}\,\)K)
\(\rho \)	1000	(kg\(\, \text {m}^{-3}\))
\(\lambda _\mathrm{p}\)	1	(W\(\, \text {m}^{-1} \,\text {K}^{-1}\))
\(\alpha \)	100	(W\(\, \text {m}^{-2} \,\text {K}^{-1}\))
\(r_\mathrm{p}\)	\(5\cdot 10^{-3}\)	(m)
\(T_\mathrm{0}\)	800	(K)
\(T_\mathrm{f}\)	300	(K)
\(t_\mathrm{1},t_\mathrm{2},t_\mathrm{3},t_\mathrm{4}\)	2,5,8,10	(s)

Heat transfer rates in sheared beds of inertial particles at high Biot numbers

Abstract

Keywords

List of symbols

Latin characters

Greek characters

Superscripts

Subscripts

1 Introduction

2 Simulation method

2.1 Particle flow model

2.2 Transport within a particle

2.2.1 Governing equations

2.3 Code architecture and parallel coupling strategy

2.4 Thermal fluxes

3 Theoretical analysis

3.1 Dimensional analysis

3.2 Effect of heat conduction within the particle

3.3 Analytical solution for heat conduction in a cooled particle bed

3.3.1 Small Biot number limit

3.3.2 High Biot number limit

4 Simple shear flow

4.1 Effect of particle stiffness on conductive fluxes

4.2 Effect of the Peclet number and shear rate on convective fluxes

4.3 Impact of the Biot number on conductive fluxes

4.4 Effect of the Peclet number on conductive flux at several Biot numbers

4.5 Regimes of conductive heat transport

5 Conclusions

Notes

Acknowledgements

Compliance with ethical standards

Conflict of interest

References

Copyright information

Authors and Affiliations

Personalised recommendations

Cite article

Reference system	Unknown quantities
Particle flow	Particle positions \(\mathbf{x}_\mathrm{i}\)
	Particle velocities \(\mathbf{v}_\mathrm{i}\)
	Angular velocity \(\varvec{\omega }_\mathrm{i}\)
Fluid flow	Fluid velocities \(\mathbf{u}\)
	Pressure p
	Scalar quantity \(\theta \) e.g., temperature
Internal thermal transport	Particle temperature T

Parameter	Min. value	Max. value
\(\phi _\mathrm{p}\)	0.3	0.64
\(\dot{\gamma }\)	\(10^{-4}\)	\(10^{-1}\)
Pe	\(10^{-2}\)	\(10^{2}\)
Bi	\(10^{-5}\)	25
\(\mu \)	0.1	Fixed
e	0.9	Fixed
\(T_\mathrm{f}\)	\((T_\mathrm{top}+T_\mathrm{bot})/2\)	Fixed