Discrete numerical modeling of loose soil with spherical particles and interparticle rolling friction

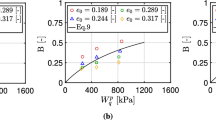
Abstract

Discrete numerical simulations were carried out to reproduce experimental results obtained on loose cohesionless soil samples subjected to triaxial tests. Periodic boundary conditions were adopted and 3D spherical discrete elements were chosen. However, to overcome excessive rolling of such an oversimplified particle’s shape, contact rolling resistance was taken into consideration. The influence of both the elastic and the plastic local parameters is discussed. It is shown that the plastic macroscopic behavior of the granular assembly depends only on the plastic parameters at the microscopic scale, and mainly on the plastic rolling moment reflecting the particle’s shape. Moreover, a procedure to obtain an initial density, ranging from loose to dense samples, is proposed by adding adhesion at contacts during the preparation phase. Finally, a calibration procedure is proposed to reproduce experimental results and the limitations of the model are discussed.

Appendix

Let $\vec {u}$, $\vec {\theta }$ define small movements of a particle relative to an initially stable configuration in which the total force and torque on the particle are $\vec {F}=\vec {T}=\vec {0}$. If the particle is involved in $N_c$ contacts and every contact remains elastic (worst case), the new force and torque induced by $\vec {u}$ and $\vec {\theta }$ can be expressed as follows, in which the translational and the rotational degrees of freedom are uncoupled (this uncoupling assumption is also found in [14]): (Note that since $\vec {F}=\vec {T}=\vec {0}$, then we can write $\varDelta \vec {F}=\vec {F}$ and $\varDelta \vec {T}=\vec {T}$):

$$\begin{aligned} \vec {F}&\simeq - \left( \sum _{c=1}^{N_c} (K_n- K_s)(\vec {n} \otimes \vec {n}) + K_s \mathbf{I}\right) \vec {u} \end{aligned}$$

(12)

$$\begin{aligned} \vec {T}&\simeq -r^2 \sum _{c=1}^{N_c} K_s (\mathbf{I}-\vec {n} \otimes \vec {n}) \vec {\theta } \end{aligned}$$

(13)

$\mathbf{I}$ being the inertia tensor of the particle and r its radius. These forces are given by neglecting the rotational term in Eq. 12 and the translational term in Eq. 13.

If contact moments ($\vec {M}_r$ and $\vec {M}_{\textit{tw}}$) are present, the moments (initially null) induced at each contact (remaining elastic) by $\vec {u}$ and $\vec {\theta }$ are:

$$\begin{aligned} \vec {M}_{\textit{tw}}&= - K_{\textit{tw}}(\vec {\theta } \cdot \vec {n})\vec {n} \nonumber \\&= - K_{\textit{tw}}(\vec {n} \otimes \vec {n})\vec {\theta }, \end{aligned}$$

(14)

$$\begin{aligned} \vec {M}_{r}&= -K_{r}(\vec {\theta }-(\vec {\theta } \cdot \vec {n})\vec {n}) \nonumber \\&= -K_{r}(\mathbf{I}-\vec {n} \otimes \vec {n})\vec {\theta }. \end{aligned}$$

(15)

where $K_r$ and $K_{\textit{tw}}$ are the rolling and twisting stiffnesses, respectively. Note that, in our study, only the rolling moment was taken into consideration. However, for generalization, we added the twisting moment here.

Adding these contributions (Eqs. 14 and 15) to the global rotational stiffness (Eq. 13) yields

$$\begin{aligned} \vec {T} \simeq -\sum _{c=1}^{N_c}\{r^2 K_s(\mathbf{I}-\vec {n} \otimes \vec {n})+ K_{\textit{tw}}\vec {n} \otimes \vec {n} + K_r(\mathbf{I}-\vec {n} \otimes \vec {n})\} \vec {\theta }\nonumber \\ \end{aligned}$$

(16)

The uncoupled equations of motion for the particle can be expressed as:

$$\begin{aligned} \vec {{\ddot{u}}}&= -\frac{\mathbf{K}_u}{M} \vec {u}, \end{aligned}$$

(17)

$$\begin{aligned} \vec {{\ddot{\theta }}}&= -\frac{\mathbf{K}_\theta }{J} \vec {\theta }, \end{aligned}$$

(18)

where $\mathbf{K}_u$ and $\mathbf{K}_\theta$ are the tensors defined by Eqs. 12 and 16 respectively, M is the mass of the particle, and J is the moment of inertia (equal to $\frac{2}{5}r^2 M$ for a sphere).

$\frac{\mathbf{K}_u}{M}$ and $\frac{\mathbf{K}_\theta }{J}$ are symmetric positive definite tensors from which six eigen values can be calculated, corresponding to six natural frequencies of the particle. The explicit centered finite difference scheme is stable for the above equations—for a single particle b—as long as $\varDelta t$ is less than $2/\sqrt{\lambda ^b_{\textit{max}}}$, $\lambda ^b_{\textit{max}}$ being the maximum eigenvalue of the particle.

A multi-body system as a whole may have natural oscillation modes combining the motion of multiple particles, with frequencies higher than the maximum frequency found for individual particles. An accurate determination of the critical timestep would thus need to consider the stiffness matrix of the system as a whole where the motion of two particles in contact would be included. For $N_b$ particles it would lead to a matrix of size $(6N_b)^2$ from which eigenvalues would have to be extracted. It can be avoided by remarking that this large assembled matrix would have every contact stiffness appearing twice in each row (once in the diagonal term and once in the column whose index corresponds to the other particle forming the contact). Since the absolute row-sum of the components can be used as an upper bound of the maximum eigenvalue (Perron-Froebenius theorem [3]) an upper bound is obtained simply by multiplying every stiffness by two when calculating the frequencies of one single particle. Equivalently, we can keep the stiffness unchanged and define the upper bound using the eigenvalues associated to individual particles as

$$\begin{aligned} \lambda _{\textit{max}} < 2\max _b(\lambda ^b_{\textit{max}}). \end{aligned}$$

(19)

[12] suggested a similar inequality without proof. Finally, a sufficient condition of stability is:

$$\begin{aligned} \varDelta t < \sqrt{\frac{2}{\max _b (\lambda ^b_{\textit{max}})}}. \end{aligned}$$

(20)

The equations of motion for a particle, (17) and (18), can be written in a simplified way considering the following assumptions:

• 1. all spheres are identical (same size and same inertia)

• 2. all contacts have the same stiffness values

• 3. the stiffness tensors, defined by Eqs. 12 and 16, are isotropic.

We note also that $K_r =\alpha _{rn}r^{2}K_n$ and $K-{\textit{tw}} = \alpha _{\textit{tw}}r^{2}K_n$. Then the uncoupled equations of motion read:

$$\begin{aligned} \vec {{\ddot{u}}}&= -\frac{N_c K_n(1+2\alpha _s)}{M} \vec {u}, \end{aligned}$$

(21)

$$\begin{aligned} \vec {{\ddot{\theta }}}&= -\frac{N_c K_n(5\alpha _s+5\alpha _{rn} +2.5\alpha _{\textit{tw}})}{M} \vec {\theta }. \end{aligned}$$

(22)