Advertisement

Granular Matter

, 18:2 | Cite as

Pressure distribution in an assembly of wooden cylinders with various aspect ratios under uniaxial confined compression

  • Piotr ParafiniukEmail author
  • Joanna Wiącek
  • Maciej Bańda
  • Marek Molenda
Open Access
Original Paper
First Online:

Abstract

Understanding how forces propagate in granular assemblages is important for equipment design and process control in many technologies. Yet, it remains poorly understood. In this study, a cuboidal assembly comprising cylinders of various lengths (aspect ratios AR ranging from 0.9 to 3.6) were subjected to uniaxial confined compression tests. Samples were vertically compressed until the top platen exerted a pressure of 50 kPa on the uppermost particles. This maximum pressure corresponds to the hydrostatic pressure of an approximately 15 m high column of chopped wood that may be encountered in real storage structures. The nonlinear loading curves were obtained depended on the aspect ratios of the cylinders. The modulus of elasticity, calculated from the linear elastic part of the stress–strain curve, monotonically decreased from 10.2 to 8.6 MPa as the aspect ratio increased from 1.2 to 3.6. The elastic modulus and volume fraction exhibited similar trends as functions of the aspect ratio. The horizontal-to-vertical pressure ratio was calculated as the horizontal pressure exerted on the wider walls to the vertical pressure exerted on the top lid during loading–unloading cycles. For ARs up to 3.6, the pressure ratio was approximately 0.31; for the longest cylinders (AR = 3.6), it decreased to approximately 0.27, probably because the assumption of the representative chamber volume was invalidated at this AR.

Keywords

Granular packings Uniaxial confined compression Packing of rods Load distribution Anisotropy 

1 Introduction

The geometrical features of granular assemblies, particularly those of packed spherical particles, have been extensively studied over the last few decades [1, 2, 3]. Understanding the geometric distribution of particles and their associated voids is relevant to diverse topics such as crystallography, chemical reactors, reinforcement of composites, fiber packings, liquid crystal arrays, random collections of rod-like molecules, and the airflow resistance of various beddings.

Compared to knowledge on geometrical features of granular packing, information regarding force propagation in granular beddings and the resulting stress–strain behaviors have yet to be clarified. Granular materials are used in numerous technological processes; thus, elucidating their mechanical behaviors is crucial for equipment design and process control. Even granular packings of spherical particles can become inherently anisotropic under gravity and friction effects. Particles with higher degrees of asymmetry will form more anisotropic deposits. Donev et al. [4] observed a sharp increase in the density and number of contacts in randomly packed assemblies of ellipsoids as the length of the packed particles increased (equivalently, as the aspect ratio, defined as the length-to-diameter ratio, increased from 1.0 to 1.5). As the aspect ratio increased beyond 1.5, the relative density decreased probably because of strong exclusion-volume effects [4]. Parkhouse and Kelly [5] examined the limiting packing density of assemblies of “spaghetti-like” fibers (diameter 1.8 mm; slenderness ranging from 6.8 to 143). The volume fraction was 0.58 for the shortest particles with an aspect ratio of 6.8, and decreased with increasing particle elongation. Lin and Ng [6] simulated the compression of assemblies of spherical and ellipsoidal particles and reported higher shear strength and less particle rotation in the ellipsoidal particles. Härtl and Ooi [7] observed that at the same porosity, non-spherical particles formed by paired spheres exhibited much higher bulk friction than single spheres because of their greater particle interlocking. These authors proposed that internal friction is a combination of contact friction and the geometric interactions between particles. They also found that bulk friction was more affected by particle aspect ratio than porosity.

Recently, the effect of particle shape on the mechanical behavior of granular materials has attracted growing interest. By virtue of discrete element method (DEM), which have developed throughout the past 20 years, these effects can be efficiently investigated. The behaviors of spheres and elongated particles have been extensively studied in numerical simulations. We have contributed to this area in our earlier work [8, 9].

To investigate the influence of particle shape on the structural properties and mechanical response of a granular assembly, Wiącek et al. [8] performed three-dimensional discrete element simulations of spherical and non-spherical particles under uniaxial confined compression. As the aspect ratio varied from 1 to 2.8, the packing density and mechanical response to the compressive load were strongly altered. The change of particle shape from spherical to oblong (aspect ratio 1 to 1.6) reduced the porosity and lateral-to-vertical pressure ratio, and increased the stiffness of the specimen. However, further elongation (aspect ratio 1.6 to 2.8) reduced the bulk density and only weakly altered the stress propagation and bulk stiffness.

Compared to knowledge on geometrical features of granular packing, information regarding the force propagation in granular beddings and the resulting stress–strain behavior remains scarce. Therefore, the objective of this work was to experimentally examine the effect of aspect ratio (diameter-to-length ratio) on the pressure distribution in a cuboidal sample of granular bedding under confined uniaxial compression (oedometric test). The granular particles are modeled as cylinders of various lengths (7 aspect ratios). The parameters of primary interest in engineering, namely, the solid fraction \(\varphi \), stress ratio k, effective elastic modulus E, and apparent coefficient of friction, were measured.

2 Method and equipment

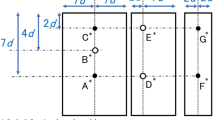
The loads exerted by a bedding of wooden cylinders on the floor and walls of a cuboidal chamber were measured in uniaxial confined compression tests. The experiment was conceptualized as an imaginary cubic section of material, which is commonly used to explain the basic ideas of continuum mechanics, such as stress components (e.g., [10]). In this configuration, the tester can characterize the bedding of granular material, including its anisotropic response to vertical axial forces acting on the center of the horizontal top plate, which rests on the upper surface of the sample. The test results should be easily interpreted by a wide range of engineers who are familiar with this handbook approach. The stress differences measured at three walls of the test chamber will determine the inherent anisotropic or non-homogeneous behavior of granular materials. A schematic of the apparatus and samples of the examined particles are shown in panels (a) and (b) of Fig. 1, respectively.
Fig. 1

a Schematic of uniaxial confined compression tester and location of load cells, b wooden pegs with various aspect ratios

The walls of the compression chamber were machined of 6 mm thick steel and galvanized. The floor and two perpendicular walls (parallel to planes XZ and YZ) were each supported on three load cells. The two YZ walls of the apparatus, (parallel to the plane of Fig. 1a) were separated by 0.12 m, while the two XZ walls were separated by 0.10 m. Gaps of 1 mm were maintained between the floor and the walls of the apparatus to exclude load transmission between the elements of the construction. The floor of the apparatus was supported on load cells FL1, FL2, and FL3, the YZ wall was supported on load cells WL4, WL5, and WL6, and the XZ wall was supported on load cells WL7, WL8, and WL9. In this configuration of the load cells, we could determine the normal forces and locate their resultant, as well as calculate the normal pressures exerted on the construction elements during the compression.

The test samples were wooden cylinders (pegs) with a nominal diameter D of 10 mm, and measured minimum and maximum axes of \(9.77 \pm 0.06\) and \(9.99 \pm 0.04\) mm, respectively. The pegs were cut from round pine wood rods (approximate length 1 m) with a circular saw. Seven sample lengths L were tested: 9.0, 11.7, 13.5, 16.2, 18.0, 27.0, and 36.0 mm (aspect ratios \(AR = L/D\) ranging from 0.9 to 3.6). The length of the longest pegs (3.6D) is the length beyond which no sharp changes in the geometrical or mechanical behaviors of the cylinder assemblies are observed. For example, in assemblies of spherocylinders examined by Zhao et al. [13], the packing density was maximized at AR = 1.5, and the coordination number increased as the aspect ratio increased to approximately AR = 3, then decreased at a slower rate.

The apparatus was inserted with a wooden rectangular tube (inside dimensions \(95\, \mathrm{mm }\times 75\, \mathrm{mm}\)), placed coaxially on the bottom of the chamber and filled with the test material. The tube was slowly lifted until a conical free surface was formed above the walls of the chamber. After the tube was removed, the free surface of the material was leveled. The sample was compressed by lowering the top cover at a load rate of 1.7 mm/min.

The vertical force on the top plate was measured by a load cell (TL10 in Fig. 1a). The sample was compressed until the normal pressure on the top plate reached its maximum of 50 kPa. Next, the sample was unloaded by lifting the top cover. Five replicate tests were performed on samples with each AR.

3 Results and discussion

3.1 Solid fraction

Figure 2 plots the solid fraction \(\phi \) of the particulate assemblies as a function of aspect ratio under a vertical pressure of 50 kPa. The \(\phi \) was lower at \(AR = 0.9\) than at AR = 1.2 (0.47 vs. 0.48). The decrease in solid fraction from 0.48 to 0.40 was observed with an increase in AR from 1.2 to 3.6, respectively. These results corroborate the findings reported in earlier experimental and numerical investigations [11, 12].

The particles behaved anomalously near \(AR \sim 0.9\), as reported in numerous earlier investigations. Donev et al. [4] found that the volume fraction of packed ellipsoidal particles sharply increases as the aspect ratio deviates slightly from unity, marking the transition from spherical to oblate, or prolate particles. They suggested that the higher density directly relates to the higher number of degrees of freedom per particle; consequently, more particle contacts are required to mechanically stabilize the packing. Philipse [12] experimentally examined random packings of various rods, and found that near AR = 1 the packing density approaches that of randomly packed spheres (0.64). At higher aspect ratios, the volume fractions markedly decrease. After mining the literature, Zhao et al. [13] reported various simulated packing densities as functions of aspect ratio. Almost all of the studies demonstrated a sharp increase in packing density when the particle shape deviated slightly from spherical. The packing density increased to a maximum as the aspect ratio increased to approximately 1.3, and thereafter decreased.
Fig. 2

Solid volume fraction in packed particles of various aspect ratios under a vertical load of 50 kPa

Fig. 3

Typical plots of force versus strain; a vertical load on the top lid, on the base of the box, on the three load cells supporting the floor, and b normal loads on the walls of the box

Zhou and Yu [11] studied the wall effect on the porosity of uniform cylindrical particles packed into cylindrical containers. They used wooden rods of diameter 2.35 mm and ARs of 2, 4, 8, and 16. In cases of negligible wall effect, the density increased as the AR reduced. At AR = 2, they obtained porosities of 0.42 (\(\phi = 0.58\)) and 0.32 (\(\phi = 0.68\)) in loose and dense packings, respectively. Philipse [12] studied packings of various rods over a wide range of AR (\(\sim \) unity to >80). Short particles, comparable to those used in the present study, were cut from plastic or wood. Near \({AR} = 1\), the volume fraction was close to that of randomly packed spheres \((\phi = 0.64)\), much higher than our volume fraction of 0.48. This inconsistency is attributed to differences in technique; Philipse [12] densified the samples by shaking them. At higher aspect ratios, the volume fractions considerably decreased. Wouterse et al. [14] similarly reported that density is maximized for nearly spherical particles and decreases at higher aspect ratios. They investigated spherocylinders and spheroids, which are similarly shaped and thus exhibit very similar packing behavior.

In the present study, a second anomaly appears at AR = 1.8, where \(\phi \) reaches a local minimum (0.435) in an otherwise monotonic tendency. The local minimum was confirmed in three additional replicate tests of samples with ARs of 1.6, 1.8, and 2.7. The probable causes of this anomaly were the test chamber dimensions, peg length, and filling method, which collectively produced a looser bedding than at ARs of 1.6 and 2.7. We intend to investigate this unanticipated effect in a future study.

3.2 Stress–strain behavior during a loading–unloading cycle

Figure 3 plots the force–strain relationships recorded during the load–unload cycle of samples with AR = 0.9. Panel (a) shows the forces recorded by the floor load cells FL1, FL2, FL3, their sum FL, and total load FL10 (recorded by the load cell mounted on the crosshead of the testing machine). The total load–strain characteristic fluctuates more than the other curves, because the top plate is less constrained than the other plates of the chamber. Tests were conducted up to a total load of 600 N. At the maximum total load, the measured floor load was 470 N, and the vertical frictional load on the walls was 130 N (21.6 % of the total load). During the initial unloading phase, the floor loads approximately followed the total loading trend until \(t= 150\) s (\(\varepsilon = 0.035\)); thereafter, they decreased more slowly than the total load. This effect is attributed to wall friction, which disturbs the release of elastic energy. FL3 (230 N) was close to the sum of FL1 and FL2 (115 N + 125 N= 240 N); thus, the floor load was fairly uniformly distributed. The total and floor loads differed by the vertical frictional load acting on the walls. As the loads were measured normal to the walls, the ratio of tangent to normal stresses might reflect the degree of mobilization of the friction.
Fig. 4

Stress ratio k as a function of strain \(\varepsilon \) during loading–unloading cycles for five samples of 9-mm long cylinders (AR = 0.9), estimated at the wider (0.12 m) walls

Figure 3b shows the forces recorded by the load cells (see Fig. 1). WL4, WL5, and WL6 supporting narrower wall, while WL7, WL8, and WL9 measured forces on the wider wall. Load cell WL6 recorded a higher load force than cells WL4 and WL5; similarly, WL9 recorded a higher load than WL7 and WL8, because the lower and upper wall locations were supported by single and paired load cells, respectively. Under maximum compression, the sum of the forces exerted on both walls was approximately 1.2 times larger at the higher location than at the lower location (106 vs. 87 N on the narrower wall, and 137 vs.113 N on the wider wall). This effect indicates an uneven distribution of horizontal load along the height of the wall; specifically, the pressure decreased downwards due to friction between the cylinders and walls.

Portions of the wall loads remained frozen after unloading, because the walls prevented complete relaxation of the elastic energy accumulated during compaction. Elastic energy was more readily released in the vertical direction, as raising the top cover frees the top surface of the bedding.

3.3 Horizontal to vertical stress ratio

3.3.1 Stress ratio during loading–unloading cycle

The horizontal-to-vertical stress ratio k was calculated as the horizontal pressure measured at the wider (0.12 m) walls to the vertical pressure measured on the top lid during the loading–unloading cycles. Five replications of the pressure ratio k versus strain \(\varepsilon \) are plotted in Fig. 4. The fluctuations in the initial compression phase reflect the particle rearrangement during compaction of the loose sample. Once the strain exceeded approximately 0.2, the fluctuations ceased and all five curves stabilized. Under a vertical pressure of 50 kPa, the k was approximately 0.33. The k of 0.33 indicates a so-called ‘active’ stress state \(\sigma _{z} > \sigma _{x}\), which typifies the loading phase of the cycle. During unloading k gradually increased and strongly fluctuated in the last unloading phase. Such behavior reflects the easier stress relaxation in the vertical direction as the top lid is raised than in the horizontal direction, where relaxation is prevented by the static walls.

3.3.2 Stress ratio dependence on particle length and wall width

The pressure ratios at walls parallel to the XZ and YZ planes did not significantly differ. Therefore, to determine the dependence of stress ratio on the aspect ratio of the particles, we measured the horizontal pressure at the wall parallel to the XZ plane (see Fig. 1a). The results are plotted in Fig. 5. Over the investigated range of ARs, the pressure ratios varied slightly, and decreased by approximately 15 % at AR = 3.6; however, the differences in k were within the range of scatter. The large error in the magnitude of k is attributed to the non-perfect replicability of the spatial structure of the samples.
Fig. 5

Stress ratio as a function of particle aspect ratio

Fig. 6

a Stress–strain relationships in five different assemblies of particles with AR = 2.7, b modulus of elasticity as a function of particle aspect ratio

The observed independence of k on aspect ratio agrees with the numerical results of Parafiniuk et al. [9], who simulated spheroids with aspect ratios ranging from 1.3 to 2.5. Moreover, it may be stated that the dimensions of the sample compared to dimensions of particles and their number were large enough to assure no influence of the walls on the test results. The most reliable experimental results in the literature are probably those of Kwade et al. [15], who measured the ks of 41 materials, and reported values of 0.3 to 0.5. Our k is lower than those of cereal seeds with 12.5 % moisture content (wheat = 0.38; rye = 0.52) obtained by Molenda and Horabik [16]. These authors obtained higher k values for more elongated or rougher-textured particles. The present results agree with those of wheat grains \((k = 0.27-0.36)\) measured by Molenda et al. [17] for three different filling methods.

Wiącek et al. [8] conducted DEM simulations of spherical and oblong particles subjected to uniaxial confined compression. As the particle AR increased from 1.0 to 1.3, the pressure ratio reduced by 25 %. A further increase in AR (from 1.3 to 1.6) reduced the pressure ratio by another 10 %. At the maximum AR of 2.8, the pressure ratio was little changed from that at AR = 1.6 and 2.12. Similar trends were reported by Parafiniuk et al. [9], who simulated cuboidal assemblies of spherical and spheroidal particles under uniaxial confined compression. They found that the pressure ratio maximizes at ARs slightly above one, and that the k(AR) values stabilize once AR exceeds 1.3.

3.4 Effective elastic modulus

Figure 6a plots the stress–strain relationships in five replications of loading–unloading cycles for assemblies of particles with AR = 2.7. The loading curves are clearly nonlinear and different. During unloading, the curves sharply decrease over a short period. This sudden change reflects the reversed direction of the moving lid. It is followed by a nearly linear phase, and a final nonlinear phase leading to zero load.

The effective elastic modulus E was calculated by Eq. (1), as recommended by Eurocode 1[18]:
$$\begin{aligned} E=H\frac{{\Delta }\sigma _z }{{\Delta }z}\left( {1-\frac{2k^{2}}{1+k}} \right) , \end{aligned}$$
(1)
where H is the height of the sample, \(\varDelta \sigma _z \) and \({\Delta }z\) denote the changes in vertical pressure and vertical displacement, respectively, and k is the stress ratio. \(H\frac{{\Delta }\sigma _z }{{\Delta }z}\) was estimated as the slope of the linear segment of the unloading curve, and k was calculated for the wider wall under a vertical pressure \(\sigma _z =50\;\mathrm{kPa}\). It should be noted that Eq. (1) assumes an isotropic continuous material. Despite this drawback, the Eurocode Standard [18] recommends Eq. (1) for rough estimates of the effective modulus of elasticity.

The modulus of elasticity E monotonically decreased from 8.64 to 7.63 MPa as the AR increased from 1.2 to 3.6. These results reasonably agree with those of dry particulate materials of plant origin under similar compaction pressure. For example, Sawicki and Swidzinski [19] obtained Es of 7 and 17 MPa for dry wheat and rice grain, respectively. Kaliyan and Morey [20] determined (inter alia) the moduli of elasticity of briquettes made of switchgrass and corn stover under various densification conditions. The E of dry corn stover in the stress range 0.9–5 MPa was 5.3 MPa. Gilbert et al. [21] measured the mechanical properties of switchgrass pellets and obtained a modulus of elasticity of approximately 8 MPa.

The strong orthotropy of wood materials is well- recognized. The present samples were cut from pine wood, which has a longitudinal elastic modulus between 6.6 and 17.4 GPa and a transverse elastic modulus between 0.2 and 1.3 GPa [22]. These values are much higher than the calculated moduli of elasticity for assemblies of cylindrical pine samples, suggesting that the spatial distribution of the particles and their contact network is much more important than the orthotropy of the wood.

Early numerical simulations of the mechanics of granular media explored 2D systems, and provided valuable findings regarding general behavior of granular materials. Rothenburg and Bathurst [23] performed simulations of planar assemblies of elliptical particles. They concluded that most of the strength effects associated with assemblages of elliptical particles are a result of their higher density of contacts. Moreover, very eccentric particles, even when densely packed, exhibited very different mechanical responses to particles of low eccentricity. As shown in Fig. 6b, the E was lower at AR = 0.9 than at AR = 1.2. This deviation from an otherwise monotonic decrease can be related to the solid fraction, which was lower in packed cylinders with an aspect ratio of 0.9 than in some samples with higher aspect ratios.

3.5 Degree of mobilization of wall friction

The degree of mobilization, or apparent coefficient of wall friction \(\mu ^{*}\) was estimated as follows:
$$\begin{aligned} \upmu ^{*}=\frac{F_{top} -F_{floor} }{F_h }, \end{aligned}$$
where \(F_{top}\), \(F_{floor}\) and \(F_{h}\) are the forces on the top plate of the chamber, the floor of the chamber, and perpendicular (horizontal) to the chamber walls, respectively. The friction was considered fully mobilized when \(\mu ^{*}\) equaled the coefficient of static friction between the wooden cylinders and the wall. The coefficient of static friction was measured as 0.27 by a Jenike shear tester. Figure 7 plots the \(\mu ^{*}\) values for cylinders with the seven aspect ratios. The mean \(\mu ^{*}\) is essentially constant \((\sim \)0.165) over the first five ARs. At ARs of 2.7 and 3.6, the \(\mu ^{*}\) reduces to approximately 0.145. Comparing the apparent and measured coefficients of friction, we infer that the mobilization of friction between the particles and walls is relatively weak. The vertical distributions of load normal to the walls are relatively uneven (see Fig. 3b), suggesting that the distributions of frictional loads are also uneven, but this inference should be examined in numerical simulations.
Fig. 7

Apparent coefficient of friction \(\mu ^{*}\) versus particle aspect ratio

4 Summary and conclusions

The geometrical properties of assemblies of variously shaped particles are important in crystallography, geology, chemical engineering (reactor fills), composites, and other branches of science and technology; however, the transmission of forces in granular beddings remains incompletely understood.

The present study focused on the mechanical behaviors of assembled wooden cylindrical particles under uniaxial confined compression. The cylinder lengths were varied as 9.0, 11.7, 13.5, 16.2, 18.0, 27.0 and 36.0 mm (ARs ranging from 0.9 to 3.6). The samples were packed into a cuboid test chamber (cross-section \(0.12\; \mathrm{m} \times 0.10\; \mathrm{m}\); height 0.10 m) and vertically compressed until the top platen exerted a pressure of 50 kPa on the uppermost particles. The solid volume fraction \(\phi \) was lower at AR = 0.9 than at AR = 1.2 (0.47 vs. 0.48); otherwise, the solid volume fraction decreased from 0.48 to 0.40 as AR increased from 1.2 to 3.6. The modulus of elasticity E, calculated from the linear elastic response, monotonically decreased from 10.2 to 8.6 MPa as AR increased from 1.2 to 3.6. At AR = 0.9, the modulus of elasticity was 9.6 MPa. The modulus of elasticity and solid fraction exhibited similar trends when plotted against the aspect ratio. The horizontal-to-vertical stress ratio (pressure ratio, k) was calculated as the horizontal pressure exerted on the wider (0.12 m) walls to the vertical pressure exerted on the top lid. The pressure ratios were approximately 0.31 at aspect ratios of 2.7 or smaller. For samples composed of the longest particles (AR = 3.6), the k was reduced to approximately 0.27.

The present results corroborate previous findings that assemblies of cylinders with ARs up to 3.6 show consistent behavior; that is, are governed by the same set of physical rules. Some of the results (e.g., \(\phi \)(AR) and E(AR)) show characteristic changes at ARs around 1.3, as reported by other researchers. Other results (e.g., k(AR)) suggest that the behaviors of packed cylinders might change between AR = 2.7 and AR = 3.6, but this suggestion requires further examination. Classifying particles shapes by their behaviors when assembled and subjected to loading would assist the design of granular materials with required characteristics. For instance, designers could test the compliance of a granular assembly under confining pressure. However, such a classification remains out of reach at present. This study provides new information that will benefit the interpretations of observed phenomena and the design optimization of granular materials. The behavioral trends and determined parameter values, when confirmed by other laboratories, can provide a basis for recommendations of design codes.

References

  1. 1.
    Farouki, O.T., Winterkorn, H.F.: Mechanical properties of granular systems. Highway Res. Rec. 52, 10–58 (1964)Google Scholar
  2. 2.
    Silbert, L.E., Ertaş, D., Grest, G.S., Halsey, T.C., Levine, D.: Geometry of frictionless and frictional sphere packings. Phys. Rev. E 65, 031304 (2002)ADSMathSciNetCrossRefGoogle Scholar
  3. 3.
    Wiącek, J., Molenda, M.: Effect of particle polydispersity on micromechanical properties and energy dissipation in granular mixtures. Particuology 16, 91–99 (2014)CrossRefGoogle Scholar
  4. 4.
    Donev, A., Cisse, I., Sachs, D., Variano, E.A., Stillinger, F.H., Conelly, R., Torquato, S., Chaikin, P.M.: Improving the density of jammed disordered packings using ellipsoids. Science 303, 990–993 (2004)ADSCrossRefGoogle Scholar
  5. 5.
    Parkhouse, J.G., Kelly, A.: The random packing of fibers in three dimensions. Proc. R. Soc. Lond. A 451, 737–746 (1995)ADSCrossRefGoogle Scholar
  6. 6.
    Lin, X., Ng, T.-T.: A three-dimensional discrete element model using arrays of ellipsoids. Géotechnique 47, 319–329 (1997)CrossRefGoogle Scholar
  7. 7.
    Härtl, J., Ooi, J.Y.: Experiments and simulations of direct shear tests: porosity, contact friction and bulk friction. Granul. Matter 10, 263–271 (2008)CrossRefGoogle Scholar
  8. 8.
    Wiącek, J., Molenda, M., Horabik, J., Ooi, J.Y.: Influence of grain shape and intergranular friction on material behavior in uniaxial compression: experimental and DEM modelling. Powder Technol. 217, 435–442 (2012)CrossRefGoogle Scholar
  9. 9.
    Parafiniuk, P., Molenda, M., Horabik, J.: Influence of particle shape and sample width on uniaxial compression of assembly of prolate spheroids examined by discrete element method. Phys. A 416, 279–289 (2014)CrossRefGoogle Scholar
  10. 10.
    Timoshenko, S.P., Goodier, J.N.: Theory of Elasticity. McGraw-Hill, New York (1970)zbMATHGoogle Scholar
  11. 11.
    Zou, R.P., Yu, A.B.: Wall effect on the packing of cylindrical particles. Chem. Eng. Sci. 51, 1177–1180 (1996)CrossRefGoogle Scholar
  12. 12.
    Philipse, A.P.: The random contact equation and its implications for (colloidal) rods in packings, suspensions, and anisotropic powders. Langmuir 12, 1127–1133 (1996)Google Scholar
  13. 13.
    Zhao, J., Li, S., Zou, R., Yu, A.: Dense random packings of spherocylinders. Soft Matter 8, 1003–1009 (2012)ADSCrossRefGoogle Scholar
  14. 14.
    Wouterse, A., Luding, S., Philipse, A.P.: On contact numbers in random rod packings. Granul. Matter 11, 169–177 (2009)CrossRefzbMATHGoogle Scholar
  15. 15.
    Kwade, A., Schultze, D., Schwedes, J.: Determination of the stress ratio in uniaxial compression tests. Part I. Powder Handl. Process. 6, 61–65 (1994)Google Scholar
  16. 16.
    Molenda, M., Horabik, J.: Mechanical Properties of Granular Agro-materials and Food Powders for Industrial Practice. Part I. Institute of Agrophysics PAS, Lublin (2005)Google Scholar
  17. 17.
    Molenda, M., Horabik, J., Ross, I.J.: Effect of filling method on load distribution in model grain bins. Trans. ASAE 39, 219–224 (1996)CrossRefGoogle Scholar
  18. 18.
    Eurocode 1, Actions on Structures. Part 4. Silos and Tanks. EN 1991-4, (2006)Google Scholar
  19. 19.
    Sawicki, A., Swidzinski, W.: Elastic moduli of non-cohesive particulate materials. Powder Technol. 96, 24–32 (1998)CrossRefGoogle Scholar
  20. 20.
    Kaliyan, N., Morey, R.V.: Constitutive model for densification of corn stover and switchgrass. Biosyst. Eng. 104, 47–63 (2009)CrossRefGoogle Scholar
  21. 21.
    Gilbert, P., Ryu, C., Sharifi, V., Swithenbank, J.: Effect of process parameters on pelletization of herbaceous crops. Fuel 88, 1491–1497 (2009)CrossRefGoogle Scholar
  22. 22.
    Hofstetter, K., Hellmich, C., Eberhardsteiner, J.: Development and experimental validation of a continuum micromechanics model for the elasticity of wood. Eur. J. Mech. A Solids 24, 1030–1053 (2005)ADSCrossRefzbMATHGoogle Scholar
  23. 23.
    Rothenburg, L., Bathurst, R.J.: Micromechanical features of granular assemblies with planar elliptical particles. Géotechnique 42, 79–95 (1992)CrossRefGoogle Scholar

Copyright information

© The Author(s) 2016

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  • Piotr Parafiniuk
    • 1
    Email author
  • Joanna Wiącek
    • 1
  • Maciej Bańda
    • 1
  • Marek Molenda
    • 1
  1. 1.Institute of AgrophysicsPolish Academy of SciencesLublin 27Poland

Personalised recommendations