Skip to main content

Advertisement

SpringerLink
Go to cart
  1. Home
  2. Granular Matter
  3. Article
Cohesive, frictional powders: contact models for tension
Download PDF
Your article has downloaded

Similar articles being viewed by others

Slider with three articles shown per slide. Use the Previous and Next buttons to navigate the slides or the slide controller buttons at the end to navigate through each slide.

Assessment of particle rearrangement and anisotropy in high-load tableting with a DEM-based elasto-plastic cohesive model

20 September 2019

Ramon Cabiscol, Jan Henrik Finke & Arno Kwade

A discrete element study of the effect of particle shape on packing density of fine and cohesive powders

13 March 2020

H. S. Elmsahli & I. C. Sinka

Peridynamic Simulation of Particles Impact and Interfacial Bonding in Cold Spray Process

16 May 2022

Baihua Ren & Jun Song

The relationship between contact network and energy dissipation in granular materials

29 August 2022

Abdurrahim Essayah, Thomas Shire & Zhiwei Gao

Particle Impact Characteristics Influence on Cold Spray Bonding: Investigation of Interfacial Phenomena for Soft Particles on Hard Substrates

22 November 2021

A. Nastic, B. Jodoin, … D. Poirier

Regularities of Friction of Multiscale Composite Materials Containing Highly Dispersed Particles of Fullerene Soot

01 March 2021

I. A. Kobykhno, F. A. Yunusov, … A. G. Kadomtsev

On the contact problem of soft-rigid interfaces: incorporation of Mindlin-Deresiewicz and self-deformation concepts

15 December 2021

Yu Tian & Kostas Senetakis

A General Load–Displacement Relationship Between Random Rough Surfaces in Elastic, Non-adhesive Contact, with Application in Metal Additive Manufacturing

15 June 2022

J. Joe, J. R. Barber & B. Raeymaekers

Numerical Investigation of the Cushion and Size Effects During Single-Particle Crushing via DEM

19 September 2020

Du-min Kuang, Zhi-lin Long, … Jie Wang

Download PDF
  • Open Access
  • Published: 27 March 2008

Cohesive, frictional powders: contact models for tension

  • Stefan Luding1,2 

Granular Matter volume 10, pages 235–246 (2008)Cite this article

  • 5743 Accesses

  • 406 Citations

  • Metrics details

Abstract

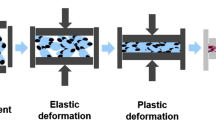
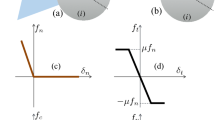
The contacts between cohesive, frictional particles with sizes in the range 0.1–10 μm are the subject of this study. Discrete element model (DEM) simulations rely on realistic contact force models—however, too much details make both implementation and interpretation prohibitively difficult. A rather simple, objective contact model is presented, involving the physical properties of elastic–plastic repulsion, dissipation, adhesion, friction as well as rolling- and torsion-resistance. This contact model allows to model bulk properties like friction, cohesion and yield-surfaces. Very loose packings and even fractal agglomerates have been reported in earlier work. The same model also allows for pressure-sintering and tensile strength tests as presented in this study.

Download to read the full article text

Working on a manuscript?

Avoid the common mistakes

References

  1. Allen M.P. and Tildesley D.J. (1987). Computer Simulation of Liquids. Oxford University Press, Oxford

    MATH  Google Scholar 

  2. Bartels G., Unger T., Kadau D., Wolf D.E. and Kertesz J. (2005). The effect of contact torques on porosity of cohesive powders. Granular Matter 7: 139

    Article  MATH  Google Scholar 

  3. Bashir Y.M. and Goddard J.D. (1991). A novel simulation method for the quasi-static mechanics of granular assemblages. J Rheol 35(5): 849–885

    Article  ADS  Google Scholar 

  4. Berger, F.: Das Gesetz des Kraftverlaufes beim Stoß. Friedr. Vieweg & Sohn AG (1924)

  5. Brendel L. (2006). Modeling of caked contacts in DEMs. Chem Eng Technol 29(11): 1355–1359

    Article  Google Scholar 

  6. Brendel, L., Dippel, S.: Lasting contacts in molecular dynamics simulations. In: Herrmann, H.J., Hovi, J.P., Luding, S. (eds) Physics of Dry Granular Media. Kluwer, Dordrecht, p 313 (1998)

  7. Brilliantov N.V., Spahn F., Hertzsch J.M. and Pöschel T. (1996). Model for collisions in granular gases. Phys Rev E 53(5): 5382

    Article  ADS  Google Scholar 

  8. Butt H.J., Cappella B. and Kappl M. (2005). Force measurements with the atomic force microscope: Technique, interpretation and applications. Surf. Sci. Rep. 59(1–6): 1–152

    Article  ADS  Google Scholar 

  9. Castellanos A. (2005). The relationship between attractive interparticle forces and bulk behavior in dry and uncharged fine powders. Adv. Phys. 54(4): 263–376

    Article  ADS  Google Scholar 

  10. Coste, C., Falcon, E., Fauve, S.: Propagations d’ondes non-linéaires dans une chaîne de bille s en contact de Hertz. In: Petit C., Pijaudier-Cabot G., Reynouard J.M. (eds) Des géomatériaux aux ouvrages: expérimentations et modélis ations, Hermes, Paris, pp 33–52 (in french, 1995)

  11. Coste C., Falcon E. and Fauve S. (1997). Solitary waves in a chain of beads under Hertz contact. Phys. Rev. E 56(5): 6104–6117

    Article  ADS  Google Scholar 

  12. Cundall P.A. and Strack O.D.L. (1979). A discrete numerical model for granular assemblies. Géotechnique 29(1): 47–65

    Google Scholar 

  13. David, C.T., Rojo, R.G., Herrmann, H.J., Luding, S.: Hysteresis and creep in powders and grains. In: Garcia-Rojo, R., Herrmann, H.J., McNamara, S. (eds) Powders and Grains 2005, Balkema, Leiden, Netherlands, pp. 291–294 (2005)

  14. David C.T., Garcia-Rojo R., Herrmann H.J. and Luding S. (2007). Powder flow testing with 2d and 3d biaxial and triaxial simulations. Particle Particle Syst. Charact. 24(1): 29–33

    Article  Google Scholar 

  15. Derjaguin B.V., Muller V.M. and Toporov Y.P. (1975). Effect of contact deformation on adhesion of particles. J. Colloid Interf. Sci. 53: 314–326

    Article  Google Scholar 

  16. Dintwa E., van Zeebroeck M., Tijskens E. and Ramon H. (2005). Torsion of viscoelastic spheres in contact. Granular Matter 7(2–3): 169–179

    Article  MATH  Google Scholar 

  17. Els, D.: Definition of roll velocity for spherical particles. Granular Matter (2006, submitted)

  18. Foerster S.F., Louge M.Y., Chang H. and Allia K. (1994). Measurements of the collision properties of small spheres. Phys. Fluids 6(3): 1108–1115

    Article  ADS  Google Scholar 

  19. Grof Z., Lawrence C.J. and Stepanek F. (2008). Computer simulation of evolving capillary bridges in granular media. Granular Matter 10(2): 93–103

    Article  Google Scholar 

  20. Heim L.O., Butt H.J., Blum J. and Schrapler R. (2008). A new method for the analysis of compaction processes in high-porosity agglomerates. Granular Matter 10(2): 89–91

    Article  Google Scholar 

  21. Herrmann, H.J., Hovi, J.P., Luding, S.: (eds) Physics of dry granular media—NATO ASI Series E 350. Kluwer, Dordrecht (1998)

  22. Hertz H. (1882). Über die Berührung fester elastischer K örper. J für die reine u angew Math 92: 136

    Google Scholar 

  23. Janssen H.A. (1895). Versuche über Getreidedruck in Silozellen. Zeitschr d Vereines deutscher Ingenieure 39(35): 1045–1049

    Google Scholar 

  24. Jenkins J.T. and Koenders M.A. (2005). Hydrodynamic interaction of rough spheres. Granular Matter 7(1): 13–18

    Article  MATH  Google Scholar 

  25. Johnson K.L. (1989). Contact Mechanics. Cambridge University Press, Cambridge

    Google Scholar 

  26. Johnson K.L., Kendall K. and Roberts A.D. (1971). Surface energy and contact of elastic solids. Proc R Soc Lond Ser A 324(1558): 301

    ADS  Google Scholar 

  27. Johnson P.C. and Jackson R. (1987). Frictional-collisional constitutive relations for granular materials, with application to plane shearing. J Fluid Mech 176: 67

    Article  ADS  Google Scholar 

  28. Kadau D., Schwesig D., Theuerkauf J. and Wolf D.E. (2006). Influence of particle elasticity in shear testers. Granular Matter 8: 34–40

    Article  Google Scholar 

  29. Kafui K.D. and Thornton C. (2000). Numerical simulations of impact breakage of spherical crystalline agglomerate. Powder Technol 109: 113–132

    Article  Google Scholar 

  30. Kappl, M., Heim, L., Butt, H.J., Luding, S., Tykhoniuk, R., Tomas, J.: From grains to powders: from single particle contact mechanics measurements to bulk powder properties. In: Garcia-Rojo, R., Herrmann, H.J., McNamara, S. (eds) Powders and Grains 2005, Balkema, Leiden, Netherlands, pp. 493–497 (2005)

  31. Kun F. and Herrmann H.J. (2000). Damage development under gradual loading of composites. J. Mater. Sci. 35(18): 4685–4693

    Article  Google Scholar 

  32. Kuwabara G. and Kono K. (1987). Restitution coefficient in a collision between two spheres. Jpn. J. Appl. Phys. 26(8): 1230–1233

    Article  ADS  Google Scholar 

  33. Labous L., Rosato A.D. and Dave R. (1997). Measurements of collision properties of spheres using high-speed video analysis. Phys. Rev. E 56: 5715

    Article  ADS  Google Scholar 

  34. Lätzel M., Luding S., Herrmann H.J., Howell D.W. and Behringer R.P. (2003). Comparing simulation and experiment of a 2d granular couette shear device. Eur. Phys. J. Eng. 11(4): 325–333

    Article  Google Scholar 

  35. Leroy B. (1985). Collision between two balls accompanied by deformation: A qualitative approach to Hertz’s theory. Am. J. Phys. 53(4): 346–349

    Article  ADS  Google Scholar 

  36. Lian G., Adams M.J. and Thornton C. (1996). Elastohydrodynamic collisions of solid spheres. J Fluid. Mech. 311: 141

    Article  ADS  MATH  Google Scholar 

  37. Lorenz A., Tuozzolo C. and Louge M.Y. (1997). Measurements of impact properties of small, nearly spherical particles. Exp. Mech. 37(3): 292–297

    Article  Google Scholar 

  38. Lubachevsky B.D. (1991). How to simulate billards and similar systems. J. Comp. Phys. 94(2): 255

    Article  ADS  MathSciNet  MATH  Google Scholar 

  39. Luding S. (1998). Collisions and contacts between two particles. In: Herrmann, H.J., Hovi, J.P. and Luding, S. (eds) Physics of dry granular media—NATO ASI Series E350, pp 285. Kluwer, Dordrecht

    Google Scholar 

  40. Luding, S.: Micro-macro models for anisotropic granular media. In: Vermeer, P.A., Ehlers, W., Herrmann, H.J., Ramm, E. (eds) Modelling of cohesive-frictional Materials, Balkema, pp 195–206 (ISBN 04 1536 023 4) (2004a)

  41. Luding S. (2004b). Molecular dynamics simulations of granular materials. In: Hinrichsen, H. and Wolf, D.E. (eds) The Physics of Granular Media, pp 299–324. Weinheim, Wiley VCH

    Google Scholar 

  42. Luding S. (2005). Anisotropy in cohesive, frictional granular media. J. Phys. Condens. Matter 17: S2623–S2640

    Article  ADS  Google Scholar 

  43. Luding, S.: About contact force-laws for cohesive frictional materials in 2d and 3d. In: Walzel, P., Linz, S., Krülle, C., Grochowski, R. (eds) Behavior of Granular Media, Shaker Verlag, pp 137–147, band 9, Schriftenreihe Mechanische Verfahrenstechnik, ISBN 3-8322-5524-9 (2006)

  44. Luding, S.: Contact models for very loose granular materials. In: Eberhard P. (ed) Symposium on Multiscale Problems in Multibody System Contacts, Springer, Heidelberg, pp. 135–150. ISBN 978-1-4020-5980-3 (2007)

  45. Luding, S., Herrmann, H.J.: Micro-macro transition for cohesive granular media. In: Diebels S. (Ed.) Bericht Nr. II-7, Inst. für Mechanik, Universität Stuttgart (2001)

  46. Luding, S., Suiker, A.: Self-healing of damaged particulate materials through sintering. Philos. Mag. (2008, submitted)

  47. Luding S., Clément E., Blumen A., Rajchenbach J. and Duran J. (1994). Anomalous energy dissipation in molecular dynamics simulations of grains: The “detachment effect”. Phys. Rev. E 50: 4113

    Article  ADS  Google Scholar 

  48. Luding S., Clément E., Blumen A., Rajchenbach J. and Duran J. (1994). The onset of convection in molecular dynamics simulations of grains. Phys. Rev. E 50: R1762

    Article  ADS  Google Scholar 

  49. Luding S., Clément E., Blumen A., Rajchenbach J. and Duran J. (1994). Studies of columns of beads under external vibrations. Phys. Rev. E 49(2): 1634

    Article  ADS  Google Scholar 

  50. Luding S., Manetsberger K. and Muellers J. (2005). A discrete model for long time sintering. J. Mech. Phys. Solids 53(2): 455–491

    Article  ADS  MATH  Google Scholar 

  51. Luding, S., Suiker, A., Kadashevich, I.: Discrete element modeling of self-healing processes in damaged particulate materials. In: Schmets, A.J.M., van der Zwaag, S. (eds) Proceedings of the 1st International Conference on Self Healing Materials, Springer series in Material Science, Berlin, Germany (ISBN 978-1-4020-6249-0 (2007)

  52. Matuttis H.G., Luding S. and Herrmann H.J. (2000). Discrete element methods for the simulation of dense packings and heaps made of spherical and non-spherical particles. Powder Technol. 109: 278–292

    Article  Google Scholar 

  53. Mindlin R.D. (1949). Compliance of elastic bodies in contact. J. Appl. Mech. 16: 259

    MathSciNet  MATH  Google Scholar 

  54. Mindlin R.D. and Deresiewicz H. (1953). Elastic spheres in contact under varying oblique forces. J. Appl. Mech. 20: 327

    MathSciNet  MATH  Google Scholar 

  55. Moreau, J.J.: New computation methods in granular dynamics. In: Powders and Grains, vol. 93. Balkema, Rotterdam, p 227 (1993)

  56. Moreau J.J. (1994). Some numerical methods in multibody dynamics: application to granular materials. Eur J Mech A 13: 93

    MathSciNet  MATH  Google Scholar 

  57. Oda M. and Iwashita K. (2000). Study on couple stress and shear band development in granular media based on numerical simulation analyses. Int. J. Eng. Sci. 38: 1713–1740

    Article  Google Scholar 

  58. Oda M. and Kazama H. (1998). Microstructure of shear bands and its relation to the mechanism of dilatancy and failure of dense granular soils. Géotechnique 48(4): 465–481

    Google Scholar 

  59. Oda, M., Iwashita, K., Kazama, H.: Micro-structure developed in shear bands of dense granular soils and its computer simulation—mechanism of dilatancy and failure. In: Fleck, N.A., Cocks, A.C.E. (eds) IUTAM Symposium on Mechanics of Granular and Porous Materials. Kluwer, Dordrecht, pp 353–364 (1997)

  60. Pao Y.H. (1955). Extension of the Hertz theory of impact to the viscoelastic case. J. Appl. Phys. 26: 1083

    Article  ADS  MATH  Google Scholar 

  61. Pöschel T. and Schwager T. (2005). Computational Granular Dynamics. Springer, Berlin

    Google Scholar 

  62. Pöschel T., Schwager T. and Brilliantov N.V. (1999). Rolling friction of a hard cylinder on a viscous plane. Eur. J. Phys. 10: 169–175

    ADS  Google Scholar 

  63. Radjai F., Jean M., Moreau J.J. and Roux S. (1996). Force distribution in dense two-dimensional granular systems. Phys. Rev. Lett. 77(2): 274

    Article  ADS  Google Scholar 

  64. Radjai F., Schäfer J., Dippel S. and Wolf D. (1997). Collective friction of an array of particles: A crucial test for numerical algorithms. J. Phys. I France 7: 1053

    Article  Google Scholar 

  65. Radjai F., Wolf D.E., Jean M. and Moreau J.J. (1998). Bimodal character of stress transmission in granular packings. Phys. Rev. Lett. 80(1): 61–64

    Article  ADS  Google Scholar 

  66. Raman C.V. (1918). The photographic study of impact at minimal velocities. Phys. Rev. 12: 442–447

    Article  ADS  Google Scholar 

  67. Rapaport D.C. (1995). The Art of Molecular Dynamics Simulation. Cambridge University Press, Cambridge

    Google Scholar 

  68. Richefeu V., Radjai F. and Youssoufi M.S.E. (2006). Stress transmission in wet granular materials. Eur. Phys. J. Eng. 21(4): 359–369

    Article  Google Scholar 

  69. Röck M., Morgeneyer M., Schwedes J., Brendel L., Wolf D.E. and Kadau D. (2008). Visualization of shear motions of cohesive powders in the true biaxial shear tester. Partic. Sci. Technol. 26: 43–54

    Article  Google Scholar 

  70. Roux, S.: Quasi-static contacts. In: Herrmann, H.J., Hovi, J.P., Luding, S. (eds) Physics of dry granular media—NATO ASI Series E 350, Kluwer, Dordrecht, p. 267 (1998)

  71. Sadd M.H., Tai Q.M. and Shukla A. (1993). Contact law effects on wave propagation in particulate materials using distinct element modeling. Int. J. Non-Lin. Mech. 28(2): 251

    Article  MATH  Google Scholar 

  72. Savkoor A.R. and Briggs G.A.D. (1977). The effect of tangential force on the contact of elastic solids in adhesion. Proc. R. Soc. Lond. A 356: 103

    Article  ADS  MATH  Google Scholar 

  73. Schäfer J., Dippel S. and Wolf D.E. (1996). Force schemes in simulations of granular materials. J. Phys. I France 6: 5–20

    Article  Google Scholar 

  74. Severens I.E.M., de Ven A.A.F.V., Wolf D.E. and Mattheij R.M.M. (2006). Discrete element method simulations of toner behavior in the development nip of the oce direct imaging print process. Granular Matter 8(3–4): 137–150

    Article  Google Scholar 

  75. Sinkovits R.S. and Sen S. (1995). Nonlinear dynamics in granular columns. Phys. Rev. Lett. 74(14): 2686

    Article  ADS  Google Scholar 

  76. Spahn F., Hertzsch J.M. and Brilliantov N.V. (1995). The role of particle collisions for the dynamics in planetary rings. Chaos Solitons Fractals 5: 1945

    Article  ADS  Google Scholar 

  77. Sperl M. (2006). Experiments on corn pressure in silo cells. Translation and comment of Janssen’s paper from 1895. Granular Matter 8(2): 59–65

    Article  MATH  Google Scholar 

  78. Suiker A.S.J. and Fleck N.A. (2004). Frictional collapse of granular assemblies. J. Appl. Mech. 71: 350–358

    Article  MATH  Google Scholar 

  79. Tanakov M.Y., Trusov L.I., Belyi M.V., Bulgakov V.E. and Gryaznov V.G. (1993). Elastically stressed state in small particles under conditions of Hertzian contacts. J. Phys. D 26: 997

    Article  ADS  Google Scholar 

  80. Thornton C. (1997). Force transmission in granular media. KONA Powder Particle 15: 81–90

    Google Scholar 

  81. Thornton C. (2000). Numerical simulations of deviatoric shear deformation of granular media. Géotechnique 50(1): 43–53

    Article  Google Scholar 

  82. Thornton C. and Antony S.J. (2000). Quasi-static deformation of a soft particle system. Powder Technol. 109(1–3): 179–191

    Article  Google Scholar 

  83. Thornton, C., Randall, C.W.: Applications of theoretical contact mechanics to solid particle system simulation. In: Micromechanics of granular media. Elsevier, Amsterdam (1988)

  84. Thornton C. and Yin K.K. (1991). Impact of elastic spheres with and without adhesion. Powder Technol. 65: 153

    Article  Google Scholar 

  85. Thornton, C., Zhang, L.: A DEM comparison of different shear testing devices. In: Kishino, Y. (ed) Powders and Grains 2001. Balkema, Rotterdam, pp. 183–190 (2001)

  86. Tighe B.P. and Sperl M. (2007). Pressure and motion of dry sand: translation of Hagen’s paper from 1852. Granular Matter 9(3/4): 141–144

    Article  Google Scholar 

  87. Tomas J. (2000). Particle adhesion fundamentals and bulk powder consolidation. KONA 18: 157–169

    Google Scholar 

  88. Tomas J. (2004). Fundamentals of cohesive powder consolidation and flow. Granular Matter 6(2/3): 75–86

    Article  MATH  Google Scholar 

  89. Tykhoniuk R., Tomas J. and Luding S. (2006). A microstructure-based simulation environment on the basis of an interface enhanced particle model. Granular Matter 8(3/4): 159–174

    Google Scholar 

  90. Valverde J.M. and Castellanos A. (2007). Compaction of fine powders: from fluidized agglomerates to primary particles. Granular Matter 9(1–2): 19–24

    Google Scholar 

  91. Vermeer, P.A., Diebels, S., Ehlers, W., Herrmann, H.J., Luding, S., Ramm, E. (eds) Continuous and Discontinuous Modelling of Cohesive Frictional Materials. Lecture Notes in Physics, vol. 568. Springer, Berlin (2001)

  92. Vermeer, P.A., Ehlers, W., Herrmann, H.J., Ramm, E.: (eds) Modelling of Cohesive-frictional materials, Balkema, Leiden, Netherlands (ISBN 04 1536 023 4) (2004)

  93. Walton K. (1978). The oblique compression of two elastic spheres. J. Mech. Phys. Solids 26: 139

    Article  ADS  MathSciNet  MATH  Google Scholar 

  94. Walton O.R. (1989). Force models for particle-dynamics simulations of granular materials. NATO ASI Ser. E Appl. Sci. 287: 367–379

    Google Scholar 

  95. Walton, O.R.: Effects of interparticle friction and particle shape on dynamic angles of repose via particle-dynamics simulation. In: Workshop: Mechanics and Statistical Physics of Particulate Materials (1994)

  96. Walton, O.R.: Elastic frictional contact models based on analysis of Mindlin (1949), private communication (1995a)

  97. Walton O.R. (1995). Force models for particle-dynamics simulations of granular materials. In: Guazzelli, E. and Oger, L. (eds) Mobile particulate systems, pp 367. Kluwer, Dordrecht

    Google Scholar 

  98. Walton O.R. and Braun R.L. (1986). Viscosity, granular-temperature and stress calculations for shearing assemblies of inelastic, frictional disks. J. Rheol. 30(5): 949–980

    Article  ADS  Google Scholar 

  99. Zhu C.Y., Shukla A. and Sadd M.H. (1991). Prediction of dynamic contact loads in granular assemblies. J. Appl. Mech. 58: 341

    Article  Google Scholar 

Download references

Open Access

This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.

Author information

Authors and Affiliations

  1. Multi Scale Mechanics, TS, CTW, UTwente, P.O. Box 217, 7500 AE, Enschede, Netherlands

    Stefan Luding

  2. Particle Technology, Nanostructured Materials, DelftChemTech, TNW, TUDelft, Julianalaan 136, 2628 BL, Delft, Netherlands

    Stefan Luding

Authors
  1. Stefan Luding
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Stefan Luding.

Rights and permissions

Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.

Reprints and Permissions

About this article

Cite this article

Luding, S. Cohesive, frictional powders: contact models for tension. Granular Matter 10, 235–246 (2008). https://doi.org/10.1007/s10035-008-0099-x

Download citation

  • Received: 22 December 2006

  • Published: 27 March 2008

  • Issue Date: June 2008

  • DOI: https://doi.org/10.1007/s10035-008-0099-x

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Keywords

  • Granular materials
  • Molecular dynamics (MD) and discrete elementmodel (DEM) force-laws
  • Friction
  • Rolling- and torsion-resistance
  • Adhesion
  • Plastic deformation
Download PDF

Working on a manuscript?

Avoid the common mistakes

Advertisement

Over 10 million scientific documents at your fingertips

Switch Edition
  • Academic Edition
  • Corporate Edition
  • Home
  • Impressum
  • Legal information
  • Privacy statement
  • Your US state privacy rights
  • How we use cookies
  • Your privacy choices/Manage cookies
  • Accessibility
  • FAQ
  • Contact us
  • Affiliate program

Not affiliated

Springer Nature

© 2023 Springer Nature Switzerland AG. Part of Springer Nature.