Introduction

Flows of energy and matter across habitat boundaries, often referred to as allochthonous subsidies, can be major determinants of ecosystem functioning (Polis and others 1997; Loreau and others 2003). Dictated by gravity, freshwater systems are sinks for terrestrial matter and therefore particularly strongly influenced by allochthonous inputs (Leroux and Loreau 2008). For example, in many boreal lakes a large fraction of consumer biomass is ultimately derived from terrestrial carbon (Cole and others 2006), which enters most lakes predominantly as dissolved organic matter (Kortelainen and others 2006). Terrestrial dissolved organic matter (tDOM) is furthermore believed to serve as a nutrient source for primary producers (Klug 2002; Kissman and others 2013; Sanders and others 2015). However, tDOM also carries light-absorbing chromophores. The resulting shading (a resource subtraction) has adverse effects on lake primary production which can override the subsidizing effects of tDOM (Karlsson and others 2009; Jones and Lennon 2015; Karlsson and others 2015). The relative importance of tDOM as a resource subsidy versus resource subtraction for lake systems is therefore a matter of debate (Jones and others 2012; Kelly and others 2014; Solomon and others 2015; Carpenter and others 2016). In particular, it is currently not well understood how the simultaneous addition of nutrients and subtraction of light that come with tDOM interact in shaping lake primary production (Seekell and others 2015a, b). Understanding these processes is important, because climate change scenarios predict tDOM supply to increase in northern lakes (Solomon and others 2015), with potentially far-reaching implications for the transfer of primary production to higher trophic levels (Jansson and others 2007; Karlsson and others 2009) and for the carbon balance of the boreal landscape (Cole and others 2007; Tranvik and others 2009).

Lake primary production is in itself spatially structured. Lacustrine primary producers are found in two distinct habitats, which are linked through opposed fluxes of the essential resources light and nutrients. Light enters lakes from above and is attenuated in the pelagic (open water) habitat before it reaches the benthic habitat at the bottom of the lake. Conversely, fueled by sinking particles from the pelagic habitat, nutrients have their highest concentration in the sediment of the benthic habitat from where they can be recycled and released back into the pelagic habitat in dissolved form. This geometry of light and nutrient supply makes resource competition between pelagic and benthic primary producers spatially asymmetric: pelagic producers shade and negatively affect the light supply to benthic producers, whereas benthic producers intercept the nutrient flux from the sediment and negatively affect the nutrient supply to pelagic producers (Hansson 1988; Genkai-Kato and others 2012; Jäger and Diehl 2014).

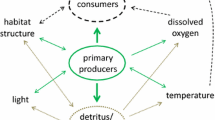
Although it is clear that input of tDOM affects resource availability and competitive interactions between benthic and pelagic primary producers, its overall effects on habitat specific and total lake primary production are not fully understood. Theoretical and empirical evidences suggest that tDOM inhibits benthic primary production through light subtraction (Figure 1, Ask and others 2009; Godwin and others 2014), whereas it may subsidize pelagic primary production with nutrients along two non-exclusive pathways: (1) by supplying nutrients bound to tDOM and (2) by shading benthic algae and thus releasing the nutrient flux from the sediment to the pelagic habitat (Figure 1, Jäger and Diehl 2014; Seekell and others 2015b; Vasconcelos and others 2016). Our understanding of the resulting net effects of tDOM on lake primary production is currently hampered by a lack of experimental assessments addressing benthic and pelagic habitats simultaneously.

Figure 1
figure 1

Hypothesized causal relationships between supply with terrestrial dissolved organic matter (tDOM), underwater light availability, pelagic nutrient concentration (soluble reactive phosphorus, SRP), gross primary production (GPP) of benthic and pelagic algae, and biomass of pelagic algae. Numbered arrows indicate the directions and signs (+/−) of hypothesized, direct causal relationships between variables. The causal link from light availability to pelagic GPP (link 7, broken arrow) was not included in the SEM model because of collinearity issues (see text).

Full size image

In this study, we investigate how input of tDOM from the terrestrial catchment interacts with cross-habitat flows of nutrients and light within lakes to shape resource competition between benthic and pelagic primary producers and total in-lake primary production. To do so, we performed an experiment in which we manipulated the concentration of tDOM in pond-scale ecosystems containing a full boreal lake community. We asked the following specific questions: does tDOM have the hypothesized (1) negative effect on benthic primary production and (2) positive effect on pelagic nutrient availability? The answer to both questions was yes, raising two follow-up questions. (3) To which extent was the positive effect of tDOM on pelagic nutrients driven by a direct nutrient subsidy and/or by a release of the nutrient flux from the sediment, triggered by the shading of benthic producers by tDOM? (4) Is the net effect of tDOM on pelagic and whole-ecosystem primary production positive or negative—that is, can the increase in pelagic nutrients outweigh the negative effect of shading? We used structural equation modeling to address question 3 and our experimental data to address questions 1, 2, and 4. We also explored questions 1–4 at a more general level by extending and numerically analyzing a process-based dynamical ecosystem model that reflects our current understanding of the nonlinear feedbacks involved in the responses of benthic and pelagic primary producers to increasing tDOM supply.

Methods

The experiment was performed at Umeå Experimental Ecosystem Facility (EXEF, 63°48′N, 20°14′E). EXEF includes a rectangular pond divided into 20 sections of which 16 were used for treatment establishment. Each section had an area of 11.5 m × 6.7 m, was 1.6 m deep except for a narrow zone near the shoreline, and had its own, separate water supply system. In summer 2011, the pond was filled with groundwater and allowed to develop a natural community, including pelagic and benthic algae and sparse floating leaf and submerged macrophytes. In May 2012, we stocked each section with a (subsequently reproducing and overwintering) fish population of three-spined stickleback (Gasterosteus aculeatus) and established two tDOM treatments: a ‘low tDOM’ control to which we continuously added groundwater with an average concentration of 1.4 g m−3 of dissolved organic carbon (DOC), and a ‘high tDOM’ treatment to which we continuously added 100-µm filtered humic water (with on average 18.7 g DOC m−3) from a mid-sized stream near the facility. As part of a broader climate impact study, the tDOM treatments were cross-classified with two temperature treatments: ambient temperature (‘amb’) and warming to 3°C above ambient temperature (‘warm’). The latter was accomplished by continuously circulating water from the warmed sections through a heat exchanger. Each tDOM by temperature treatment was replicated four times.

Warming and tDOM additions were maintained from May 10, 2012, to October 6, 2012, interrupted during winter to allow for a regular ice cover, and resumed from May 16, 2013, to October 3, 2013 (Julian days 136–276). Results from the summer season 2012—when we did not measure all state variables depicted in Figure 1, are described in Vasconcelos and others (2016). Here, we report results from the summer season 2013 with a focus on the tDOM treatments, which were characterized as follows. On May 16, 2013, the water supplies to both high and low tDOM treatments were set to 4 m3 day−1 to mimic a 1-week spring flow. Thereafter, a continuous input of 1.14 m3 day−1 was applied, corresponding to a daily exchange rate of 0.9% of the water volume during the rest of the season. Average concentrations in the incoming humic and groundwater and the resulting daily additions of DOC and nutrients to the high and low tDOM treatments are summarized in Table 1. Notably, DOC additions were 13-fold higher, and total phosphorus (TP) additions were 17-fold higher in the high versus low tDOM treatments. In order to focus the experiment on the interaction between phytoplankton and sediment-dwelling benthic algae, we cut and removed an existing sparse macrophyte cover on Julian day 156.

Table 1 Temporal Averages (mean ± 1SD) of the Concentrations of Dissolved Organic Carbon (DOC), Soluble Reactive Phosphorus (SRP), Total Phosphorus (TP), and Dissolved Inorganic Nitrogen (DIN) in the Humic Water and Groundwater Added to the High and Low tDOM Treatments, Respectively
Full size table

Physical, Chemical, and Biological Variables

Water temperature and vertical profiles of photosynthetic active radiation (PAR, used to calculate the vertical light attenuation coefficient, kd) were determined as in Vasconcelos and others (2016). Temperature profiles indicated that the water column was always well mixed. We therefore calculated average light in the mixed water column (Imix) and light at the sediment surface (IZmax), expressed as percentages of incident PAR, as

$$ I_{\text{mix}} = 100 \cdot {{\left[ {1 - \exp \left( { - k_{d} \cdot z_{\hbox{max} } } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {1 - \exp \left( { - k_{d} \cdot z_{\hbox{max} } } \right)} \right]} {\left( {k_{d} \cdot z_{\hbox{max} } } \right)}}} \right. \kern-0pt} {\left( {k_{d} \cdot z_{\hbox{max} } } \right)}}, $$
(1)
$$ I_{{z_{\hbox{max} } }} = 100 \cdot \exp \left( { - k_{d} \cdot z_{\hbox{max} } } \right), $$
(2)

where zmax is the depth of the water column (1.6 m).

Every third week, starting on Julian day 136, we took integrated water samples from the upper meter of the water column in each experimental section. Water samples were filtered (0.45 µm) prior to determining the concentrations of soluble reactive phosphorus (SRP) and dissolved inorganic nitrogen (DIN) under flow injection analysis (FIA, Foss, Denmark). Concentrations of dissolved organic carbon (DOC) and chlorophyll a (Chl a) were determined as in Vasconcelos and others (2016). Treatment effects on DIN are not further reported here because molar DIN:TP ratios exceeded 30 in 80% of all available measurements throughout the experiment, indicating that phosphorus was the limiting nutrient for primary producers (Bergström 2010).

In each experimental section, we estimated gross primary production (GPP) in the benthic and pelagic habitats (= benthic and pelagic GPP) from oxygen dynamics recorded during 48-h in situ incubations. Incubations were performed on four occasions (Julian days 161–165, 196–200, 242–247, and 273–277) as described in Rodríguez and others (2016), and oxygen dynamics were converted into units of carbon assuming a C:O2 conversion factor of 0.375 g/g (Wetzel and Likens 2000).

Data Analysis

We analyzed treatment responses using the temporally averaged mean values of all relevant variables (Figure 1) over a 113-day window ranging from Julian day 161 to 273, starting and ending with the first (June 10) and the last (September 30) measurement of benthic and pelagic GPP, respectively. Temporal averaging was done by integration of linearly interpolated measurements over the selected time window. Water temperatures and DOC concentrations were relatively constant during the time window, with the exception of a 6°C temperature decline in the last week (see Appendix S1).

We analyzed the data in two steps. In a first step, we used two-way ANOVA to test for treatment effectiveness (differences in DOC and temperature between treatments) and for effects of the treatments on the production of benthic and pelagic algae, on biomass of pelagic algae and on the availability of the resources light (characterized by kd, Imix, and Izmax) and SRP. Data were log-transformed when necessary to fulfill ANOVA requirements. All ANOVAs were run on R software using the ez package (R Development Core Team 2013; Lawrence 2015).

In a second step, we used piecewise structural equation modeling (piecewise SEM) to statistically tease apart and quantify direct and indirect effects of tDOM on the resources light and SRP and on interactions and feedbacks between benthic and pelagic primary producers. Piecewise SEM can be applied to data with small sample sizes because it estimates path coefficients one at a time and then pieces these links together to build a unique causal model (Lefcheck 2016). Piecewise SEM uses the d-separation test (Fisher’s C) to evaluate whether the causal model misses important links (a P value > 0.05 indicates that a model is acceptable, Shipley 2002.) We performed piecewise SEM on the temporally averaged mean values of all state variables included in Figure 1 using R software with the package ‘piecewiseSEM’ (R Core Team 2013; Lefcheck 2016). Data were log-transformed to fulfill the analysis requirements.

A potential problem with piecewise SEM is the presence of loops and collinearities, which can affect the estimation of path coefficients and misguide the interpretation of causal relationships (Lefcheck 2016). In our causal model, there are two loops: (1) pelagic GPP → pelagic algal biomass → light availability → pelagic GPP (links 5–6–7 in Figure 1), and (2) light availability → benthic GPP → SRP → pelagic GPP → pelagic algal biomass → light availability (links 2–3–4–5–6 in Figure 1). We initially ran piecewise SEM on the full causal model with both loops included (Appendix S2). This model had poor statistical support (AICc = − 185.6) compared to the final model (AICc = − 262.6) and returned one biologically implausible sign—a negative sign for link 7 in the first loop (that is, a negative effect of increased light availability on pelagic GPP), which was not statistically significant (Appendix S2). It is highly unlikely that depth-integrated pelagic GPP suffered from light inhibition in the low tDOM treatment, which then would have been alleviated in the high tDOM treatment. Instead, the covariance structure of the data (tDOM correlated strongly, but with opposite signs, with light availability, IZmax, and strongly positively with pelagic GPP) made it impossible to detect the expected positive effect of increased light availability on pelagic GPP, which was presumably weak (see discussion section Direct effects of tDOM on resource availability). We therefore removed link 7 from the final model. In contrast, breaking the second loop by excluding link 6 (a negative effect of pelagic Chl a on the light IZmax which was statistically significant) did not affect the estimates of any other path coefficients. We therefore kept link 6 in the final model.

Because the estimates of path coefficients related to the tDOM treatments could be influenced by the temperature treatments, we also analyzed an SEM that included effects of temperature on algal biomass and GPP [see Vasconcelos and others (2016) for mechanistic details on expected temperature effects]. The model including both tDOM and temperature effects had poor statistical support (AICc = − 105.6), and path coefficients of potential temperature effects were not statistically significant, except for a negative link from temperature to pelagic Chl a (Appendix S3). Including temperature links in the piecewise SEM also only marginally altered the estimates of path coefficients shared by the model excluding temperature effects (Appendix S3). In the results section, we therefore present the model with only tDOM effects, which had by far the highest statistical support (AICc = − 262.6).

Dynamical Ecosystem Model

The dynamical ecosystem model is an extension of a model of competition between benthic and pelagic primary producers developed by Jäger and Diehl (2014). It is described in Appendix S4 and summarized in Tables S4.1 and S4.2. In short, the model describes the dynamics of all state variables (light attenuation, benthic and pelagic mineral nutrients, sediment nutrients, benthic and pelagic algal biomass) and process rates (nutrient transformations and fluxes, benthic and pelagic GPP) that are explicitly or implicitly involved in the processes depicted in Figure 1.

We used the model to explore the influence of tDOM on aquatic primary production under two extreme, contrasting scenarios concerning the availability of organic nutrients bound to tDOM: (i) when entering the lake, all tDOM-bound nutrients become instantly available to aquatic producers; (ii) alternatively, tDOM-bound nutrients are completely unavailable to aquatic producers. Real systems are most likely somewhere in-between these two scenarios, which bracket all intermediate cases of partial availability of tDOM-bound nutrients and, thus, enable a comprehensive theoretical assessment of the relative importance of the direct and indirect pathways of tDOM effects on benthic and pelagic primary production. For completeness, we also explored a third, intermediate scenario where half of the nutrients bound to tDOM are assumed to become available.

The equation systems describing scenarios i–iii differ in the numerical values of a single term, a0,1cDOMDOM, describing the conversion of externally supplied, tDOM-bound nutrients into nutrients available to pelagic producers (see Appendix S4 and eq. E3 in Table S4.1 for details). Here, DOM is the tDOM concentration in incoming water from the catchment, cDOM is the nutrient to carbon quota of incoming tDOM, and a0,1 is a dummy variable that equals 1 in scenario i (tDOM-bound nutrients are fully available), equals 0 in scenario ii (tDOM-bound nutrients are unavailable), and equals 0.5 in scenario iii (half of all tDOM-bound nutrients are available). Scenario ii has been explored extensively in Jäger and Diehl (2014) and Vasconcelos and others (2016), whereas scenarios i and iii are novel. For all scenarios, we numerically explored the influence of a large gradient in external tDOM supply on equilibrium values of underwater light, nutrients and primary production in a system that matches the physical setting of the experimental pond sections (uniform water depth 1.6 m, well-mixed water column, water residence time 100 days).

Results

Treatment Effectiveness and Light Climate

In the ambient, low tDOM treatment, DOC concentrations were fairly constant at approximately 4 g m−3, whereas water temperatures hovered around 15–20°C for most of the time (Appendix S1). The manipulations of tDOM loading and temperature were highly effective. Averaged over Julian days 161–273, DOC was 2.8 times higher in high versus low tDOM sections (Figure 2), and warmed sections were 2.8°C warmer than ambient sections (Appendix S1), with no interaction between tDOM and temperature treatments (Table 2).

Figure 2
figure 2

Responses of DOC, light availability at depth zmax (Izmax), SRP, benthic, pelagic, and total (= benthic + pelagic) GPP, and pelagic biomass (Chl a) to the tDOM and temperature treatments. White bars = low tDOM; black bars = high tDOM; amb = ambient temperature; warm = elevated temperature. Shown are treatment means +1 SE. Also shown are the results of the piecewise SEM with the highest statistical support (AICc = − 262.6, Δ AICc to next best model = − 77.9). Arrows indicate the direction of causality, and numbers near arrows are standardized path coefficients. All links are statistically significant at P < 0.05. Shown above each dependent variable is the R2 value of the path(s) explaining that variable. Note that total GPP is not included in the SEM.

Full size image
Table 2 P Values of Two-way ANOVAS of the Effects of Terrestrial Dissolved Organic Matter (tDOM), Warming, and Their Interaction (tDOM * Warming) on Water Temperature, Dissolved Organic Carbon (DOC), Light Attenuation (kd), Light in the Benthic (IZmax) and Pelagic (Imix) Habitats, Benthic Primary Production (GPP), Soluble Reactive Phosphorus (SRP), Pelagic GPP and Chl a, and Total GPP (= benthic plus pelagic GPP)
Full size table

The vertical light attenuation coefficient kd was on average 2.5 times higher in high versus low tDOM sections (2.34 vs. 0.92 Table 2). This implied that light supply to the benthic habitat (IZmax, equation 2) was 25 versus 3.6% of incoming light and that light supply to the pelagic habitat (Imix, equation 1) was 54 versus 28% of incoming light in high versus low tDOM sections, respectively (Figure 2, Table 2). Warming had no effect on the light supply to the benthic and pelagic habitats (Table 2).

Primary Producers and Mineral Nutrients

Benthic and pelagic primary production responded in opposite ways to increasing tDOM supply. Benthic GPP was lower, while pelagic GPP was higher in the high compared to the low tDOM sections (Figure 2, Table 2). As a consequence, the average contribution of benthic GPP to total (= pelagic + benthic) GPP was 37% in the low tDOM treatment compared to only 13% in the high tDOM treatment. Correspondingly, the contribution of pelagic GPP to total GPP was 63% and 87% in the low versus high tDOM treatments, respectively. Total GPP was approximately 1.5 times higher in high versus low tDOM sections (Figure 2, Table 2). Pelagic chlorophyll concentration was higher in the high than in the low tDOM sections and was negatively affected by warming (Figure 2, Table 2). Soluble reactive phosphorus (SRP) responded positively to increased tDOM supply and negatively to warming. SRP was on average 1.5 times higher in high versus low tDOM sections and 1.2 times higher in ambient versus warm sections (Figure 2, Table 2). There was no interaction between warming and tDOM effects on any response variable (Table 2).

Piecewise SEM Results

The piecewise SEM in Figure 2 accounted for 45 to 92% of the variance in the response variables (Figure 2), and the d-separation test (Fisher’C = 9.45, P value = 0.89) indicates that the SEM did not miss important links. In agreement with our hypotheses, the SEM supported the following direct causal links: a positive effect of tDOM on SRP, a negative effect of tDOM on light availability in the benthic habitat (IZmax), a positive effect of IZmax on benthic GPP, a negative effect of benthic GPP on SRP, a positive effect of SRP on pelagic GPP, a positive effect of pelagic GPP on pelagic algal biomass, and a negative effect of pelagic algal biomass on IZmax (Figure 2). A comparison of the strength of the direct path from tDOM to SRP (link 8 in Figure 1, standardized path coefficient = + 0.55) with the strength of the indirect path from tDOM to SRP via IZmax and benthic GPP (links 1–3 in Figure 1, product of the standardized path coefficients = + 0.27) suggests that the direct path was quantitatively about two times as important as the indirect path.

Dynamical Model Output

Figure 3 shows representative numerical examples of equilibrium GPP, light and nutrient conditions along a gradient of increasing tDOM concentration for scenarios i–iii. For greater generality (see discussion), the x-axes in Figure 3 are scaled as optical depth of the water column, OD = kd·zmax rather than tDOM concentration. For the chosen model parameterization, the light attenuation coefficient kd is primarily driven by tDOM and only to a small extent by light attenuation from pelagic algae (see caption of Figure 3). Optical depth is therefore roughly proportional to tDOM concentration, with one unit of OD corresponding to an approximate tDOM concentration of 3 g C m−3 at the assumed water column depth zmax of 1.6 m. Note that the depicted qualitative patterns along the OD (= tDOM) gradient are general, that is, they do not depend on the specific parameterization of the example in Figure 3.

Figure 3
figure 3

Example of equilibrium model predictions for A light in the pelagic (Imix) and benthic (IZmax) habitats, B benthic GPP, C, E total pelagic phosphorus (= dissolved mineral phosphorus + phosphorus in pelagic algae), D pelagic GPP, and F total (= benthic + pelagic) GPP along a gradient of increasing tDOM concentration, expressed as optical depth (OD). Optical depth equals kd·zmax with kd = kA A* + kDOM DOM, where A* and DOM are the concentrations of pelagic algae (at equilibrium) and tDOM, respectively, kA and kDOM are specific light attenuation coefficients, and zmax is water column depth (set to 1.6 m). Panels B–F show scenarios where tDOM-bound phosphorus is completely unavailable (a0,1 = 0, model scenario ii, dotted lines), partly available (a0,1 = 0.5, model scenario iii, broken lines), and fully available (a0,1 = 1, model scenario i, solid lines) to pelagic producers. The approximate ranges of optical depths encountered in the low (white bars) and high (gray bars) experimental tDOM treatments are indicated. Panel E illustrates how the direct and indirect contributions of tDOM to total pelagic phosphorus (TP) can be partitioned. At a given optical depth, colored bars represent the contributions to TP coming from different sources: blue = surface inflow of dissolved mineral P (assumed to be independent of tDOM concentration, horizontal broken line); green = sediment inflow of dissolved mineral P (driven by shading of benthic algae by tDOM and pelagic algae); yellow = surface inflow of dissolved organic P bound to tDOM. The summed bars illustrate how the relative sizes of tDOM contributions to TP via the direct (yellow = D) and indirect (green = T) pathways can be calculated as D/(D + T) and T/(D + T), respectively. Note that these relative contributions shift with increasing optical depth (= increasing tDOM supply).

Full size image

The following patterns emerge. Average light in the mixed pelagic water column, Imix, declines gradually with increasing optical depth, whereas light at the sediment surface, IZmax, declines much more rapidly and is considerably lower than Imix at all optical depths (Figure 3A). Consequently, benthic GPP becomes increasingly light-limited and declines abruptly to zero at a rather moderate level of OD (Figure 3B). When tDOM-bound nutrients are unavailable (scenario ii), benthic GPP decreases monotonically with increasing OD, whereas benthic GPP initially benefits from increasing OD when tDOM-bound nutrients become partly or fully available (scenarios i and iii, Figure 3B). The latter occurs, because tDOM-derived nutrients sequestered by pelagic algae sink to the bottom and stimulate benthic GPP after being mineralized in the sediment (see Figure S4.4). For the specific parameterization used in Figure 3, light limitation of benthic GPP becomes overwhelming at an OD > 3 in all three scenarios, and benthic GPP becomes zero when OD is equal to or greater than 4.4. This corresponds to an approximate tDOM concentration of 12 g C m−3.

In contrast, pelagic GPP initially increases with increasing tDOM supply in all three scenarios. In scenario ii, where tDOM nutrients are unavailable, this occurs over the OD range where benthic GPP declines (dotted lines in Figure 3B, D) and, consequently, a larger fraction of sediment nutrients can reach the mixed water column, thus alleviating pelagic nutrient limitation. Once benthic producers are extinct, any further increase in OD has no further positive effect on the nutrient flux from the sediment to the water column, but continues to reduce the light supply; consequently, pelagic GPP starts to decrease with increasing tDOM supply (increasing OD) in scenario ii (dotted line in Figure 3D). In contrast, in scenarios i and iii, pelagic algae benefit from increasing tDOM supply even after benthic producers are extinct, because of the release of tDOM-bound nutrients; eventually, however, release from nutrient limitation cannot compensate for increasing light limitation, and pelagic GPP declines at very high tDOM supply (broken and solid lines at high OD in Figure 3D). Pelagic GPP, and also total GPP, therefore show hump-shaped relationships to OD supply under all scenarios, but are always highest in scenario i where tDOM-bound nutrients are assumed to be fully available to pelagic producers (Figure 3D, F).

Discussion

We have reported results from a replicated, large-scale field experiment investigating how input of terrestrial organic matter shapes primary production and resource competition between benthic and pelagic producers. We focused on relatively shallow systems and on the input of tDOM as the primary driver of cross-habitat fluxes, because small, shallow lakes are the most abundant lake type in the boreal landscape (Downing and others 2006), and because tDOM is typically the most important external source of organic carbon and nutrients to northern lakes, but also highly variable among lakes (Wilkinson and others 2013; Seekell and others 2015a). Our specific research questions can be placed into three categories. (1) What are the direct effects of tDOM on the availability of limiting resources to pelagic and benthic producers? (2) What are the indirect effects of tDOM on resource availability? (3) What is the net result of the direct and indirect effects of tDOM on benthic, pelagic, and total primary production? Below, we discuss these questions in order, making use of both our experimental data and the output from our dynamical ecosystem model.

Direct Effects of tDOM on Resource Availability

We hypothesized two direct effects of tDOM on resource availability to producers. First, the underwater light supply should decrease with increasing tDOM input. Although it comes as no surprise that this hypothesis was confirmed, we also quantified the absolute and relative strengths of tDOM effects on light supply to benthic versus pelagic producers. The absolute reduction in light supply from low to high tDOM was similar in both habitats, but the relative reduction was much stronger in the benthic habitat. At high tDOM, benthic algae received only 3.6% of incident radiation, whereas pelagic algae received approximately 28%. In the high tDOM treatment, light was thus much more limiting to benthic than to pelagic producers, reflecting a fundamental asymmetry: benthic producers are inevitably more sensitive to increasing light attenuation than pelagic producers, because the former only receive light that has traveled through the entire pelagic habitat. Consequently, light in the benthic habitat falls below the conventional compensation point for photosynthesis (1% of incident radiation, calculated from equation 2) already at an optical depth of 4.6 (Figure 3A, Krause-Jensen and Sand-Jensen 1998). In contrast, pelagic producers always receive full incident radiation at the water surface. Average light in the water column Imix therefore decreases more slowly with optical depth, and an optical depth of 100 (calculated from equation 1) is required for Imix to fall below the compensation point in a well-mixed pelagic habitat. Our high tDOM treatment (mean optical depth 3.74) was thus close to the compensation point for benthic producers but still very far from the compensation point for pelagic producers. Note that the compensation point for photosynthesis balances GPP only against algal respiration losses, but ignores other losses. Consequently, our dynamical model predicts pelagic algae to go extinct at a considerably lower optical depth than 100 (Figure 3D, S4.3d), because they are assumed to suffer from additional losses through sinking and washout.

Second, the concentrations of limiting nutrients should increase with increasing tDOM supply if tDOM-bound organic nutrients are at least partly mineralized. This hypothesis was supported by a positive direct effect of tDOM on SRP in the SEM, which is in line with the general observation of a positive correlation between SRP and water color in Swedish forest lakes (Meili 1992). Yet, the SEM suggests that direct release of tDOM-bound phosphorus was not the only contribution to pelagic nutrients in the high tDOM treatment. We explore the contribution of the indirect pathway involving nutrient release from the sediment in the next section.

Indirect Effects of tDOM on Resource Availability

We hypothesized two indirect effects of tDOM on resource availability to producers. First, if tDOM benefits pelagic producers, this should feedback on the underwater light climate through increased shading. We did indeed observe a 35% increase in pelagic chlorophyll in the high tDOM treatment. Yet, the path coefficient from pelagic chlorophyll to the light extinction coefficient kd was only weakly positive. The likely reason for this weak feedback is that the contribution of pelagic algae to light extinction was small compared to the contribution of tDOM, as is typical for unproductive humic lakes (Ask and others 2009). Average pelagic chlorophyll concentrations were 5.8 versus 4.3 mg Chl a m−3 in the high versus low tDOM treatments. Using the 10 and 90% quantiles from a literature review of chlorophyll-specific attenuation coefficients of phytoplankton (Krause-Jensen and Sand-Jensen 1998), this difference in chlorophyll concentration corresponds to an estimated difference in light attenuation of 0.02–0.06 m−1. Pelagic chlorophyll thus likely contributed only 1.5–5% to the increase in light attenuation between low and high tDOM treatments, with most of the remaining light attenuation being directly attributable to tDOM.

Second, the strong, direct contribution of tDOM to light attenuation should reduce the growth of benthic primary producers and thus indirectly enhance the flux of nutrients from the sediment to the pelagic habitat. This prediction was supported by the SEM, which estimated the contribution of the indirect pathway from tDOM to pelagic nutrients to be 50% as large as the direct pathway. It is generally very difficult to address this issue with more direct evidence, such as bioassays of the availability of tDOM-bound nutrients and measurements of nutrient fluxes out of the sediment. We are not aware of any study that has measured both processes simultaneously, but we can use our model to illustrate how the two pathways can, in principle, be partitioned. Figure 3E illustrates that the direct contribution of tDOM-bound nutrients to total pelagic nutrients equals the difference D between model scenarios (i) and (ii). The relative contribution of the direct pathway from tDOM to pelagic nutrients can then be calculated as the ratio D/(D + T), where T is the contribution of tDOM to pelagic nutrients via the indirect pathway (see Figure 3E for details).

Figure 3E illustrates three things. First, it indicates that a significant contribution of the indirect pathway from tDOM to pelagic nutrients (via release of sediment nutrients) is a plausible and robust outcome. Note, however, that the numerical examples in Figure 3 are not intended to be quantitative descriptions of the experimental system, but only illustrations of scenarios (i)–(iii) using plausible, generic parameter values. Second, Figure 3E suggests an experimental procedure by which the relative contributions of the direct and indirect pathways from tDOM to pelagic nutrients could be estimated. What is required are experiments in which tDOM treatments (represented by the solid line in Figure 3E) are combined with control treatments (represented by the dotted line) in which only light attenuation is manipulated, and thus, only the indirect pathway is operating. This could be accomplished by mimicking the light-attenuating properties of tDOM through addition of an inert dye or, in smaller systems, through manipulation of light attenuation by mesocosm walls (Diehl and others 2002, 2015).

Finally, the model suggests that the indirect pathway from tDOM to pelagic nutrients can give rise to highly nonlinear system responses, including abrupt shifts in benthic and pelagic GPP beyond a threshold in optical depth. While our experiment was not designed to address such nonlinearities, their existence is indeed suggested by lake data covering continuous gradients in DOC and nutrient concentrations (Vadeboncoeur and others 2003; Ask and others 2009; Godwin and others 2014). Such rapid state shifts can be dramatically accentuated by additional positive feedbacks from tDOM such as the development of anoxia, which abruptly promote the release of nutrients from the sediment (Genkai-Kato and others 2012; Brothers and others 2014).

Net Effects of tDOM on Primary Producers in Shallow Versus Deep Systems

As described in the previous section, our data clearly indicate that the indirect effect of tDOM on light (via shading from pelagic chlorophyll) was much weaker than the direct one (via shading by tDOM), whereas the indirect effect of tDOM on pelagic nutrients (via release of sediment nutrients) was of comparable strength as the direct one (via release of tDOM-bound nutrients). Regardless of the underlying mechanism, the net effects of our tDOM addition were negative for benthic production and positive for pelagic production, which is consistent with model simulations (Figure 3B, D). As a consequence, increased tDOM supply shifted resource competition between benthic and pelagic producers in favor of pelagic algae, moving the system from a state of a significant benthic contribution (benthic algae accounting for 37% of total GPP) to a state strongly dominated by pelagic production (benthic algae accounting for only 13% of total GPP).

Interestingly, total (= benthic + pelagic) GPP was highest in the high tDOM treatment, suggesting that primary producers were overall less resource limited at high than at low tDOM supply. A likely mechanism is that, at high tDOM supply, both tDOM-bound nutrients and sediment nutrients formerly used by benthic algae became available to pelagic algae, while pelagic light supply was still relatively high (Imix = 28% of incident PAR; note that this is higher than the light supply to benthic algae at low tDOM, IZmax = 25%, Figure 3A). More generally, it has been proposed that the influence of tDOM on total lake primary production shifts sign at some threshold tDOM supply, with tDOM effects being positive in clear, nutrient-limited lakes and negative in humic, light-limited lakes (Solomon and others 2015; Seekell and others 2015b). Based on data from boreal and arctic lakes, Seekell and others (2015a) suggested that this threshold occurs around a concentration of 4.8 g DOC m−3.

It is, however, unlikely that a single threshold concentration applies to lakes of different depths, because the negative effect of a given tDOM concentration on underwater light supply increases with lake depth. Thus, optical depth should be a more general descriptor of the effect of tDOM on the underwater light environment than DOC concentration (Figure 3). Finstad and others (2014), who studied tDOM relationships with fish production, did indeed observe that shallow lakes switch from positive to negative tDOM effects at higher terrestrial carbon loads than deeper lakes. Yet, also optical depth cannot fully embody all possible effects of tDOM on primary production, because feedbacks on nutrients scale nonlinearly with lake depth (for example, the dilution of sediment-derived nutrients in the water column) and/or depend on the bioavailability of tDOM-bound nutrients (note that the optical depth at which total GPP is predicted to peak differs depending on the availability of tDOM-bound phosphorus, Figure 3F). It is therefore unlikely that a single number can be found (be it optical depth or tDOM concentration) at which primary production peaks across a heterogeneous set of lakes.

Potential Role of Grazing in the Experimental System

The structures of both the SEM (Figure 1) and the dynamical ecosystem model (Table S4.1), as well as our interpretation of the experimental data, are all based on the assumption that specific algal grazing losses were constant and relatively small in our experimental system. We believe that these assumptions are well justified, both conceptually and empirically. Conceptual support comes from an extension of the dynamical model that includes benthic and pelagic grazers and carnivorous fish, which approximates the trophic structure of the experimental pond community. That model predicts that fish control grazers at low levels and release primary producers from grazing pressure (Vasconcelos 2017), which is in agreement with observations. Benthic invertebrate dry biomass was less than 0.55 g m−2, and zooplankton dry biomass was less than 3 mg m−3 in all treatments, suggesting that predation pressure by invertebrate feeding fish (sticklebacks) was very high (Vasconcelos 2017; see also Hedström and others 2017). We therefore conclude that grazing is unlikely to interfere with our interpretation of the experimental observations.

Conclusions and Outlook

We have shown that aquatic primary production increased in response to increased organic matter input from terrestrial sources over the range of environmental conditions (pond depth and tDOM concentrations) covered by our experiment. At first glance, tDOM seemed to act primarily as a resource subsidy for pelagic primary producers, with organic nutrients bound to tDOM being the putative resource. Yet, our detailed analyses revealed that a direct positive effect of tDOM-bound nutrients was not sufficient to explain the results and that tDOM also acted as a resource subtraction by shading primary producers. The overall positive effect of tDOM on aquatic production therefore involved complex, spatially organized feedbacks, where terrestrial DOM inputs triggered alterations in the flows of light and nutrients between habitats within the aquatic system, which, in turn, altered the absolute and relative contributions of benthic and pelagic algae to total primary production.

Understanding these processes is important, because climate change scenarios predict terrestrial DOM supply to increase in northern lakes (Finstad and others 2016), and tDOM affects both the carbon balance of lakes (Cole and others 2007) and biomass production at higher trophic levels (Finstad and others 2014; Karlsson and others 2015). Although we believe that the dynamical model illustrated in Figure 3 provides a useful framework to guide future research (including model extensions to higher trophic levels), important components of this framework still need to be investigated more closely. In particular, detailed empirical assessments of the availability of tDOM-bound nutrients and of nutrient fluxes across the sediment–water interface should be a high priority.