Abstract
Although stream ecosystems are recognized as an important component of the global carbon cycle, the impacts of climate-induced hydrological extremes on carbon fluxes in stream networks remain unclear. Using continuous measurements of ecosystem metabolism, we report on the effects of changes in snowmelt hydrology during the anomalously warm winter 2013/2014 on gross primary production (GPP), ecosystem respiration (ER), and net ecosystem production (NEP) in an Alpine stream network. We estimated ecosystem metabolism across 12 study reaches of the 254 km2 subalpine Ybbs River Network (YRN), Austria, for 18 months. During spring snowmelt, GPP peaked in 10 of our 12 study reaches, which appeared to be driven by PAR and catchment area. In contrast, the winter precipitation shift from snow to rain following the low-snow winter in 2013/2014 increased spring ER in upper elevation catchments, causing spring NEP to shift from autotrophy to heterotrophy. Our findings suggest that the YRN transitioned from a transient sink to a source of carbon dioxide (CO2) in spring as snowmelt hydrology differed following the high-snow versus low-snow winter. This shift toward increased heterotrophy during spring snowmelt following a warm winter has potential consequences for annual ecosystem metabolism, as spring GPP contributed on average 33% to annual GPP fluxes compared to spring ER, which averaged 21% of annual ER fluxes. We propose that Alpine headwaters will emit more within-stream respiratory CO2 to the atmosphere while providing less autochthonous organic energy to downstream ecosystems as the climate gets warmer.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Stream ecosystems receive terrestrial deliveries of organic carbon (OC), which can be degraded and mineralized to carbon dioxide (CO2) that ultimately outgasses to the atmosphere (Cole and others 2007; Battin and others 2009; Raymond and others 2013; Hotchkiss and others 2015). Within stream networks, low-order streams dominate CO2 outgassing fluxes (Raymond and others 2013; Hotchkiss and others 2015; Schelker and others 2016). Terrestrial OC that is not mineralized in streams is buried in floodplains or routed downstream to fuel ecosystem respiration (ER) in larger rivers, estuaries, and coastal waters (Bauer and others 2013). Gross primary production (GPP) in streams also contributes to stream ER; the balance between GPP and ER (including heterotrophic and autotrophic aerobic respiration) determines net ecosystem production (NEP). Autotrophy (i.e., NEP > 0) in streams seems to be limited to windows of favorable light conditions and extended baseflow when reduced hydraulic stress enables the accrual of primary producers (Roberts and others 2007; Hall and others 2015). However, most inland waters, and particularly streams, are heterotrophic (that is, NEP < 0) on daily to annual scales (Vannote and others 1980; Battin and others 2008; Hoellein and others 2013), indicating a reliance on terrestrial OC fueling ecosystem respiration (Fisher and Likens 1973; Lovett and others 2006).
Aquatic ecosystem metabolism has been proposed to serve as a sentinel of climate change (Williamson and others 2008). Given the temperature sensitivity of metabolism, increasing streamwater temperatures due to climate change could increase GPP and ER (Demars and others 2011; Perkins and others 2012; Yvon-Durocher and others 2012; Demars and others 2016). Flow regime of streams and rivers will also shift with climate change (Botter and others 2013). Increasing flood frequency and drought will likely have a strong influence on stream ecosystem metabolism (Hall 2016), as hydrology drives benthic biomass and terrestrial OC deliveries and transport (Uehlinger 2006; Roberts and others 2007). At the stream network scale, however, the effects of climate change and particularly of hydrological extremes on ecosystem metabolism are elusive at present.
Snow-dominated ecosystems are particularly vulnerable to climate change (Barnett and others 2005) with forecasted precipitation shifts from snow to rain in winter and with consequences for snowmelt hydrology in spring (Adam and others 2009; Berghuijs and others 2014). These consequences of reduced snowpack include spring snowmelt occurring earlier coupled with a reduction in the amount of snowmelt-derived runoff into stream networks (Adam and others 2009). Although snow- and ice-dominated aquatic ecosystems in high latitudes are relevant for global carbon fluxes due to extensive C storage and mobilization (Lapierre and others 2013), little is known about the relevance of alpine streams for carbon fluxes (except see Uehlinger and Naegeli 1998; Uehlinger 2006). Understanding the response of stream metabolism to altered snowmelt hydrology is therefore critical to better predict impacts of global warming on carbon fluxes in alpine ecosystems. We hypothesized that shifting from snow to rain potentially has consequences for ecosystem metabolism as the timing of increasing PAR decouples from the onset of snowmelt when the potential drivers of ecosystem metabolism are also highest. Although PAR is crucial for GPP, spring snowmelt flushes terrigenous resources into and through stream networks (Boyer and others 1997), including DOC, which may stimulate ER, and nutrients, that may increase both ER and GPP. In contrast, we hypothesized that a spring following a winter with low snow would reduce or alter the timing of delivery of nutrients and DOC to the stream network in coinciding with increasing light intensity resulting in lower GPP and ER, thus reducing the overall NEP. Alternatively, with reduced snowmelt-delivery, streamwater temperature could be higher following reduced snowmelt influence, thus increasing ER resulting in increased heterotrophy and ultimately increased CO2 to the atmosphere. Using 18-months of daily estimates of stream metabolism, we studied the impacts of altered snowmelt hydrology on ecosystem metabolism and carbon cycling in an Alpine stream network encompassing two winter/spring time periods with differing snowmelt hydrology. In comparison with the 2012/2013 winter, the 2013/2014 winter was unusually warm with worldwide temperature and precipitation anomalies carrying signatures of climate change (Davies 2015; World Meteorological Organization 2015). We expected effects of contrasting snowmelt hydrology on spring stream GPP, ER and NEP, and impacts of ecosystem metabolism during snowmelt on the annual metabolism across the stream network.
Methods
Study Site
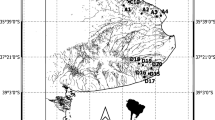
The Ybbs River Network (YRN, Austria) drains a subalpine catchment (254 km2) ranging from 532 to 1893 m above sea level (m.a.s.l.). Geology is dominated by calcareous rock, and land use is characterized by forests (82%), alpine meadows (11%) and a mix (7%) of agriculture, settlements, and bare rock at high elevations. Our study reaches were distributed across the YRN (Figure 1) and ranged from 1st to 4th Strahler order with mean catchment elevation from 795 to 1266 m a.s.l. (Table 1).
Ybbs River Network (YRN) located in lower Austria. Yellow points and ID numbers in the map refer to study sites; red points highlight gauging stations used for stream flow and snowmelt model calibration. Time series of daily gross primary production (GPP), ecosystem respiration (ER), and net ecosystem production (NEP) from 12 streams in the YRN; all fluxes are given as g O2 m−2 day−1. The orange and blue bands highlight the spring following the high-snow winter (HS, 2012/2013) and low-snow winter (LS, 2013/2014), respectively. Boxplots indicate the upper and lower 75th percentile, and the median value of GPP, ER, or NEP, the tail represents the smallest or largest values within 1.5 times the size of the box, open circles are considered as outliers. GPP, ER, or NEP during HS (orange) were significantly higher or lower than LS (blue) as indicated by the asterisk (p < 0.05).
Climate Trends
The 2013/2014 winter was the second warmest winter recorded in Austria over the last 247 years; besides elevated temperatures, it had unusual precipitation patterns with reduced snowpack along the northern flank of the Alps (ZAMG 2015). The comparison showed that air temperature, as measured in Lunz am See located at the center of the YRN, averaged −1.5 ± 3.9 and 0.8 ± 3.2°C (mean ± standard deviation) during the 2012/2013 and 2013/2014 winter (1 December–28 February), respectively; for comparison, the long-term average (1909–2015) was −2.3 ± 1.8°C. Similarly, the 2012/2013 winter had 40 snow days and 18 rain days, whereas the 2013/2014 winter had 6 snow days and 33 rain days (see supplementary information, Figure S1). Consequently, cumulative new snow in Lunz am See was 271 cm in the 2012/2013 winter compared to 32 cm in the 2013/2014 winter. Therefore, we refer to the 2012/2013 and 2013/2014 winters as high-snow (HS) and low-snow (LS) winters, respectively.
Snowmelt Modeling
We estimated the contribution of snowmelt to streamflow using a spatially explicit hydrological model (Schaefli and others 2014). We simulated rainfall/snowfall separation, snowpack evolution, snowmelt, evapotranspiration, soil moisture dynamics, surface and subsurface runoff generation at the sub-catchment scale, as the basic sub-units describing the spatial structure of the model domain. The hydrologic response of each sub-catchment was routed through the stream network to obtain water fluxes at any study reach. For this, we used the river network delineated from a digital elevation model of the region, with channel heads identified through comparison with topographic maps and field surveys. We used meteorological data collected at the weather station situated in Lunz am See (Figure 1), which included precipitation, temperature, and duration of sunshine at an hourly time scale. We assumed precipitation and duration of sunshine to be uniform across the catchment area. To account for temperature changes with elevation, we distributed temperature data among the different sub-catchments assuming a calibrated lapse rate constant in time (supplementary information, Table S1). Temperature and sunshine data were used to estimate potential evapotranspiration through the Priestley–Taylor method (1972). And finally, we used temperature data to determine the type of precipitation (rainfall vs snow) and to estimate snowmelt through a temperature-index approach (Schaefli and others 2014).
Using a Monte Carlo approach, we calibrated 11 model parameters (supplementary information, Table S1) by contrasting hourly simulated and measured stream discharge from two gauging stations (Figure 1) from January 2012 to December 2014. For this, we ran the model for 1 million parameter sets sampled through a Latin hypercube built from uniform distributions spanning physically reasonable parameter ranges (supplementary information, Table S1). We evaluated the goodness of fit of each parameter set for both stream sections via the Nash–Sutcliffe performance criterion (Nash and Sutcliffe 1970), which evaluates the fit of simulated discharge Q s to observed discharge Q o compared to the simplest possible model, that is, the mean of the observed discharge over the entire period \( \bar{Q}_{\text{o}} \):
Here, t i is the ith timestep of simulation. Values lower than zero indicate that the model reproduces the data worse than the mean observed discharge. Finally, the parameter set with the best sum of NS over the two gauging stations located on the main stem of the YRN (NS = 0.78 and 0.73 for the downstream and upstream located stations (see Figure 1), respectively) was selected (supplementary information, Table S1) and used to model discharge Q and snowmelt contribution for each study site on a daily basis. Further details on model formulation and calibration are given in Schaefli and others (2014).
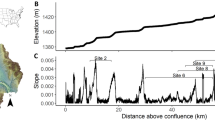
Based on the outcome of the hydrological model, we selected a window from 1 March to 13 May, encompassing a total of 74 days, to compare spring snowmelt hydrology and ecosystem metabolism across the YRN following a high-snow (HS, 2012/2013) and low-snow winters (LS, 2013/2014). We selected this spring window of 1 March–13 May based on the snowmelt hydrograph and when the snowmelt signature was apparent within the stream discharge hydrograph, which also encompassed the onset of increased photosynthetic active radiation (PAR) (Figure 2). To compare total spring snowmelt between years (that is, spring following the 2012/2013 HS or the 2013/2014 LS winter) and across the elevation gradient in the YRN, we analysed cumulative snowmelt (m3) during the selected window per catchment area (m2) as a function of year interacting with mean catchment elevation (m) in an Analysis of Covariance (ANCOVA) where cumulative snowmelt (per catchment area) = elevation × year (supplementary information, Figure S2).
Time-series of photosynthetic active radiation (PAR, lux), stream discharge (Q m3 s−1) and modeled snowmelt (m3 s−1) from site 8, a 4th-order stream in the Ybbs River Network (YRN). Negative snowmelt indicates freezing and negative light occurred when the light sensor was buried in mud due to disturbance from horses. The orange and blue bands highlight the spring snowmelt window following a high-snow winter (HS, 2012/2013) and low-snow winter (LS, 2013/2014), respectively.
Ecosystem Metabolism
We used changes in streamwater dissolved oxygen concentration to estimate daily GPP and ER (Odum 1956). Dissolved oxygen (DO) and temperature were measured in situ every 5-min with HOBO dissolved oxygen loggers (Onset®). We modeled diel DO to estimate daily gross primary production (GPPd) and ecosystem respiration (ERd, as a negative flux representing aerobic respiration) using the following equation (Van de Bogert and others 2007; Hotchkiss and Hall 2014; Hall and others 2015):
where DOt is measured DO (g m−3) at time t. Δt (d) is the time step of analysis. Zd (m) is the daily average stream depth calculated from modeled Q based on scaling relationships explicitly for the Ybbs River Network (YRN) from Ceola and others (2014). PARt is the photosynthetic active radiation (lux) measured at each study reach using HOBO light loggers (Onset®), at time t, whereas \( \sum{\text{PAR}}_{\text{d}} \) is the average light intensity for day d. The equation assumes that GPP linearly varies with PAR while ER is constant during the day. The reaeration coefficient, \( k_{{{\text{O}}_{2} }} \) (day−1), corrected for streamwater temperature (T), was estimated from the reaeration coefficient standardized at 20°C. The daily reaeration coefficient, standardized at 20°C (k 20 day−1), was estimated from a k 20 versus mean daily modeled Q relationship where \( k_{{{\text{O}}_{2} }} \) = k 20/1.0241(T−20) (Bott 2006). Detail on the estimation of \( k_{{{\text{O}}_{2} }} \), which was based on a combination of tracer gas releases and night-time regression, along with fitting \( k_{{{\text{O}}_{2} }} \) versus Q, is provided below. DOsat refers to DO concentration (g m−3) at 100% saturation given stream temperature and site-specific elevation-adjusted barometric pressure (Garcia and Gordon 1992), which was continuously measured at the weather station in Lunz am See. Assuming normally distributed observation error, GPPd (g O2 m2 day−1) and ERd (g O2 m2 day−1) were estimated by fitting equation 2 relative to the measured DO data using the nlm function in R (R Core Team 2015) to choose the parameters that minimized the normal negative log likelihood (Hilborn and Mangel 1997). We used several different starting parameter values to ensure proper minimization of the model (Hall and others 2015). Out of approximately 575 potential metabolism days, for most of our sites, we were able to estimate GPP and ER for on average 485 days. We excluded any negative GPP or positive ER, approximately 8–15 days for each site. Estimates of GPP and ER were also excluded based on the visual inspection of predicted versus observed dissolved oxygen for every metabolism day. This step also served to visually check the quality of the dissolved oxygen data as well (for example, lack of a diel curve, noise in the data), and resulted in the exclusion of on average 40 days. Additional gaps in our data were due to maintenance and downloading (for most sites, around 30 days in total for the duration of the study), or malfunctioning and loss of sensors.
Reaeration Estimation
We conducted a total of 53 propane releases across 11 of our 12 study reaches. We defined propane addition reaches to have a minimal travel time of 20 min, which resulted in reaches ranging from 49 (site 5) to 788 m (site 11) across our study sites. The most downstream station coincided with the location of the dissolved oxygen sensor and the upper sampling station was situated far enough distance downstream of the propane addition to allow for mixing. Propane was added until concentration reached equilibrium, which was estimated by the fourfold travel time of a packet of water to travel through the study reach (Stream Solute Workshop 1990). Travel time and stream discharge Q at each sampling station were estimated for each release from a ‘slug’ addition of sodium chloride. At equilibrium (‘plateau’) conditions, we collected five replicate 40 ml water samples from an upper and lower sampling site within the release reach and gas concentration therein was measured using a Gas Chromatograph (Agilent). The reaeration coefficient of propane was calculated from the difference in dilution-corrected gas concentrations from the upper and lower sampling stations following Peter and others (2014). To calculate \( k_{{{\text{O}}_{2} }} \) (day−1) from the propane reaeration coefficient, we use the following equation:
where \( k_{{{\text{O}}_{2} }} \) (day−1) is the reaeration coefficient for oxygen and k propane (day−1) is the reaeration coefficient for propane. The temperature-sensitive Schmidt number for oxygen (\( Sc_{{{\text{O}}_{2} }} \)) and propane (Sc propane) refers to the ratio of kinematic viscosity of water and the diffusion coefficient (Wanninkhof 1992).
We also estimated reaeration using the night-time regression approach (Hornberger and Kelly 1975; Izagirre and others 2007). We regressed the change in oxygen per unit of time versus the oxygen saturation deficit (DOsat−DOt) from sunset to sunrise. The slope of this relationship for each night corresponds to \( k_{{{\text{O}}_{2} }} \) (day−1). Similar to Izagirre and others (2007), we only kept estimates of \( k_{{{\text{O}}_{2} }} \) from significant night-time regressions (p < 0.05), and given the variability of this estimate (Aristegi and others 2009), we also only kept those estimates where R 2 > 0.35. This latter step also ensured exclusion of inaccurate estimates identified as significant due to the high number of data points (>100) provided by automatic sensor (every 5 min) logging.
We combined \( k_{{{\text{O}}_{2} }} \) estimates from both tracer gas releases and night-time regression to generate rating curves of the reaeration coefficient on Q for each site. For this, we used k 20 (day−1), which is \( k_{{{\text{O}}_{2} }} \) standardized to 20°C from stream temperature (T) where k 20 = \( k_{{{\text{O}}_{2} }} \) × 1.0241(T−20) (Table 2; Bott 2006), in either linear or logarithmic models, which we selected based on R 2. Despite statistically insignificant relationships between k 20 and Q for all of our sites (see Table 2) we used the best-fit rating curve and daily Q to predict \( k_{{{\text{O}}_{2} }} \) as varying on a daily basis for each site (Izagirre and others 2007), as fixing k 20 for estimating 450+ days of continuous ecosystem metabolism would not have been appropriate. This approach has been identified as reliable and robust compared to using empirical models for \( k_{{{\text{O}}_{2} }} \) prediction (Aristegi and others 2009).
Nutrients and Dissolved Organic Carbon
We collected monthly streamwater for N–NO3 (µg l−1), N–NH4 (µg l−1), P–PO4 (µg l−1), and dissolved organic carbon (DOC, mg l−1) concentrations in March and April of each year. Nutrient samples were sterile-filtered (0.2 μm) into sterile Falcon® tubes, and DOC samples were filtered using pre-combusted (450°C) glass-fiber filters (GFF) into acid-washed, pre-combusted 40 ml glass vials. Each month, duplicate nutrient samples and 4 replicate DOC samples were taken from each site for a total of 4 and 8 samples for nutrients and DOC, respectively. Samples for nutrient and DOC analyses were kept cold in the dark pending analyses (within 2 days) using a continuous flow analyser (FlowSys, SYSTEA, Analytical Technologies) and a Sievers (5310C, GE Analytical Instruments) TOC analyser, respectively. Because N–NH4 and P–PO4 concentrations were often at or below analytical detection limits (4 and 2 μg l−1 for N–NH4 and P–PO4, respectively), we excluded these data from any explanatory statistical analyses and used only N–NO3 concentration data.
Benthic Chlorophyll a
We collected samples for benthic chlorophyll a as a proxy for algal biomass. Every month, we randomly collected 6 rocks from each study reach, and kept them frozen pending further analysis. Within a month, biofilms were removed from the rocks using plastic brushes and the resulting slurry was filtered onto GFF-filters, which were then extracted in 90% acetone and analysed spectrophometrically for chlorophyll a (Lorenzen 1967).
Statistical Analyses
To test if spring snowmelt ecosystem metabolism significantly differed following HS and LS winters for each stream, we used a generalized least squares model for each site (gls function from the nlme package in R software) with an autocorrelation structure (AR(2)) and allowing different variances across years to account for heterogeneity (Zuur and others 2009). We used a two-way ANOVA to test the effect of site and year (HS vs LS spring) and the interaction effect of site and year on spring snowmelt nitrate and DOC concentrations.
We further investigated the effects of spring snowmelt on ecosystem metabolism across the YRN by a combined analysis with known drivers of ecosystem metabolism. For this, we used cumulative spring GPP, ER, and NEP integrated over 74 days for each year. In a first step, we regressed these metabolism estimates on known drivers using linear mixed effect models with site as a random effect (Zuur and others 2009). As drivers for cumulative snowmelt GPP, we considered the combination of catchment area, light, and N–NO3 concentration. As ER appeared to be driven by autotrophic respiration across the catchment (Figure 1), we predicted cumulative snowmelt GPP along with N–NO3 and DOC concentrations, and streamwater temperature as controls on cumulative snowmelt ER. Finally, as NEP is the balance of GPP and ER, we predicted that the variability in cumulative snowmelt NEP could be explained by catchment area, N–NO3 and DOC concentrations and PAR.
We fitted our proposed models using the lme function (lmer package) in R (R Core Team 2015). Parsimonious models were selected based on Akaike Information Criterion (AICc) and model fit, which was assessed based on R 2 marginal (\( R^{2}_{\text{fixed}} \), fixed factors only) and R2 conditional (\( R^{2}_{\text{cond}} \), full model, package MuMIn, Nakagawa and Schielzeth 2012). The second step of our analysis, which targeted actual snowmelt effects and differences between years, was based on the pre-selected most parsimonious models for cumulative GPP, ER, and NEP from step 1. Here, we ran the same model, but included elevation × year as fixed factors. Mean catchment elevation and year (HS, 2012/2013 and LS, 2013/2014) explained spring snowmelt almost entirely (supplementary information, Figure S2); therefore, we tested elevation × year as controls on ecosystem metabolism during springtime snowmelt. For graphical representation, we used the overall model (i.e., final model of step 1, including elevation × year of step 2) to compute partial residuals (or adjusted Y) as
where Y stands for GPP, ER, or NEP and x j is the matrix of up to 2 drivers considered in step 1 with their best-fit regression slopes given by β j . These adjusted responses are freed from effects of commonly known drivers identified as important in step 1, but contain variation due to catchment elevation, year, and their interaction plus random effect and error.
Carbon Fluxes
We converted metabolic fluxes from oxygen to carbon by assuming a 1:1 molar ratio of O2 to CO2 (Hall and others 2016) and calculated organic C spiraling lengths (S OC) based on heterotrophic respiration, stream discharge, and DOC concentration. For each day from each metabolism site, we calculated S OC where S OC = (Q × [DOC])/(−HR × w) (Newbold and others 1982; Hall and others 2016); Q is modeled daily discharge (m3 day−1) and w (m) is width calculated from Q using scaling relationships (Ceola and others 2014). [DOC] is the mean DOC concentration (g m−3) from March and April. We estimated heterotrophic respiration (HR, g C m−2 day−1) from GPP (g C m−2 day−1) and ER (g C m−2 day−1) by assuming that HR = ER − 0.39 GPP. The coefficient of 0.39 was computed using quantile regression at the 90th percentile on all the spring snowmelt metabolism estimates from the YRN following Hall and Beaulieu (2013) and Hall and others (2016) (supplementary information). Lastly, we calculated mineralization velocity (V f , m day−1), as the ratio between HR and [DOC] (Newbold and others 1982; Hall and others 2016). Similar to our approach to investigate the drivers of spring snowmelt ecosystem metabolism, we analysed V f and S OC (as log S OC) of both HS and LS springs across the YRN using linear mixed effect models (lme function, R Core Team 2015), with elevation × year and site as fixed and random factors, respectively. We also calculated potential maximum reach length of each of our metabolism reaches based on the distance between the nearest upstream and downstream tributaries (similar to Hall and others 2016).
To quantify snowmelt metabolism at the annual scale, we estimated any missing values using linear interpolation between data points. Given the 18 months of daily estimates of ecosystem metabolism, to estimate annual metabolism to encompass and compare years with HS and LS winters, there would be approximately a 6-month overlap of the annual estimates. Therefore, we calculated annual rates of ecosystem metabolism (g C m−2 y−1) to encompass the HS window. Annual metabolism estimates represent the total cumulative flux from 1 November 2012 to 31 October 2013.
Results
Spring Snowmelt Hydrology
Based on modeled snowmelt and streamflow discharge, our defined spring snowmelt window (74 days, 1 March–13 May) encapsulated on average 61% [95% Confidence Interval (CI) 44–72%] and 26% (CI 24–30%) of the total snowmelt contributions of the 2012/2013 and 2013/2014 winter, respectively (supplementary information, Table S2). Snowmelt contributed on average 71% (CI 54–86%) and 30% (CI 17–52%) to total winter and spring (1 December–13 May) discharge in high-snow (HS) and low-snow (LS) years, respectively, with the residual discharge likely attributable to baseflow and rain (supplementary information, Table S2). Spring discharge owing to snowmelt increased disproportionately with elevation between HS and LS winter (supplementary information, Figure S2).
Relationships between A cumulative spring gross primary production (GPP, g O2 m−2) adjusted for catchment area (log) and PAR, B ecosystem respiration (ER, g O2 m−2) adjusted for GPP, and C net ecosystem production (NEP, g O2 m−2) adjusted for the effect of catchment area (log, km2) versus mean catchment elevation (m) for snowmelt after high-snow (HS, 2013) and low-snow (LS, 2014) winters. Lines are the linear fits as estimated from the best-fit linear mixed effect model (Table 3). Arrows indicate the metabolic shift from HS to LS for each study stream in the Ybbs River Network.
Stream Metabolism
Stream metabolism varied throughout the year and across YRN with seasonal patterns of ER often mirroring those of GPP (Figure 1). Overall GPP ranged from 0.01 to 29.1 g O2 m−2 day−1. In 10 out of 12 streams GPP peaked in spring, whereas at two sites (7 and 9), GPP peaked in summer at low discharge, and at one site (6), GPP peaked during both spring and summer (Figure 1). ER ranged from −54.2 to −0.04 g O2 m−2 day−1 across the YRN. NEP values ranged from −41.3 to 15.7 g O2 m−2 day−1, with consistent sequences of autotrophy primarily restricted to spring snowmelt across the YRN. Spring snowmelt following a HS (2012/2013) winter had significantly (paired t test: p < 0.05) more autotrophic days (average 20, range 0–61 days) than spring snowmelt following a LS (2013/2014) winter (average 8, range 0–38 days).
Total spring ecosystem metabolism varied markedly between years during snowmelt (Figure 1). We found that cumulative spring GPP integrated over 74 days, as indicated by the results of linear mixed effects models, increased with catchment size (log) and PAR, yet we found no effect of elevation or year (HS or LS) (Table 3; Figure 3) on GPP. Cumulative ER increased with cumulative spring GPP. The interaction effect of year × elevation was significant, when added to the cumulative ER model (Table 3). Results of this model indicated that ER decreased (more to less negative) with elevation following a HS winter, but not after a LS winter (Table 3; Figure 3). Cumulative NEP increased (from a more negative to a less negative or positive flux) with catchment size and PAR. Also here, the addition of elevation × year to the NEP model was significant (Table 3). NEP moved toward autotrophy with increasing catchment elevation following the HS winter but not following the LS winter (Figure 3). In 66% of the streams, cumulative ecosystem metabolism during snowmelt became more autotrophic following a HS winter, which was particularly pronounced for streams draining higher elevation and pristine catchments (Figure 3). This pattern was not found for the largest stream in the YRN (site 8) with an open canopy with elevated PAR (supplementary information, Table S3) and within a lower-elevation sub-catchment (sites 1, 3, 4, and 5).
Benthic Chlorophyll a
Throughout the 18 months of metabolism estimates, monthly means (n = 6 at each site) of benthic chlorophyll a ranged from 0.5 to 348 mg m−2 across the YRN (Figure 4). Two sites, 7 and 9, where GPP peaked in summer, and not spring, had the lowest average chlorophyll a (14 and 20 mg m−2), whereas the highest elevation site (12) had highest average chlorophyll a (143 mg m−2). Across the YRN, chlorophyll a was lowest in late January 2013 (13 mg m−2) and late June 2013 (21 mg m−2), following storm events just prior to sampling (Figure 4). Chlorophyll a peaked in March and April (2013), following a HS winter where average chlorophyll a was 104 mg m−2 in April and 91 mg m−2 in March. In comparison, the following spring in 2014, following a LS winter, average monthly chlorophyll a across all 12 sites was 49 and 37 mg m−2 in March and April, respectively.
Mean (n = 6) benthic chlorophyll a (mg m−2) for each ecosystem metabolism study site for each date sampled. Vertical lines are ±1 standard error. The black line and gray bands represent the average and standard error of all estimates of chlorophyll a across all sites per date. The orange and blue bands highlight the spring snowmelt window following high-snow winter (HS, 2012/2013) and low-snow winter (LS, 2013/2014), respectively.
A Spiraling length (natural log-transformed S oc, km−2) and B mineralization velocity (V f , m day−1) plotted against mean catchment elevation for each ecosystem metabolism site. Lines depict the linear fit from linear mixed effect models for spring following a high-snow winter (HS, 2012/2013, orange) and a low-snow winter (LS, 2013/2014) where lnSoc_HS = −2.6 + 0.004 × elevation, lnSoc_LS = 0.4 + 0.001 × elevation, \( R^{2}_{\text{fixed}} \) = 0.11, \( R^{2}_{\text{cond}} \) = 0.92 and V f_HS = 8.3 + 0.006 × elevation, V f_LS = 0.6 + 0.001 × elevation, \( R^{2}_{\text{fixed}} \) = 0.24, \( R^{2}_{\text{cond}} \) = 0.61).
Spring Snowmelt Carbon Spiraling Length and Mineralization Velocity
Across the YRN, S OC averaged 5.3 km (95% CI 0.2–34.7) in spring following a HS winter and 3.4 km (95% CI 0.2–13.4) following a LS winter, exceeding the average stream length of 1.3 ± 0.9 km (mean ± standard deviation) (supplementary information, Table S4). The results of the linear mixed effect model (S OC ~ elevation × year, with site as a random variable) indicated that mean S OC increased with catchment elevation following a HS winter, but did not change with elevation following a LS winter (Figure 5). Spring V f after a HS winter averaged 2.5 (95% CI 0.3–11.1 m day−1) and 1.8 m day−1 (95% CI 0.4–5.5 m day−1) following a LS winter (supplementary information, Table S4). Using a similar model approach to model S OC, mean V f decreased with elevation following a HS winter, but increased slightly following a LS winter (Figure 5).
Annual Estimates of Ecosystem Metabolism
On an annual basis, all study sites were heterotrophic but were autotrophic during spring (1 March–13 May) at four sites following the HS (2013) winter and only the largest stream (site 8) in 2014 following the LS winter (Figure 6). Annual GPP ranged from 62 to 1031 g C m−2 y−1 (supplementary information, Table S5; Figure 6) with spring metabolism accounting for on average 33% (range 15–60%) of the annual GPP flux. Spring ER accounted on average for 21% (range 11–34%) of the annual ER fluxes, which ranged from −457 to −1735 g C m−2 y−1 across all sites. The lowest percentage of spring GPP and ER contribution to annual fluxes was from one sub-catchment (sites 7 and 9), where GPP peaked in the summer. Conversely, highest contributions of spring GPP and ER to annual fluxes were in the low-elevation sub-catchment (sites 1, 2, 3, 4), where reaches were more forested. Annual NEP fluxes trended toward decreasing heterotrophic (more negative to less negative) fluxes with mean catchment elevation (Figure 6) and ranged from −1036 to −140 g C m−2 y−1.
A Ybbs River Network (YRN) cumulative spring ecosystem respiration (ER, g C m−2) versus cumulative spring gross primary production (GPP, g C m−2) following high- (HS, orange) and low-snow (LS, blue) winters. The line represents the 1:1 relationship between ER (as a negative flux) and GPP. B 2013 YRN annual and cumulative spring (HS) GPP, ER, and C net ecosystem production (NEP, g C m−2 y−1) by mean catchment elevation. The annual estimates (darker bars) are the sum of the spring snowmelt ecosystem metabolism estimates (lighter bars) and the estimates from the remaining portion of the year.
Discussion
Spring Snowmelt
The spring snowmelt window captured 61 and 26% of modeled snowmelt for spring following HS and LS winters, respectively. Following a LS winter (2013/2014), there was a less distinct pulse of snowmelt as observed in the preceding year following a HS (2012/2013) winter. The window we selected for our analyses did not capture the early pulses of snowmelt in the 2014 late winter/spring, likely due to the warmer winter (Figure 2). Shifting the snowmelt window into February for 2014 (LS) to compare an equivalent snowmelt in 2013 (HS), we would have likely captured a period of substantially lower light availability in 2014 (Figure 2). For instance, mean PAR in February across the YRN was 2.5-fold lower than the mean PAR in March. Furthermore, given the daily estimates of NEP (see Figure 1), it is also likely that the window of autotrophy was not simply shifted earlier in the spring following a LS winter. NEP was not less negative or positive before the spring snowmelt window (Figure 1), thereby providing further evidence that GPP did not simply shift earlier in the year. Therefore, our approach of using the same calendar dates (that is, 1 March–13 May) for each year equalized potential PAR that drives GPP.
Reaeration Estimation
Estimation of reaeration in streams is critical to properly estimate ecosystem metabolism (Mulholland and others 2001). We recognize the potential error associated with the rating curves based on discharge and the combined \( k_{{{\text{O}}_{2} }} \) estimates from propane releases and night-time regressions (Table 2). For instance, for sites 4 and 9, we were unable to establish a statistically significant rating curve, as it was also found in Basque streams (Izagirre and others 2008). Also similar to Izagirre and others (2008), the relationship between k 20 and Q varied between sites. For instance, for over half of our sites, the relationship between k 20 and Q included natural log-transformed estimates of Q. Although we did not test this effect, log-transformed Q could mask error of our estimates of k 20, given any deviation from the prediction on a log scale would result in a larger error compared to a non-log scale relationship. Furthermore, propane releases were not successful in our larger streams (for example, site 8), where not enough propane could be introduced into the streamwater; here we relied on night-time regressions. In site 11, we succeeded in 2 propane releases but there was a mismatch between the results of the propane release and the night-time regressions and we therefore excluded the \( k_{{{\text{O}}_{2} }} \) estimates from the propane releases from the model for this site (Table 2). Although we did not attempt to model \( k_{{{\text{O}}_{2} }} \), along with GPP and ER, this approach would be possible for future studies and especially feasible given that empirical estimates of \( k_{{{\text{O}}_{2} }} \), from propane releases or night-time regression, can be used to inform such model approaches as described by Holtgrieve and others (2010), Grace and others (2015) or the relatively new R package, streamMetabolizer (Appling and others 2016).
Seasonal Ecosystem Metabolism
Seasonal patterns and ranges of GPP and ER agree with previous studies on stream metabolism measured over multiple years (Uehlinger 2006; Roberts and others 2007; Hall and others 2015). Streams were heterotrophic throughout most of the year with windows of autotrophy. The observation of autotrophic days during spring snowmelt corroborates previous work on the temporal dynamics of CO2 in an Alpine stream and showing that snowmelt conditions turn streams into transient sinks of atmospheric CO2 (Peter and others 2014).
Increasing autotrophy at high discharge seems counterintuitive because elevated discharge may disturb benthic algae and therefore depress GPP. For instance, others have reported prolonged autotrophy during baseflow in spring or summer, which was punctuated by storms reducing GPP (Uehlinger 2006; Roberts and others 2007; Beaulieu and others 2013). While we observed a decrease in both GPP and ER following large rain events resulting in high stream discharge spates throughout the study period (Figure 1), snowmelt in the YRN differs from storm spates in that it is a sustained (Peter and others 2014; Fasching and others 2015), but likely non-scouring, increase in stream flow. Evidence from the monthly chlorophyll a estimates further indicated that snowmelt in the YRN was not scouring during both years. Throughout the 18 months of data collection, chlorophyll a was depressed after 2 large storm events in early January 2013 and early June 2014, where it took several months after these storms for the stream benthic biofilms to recover (Figure 4). In contrast, chlorophyll a peaked in spring during snowmelt following both winters. We suggest that other factors such as more light due to seasonal variation and higher nutrient concentrations may over-ride possible negative effects on benthic primary producers during increasing discharge in spring. Furthermore, snowmelt as a recurrent and predictable event in the YRN (Peter and others 2014; Fasching and others 2015), may have led to adaptations of the primary producers to the natural flow regime (Lytle and Poff 2004; Val and others 2016). Therefore, we propose that autotrophy during spring snowmelt imparts a distinct fingerprint on the annual metabolism that, in the context of the emerging Stream Biome Gradient Concept (Dodds and others 2015), may prove characteristic for snow-dominated alpine streams.
Drivers of Spring Ecosystem Metabolism
Across the YRN, spring ecosystem metabolism was shaped by a combination of catchment size, light, and likely snowmelt-associated factors, such as temperature and nutrient delivery, which varied following HS and LS winters across elevation. PAR and catchment size drove total cumulative spring snowmelt GPP (Table 3). This result supports predictions of the River Continuum Concept (RCC) (Vannote and others 1980) positing increased light availability and therefore higher GPP as channels widen along the continuum from headwaters to larger reaches downstream. PAR was also detected as a driver of ecosystem GPP by cross-biome studies (Mulholland and others 2001; Bernot and others 2010) and continuous measurements in single streams (Roberts and others 2007; Beaulieu and others 2013; Dodds and others 2013; Griffiths and others 2013; Hall and others 2015). ER was positively related to GPP, a finding similar to other studies with continuous measurements of ecosystem metabolism within single streams (Uehlinger 2006; Roberts and others 2007; Beaulieu and others 2013; Dodds and others 2013; Griffiths and others 2013; Roley and others 2014). This suggests that autotrophic respiration likely comprised a large proportion of ecosystem respiration (Hall and Beaulieu 2013). While we found no temperature effect on ER, a combination of factors contributing to the umbrella effect of snowmelt could be responsible for the decrease in ER with elevation following a HS winter. For instance, although streamwater temperature significantly decreased with elevation (mean streamwater temperature (T) = 9.0 − 0.004 elevation + 0.8 year, adjusted r 2 = 0.51, P < 0.001) and DOC and N–NO3 concentrations varied across the YRN (supplementary information, Table S3), we found no statistically significant effect of these potential drivers on ER. Likely, a combination of drivers, such as stream discharge and delivery of DOC to the stream network, could explain the patterns of spring ER across the YRN. For instance, as discussed below, the combination of increased DOC concentration and stream discharge with elevation could have led to more export rather than mineralization of organic carbon, resulting in reduced ER following a HS winter. Conversely, lower stream discharge following a LS winter could have contributed to higher residence time of the water, and therefore increased the capacity of ER via mineralization of DOC (Casas-Ruiz and others 2017). However, given the data, we can only speculate, but ER was likely driven by a combination of factors associated with snowmelt such as streamwater temperature along with nutrient and organic carbon delivery occurring at a different time scale or other drivers that we did not measure in the YRN.
Changes in ER, rather than GPP, may drive the balance between autotrophy and heterotrophy. For instance in the YRN, although cumulative spring GPP was not apparently driven by hydrology (rather PAR and catchment area), inter-annual differences in ER could be associated with differences in spring hydrology following the HS and LS winters given the interaction effect of elevation × year. For instance, climate-induced changes to stream hydrology driving annual frequency of seasonal ER patterns, but not GPP, was detected from wavelet analyses of 15-years of continuous data in the Ebro River basin located in the Iberian Peninsula of Spain (Val and others 2016). Also in the Thur River, Switzerland, ecosystem metabolism moved toward autotrophy over a 15-year study, which was attributable to a reduction in nutrients depressing ER, whereas GPP remained constant over 15-years (Uehlinger 2006). Conversely, in a suburban stream in Ohio, USA (Beaulieu and others 2013) and a forested headwater stream in Tennessee, USA (Roberts and others 2007), inter-annual differences in spring GPP were attributable to the timing of scouring storm flows which reduced GPP. For the YRN, we suggest that catchment size principally shaped spring NEP by driving GPP, but that ER drove NEP toward autotrophy as it decreased with mean catchment elevation following a HS winter (Figure 3).
Our model did not retain streamwater N–NO3 and DOC concentrations as predictors although they varied significantly among streams and between springs following HS and LS winters (supplementary information, Table S3). As N–NH4 and P–PO4 concentrations were low, these labile forms of N and P were likely limiting for ecosystem metabolism. Presumably our monthly sampling for streamwater nutrients and DOC was too coarse to capture solute flushing from the catchments into the streams during snowmelt (Boyer and others 1997) and was therefore likely limited in statistically explaining variation in ecosystem metabolism in this study.
Carbon Cycling
Our estimates of S OC were lower and V f were higher than those reported from larger rivers (Q > 14 m3 s−1, Hall and others 2016), which stresses the importance of headwaters for carbon retention and cycling (Battin and others 2008). Patterns of S OC across the YRN likely reflected the influence of stream discharge on the spiraling length (Newbold and others 1982). The mean S oc increased with catchment elevation following a HS winter more so than a following a LS winter (Figure 5), a pattern which followed the trend in snowmelt across the catchment (supplementary information, Figure S2).
In comparison, V f decreased with elevation following a HS winter, a pattern similar to total spring ER (Figure 3). Furthermore, although our temporal sampling of DOC likely did not capture all of the flushing of DOC into the YRN, the average DOC load was greater following a HS than a LS winter [249 (95% CI 4–1399) vs 130 kg day−1 (95% CI 3–704) calculated from mean Q × mean DOC per site and year]. Coupled with higher loads, DOC concentrations increased with mean catchment elevation following a HS winter, but not a LS winter (linear mixed effect model; DOC ~ elevation × year, DOCHS = 0.08 + 0.0016 × elevation, DOCLS = 1.95 − 0.0002 × elevation, \( R^{2}_{\text{fixed}} \) = 0.14, \( R^{2}_{\text{cond}} \) = 0.77). Therefore, following a HS winter, V f tracked the coupling of decreasing ER and increasing DOC concentrations across the elevation gradient. This coupling indicated that at lower elevations following a HS winter, there was less DOC, but increased mineralization relative to a LS spring. In comparison, at higher elevations, there was more DOC relative to LS spring, but decreased mineralization rates, indicating export of DOC following a HS winter. This relative export versus mineralization of C between springs following HS versus LS winters tracked the elevation, and subsequently the snowmelt (supplementary information, Figure S2) gradients across the YRN, indicating that snowmelt is indeed a driver of C cycling in this subalpine stream network. These findings indicate that climate change scenarios of reduced snow pack, and therefore reduced snowmelt (Beniston 2012), would impact C cycling in subalpine stream networks. Although the delivery of terrestrial C would be reduced with reduced snowmelt, increased residence time due to decreased stream discharge coupled with increased streamwater temperatures likely would increase C mineralization (Yvon-Durocher and others 2012; Casas-Ruiz and others 2017). Increased C mineralization would lead to more in-stream CO2 production and reduced export of C to downstream ecosystems. Therefore, compared to current estimates (for example, Hotchkiss and others 2015), the contribution of CO2 from low-order, headwater streams could increase in subalpine stream networks under warming climate change predictions.
Annual Ecosystem Metabolism
Spring snowmelt GPP had a greater contribution to annual ecosystem metabolism fluxes than ER. We found consistent sequences of autotrophy remained restricted to spring snowmelt across the YRN in 10 out of 12 study reaches. When we compare this window to annual metabolic carbon fluxes, we found that the contribution of GPP during the 74-day spring snowmelt (that is, 20% of the time of an annual cycle) contributed an average of 33% of the annual GPP fluxes following a HS winter. Given that these contributions are higher than would be anticipated from 74 days (that is, 20%) indicates that GPP during spring snowmelt is indeed a significant autochthonous carbon flux on an annual basis. In contrast, ER during snowmelt contributed on average 21% to the annual respiratory carbon fluxes across the YRN. Similarly, in a 1st-order forested stream, the magnitude of the spring algal bloom coupled with the timing of storm spates that could either depress GPP or increase ER or both, drove annual estimates of GPP (Roberts and others 2007). Within lower-elevation, forested catchments in the YRN, spring GPP had a greater contribution (40–50%) to annual fluxes compared to higher elevation sites (25–32%), which likely received more PAR. The importance of PAR to seasonal and annual ecosystem metabolism cycles was found in the Thur River where stochastic events drove daily patterns of ecosystem metabolism but the annual solar cycle drove seasonal patterns (Uehlinger 2006).
Our study reaches were heterotrophic on an annual basis with annual NEP ranging tenfold across the YRN (Figure 6). This finding coincides with previous studies of continuous ecosystem metabolism (Uehlinger 2000, 2006; Roberts and others 2007; Dodds and others 2013; Griffiths and others 2013) and the role of heterotrophy in fluvial ecosystems (Battin and others 2008). The range in annual NEP, GPP, and ER fluxes across the YRN encompassed the relatively few available data on annual ecosystem metabolism fluxes estimated from continuous data (Figure 7). We did not detect any obvious correlations in annual GPP and ER fluxes across the YRN or across the range of values previously published. However, if we excluded data from the Mississippi River, representing an exceptionally large catchment, annual NEP trended from more negative to a less negative flux with increasing catchment area (NEP = 39.4 × log(A) − 575.8, R 2 = 0.22, p = 0.04). Recognizing that this trend is from only 17 streams and rivers, with 12 from YRN, this finding coincides with a meta-analysis of daily estimates of GPP to ER ratios moving toward autotrophy with increasing stream discharge (Hall and others 2016) and supports the RCC (Vannote and others 1980). With the advent of more reliable and affordable oxygen sensors and the capability to analyse continuous oxygen data to estimate ecosystem metabolism (Hall 2016), in the future, data on annual fluxes of GPP, ER, and NEP will likely become more common and begin to fill the data gaps needed to start to tease apart what drives annual fluxes, at both spatial and temporal scales, in fluvial ecosystems. Combining long-term measurements of ecosystem metabolism with large-scale C budget approaches to quantify the inputs and outputs of OC seems to be a promising next step in quantifying C budgets in stream networks.
A The YRN annual ecosystem respiration (ER, g C m−2 y−1) and gross primary production (GPP, g C m−2 y−1) fell within range of other published estimates from small streams to large rivers. The line represents the 1:1 line of annual ER (as a negative flux) to GPP. B The estimates of annual net ecosystem production (NEP, g C m−2 y−1) from this study in the Ybbs River Network (YRN) along with other published estimates increased with catchment size (km2). The line represents the linear relationship between annual NEP and catchment size (log(A), NEP = 39.4 × log(A) − 575.8, R 2 = 0.22, p = 0.04), excluding NEP estimates from the Mississippi River catchment. References for published annual estimates of ecosystem metabolism can be found in the supplementary information, Table S5.
In conclusion, our findings suggest that as climate changes with precipitation shifts (Berghuijs and others 2014) and receding snow (Beniston 2012) in the alpine regions, stream networks become more heterotrophic and thereby even larger sources of in-stream respiratory CO2 to the atmosphere during spring snowmelt. Concomitantly, less OC, both of terrestrial and autochthonous origin, is exported downstream with potential consequences for the carbon cycle in large rivers and coastal waters. Predictions of the feedbacks between carbon cycling and climate change will improve as we better assess and quantify the carbon fluxes through stream networks.
References
Adam JC, Hamlet AF, Lettenmaier DP. 2009. Implications of global climate change for snowmelt hydrology in the twenty-first century. Hydrol Process 23:962–72.
Appling AP, Hall RO Jr., Arroita M, Yackulic CB. 2016. streamMetabolizer: models for estimating aquatic photosynthesis and respiration. R package version 0.9.32. https://github.com/USGS-R/streamMetabolizer.
Aristegi L, Izagirre O, Elosegi A. 2009. Comparison of several methods to calculate reaeration in streams, and their effects on estimation of metabolism. Hydrobiologia 635:113–24.
Barnett TP, Adam JC, Lettenmaier DP. 2005. Potential impacts of a warming climate on water availability in snow-dominated regions. Nat Geosci 438:303–9.
Battin TJ, Kaplan LA, Findlay S, Hopkinson CS, Hopkinson CS, Marti E, Packman AI, Newbold JD, Sabater F. 2008. Biophysical controls on organic carbon fluxes in fluvial networks. Nat Geosci 1:95–100.
Battin TJ, Luyssaert S, Kaplan LA, Aufdenkampe AK, Richter A, Tranvik LJ. 2009. The boundless carbon cycle. Nat Geosci 2:598–600.
Bauer JE, Cai W-J, Raymond PA, Bianchi TS, Hopkinson CS, Regnier PAG. 2013. The changing carbon cycle of the coastal ocean. Nat Geosci 504:61–70.
Beaulieu JJ, Arango CP, Balz DA, Shuster WD. 2013. Continuous monitoring reveals multiple controls on ecosystem metabolism in a suburban stream. Freshw Biol 58:918–37.
Beniston M. 2012. Is snow in the Alps receding or disappearing? Wiley Interdiscip Rev Clim Change 3:349–58.
Berghuijs WR, Woods RA, Hrachowitz M. 2014. A precipitation shift from snow towards rain leads to a decrease in streamflow. Nat Clim Change 4:583–6.
Bernot MJ, Sobota DJ, Hall RO Jr, Mulholland PJ, Dodds WK, Webster JR, Tank JL, Ashkenas LR, Cooper LW, Dahm CN, Gregory SV, Grimm NB, Hamilton SK, Johnson SL, McDowell WH, Meyer JL, Peterson B, Poole GC, Valett HM, Arango C, Beaulieu JJ, Burgin AJ, Crenshaw C, Helton AM, Johnson L, Merriam J, Niederlehner BR, O’Brien JM, Potter JD, Sheibley RW, Thomas SM, Wilson K. 2010. Inter-regional comparison of land-use effects on stream metabolism. Freshw Biol 55:1874–90.
Bott TL. 2006. Primary productivity and community respiration. In: Hauer FR, Lamberti GA, Eds. Methods in stream ecology, 2nd ed. San Diego: Elsevier. pp 663–90.
Botter G, Basso S, Rodriguez-Iturbe I, Rinaldo A. 2013. Resilience of river flow regimes. Proc Natl Acad Sci USA 110:12925–30.
Boyer EW, Hornberger GM, Bencala KE, McKnight DM. 1997. Response characteristics of DOC flushing in an alpine catchment. Hydrol Process 11:1635–47.
Casas-Ruiz JP, Catalán N, Gómez-Gener L, von Schiller D, Obrador B, Kothawala DN, Lópex P, Sabater S, Marcé R. 2017. A tale of pipes and reactors: controls on the in-stream dynamics of dissolved organic matter in rivers. Limnol Oceanogr. doi:10.1002/lno.10471.
Ceola S, Bertuzzo E, Singer G, Battin TJ, Montanari A, Rinaldo A. 2014. Hydrologic controls on basin-scale distribution of benthic invertebrates. Water Resour Res 50:2903–20.
Cole JJ, Prairie JR, Caraco NF, McDowell WH, Tranvik LJ, Striegl RG, Duarte CM, Kortelainen P, Downing JA, Middelburg JJ, Melack JM. 2007. Plumbing the global carbon cycle: integrating inland waters into the terrestrial carbon budget. Ecosystems 10:172–85.
Davies HC. 2015. Weather chains during the 2013/2014 winter and their significance for seasonal prediction. Nat Geosci 8:833–7.
Demars BOL, Russel Manson J, Ólafsson JS, Gíslason GM, Gudmundsdóttir R, Woodward G, Reiss J, Pichler DE, Rasmussen JJ, Friberg N. 2011. Temperature and the metabolic balance of streams. Freshwater Biology 56:1106–21.
Demars BOL, Gíslason GM, Ólafsson JS, Manson JR, Friberg N, Hood JM, Thompson JJD, Freitag TE. 2016. Impact of warming on CO2 emissions from streams countered by aquatic photosynthesis. Nat Geosci 8:833–7.
Dodds WK, Veach AM, Ruffing CM, Larson DM, Fischer JL, Costigan KH. 2013. Abiotic controls and temporal variability of river metabolism: multiyear analyses of Mississippi and Chattahoochee River data. Freshw Sci 32:1073–87.
Dodds WK, Gido K, Whiles MR, Daniels MD, Grudzinski BP. 2015. The stream biome gradient concept: factors controlling lotic systems across broad biogeographic scales. Freshw Sci 34:1–19.
Fasching C, Ulseth AJ, Schelker J, Steniczka G, Battin TJ. 2015. Hydrology controls dissolved organic matter export and composition in an Alpine stream and its hyporheic zone. Limnol Oceanogr 61:558–71.
Fisher SG, Likens GE. 1973. Energy flow in Bear Brook, New Hampshire: an integrative approach to stream ecosystem metabolism. Ecol Monogr 43:421–39.
Garcia HE, Gordon LI. 1992. Oxygen solubility in seawater—better fitting equations. Limnol Oceanogr 37:1307–12.
Grace MR, Giling DP, Hladyz S, Caron V, Thompson RM, Mac NR. 2015. Fast processing of diel oxygen curves: estimating stream metabolism with BASE (Bayesian single-station estimation). Limnol Oceanogr Methods 13:103–14. doi:10.1002/lom3.10011.
Griffiths NA, Tank JL, Royer TV, Roley SS. 2013. Agricultural land use alters the seasonality and magnitude of stream metabolism. Limnol Oceanogr 58:1513–29.
Hall RO Jr. 2016. Metabolism of streams and rivers. In: Jones JB, Stanley EH, Eds. Stream ecosystems in a changing environment. Amsterdam: Elsevier. p 151–80.
Hall RO Jr, Beaulieu JJ. 2013. Estimating autotrophic respiration in streams using daily metabolism data. Freshw Sci 32:507–16.
Hall RO Jr, Yackulic CB, Kennedy TA, Yard MD, Rosi-Marshall EJ, Voichick N, Behn KE. 2015. Turbidity, light, temperature, and hydropeaking control primary productivity in the Colorado River, Grand Canyon. Limnol Oceanogr 60:512–26.
Hall RO Jr, Tank JL, Baker MA, Rosi-Marshall EJ, Hotchkiss ER. 2016. Metabolism, gas exchange, and carbon spiraling in rivers. Ecosystems 19:73–86.
Hilborn R, Mangel M. 1997. The ecological detective: confronting models with data. Princeton, NJ: Princeton University Press. p 315p.
Hoellein TJ, Bruesewitz DA, Richardson DC. 2013. Revisiting Odum (1956): a synthesis of aquatic ecosystem metabolism. Limnol Oceanogr 58:2089–100.
Holtgrieve GW, Schindler DE, Branch TA, A’mar ZT. 2010. Simultaneous quantification of aquatic ecosystem metabolism and reaeration using a Bayesian statistical model of oxygen dynamics. Limnol Oceanogr 55:1047–62.
Hornberger GM, Kelly MG. 1975. Atmospheric reaeration in a river using productivity analysis. J Environ Eng Division ASCE 101:729–39.
Hotchkiss ER, Hall RO. 2014. High rates of daytime respiration in three streams: use of δ18O2 and O2 to model diel ecosystem metabolism. Limnol Oceanogr 59:798–810.
Hotchkiss ER, Hall RO Jr, Sponseller RA, Butman D, Klaminder J, Laudon H, Rosvall M, Karlsson J. 2015. Sources of and processes controlling CO2 emissions change with the size of streams and rivers. Nat Geosci 8:696–9.
Izagirre O, Bermejo M, Pozo J, Elosegi A. 2007. RIVERMET©: an excel-based tool to calculate river metabolism from diel oxygen–concentration curves. Environ Modell Softw 22:24–32.
Izagirre O, Agirre U, Bermejo M, Pozo J, Elosegi A. 2008. Environmental controls of whole-stream metabolism identified from continuous monitoring of Basque streams. J N Am Benthol Soc 27:252–68.
Lapierre J-F, Guillemette F, Berggren M, del Giorgio PA. 2013. Increases in terrestrially derived carbon stimulate organic carbon processing and CO2 emissions in boreal aquatic ecosystems. Nat Commun. doi:10.1038/ncomms3972.
Lorenzen CJ. 1967. Determination of chlorophyll and pheo-pigments: spectrophotometric equations. Limnol Oceanogr 12:343–6.
Lovett GM, Cole JJ, Pace ML. 2006. Is net ecosystem production equal to ecosystem carbon accumulation? Ecosystems 9:152–5.
Lytle DA, Poff N. 2004. Adaptation to natural flow regimes. Trends Ecol Evol 19:94–100.
Mulholland PJ, Fellows CS, Tank JL, Grimm NB, Webster JR, Hamilton SK, Marti E, Ashkenas L, Bowden WB, Dodds WK, McDowell WH, Paul MJ, Peterson BJ. 2001. Inter-biome comparison of factors controlling stream metabolism. Freshw Biol 46:1503–17.
Nakagawa S, Schielzeth H. 2012. A general and simple method for obtaining R2 from generalized linear mixed-effects models. O’Hara RB, editor. Methods Ecol Evol 4:133–42.
Nash JE, Sutcliffe JV. 1970. River flow forecasting through conceptual models part I—a discussion of principles. J Hydrol 10:317–29.
Newbold JD, Mulholland PJ, Elwood JW, O’Neill RV. 1982. Organic-carbon spiralling in stream ecosystems. Oikos 38:266–72.
Odum HT. 1956. Primary production in flowing waters. Limnol Oceanogr 1:102–17.
Perkins DM, Yvon-Durocher G, Demars BOL, Reiss J, Pichler DE, Friberg N, Trimmer M, Woodward G. 2012. Consistent temperature dependence of respiration across ecosystems contrasting in thermal history. Global Change Biol 18:1300–11.
Peter H, Singer GA, Preiler C, Chifflard P, Steniczka G, Battin TJ. 2014. Scales and drivers of temporal pCO2 dynamics in an Alpine stream. J Geophy Res Biogeosci. doi:10.1002/2013JG002552.
Priestley CHB, Taylor RJ. 1972. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon Weather Rev 100:81–92.
R Core Team. 2015. R: a language and environment for statistical computing, Vienna, Austria. Vienna: R Foundation for Statistical Computing.
Raymond PA, Hartmann J, Lauerwald R, Sobek S, McDonald C, Hoover M, Butman D, Striegl R, Mayorga E, Humborg C, Kortelainen P, Dürr H, Meybeck M, Ciais P, Guth P. 2013. Global carbon dioxide emissions from inland waters. Nat Geosci 503:355–9.
Roberts BJ, Mulholland PJ, Hill WR. 2007. Multiple scales of temporal variability in ecosystem metabolism rates: results from 2 years of continuous monitoring in a forested headwater stream. Ecosystems 10:588–606.
Roley SS, Tank JL, Griffiths NA, Hall RO Jr, Davis RT. 2014. The influence of floodplain restoration on whole-stream metabolism in an agricultural stream: insights from a 5-year continuous data set. Freshw Sci 33:1043–59.
Schaefli B, Nicótina L, Imfeld C, Da Ronco P, Bertuzzo E, Rinaldo A. 2014. SEHR-ECHO v1.0: a spatially explicit hydrologic response model for ecohydrologic applications. Geosci Model Dev 7:2733–46.
Schelker J, Singer GA, Ulseth AJ, Hengsberger S, Battin TJ. 2016. CO2 evasion from a steep, high gradient stream network: importance of seasonal and diurnal variation in aquatic pCO2 and gas transfer. Limnol Oceanogr 61:1826–38. doi:10.1002/lno.10339.
Stream Solute Workshop. 1990. Concepts and methods for assessing solute dynamics in stream ecosystems. J N Am Benthol Soc 9:95–119.
Uehlinger U. 2000. Resistance and resilience of ecosystem metabolism in a flood-prone river system. Freshw Biol 45:319–32.
Uehlinger U. 2006. Annual cycle and inter-annual variability of gross primary production and ecosystem respiration in a floodprone river during a 15-year period. Freshw Biol 51:938–50.
Uehlinger U, Naegeli MW. 1998. Ecosystem metabolism, disturbance, and stability in a prealpine gravel bed river. J N Am Benthol Soc 17:165–78.
Val J, Chinarro D, Pino MR, Navarro E. 2016. Global change impacts on river ecosystems: a high-resolution watershed study of Ebro river metabolism. Sci Total Environ 569–570:774–83.
Van de Bogert MC, Carpenter SR, Cole JJ, Pace ML. 2007. Assessing pelagic and benthic metabolism using free water measurements. Limnol Oceanogr Methods 5:145–55.
Vannote RL, Minshall GW, Cummins KW, Sedell JR, Cushing CE. 1980. The river continuum concept. Can J Fish Aquat Sci 37:130–7.
Wanninkhof R. 1992. Relationship Between wind-speed and gas-exchange over the ocean. J Geophys Res 97:7373–82.
Williamson CE, Dodds W, Kratz TK, Palmer MA. 2008. Lakes and streams as sentinels of environmental change in terrestrial and atmospheric processes. Front Ecol Environ 6:247–54.
World Meteorological Organization. 2015. WMO statement on the status of the global climate in 2014. p. 24.
Yvon-Durocher G, Caffrey JM, Cescatti A, Dossena M, Giorgio PD, Gasol JM, Montoya JM, Pumpanen J, Staehr PA, Trimmer M, Woodward G, Allen AP. 2012. Reconciling the temperature dependence of respiration across timescales and ecosystem types. Nat Geosci 487:472–7.
ZAMG. 2015. HISTALP Langzeitklimareihen - Österreich Winterbericht 2013/14. p. 7.
Zuur A, Ieno EN, Walker N, Saveliev AA, Smith GM. 2009. Mixed effects models and extensions in ecology with R. New York: Springer Science & Business Media. p 574.
Acknowledgments
We are most grateful to Robert Hall Jr. and Emily Bernhardt for discussions and advice on an earlier version of the manuscript. We thank three anonymous reviewers for helpful and constructive comments, which led to great improvement of the manuscript. We acknowledge the help of Gertraud Steniczka, Christian Preiler, and Edurne Estevez Caño in the laboratory and in the field, and Antony Davison for advice on the statistics. Financial support came from the Austrian Science Foundation (Y420-B17) and from the Swiss Science Foundation (200021_163015) to TJB. All data are available upon request to amber.ulseth@epfl.ch or tom.battin@epfl.ch.
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors contributions
AJU, TJB, GAS and JS conceived of and designed the study, AJU and GAS performed the research, AJU, GAS, and EB analysed data, AJU, EB, and GAS contributed methods and model approaches, and AJU and TJB wrote the paper.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ulseth, A.J., Bertuzzo, E., Singer, G.A. et al. Climate-Induced Changes in Spring Snowmelt Impact Ecosystem Metabolism and Carbon Fluxes in an Alpine Stream Network. Ecosystems 21, 373–390 (2018). https://doi.org/10.1007/s10021-017-0155-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10021-017-0155-7