Advertisement

Ecosystems

, Volume 17, Issue 3, pp 550–566 | Cite as

Large-Scale Spatial Dynamics of Intertidal Mussel (Mytilus edulis L.) Bed Coverage in the German and Dutch Wadden Sea

  • Eelke O. Folmer
  • Jan Drent
  • Karin Troost
  • Heike Büttger
  • Norbert Dankers
  • Jeroen Jansen
  • Marnix van Stralen
  • Gerald Millat
  • Marc Herlyn
  • Catharina J. M. Philippart
Open Access
Article
First Online:
Received:
Accepted:

Abstract

Intertidal blue mussel beds are important for the functioning and community composition of coastal ecosystems. Modeling spatial dynamics of intertidal mussel beds is complicated because suitable habitat is spatially heterogeneously distributed and recruitment and loss are hard to predict. To get insight into the main determinants of dispersion, growth and loss of intertidal mussel beds, we analyzed spatial distributions and growth patterns in the German and Dutch Wadden Sea. We considered yearly distributions of adult intertidal mussel beds from 36 connected tidal basins between 1999 and 2010 and for the period 1968–1976. We found that in both periods the highest coverage of tidal flats by mussel beds occurs in the sheltered basins in the southern Wadden Sea. We used a stochastic growth model to investigate the effects of density dependence, winter temperature and storminess on changes in mussel bed coverage between 1999 and 2010. In contrast to expectation, we found no evidence that cold winters consistently induced events of synchronous population growth, nor did we find strong evidence for increased removal of adult mussel beds after stormy winter seasons. However, we did find synchronic growth within groups of proximate tidal basins and that synchrony between distant groups is mainly low or negative. Because the boundaries between synchronic groups are located near river mouths and in areas lacking suitable mussel bed habitat, we suggest that the metapopulation is under the control of larval dispersal conditions. Our study demonstrates the importance of moving from simple habitat suitability models to models that incorporate metapopulation processes to understand spatial dynamics of mussel beds. The spatio-dynamic structure revealed in this paper will be instrumental for that purpose.

Keywords

population synchronization connectivity supply side ecology larvae habitat suitability spatial autocorrelation spatial stability dynamic ecosystem Mytilus edulis Getis Ord statistic 

Introduction

Reef-building bivalves such as intertidal blue mussel (Mytilus edulis) are important for the community composition and functioning of coastal ecosystems for various reasons. Intertidal mussel beds provide structural heterogeneity on otherwise homogeneous mudflats and thus provide habitat for other species (Gutiérrez and others 2003; Buschbaum and others 2009; van der Zee and others 2012). Mussels may compete with other suspension feeders by consuming large amounts of phytoplankton (Kamermans 1994; Cadée and Hegeman 2002). Consequently, secondary production and biomass of intertidal mussel beds is high (Asmus 1987) making them an important food resource for, amongst others, birds and crabs (Nehls and others 1997). Mussels may also promote planktonic primary production by accelerating nutrient cycling (Asmus and Asmus 1991) and local benthic primary production by deposition of nutrient-rich feces and pseudofeces. Lastly, mussel beds may locally reduce hydrodynamic forces which influences local sediment properties (Widdows and Brinsley 2002). To develop a better understanding of the roles that intertidal mussel beds play in coastal ecosystems, it is important to identify the main determinants of mussel bed distributions and dynamics. Insight into spatial distributions, habitat suitability, reproduction, dispersal, settlement, and survival are prerequisites to understand and model large-scale spatio-temporal variability of marine bivalve populations. The purpose of the present paper is to foster our understanding of long-term spatio-temporal development of adult intertidal mussel bed distributions in the Wadden Sea as a step towards the development of spatial metapopulation models of blue mussels.

Spatial distributions and dynamics of intertidal mussel beds are determined by the combination of larval supply, settlement and various post-settlement loss processes which in their turn depend on the interplay of large-scale hydrodynamic forces and small-scale facilitation (van de Koppel and others 2005, 2012). The blue mussel is a gonochoric bivalve species with a flexible reproductive strategy that adjusts spawning according to environmental conditions (Gosling 1992b). Larvae and settling individuals are observed in spring, summer, and autumn (Bayne 1976; Pulfrich 1996; de Vooys 1999; Philippart and others 2012). Dispersal of the pelagic planktotrophic mussel larvae is strongly determined by water currents (Levin 2006; Metaxas and Saunders 2009; Carson and others 2010; White and others 2010) and the duration of the planktonic larval stage which depends on environmental factors such as food availability, temperature, and salinity (Gosling 1992b). Blue mussel larvae have been estimated to reside in the water column for approximately 3–5 weeks (Gosling 1992b; de Vooys 1999). When larvae reach a size of approximately 0.2 mm they settle and produce byssus threads to attach to substrata and to each other which protects them from dislodgement due to currents and waves (Bayne 1964, 1976; De Blok and Tan-Maas 1977; McGrath and others 1988). Important substrata on the intertidal soft sediments in the Wadden Sea are adult mussels, Pacific oysters (Crassostrea gigas), cockles (Cerastoderma edule), beds of dead shells, protruding tubes of Lanice conchilega (Callaway 2003), macroalgae and seagrass (Pulfrich 1996; wa Kangeri and others 2013). Bed formation results in increased bottom surface roughness which reduces hydrodynamic force (Widdows and Brinsley 2002; Donker and others 2012). Intertidal mussel beds that have established on soft sediments provide substratum for attachment and shelter of postlarvae which results in positive feedback between mussel bed presence and local recruitment allowing a bed to persist over long time spans (Bayne 1964; McGrath and others 1988; Gutiérrez and others 2003; Herlyn and others 2008). Foundations of dead shells which are built up underneath mussel beds may also provide substratum for postlarvae thereby upholding the positive feedback even when living mussels have disappeared (Herlyn and others 2008). Settlement may, however, also occur outside mussel beds or shell foundations in years when there are large quantities of settlers. Predation by shrimp and crabs (van der Veer and others 1998; Andresen and van der Meer 2010) is an important loss factor shortly after settlement while waves and currents (Nehls and Thiel 1993; Brinkman and others 2002; Hammond and Griffiths 2004; Herlyn and others 2008; Donker and others 2012) and ice-scouring during cold winters (Strasser and others 2001) may be important during all life stages of mussels and mussel beds.

Adult bivalve population sizes may fluctuate vigorously as a consequence of high temporal variation in larval supply, early stage survival and variation in adult mortality rate (Thorson 1950; Gosling 1992a; Beukema and others 1993, 2001, 2010; Caley and others 1996; van der Meer and others 2001; Levin 2006). In the Wadden Sea, Macoma balthica, Cerastoderma edule, Mya arenaria, and Mytilus edulis often show recruitment peaks after cold winters (Beukema and others 2001; Strasser and others 2003). Bivalve recruitment peaks following cold winters have also been observed in other northwestern European seas and estuaries such as the Swedish west coast (Möller 1986) and the Wash, UK (Young and others 1996). Various explanations have been suggested for this. First, adults produce more or larger eggs under cold conditions because lower maintenance metabolism is required, thus leaving more energy for gonad production (Honkoop and van der Meer 1998). It should be noted, however, that the experiment that Honkoop and van der Meer (1998) performed with Macoma balthica shows that the temperature effect on gonad production is rather small. Secondly, bivalve spawning may occur earlier in the season after warm winters which may lead to a temporal mismatch with the spring bloom of phytoplankton (which, inter alia, depends on light conditions) which decreases recruitment (Philippart and others 2003). The third line of explanations concerns the temperature-related phenology of mussels and their main crustacean predators, shore crab Carcinus maenas and brown shrimp Crangon crangon (van der Veer and others 1998; Andresen and van der Meer 2010). Specifically, post-settlement survival on intertidal flats is relatively high after cold winters because of lower densities or later arrival of shrimps and crabs (Beukema 1991, 1992; Young and others 1996; Strasser and Günther 2001). Reduced densities or later arrival of predators leads to a larger proportion of young bivalves to grow too large to be handled and consumed by predators (Philippart and others 2003; Beukema and Dekker 2005). Mortality of adult bivalves may also peak during cold winters because frost is lethal for cockles (Cerastoderma edule) and ice-scouring may eradicate intertidal mussel beds (Strasser and others 2001; Büttger and others 2011).

The observation that recruitment peaks often follow cold winters suggests that winter temperature drives large-scale spatial population synchronization because winter temperatures are correlated over large geographic ranges. Particularly, Beukema and others (2001) show that recruitment of the bivalve species Macoma balthica, Cerastoderma edule, and Mya arenaria is spatially synchronized between three distant locations in the western Dutch and western German Wadden Sea between 1973 and 1999 (Mytilus was not included in the monitoring in two of the three sites).

Synchronous dynamics on smaller spatial scales can result from spatial autocorrelation in more regional growth determinants. For instance, diverging regional trends in food availability, predation, and hydrodynamic impact could lead to distinct synchronization patterns between regions. Synchronous dynamics among nearby populations can also result from distance-limited dispersal of larvae between populations (Bjørnstad and others 1999; Ranta and others 2006). The supply of planktonic larvae in a particular region depends on the proximity of larvae sources and hydrodynamic transport toward the region (Levin 2006) and, to a certain extent, also on larval swimming behavior (Knights and others 2006). As the swimming capacity of larvae is limited relative to water currents, the spatial connectivity of the mussel populations, and therefore the degree of population synchrony, will largely depend on regional geomorphology and currents during the larval stage (Young and others 1996; McQuaid and Phillips 2000; Gilg and Hilbish 2003; Watson and others 2010).

Temperature, the spatially diverging growth determinants and dispersal will lead to characteristic signatures in spatial population covariance. That is, the spatial range over which the determinants operate, will show up in the spatial range of population synchronization (Bjørnstad and others 1999). If temperature is the dominant determinant, it is expected that synchronization will be observed in the entire population. If regionally distinct determinants are important then synchronization patterns will show autocorrelation on a regional scale. And more specifically, if geomorphology and hydrodynamic transport are important determinants of population synchronization, physical barriers such as rivers will show up as boundaries of synchronizing populations. Because temperature and the regional mechanisms operate simultaneously, the temperature effect must dominate the regional mechanisms to achieve visible synchronization at a large spatial scale. Similarly, regional effects must be pronounced in order to show up if there are strong temperature effects.

The objective of this study is to obtain insight into the distribution and dynamics of intertidal mussel beds in the Wadden Sea by exploring large scale spatio-temporal trends and scale-dependent population synchronizations. First, we compare the mean spatial distribution of intertidal mussel beds for the period 1999–2010 with the spatial distribution of the period 1968–1976 to get insight into long-term spatial variability and into the determinants of habitat suitability. Secondly, we analyze spatial patterns in the synchronization of intertidal mussel bed dynamics for the period 1999–2010. Thirdly, we use a stochastic growth model to analyze the impacts of winter temperature and storminess on intertidal mussel bed dynamics for the period 1999–2010 while controlling for density dependence. The analyses presented here aim to stimulate the development of spatially explicit metapopulation models including habitat suitability, resource dynamics and hydrodynamic connectivity. Insight into these factors is relevant from a management and conservation point of view where insight into long-term variability and natural establishment of intertidal mussel beds is a basic requirement.

Methods

Study Region and Tidal Basins

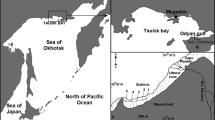
The Wadden Sea (52°57′–55°37′N, 4°44′–8°12′E) is a shallow sea located in the southeastern part of the North Sea bordering the coastal mainland of Denmark, Germany, and the Netherlands (Figure 1) [For a recent description of the biotic and abiotic properties of the Wadden Sea see Philippart and Epping (2010)]. It is one of the world’s largest coherent systems of intertidal sand and mud flats (Reise 2005; Reise and others 2010). The area contains coastal waters, intertidal sandbanks, mudflats, shallow subtidal flats, drainage gullies and deeper inlets and channels. The Elbe, Weser, and Ems are the main rivers discharging into the Wadden Sea (Figure 1) with average freshwater run-off of 700, 310, and 125 m3 s−1, respectively (Philippart and Epping 2010). Freshwater also enters the Wadden Sea at an average rate of approximately 470 m3 s−1 through two sluices in the dike (“Afsluitdijk”) in tidal basin 39 (van Raaphorst and de Jonge 2004). Tidal currents and exposure to waves differ between regions due to differences in tidal range, geomorphology, fetch, and the occurrence of barrier islands (Figure 1). Tidal amplitudes range between 1.5 and 3.0 m in the Northern (Tidal Basins 1–10; henceforth TB denotes “tidal basin”) and Southern (TB 23–39) Wadden Sea and are greater than 3.0 m in the central part (TB 11–22) (Staneva and others 2009). The moderate and stormy winds in the area are mainly southwesterly.
Figure 1

The 39 tidal basins of the Wadden Sea with average intertidal mussel bed coverage over the years 1999–2010. Intertidal mussel bed coverage is defined as the percentage of tidal flat area that is covered by mussel beds. The intertidal flats in tidal basins 1–3 in Denmark are colored gray because no comparable mussel bed data were available. The names of the weather stations are printed against a yellow background to clearly distinguish them from the region names. The geographic extent ranges between 52°57′–55°37′ North and 4°44′–8°12′ East (Color figure online).

The area can be divided into tidal basins which are natural geomorphological and hydrodynamic subunits. A tidal basin is delineated by the mainland, barrier islands, tidal divides and it connects to the North Sea via tidal inlets (Figure 1). The volume of water that is being exchanged with the North Sea through tidal inlets is much larger than the volume of water that is displaced between neighboring tidal basins (Ridderinkhof and others 1990). We use tidal basins as units of observation because locations within tidal basins share various morphological, hydrodynamic, and trophic properties that are relevant for the abundance of mussel beds (van Beusekom and others 2012). Furthermore, the turnover time of a tidal basin—defined by Ridderinkhof and others (1990) as the time necessary to reduce the mass present in a basin to a fraction e−1 of the original mass—is relevant for the transport of larvae between tidal basins. In particular, Ridderinkhof and others (1990) show that the smaller tidal basins in the Dutch Wadden Sea have short turnover times between 8 and 10 tidal periods (one tidal period is approximately 12.5 h) whereas larger tidal basins such as the Ems (Figure 1, TB 30) estuary have turnover times of 25 tidal periods.

Data

We used two data sets on mussel bed distributions from two periods. The first consists of data collected in 36 tidal basins in the German and Dutch Wadden Sea (Figure 1) for the period 1999–2010. The Danish tidal basins (TB 1–3 and the Northern part of TB 4) were not included in this study because in these basins an incomparable survey protocol was applied and surveys took place every 2 years rather than every year. Annual mapping of mussel bed contours in Schleswig-Holstein (TB 4–18), Germany, Lower Saxony (TB 18–30), Germany and the Netherlands (TB 30–39) was performed on the basis of a common definition of a mussel bed (de Vlas and others 2005) and according to trilateral TMAG agreements (TMAG = Trilateral Monitoring and Assessment Group 1997). TB 4 refers to the southern half of the tidal basin only because the northern half is located in Denmark and not surveyed in a comparable fashion. The contours of visited mussel beds were determined by a combination of aerial surveys, aerial photographs, and by walking around the bed with a hand-held GPS device following the TMAG protocol (de Vlas and others 2005). In Schleswig-Holstein intertidal mussel beds were monitored by BioConsult SH since 1998; in Lower Saxony by NLPV and NLWKN since 1994 (except for 1995 and 1998); in the Netherlands by IMARES and MarinX since 1995. The largest complete and homogeneous data set thus results from the period 1999–2010. Region specific survey details are described below.

In Schleswig-Holstein aerial photographs were taken annually (except for the years 2006 and 2009) with scale of 1:15.000 or 1:25.000. The photographs were checked visually and the contours of ascertained mussel beds were digitized and included in a GIS. Results were combined with field surveys. Each year about 40% of the mussel bed locations were visited. For those locations where field surveys were not possible, aerial photographs provided the only source of information. For the beds not visited in 2006 and 2009 it was assumed that the contours were the same as the year before. It is noted, however, that during the field campaigns in 2006 and 2009 new beds and the disappearance of beds were observed.

In Lower Saxony contours of mussel beds were determined on the basis of black and white aerial photographs with a scale of 1:15.000. Since 2006 true color photographs with a scale of 1:20.000 have been used. Photographs were analyzed with a stereoscope and contours of mussel beds were digitized and included in a GIS. For the year 2010 digital orthophotos were used and digital mapping of the contours was done on screen. Results were validated in the field.

In the Netherlands, aerial inspection flights were carried out in spring prior to the field survey to assess whether the beds that were mapped in the previous year were still present, whether there were new seed beds, and whether large portions of beds had disappeared. Locations where changes were observed during flights were prioritized during the field surveys. The available time was usually not sufficient to map all mussel beds by means of GPS. The percentage of bed locations that were surveyed in the field was between 40 and 95%. For beds not visited it was assumed that the contour is the same as in the preceding year if the aerial survey confirmed the presence. When a bed is visited in a following year the contour in the missing year is estimated on the basis of the contours before and after the missing year. The polygon vector files describing the contours of the mussel beds were imported into a GIS. The online supplementary appendix A provides further details of the survey protocols and institutes.

In all three areas, according to the TMAG protocol, beds qualify as mussel beds if the percentage cover by mussels is 5% or more. In the period 1999–2010, mussel beds may have contained Pacific oysters (Crassostrea gigas) which were first observed in the western Dutch Wadden Sea (TB 39) in late 1970s (Fey and others 2010; Troost 2010) and in the central Wadden Sea (TB 26) in 1998 and in the northern Wadden Sea (TB 4 and 5) in the early 1990s (Wehrman and others 2000). During the winter 2009/2010 ice-scouring destroyed mussel beds in Schleswig-Holstein (Büttger and others 2011). To avoid bias caused by removal of mussel beds by ice-scouring, we excluded from the analysis growth estimates from TB 4–18 for the year 2009.

The second data set is a compilation of mussel bed contours for the entire Wadden Sea based on aerial photographs recorded in 1968, 1973, 1974, 1975, and 1976 (Dijkema and others 1989). The methodology used by Dijkema and others (1989) differs from the methodology used to obtain the 1999–2010 data set. In particular, mussel beds were demarcated on the basis of stereoscopy of aerial photographs and the contours around mussel beds were drawn more loosely and wider than for the 1999–2010 data set. Although comparison of absolute areas between the data sets is not possible, it is nevertheless possible to compare spatial patterns in relative abundances.

Maps of the intertidal areas and of land boundaries were provided by the Common Wadden Sea Secretariat (CWSS), Wilhelmshaven. The intertidal area was assumed to be constant over the period 1968–2010. A vector file representing the tidal basins (Figure 1) was obtained from Kraft and others (2011). All spatial data were organized in a GIS. Lambert Azimuthal Equal Area projection (using the ETRS89 datum; EPSG code 3035) was used to obtain true area representation over the full study area.

To investigate the effects of winter temperature and storminess on the dynamics of mussel bed coverage we made use of air temperature and wind measurements from different weather stations in the Wadden Sea area. The weather stations are all located near the coastline (Figure 1). German temperature data were obtained from the German Meteorological Service (www.dwd.de) for the stations List auf Sylt, Cuxhaven, Norderney and Emden. We used German wind measurements from the stations List auf Sylt and Norderney only because the storminess at the stations Cuxhaven and Emden is substantially lower than at the other stations because they are located more land inwards. Dutch temperature and wind data were obtained from the Royal Netherlands Meteorological Institute (www.knmi.nl) for the stations Lauwersoog, Hoorn Terschelling, Vlieland and De Kooy. A measure for winter severity (T) was obtained by calculating the Hellmann number which is the absolute value of the sum of the daily average temperatures below zero degree Celsius for the period 1 November to 31 March. It is noted that a strong correlation between air- and water-temperature has been observed over a long period of time in the western Dutch Wadden Sea (TB 39 in Figure 1) suggesting that air temperature is a solid indicator for water temperature (van Aken 2008). We defined storminess as the number of days with average wind speed greater than 15 m/s (~7 Bft) in the period 1 August through 30 June. Mussel bed growth rates were related to the Hellman number of the preceding winter (1 November–31 March) and the storminess of the following period (1 August–30 April). For instance, growth between 2005 and 2006 (and labelled R 2005) is related to the Hellman number over the period 1 November 2004 and 31 March 2005 and the storminess between 1 August 2005 and 30 April 2006. For each tidal basin we used the weather data from the nearest weather station (stations Cuxhaven and Emden are excluded for wind). The nearest weather station is defined as the one with the shortest straight line distance from the centroid of the tidal basin.

Statistical Models

Mussel Bed Area Per Tidal Basin and Spatial Clustering

We define mussel bed area per tidal basin (A i ) as the sum of the areas of the mussel bed polygons intersecting with the tidal basins. Mussel bed coverage per tidal basin i (C i in %) is the percentage of total intertidal flat area that is covered by mussel beds. For the period 1999–2010 we calculate yearly sets of coverages and the mean coverage over the period; for the period 1968–1976 only one set of mussel bed coverage can be calculated.

Ord and Getis (1995) have developed two local statistics, G i and G i * , to evaluate the degree of spatial clustering around a focal location, i. Statistic G i excludes location i from the cluster whereas G i * includes it. The G and G* statistics express the sum of the values in the vicinity of a particular location as the proportion of the sum of the values for the entire area. G and G* are positive when the mean of a cluster is greater than the overall mean and negative when it is less. Specifically, the statistics identify those clusters of locations with values higher or lower in magnitude than might occur by chance. G and G* are similar to the z score in that they indicate how many standard deviations a value is above or below the mean. For the mean, the standard deviation and testing of the G and G* statistics, see Getis (2009). We use the G* statistic because we are interested in the degree of clustering rather than in the influence of observation i on the value of j (Getis 2009). We use the G* to identify clusters of tidal basins with high and low values of mean mussel bed coverage for the periods 1999–2010 and 1968–1976. Following the notation in Getis (2009) G i * is defined as follows:
$$ {G_{i}^{ *} = \frac{{\sum\limits_{j = 1}^{n} {w_{ij} \left( d \right)C_{j} - W_{i}^{ *} \overline{C} } }}{{s\sqrt {\frac{{\left( {nS_{{ 1 {\text{i}}}}^{ *} - W_{i}^{ * 2} } \right)}}{n - 1}} }}}, $$
$$ W_{i}^{*} = \sum\limits_{{j = 1}}^{n} {w_{{ij}} \left( d \right)} \;{\text{and}}\;S_{{1i}}^{*} = \sum\limits_{{j = 1}}^{n} {w_{{ij}}^{2} } \quad {\text{for}}\;{\text{all}}\;j $$
where w ij (d) is the spatial weight describing the topological relationships between tidal basins i and j as a function of the distance (d) between their centroids. It equals 1 if the distance is less than 30 km and 0 otherwise (note that w ii = 1). We take the cut-off distance of 30 km to avoid isolation of large tidal basins. A large cut-off distance would lead to large numbers of neighbors for the smaller tidal basins. The maximum distance between centroids of neighboring tidal basins is 28 km (TB 37 and TB 36) and the shortest about 6 km (TB 16 and TB 15). \( {\overline{C} } \) and s are the mean and standard deviation of the coverages of mussel beds for the 36 tidal basins. A cluster of large positive values of G i * indicates a hotspot of tidal basins whereas a cluster of large negative values indicates a cold spot.

Growth, Density Dependence, Winter Temperature and Storminess

We calculated relative yearly mussel bed growth rate per tidal basin i (R i,t ) as the difference in the percentage coverages of mussel beds between successive years divided by the mean coverage of tidal basin i in the period 1999–2010,
$$ {R_{i,t} = \frac{{C_{i,t + 1} - C_{i,t} }}{{\bar{C}_{i} }}}, $$
where C i,t is the mussel bed coverage in tidal basin i in year t and \( {\bar{C}_{i} } \) is the mean mussel bed coverage of tidal basin i for the period 1999–2010. Mussel bed growth rates for the years 1999 to 2009 are calculated for the 25 tidal basins with mean coverage greater than 0.2%.
We tested for density dependence and the effects of Hellmann temperature (T) of the preceding winter and storminess (S) during the following season on growth rate (R) by means of a first-order linear model (Royama 1992). Because we had no a priori expectations of the functional form, we also considered nonlinear relationships between the dependent variable R and the explanatory variables coverage (C), T and S by also including their squared terms. We also considered interactions between T and C and between S and C to investigate whether the effects of the Hellmann temperature and storminess depend on mussel bed coverage. The first-order linear model can be written as:
$$ R_{{i,t}} = \beta _{0} + \beta _{1} C_{{i,t}} + \beta _{2} T_{{i,tp}} + \beta _{3} S_{{i,tf}} + \beta _{4} C_{{i,t}}^{2} + \beta _{5} T_{{i,tp}}^{2} + \beta _{6} S_{{i,tf}}^{2} + \beta _{7} C_{{i,t}} T_{{i,tp}} + \beta _{8} C_{{i,t}} S_{{i,tf}} $$
T i,tp denotes the Hellmann temperature of the winter preceding time t in tidal basin i (e.g., growth in year 2005 depends on the temperature of winter 2004/2005). S i,tf denotes the storminess during the season following time t in tidal basin i (for example, growth in year 2005 depends on the storminess of the season 2005/2006). We used linear-mixed effects models (LMM) to account for possible differences between tidal basins and years. Particularly, the effects of C, and S were allowed to differ by tidal basin and year by including them as random slopes. We did not model T with a random effect to keep the number of variables with random effects low to avoid unwieldy models. The observations were weighted by \( {\bar{C}_{i} } \) to account for the fact that the relative changes in coverage are more precisely determined in the tidal basins with large \( {\bar{C}_{i} } \). Following, Bolker and others (2009) we used restricted maximum likelihood (REML) estimation.

The original distribution of R was leptokurtotic with positive and negative tails which resulted in heteroscedastic model residuals. We therefore normalized the distribution of R by using the power transformation (|R| λ sgn(R) − 1)/λ; λ > 0 (Bickel and Doksum 1981). The value of λ was selected on the basis of the distribution of the residuals. We checked for normality and homogeneity by visual inspections of plots of residuals against fitted values. We set λ = 0.5 which yielded satisfactory results.

We used the following two-step model selection procedure. Step 1: We started by estimating the full model which included all fixed effects and the random intercepts and slopes for C and S for both the levels “tidal basin” and “year”. We removed the random slopes (from both levels) in order of increasing standard deviation starting with the random slope with the lowest standard deviation. The successive models were compared on the basis of likelihood ratios. If the p-value for the likelihood ratio test (LRT) was greater than 0.05, preference was given to the simpler model. The random intercepts for the levels “tidal basin” and “year” were retained to meet the assumption of homoscedasticity. Step 2: Given the obtained random effects structure, we estimated all plausible nested models by setting coefficients of the fixed effects at zero (or removing their variables from the model). Models including quadratic terms and interactions were only considered if the lower order effects were also in the model. The estimated models were ranked in order of increasing AIC levels (Burnham and Anderson 1998).

Synchronization

Synchronization is defined as the correlation between the yearly mussel bed growth rates of the tidal basins. We consider the correlation in yearly growth rate rather than the correlation in coverages because coverages may be affected by temporal trends (Turchin 2003). For each tidal basin pair, synchronization is calculated using Pearson’s correlation coefficient (r). To avoid possible influence of tidal basins with low mussel bed coverages, the correlation coefficients are calculated between tidal basins with average coverage greater than 0.2%. This resulted in a symmetric 25 × 25 correlation matrix. The correlation matrix for the entire data set—that is, the data set including the tidal basins for which the average coverage is less than or equal to 0.2%—is presented in the online appendix B. We visualized the correlation matrix by plotting ellipses shaped as contours of a bivariate normal distribution with unit variance and correlation r. The points of the contour are given by \( {\left( {x,y} \right) = \left( {{ \cos }\left( {\theta + \frac{d}{ 2}} \right),{ \cos }\left( {\theta - \frac{d}{ 2}} \right)} \right)} \) and d = arccos(r) where θ ϵ [0, 2π] (Murdoch and Chow 1996).

We used R 2.15.2 (R Development Core Team 2009) for data handling, estimation, and plotting. For spatial data handling and statistics we used the R packages sp (Pebesma and Bivand 2005; Bivand and others 2008), rgeos (Bivand and Rundel 2011), rgdal (Keitt and others 2011). For mixed modeling we used the R package lme4 (Bates and others 2012). For plotting we used ellipse (Murdoch and Chow 1996, 2012) and ggplot2 (Wickham 2009).

Results

Mean Mussel Bed Coverage and Spatial Stability

The mean mussel bed coverages strongly varied between the tidal basins (Figure 1). The highest mean coverages were found in the tidal basins in the eastern part of the Dutch Wadden Sea (TB 31–36) and in the western part of Lower Saxony (TB 22–TB 29). In some of the areas mean coverage ranged between 4 and 6% of the intertidal area. The coverages were low in the northern tidal basins in Schleswig-Holstein (TB 4–10) (between 0 and 1.5%) whereas mussel beds were virtually absent in TB 11–18. The coverages were also relatively low (<0.5%) in the western Dutch Wadden Sea (TB 37–39).

The spatial variation in mussel bed coverages presented in Figure 1 is more clearly visible in the left panel of Figure 2 which shows the distribution of mussel bed hot and cold spots (that is, the G* statistic) for the same period. The right panel shows G* for the 1968–1976 period. In both periods the hotspots are situated in the eastern Dutch Wadden Sea and in western Lower Saxony while the cold spots are situated in northern Schleswig-Holstein and in the western Dutch Wadden Sea. The highest G* value occurred in western Lower Saxony in the period 1968–1976 and in the eastern Dutch Wadden Sea in the period 1999–2010.
Figure 2

Getis-Ord hot- and cold spot maps for average intertidal mussel bed coverages for the periods 1999–2010 and 1968–1976 (Color figure online).

Temporal Trends and Synchronization

Figure 3 shows for each tidal basin the trend in mussel bed coverage over the period 1999–2010. The yearly fluctuations are high in the tidal basins where the average coverages are high and much lower in the tidal basins with low average coverages. For example, the coverages fluctuate irregularly between 0 and 8% in the eastern Dutch Wadden Sea (TB 31–36) whereas the yearly changes in coverage in northern Schleswig-Holstein (TB 4, 6, 7, 9, and 10) are more regular and range between 0 and 2.5%. Figure 3 also shows that tidal basins in each other’s vicinity show similar fluctuation patterns. For instance, TB 22–26 in Lower Saxony show a peak in the year 2000 after which the coverages decrease until 2006 after which there is a slight and regular increase. In the eastern Dutch Wadden Sea (TB 31, 32, 34, 35, 36), a peak is observed in 2002, after which the coverages decline, until a second peak is observed in most of the tidal basins in 2006. The growth in the eastern Dutch Wadden Sea in 2002 and 2006 is not observed in the German (TB 4–30) or western Dutch Wadden Sea (TB 37–TB 39).
Figure 3

Intertidal mussel bed coverage (%) of the tidal flats for 36 tidal basins for the period 1999–2010. The numbers in the strips of the panels represent the tidal basin number (see Figure 1).

Figure 4 shows the correlation in mussel bed growth between all tidal basins with average coverages above 0.2%. The figure shows three blocks of tidal basins with synchronic dynamics. The most northerly synchronic block (TB 4–10) is located in northern Schleswig-Holstein. The second synchronic block (TB 19–30) is bordered by the river Elbe (TB 18) in the east and by the Ems estuary (TB 30) in the west. The dynamics of the relatively small TB 20 are not synchronized with the other tidal basins in the block. The third block of synchronic tidal basins (TB 30–39) is located in the Dutch Wadden Sea. Within the three blocks the correlation between tidal basins is highest within the centers of the blocks and decreases with distance between the tidal basins. Although short-distance synchronization dominates, long-distance synchronization is also observed between the blocks consisting of TB 36, 37, and 39; and TB 19, 20, and 22, respectively.
Figure 4

Ellipse matrix of the correlations between yearly intertidal mussel bed growth rates of the tidal basins for which the average coverage was greater than 0.2%. The ellipses are the contours of a bivariate normal distribution with unit variances and Pearson’s correlation coefficient r (Murdoch and Chow 1996). In the case of positive correlation, the color of the ellipse is blue. In the case of negative correlation, the color is red. The intensity of the color relates to the (absolute) size of the correlation coefficient. Correlations of the elements along the diagonal are always 1 and not informative and thus not presented. The ellipse matrix for all tidal basins is presented in the supplementary appendix B (Color figure online).

Mussel Bed Growth Models

In the full model of step 1—that is, the model including all fixed effects and random intercepts and random slopes for coverage and storminess at the levels tidal basin and year—the relative standard deviation of the random slope of coverage in level tidal basin was small. Accordingly, the likelihood ratio test showed that deleting this random effect from the full model did not cause a significant reduction in likelihood and thus preference was given to the simpler model (Table 1, model 4). This elimination procedure was continued until only the intercept at the levels of tidal basin and storminess at the year level remained as random effects. On the basis of the thus obtained random effects model (that is, random intercept for tidal basin level and storminess at the year level) all nested fixed effects models were estimated and ordered by AIC (Table 2). The best model only includes a negative term for C suggesting that negative density-dependent processes are acting (−0.160, SE 0.024). The second best model in terms of AIC—which is considerably worse than the best model (ΔAIC = 4.486)—indicated in addition to a negative effect of C a slight positive but highly insignificant effect of storminess (S). The third best model (ΔAIC = 5.512) also indicated a negative effect of C and a positive effect of C 2 suggesting that the negative effect of coverage leveled of at high values of C. Models 4 and 5 fit the data substantially worse than models 1–3 (ΔAIC ≥ 7.859). Model 4 shows a negative effect of S and a positive effect of S 2 in addition to the negative C effect. Model 5 shows a positive but highly insignificant effect of S but a negative and significant interaction between C and S. Winter severity (T) does not show up as a predictor in the models 1–5. The variance of the random effects at the year level indicated considerable heterogeneity across years while the variance across tidal basin is very low.
Table 1

Selection of Random Effects of the Linear Mixed Models of Mussel Bed Growth

Model

TB level

SD

Year level

SD

X 2

Df

P value

1

Intercept

0.232

Intercept

0.341

   
 

Residual

  

0.958

   

2

Intercept

0.100

Intercept

S

0.706

0.279

21.421

2

<0.000

 

Residual

  

0.922

   

3

Intercept

0.153

Intercept

C

S

0.707

0.106

0.296

2.141

3

0.544

 

Residual

  

0.882

   

4

Intercept

C

0.326

0.128

Intercept

C

S

0.587

0.129

0.254

3.375

2

0.185

 

Residual

  

0.856

   

5

Intercept

C

S

0.227

0.103

0.045

Intercept

C

S

1.514

0.258

2.521

0.000

3

1.000

 

Residual

  

0.844

   

C = intertidal mussel bed coverage (%); S = storminess; TB = tidal basin. In this stage of the model selection procedure the fixed effects (C, C 2, T, T 2, S, S 2, C × S, C × T) remain unchanged. The column SD gives the standard deviations for the random effects of the intercept, C and S for the levels TB and Year. The columns χ 2, Df, and the P value present the relevant outcomes of the χ 2 tests. The number of observations is 269 after removing the observations that were possibly influenced by ice-scouring; the number of tidal basins is 25 (viz. the ones that fit the criterion of mean coverage greater than 0.2%) and the number of years is 11.

Table 2

Regression Table with the Full and the Five Best Mixed-Effects Models for Mussel Bed Growth Rate Selected on the Basis of AIC Values

 

Full Model

Model 1

Model 2

Model 3

Model 4

Model 5

Intercept

−1.618

−1.894

−1.955

−1.730

−1.718

−2.079

 

(−0.303)

(0.098)

(0.229)

(0.124)

(0.223)

(0.234)

C

−0.277

−0.160

−0.158

−0.322

−0.136

−0.099

 

(−0.078)

(0.024)

(0.024)

(0.072)

(0.024)

(0.034)

C 2

0.028

  

0.024

  
 

(0.009)

  

(0.009)

  

S

−0.114

 

0.024

 

−0.290

0.111

 

(0.169)

 

(0.087)

 

(0.142)

(0.094)

S 2

0.046

   

0.069

 
 

(0.029)

   

(0.026)

 

T

−0.001

     
 

(0.008)

     

T 2

−0.000

     
 

(0.000)

     

C × S

−0.040

    

−0.041

 

(0.016)

    

(0.015)

C × T

−0.000

     
 

(0.001)

     

Random effects

      

Intercept for TB

0.010

0.019

0.019

0.012

0.015

0.023

Intercept for year

0.498

0.427

0.471

0.416

0.360

0.470

S for year

0.078

0.061

0.068

0.061

0.060

0.070

residual

0.851

0.868

0.868

0.864

0.866

0.856

ΔAIC

  

4.486

5.512

7.859

8.188

AIC

990.216

930.489

934.975

936.001

938.348

938.677

BIC

1040.542

955.651

963.733

964.758

970.700

971.030

Deviance

962.216

916.489

918.975

920.001

920.348

920.677

Log-likelihood

−481.108

−458.244

−459.488

−460.000

−460.174

−460.339

C = mussel bed coverage (%); S = storminess; TB = tidal basin. Standard errors in parentheses underneath the regression coefficients. The number of observations (269) is the same as in Table 1.

Discussion and Conclusions

We analyzed the spatial variability of the coverage of mussel beds in the international Wadden Sea on the basis of data collected in the periods 1968–1976 and 1999–2010. Within each period, notable regional differences in mussel bed coverages were observed. Between the periods, however, these distribution patterns were remarkably stable in that the regions that were densely populated in the period 1968–1976 were also densely populated in the period 1999–2010. The highest coverages occur in the relatively small and sheltered tidal basins in the eastern Dutch and in the western Lower Saxon Wadden Sea whereas mussel beds were virtually absent in tidal basins that are not sheltered by barrier islands (TB 11–18). The strikingly stable mussel bed distributions may be explained by the regionally variable levels of exposure to hydrodynamic forces which are relatively constant on the scales of decades.

Although analysis of long-term regional differences in mussel bed coverage provides insight into the relatively invariable determinants of habitat suitability, analysis of year-to-year variability including spatial synchrony, sheds light on the determinants of short-term dynamics. We expected that yearly increases in coverage would be explained by episodic recruitment events following cold winters and that decreases would occur during stormy winter seasons. In particular, previous studies performed at various locations have shown that bivalve recruitment events are often preceded by cold winters (Möller 1986; Young and others 1996; Beukema and others 2001; Strasser and others 2003) which has led to the commonly held view that winter severity is the main driver of bivalve recruitment events and population synchronization in North West Europe. Because winter temperatures are strongly correlated in the entire study region (Figure 5) we hypothesized that growth peaks would show up at the same time throughout the entire study area. If regional growth determinants or larval dispersal would dominate, then population synchronization would show up at smaller spatial scales. Our analyses did not show that cold winters systematically induced increases in mussel bed coverages. Nor did we find strong evidence for negative effects of storminess. We did find, however, that synchronic growth was constricted to confined blocks of tidal basins bordered by hydrodynamic barriers such as rivers and large extents of unsuitable habitats. These results point toward the importance of considering larval transport and early stage survival to further develop understanding of the spatial dynamics of mussel beds in the Wadden Sea. The importance of larval transport has also been demonstrated for coastal mussel populations in southwest England (Gilg and Hilbish 2003) and the southeast South Africa (McQuaid and Phillips 2000) where coastal circulation is an important determinant of larval dispersal. Although our hypothesis and results are consistent with findings from other systems, we do not rule out alternative explanations. For instance, regional differences in the change of eutrophication (van Beusekom and others 2012) and carrying capacity or predation rates could lead to regional differences in vital rates which could cause the observed synchronization patterns. Another possible cause of diverging dynamics in the separate blocks may be related to local hydrodynamic disturbances which were not detected by regressing adult mussel bed dynamics on storminess. To distinguish between the above-mentioned hypotheses it is important to obtain detailed long-term spatial data on competition and food limitation, reproductive capacity and output, early stage predation, recruitment, hydrodynamic disturbance and transport. In this context it is also important to have better understanding of the positive and negative interactions between Pacific oysters and mussels. Particularly, mussels and oysters benefit from each other in that they provide suitable substrate but they suffer from each other due to competition for food resources. The long-term consequences of the establishment of Pacific oyster populations for mussel populations will depend on the responses of both populations to environmental conditions and on the interactions between the populations.
Figure 5

Winter severity and storminess for the different weather stations along the Wadden Sea coast. Winter severity or the Hellmann temperature was calculated as the absolute value of the sum of the daily average temperatures that were below zero degrees Celsius for the period 1 November–31 March. Storminess is defined as the number of days with average wind speed greater than 15 m/s (~7 Bft) in the period 1 August–30 June (Color figure online).

The fact that we did not find a temperature effect on growth does not imply that temperature may not have an effect on the long-term dynamics and sustainment of intertidal mussel beds at all. There are several reasons why we might have missed to detect a winter temperature effect. Firstly, our time series covered the period 1999–2010 which was relatively warm. Beukema and others (2001), who did find a temperature effect, used data for the period 1969–1999 which contained several cold winters. In particular, the severe winters of 1978/1979 and 1995/1996 were followed by extraordinary recruitment events for different species of bivalves including Mytilus edulis. The study of Möller (1986) also included the year 1979 after which an eightfold increase in the numerical density of Mya arenaria was observed. The study of Strasser and others (2003) focused on recruitment of several species of bivalves in the whole Wadden Sea following the cold winter of 1995/1996. They found higher than average densities of recruits of Cerastoderma edule in 1996 in the entire Wadden Sea. For the species Macoma balthica and Mya arenaria higher than average recruitment was only observed in the southern Wadden Sea. It is therefore possible that we would have found statistically significant temperature effects if our time series had included more and colder winters. It is important to note, however, that cold winters are not a prerequisite for high recruitment events as relatively mild winters may also be followed by high recruitment events. For instance, after the relatively mild winters of 1974/1975 and 1990/1991, Beukema and others (2001) found high densities of recruits for different species of bivalves. And in our data set the mild winters of 2000/2001 and 2004/2005 were followed by substantial increases of adult mussel beds in the Dutch Wadden Sea (observed as peaks in 2002 and 2006). Because cold winters are expected to occur less frequently in the future due to climate change, the factors underlying recruitment after relatively warm winters will become increasingly important determinants of bivalve metapopulations. Another potential cause of the absence of a winter temperature effect is that loss processes operate between the moments of recruitment and the surveys of adult mussel beds which may distort the correlation between winter temperature and mussel bed growth to some extent. This implies that winter temperature effects might be more easily detected for endobenthic species such as Macoma balthica than for epibenthic species that are more vulnerable to hydrodynamic disturbance. Note, however, that we did observe bivalve-characteristic episodic growth peaks by considering yearly changes in the coverage of adult mussel beds (Figure 3).

The absence of evidence of a storminess effect in the growth model does not imply that storminess does not influence mussel bed dynamics. The absence of a storminess effect may be explained by the fact that we considered dynamics of adult mussel beds while especially settlement and newly settled mussel beds are sensitive to hydrodynamic disturbance and storminess because individual mussels have not yet attached themselves firmly to the sediment and each other. As a result establishment and development of adult mussel beds tends to occur at relatively sheltered locations where the impact of storms on adult beds is relatively low. For example, Nehls and Thiel (1993)—who studied survival of mussel beds including newly recruited mussel beds—found that only 49 out of 94 beds survived their first winter and that all of the surviving beds were located in sheltered areas. These areas were also found to be populated with mussel beds in several decades before and after their investigation. Our paper concerns the dynamics of adult mussel beds which implies that we are analyzing the dynamics of beds that already survived the initial young stages and thus occur in relatively sheltered locations only.

The limitation of our empirical approach to detect storminess effects could be cleared up by integrating observations of young and adult intertidal mussel beds with hydrodynamic models (Donker and others 2012). Although such integrated models provide insight into the mechanic interactions between hydrodynamic forces and intertidal mussel beds, the approach will be difficult to apply to large temporal and spatial scales for the following two main reasons. Firstly, the hydrodynamic conditions of all the relevant locations—which include tides, wind and fetch—need to be known which requires very detailed data sets, extensive monitoring and complex and computer intensive modeling. Secondly, because waves and currents are attenuated when they travel over the rough mussel bed surfaces, they cannot be considered independent variables. Yet, it would be useful to have more insight into the long-term impacts of waves and currents on the tidal flats in order to identify suitable mussel bed habitat in terms of hydrodynamics independently of the observations presented in this paper.

In this paper, we have suggested that synchronic spatial population dynamics within blocks of neighboring tidal basins may result from distance-dependent dispersal of larvae. In particular, larvae that are produced in one tidal basin may be transported to hydrodynamically connected tidal basins. This suggestion is supported by the fact that the borders of the synchronic blocks are located at tidal basins with estuaries and rivers (in which water currents form a barrier toward the next tidal basins) and at regions that lack suitable habitat. As mentioned above, the turnover time for the Ems estuary (Figure 1, TB 30) is substantially longer than the turnover times for the other Dutch tidal basins (Ridderinkhof and others 1990) so that the chance for a larva to survive the time it takes to pass the estuary and arrive at suitable habitat is relatively low. The chance to survive the passing of the Elbe estuary (TB 18) and arrive at suitable habitat would conceivably be even lower. Our results, that is, that the population dynamics within the blocks separated by the Ems and Elbe estuaries are distinct, are in line with this observation. Hydrodynamic transport modeling, on the basis of tides and wind, could elucidate possible fates of mussel larvae and provide insight into the connectivity of suitable habitat patches within tidal basins. This type of modeling would help to provide insight into the structure of the metapopulation network and would be able to show which subpopulations produce larvae with high survival and settling probability. In addition to water movement, the characteristics of the water affecting larval growth and development (such as food availability, salinity, and temperature) should be considered (Metaxas and Saunders 2009). Particularly, a lower growth- and development rate during the larval phase increases the time a larva needs to complete development which increases the risk of being predated by ctenophores and benthic feeders or of being transported offshore (Young and others 1998; Philippart and others 2003; Metaxas and Saunders 2009). Hydrodynamic connectivity modeling and water quality measurements in combination with larval requirements could provide a framework for the development of a dispersal model describing the corridors between suitable habitats from the perspective of larvae.

In the Wadden Sea there is high quality, comparable long-term distribution data available for intertidal mussel beds but not for subtidal mussel beds. Because our quantitative analyses required homogeneous data we have focused on intertidal mussel beds only. Subtidal mussel populations may, however, influence the dynamics of intertidal populations by producing larvae that end up in the intertidal and vice versa. Hence, a complete model of spatial population dynamics would include survival, production, dispersal, and settlement of both intertidal and subtidal populations.

The spatial configuration of suitable habitat and population growth dynamics presented in this paper is relevant from a natural resource management perspective. If it is combined with the outcomes of further research suggested above, it will be possible to pinpoint those locations and sub-populations that are of pivotal importance for the resilience of the metapopulation of mussel beds and hence require special protection.

Notes

Acknowledgments

This study was financially supported by the Waddenfonds, province of Noord Holland and the Program towards a rich Wadden Sea. We thank the following organizations for supporting the intertidal mussel bed surveys and providing data: 1. The Schleswig-Holstein Agency for Coastal Defence, National Park and Marine Conservation—National Park Authority, 2. National Park Administration Wadden Sea Lower Saxony and The Lower Saxonian Agency for Water Management, Coastal Protection and Nature Conservation, 3. IMARES. The Alfred-Wegner-Institute (Sylt) kindly provided aerial photographs. We thank Dietmar Kraft for constructing the vector file with the tidal basins and Carola van Zweeden for GIS database management of IMARES data. We are very grateful to Folkert de Jong for stimulating an international and comparative approach. We thank our colleagues Jaap van der Meer, Ulrich Callies, Theunis Piersma, Sofia Saraiva and David Thieltges for discussion and Jaap van der Meer, Jan Beukema and Peter Herman for providing challenging and valuable comments on the manuscript. Finally, we thank the anonymous reviewer and the non-anonymous reviewer Dr. Martin Thiel for their critical and useful comments.

Supplementary material

10021_2013_9742_MOESM1_ESM.doc (320 kb)
Supplementary material 1 (DOC 320 kb)

References

  1. Andresen H, van der Meer J. 2010. Brown shrimp (Crangon crangon, L.) functional response to density of different sized juvenile bivalves Macoma balthica (L.). J Exp Mar Biol Ecol 390:31–8.CrossRefGoogle Scholar
  2. Asmus H. 1987. Secondary production of an intertidal mussel bed community related to its storage and turnover compartments. Mar Ecol Prog Ser 39:251–66.CrossRefGoogle Scholar
  3. Asmus RM, Asmus H. 1991. Mussel beds: limiting or promoting phytoplankton? J Exp Mar Biol Ecol 148:215–32.CrossRefGoogle Scholar
  4. Bates D, Maechler M, Bolker B. 2012. lme4: Linear mixed-effects models using S4 classes. http://CRAN.R-project.org/package=lme4.
  5. Bayne BL. 1964. Primary and secondary settlement in Mytilus edulis L. (mollusca). J Animal Ecol 33:513.CrossRefGoogle Scholar
  6. Bayne BL. 1976. Marine mussels, their ecology and physiology. Cambridge: Cambridge University Press.Google Scholar
  7. Beukema JJ. 1991. The abundance of shore crabs Carcinus maenas (L.) on a tidal flat in the Wadden Sea after cold and mild winters. J Exp Mar Biol Ecol 153:97–113.CrossRefGoogle Scholar
  8. Beukema JJ. 1992. Dynamics of juvenile shrimp Crangon crangon in a tidal-flat nursery of the Wadden Sea after mild and cold winters. Mar Ecol Prog Ser 83:157–65.CrossRefGoogle Scholar
  9. Beukema JJ, Dekker R. 2005. Decline of recruitment success in cockles and other bivalves in the Wadden Sea: possible role of climate change, predation on postlarvae and fisheries. Mar Ecol Prog Ser 287:149–67.CrossRefGoogle Scholar
  10. Beukema JJ, Essink K, Michaelis H, Zwarts L. 1993. Year-to-year variability in the biomass of macrobenthic animals on tidal flats of the Wadden Sea: how predictable is this food source for birds? J Sea Res 31:319–30.CrossRefGoogle Scholar
  11. Beukema JJ, Dekker R, Essink K, Michaelis H. 2001. Synchronized reproductive success of the main bivalve species in the Wadden Sea: causes and consequences. Mar Ecol Prog Ser 211:143–55.CrossRefGoogle Scholar
  12. Beukema JJ, Dekker R, Philippart CJM. 2010. Long-term variability in bivalve recruitment, mortality, and growth and their contribution to fluctuations in food stocks of shellfish-eating birds. Mar Ecol Prog Ser 414:117–30.CrossRefGoogle Scholar
  13. Bickel PJ, Doksum KA. 1981. An analysis of transformations revisited. J Am Stat Assoc 76:296–311.CrossRefGoogle Scholar
  14. Bivand RS, Rundel C. 2011. rgeos: Interface to Geometry Engine-Open Source (GEOS). http://CRAN.R-project.org/package=rgeos.
  15. Bivand R, Pebesma EJ, Gómez-Rubio V. 2008. Applied spatial data analysis with R. New York: Springer.Google Scholar
  16. Bjørnstad ON, Ims RA, Lambin X. 1999. Spatial population dynamics: analyzing patterns and processes of population synchrony. Trends Ecol Evol 14:427–32.PubMedCrossRefGoogle Scholar
  17. Bolker BM, Brooks ME, Clark CJ, Geange SW, Poulsen JR, Stevens MHH, White JSS. 2009. Generalized linear mixed models: a practical guide for ecology and evolution. Trends Ecol Evol 24:127–35.PubMedCrossRefGoogle Scholar
  18. Brinkman A, Dankers N, Van Stralen M. 2002. An analysis of mussel bed habitats in the Dutch Wadden Sea. Helgoland Mar Res 56:59–75.CrossRefGoogle Scholar
  19. Burnham KP, Anderson DR. 1998. Model selection and inference: a practical information—theoretic approach. New York: Springer.CrossRefGoogle Scholar
  20. Buschbaum C, Dittmann S, Hong J-S, Hwang I-S, Strasser M, Thiel M, Valdivia N, Yoon S-P, Reise K. 2009. Mytilid mussels: global habitat engineers in coastal sediments. Helgoland Mar Res 63:47–58.CrossRefGoogle Scholar
  21. Büttger H, Nehls G, Witte S. 2011. High mortality of Pacific oysters in a cold winter in the North-Frisian Wadden Sea. Helgoland Mar Res 65:525–32.CrossRefGoogle Scholar
  22. Cadée GC, Hegeman J. 2002. Phytoplankton in the Marsdiep at the end of the 20th century; 30 years monitoring biomass, primary production, and Phaeocystis blooms. J Sea Res 48:97–110.CrossRefGoogle Scholar
  23. Caley M, Carr M, Hixon M, Hughes T, Jones G, Menge B. 1996. Recruitment and the local dynamics of open marine populations. Ann Rev Ecol Syst 27:477–500.CrossRefGoogle Scholar
  24. Callaway R. 2003. Long-term effects of imitation polychaete tubes on benthic fauna: they anchor Mytilus edulis (L.) banks. J Exp Mar Biol Ecol 283:115–32.CrossRefGoogle Scholar
  25. Carson HS, López-Duarte PC, Rasmussen L, Wang D, Levin LA. 2010. Reproductive timing alters population connectivity in marine metapopulations. Curr Biol 20:1926–31.PubMedCrossRefGoogle Scholar
  26. de Blok JW, Tan-Maas M. 1977. Function of byssus threads in young postlarval Mytilus. Nature 267:558.CrossRefGoogle Scholar
  27. de Vlas J, Brinkman AG, Buschbaum C, Dankers N, Herlyn M, Kristensen PS, Millat G, Ruth M, Steenbergen J, Wehrmann A. 2005. Intertidal Blue Mussel Beds. Trilateral Monitoring and Assessment Group, Common Wadden Sea Secretariat, Wilhelmshaven, Germany.Google Scholar
  28. de Vooys CGN. 1999. Numbers of larvae and primary plantigrades of the mussel Mytilus edulis in the western Dutch Wadden Sea. J Sea Res 41:189–201.CrossRefGoogle Scholar
  29. Dijkema KS, van Thienen G, van Beek JG. 1989. Habitats of the Netherlands, German and Danish Wadden Sea. Texel: Research Institute for Nature Management, Veth Foundation, Leiden.Google Scholar
  30. Donker JJA, van der Vegt M, Hoekstra P. 2012. Wave forcing over an intertidal mussel bed. J Sea Res 82:54–66.CrossRefGoogle Scholar
  31. Fey F, Dankers N, Steenbergen J, Goudswaard K. 2010. Development and distribution of the non-indigenous Pacific oyster (Crassostrea gigas) in the Dutch Wadden Sea. Aquac Int 18:45–59.CrossRefGoogle Scholar
  32. Getis A. 2009. Spatial Autocorrelation. Handbook of applied spatial analysis, software tools, methods and applications. Heidelberg: Springer. p 255–78.Google Scholar
  33. Gilg M, Hilbish T. 2003. The geography of marine larval dispersal: coupling genetics with fine-scale physical oceanography. Ecology 84:2989–98.CrossRefGoogle Scholar
  34. Gosling EG. 1992a. Ecology of bivalves. In: The mussel Mytilus: ecology, physiology, genetics, and culture. Developments in aquaculture and fisheries science. Amsterdam: Elsevier. pp 44–86.Google Scholar
  35. Gosling EG. 1992b. Reproduction, settlement and recruitment. In: The mussel Mytilus: ecology, physiology, genetics, and culture. Developments in aquaculture and fisheries science. Amsterdam: Elsevier. pp 131–168.Google Scholar
  36. Gutiérrez JL, Jones CG, Strayer DL, Iribarne OO. 2003. Mollusks as ecosystem engineers: the role of shell production in aquatic habitats. Oikos 101:79–90.CrossRefGoogle Scholar
  37. Hammond W, Griffiths CL. 2004. Influence of wave exposure on South African mussel beds and their associated infaunal communities. Mar Biol 144:547–52.CrossRefGoogle Scholar
  38. Herlyn M, Millat G, Petersen B. 2008. Documentation of sites of intertidal blue mussel (Mytilus edulis L.) beds of the lower Saxonian Wadden Sea, southern North Sea (as of 2003) and the role of their structure for spatfall settlement. Helgoland Mar Res 62:177–88.CrossRefGoogle Scholar
  39. Honkoop PJ, van der Meer J. 1998. Experimentally induced effects of water temperature and immersion time on reproductive output of bivalves in the Wadden Sea. J Exp Mar Biol Ecol 220:227–46.CrossRefGoogle Scholar
  40. Kamermans P. 1994. Similarity in food source and timing of feeding in deposit- and suspension-feeding bivalves. Mar Ecol Prog Ser 104:63.CrossRefGoogle Scholar
  41. Keitt TH, Bivand R, Pebesma E, Rowlingson B (2011) rgdal: bindings for the geospatial data abstraction library. http://CRAN.R-project.org/package=rgdal.
  42. Knights AM, Crowe TP, Burnell G. 2006. Mechanisms of larval transport: vertical distribution of bivalve larvae varies with tidal conditions. Mar Ecol Prog Ser 326:167–74.CrossRefGoogle Scholar
  43. Kraft D, Folmer EO, Meyerdirks J, Stiehl T. 2011. Data inventory of the tidal basins in the trilateral Wadden Sea. Leeuwarden: Programma naar een Rijke Waddenzee.Google Scholar
  44. Levin LA. 2006. Recent progress in understanding larval dispersal: new directions and digressions. Integr Comp Biol 46:282–97.PubMedCrossRefGoogle Scholar
  45. McGrath D, King PA, Gosling EM. 1988. Evidence for the direct settlement of Mytilus edulis larvae on adult mussel beds. Mar Ecol Prog Ser 47:103–6.CrossRefGoogle Scholar
  46. McQuaid C, Phillips T. 2000. Limited wind-driven dispersal of intertidal mussel larvae: in situ evidence from the plankton and the spread of the invasive species Mytilus galloprovincialis in South Africa. Mar Ecol Prog Ser 201:211–20.CrossRefGoogle Scholar
  47. Metaxas A, Saunders M. 2009. Quantifying the ‘Bio-’ components in biophysical models of larval transport in marine benthic invertebrates: advances and pitfalls. Biol Bull 216:257–72.PubMedGoogle Scholar
  48. Möller P. 1986. Physical factors and biological interactions regulating infauna in shallow boreal areas. Mar Ecol Prog Ser 30:33–47.CrossRefGoogle Scholar
  49. Murdoch DJ, Chow ED. 1996. A graphical display of large correlation matrices. Am Stat 50:178–80.Google Scholar
  50. Murdoch D, Chow ED. 2012. ellipse: functions for drawing ellipses and ellipse-like confidence regions. http://CRAN.R-project.org/package=ellipse.
  51. Nehls G, Thiel M. 1993. Large-scale distribution patterns of the mussel Mytilus edulis in the Wadden Sea of Schleswig-Holstein: do storms structure the ecosystem? J Sea Res 31:181–7.CrossRefGoogle Scholar
  52. Nehls G, Hertzler I, Scheiffarth G. 1997. Stable mussel Mytilus edulis beds in the Wadden Sea: they’re just for the birds. Helgolander Meeresuntersuchungen 51:361–72.CrossRefGoogle Scholar
  53. Ord JK, Getis A. 1995. Local spatial autocorrelation statistics: distributional issues and an application. Geogr Anal 27:286–306.CrossRefGoogle Scholar
  54. Pebesma EJ, Bivand R. 2005. Classes and methods for spatial data in R. R News 5:9–13.Google Scholar
  55. Philippart CJM, Epping HG. 2010. The Wadden Sea: a coastal ecosystem under continuous change. In: Kennish MJ, Paerl HW, Eds. Coastal lagoons: critical habitats of environmental change. Marine science book series. Boca Raton: Taylor & Francis.Google Scholar
  56. Philippart CJM, van Aken HM, Beukema JJ, Bos OG, Cadée GC, Dekker R. 2003. Climate-related changes in recruitment of the bivalve Macoma balthica. Limnol Oceanogr 48:2171–85.CrossRefGoogle Scholar
  57. Philippart CJM, Amaral A, Asmus R, van Bleijswijk J, Bremner J, Buchholz F, Cabanellas-Reboredo M, Catarino D, Cattrijsse A, Charles F, Comtet T, Cunha A, Deudero S, Duchêne J-C, Fraschetti S, Gentil F, Gittenberger A, Guizien K, Gonçalves JM, Guarnieri G, Hendriks I, Hussel B, Vieira RP, Reijnen BT, Sampaio I, Serrao E, Pinto IS, Thiebaut E, Viard F, Zuur AF. 2012. Spatial synchronies in the seasonal occurrence of larvae of oysters (Crassostrea gigas) and mussels (Mytilus edulis/galloprovincialis) in European coastal waters. Estuar Coast Shelf Sci 108:52–63.CrossRefGoogle Scholar
  58. Pulfrich A. 1996. Attachment and settlement of post-larval mussels (Mytilus edulis L.) in the Schleswig-Holstein Wadden Sea. J Sea Res 36:239–50.CrossRefGoogle Scholar
  59. Ranta E, Kaitala V, Lundberg P. 2006. Ecology of populations. Cambridge: Cambridge University Press.Google Scholar
  60. R Development Core Team. 2009. R: A Language and Environment for Statistical Computing.Google Scholar
  61. Reise K. 2005. Coast of change: habitat loss and transformations in the Wadden Sea. Helgoland Mar Res 59:9–21.CrossRefGoogle Scholar
  62. Reise K, Baptist MJ, Burbridge P, Dankers N, Fischer L, Flemming B, Oost AP. 2010. The Wadden Sea 2010: a universally outstanding tidal wetland. Wilhelmshaven: CWSS.Google Scholar
  63. Ridderinkhof H, Zimmerman JTF, Philippart ME. 1990. Tidal exchange between the North Sea and Dutch Wadden Sea and mixing time scales of the tidal basins. J Sea Res 25:331–50.CrossRefGoogle Scholar
  64. Royama T. 1992. Analytical population dynamics. London: Chapman & Hall.CrossRefGoogle Scholar
  65. Staneva J, Stanev EV, Wolff JO, Badewien TH, Reuter R, Flemming B, Bartholom , Bolding K. 2009. Hydrodynamics and sediment dynamics in the German Bight. A focus on observations and numerical modelling in the East Frisian Wadden Sea. Cont Shelf Res 29:302–19.CrossRefGoogle Scholar
  66. Strasser M, Günther C-P. 2001. Larval supply of predator and prey: temporal mismatch between crabs and bivalves after a severe winter in the Wadden Sea. J Sea Res 46:57–67.CrossRefGoogle Scholar
  67. Strasser M, Reinwald T, Reise K. 2001. Differential effects of the severe winter of 1995/1996 on the intertidal bivalves Mytilus edulis, Cerastoderma edule and Mya arenaria in the Northern Wadden Sea. Helgoland Mar Res 55:190–7.CrossRefGoogle Scholar
  68. Strasser M, Dekker R, Essink K, Günther CP, Jaklin S, Kröncke I, Madsen PB, Michaelis H, Vedel G. 2003. How predictable is high bivalve recruitment in the Wadden Sea after a severe winter? J Sea Res 49:47–57.CrossRefGoogle Scholar
  69. Thorson G. 1950. Reproductive and larval ecology of marine bottom invertebrates. Biol Rev 25:1–45.PubMedCrossRefGoogle Scholar
  70. TMAG—Trilateral Monitoring and Assessment Group. 1997. TMAP manual. The Trilateral Monitoring and Assessment Program (TMAP). Common Wadden Sea Secretariat, Wilhelmshaven, Germany.Google Scholar
  71. Troost K. 2010. Causes and effects of a highly successful marine invasion: case-study of the introduced Pacific oyster Crassostrea gigas in continental NW European estuaries. J Sea Res 64:145–65.CrossRefGoogle Scholar
  72. Turchin P. 2003. Complex population dynamics: a theoretical/empirical synthesis. Princeton, NJ: Princeton University Press.Google Scholar
  73. van Aken HM. 2008. Variability of the water temperature in the western Wadden Sea on tidal to centennial time scales. J Sea Res 60:227–34.CrossRefGoogle Scholar
  74. van Beusekom JEE, Buschbaum C, Reise K. 2012. Wadden Sea tidal basins and the mediating role of the North Sea in ecological processes: scaling up of management? Ocean Coastal Manage 68:69–78.CrossRefGoogle Scholar
  75. van de Koppel J, Rietkerk M, Dankers N, Herman PM. 2005. Scale-dependent feedback and regular spatial patterns in young mussel beds. Am Nat 165:66–77.CrossRefGoogle Scholar
  76. van de Koppel J, Bouma TJ, Herman PMJ. 2012. The influence of local- and landscape-scale processes on spatial self-organization in estuarine ecosystems. J Exp Biol 215:962–7.PubMedCrossRefGoogle Scholar
  77. van der Meer J, Beukema JJ, Dekker R. 2001. Long-term variability in secondary production of an intertidal bivalve population is primarily a matter of recruitment variability. J Animal Ecol 70:159–69.CrossRefGoogle Scholar
  78. van der Veer HW, Feller RJ, Weber A, Witte J. 1998. Importance of predation by crustaceans upon bivalve spat in the intertidal zone of the Dutch Wadden Sea as revealed by immunological assays of gut contents. J Exp Mar Biol Ecol 231:139–57.CrossRefGoogle Scholar
  79. van der Zee E, van der Heide T, Donadi S, Eklöf J, Eriksson B, Olff H, van der Veer H, Piersma T. 2012. Spatially extended habitat modification by intertidal reef-building bivalves has implications for consumer–resource interactions. Ecosystems 15:664–73.CrossRefGoogle Scholar
  80. van Raaphorst W, de Jonge VN. 2004. Reconstruction of the total N and P inputs from the IJsselmeer into the western Wadden Sea between 1935–1998. J Sea Res 51:109–31.CrossRefGoogle Scholar
  81. wa Kangeri AK, Jansen JM, Barkman BR, Donker JJA, Joppe DJ, Dankers NMJA. 2013. Perturbation induced changes in substrate use by the blue mussel, Mytilus edulis, in sedimentary systems. J Sea ResGoogle Scholar
  82. Watson JR, Mitarai S, Siegel DA, Caselle JE, Dong C, McWilliams JC. 2010. Realized and potential larval connectivity in the Southern California Bight. Mar Ecol Progr Ser 401:31–48.CrossRefGoogle Scholar
  83. Wehrmann A, Herlyn M, Bungenstock F, Hertweck G, Millat G. 2000. The distribution gap is closed—first record of naturally settled Pacific oysters (Crassostrea gigas) in the East Frisian Wadden Sea, North Sea. Senckenbergiana Maritima 30:153–60.CrossRefGoogle Scholar
  84. White C, Selkoe KA, Watson J, Siegel DA, Zacherl DC, Toonen RJ. 2010. Ocean currents help explain population genetic structure. Proc R Soc B 277:1685–94.PubMedCentralPubMedCrossRefGoogle Scholar
  85. Wickham H. 2009. ggplot2: elegant graphics for data analysis. New York: Springer. http://had.co.nz/ggplot2/book.
  86. Widdows J, Brinsley M. 2002. Impact of biotic and abiotic processes on sediment dynamics and the consequences to the structure and functioning of the intertidal zone. J Sea Res 48:143–56.CrossRefGoogle Scholar
  87. Young E, Bigg G, Grant A. 1996. A statistical study of environmental influences on bivalve recruitment in the Wash, England. Mar Ecol Prog Ser 143:121–9.CrossRefGoogle Scholar
  88. Young EF, Bigg GR, Grant A, Walker P, Brown J. 1998. A modelling study of environmental influences on bivalve settlement in The Wash, England. Mar Ecol Prog Ser 172:197–214.CrossRefGoogle Scholar

Copyright information

© The Author(s) 2014

Open AccessThis article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.

Authors and Affiliations

  • Eelke O. Folmer
    • 1
  • Jan Drent
    • 1
  • Karin Troost
    • 2
  • Heike Büttger
    • 3
  • Norbert Dankers
    • 4
  • Jeroen Jansen
    • 4
  • Marnix van Stralen
    • 5
  • Gerald Millat
    • 6
  • Marc Herlyn
    • 7
  • Catharina J. M. Philippart
    • 1
  1. 1.Department of Marine EcologyRoyal Netherlands Institute for Sea Research (NIOZ)Den Burg, TexelThe Netherlands
  2. 2.Institute for Marine Resources & Ecosystem StudiesYersekeThe Netherlands
  3. 3.BioConsult SHHusumGermany
  4. 4.Institute for Marine Resources & Ecosystem StudiesTexelThe Netherlands
  5. 5.ScharendijkeThe Netherlands
  6. 6.National Park Administration Wadden Sea Lower SaxonyWilhelmshavenGermany
  7. 7.Niedersächsischer Landesbetrieb für Wasserwirtschaft, Küsten- und NaturschutzNorderneyGermany

Personalised recommendations