Estimating Uncertainty in Ecosystem Budget Calculations

Abstract

Ecosystem nutrient budgets often report values for pools and fluxes without any indication of uncertainty, which makes it difficult to evaluate the significance of findings or make comparisons across systems. We present an example, implemented in Excel, of a Monte Carlo approach to estimating error in calculating the N content of vegetation at the Hubbard Brook Experimental Forest in New Hampshire. The total N content of trees was estimated at 847 kg ha⁻¹ with an uncertainty of 8%, expressed as the standard deviation divided by the mean (the coefficient of variation). The individual sources of uncertainty were as follows: uncertainty in allometric equations (5%), uncertainty in tissue N concentrations (3%), uncertainty due to plot variability (6%, based on a sample of 15 plots of 0.05 ha), and uncertainty due to tree diameter measurement error (0.02%). In addition to allowing estimation of uncertainty in budget estimates, this approach can be used to assess which measurements should be improved to reduce uncertainty in the calculated values. This exercise was possible because the uncertainty in the parameters and equations that we used was made available by previous researchers. It is important to provide the error statistics with regression results if they are to be used in later calculations; archiving the data makes resampling analyses possible for future researchers. When conducted using a Monte Carlo framework, the analysis of uncertainty in complex calculations does not have to be difficult and should be standard practice when constructing ecosystem budgets.

Lack of Error in Ecosystem Budgets

There are many sources of uncertainty in nutrient budgets for forested ecosystems. Some sources of uncertainty are well understood and commonly reported, such as the variability reflected in replicate plots. For systems of small stature, such as grasslands or tundra, ecosystem nutrient stocks can be assessed independently on multiple plots, and reporting the variation across plots is sufficient to describe the uncertainty in the estimates. Forest nutrient budgets, however, require the use of allometric equations to estimate the biomass of tree components. The uncertainty in these equations should be included in estimates of uncertainty in nutrient budgets, along with the uncertainty in nutrient concentrations of tissues and the measurement and sampling error. To our knowledge, the uncertainty in all these components has never been propagated through a calculation of nutrient contents of a forest.

In principle, the uncertainty associated with any calculation can be derived analytically from the reported uncertainty in the components (Taylor 1996; Lo 2005). In practice, however, analytical error propagation is problematic in situations where the calculations are difficult to represent mathematically or the coefficients of variation are high (>30%) (Harmon and others 2007). Gaussian error propagation uses partial derivatives to estimate errors associated with changes in parameters, but the slope is an inaccurate approximation of a non-linear effect especially if the uncertainties are large. Many of the equations used in ecosystem budgets are non-linear. For example, allometric equations for tree biomass are commonly logarithmic (Jenkins and others 2003), and equations that predict tree height from diameter may follow a saturating function (Canham and others 1994). One equation for forest floor mass involves a combination of exponential decay and logistic growth with six parameters (Covington 1981).

Monte Carlo simulation of error is an attractive alternative to analytical solutions. It can be employed to propagate parameter uncertainty in any set of equations. For equations of even moderate complexity, the Monte Carlo approach requires fewer assumptions and is far easier to implement than analytical approaches (Press and others 1986, p. 531). Monte Carlo propagation of uncertainty in tree biomass equations has been applied to tropical (Chave and others 2004), temperate hardwood (Fahey and others 2005), and boreal coniferous forests (Hermle and others 2010); temperate conifer plantations (Sicard and others 2006); and oak woodlands (Harmon and others 2007).

In the environmental sciences, there is a need for better characterization of all aspects of data uncertainties, for example, to better inform policy decisions (Ascough and others 2008). Monte Carlo simulation offers a tractable, flexible, and robust approach. Our goal in this paper is to make the calculation of error less daunting for ecosystem scientists. With data from the Hubbard Brook Experimental Forest in New Hampshire, USA, we provide step-by-step instructions for calculating the uncertainty in the nitrogen content of trees. We use the Monte Carlo approach to incorporate the reported errors of the components into the final estimate. We include measurement uncertainty and inter-plot variation to demonstrate how they should be represented and to allow all these sources of uncertainty to be compared. To minimize technical obstacles, we implement our example in a common spreadsheet format (Excel, http://www.microsoft.com), but note that this type of analysis could be conducted using any of a variety of other environments, such as R (http://www.r-project.org), Matlab (http://www.mathworks.com), or SAS (http://www.sas.com).

The Monte Carlo Approach

The Monte Carlo approach to estimating uncertainty is conceptually straightforward (Press and others 1986). The equations of interest are repeatedly evaluated using parameter values randomly selected from their known (or assumed) probability distributions. The random generation of the parameters should ideally account for any covariance structure in their joint probability distributions. After applying the equations many times, the resulting large number of predictions can be used to define the probability distribution of the propagated error.

Uncertainty in the allometric relationships can be represented in various ways. One approach is to use the variation in the parameter estimates. For example, parameters can be simulated by resampling with replacement the original allometric data (Chernick 2008). Alternatively, estimates can be calculated for each iteration from the variance and covariance matrix of the parameters (Sicard and others 2006). However, neither the data nor the joint probability distributions of the parameters are typically available. Instead, error estimates are often provided for the dependent variables calculated with the biomass equations (Jenkins and others 2003). Thus, an alternative approach is to use these estimates of the model uncertainty (such as the root mean square error of the residual) to perturb the regression line by a randomly sampled amount at each Monte Carlo iteration. In this section, we illustrate the Monte Carlo procedure applied to a single parameter (in the case of N concentration) and to model uncertainty (in the case of height and biomass).

The example we have chosen is estimating error of the N content of aboveground biomass in the northern hardwood forest at Hubbard Brook. This calculation requires, for each tree species, equations relating tree height to diameter (Equation 1), equations relating the biomass of various tissue types to height and diameter (Equation 2), and estimates of tissue N concentration (Equation 3). Specifically,

$$ { \log }\left( H \right) = a + b\,{ \log }\,\left( {\text{DBH}} \right) + \varepsilon_{H} $$

(1)

$$ { \log }\left( {B_{i} } \right) = m + n\,{ \log }\left( {0.5H\pi \left( {{\text{DBH}}/2} \right)^{2} } \right) + \varepsilon_{{B_{i} }} $$

(2)

$$ N_{\text{T}} = \sum\limits_{i} {\left( {B_{i} \left( {N_{i} + \varepsilon_{{N_{i} }} } \right)} \right)} $$

(3)

where H is the tree height; DBH is the tree diameter at breast height (1.37 m); B _i is the biomass of tissue i; N _T is the total N in the tree; N _i is the concentration of N in tissue i; a, b, m, and n are parameters; and ε _H , $\varepsilon_{{B_{i} }}$, and $\varepsilon_{{N_{i} }}$ are residual errors for the height, biomass equations, and the estimates of N concentration of tissue i, respectively. We have estimates of the error associated with the N concentration of the tissues ($\sigma_{{N_{i} }}$) from Likens and Bormann (1970). For the height and biomass equations, Whittaker and others (1974) provided estimates for σ _H and $\sigma_{{B_{i} }}$, rather than the standard deviations of parameters a, b, m, and n; we therefore based the Monte Carlo analysis on the residual error terms ε _H , $\varepsilon_{{B_{i} }}$, and $\varepsilon_{{N_{i} }}$. We assumed that these error terms ε _H , $\varepsilon_{{B_{i} }}$, and $\varepsilon_{{N_{i} }}$ were independent of one another and normally distributed with a zero mean and with standard deviations described under “Advice on Selecting Error Terms”.

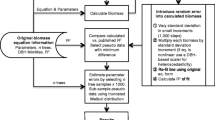
The estimation of the probability distribution of N _T requires generating random values for all the error terms at each iteration of the Monte Carlo (Figure 1). Then the reported diameters for the trees and the parameters associated with the different species and tissue types can be used to calculate a value of N _T using Equations (1)–(3). Repeating the calculation with new random numbers many times makes it possible to accumulate estimates of the mean and variance and other statistics of interest of all previous Monte Carlo estimates of N _T . A sufficient sample size is achieved when the mean and standard deviation settle to acceptably constant values (Figure 2).

Figure 1

Flowchart of the steps in the Monte Carlo calculation of uncertainty in N content of a forest using sample plots and the uncertainty in tree measurement, allometric relationships, and tissue concentrations.

Figure 2

Mean and standard deviation of N content of aboveground vegetation at Hubbard Brook as a function of the number of Monte Carlo iterations. The different lines represent results from five independent Monte Carlo simulations.

A Case Study Implemented in Excel

We implemented the Monte Carlo approach to error estimation of the N content of aboveground biomass at Hubbard Brook Experimental Forest, New Hampshire using Excel (Microsoft Excel 2002 and 2007 and Microsoft Excel X and 2008 for Mac, Microsoft Corporation, Redmond, WA). In addition to the uncertainty in the biomass equations (Equations 1 and 2) and the parameter uncertainty associated with N concentrations (Equation 3), our example includes the measurement precision in tree diameters and the uncertainty associated with sampling plots to characterize the ecosystem.

We randomly selected plots from the network of 0.05-ha plots distributed across the Hubbard Brook Valley (Schwarz and others 2003). We confined our sampling to the plots in the northern hardwood forest type (n = 140). All trees 9.5-cm DBH or greater were measured during 1994–1995 and identified to species (Solomonoff 2007). We used allometric equations constructed from trees sampled at Hubbard Brook in 1965 (Whittaker and others 1974) and tissue chemistry from trees sampled in 1966–1967 (Likens and Bormann 1970). We calculated parabolic volume from the measured DBH and the predicted height (calculated using DBH-height regressions reported in Whittaker and others 1974). We use parabolic volume rather than tree diameter to predict biomass at Hubbard Brook because the relationship of tree height to diameter can vary with elevation (Whittaker and others 1974).

The Excel workbook was organized to keep the parameters (and randomly sampled error terms) describing biomass and nutrient concentrations in separate spreadsheets, organized by tissue type and species. The calculations of tree and stand biomass and nutrient contents were calculated on a spreadsheet that started with the tree inventory data in two columns, giving the species (important as an index variable) and diameter of each tree. This spreadsheet had columns for estimates of biomass by tissue type, more columns for estimated N content by tissue type, columns for the sum of biomass and sum of N content, and hundreds or thousands of rows for the trees. All of these results changed with each iteration of the Monte Carlo. At the bottom of the set of trees representing each plot, we summed the values of the biomass and N content estimates. A single estimate of the ecosystem values was randomly selected based on the mean and standard error of these plots. To document the contribution of the other sources of error to the uncertainty in N content, we used 15 plots. We also used 5, 10, 20, 30, 40, or 60 plots, with all sources of error included, to quantify the effect of sampling intensity on the total uncertainty.

The entire sequence of calculations (Figure 1) is carried out in Excel when any cell is changed. In the Monte Carlo, because of the random number queries, the estimates for each tree and the sums for the plots all change with every update. To accumulate multiple estimates of the ecosystem values requires copying the values into a list of results, which we did in a separate spreadsheet. The error statistics can be computed from any number of rows, and the values compared until the number of iterations is sufficient to give a reproducible result (Figure 2). In this example, 100 iterations were enough to estimate the mean biomass and the standard deviation with an uncertainty of about 1% of the mean.

Uncertainty in the Nitrogen Content of Biomass

Calculated without uncertainty, the N in biomass in mid-elevation hardwoods at Hubbard Brook averaged 847 kg ha⁻¹, based on fifteen 0.05-ha plots. Using the Monte Carlo approach to estimate the uncertainty in tree measurement, allometric equations, N concentrations, and plot variability, we obtained a mean estimate of 869 kg ha⁻¹ with a standard deviation of 66 kg ha⁻¹, or 8% of the mean (Table 1 and Figure 2). The difference between the N content without error and the resampled mean reflects a bias in the resampling procedures (less than 3% in this case). The mean of the Monte Carlo estimates is higher than the mean calculated without error, because of the logarithmic equations for height and biomass.

Table 1 Uncertainty in Estimation of N Content of Trees at Hubbard Brook, Reported as (a) the Coefficient of Variation (the Standard Deviation Divided by the Mean) and (b) kg N/ha of 100 Monte Carlo Iterations

In addition to Monte Carlo calculations that combined all sources of error, we made calculations with each source of error alone. The uncertainty in the height of the trees (Equation 1) contributed 3% uncertainty to the total N budget, expressed as the standard deviation divided by the mean (the coefficient of variation). The uncertainty in the biomass equations (Equation 2) contributed 4% uncertainty. The standard error of the N concentrations in tissues (Equation 3) contributed 3%. Plot variability contributed 6%, with a sample of fifteen 0.05-ha plots. The measurement error of tree diameters contributed only 0.02%. The sum of the individual sources of error, reported in units of coefficient of variation or kg N/ha (Table 1), is much greater than the uncertainty from the Monte Carlo simulations with all errors combined. The variance of a sum is the sum of the variances (Taylor 1996); the sum of standard deviations is not meaningful. In this case, squaring the standard deviations of the errors of individual sources and summing them approximates the square of the standard deviation of the errors of combined sources.

We investigated the effect of sampling intensity on uncertainty by selecting different numbers of plots (Table 1). With only five plots, the uncertainty in N contents of the ecosystem was 15%. With 30–60 plots, it was 7%. Adding more plots cannot reduce the uncertainty below that contributed by the other sources, which was 7%. Plot-sampling error alone was only 3% with 60 plots.

The uncertainties associated with the allometric equations describing tree biomass (Whittaker and others 1974) are quite low; these equations were among the best fit (93rd percentile) of 180 equations compiled by Jenkins and others (2004). Most other allometric equations would contribute more uncertainty to the nutrient content of vegetation than our example shows.

The Monte Carlo analysis can provide information about which of the equations are most important to improve, based on their effect on overall uncertainty (Table 1). This is not the same as the uncertainty in the individual equations, because some equations are more important than others to the final result. For example, although the uncertainty in the equation for bark biomass is higher than that for wood biomass (Whittaker and others 1974), this uncertainty contributes less to the uncertainty in total biomass N, because the wood contains so much more N than the bark. In this data set, branches have both high uncertainty in the biomass equation and high N content, and thus contribute the greatest uncertainty (in kg N/ha) to the overall estimate of N in biomass at Hubbard Brook (Table 1b).

Advice on Selecting Error Terms

Selecting the appropriate component error terms for an uncertainty analysis using Monte Carlo simulation depends on the question being asked (Harmon and others 2007). To describe the variation in the population or the uncertainty in estimates of individuals, the standard deviation is the appropriate term to use. To describe uncertainty in the estimate of the population mean, the standard error of the mean should be used.

The question that we addressed in our example was the uncertainty in the ecosystem total of N in trees, which is the uncertainty in the mean. Therefore, we used the means and standard errors of the N concentrations for the tissues of each species to define the uncertainty in N concentrations (Equation 3). This variation is smaller than the measured variation in tissue concentrations (the standard deviation). This choice is easy to understand in the case of a single parameter.

For a regression equation, uncertainty is described by the variation around the fitted equation. The standard deviation of the dependent variable based on the regression model, $s_{y \cdot x}$, is calculated as

$$ S_{y \cdot x} = \sqrt {{\frac{{\sum {\left( {y_{i} - \hat{y}_{i} } \right)}^{2} }}{n - 2}}} $$

(4)

where y refers to the dependent variable (log₁₀ of tree height or tissue biomass, in our example); y _i is the observed and $\hat{y}_{i}$ is the predicted value of the ith observation, and n is the number of observations used to estimate the regression equation (Snedecor and Cochran 1989, p. 162).

The uncertainty associated with regression predictions also depends on the value of the independent variable x, in our case log₁₀ (DBH). The uncertainty described by the standard deviation of the regression, $S_{y \cdot x}$ (Equation 4), describes the error at the mean value of the observations in the regression data set, $\bar{x}.$ The uncertainty in predicting y increases as values of x depart from this mean. Finally, the uncertainty in the regression prediction also depends on the number of observations in the regression data set, n. For the error terms in Equations (1) and (2), we used the error appropriate to an estimate of the mean of y at a specified value of x, $s_{\text{m}}$ (Snedecor and Cochran 1989, p. 164):

$$ s_{\text{m}} = s_{y \cdot x} \sqrt {{\frac{1}{n}} + {\frac{{(x - \bar{x})^{2} }}{{\sum\nolimits_{i = 1}^{n} {(x_{i} - \bar{x})^{2} } }}}} $$

(5)

The uncertainty in predicting the value of y for an individual from regression, $s_{\text{p}}$, is larger, analogous to the standard deviation compared to the standard error (Snedecor and Cochran 1989, p. 166):

$$ s_{\text{p}} = s_{y \cdot x} \sqrt {1 + {\frac{1}{n}} + {\frac{{(x - \bar{x})^{2} }}{{\sum\nolimits_{i = 1}^{n} {(x_{i} - \bar{x})^{2} } }}}} $$

(6)

The use of Equation (5) or (6) requires the number of observations in the regression, the mean of the x observations, and the sum of squared deviations of the x, $(x_{i} - \bar{x})^{2}$. Because these statistics are not commonly reported, some researchers have chosen to represent the uncertainty in the biomass equations using only the standard deviation of the regression (Equation 4) (Chave and others 2004; Fahey and others 2005). This approach results in an overestimate of the uncertainty in the population mean (Equation 5), but an underestimate of the uncertainty in the individual estimates (Equation 6).

Advice on Applying Error Terms

As a general rule, errors should be generated to simulate the measurement and analytical procedures. In this sense, every Monte Carlo iteration is like a resampling of the study. For example, measurement uncertainty applies independently for each measurement. In our case study, we randomly sampled the measurement uncertainty in DBH for every tree in our sample. The errors are as likely to be positive as negative, and they tend to cancel out. In contrast, at each iteration, we simulated a single set of allometric equations and a single set of N-concentration parameters and applied them to all the trees to estimate N _T.

It is possible to select the right form of error but to apply it incorrectly. A common mistake is to apply parameter uncertainty independently for each observation in the data set. To calculate uncertainty in the ecosystem total, we are interested not in the variation from tree to tree, but in the possible inaccuracy of the equation describing the average tree. For example, consider the equation for the mass of the branches of a sugar maple tree, which has high uncertainty. If this equation is inaccurate, then this error applies equally to every sugar maple tree in the sample. For this reason, we sample the error terms in the table of parameters in Excel, not in the list of trees. Each tree is calculated with the same sample of the error term (or sample of the parameter, in the case of nitrogen concentration), until the next iteration of the Monte Carlo.

The same argument applies when comparing ecosystem totals across multiple plots or sites. It is important to apply the parameter uncertainty simultaneously for all observations at each iteration of the Monte Carlo. Using the same example as before, if Whittaker’s equation is in error about the branches of sugar maple trees, it is equally so for all the trees in the population. This source of error does not contribute as much to the uncertainty in detecting differences between plots or between sites as it does to the uncertainty in the mean.

Our case study illustrates the sampling of multiple plots. We used the same parameters, sampled with error, at each iteration of the Monte Carlo, and at each iteration, we estimated the ecosystem total as a random sample based on the mean and standard error of the plot totals. To compare two sites each with multiple plots (not illustrated in this paper), we would compute the t statistic for the site difference at each iteration of the Monte Carlo, and report the proportion of all iterations with a significant t. To compare more than two sites, the proportion of significant results of analysis of variance would be reported for many iterations. A confidence of 95% in the difference across sites would be indicated if more than 95% of the Monte Carlo iterations produced a significant difference.

Designing a flowchart (Figure 1) can help to plan the sequence of calculations. Using a programming language would make the structure of the calculations more explicit than in Excel. The implementation of a Monte Carlo calculation is not difficult; conceptualizing the approach to take is more challenging.

Sources of Error Not Included in this Example

We assumed, in this illustration, that the error in each of the equations was independent of all the others. This assumption certainly is not always true. For example, in stream water fluxes, some elements are at higher concentrations when water flux is high, while others are diluted at high volumes. Relationships among the parameters could be included in a Monte Carlo simulation, by sampling from a multivariate distribution, if these relationships are known. Correlations among parameters can also be treated mathematically (Taylor 1996).

The propagation of error does not require that the variables be normally distributed. We used a normal distribution of error in this illustration, consistent with the assumptions of Whittaker’s regression models (Whittaker and others 1974). If a distribution is known to be non-normal, then the actual distribution should be used in the random resampling procedure.

There are other sources of errors in measurement, which are not addressed in this approach. We have treated all the errors as random perturbations with mean zero. Systematic errors, which lead to bias, have not been accounted for. For example, we represent minor species using the equations developed for the major species, such as the substitution of sugar maple for red maple (Whittaker and others 1974). Regression equations are commonly used at sites other than those at which they were developed, which introduces uncertainty not described by the uncertainty in the regression model (Harmon and others 2007).

Laboratory procedures are prone to error; there are some values of tissue concentration in the original Hubbard Brook data set (Likens and Bormann 1970), which were not borne out by later measurements (Siccama and others 1994). Analytical uncertainty is often not reported but is usually small compared to variation across samples (in this case, by tree; Likens and Bormann 1970).

Log-transformed equations like the ones we used for estimating height (Equation 1) and biomass (Equation 2) systematically underestimate the values when back transformed (Baskerville 1972). This bias can be corrected using the standard deviation of the regression (Equation 4) and the sample size, which are commonly reported (Sprugel 1983). Jenkins and others (2003) question whether this correction factor is an improvement. The decision regarding the correction factor is important to the accuracy of nutrient budgets, but it does not contribute to the uncertainty analysis.

Conclusions

Ecosystem biomass and nutrient budgets have commonly reported sampling error derived from replicate plots, but few have included in their error analysis the uncertainty in allometric regressions or nutrient concentrations. The variation across sampling plots may be the largest source of uncertainty, as shown in this example from northern hardwoods and in our previous work in this forest type (Fahey and others 2005) and in oak woodlands (Harmon and others 2007). However, estimates of uncertainty that exclude other sources of error are biased, in that the true uncertainty is greater than that reported when only the sampling error is considered.

Propagating parameter and equation uncertainty in ecosystem budgets is not difficult. When the allometric equations we used here were published, the authors wrote, “The problem of confidence limits for treatment of forest samples by logarithmic regression is unsolved” (Whittaker and others 1979). Since that time, advances in computing technology have made it relatively easy to make the necessary calculations on a personal computer, using spreadsheets, computer programs, or specialized software. Designing an appropriate analysis is probably more difficult than implementing it.

We contend that reporting uncertainty in the result of ecosystem calculations should be standard practice. It is important to the audience who will make use of the result; it also has a benefit to researchers who want to know how best to improve an estimate. When making use of results reported by others, we often depend on reported error statistics. In the case of regression equations, we would ideally use not just the standard deviation of the regression, but also the mean and sum of squared deviations of the independent variable (Equation 5 or 6). These can be calculated from archived data, which are also necessary for resampling approaches (Chernick 2008). Providing this information will enable future users to properly evaluate the uncertainty introduced by use of the equations.

Appendices

Appendices

Step-by-Step Implementation in Excel

In each iteration of the Monte Carlo, we accounted for measurement error in the tree DBH measurements (± 0.05 cm, Solomonoff 2007) by randomly generating an error term for the DBH of each tree (Figure 1). Specifically, the error term was a random normal deviate with a mean of zero and σ _d of 0.05 cm. This error was calculated independently for each tree in the inventory. This is the only measured variable in this illustration; the other variables are calculated from previously reported parameters.

The next step of the calculation was to estimate tree height as a function of diameter and species (Equation 1). The tree species was used as an index variable to look up the parameters a and b. The error term for the DBH-height equation, ε _Hi , was simulated as a random normal deviate with a mean of zero and σ _Η. In this implementation, σ _Ηι was based on the reported error of the regression (Whittaker and others 1974) corrected for the sample size and the deviation of each tree from the mean tree in Whittaker’s sample (Equation 5).

Unlike the error in tree diameter, which was independently estimated for each tree, ε _Hi was used for all trees of a given species in the data set for each iteration of the Monte Carlo. An error in the height equation affects all the trees simultaneously, whereas an error in diameter measurement pertains to a single tree. In the Excel implementation, this means that the parameter and equation errors must be included in the lookup tables, so that for each iteration of the ecosystem calculation, the same random sample of each error is used.

Next, the height of each tree was used to calculate its parabolic volume. The geometric formula for parabolic volume, 0.5 Hπ(DBH/2)², was evaluated without additional error terms.

To calculate the biomass of tree tissues as a function of parabolic volume (Equation 2), we used tree species to index the parameter values in a lookup table and error terms (ε _Bi ) generated as random normal deviates with a mean of zero and standard deviation σ _βι . Similar to tree height, σ _βι was calculated from the reported error of the regression estimate (Whittaker and others 1974; Equation 5). Then the N content of each tissue type (Equation 3) was calculated from this biomass and the N concentration for each species and tissue type, which was obtained from a final lookup table. Uncertainty in N concentration was included as a random normal deviate with a mean of zero and σ _Νι defined by the reported standard error of the replicate tissue samples (Likens and Bormann 1970).

For each of the plots in the sample of the ecosystem, the mass and nutrient contents by tissue for all the trees in each plot were summed, with no error added by summing. The mean and standard error of these plots were used to randomly generate a single estimate of the ecosystem values, and the results were accumulated in another spreadsheet in which each line represented one iteration of the Monte Carlo simulation.

The Excel workbook with our data and the Monte Carlo results are available at http://www.esf.edu/for/yanai/Uncertainty/Yanai_Ecosystem_Error.xls.

Random number generation

The random number generator in Excel, RAND(), returns a number between 0 and 1 with even distribution. To generate the normal random error estimates, we used NORMINV(RAND(), mean, standard deviation), with the mean and standard deviation referencing cells with those values.

Lookup Tables in Excel

It is important that each iteration of the Monte Carlo apply the same error estimates for equations 1, 2, and 3 to all the trees in the data set. For this reason, the random generation of errors cannot be contained in the equations that are repeated in each line of the stand inventory (calculating height or biomass from DBH, for example). If the error terms are generated in a parameter table, they will change with each new calculation (iteration) but they will be constant across all the trees in the inventory.

We used the VLOOKUP function in Excel to reference the parameters and the error terms in the biomass equations and nutrient concentrations. In our example, the parameters for height, biomass, and nutrient concentration are each a table, with tree species as the index variable. VLOOKUP requires three arguments. The first gives the index variable (the species of the tree). The second gives the location of the table. The third specifies in which column of the table you want to look up a value. Note that the index variable must be in alphabetical order.

Tricks and Tools in Excel

The results of each iteration of the Monte Carlo are copied and pasted (Edit, Paste Special, Values) into a list of results where they will not be updated with the next iteration. This process goes more quickly if you add the “Paste Values” button to your toolbar. Depending on your version, you might find this under: Tools, Customize, Commands, Edit, Paste Values. Or the sequence of menu selections may be: View, Customize Toolbars and Menus. You can also create a keyboard shortcut for this operation.

By default, Excel automatically recalculates the value of every formula when any cell is changed. This can take some time for thousands of trees. When modifying a spreadsheet, you can turn this feature off, in Excel Preferences, Calculations, Manually. There is a keyboard shortcut to “calculate now.” When running the Monte Carlo simulations, you will need to turn the automatic calculation back on.

We made many mistakes while building our Monte Carlo spreadsheets. As always, it helps to test the parts before assembling the whole. The uncertainty in biomass and nutrient concentrations can be implemented for a single tree, and the sampled variance can be compared to the expected variance. A spreadsheet that has only one tree calculated many times with random error each time can be useful for trouble-shooting. Graphing the relationships represented by the component equations can help to reveal unexpected problems.

You may find it useful to graph your outputs as a function of the number of iterations (Figure 2). Doing so for multiple independent Monte Carlo runs allows you to visualize the rate of diminishing uncertainty in your estimate of uncertainty.