Abstract
Soil erosion negatively affects crop yields and may have contributed to the collapse of ancient civilizations. Whether erosion may have such an impact on modern societies as well, is subject to debate. In this paper we quantify the relationship between crop yields and soil water available to plants, the most important yield-determining factor affected by erosion, at the European scale. Using information on the spatial distribution of erosion rates we calculate the potential threat of erosion-induced productivity losses. We show that future reductions in productivity in Europe as a whole are relatively small and do not pose a substantial threat to crop production within the coming century. However, within Europe there is considerable variability, and although productivity in northern Europe is not likely to be significantly reduced by soil erosion, for the southern countries the threat of erosion-induced productivity declines is stronger.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
There is little doubt that soil erosion has a detrimental effect on global soil resources. The depletion of the soil has led to major instability and undoubtedly contributed to the collapse of relatively advanced societies in the past, such as the isolated civilizations of Easter Island and Iceland (Diamond 2004). Societies on large landmasses were probably also affected by soil degradation. Evidence suggests that the fall of the Mayan civilization was related to problems of soil erosion (Jacob and Hallmark 1996), whereas in ancient China soil degradation was found to be one of the decisive factors leading to the relocation of population centres (Duan and others 1998). Archaeological evidence also points to severe soil erosion in Greece during ancient Greek times (Vanandel and others 1990), which may have contributed significantly to the collapse of Greek civilization (Runnels 1995).
Soil erosion continues to have detrimental effects on global soil resources. Some claim that during the last 40 years nearly one-third of the world’s arable land has been lost through erosion and continues to be lost at a rate of more than ten million hectares per year (Pimentel and others 1995). A recent study by Wilkinson and McElroy (2007) estimates that soil loss from global farmlands is currently running at a rate of more than 6 t ha−1 y−1, which is more than 15 times the estimated average rate of erosion (0.42 t ha−1 y−1) during the whole Phanerozoic Era, a period of 542 million years spanning the Lower Cambrian to the Tertiary Pliocene. Current land abandonment in some parts of Europe has probably been driven by soil erosion (Bakker and others 2005a), whereby abandoned areas have reverted to unproductive scrubland. It seems likely that modern societies and landscapes are threatened by the loss of crop yields and subsequent land abandonment if soil erosion continues to degrade soil resources.
Although the problem has received much attention recently (Conway and Toenniessen 1999; Tilman and others 2002; McNeill and Winiwarter 2004), there is no quantitative information about the effects of past or future erosion on agricultural productivity at either the regional or national level (Trimble and Crosson 2000; Yaalon and Arnold 2000). Despite claims that during the past 50 years soil loss by erosion has been a serious problem, the current and potential future consequences of this loss are not known. Inferences made from the synchronicity of soil erosion events and societal changes are not based on quantitative assessments of the impact of soil erosion on agricultural productivity. Likewise, the analogy between the collapse of ancient societies and the risks facing modern society is based on assumptions that have not been tested. Hence, the extent to which soil erosion is indeed a significant threat to the agricultural productivity of modern societies remains a subject for debate (Crosson 1997).
Soil erosion has a detrimental effect on soil quality for agricultural production because erosion degrades soil functions for crop growth such as the supply of water, nutrients and rooting space. These effects have been demonstrated through numerous experiments conducted on plots where erosion was either simulated by artificial desurfacing (Mbagwu and others 1984; Dormaar and others 1986; Gollany and others 1992; Malhi and others 1994; Tanaka 1995; Larney and others 2000), or by comparing yield on strongly eroded areas with yield on less eroded areas (Bramble-Brodahl and others 1984; Busacca and others 1984; White and others 1984; Mielke and Schepers 1986; Olson and Carmer 1990; Kosmas and others 2001). The reported results, however, show a wide variability and a systematic overestimation of the effects due to the use of flawed methodologies may explain a large part of the research results (Bakker and others 2004). Nevertheless, systematic analysis of the available data allowed some general conclusions to be drawn: under intense, mechanized agriculture, yield reductions at the field scale are of the order of 4% for each 0.1 m of soil loss. This finding applies to European and North American studies, where yield reductions could generally be attributed to a reduction in rooting depth and/or plant available water (for example, Olson and others 1999; Bakker and others 2004).
The results of such field experiments cannot directly be extrapolated to a regional or national level. The effects of erosion on crop productivity may vary per agro-ecological zone and the effects may also depend on the scale level studied. Within larger spatial units, compensatory effects may occur: regional productivity may be maintained by the simple reallocation of arable land to less erosion-prone areas with arable areas becoming permanent grassland or forest (Bakker and others 2005a). Furthermore, inclusion of depositional areas within the spatial unit studied may offset the negative effect of erosion upslope, as deposition may improve soil properties and productivity may increase.
As the extrapolation of field results to the regional scale is questionable, it is appropriate to explore other approaches to assess the relationship between erosion and crop productivity. If a relationship between crop productivity and soil properties affected by erosion could be established directly at the regional scale and if data on the spatial distribution of soil erosion were available, it would be possible to assess the effect of soil erosion on crop productivity at the regional scale.
In this paper we attempt to quantify the effects of erosion on the future evolution of agricultural productivity in Europe, based on quantitative information on: (1) the relationship between crop productivity and soil depth and soil water availability; (2) the effect of erosion on soil depth and soil water availability; and (3) information on the spatial distribution of soil erosion.
Methods
Data
Soft wheat (Triticum aestivum L.) was chosen as an indicator crop. Wheat is widely cultivated over a broad range of climatic conditions and its susceptibility to erosion is representative of many other common crops with similar rooting depths and water requirements. Annual yield data were derived for Germany, France and Greece from national statistical offices at the NUTS3 level (Nomenclature of Territorial Units for Statistics level 3). This provided a total of 300 observations. These data were averaged over the period 1991–2000.
In the intensively cultivated agro-ecosystems of Europe, it is reasonable to assume that fertilizer applications compensate for erosion-induced nutrient shortages and so, nutrients are not important in controlling crop productivity. Previous research has shown that under these conditions rooting space and water availability are the main soil-related limiting factors for crop yields (for example, Olson and others 1999; Bakker and others 2004). We combined available rooting space and water availability into a single variable, the total Soil Water Available to Plants (SWAP) that is assumed to be the most important variable controlling the effect of erosion on crop yields. SWAP is analogous to the available water capacity (AWC) defined by Salter and Williams (1965) as the volume of water held between wilting point and field capacity. SWAP was originally defined by Thomasson (1979) and is calculated as the product of soil depth and volumetric water content for that depth, integrated down to the normal rooting depth of a specified crop. In the case of wheat growth in Europe, the maximum rooting depth is considered to be 1.20 m (Thomasson 1979). In principle, SWAP is the quantity of water (mm) held between field capacity (5 kPa) and the permanent wilting point (1,500 kPa), which for a soil growing cereals is the sum of two components: the water held at low suctions 5–200 kPa between 0 and 1.2 m depth and the water held at higher suctions 200–1,500 kPa between 0 and 0.5 m depth (Jones and others 2000). The assumption here is that cereal crops with a short growing season have limited opportunity to exploit fully the available water between field capacity and wilting point at depths below 0.5 m because only a small proportion of the root system extends below 0.5 m depth (Thomasson 1979). In the case of shallow soils, the integration of available water with depth is terminated at a barrier to rooting such as a layer of rock if this is shallower than 1.2 m. The SWAP data used in this study were derived from the European Soil Database (King and others 1994, 1995). These data were interpolated to 1 km × 1 km grid for use by the Pan European Soil Erosion Risk Assessment project (PESERA; Kirkby and others 2004).
The soil erosion data were derived from the PESERA model (run at the 1 km resolution, in October 2003, for the whole of Europe). The PESERA model is a spatially distributed process-based water erosion model that was specifically developed to be applicable at the regional scale using information on topography, land cover and climate that is available at that scale (Kirkby and others 2004). Initial validation of PESERA has shown that the model is able to reproduce the observed spatial variations in erosion rates within Europe rather well, although predictions for individual grid cells or small catchments may show considerable deviations (Van Rompaey and others 2003a, b). It is important to note that PESERA only predicts water erosion by rill and inter-rill, whereas other forms of erosion, caused by wind and tillage are not simulated even though these may be important. However, wind erosion is limited to certain areas within Europe and average wind erosion rates are relatively low. Tillage erosion is more widespread and is often more important than water erosion at the field scale, but it generally leads to soil redistribution within the field rather than significant soil export from the field.
Deriving the SWAP-Yield Relationship
An important complication when assessing the effects of (erosion-induced) reductions in SWAP on crop yields is that SWAP is, at the regional scale, correlated with climate and economic variables that also affect yields. Finding a strong correlation between SWAP and yields may lead to a false conclusion that this relationship is causal. In practice, it may be a climatic variable such as potential evapo-transpiration that is causally related to productivity and at the same time correlated to SWAP, because in Europe high evapo-transpiration rates occur in semi-arid areas that generally have slow soil-formation rates and therefore thin soils (Selby 1991). Likewise, economic variables show a similar trend to SWAP along a north–south axis across Europe, for which a number of explanations may exist. Therefore, we need to assess the true relationship between SWAP and yields, that is, the pseudo-isolated effect of SWAP (Cook 1998; Morrison 2000), controlled for important climate and economic variables.
The following additional data were also collected: annual rainfall and mean annual temperature over the period 1991–2000 from the Advanced Terrestrial Ecosystem Analysis and Modelling (ATEAM) project database (an EU-funded project, contract No: EVK2-2000-00075, http://www.pik-potsdam.de/ateam/ateam.html); annual incoming global radiation was calculated from the empirical formula of Linacre (1969) using only latitude as input, and; potential evapo-transpiration was calculated from temperature and incoming global radiation using the empirical relationship of Jensen and Haise (1963). These data were aggregated to the NUTS3 level. National and local Gross Domestic Products (GDP) were derived from the EUROSTAT database at the NUTS3 level (local GDP) and at the country level (national GDP) (http://www.ec.europa.eu/eurostat).
Interactions with economic and climatic variables, as well as controlling for confounding variables, were also taken into account. Both confounding and interaction involve the assessment of an association between two or more variables (that is, the regression coefficient) so that any additional variables affecting this association are accounted for (Kleinbaum and others 1998).
Thus, with respect to confounding and interaction, the following hypotheses were tested:
-
(1)
The regression coefficient of SWAP depends on the values of annual rainfall, potential annual evapo-transpiration and input level (local GDP): when rainfall and input levels are high, the coefficient is small, that is, the relationship is less strong. When potential evapo-transpiration is high, the coefficient is large, that is, the relationship is strong. Hence, interaction is hypothesized to occur between SWAP and rainfall, potential evapo-transpiration and local GDP.
-
(2)
The regression coefficient of SWAP is confounded by mean annual temperature, net incoming solar radiation and national GDP (that is, these factors affect yields in a similar way to SWAP). To assess the proper coefficient of SWAP, these variables should be controlled.
Furthermore, the effect of SWAP may be non-linear. As observed in many experiments on the productivity response to erosion, reductions that are caused by restrictions in soil depth and/or water availability tend to become more severe with incremental soil loss (Bakker and others 2004). Conversely, when SWAP increases beyond the crop’s water requirements, the effect is expected to be weak or even absent. Therefore, the effect is expected to become stronger with lower SWAP values, and weaker with higher SWAP values.
Interaction was assessed, prior to confounding, by examining the added value of an interaction term (that is, the product of the interacting variables) to the model fit. Only interactions that had significant added value at the 95% probability-interval were taken into account. Variables for which the hypothesis of interaction was rejected were also tested for confounding.
Confounding was assessed by comparing the regression coefficient of SWAP on yields when only SWAP was in the model, with the regression coefficient of SWAP when radiation, temperature and national GDP were included. There are no statistical tests to assess confounding and a judgment needs to be made about whether or not the difference is considered to be negligible or not (Kleinbaum and others 1998). We considered, therefore, changes in the regression coefficient of SWAP of more than 5%, following the addition of another variable, to be large enough to consider the added variable as a confounder. The non-linearity of SWAP was evaluated by testing the significance (P < 0.05) of a squared SWAP term, next to SWAP.
Spatially Explicit Projection of Erosion-Induced Yield Losses 100 Years from Now
When assessing the effect of erosion-induced reductions in SWAP on future productivity, consideration should be given to the role of technological innovation. We know that in the past yields have increased strongly as a result of advances in technology (Ewert and others 2005, 2007), but whether or not this trend will continue in the future is uncertain (Ewert and others 2005; Rounsevell and others 2005, 2006). Some scientists claim that trends will continue to boost yield growth at similar rates to those of the past (Ewert and others 2007), whereas others conclude that yield increases will slow due to biophysical constraints on plant productivity (Kindal and Pimentel 1994; Amthor 1998; Hafner 2003). As the role of technology in the future is uncertain, two extreme scenarios were explored in this paper to capture the range of uncertainties. The first scenario assumed that increases in yields will continue at the same rate as now, that is, a linear extrapolation of current trends into the future. Current trends were assumed to be an annual increase of 1% of the yield (see Bakker and others 2005b). The second scenario assumed that yields have peaked and that no more increase will occur. Both scenarios are unlikely, but they indicate the widest range of possible outcomes. A third scenario, the United Nations Environmental Programme scenario, assumed a continued increase in productivity until 2025 (that is, a linear extrapolation of current trends) and after that a decrease in yield increase rate to about 87% of the current value (UNEP 1997).
For Austria, the Netherlands, Belgium, Luxembourg, Denmark, Ireland, Spain, Portugal and Italy, yield data were not available. For these countries, yields were estimated using a regression model that was based on SWAP, potential evapo-transpiration, mean annual temperature and local and national GDP data (see Bakker and others 2005b for details).
Using the PESERA erosion rates, a map was created of the relative wheat yield reductions in 100 years from now. First, PESERA erosion rates (available at the 1 km2 scale) were aggregated to the NUTS3 level, whereby only erosion on arable land [that is, non-irrigated arable land, irrigated arable land and permanent crops according to the CORINE2000 classification (EEA 2004)] was considered, resulting in average erosion rates in t ha−1 y−1 on arable land per NUTS3 region. To convert these erosion rates into reductions of SWAP, we assumed an average dry bulk density of 1,300 kg m−3 for topsoil and an average volumetric water content of 150 mm m−1 (for silty soils this value is higher, whereas for sandy and clayey soils it is lower). This implies that 1 t ha−1 of erosion equals a loss in soil depth of approximately 7.7 × 10−2 mm and a SWAP loss of 1.16 × 10−2 mm. The resulting erosion-induced SWAP losses were multiplied by the regression coefficient to obtain yield loss. The yield loss was expressed as a fraction of the future yield.
Results
General Statistics
Table 1 summarizes the general statistics for all variables in the dataset containing the NUTS3 units of France, Germany and Greece. Average yields per NUTS3 unit vary from 1.43 t ha−1 y−1 in Greece to more than 9 t ha−1 y−1 in northern Germany. Soil erosion rates range from almost nothing to nearly 18 t ha−1 y−1. The climatic gradient is strong, as are the differences in the economic environment. For a more detailed description of these variables see Bakker and others (2005b).
Assessing the Effect of SWAP on Wheat Yields
The initial regression equation with only SWAP as the independent variable has a regression coefficient of 4.71 × 10−2 (Table 2), meaning that yields differ on average by 4.71 × 10−2 t ha−1 y−1 between areas that show 1 mm difference in SWAP. The quadratic term has a significant, negative coefficient when included in the model, meaning that the effect of SWAP on yields grows stronger as SWAP declines, which is to be expected.
Of the interaction terms, only the product of local GDP with SWAP is significant next to SWAP, meaning that the effect of SWAP reductions is less important in regions with a higher local GDP. The quadratic term of SWAP is no longer significant when the interaction term is included, and is therefore removed. Including rainfall in the regression does not affect the regression coefficient(s) of SWAP or the interaction term, so the hypothesis that rainfall confounds with SWAP can be rejected, and rainfall is left out of the regression. When potential evapotranspiration was included in the model the SWAP regression coefficient was 2.69 × 10−2. As this is more than a 5% change, potential evapo-transpiration is considered to be an important confounder. The interaction term of SWAP with local GDP becomes non-significant when potential evapotranspiration is introduced, and was therefore removed from the regression.
When solar radiation is included in the model, the coefficient of SWAP becomes even smaller (2.24 × 10−2), but adding solar radiation makes potential evapotranspiration redundant (non-significant and uncertain parameter estimate). Thus, solar radiation, rather than potential evapotranspiration, is considered to be the confounder. Potential evapotranspiration is therefore excluded from the equation.
Mean annual temperature, next to solar radiation, did not affect the regression coefficient of SWAP. Adding national GDP changes the regression coefficient of SWAP slightly, from 2.24 × 10−2 to 2.08 × 10−2, which is nevertheless more than a 5% change, so the hypothesis that national GDP confounds with SWAP is accepted. The quadratic term of SWAP as well as the interaction term with local GDP remained insignificant.
The final coefficient of SWAP is thus estimated at 2.08 × 10−2, which is the adjusted estimate when correcting for the effect of national GDP and solar radiation on yields.
Comparison with Field Data
The observed regression coefficient of SWAP derived at the NUTS3 level can now be used to calculate yield losses in response to SWAP reductions by erosion. If we assume that an average soil has a plant-available volumetric water content of about 150 mm m−1, then a soil loss of 0.1 m would correspond to a SWAP reduction of 15 mm. The estimated regression coefficient of 2.08 × 10−2 for SWAP implies that a soil loss of 0.1 m would result in a yield loss of 0.31 t (0.1 m equals 15 mm, times 2.08 × 10−2 t mm−1 = 0.31 t). If we compare this reduction to the average yield of 6.31 t ha−1 y−1(Table 1) we arrive at a relative loss of 4.9%, which is close to the average yield loss of 4.3% per 0.1 m of soil loss from a regression analysis of the field data collected using the ‘comparing plots’ method (Bakker and others 2004).
Some comparisons with individual experiments can also be made. Mokma and Sietz (1992) found yield differences of 17.8% when comparing a soil of 0.92 m depth to a soil of 0.56 m depth in south-central Michigan. Assuming a plant available volumetric water content of 150 mm m−1, the two soils correspond to SWAP values of 138 and 84 mm, respectively. The regression coefficient derived here translates this into a reduction of 1.1 t ha−1, which equals a loss of 16% relative to an assumed yield of 7 t ha−1 y−1 for the 0.92 m soil. Likewise, Schumacher and others (1994) found yield reductions of 7% when comparing a 0.75-m depth soil to a 0.59-m depth soil in the north-central United States. Assuming again volumetric water content of 150 mm m−1, the two soils have SWAP values of 113 and 89 mm, respectively. The regression coefficient derived in this research translates this in a reduction of 0.5 t ha−1 y−1, which equals a loss of 8% relative to an assumed productivity of 6 t ha−1 y−1 for a 0.75 m depth soil. To investigate the effect of very severe erosion, Schumacher and others (1994) compared a 0.69 m depth soil with a 0.20 m depth soil, for which they found a 26% yield difference. Assuming a SWAP of respectively 103 and 35 mm, we find a yield difference of 1.4 t ha−1 y−1, which equals a reduction of 25% relative to an assumed productivity of 5.5 t ha−1 y−1 for a 0.69 m soil.
Spatially Explicit Projection of Erosion-Induced Yield Reductions 100 Years from Now
The obtained regression coefficient can be used to assess the effect of erosion on future yields in Europe. In Table 3 the effect of erosion on yields in the future is shown for three different European agro-ecosystems, ranging from highly productive agriculture with relatively low erosion rates to the marginal systems with low productivity and high erosion rates assuming the three scenarios described above (continuing trends, ceasing trends and the UNEP scenario). For the three scenarios and the three agro-ecosystems, yields were calculated with and without erosion. The percentages shown are the difference in yields between the erosion and the non-erosion variant, proportional to the yield of the non-erosion variant.
In the intensive, low erosion agro-ecosystems the impact of erosion is small, but it increases with smaller yields, smaller trends in yields and increasing erosion rates. Yield reductions are maximum 12% and this value is only reached for a marginal agricultural system.
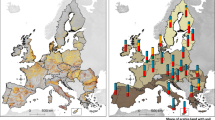
In Figure 1, the projected relative productivity losses after 100 years are shown for the countries studied, based on the UNEP scenario. For large parts of Northern Europe the effect of erosion on productivity is negligible, whereas in southern Europe the effect of erosion is clearly manifest. In Greece, erosion-induced yield reductions sometimes exceed 15%, which is partly attributable to the high erosion rates and partly to the low yields. Absolute yield losses after 100 years incidentally exceed 0.5 t ha−1 y−1 in France (Pyrenees-Atlantiques), Italy (Sondrio, Perugia) and Portugal (Pinhal Interior Sul).
In Figure 2 the projected relative productivity losses after 100 years are depicted per country, based on the UNEP scenario. Greece has the highest foreseen reduction of up to 3.8%, followed by Portugal (3.1%), Spain (2.4%) and Italy (2.4%).
Analysis
A statistical analysis shows that the impact of SWAP on yields confounds with the impacts of climate and economic variables. The non-linearity of the impact of SWAP on yields was obscured when confounding variables were entered into the regression. Correcting for this confounding has resulted in an impact of SWAP on yield equal to a 20.8 kg ha−1 y−1 difference between units that differ 1 mm in SWAP. If this relationship is projected along moderate yield increases, erosion-induced yield losses in Europe will amount to a few percentage points in the coming century. Effects of erosion-induced losses in soil nutrients were not taken into account, but in the case of Europe the application of fertilizers is likely to compensate for any loss in intrinsic soil fertility. This may not be the case in other parts of the world, so the results presented here cannot be extrapolated outside of Europe.
The erosion-induced yield reductions found here are of a similar magnitude to those derived at the plot-scale suggesting that the hypothesized scale effects may be absent. This implies that: (1) the reallocation of land use within NUTS3-units to avoid erosion prone areas or to abandon strongly eroded areas rarely happens (due to regulations, lack of farmers’ perception of the problem of erosion, or due to a lack of available land); and/or (2) that the possible positive effects of deposition are unable to offset the negative effects of erosion. Consequently, for these two reasons erosion impacts directly on agricultural productivity.
Where compensation does occur, that is, down slope areas profiting from water and sediment supply from upslope areas, then the in-situ effects of erosion on productivity must be larger than the 20.8 kg ha−1 y−1 per 1 mm SWAP loss.
The results shown in Table 3 and Figures 1 and 2 indicate that erosion will not have a strong impact on productivity in highly productive agro-ecosystems. Erosion rates here are generally low, and the erosion induced SWAP reductions result in yield reductions that are very small compared to the overall production. In more marginal agro-ecosystems, however, the impact of erosion induced SWAP reductions on productivity can be important. In southern Europe, due to both severe erosion in ancient times and slow soil formation rates (typical for Mediterranean climates, because of low rainfall and quick mineralization of carbon), soils are stony and shallow and wheat yields are low. Here, erosion-induced reductions from 6 to 12% are projected to occur in the next 100 years, depending on the contribution of technological innovations to productivity increases. At the national level (Figure 2) agricultural productivity in Greece in 100 years from now is likely to be reduced by approximately 3.5% as a result of soil erosion. Also in Portugal, Italy and Spain, reductions are considerable, provided that erosion rates on agricultural land in these countries are as high as the PESERA model predicts.
Despite these regional differences, the hypothesis that erosion poses a serious threat to Europe’s agricultural production is not likely to be correct under current land use and current erosion rates. Development of artificial fertilizers on the one hand, and the strong increasing trends of yields are likely to have made modern agriculture less sensitive to the harmful effects of erosion, compared to agriculture in ancient civilizations as those mentioned in the introduction. It should nevertheless also be taken into account that the time scale used in this study is relatively short. We show that the agricultural productivity of Europe is not directly threatened in the next 100 years, but the lifespan of a civilization far exceeds this time period. Although the effects identified are relatively minor over 100 years, they can be of major importance at the millennial time scale.
Conclusion
Although erosion may have threatened food supplies in the past, it appears that for Europe technological innovations make agricultural productivity more resistant to the detrimental impacts of soil loss. From the quantitative relationships presented in this paper we conclude that crop yields in Europe are unlikely to be significantly reduced by current levels of soil erosion within the coming century. There is nevertheless considerable spatial variability in the effect of erosion. For the Mediterranean area the threat of erosion-induced yield reductions is stronger than it is for Northern Europe. Greece is likely to suffer the largest reductions, followed by Portugal, Italy, Spain and the south of France. Furthermore, the observed yield reductions due to reductions in SWAP appear to be consistent across scales, which implies that soft wheat is not reallocated to more favorable areas to maintain productivity.
These conclusions hold for (1) Europe, albeit more for the temperate zone than for the semi-arid zone; for (2) current erosion rates and for (3) current agricultural land use. In regions where nutrients are a potentially limiting factor, such as parts of Sub Saharan Africa, impacts of erosion may be much larger. If erosion rates accelerate, for example, due to climatic change, yield reductions may become stronger. If agriculture were to expand to more marginal areas, yield reductions would also become stronger.
The fact that erosion is no direct threat to agricultural productivity does not imply that it should not be controlled, as the harmful effects of soil erosion on the environment should not be ignored. Increasing production inputs to compensate for nutrient losses arising from erosion has negative effects on the sustainability of agricultural practices. This includes the increasing costs and carbon emissions of fertilizer manufacture and the offsite effects of fertilizer, pesticide, and herbicide runoff on the fragile ecological balances of many terrestrial and aquatic ecosystems. The focus of future discussions on the impacts of erosion should therefore include the complex relationships between agricultural needs, productivity, and the ecological and social impacts rather than productivity alone.
References
Amthor JS. 1998. Perspective on the relative insignificance of increasing atmospheric CO2 concentration to crop yield. Field Crops Res 58:109–127
Bakker MM, Govers G, Rounsevell MDA. 2004. The crop productivity–erosion relationship: an analysis based on experimental work. Catena 57:55–76
Bakker MM, Govers G, Kosmas C, Vanacker V, Van Oost K, Rounsevell MDA. 2005a. Soil erosion as a driver of land-use change. Agric Ecosyst Environ 105:467–481
Bakker MM, Govers G, Ewert F, Rounsevell M, Jones R. 2005b. Wheat variability as a function of climate, soil and economic variables along a climatic gradient. Agric Ecosyst Environ 110:195–209
Bramble-Brodahl M, Fosberg MA, Walker DJ, Falen AL. 1984. Changes in soil productivity related to changing topsoil depth on two Idaho Palouse soils. Erosion and soil productivity. American society of Agricultural engineers, New Orleans, Louisiana
Busacca AJ, McCool DK, Papendick RI, Young DL. 1984. Dynamic impacts of erosion processes on productivity of soils in the Palouse. In: American society of Agricultural engineers, Eds. Erosion and soil productivity. New Orleans, Louisiana, pp 152–69
Conway G, Toenniessen G. 1999. Feeding the world in the twenty-first century. Nature 402:C55–C58
Cook ML. 1998. Property rights constraints in collective action: the case of US Agriculture Producer Groups (draft). In: 2nd Conference of the International Society of New Institutional Economics
Crosson PR. 1997. Will erosion threaten agricultural productivity? Environment 39:4–9, 29–31
Diamond J. 2004. The enigmas of Easter Island by Flenley J, Bahn P. New York review of books. New York Review, New York
Dormaar JF, Lindwall CW, Kozub GC. 1986. Restoring productivity to an artificially eroded dark brown chernozemic soil under dryland conditions. Can J Soil Sci 66:273–285
Duan CQ, Gan XC, Wang J, Chien PK. 1998. Relocation of civilization centers in ancient China: environmental factors. AMBIO 27:572–575
EEA. 2004. Corine land cover 2000. European Environmental Agency, Copenhagen
Ewert F, Porter JR, Rounsevell M. 2007. Crop models, CO2, and climate change. Science 315:459–460
Ewert F, Rounsevell MDA, Reginster I, Metzger M, Leemans R. 2005. Future scenarios of European agricultural land use. I: estimating changes in crop productivity. Agric Ecosyst Environ 107:101–116
Gollany HT, Schumacher TE, Lindstrom MJ, Evenson PD, Lemme GD. 1992. Topsoil depth and desurfacing effects on properties and productivity of a typic Argiustoll. Soil Sci Soc Am J 56:220–225
Hafner S. 2003. Trends in maize, rice, and wheat yields for 188 nations over the past 40 years: a prevalence of linear growth. Agric Ecosyst Environ 97:275–283
Jacob JS, Hallmark CT. 1996. Holocene stratigraphy of Cobweb Swamp, a Maya wetland in northern Belize. Geol Soc Am Bull 108:883–891
Jensen ME, Haise HR. 1963. Estimating evapotranspiration from solar radiation. J Irrig Drain Div. ASCE 89:15–41
Jones RJA, Zdruli P, Montanarella L. 2000. The estimation of drought risk in Europe from soil and climatic data. In: Vogt JV, Somma F, Eds. Drought and Drought Mitigation in Europe. Kluwer. The Netherlands, pp 133–146
JRC. 2007. http://www.eusoils.jrc.ec.europa.eu/ESDB_Archive/pesera/pesera_data.html. Accessed 07 May 2007
Kindal HW, Pimentel D. 1994. Constraints on the expansion of the global food supply. Ambio 23:198–205
King D, Daroussin J, Tavernier R. 1994. Development of a soil geographical database from the soil map of the European Communities. Catena 21:37–26
King D, Le Bas C, Daroussin J, Thomasson AJ, Jones RJA. 1995. The EU map of soil water available for plants. In: King D, Jones RJA, Thomasson AJ, Eds. European land information systems for agroenvironmental monitoring. Office for Official Publications of the European Communities, Luxembourg, pp 131–142
Kirkby M, Jones RJA, Irvine B, Gobin A, Govers G, Cerdan O, Van Rompaey A, Le Bissonnais Y, Daroussin J, King D, Montanarella L, Grimm M, Vieillefont V, Puigdefabregas J, Boer M, Kosmas C, Yassoglou N, Tsara M, Mantel S, van Lynden G, Hunting J 2004. Pan-European soil erosion risk assessment: the PESERA Map. European Soil Bureau Research Report. Office for Official Publications of the European Communities, European Soil Bureau, Luxembourg, pp 18
Kleinbaum DG, Kupper LL, Muller KE, Nizam A 1998. Applied regression analysis and other multivariable methods. Brooks/Cole publishing company, CA
Kosmas C, Gerontidis S, Marathianou M, Detsis B, Zafiriou T, Muysen Wv, Govers G, Quine T, Vanoost K. 2001. The effects of tillage displaced soil on soil properties and wheat biomass. Soil Tillage Res 58:31–44
Larney FJ, Olson BM, Janzen HH, Lindwall CW. 2000. Early impacts of topsoil removal and soil amendments on crop productivity. Agron J 92:948–956
Linacre ET. 1969. Empirical relationships involving the global radiation intensity and ambient temperature at various latitudes and altitudes. Archiv Meteor Geophys Bioklim B12:1–20
Malhi SS, Izaurralde RC, Nyborg M, Solberg ED. 1994. Influence of topsoil removal on soil fertility and barley growth. J Soil Water Conser 49:96–101
Mbagwu JSC, Lal R, Scott TW. 1984. Effects of desurfacing of Alfisols and Ultisols in Southern Nigeria: I. Crop performance. Soil Sci Soc Am J 48:828–833
McNeill JR, Winiwarter V. 2004. Breaking the sod: Humankind, history, and soil. Science 304:1627–29
Mielke LN, Schepers JS. 1986. Plant response to topsoil thickness on an eroded loess soil. J Soil Water Conserv 41:59–63
Mokma DL, Sietz MA. 1992. Effects of soil erosion on corn yields on Marlette soils in south-central Michigan. J Soil Water Conserv 47:325–327
Morrison D. 2000. Causality and Covariance Models. Australia: University of Western Australia
Olson KR, Carmer SG. 1990. Corn yield and plant population differences between eroded phases of Illinois soils. J Soil Water Conserv 45:562–566
Olson KR, Mokma DL, Lal R, Schumacher TE, Lindstrom MJ. 1999. Erosion impacts on crop yield for selected soils of the north central United States. In: Lal R (ed). Soil quality and soil erosion. Soil and water conservation society, Ankeny, Iowa, pp 259–283
Pimentel D, Harvey C, Resosudarmo P, Sinclair K, Kurz D, Mcnair M, Crist S, Shpritz L, Fitton L, Saffouri R, Blair R. 1995. Environmental and economic costs of soil erosion and conservation benefits. Science 267:1117–23
Rounsevell M, Reginster I, Araújo MB, Carter TR, Dendoncker N, Ewert F, House JI, Kankaanpää S, Leemans R, Metzger M, Schmit C, Smith P, Tuck G. 2006. A coherent set of future land use change scenarios for Europe. Agric Ecosyst Environ 114:57–68
Rounsevell MDA, Ewert F, Reginster I, Leemans R, Carter TR. 2005. Future scenarios of European agricultural land use II. Projecting changes in cropland and grassland. Agric Ecosyst Environ 107:117–35
Runnels CN. 1995. Environmental degradation in Ancient-Greece. Sci Am 272:96–99
Salter PJ, Williams JB. 1965. The influence of texture on the moisture characteristics of soils. II. Available-water capacity and moisture release characteristics. J Soil Sci 16:310–317
Schumacher TE, Lindstrom MJ, Mokma DL, Nelson WW. 1994. Corn yield: erosion relationships of representative loess and till soils in the North-Central United States. J Soil Water Conserv 49:77–81
Selby MJ 1991. Hillslope materials and processes. Oxford: Oxford university press
Tanaka DL 1995. Spring wheat straw production and composition as influenced by topsoil removal. Soil Sci Soc Am J 59:649–654
Thomasson AJ 1979. Assessment of average soil droughtiness. In: Jarvis MG, Mackney D, Eds. Soil survey applications. Soil Survey Technical Monograph, Harpenden, UK, pp 43–50
Thomasson AJ. 1995. Assessment of soil water reserves available for plants (SWAP): a review. In: King D, Jones RJA, Thomasson AJ, Eds. European land information systems for agro-environmental monitoring. European Commision, Luxembourg, pp 115–130
Tilman D, Cassman KG, Matson PA, Naylor R, Polasky S. 2002. Agricultural sustainability and intensive production practices. Nature 418:671–677
Trimble SW, Crosson PR. 2000. U.S. Soil erosion rates—Myth and reality. Science 289:248–250
UNEP. 1997. Global environment outlook - 1. New York: UNEP
Van Rompaey AJJ, Bazzoffi P, Jones RJA, Montanarella L, Govers G. 2003a. Validation of soil erosion risk assessment in Italy. In: European soil bureau, Luxembourg, pp 25
Van Rompaey AJJ, Vieillefont V, Jones RJA, Montanarella L, Verstraeten G, Bazzoffi P, Dostal T, Krasa J, de Vente J, Poesen J. 2003b. Validation of soil erosion estimates at European Scale. European Soil Bureau, Brussels, pp 25
Vanandel TH, Zanger E, Demitrack A. 1990. Land-use and soil-erosion in prehistoric and historical Greece. J Field Archaeol 17:379–396
White AW, Bruce RR, Thomas AW, Langdale GW, Perkins HF. 1984. Characterizing productivity of eroded soils in the Southern Piedmont. In: Erosion and soil productivity. American society of Agricultural engineers, New Orleans, Louisiana
Wilkinson BH, McElroy BJ 2007. The impact of humans on continental erosion and sedimentation. Geol Soc Am Bull 119:140–156
Yaalon DH, Arnold RW. 2000. Attitudes toward soils and their societal relevance: then and now. Soil Sci 165:5–12
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License ( https://creativecommons.org/licenses/by-nc/2.0 ), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Bakker, M.M., Govers, G., Jones, R.A. et al. The Effect of Soil Erosion on Europe’s Crop Yields. Ecosystems 10, 1209–1219 (2007). https://doi.org/10.1007/s10021-007-9090-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10021-007-9090-3