1 Introduction

A consumption good can be differentiated depending on, for example, production procedures, as are organic vegetables from non-organic vegetables. Diesel trains and electric trains might provide similar transportation services. Electricity can be generated by thermal power and nuclear power, or by the ostensibly greener modes of water power, solar power, and wind power. Even household energy needs can be satisfied with either electricity or (natural) gas. The production procedures of these goods might differ in terms of environmental damage or burdens. Producing firms might be private or public. Moreover, consumers are aware of the environmental friendliness and environmental costs in goods production.Footnote 1 Therefore, these goods might be regarded as differentiated goods by consumers even if their consumption provides the same physical benefits to consumers.

This paper presents consideration of a mixed duopolistic market in which firms undertake environmental R&D investment to improve environmental friendliness of production. Recently, it has often been suggested that partially privatizing a public firm improves social welfare in various respects (e.g., Matsumura 1998; Matsumura and Kanda 2005). Our purposes are to present an analysis of public firm privatization effects on the environment and on social welfare in a mixed duopolistic market, in which consumers are aware of the differentiated environmental friendliness of market goods. The two firms are assumed to be domestically owned: one is public. The public firm is concerned about the environment.

Many reports describe analyses of partial privatization in a mixed oligopoly: Fujiwara (2007) reports that partial privatization is optimal with respect to product differentiation in a fixed number of firms. Cato (2008) demonstrates that, with sufficiently negative environmental externalities, a mixed oligopoly is socially preferred to a private oligopoly. Gil-Moltó et al. (2011) were the first to report a study of R&D subsidies in a mixed oligopoly. Pal and Saha (2015) assume for their analysis of a pollution tax and privatization and demonstrate that partial privatization is optimal. They also illustrate that when the public firm is concerned about the environment, privatization improves the environment. Ouattara (2019) develops the Haruna and Goel (2018) model to demonstrate that although an increased degree of privatization worsens the environment, it increases social welfare. Haruna and Goel (2018) assume a pollution tax for their analysis and report that privatization tends to worsen the environment by comparing private duopoly and mixed duopoly. Lee and Park (2020) report that when R&D costs are low, privatization is socially undesirable.Footnote 2 In contrast to our findings, most of the studies explained above investigate R&D expenditures (abatement expenditures) to reduce goods production costs.

We construct a model of a mixed duopoly, basing it on a differentiated duopoly model described by Yakita and Yamaguchi (2011), who formalize consumers’ environmental awareness and the environmental friendliness of consumption goods. Consumers do not differentiate goods physically per se, but differentiate them according to their environmental friendliness. For instance, organic tomatoes and non-organic tomatoes are both tomatoes, i.e., a consumption good, but they are differentiated and usually sold at different prices. The environmental friendliness of the goods’ production is evaluated endogenously in light of a firm’s R&D activities.Footnote 3 The private firm simply maximizes profit, whereas the public firm maximizes the objective function, which is the weighted average of its profit and social welfare from the market. The main results are the following. The increased degree of privatization of the public firm degrades its environmental R&D investment. The reduced R&D investment consequently lowers the environmental friendliness of public firm’s goods. Then, through R&D spillovers, it lowers that of a private firm’s goods. Consequently, privatization of the public firm worsens the environment and decreases goods consumption.

The paper is structured as follows. The next section introduces a model. Section 3 presents a two-stage Nash equilibrium for a given degree of privatization. Section 4 reports the effects of an increase in the degree of privatization. The last section concludes the paper.

2 Model

The model is structured as a three-stage game among a private and public firm and government. At stage zero, government commits to the degree of privatization of a public firm. At stage one, the partially public firm and a private firm undertake environmental R&D investment to improve the environmental friendliness of their outputs while accepting the R&D investment of another firm as given. Finally, at stage two, both firms compete in the mixed duopoly market. The private firm maximizes its profit whereas the public firm maximizes the weighted average of its profit and social welfare. The game is solved by backward induction to obtain its subgame perfect equilibrium for the last two stages. The degree of privatization of the public firm affects the subgame perfect Nash equilibrium.

We assume the utility function of a representative consumer as

$$ U = x_{0} + x_{1} - \frac{{x_{0}^{2} }}{{u_{0}^{2} }} - \frac{{x_{1}^{2} }}{{u_{1}^{2} }} + M. $$
(1)

Therein, variables \(x_{0}\) and \(x_{1}\) respectively represent the amount of consumption goods provided by a public firm and by a private firm, whereas \(u_{0}\) and \(u_{1}\) respectively denote the environmental friendliness of the two goods. In addition, \(M = Y - \sum\nolimits_{0}^{1} {p_{i} x_{i} }\) represents the quantity of outside composite goods, where \(Y\) stands for the income level and \(p_{i}\) signifies the price of goods \(x_{i}\) (\(i = 0,1\)). For analytical purposes, we assume that these two goods are physically equivalent, but that they differ in terms of their respective degrees of environmental friendliness. Consumers are clearly aware of differences in the degree of environmental friendliness of goods. If environmental friendliness differs in terms of the consumers’ environmental awareness, i.e., if \(u_{0} \ne u_{1}\), then two goods \(x_{0}\) and \(x_{1}\) are not perfectly substitutable. In this sense, the market for these goods can be regarded as having a differentiated duopolistic market structure. Regarding the effects of public firm privatization, we assume that substitutability between two goods can be negligible in terms of consumer demand.Footnote 4

The inverse demands are, respectively,

$$ p_{i} = 1 - \frac{{2x_{i} }}{{u_{i}^{2} }}\,\,(i = 0,1). $$
(2)

Environmental awareness depends on the degree of environmental friendliness, which is determined by a firm’s environmental R&D investment. In this sense, the degree of differentiation is endogenous in this study.

Although the two goods are differentiated, the production cost per unit is common at \(c(<1)\) for both goods. Profit maximization of the private firm is conducted to maximize \(\pi_{1} = N(p_{1} - c)x_{1}\), which can be rewritten as

$$ \pi_{1} = N\left(1 - c - \frac{{2x_{1} }}{{u_{1}^{2} }}\right)x_{1} , $$
(3)

where \(N\) represents the number of consumers. The number of consumers is assumed to be constant. From the first-order condition for profit maximization, we obtain

$$ x_{1} = \frac{1 - c}{4}u_{1}^{2} . $$
(4)

As the environmental friendliness of private goods increases, demand for it increases, although the price becomes high (see (2)).

Following reports of the literature such as that by Beladi and Chao (2006), the objective of the partially public firm is given by the weighted average of its profit and social welfare from the differentiated market goods as

$$ \Pi_{0} = \theta \pi_{0} + (1 - \theta )(CS + \pi_{0} + \pi_{1} ) = \pi_{0} + (1 - \theta )(CS + \pi_{1} ), $$
(5)

where \(CS\) denotes the consumer surplus, i.e.,

$$ CS = N(U - p_{0} x_{0} - p_{1} x_{1} ) = N\left(\frac{{x_{0}^{2} }}{{u_{0}^{2} }} + \frac{{x_{1}^{2} }}{{u_{1}^{2} }}\right), $$
(6)

and where parameter \(\theta\) denotes the degree of privatization of the public firm (\(0 \le \theta < 1\)).Footnote 5 The public firm’s profit is given as \(\pi_{0} = N(p_{0} - c)x_{0}\). It is noteworthy that R&D investment costs do not appear in the maximization at this stage because they are expended in the earlier stage as sunk costs. The problem of the public firm is to maximize the objective function with respect to \(x_{0}\). From the first-order condition, we obtain

$$ x_{0} = \frac{1 - c}{{2(1 + \theta )}}u_{0}^{2} . $$
(7)

The degree of privatization discourages consumers from demanding the goods provided by the public firm, given the firm’s environmental friendliness.

The degree of environmental friendliness of a product is determined by a firm’s environmental R&D investments. Environmental R&D must be undertaken in advance of goods production. The investment expenditure is a sunk cost for goods production.Footnote 6 We assume that both public and private firms have identical environmental R&D technology for environmental friendliness of goods. Following Symeonidis (2003) and Yakita and Yamauchi (2011), the following relation between the degree of environmental friendliness and R&D investment is assumed as

$$ u_{i} = \alpha\left (R_{i}^{1/4} + \rho R_{j}^{1/4}\right )\,\,(i,j = 0,1;i \ne j), $$
(8)

where \(R_{i}\) stands for the amount of R&D investment of the producer of goods \(x_{i}\) (\(i,j = 0,1;i \ne j\)), \(\alpha\) is a positive constant, and \(\rho\) signifies technological spillovers in R&D investments (\(0 < \rho < 1\)). Firm \(j\)’s environmental R&D investment improves the environmental friendliness of firm \(i\) through spillover effects (\(i,j = 0,1\); \(i \ne j\)).

3 Two-stage subgame perfect equilibrium for a given degree of privatization

From the firm’s choices of quantities \(x_{i}\) at the second stage subgame, the profit of private firm 1 is obtained from (3) as

$$ \pi_{1} = \frac{{N(1 - c)^{2} }}{8}u_{1}^{2} . $$
(9)

The value of the objective function of the public firm 0 is obtained from (5) as

$$ \Pi_{0} = \frac{{N(1 - c)^{2} }}{2}\left[\frac{{u_{0}^{2} }}{2(1 + \theta )} + \frac{{3(1 - \theta )u_{1}^{2} }}{8}\right], $$
(10)

for a given degree of privatization. At the preceding stage, i.e., at stage one, each firm chooses its environmental R&D investment to maximize the net-of-R&D investment value of the objective function, i.e., \(\pi_{1} - R_{1}\) and \(\Pi_{0} - R_{0}\) respectively, given the choice of the other firm. The degree of privatization of public firm is chosen by government to maximize social welfare in the earlier stage.

From the first-order conditions for R&D investment optimization, we obtain the equilibrium R&D investments \((R_{0} ,R_{1} )\) satisfying the following two equations: using (9) as

$$ R_{1}^{ - 1/2} + \rho R_{0}^{1/4} R_{1}^{ - 3/4} = \frac{16}{{N(1 - c)^{2} \alpha^{2} }}. $$
(11)

Then, using (10),

$$ \left(\frac{1}{1 + \theta } + \frac{{3(1 - \theta )\rho^{2} }}{4}\right)R_{0}^{ - 1/2} + \rho \left(\frac{1}{1 + \theta } + \frac{3(1 - \theta )}{4}\right)R_{1}^{1/4} R_{0}^{ - 3/4} = \frac{8}{{N(1 - c)^{2} \alpha^{2} }}. $$
(12)

The second-order conditions for the R&D investment optimization are satisfied respectively as

$$ \frac{{\partial^{2} \pi_{1} }}{{\partial R_{1}^{2} }} = \frac{{N(1 - c)^{2} \alpha }}{64}\left(\alpha R_{1}^{ - 6/4} - 3R_{1}^{ - 7/4} u_{1}\right ) < 0\,\,\,{\text{and}} $$
(13)
$$ \frac{{\partial^{2} \Pi_{0} }}{{\partial R_{0}^{2} }} = - \frac{{N(1 - c)^{2} \alpha^{2} }}{16}\left[\left(\frac{1}{1 + \theta } + \frac{{3(1 - \theta )\rho^{2} }}{4}\right)R_{0}^{{ - \frac{3}{2}}} + \frac{3\rho }{2}\left(\frac{1}{1 + \theta } + \frac{3(1 - \theta )}{4}\right)R_{1}^{\frac{1}{4}} R_{0}^{{ - \frac{7}{4}}} \right]\,\,\, < 0 $$
(14)

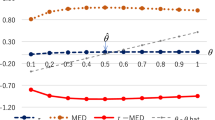
Therefore, if R&D investments satisfying (11) and (12) exist, then these are the solution for the mixed duopoly \((R_{0} ,R_{1} )\), i.e., a subgame perfect Nash equilibrium. From (11)–(14), one can obtain the best response functions of firm’s R&D investment, \(R_{0} (R_{1} )\) for the public firm and \(R_{1} (R_{0} )\) for the private firm. The best response functions are presented in Fig. 1. We can demonstrate that these functions are increasing. For analytical purposes, we assume that a Nash equilibrium \((R_{0}^{N} ,R_{1}^{N} )\) exists. The stable condition of the equilibrium is given as \(R_{1} ^{\prime}(R_{0} ) > R_{0} ^{\prime}(R_{1} )\), which can be written from (11) and (12) as

$$ D \equiv \frac{{\partial^{2} \Pi_{0} }}{{\partial R_{0}^{2} }}\frac{{\partial^{2} \pi_{1} }}{{\partial R_{1}^{2} }} - \frac{{[\rho N(1 - c)^{2} \alpha^{2} ]^{2} }}{{2^{11} }}\left[\frac{1}{1 + \theta } + \frac{3(1 - \theta )}{4}\right](R_{0} R_{1} )^{ - 3/2} > 0. $$
(15)

As spillover effects become smaller, i.e., as \(\rho \to 0\), the respective left-hand sides of (11) and (12) become \(R_{1}^{ - 1/2}\) and \(R_{0}^{ - 1/2} /(1 + \theta )\). From (11) and (12), we have \(2/(1 + \theta ) = (R_{0} /R_{1} )^{1/2}\). Therefore, because \(0 \le \theta < 1\), it can be demonstrated that if spillover effects are sufficiently small, then \(R_{0}^{N} > R_{1}^{N}\). Environmental R&D investment of a public firm is likely to be greater than that of a private firm with small spillovers.Footnote 7

Fig. 1
figure 1

Best response functions and Nash equilibrium R&D investment

Full size image

The upward-sloping best reaction function shows that R&D investments are strategic complements. An increase in \(R_{i}\) increases \(u_{i}\) and at the same time increases \(u_{j}\) through spillovers. These increased perceptions of consumers about environmental friendliness stimulate consumer demand for goods because of their environmental awareness. The enhanced demand gives firms incentives to increase environmental R&D investments. Such strategic complementarity derives from spillovers, as described by Gil-Moltó et al. (2011). If no spillover exists, i.e., if \(\rho = 0\), then the R&D investments of firms are respectively determined independently, as shown in (11) and (12), i.e., with no strategic complementarity.

4 Increases in the degree of partial privatization

Next, we present an analysis of the effects of the degree of partial privatization \(\theta\) on environmental R&D behaviors of the two firms at Nash equilibrium. From (11) and (12) we obtain

$$ \left( {\begin{array}{*{20}c} {\frac{{\partial^{2} \pi_{1} }}{{\partial R_{1}^{2} }}} & {\frac{{\rho N(1 - c)^{2} \alpha^{2} }}{64}(R_{0} R_{1} )^{ - 3/4} } \\ {\frac{{\rho N(1 - c)^{2} \alpha^{2} }}{32}[\frac{1}{1 + \theta } + \frac{3(1 - \theta )}{4}](R_{0} R_{1} )^{ - 3/4} } & {\frac{{\partial^{2} \Pi_{0} }}{{\partial R_{0}^{2} }}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{{dR_{1} }}{d\theta }} \\ {\frac{{dR_{0} }}{d\theta }} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 0 \\ { - \frac{{\partial^{2} \Pi_{0} }}{{\partial \theta \partial R_{0} }}} \\ \end{array} } \right), $$
(16)

where \(\partial^{2} \pi_{1} /\partial R_{1}^{2}\) and \(\partial^{2} \Pi_{0} /\partial R_{0}^{2}\) are given respectively by (13) and (14), and where

$$ - \frac{{\partial^{2} \Pi_{0} }}{{\partial \theta \partial R_{0} }} = \frac{{N(1 - c)^{2} \alpha^{2} }}{8}\left\{ \left[\frac{1}{{(1 + \theta )^{2} }} + \frac{{3\rho^{2} }}{4}\right]R_{0}^{ - 1/2} + \rho \left[\frac{1}{{(1 + \theta )^{2} }} + \frac{3}{4}\right]R_{1}^{1/4} R_{0}^{ - 3/4} \right\} > 0. $$
(17)

Therefore, from (13)–(15), we obtain

$$ \frac{{dR_{0} }}{d\theta } = - \frac{{\partial^{2} \pi_{1} }}{{\partial R_{1}^{2} }} \cdot \frac{{\partial^{2} \Pi_{0} }}{{\partial \theta \partial R_{0}^{{}} }}/D < 0\,\,\,{\text{and}} $$
(18)
$$ \frac{{dR_{1} }}{d\theta } = \frac{{\rho N(1 - c)^{2} \alpha^{2} }}{64}(R_{0} R_{1} )^{ - 3/4} \cdot \frac{{\partial^{2} \Pi_{0} }}{{\partial \theta \partial R_{0}^{{}} }}/D < 0. $$
(19)

An increase in the degree of privatization reduces the environmental R&D investment of both firms when R&D investment spillovers exist. The increased degree of privatization of public firm lowers social welfare stemming from the consumer surplus, inducing the public firm to decrease its output, as shown in (7). The reduction of output production gives an incentive to reduce its R&D investment. This response of the public firm decreases the environmental friendliness of the private firm’s output through spillover effects, thereby decreasing consumer demand for the private firm’s goods. Therefore, the increased degree of privatization of the public firm also decreases the incentive for R&D investment of the private firm. Consequently, if public firms are concerned about the environment, then privatization of the public firms worsens the environment.Footnote 8

Effects of the increased degree of privatization can be represented by a leftward shift of the best response function \(R_{0} (R_{1} )\) in Fig. 1. With R&D spillovers, the best response function \(R_{1} (R_{0} )\) is upward sloping. Therefore, the shift of \(R_{0} (R_{1} )\) decreases both \(R_{0}\) and \(R_{1}\). With no spillovers, response function \(R_{1} (R_{0} )\) is horizontal. For that reason, \(R_{1}\) remains constant. This result contrasts with that presented by Gil-Moltó et al. (2011) for which the status of goods as strategic substitutes or strategic complements depends on the strength of spillover effects brought about by cost-reducing R&D investments.

Effects of the increased degree of privatization of public firms on environmental friendliness and consumption levels are presented in Table 1.Footnote 9

Table 1 Effects of increased degree of privatization (\(\rho > 0\))
Full size table

The effect on the utility of a representative consumer is given as

$$ \frac{dU}{{d\theta }} = \frac{{(1 - c)u_{0} }}{1 + \theta }\{ [1 - \frac{1 - c}{{2(1 + \theta )}}]\frac{{du_{0} }}{d\theta } - \frac{{u_{0}^{{}} }}{2(1 + \theta )}(1 - \frac{1 - c}{{1 + \theta }})\} \, + \frac{{(1 - c)u_{1} }}{2}(1 - \frac{1 - c}{4})\frac{{du_{1} }}{d\theta } < 0. $$
(20)

We also obtain

$$ \frac{dW}{{d\theta }} = N(1 - c)^{2} \left[\frac{{(1 + 2\theta )u_{0} }}{{2(1 + \theta )^{2} }}\frac{{du_{0} }}{d\theta } + \frac{{3u_{1}^{{}} }}{8}\frac{{du_{1} }}{d\theta } - \frac{{\theta u_{0}^{2} }}{{2(1 + \theta )^{3} }}\right] < 0, $$
(21)

where \(W = CS + \pi_{0} + \pi_{1}\) represents the social welfare level. Therefore, increases in the degree of privatization of a public firm lowers both a consumer’s utility of the market goods and social welfare. The negative social welfare effect of public firm privatization is reported in the literature (e.g., Haruna and Goel 2018). Nevertheless, few reports of the relevant literature have described that environmental R&D spillovers enhance the negative welfare effect through strategic complementarity. Furthermore, the result of the monotonic negative effect of privatization in our case of the endogenous degree of goods differentiation contrasts against optimal partial privatization with respect to the substitutability of differentiated goods (inverted U-shape with respect to goods substitutability), as described in Fujiwara (2007) and Pal and Saha (2015).Footnote 10 They do not consider consumers’ environmental awareness.

5 Concluding remarks

We have demonstrated that an increase in the degree of partial privatization of public firms lowers environmental R&D investment of a public firm and have demonstrated that the lowered R&D investment of the public firm also lowers that of the private firm through R&D investment spillovers. These decreased R&D investments reduce the environmental friendliness of consumption goods. Consumers who are aware of environmental friendliness decrease their consumption of market goods. Therefore, if a public firm is concerned about the consumer surplus, then the increased degree of privatization might be socially undesirable. This conclusion is consistent with that reported, for example, in Gil-Moltó et al. (2011), although that study includes no consideration of partial privatization. It is noteworthy that our results indicate that even if firms are private, they might improve the environment by consideration of social welfare (as encouraged by the Social Value Act).

Our simple model includes some deficiencies. First, we have assumed that the consumption goods are clearly, or perfectly, differentiated by individuals who are aware of environmental friendliness. However, some people are not so aware of the environmental friendliness of goods. In such cases, goods are substitutable. That substitutability might moderate the declining demand of both goods, thereby mitigating the effects of public firm privatization, although the model might become extremely complicated.Footnote 11

Next, we considered privatization solely as a policy instrument. Governments have other policy instruments: other studies assume multiple policy instruments (e.g., R&D subsidies and privatization, as reported by Gil-Moltó et al. 2011). Environmental externalities in oligopolistic markets are well known to involve multiple inefficiencies. Therefore, multiple policy instruments must retain efficient solutions (e.g., Yin 2003). Consideration of other policies is left as a subject for future study.

5.1 Appendix substitutability between differentiated goods

Representing the inverse measure of the degree of horizontal product differentiation between varieties \(x_{0}\) and \(x_{1}\) by parameter \(\sigma \in (0,1)\), the two goods become independent when \(\sigma \to 0\) as in the text. As \(\sigma \to 1\), the two goods become substitutes. With \(\sigma \in (0,1)\), the utility function can be written as

$$ U = x_{0} + x_{1} - \frac{{x_{0}^{2} }}{{u_{0}^{2} }} - \frac{{x_{1}^{2} }}{{u_{1}^{2} }} - 2\sigma \frac{{x_{0} }}{{u_{0} }}\frac{{x_{1} }}{{u_{1} }} + M. $$
(22)

The inverse demand functions become

$$ p_{i} = 1 - \frac{{2x_{i} }}{{u_{i}^{2} }} - 2\sigma \frac{{x_{j} }}{{u_{i} u_{j} }}\,(i,j = 0,1;\,i \ne j). $$
(23)

The public firm objective becomes

$$ \Pi_{0} = N\left\{ (1 - c)[x_{0} + (1 - \theta )x_{1} ] - (1 + \theta )\frac{{x_{0}^{2} }}{{u_{0}^{2} }} - (1 - \theta )\frac{{x_{1}^{2} }}{{u_{1}^{2} }} - 2\sigma \frac{{x_{0} x_{1} }}{{u_{0} u_{1} }}\right\} , $$
(24)

from which we obtain the optimal output level for given environmental friendliness as

$$ x_{0} = (1 - c - 2\sigma \frac{{x_{1} }}{{u_{0} u_{1} }})\frac{{u_{0}^{2} }}{2(1 + \theta )}. $$
(25)

The optimal output level is

$$ x_{1} = (1 - c - 2\sigma \frac{{x_{0} }}{{u_{0} u_{1} }})\frac{{u_{1}^{2} }}{4}, $$
(26)

which is obtained by maximizing profit \(\pi_{1} = N(1 - c - \frac{{2x_{1} }}{{u_{1}^{2} }} - 2\sigma \frac{{x_{0} }}{{u_{0} u_{1} }})x_{1}\) with respect to \(x_{1}\) for a given degree of environmental friendliness of goods.

From (25) and (26), we obtain a subgame perfect Nash equilibrium as

$$ x_{0} = \frac{{(1 - c)(2u_{0} - \sigma u_{1} )u_{0} }}{{2[2(1 + \theta ) - \sigma^{2} ]}}\,\,\,\,{\text{and}} $$
(27)
$$ x_{1} = \frac{{(1 - c)[(1 + \theta )u_{1} - \sigma u_{0} ]u_{1} }}{{2[2(1 + \theta ) - \sigma^{2} ]}}. $$
(28)

These values respectively correspond to (7) and (4) in the text. The profit of the private firm in the equilibrium is

$$ \pi_{1} = \frac{{N(1 - c)^{2} [(1 + \theta )u_{1} - \sigma u_{0} ]^{2} }}{{2[2(1 + \theta ) - \sigma^{2} ]^{2} }}. $$
(29)

The value of the objective of the public firm is

$$ \Pi_{0} = \frac{{(1 - c)^{2} }}{{4[2(1 + \theta ) - \sigma^{2} ]^{2} }}\{ (1 + \theta )(2u_{0} - \sigma u_{1} )^{2} + 3(1 - \theta )[(1 + \theta )u_{1} - \sigma u_{0} ]^{2} \, + 2\sigma (1 - \theta )(2u_{0} - \sigma u_{1} )[(1 + \theta )u_{1} - \sigma u_{0} ]\} . $$
(30)

The R&D investment of the private firm improves the environmental friendliness of its own goods and indirectly improves that of the rival’s goods through spillovers. However, the improved friendliness of the rival’s goods might affect the profit negatively through goods substitution when \(\sigma\) is great, as might be apparent from (29). Therefore, it is difficult to derive Nash equilibrium R&D investments (\(R_{0}\),\(R_{1}\)) of the public and the private firm to maximize \(\Pi_{0} - R_{0}\) and \(\pi_{1} - R_{1}\), respectively, explicitly. There are many cases depending on the relative magnitudes of parameters \(\sigma\) and \(\rho\). Therefore, we cannot derive effects of the degree of privatization of the public firm on the R&D investments of both firms explicitly.

Letting \(\sigma \to 0\) in (29) and (30), these conditions approach (9) and (10) in the text. Therefore, if the substitutability between goods differentiated in terms of environmental friendliness is sufficiently small, then the analyses in the text applies. If otherwise the substitutability is great, then we cannot a priori rule out a case in which R&D investments increase with the degree of public firm privatization, thereby improving the environment. However, if goods are differentiated by consumers in terms of environmental friendliness, then the substitutability is apparently small.