Analyses of biped walking posture by dynamical-evaluating index

Abstract

In this paper, biped walking posture and design are evaluated through dynamic reconfiguration manipulability shape index (DRMSI). DRMSI is the concept derived from dynamic manipulability and reconfiguration manipulability with remaining redundancy. DRMSI represents the ability of dynamical system of manipulators possessing shape changing acceleration in task space by normalized torque inputs, while the hand motion is assigned as the primary task. Besides, we use visual lifting approach to stabilize the walking and stop falling down. In this research, the primary task is to make the position of the head direct to the desired one as much as possible. And realizing the biped walking is the second task. This research indicates that proposed dynamical-evaluating index is effective in evaluating the biped walking motion and biped humanoid robot has the adjustable configuration to walk with higher flexibility. Flexibility represents the dynamical shape changeability of humanoid robot based on redundancy of the humanoid robot with the premise of the primary task given to keeping the head position high.

1 Introduction

Many researchers made their efforts to control humanoid walking and proposed many effective methods to measure walking flexibility. And, ZMP-based walking motion is considered as the most effective method, which has been certified as a useful control method to increase stability of practical biped walking in the real world, because it can make sure that the humanoid can get the balance of walking and standing by keeping the ZMP within the convex hull of supporting area [1]. Nakamura et al. [2] showed the way of representing the connection between motions and environment based on the dynamical equation of motion and put into execution on the human. Stability of walking including slipping is influenced by some elements such as the gain parameters of visual lifting approach [3,4,5,6], the friction coefficient of the floor while slipping [7, 8], length and mass of links and joints. And these elements can change stance of legs and efficiency of energy while walking. Therefore, some dynamical measurements are proposed to evaluate the stability of walking, such as high walking velocity with low-energy consumption and walking distance with certain energy consumption. Besides, since dimension number of biped walking dynamical states is variable with the condition of contacting between floor and feet, some dynamical measurements discussing continually dynamical shape changeability of humanoid according to the bipedal gaits’ varieties are required.

Fig. 1

Applications of DRME for humanoid robot

Fig. 2

Walking on uneven floor with a no-singular configuration, b partially singular configuration

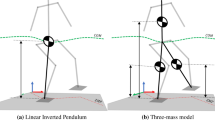
Humanoid robots execute some tasks like riding the bicycle and walking with redundancy. Thus, we describe dynamical redundancy of humanoid biped walking in this paper, explaining the concept of dynamical reconfiguration manipulability shape index (DRMSI) [9]. That evaluates dynamical shape changeability of a dynamical system which can potentially produce a motion in a workspace with normalized input torques. We have applied DRMSI to the biped walking where primary task is assigned to keep the head height to stop falling down during the walking process. The concept is illustrated in Fig. 1. Simulations show that the value of dynamical reconfiguration manipulability ellipsoids (DRMEs) [9, 10] is affected by the change of the human’s waist height based on visual lifting approach. It indicates that DRMSI also can be one of the dynamical measurements used to evaluate dynamical shape changeability and the stability of walking in our study.

Appearance of biped robot walking on the uneven floor is shown in Fig. 2. Considering the condition of executing task-1 (keeping the height of head) and task-2 (lowering the height of waist) is set. These tasks can be executed under an assumption that humanoid’s eyes should be directed to target object during the walking process. Walking direction is along the y-axis. There is space for z-acceleration of waist in (a), which enables robot to execute task-1 and task-2 simultaneously together. However, there is no space for z-acceleration of waist in (b), task-1 can be executed but task-2 cannot be executed since head will be lower if the foot approaches floor. We find that humanoid robot can adjust suitable configuration by changing the visual-lifting gains in VLA to improve walking stability on the even floor based on the value of DRMSI with remaining redundancy from simulation results.

2 Dynamical biped walking model

Fig. 3

Definition of biped-walking model, $\textcircled {1}$–$\textcircled {17}$ represents link number, – is joint number, $q_1$–$q_{17}$ is joint angles

Table 1 Physical parameters

The biped-walking robot in Fig. 3 is discussed in this paper, Table 1 shows length $l_i$ (m), mass $m_i$ (kg) of links and coefficient of joints’ viscous friction $d_i\, (\hbox {N}\,\hbox {m}\,\hbox {s}/\hbox {rad}$), which are determined by [11]. This model is simulated as a serial-link manipulator having branches and represents rigid whole body such as feet including toe, torso, arms and so on and is up to 17 degree-of-freedom (DoFs). Though motion of legs is limited in sagittal plane, it possesses many walking gaits since the robot has flat-sole feet and kicking torque. In this paper, the foot named as link-1 is defined as “supporting-foot” and the other foot named as link-7 is defined as “free foot” (“contacting-foot” when the floating foot contacts with ground) according to gaits. When the contacting-foot stop slipping which indicates that static friction force is exerted to the foot, the contacting-foot switches to supporting-foot and the previous supporting-foot is transferred into free foot if it was isolated from the floor.

3 Dynamic reconfiguration manipulability

Motion equation of serial-link manipulators can be written as

$$\begin{aligned} {\varvec{M}}({\varvec{q}})\ddot{{\varvec{q}}}+{\varvec{h}}({\varvec{q}}, \dot{{\varvec{q}}})+{\varvec{g}}({\varvec{q}})+{\varvec{D}}\dot{{\varvec{q}}}={\varvec{\tau }} , \end{aligned}$$

(1)

where ${\varvec{q}}$ represents the angle matrix of manipulators, ${\varvec{M}}({\varvec{q}}) \in R^{n \times n}$ represents inertia matrix, ${\varvec{h}}({\varvec{q}}, \dot{{\varvec{q}}}) \in R^{n}$ and ${\varvec{g}}({\varvec{q}}) \in R^{n}$ represent vectors of Coriolis force, centrifugal force and gravity, ${\varvec{D}}=\text {diag}[d_1, d_2, \ldots , d_{n}]$ is matrix representing coefficients of joints’ viscous friction and ${\varvec{\tau }} \in R^{n}$ represents joint torque. The kinematic equation of manipulators, the relation between the jth link’s velocity $\dot{{\varvec{r}}}_j \in R^m$ and the angular velocity $\dot{{\varvec{q}}} \in R^n$ is described by

$$\begin{aligned} \dot{{\varvec{r}}}_j={\varvec{J}}_{j}\dot{{\varvec{q}}}\quad (j=1,2,\ldots ,n) . \end{aligned}$$

(2)

Then, ${\varvec{J}}_{j} \in R^{m \times n}$ can be described as Jacobian matrix, which is a function of angle ${\varvec{q}}$. In this section, m represents the dimension of workspace and n represents the number of links. Differentiating calculation of (2), we can obtain acceleration of jth link $\ddot{{\varvec{r}}}_j$ shown as (3).

$$\begin{aligned} \ddot{{\varvec{r}}}_j={\varvec{J}}_j({\varvec{q}})\ddot{{\varvec{q}}}+\dot{{\varvec{J}}}_j({\varvec{q}})\dot{{\varvec{q}}} . \end{aligned}$$

(3)

Then, we can obtain (4) by putting (3) into (1).

$$\begin{aligned} \ddot{{\varvec{r}}}_j-\dot{{\varvec{J}}}_j\dot{{\varvec{q}}}={\varvec{J}}_j{\varvec{M}}^{-1}[\tau -{\varvec{h}}({\varvec{q}},\dot{{\varvec{q}}})-{\varvec{g}}({\varvec{q}})-{\varvec{D}}\dot{{\varvec{q}}}]. \end{aligned}$$

(4)

Here, two variables are defined as follows:

$$\begin{aligned}&\tilde{{\varvec{\tau }}}{\mathop {=}\limits ^{\bigtriangleup }} {\varvec{\tau }} -{\varvec{h}}({\varvec{q}},\dot{{\varvec{q}}})-{\varvec{g}}({\varvec{q}})-{\varvec{D}}\dot{{\varvec{q}}}, \end{aligned}$$

(5)

$$\begin{aligned}&\ddot{\tilde{{\varvec{r}}}}_j{\mathop {=}\limits ^{\bigtriangleup }} \ddot{{\varvec{r}}}_j-\dot{{\varvec{J}}}_j\dot{{\varvec{q}}}={\varvec{J}}_j\ddot{{\varvec{q}}}. \end{aligned}$$

(6)

Then, (4) can be rewritten as

$$\begin{aligned} \ddot{\tilde{{\varvec{r}}}}_j={{\varvec{J}}}_j{\varvec{M}}^{-1}\tilde{{\varvec{\tau }}}\quad (j=1,2,\ldots ,n). \end{aligned}$$

(7)

Here, the desired end-effector’s acceleration $\ddot{\tilde{{\varvec{r}}}}_{nd}$ is considered as a primary task. Putting $j=n$ into (7), the desired $\ddot{\tilde{{\varvec{r}}}}_{j}$ is written into $\ddot{\tilde{{\varvec{r}}}}_{nd}$, and (4) can be expressed [12].

$$\begin{aligned} \ddot{\tilde{{\varvec{r}}}}_{nd}={{\varvec{J}}}_n{\varvec{M}}^{-1}\tilde{{\varvec{\tau }}}. \end{aligned}$$

(8)

From (8), $\tilde{{\varvec{\tau }}}$ is obtained in (9).

$$\begin{aligned} \tilde{{\varvec{\tau }}}= & {} ({\varvec{J}}_{n}{\varvec{M}}^{-1})^{+} \ddot{\tilde{{\varvec{r}}}}_{nd}\nonumber \\&+ [ {\varvec{I}}_{n} - ({\varvec{J}}_{n}{\varvec{M}}^{-1})^{+}({\varvec{J}}_{n}{\varvec{M}}^{-1}) ]\, ^1{\varvec{l}}, \end{aligned}$$

(9)

${}^1{\varvec{l}}$ represents an arbitrary vector when ${}^1{\varvec{l}} \in R^{n}$. The left superscript $``1''$ of ${}^1{\varvec{l}}$ represents the first dynamic reconfiguration subtask. In the right side of (9), the first part describes the solution of minimizing $\tilde{{\varvec{\tau }}}$ in the null room of ${\varvec{J}}_{n}{\varvec{M}}^{-1}$ during executing $\ddot{\tilde{{\varvec{r}}}}_{nd}$.

The second part expresses the elements of torques at each joint, which can change the configuration of manipulator despite the influence of arbitrary $\ddot{\tilde{{\varvec{r}}}}_{nd}$ as end-effector acceleration. In this research, $^1\ddot{\tilde{{\varvec{r}}}}_{nd}$ is defined as the desired acceleration for a higher level dynamic reconfiguration control system and $^1 \ddot{\tilde{{\varvec{r}}}}_{jd}$ is acceleration for ordinary dynamic reconfiguration. The relation between $^1 \ddot{\tilde{{\varvec{r}}}}_{jd}$ and $\ddot{\tilde{{\varvec{r}}}}_{nd}$ is described in (10) by substituting (9) into $^1\ddot{\tilde{{\varvec{r}}}}_{jd}={{\varvec{J}}}_j{\varvec{M}}^{-1}\tilde{{\varvec{\tau }}}$.

$$\begin{aligned} ^1\ddot{\tilde{{\varvec{r}}}}_{jd}= & {} {\varvec{J}}_{j}{\varvec{M}}^{-1} ({\varvec{J}}_{n}{\varvec{M}}^{-1})^{+} \ddot{\tilde{{\varvec{r}}}}_{nd} \nonumber \\&\,+\,{\varvec{J}}_{j}{\varvec{M}}^{-1} [ {\varvec{I}}_{n} - ({\varvec{J}}_{n}{\varvec{M}}^{-1})^{+}({\varvec{J}}_{n}{\varvec{M}}^{-1}) ]\, ^1{\varvec{l}}. \end{aligned}$$

(10)

Here, two new variables are defined in the following equations:

$$\begin{aligned}&\varDelta ^1\ddot{\tilde{{\varvec{r}}}}_{jd}{\mathop {=}\limits ^{\bigtriangleup }} ^1\ddot{\tilde{{\varvec{r}}}}_{jd} - {\varvec{J}}_{j}{\varvec{M}}^{-1} ({\varvec{J}}_{n}{\varvec{M}}^{-1})^{+} \ddot{\tilde{{\varvec{r}}}}_{nd}, \end{aligned}$$

(11)

$$\begin{aligned}&^1{\varvec{\varLambda }}_{j}{\mathop {=}\limits ^{\bigtriangleup }} {\varvec{J}}_{j}{\varvec{M}}^{-1} [ {\varvec{I}}_{n} - ({\varvec{J}}_{n}{\varvec{M}}^{-1})^{+}({\varvec{J}}_{n}{\varvec{M}}^{-1}) ]. \end{aligned}$$

(12)

In (11), $\varDelta ^1\ddot{\tilde{{\varvec{r}}}}_{jd}$ is called “the first dynamic reconfiguration acceleration”. In (12), $^1{\varvec{\varLambda }}_j$ is a ${m{\times }n}$ matrix called “the first dynamic reconfiguration matrix”. And then, (10) can be rewritten as

$$\begin{aligned} \varDelta ^1\ddot{\tilde{{\varvec{r}}}}_{jd} = \,^1{\varvec{\varLambda }}_{j} \,^1{\varvec{l}}. \end{aligned}$$

(13)

The relation between $^1\ddot{\tilde{{\varvec{r}}}}_{jd}$ and $\varDelta ^1\ddot{\tilde{{\varvec{r}}}}_{jd}$ is shown in Fig. 4. The key is to adjust $^1{\varvec{l}}$ to generate $\varDelta ^1\ddot{\tilde{{\varvec{r}}}}_{jd}$.

Solving $^1{\varvec{l}}$ in (13) as

Fig. 4

Configuration change of intermediate links during manipulator executing task

$$\begin{aligned} ^1{\varvec{l}} = \,^1{\varvec{\varLambda }}^{+}_{j} \varDelta {}^1\ddot{\tilde{{\varvec{r}}}}_{jd} +\left( {\varvec{I}}_n - \,^1{\varvec{\varLambda }}^{+}_{i}\,^1{\varvec{\varLambda }}_{j}\right) \,^2{\varvec{l}}. \end{aligned}$$

(14)

In (14), $^2{\varvec{l}}$ is an arbitrary vector satisfying $^2{\varvec{l}} \in R^{n}$. If $^1{\varvec{l}}$ is restricted by $\Vert {}^1{\varvec{l}}\Vert \le 1$. ${}^1{\varvec{l}}$ has same dimension as $\tilde{{\varvec{\tau }}}$, which could be understood from (9). Then ${}^1{\varvec{l}}$ in (9) could be thought to be new input torque. Therefore, $\Vert {}^1{\varvec{l}}\Vert \le 1$ means all input torques are restricted equally. Then by inputting (14) to $\Vert {}^1{\varvec{l}}\Vert = {}^1{\varvec{l}}^T{}^1{\varvec{l}} \le 1$. The following relation can be derived, which means ellipsoid made by $\Vert {}^1{\varvec{l}}\Vert \le 1$. This procedure has been known as normalization. Then we have

$$\begin{aligned} {\varDelta {}^1\ddot{\tilde{{\varvec{r}}}}_{jd}}^{T} \left( {}^1{\varvec{\varLambda }}^{+}_{j}\right) ^{T} {}^1{\varvec{\varLambda }}^{+}_{j} \varDelta {}^1\ddot{\tilde{{\varvec{r}}}}_{jd} \le 1. \end{aligned}$$

(15)

If rank$(^1{\varvec{\varLambda } }_{i})=m$, (15) represents an m-dimensional space ellipsoid, satisfying

$$\begin{aligned} \varDelta {}^1\ddot{\tilde{{\varvec{r}}}}_{jd} = {}^1{\varvec{\varLambda }}_{j} {}^1{\varvec{\varLambda }}^{+}_{j} \varDelta {}^1\ddot{\tilde{{\varvec{r}}}}_{jd} ,\quad \varDelta {}^1\ddot{\tilde{{\varvec{r}}}}_{jd} \in R^m, \end{aligned}$$

(16)

which means that $\varDelta ^1\ddot{\tilde{{\varvec{r}}}}_{jd}$ can be arbitrarily obtained in m-dimensional space and (15) always has the value $^1{\varvec{l}}$ satisfying all $\varDelta ^1\ddot{\tilde{{\varvec{r}}}}_{jd} \in R^{m}$. Besides, if rank$(^1{\varvec{\varLambda } }_{j})=r<m$, ${\varDelta }\ddot{\tilde{{\varvec{r}}}}_{jd}$ is not obtained arbitrarily in $R^m$. Therefore, we name reduced ${\varDelta }\ddot{\tilde{{\varvec{r}}}}_{jd}$ after ${\varDelta }^1\ddot{\tilde{{\varvec{r}}}}^{*}_{jd}$. Then (15) can be denoted as the following equation:

$$\begin{aligned}&\left( \varDelta {}^1\ddot{\tilde{{\varvec{r}}}}^{*}_{jd}\right) ^T \left( ^1{\varvec{\varLambda }}^{+}_{j}\right) ^{T} \,^1{\varvec{\varLambda }}^{+}_{j} \varDelta {}^1\ddot{\tilde{{\varvec{r}}}}^{*}_{jd} \le 1, \nonumber \\&\left( \varDelta {}^1\ddot{\tilde{{\varvec{r}}}}^{*}_{jd} = {}^1{\varvec{\varLambda }}_{j} {}^1{\varvec{\varLambda }}^{+}_{j} \varDelta {}^1\ddot{\tilde{{\varvec{r}}}}_{jd}\right) . \end{aligned}$$

(17)

Equation (17) denotes an r-dimensional ellipsoid on immediate link j. Then, the matrix ${\varvec{\varLambda }}$ is denoted by the singular value dissolution:

$$\begin{aligned} ^1{\varvec{\varLambda }}_j=^1{\varvec{U}}_j ^1{\varvec{\Sigma }}_j ^1{\varvec{V}}_j^T. \end{aligned}$$

(18)

In (18), $^1{\varvec{U}} \in R^{m \times m}$ and $^1{\varvec{V}}\in R^{n \times n}$ denote orthogonal matrixes, and r is the number of non-zero singular values of $^1{\varvec{\varLambda }}_j$ ($\sigma _{j,1}{\ge }\,\,{\cdots }\,\,{\ge }\sigma _{j,r}>0$). Besides, $r\,{\le }\,m$ since rank$( ^1{\varvec{\varLambda }}_j)=r\,{\le }\,m$. Thus, when the end-effector of manipulator executes some tasks, dynamic reconfiguration capability of jth link can be denoted as

$$\begin{aligned} ^1w_{j} = ^1\sigma _{j,1} \cdot ^1\sigma _{j,2} \ldots ^1\sigma _{j,r} \end{aligned}$$

(19)

Here, we name ${}^1w_{j}$ in (19) as dynamic reconfiguration manipulability measure (DRMM) [9], indicating the degree of that reconfiguration acceleration of jth link can be generated for arbitrary direction. And then, volume of dynamic reconfiguration manipulability ellipsoid (DRME) at the jth link is described by referring and using the same concept given by page 131 in [13] as

$$\begin{aligned} ^1V_{DRj}= & {} c_m \cdot {}^1w_{j} , \end{aligned}$$

(20)

$$c_{m}= \left\{ \begin{array}{*{20}l} \frac{2(2\pi )^{(m-1)/2}}{1\cdot 3 \ldots (m-2)m}, \,\quad \,{\text {when}} \,m\, {\text {is odd }}. \\ \frac{(2\pi )^{m/2}}{2\cdot 4 \ldots (m-2)m}, \quad {\text { when}} \,m \,{\text {is even }}. \end{array} \right.$$

(21)

Since the coefficient $c_{m}$ given as (21) is a constant when m is fixed, the volume is proportional to ${}^1w_{j}$. Hence, we can regard ${}^1w_{j}$ as a representative measure.

To consider dynamic reconfiguration measure of the whole manipulator links, we explain again Dynamic reconfiguration manipulability shape index (DRMSI) for the readers’ convenience based on previous work [9] and the concept was proposed by [12] as follows:

$$\begin{aligned} ^1W_{DR} = \sum _{j=1}^{n-1} \,a_j \,\,^1V_{DRj}. \end{aligned}$$

(22)

Here, $a_j$ is unit adjustment between different dimension. In this paper, singular-values increase a hundredfold to enlarge value of ellipsoids, compared to ellipses or line segments.

Fig. 5

Concept of visual lifting approach

4 Visual lifting approach

Visual lifting approach has been proposed [14, 15], which can improve the stability of biped standing and walking as shown in Fig. 5. We apply a model-based matching method to measure the posture of a static target object described by ${\varvec{\psi }}(t)=[X_{\text {head}}(t), Y_{\text {head}}(t), Z_{\text {head}}(t),\phi _{\text {head}}(t), \theta _{\text {head}}(t),\psi _{\text {head}}(t)]$ representing the position and orientation of robot’s head based on $\Sigma _{H}$. The relatively desired head posture coordinate of $\Sigma _{{R}}$ (coordinate of reference target object) and the current head posture coordinate $\Sigma _\text {H}$ are predefined by Homogeneous Transformation as ${^{H}{\varvec{T}}_\text {R}}$. The difference between the desired head posture coordinate $\Sigma _{H_\text {d}}$ and the current head posture coordinate $\Sigma _{H}$ is defined as ${^H{\varvec{T}}_{H_\text {d}}}$, it can be described by:

$$\begin{aligned} {^H{\varvec{T}}_{H_\text {d}}({\varvec{\psi }}_\text {d}(t), {\varvec{\psi }}(t))} = {^H{\varvec{T}}_{\text {R}}}({\varvec{\psi }}(t))\cdot {^{H_\text {d}}{\varvec{T}}_{\text {R}}}^{-1}({\varvec{\psi }}_\text {d}(t)), \end{aligned}$$

(23)

where ${^H{\varvec{T}}_{\text {R}}}$ is calculated by ${\varvec{\psi }}(t)$. ${\varvec{\psi }}(t)$ can be measured by online visual posture evaluation proposed by [16]. However, we assume that this parameter is given directly. Here, the force is considered to be directly proportional to $\delta {\varvec{\psi }}(t)$, which is exerted on the head to minimize the deviation $\delta {\varvec{\psi }}(t)(={\varvec{\psi }}_\text {d}(t)-{\varvec{\psi }}(t))$ calculated from ${^H{\varvec{T}}_{H_\text {d}}}$. The deviation of the robot’s head posture is caused by gravity force and the influence of walking dynamics. The joint torque ${\varvec{\tau }}_\text {h}(t)$ lifting the robot’s head up and forward is donated:

$$\begin{aligned} {\varvec{\tau }}_\text {h}(t) = {\varvec{J}}_\text {h}({\varvec{q}})^T{\varvec{K}}_{\text {p}}\delta {\varvec{\psi }}(t), \end{aligned}$$

(24)

where ${\varvec{J}}_\text {h}({\varvec{q}})=[{\varvec{J}}_{hx}({\varvec{q}}), {\varvec{J}}_{hy}({\varvec{q}}), {\varvec{J}}_{hz}({\varvec{q}})]^T$ is Jacobian matrix of the head posture against joint angles ${\varvec{q}}$ from supporting foot to head including $q_1, q_2, q_3, q_4, q_8, q_9, q_{10}, q_{17}$, and ${\varvec{K}}_{p}=[K_{px}, K_{py},K_{pz}]$ is lifting proportional gain like impedance control changing the impedance by changing damping and spring coefficients that can adjust joint torque ${\varvec{\tau }}_\text {h}(t)$ to desired one where $K_{pz}$ is visual-lifting gain adjusting visual feedback torque inputs along z-axis direction that can keep the head height targeting the desired one as much as possible and determine that humanoid robots walk like humans or monkeys. $K_{pz}$ also has special ranges to stabilize the walking. We apply these inputs to stop falling down caused by the influence of gravity or dangerous slipping gaits happening unpredictably during walking progress. We stress that the input torque for non-holonomic joint such as joint-1, $\tau _{h_1}$ in ${\varvec{\tau }}_h(t)$ in (24) is zero for its free joint. $\delta {\varvec{\psi }}(t)$ can show the deviation of the humanoid’s position and orientation; however, only position is discussed in this study.

5 Stability analyses of biped walking by dynamical-evaluating index

In the environment that sampling time is set as $2.0 \times 10^{-4}$ (s) and coefficients of friction between the foot and the ground are set as $\mu _s =1.0$ (static friction coefficient), $\mu _k=0.7$ (viscous friction coefficient), the walking simulations are done. The desired position of head is set as ${\varvec{\psi _\text {d}}}=[0,0,2.30$ (m)].

Concerning simulation environment, we used “Borland C++ Builder Professional Ver. 5.0” to make simulation program and “OpenGL Ver. 1.5.0” to display humanoid’s time-transient configurations.

In this section, the dynamical shape changeability and stability of biped-walking based on VLA are analyzed according to data obtained from the simulations. In the simulations, we change ${\varvec{K}}_{p}=[K_{px}, K_{py},K_{pz}]$ in VLA to analyze this walking motion under different circumstances. Thus, we did 54 cases of simulations by changing the ${\varvec{K}}_p$, where $K_{px}\in [10,20,30], K_{py}\in [190,290,390],K_{pz}\in [800,900,1000, 1100,1200]$. $K_{pz}$ is set as six kinds of values to find the range of $K_{pz}$, which can be used to stabilize the walking. The results of simulations are shown in Table 2, where we can know the walking states, number of steps, walking time, stride and average of DRMSI, which can be used to analyze the dynamical shape changeability and stability of the biped walking.

We can see that stride of stabilized walking changes among the range from 0.328 to 0.451 (m) and stride on unstable walking is fewer than 0.328[m] from Table 2. And we can also find that stride of walking decreases when $K_{py}$ increases and $K_{py}$ has no influence on stride from case (10) to case (18) where $K_{pz}=900$. Comparing case (16), (25), (34) and (43) where $K_{px}=10$ and $K_{py}=390$, we can find that stride increases from 0.342 to 0.451 (m). Therefore, $K_{py}$ and $K_{pz}$ has opposite influence on stride and $K_{px}$ has no influence on stride, which is easy to understand when we analyze from the influence of resolution of torque ${\varvec{\tau }}_\text {h}(t)$ in (24) into x-, y- and z-axis direction, respectively, on stride.

Since Table 2 also shows the number of steps and total walking time, we can calculate the walking period easily. When humanoid robot can stabilize the biped walking from case (10) to case (36) and from case (43) to case (45) during 30 (s), we compare the number of steps to compare the walking period. Then, we find that change of $K_{px}$ has no influence on walking period from case (10) to case (13) where number of steps is 61 and when increase of $K_{py}$ and $K_{pz}$ has influence on walking period representatively since acceleration along y-axis and z-axis direction also increases representatively. Comparing the number of steps in case (10), (13) and (16), we can see that walking period decreases when $K_{py}$ increases. Comparing the number of steps in case (16), (25), (34) and (43), we can see that walking period increases when $K_{pz}$ increases.

Figure 6 shows the screenshot of walking states corresponding to DRMSI in case (36). Points A and F represent that connecting foot surface-connects with ground. From point A to point B, surface-connecting foot switches to supporting-foot. Walking states between point B and point C represent supporting-foot surface-connects with ground. Walking states between points C and point F represent supporting-foot point-connects with ground. From this figure, we can find that DRMSI changes according to walking states, which indicates DRMSI is determined by the configuration of humanoid robot.

Fig. 6

Screenshot of walking states corresponding to DRMSI in case (36)

Table 2 Results of simulation in 54 cases

Fig. 7

Height of head and waist in cases (9), (18), (28), (36), (45), (54) corresponding to a–f, respectively. Since appropriate gain sets can make the humanoid robot stabilize walking motion, height of head and waist changes periodically in a small range-like cases (18), (28), (36) and (45). However, in cases (9) and (54), the height of head and waist changes aperiodically and becomes lower, which shows that humanoid robot has a tendency to fall down or has fallen down

Fig. 8

Average of DRMSI in biped walking. a Average of DRMSI by setting $K_{px}$ and $K_{py}$ with $K_{pz}$ fixed at $K_{pz}=800$ from case (1) to case (9). b Average of DRMSI by setting $K_{px}$ and $K_{py}$ with $K_{pz}$ fixed at $K_{pz}=900$ from case (10) to case (18). c Average of DRMSI by setting $K_{px}$ and $K_{py}$ with $K_{pz}$ fixed at $K_{pz}=1000$ from case (19) to case (27). d Average of DRMSI by setting $K_{px}$ and $K_{py}$ with $K_{pz}$ fixed at $K_{pz}=1100$ from case (28) to case (36). e Average of DRMSI by setting $K_{px}$ and $K_{py}$ with $K_{pz}$ fixed at $K_{pz}=1200$ from case (37) to case (45). f Average of DRMSI by setting $K_{px}$ and $K_{py}$with $K_{pz}$ fixed at $K_{pz}=1300$ from case (46) to case (54). We can see that when $K_{px}$ is set from 10 to 30, there is almost no change about average of DRMSI such as case (1) $\rightarrow$ case (2) $\rightarrow$ case (3), case (4) $\rightarrow$ case (5) $\rightarrow$ case (6), case (7) $\rightarrow$ case (8) $\rightarrow$ case (9) and so on. On the other hand, when $K_{py}$ is set from 190 to 390, there is a small range of change about average of DRMSI in cases those can keep walking which are shown b–d such as case (10) $\rightarrow$ case (13) $\rightarrow$ case (16), case (11) $\rightarrow$ case (14) $\rightarrow$ case (17), case (12) $\rightarrow$ case (15) $\rightarrow$ case (18). Therefore, $K_{px}$ and $K_{py}$ have small effect on DRMSI, indicating that $K_{px}$ and $K_{py}$ are not necessary issues for stabilizing the biped walking

Fig. 9

Screenshot of walking states in cases (1), (4), (28), (37). Dynamical reconfiguration manipulability ellipsoids (DRMEs) degraded into small ellipses and line segments when humanoid robots tended to fall down shown like cases (1), (4), (37). DRMSI is calculated from the total volume of ellipsoids, ellipses and line segments appearing on each intermediate link of humanoid from the supporting foot to head. Hence, DRMSI becomes small while the region of unstable walking appears and humanoid tends to fall down. However, in case (37), humanoid robots can stabilize walking very well while region of stable walking appears, and all the DRMEs is larger than the states of falling down. From this point, we think that DRMSI is an effective measurement to evaluate the dynamical shape changeability

Fig. 10

Effect of gain $K_{pz}$ on DRMSI. a The change of average of DRMSI by setting $K_{px}$ and $K_{pz}$ with $K_{py}$ fixed at $K_{py}=390$. b The change of average of DRMSI by setting $K_{py}$ and $K_{pz}$ with $K_{px}$ fixed at $K_{px}=10$. a $K_{pz}$ has more influence on DRMSI than $K_{px}$. b $K_{pz}$ has more influence on DRMSI than $K_{py}$. And $K_{pz}$ is also influential in the change of stride by comparing the stride of case (1), case (10), case (19), case (28), case (37), case (46) in Table 2. Comparing the average of DRMSI, we find it important to keep the balance when setting $K_{px}$, $K_{py}$ and $K_{pz}$ for obtaining the larger DRMSI. From two figures, some cases enclosed in two red cycles represent humanoid robot can stabilize the walking. And maximum and minimum of average of DRMSI are marked in b corresponding to case (28) and case (37) representatively, indicating that DRMSI can be used to evaluate the dynamical shape changeability and stability of walking motion. Hence, we can conclude that when $K_{pz}$ increases in certain range from 900 to 1200 with the balance setting of $K_{px}$ and $K_{py}$, DRMSI also increases. And the gains setting in case (28) is the best combination of $K_{px}$, $K_{py}$, $K_{pz}$

Figure 7 shows the height of head and waist in cases (9), (18), (28), (36), (45), (54) corresponding to figures a–f, respectively. Since appropriate gain sets can make the humanoid robot stabilize walking motion, height of head and waist changes periodically in a small range-like cases (18), (28), (36) and (45) shown in Fig. 7. However, in cases (9) and (54), the height of head and waist changes aperiodically and becomes lower, which shows that humanoid robot has a tendency to fall down or has fallen down shown in Fig. 7.

Figure 8 shows the average of DRMSI. From the figure, we can see that when $K_{px}$ is set from 10 to 30, there is almost no change about average of DRMSI such as case (1) $\rightarrow$ case (2) $\rightarrow$ case (3), case (4) $\rightarrow$ case (5) $\rightarrow$ case (6), case (7) $\rightarrow$ case (8) $\rightarrow$ case (9) and so on. On the other hand, when $K_{py}$ is set from 190 to 390, there is a small range of change about average of DRMSI in cases those can keep walking which are shown in Fig. 8b–d such as case (10) $\rightarrow$ case (13) $\rightarrow$ case (16), case (11) $\rightarrow$ case (14) $\rightarrow$ case (17), case (12) $\rightarrow$ case (15) $\rightarrow$ case (18). Therefore, $K_{px}$ and $K_{py}$ have small effect on DRMSI, indicating that $K_{px}$ and $K_{py}$ are not necessary issues for stabilizing the biped walking.

Figure 9 shows the screenshot of walking states in cases (1), (4), (28), (37). Dynamical reconfiguration manipulability ellipsoids (DRMEs) degraded into small ellipses and line segments when humanoid robots tended to fall down shown like cases (1), (4), (37) in Fig. 9. And DRMSI is calculated from the total volume of ellipsoids, ellipses and line segments appearing on each intermediate link of humanoid from the supporting foot to head. Hence, DRMSI becomes small while the region of unstable walking appears and humanoid tends to fall down. However, in case (37), humanoid robots can stabilize walking very well while region of stable walking appears, and all the DRMEs are larger than the states of falling down. From this point, we think that DRMSI is an effective measurement to evaluate the dynamical shape changeability.

Then, we set $K_{pz}$ as 800, 900, 1000, 1100, 1200 and 1300 representatively to do walking simulations. Figure 10a shows that $K_{pz}$ has more influence on DRMSI than $K_{px}$. Figure 10b shows that $K_{pz}$ has more influence on DRMSI than $K_{py}$. And $K_{pz}$ is also influential in the change of stride by comparing the stride of case (1), case (10), case (19), case (28), case (37), case (46) in Table 2. Comparing the average of DRMSI, we find it important to keep the balance when setting $K_{px}$, $K_{py}$ and $K_{pz}$ for obtaining the larger DRMSI. From two figures, some cases enclosed in two red cycles represent humanoid robot can stabilize the walking. And maximum and minimum of average of DRMSI are marked in Fig. 10b corresponding to case (28) and case (37) representatively, indicating that DRMSI can be used to evaluate the dynamical shape changeability and stability of walking motion. From Fig. 10, we can conclude that when $K_{pz}$ increases in certain range from 900 to 1200 with the balance setting of $K_{px}$ and $K_{py}$, DRMSI also increases. And the gains setting in case (28) is the best combination of $K_{px}$, $K_{py}$, $K_{pz}$. This conclusion can be used to stabilize the biped walking.

6 Conclusion

In this paper, we explained the proposed DRMSI and visual-lifting approach. Then we did 54 cases of simulations by changing the visual-lifting gain ${\varvec{K}}_p$. Then we found the best combination of $K_{pi}\,(i=x, y, z)$ to keep the walking being kept in a continuous and sustainable stepping.