Non-solvable Groups whose Character Degree Graph has a Cut-Vertex. I

Abstract

Let G be a finite group. Denoting by $\textrm{cd}(G)$ the set of degrees of the irreducible complex characters of G, we consider the character degree graph of G: this is the (simple undirected) graph whose vertices are the prime divisors of the numbers in $\textrm{cd}(G)$, and two distinct vertices p, q are adjacent if and only if pq divides some number in $\textrm{cd}(G)$. In the series of three papers starting with the present one, we analyze the structure of the finite non-solvable groups whose character degree graph possesses a cut-vertex, i.e. a vertex whose removal increases the number of connected components of the graph.

1 Introduction

Given a finite group G, let $\textrm{cd}(G) = \{\chi (1) ~|~ \chi \in \textrm{Irr}(G)\}$ be the set of the degrees of the irreducible complex characters of G. This set has been extensively studied, on its own account as well as in relation to the structure of the group G. The character degree graph (or degree graph) $\Delta (G)$ is the simple undirected graph related to the set $\textrm{cd}(G)$ as follows: the vertex set $\textrm{V}(G)$ of $\Delta (G)$ consists of all prime numbers dividing the degree of some irreducible character of G, and two distinct vertices p, q are adjacent in $\Delta (G)$ if and only if the product pq divides some irreducible character degree of G. Several results in the literature illustrate that graph-theoretical features of $\Delta (G)$ are significantly linked to the structure of G. For a detailed account on this subject, we refer to the expository paper [20].

As an important example, we mention that the number of connected components of $\Delta (G)$ is in general at most three [24], and at most two if G is solvable. The structure of the finite groups whose degree graph is disconnected is described in [19] for the solvable case, and in [22] for the non-solvable case.

As a further step in the study of the connectivity properties of the degree graph, it is natural to consider the question about the existence of a cut-vertex, i.e. a vertex whose removal yields a resulting graph with more connected components than the original one. A graph that is connected and has a cut-vertex is said to have connectivity degree 1, which is the smallest degree of connectivity of a connected graph. The finite solvable groups G such that $\Delta (G)$ has connectivity degree 1 are investigated in [21]; among other things, it is shown ([21, Theorem 1.1]) that in this case $\Delta (G)$ has a unique cut-vertex.

We also mention that the finite groups G whose degree graph $\Delta (G)$ has connectivity degree 1, and which satisfy the strong assumption (studied in [1], and implying non-solvability) that the complement graph of $\Delta (G)$ is non-bipartite, are described in [11].

In the series of three papers starting with the present one, we give a complete classification of all finite non-solvable groups whose degree graph has a cut-vertex (see Theorems A, B and C in Section 2). It turns out that the structure of the relevant groups, as well as of the corresponding degree graphs, is significantly restricted and, quite surprisingly, does not fall too far from the structure of the finite non-solvable groups with a disconnected degree graph (see [22] or Theorem 3.7). As an interesting feature, we mention that in all cases (similarly to the situation for solvable groups) a degree graph $\Delta (G)$ with connectivity degree 1 has a unique cut-vertex (Corollary D).

The structure of the finite non-solvable groups whose character degree graph has connectivity degree 1 can be generally described as follows. Such a group G has a unique non-solvable composition factor S, belonging to the following short list of isomorphism types: $\mathrm{{PSL}}_2(t^a)$, $\mathrm{{Sz}}(2^a)$, $\mathrm{{PSL}}_3(4)$, $\mathrm{{M}}_{11}$, $\mathrm{{J}}_1$; moreover, if $S \not \cong \mathrm{{PSL}}_2(t^a)$, then G has a (minimal) normal subgroup isomorphic to S (Theorem 4.1). Furthermore, $\textrm{V}(G) = \textrm{V}(S) \cup \{p\} = \textrm{V}(G/R) \cup \{p\}$, where R is the solvable radical of G and p is the cut vertex of $\Delta (G)$ (Theorem 3.16). We also remark that in all cases, except possibly when the non-abelian simple section S is isomorphic to the Janko group $\mathrm{{J}}_1$, the cut-vertex p of $\Delta (G)$ is a complete vertex (i.e. it is adjacent to all other vertices) of $\Delta (G)$; moreover, the graph $\Delta (G) - p$ obtained from $\Delta (G)$ by removing the vertex p (and all edges incident to p) has exactly two connected components, which are complete graphs. Rather remarkably, one of them consists of a single vertex, and hence our results give also a description of the finite non-solvable groups G such that $\Delta (G)$ has a cut-edge, i.e. an edge whose removal increases the number of connected components of the graph.

In Section 2 of this paper, we present the complete statement of our main results Theorem A, Theorem B and Theorem C, as well as a discussion concerning the degree graphs associated to the relevant groups with some figures and comments. After another preliminary section, in Section 4 we prove Theorem A under the assumption that the non-abelian simple section S of the group is not isomorphic to a projective special linear group $\textrm{PSL}_2(t^a)$. The case $S \cong \textrm{PSL}_2(t^a)$ requires a much longer and rather technical analysis, which will be carried out in the forthcoming papers [8] and [9], where the proof of Theorem A and Theorem B will be completed. Finally, in Section 5 we prove Theorem C, which provides the classification the finite non-solvable groups G such that $\Delta (G)$ is not connected and has a cut-vertex, and that is rather directly derived from the classification in [22].

We close this introductory section by recalling that results about the degree graph of finite groups often have a counterpart concerning the prime graph built on the set of conjugacy class sizes of groups. The analogue of the problem here considered is studied in [10], where a classification of the finite groups whose prime graph on conjugacy class sizes has a cut-vertex is provided. However, the situation in that context turns out to be significantly different from the present one, since the relevant groups turn out to be solvable of Fitting height at most three and, moreover, there are cases in which the relevant graphs have two cut-vertices.

Not surprisingly, in this paper we use results that depend on the classification of the finite simple groups. Every group considered in the following discussion is tacitly assumed to be a finite group.

2 The Classification

Given a group G, we denote by $R = R(G)$ the solvable radical (i.e. the largest solvable normal subgroup), and by $K = K(G)$ the solvable residual (i.e. the smallest normal subgroup with a solvable factor group) of G. Equivalently, K(G) is the last term of the derived series of G. Also, as customary, $\pi (n)$ denotes the set of all prime divisors of a positive integer n, and we write $\pi (G)$ for $\pi (|G|)$.

This section is entirely dedicated to presenting the statement of the main theorems (Theorem A, Theorem B and Theorem C), the proof of which begins in the present paper as specified in the Introduction. The first two theorems treat the connected case, and can be regarded as two parts of the same result (in fact, they are stated separately only to improve clarity of the exposition and readability): the former deals with groups with no composition factors isomorphic to $A_5$, whereas the latter covers the complementary situation. On the other hand, the disconnected case is analyzed in Theorem C. The rest of the section also presents the associated degree graphs, with some figures and comments.

In order to clarify the statements we also mention that, for $H = \textrm{SL}_2(t^a)$ (where t is a prime), an H-module V over the field $\mathbb {F}_t$ with t elements is called the natural module for H if V is isomorphic to the standard module for $\textrm{SL}_2(t^a)$, i.e. the two dimensional vector space over the field $\mathbb {F}_{t^a}$ (or any of its Galois conjugates) acted upon by matrix multiplication, seen as an $\mathbb {F}_t[H]$-module. We will freely use this terminology also referred to the conjugation action of a group on a suitable elementary abelian normal subgroup.

Theorem A

Let G be a non-solvable group with no composition factors isomorphic to $\textrm{SL}_2(4)\cong A_5$, let R and K be, respectively, the solvable radical and the solvable residual of G, and let p be a prime number. Then the graph $\Delta (G)$ is connected and has cut-vertex p, if and only if G/R is an almost simple group, $\textrm{V}(G) = \pi (G/R)\cup \{p\}$ and, denoting by S the socle of G/R, one of the following holds.

• (a) S is isomorphic to ${\textrm{Sz}}(2^a)$. In this case, $K\cong S$ is a minimal normal subgroup of G, $a\ge 3$ is a prime, $p=2^a-1$ and $\textrm{V}(G/K)\subseteq \{p\}$.

• (b) S is isomorphic to ${\textrm{PSL}}_3(4)$. In this case, $K\cong S$ is a minimal normal subgroup of G, $|G:KR|\in \{1,3\}$, $p=5$ and $\textrm{V}(G/K)\subseteq \{5\}$.

• (c) S is isomorphic to ${\text {M}}_{11}$. In this case, $K\cong S$ is a minimal normal subgroup of $G=K\times R$, $p=5$ and $\textrm{V}(G/K) = \textrm{V}(R)\subseteq \{5\}$.

• (d) S is isomorphic to ${\textrm{J}}_1$. In this case, $K\cong S$ is a minimal normal subgroup of $G=K\times R$, $p=2$ and $\textrm{V}(G/K) = \textrm{V}(R)\subseteq \{2\}$.

• (e) S is isomorphic to $\textrm{PSL}_2(t^a)$, where t is an odd prime and $t^a>5$. In this case |G/KR| is not a multiple of t, $p\ne t$, and one of the following holds.

  • (i) K is isomorphic to $S\cong \textrm{PSL}_2(t^a)$ or to $\textrm{SL}_2(t^a)$, and $\textrm{V}(G/K)=\{p\}$.

  • (ii) K contains a minimal normal subgroup L of G such that K/L is isomorphic to $\textrm{SL}_2(t^a)$ and L is the natural module for K/L; moreover, $\textrm{V}(G/K)=\{p\}$.

  • (iii) $t^a=13$ and $p=2$. K contains a minimal normal subgroup L of G such that K/L is isomorphic to $\textrm{SL}_2(13)$, and L is one of the two 6-dimensional irreducible modules for $\textrm{SL}_2(13)$ over $\mathbb {F}_3$. Moreover, $\textrm{V}(G/K)\subseteq \{2\}$.

• (f) S is isomorphic to $\textrm{SL}_2(2^a)$, where $a> 2$, and one of the following holds.

  • (i) $K\cong S$ is a minimal normal subgroup of G; also, either $\textrm{V}(G/K) \cup \pi (G/KR)=\{2\}$ and $p=2$, or G/KR has odd order, $p\ne 2$ and $\textrm{V}(G/K)=\{p\}$.

  • (ii) K contains a minimal normal subgroup L of G such that K/L is isomorphic to $\textrm{SL}_2(2^a)$ and L is the natural module for K/L; also, G/KR has odd order, $p\ne 2$, $\textrm{V}(G/K)=\{p\}$ and, for a Sylow 2-subgroup T of G, we have $T'=(T\cap K)'$.

In all cases except in case (d) when R is abelian, p is a complete vertex of $\Delta (G)$; furthermore, in all cases, p is the unique cut-vertex of $\Delta (G)$.

Theorem B

Let G be a (non-solvable) group having a composition factor isomorphic to $\textrm{SL}_2(4)\cong A_5$, let R and K be, respectively, the solvable radical and the solvable residual of G, and let p be a prime number. Then the graph $\Delta (G)$ is connected and has a cut-vertex p, if and only if G/R is an almost simple group with socle isomorphic to $\textrm{SL}_2(4)$, $\textrm{V}(G) = \{2,3,5\}\cup \{p\}$, and one of the following holds.

• (a) K is isomorphic either to $\textrm{SL}_2(4)$ or to $\textrm{SL}_2(5)$, and $\textrm{V}(G/K) =\{p\}$; if $p=5$, then $K\cong \textrm{SL}_2(4)$ and $G=K\times R$.

• (b) K contains a minimal normal subgroup L of G with $|L| = 2^4$. Moreover, $G = KR$ and

  • (i) either L is the natural module for K/L, $p \ne 2$ and $\textrm{V}(G/K)=\{p\}$,

  • (ii) or L is isomorphic to the restriction to K/L, embedded as $\Omega _4^-(2)$ into $\textrm{SL}_4(2)$, of the standard module of $\textrm{SL}_4(2)$. Moreover, $p = 5$, $G=K\times R_0$, where $R_0=\textbf{C}_{G}(K)$, and $\textrm{V}(R_0)=\textrm{V}(G/K) \subseteq \{ 5\}$.

• (c) K contains a minimal normal subgroup L of G such that K/L is isomorphic to $\textrm{SL}_2(5)$, and

  • (i) either L is the natural module for K/L, $p\not =5$ and $\textrm{V}(G/K)=\{p\}$,

  • (ii) or L is isomorphic to the restriction to K/L, embedded in $\textrm{SL}_4(3)$, of the standard module of $\textrm{SL}_4(3)$, $p=2$ and $\textrm{V}(G/K)\subseteq \{2\}$.

In all cases, p is a complete vertex and the unique cut-vertex of $\Delta (G)$.

Finally, in order to complete the discussion, we provide a characterization of the non-solvable groups whose degree graph is disconnected and has a cut-vertex.

Theorem C

Let G be a non-solvable group, R the solvable radical of G, K the solvable residual of G and p a prime number. Then $\Delta (G)$ is a disconnected graph with cut-vertex p if and only if K is isomorphic to either $\textrm{PSL}_2(t^a)$ or $\textrm{SL}_2(t^a)$ (where t is a prime and $t^a\ge 4$), G/K is abelian, $|G:KR| = p^b$ with $b \ge 0$, and one of the following holds.

• (a) t is odd, $p=2$, $t^a\not =9$ and $t^a$ is neither a Fermat nor a Mersenne prime.

• (b) $t=2$, $t^a \ne 4$, $p \ne 2$ and $b \ge 1$.

Moreover, p is the unique cut-vertex and a complete vertex of $\Delta (G)$.

As a consequence of the above results and of Theorem 1.1 of [21] we have:

Corollary D

For every group G, the degree graph $\Delta (G)$ has at most one cut-vertex.

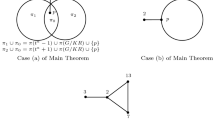
Regarding the (connected) graphs associated with the groups of Theorem A, they are represented in Fig. 1except for those related to case (e)(i), and to case (f)(i) when $p\ne 2$ (note that the dashed edge represented in Fig. 1 case (d) is actually in the graph if and only if $\textrm{V}(R)=\{2\}$). For the two missing families of graphs we provide next a description.

Recall that, given two graphs $\varGamma _1$ and $\varGamma _2$ with vertex sets $\textrm{V}(\varGamma _1)$ and $\textrm{V}(\varGamma _2)$ respectively, the join of $\varGamma _1$ and $\varGamma _2$ is defined as the graph $\varGamma _1*\varGamma _2$ whose vertex set is $\textrm{V}(\varGamma _1) \cup \textrm{V}(\varGamma _2)$, and two vertices are adjacent if and only if either one of them is in $\textrm{V}(\varGamma _1)$ and the other one in $\textrm{V}(\varGamma _2)$, or they are vertices of the same $\varGamma _i$ and they are adjacent in $\varGamma _i$.

Now, consider a group G as in case (e)(i) of Theorem A, and adopt the notation of that theorem. Defining $\varGamma _1$ to be the complete graph whose vertex set is $\{2\}\cup \pi (G/KR)$, and $\varGamma _2$ to be the graph consisting of two complete connected components with vertex sets $\pi (t^a-1)-\textrm{V}(\varGamma _1)$ and $\pi (t^a+1)-\textrm{V}(\varGamma _1)$ respectively, it turns out that $\Delta (G/R)$ is a graph with two connected components: one of them consists of t only, whereas the other is $\varGamma _1*\varGamma _2$ (this follows, for instance, from [30, Theorem A]). Given that, it is not difficult to see that $\Delta (G)$ is obtained starting from this $\Delta (G/R)$ and then connecting the vertex p (regardless if it is already in $\pi (G/R)$ or not) with all the other vertices.

Similarly, if G is as in case (f)(i) of Theorem A for $p\ne 2$, one defines $\varGamma _1$ to be the complete graph whose vertex set is $\pi (G/KR)$, and $\varGamma _2$ to be the graph with two complete connected components of vertex sets $\pi (2^a-1)-\textrm{V}(\varGamma _1)$ and $\pi (2^a+1)-\textrm{V}(\varGamma _1)$, respectively. Then $\Delta (G/R)$ is as above (with 2 playing the role of t, of course) and $\Delta (G)$ is also obtained in the same way as above.

Moving to Theorem B, the graphs arising from it are displayed in Fig. 2 only in the case when the cut-vertex p is not already in the set $\pi (G/R)=\{2,3,5\}$. The missing graphs can be easily described: they are all the paths of length 2 with vertex set $\{2,3,5\}$. Of course, there are three of them and they all occur: for instance, all these graphs occur as $\Delta (G)$ for G as in case (a) of Theorem B (it is enough to consider the direct product $\textrm{SL}_2(4)\times R$, where R is a non-abelian q-group, for $q\in \{2,3,5\}$). It is also clear that case (b)(ii) is associated to the path $2-5-3$, and case (c)(ii) to the path $3-2-5$.

Finally, the (disconnected) graphs related to the groups of Theorem C are displayed in Fig. 3.

Fig. 1

Graphs arising from Theorem A $(\pi =\pi (G/R)\cup \{p\}$)

Fig. 2

Graphs arising from Theorem B when $p\not \in \{2,3,5\}$

Fig. 3

Graphs arising from Theorem C

3 Preliminary Results

A simple undirected graph $\Delta = (V, E)$ is defined by its vertex set $V = \textrm{V}(\Delta )$ and its edge set $E = \textrm{E}(\Delta )$, which is a subset of the set $V^{[2]}$ (consisting of the subsets of size 2 of V). The graph $\Delta$ is said to be complete if $E = V^{[2]}$. When $\Delta = \Delta (G)$ is the degree graph of a group G, we will write $\textrm{V}(G)$ for $\textrm{V}(\Delta )$ and $\textrm{E}(G)$ for $\textrm{E}(\Delta )$.

A graph $\Delta _0 = (V_0, E_0)$ is a subgraph of $\Delta = (V, E)$ if $V_0 \subseteq V$ and $E_0 \subseteq E \cap V_0^{[2]}$; $\Delta _0$ is an induced subgraph of $\Delta$ if $E_0 = E \cap V_0^{[2]}$; we remark that an induced subgraph of $\Delta$ is uniquely determined by the choice of its vertex set $V_0$. For $X \subset V$, we denote by $\Delta - X$ the subgraph of $\Delta$ induced by the vertex set $V - X$ (i.e. the subgraph obtained by ‘deleting’ the vertices in X and all the edges incident to them). If $X = \{v\}$, we simply write $\Delta -v$.

A graph $\Delta$ is connected if every pair of vertices u and v is linked by a path in $\Delta$. For $k \ge 0$, $\Delta$ is k-connected if $|\textrm{V}(\Delta )| >k$ and $\Delta - X$ is connected for every $X \subseteq V$ such that $|X| = k$. The largest integer k such that $\Delta$ is k-connected is called the connectivity degree of $\Delta$. So, a disconnected graph has connectivity degree 0, while a graph $\Delta$ has connectivity degree 1 if and only if $|\textrm{V}(\Delta )| \ge 2$, $\Delta$ is connected, and there exists a vertex $v \in \textrm{V}(\Delta )$ such that $\Delta - v$ is disconnected; in this case, v is called a cut-vertex of $\Delta$. A vertex v of a graph $\Delta$ is said to be complete if v is adjacent to every other vertex of $\Delta$. It is easily seen that a graph with at least three vertices and that possesses at least two complete vertices is 2-connected. A complete subgraph is called a clique. We refer to [6] for further background in graph theory.

Throughout the paper some standard facts of character theory, such as Clifford correspondence, Gallagher’s theorem, properties of character extensions (see [17]) and coprime actions (see [3]) will be used without references.

A basic result for the subject at hand, is the following consequence of the Ito–Michler’s theorem, that describes the set of the vertices of the degree graph of a finite group.

Proposition 3.1

Let G be a group and p a prime number. Then $p \not \in \textrm{V}(G)$ if and only if G has a normal abelian Sylow p-subgroup.

We also mention that, as a consequence of Clifford theory, if H is isomorphic either to a normal subgroup or to a factor group of a group G (even more generally, to a subnormal section of G), then $\Delta (H)$ is a subgraph of $\Delta (G)$.

As an important reference for our discussion, we recall some properties of the degree graphs of the non-abelian simple groups [29].

Lemma 3.2

([29, Theorem 5.2]) Let $S \cong \textrm{PSL}_2(t^a)$ or $S \cong \textrm{SL}_2(t^a)$, with t prime and $a \ge 1$. Let $\pi _{+} = \pi (t^a+1)$ and $\pi _{-} = \pi (t^a-1)$. For a subset $\pi$ of vertices of $\Delta (S)$, we denote by $\Delta _{\pi }$ the subgraph of $\Delta = \Delta (S)$ induced by the subset $\pi$. Then

• (a) if $t=2$ and $a \ge 2$, then $\Delta (S)$ has three connected components, $\{t\}$, $\Delta _{\pi _{+}}$ and $\Delta _{\pi _{-}}$, and each of them is a complete graph.

• (b) if $t > 2$ and $t^a > 5$, then $\Delta (S)$ has two connected components, $\{t\}$ and $\Delta _{\pi _{+} \cup \pi _{-}}$; moreover, both $\Delta _{\pi _{+}}$ and $\Delta _{\pi _{-}}$ are complete graphs, no vertex in $\pi _{+} - \{ 2 \}$ is adjacent to any vertex in $\pi _{-} - \{ 2\}$ and 2 is a complete vertex of $\Delta _{\pi _{+} \cup \pi _{-}}$.

Lemma 3.3

([29, Theorem 4.1]) Let $S \cong \textrm{Sz}(q)$, where $q = 2^a \ge 8$ and a is odd. Then $\Delta (S)$ has vertex set $\pi (S) = \{2\} \cup \pi _0$, where $\pi _0 = \pi ((q-1)(q^2+1))$, the set $\pi _0$ induces a complete subgraph of $\Delta (G)$ and the vertex 2 is adjacent only to the primes in $\pi _1 = \pi (q-1)$ in $\Delta (S)$.

Theorem 3.4

[29] Let G be a non-abelian simple group.

• (a) If $\Delta (G)$ is not a complete graph, then G is isomorphic to one of the following groups: $\textrm{M}_{11}$, $\textrm{M}_{23}$, $\textrm{J}_1$, $\textrm{A}_5 \cong \textrm{PSL}_2(4) \cong \textrm{PSL}_2(5)$, $\textrm{A}_6 \cong \textrm{PSL}_2(9)$, $\textrm{A}_8 \cong \textrm{PSL}_4(2)$, $\textrm{PSL}_2(t^a)$ (t prime, $t^a\ge 4$), $\textrm{PSL}_3(t^a)$ for suitable values of $t^a$ (t prime), $\textrm{PSU}_3(t^{2a})$ for suitable values of $t^{a}$ (t prime, $t^a> 2$), $\textrm{Sz}(2^a)$ (a odd, $a \ge 3$).

• (b) Either $\Delta (G)$ is 2-connected or G is isomorphic to one of the following groups: $\textrm{M}_{11}$, $\textrm{J}_1$, $\textrm{PSL}_2(t^a)$ (t prime, $t^a\ge 4$), $\textrm{PSL}_3(4)$, $\textrm{Sz}(2^a)$ (a odd, $a \ge 3$ and $2^a-1$ a prime number).

• (c) $\Delta (G)$ is disconnected if and only if $G \cong \textrm{PSL}_2(t^a)$ (t prime, $t^a\ge 4$).

Proof

The list (a) of the simple groups with a non-complete degree graph is given in [29], as well as the structure of the relevant graphs. In particular, one can immediately check that $\Delta (\mathrm{{A}}_8)$ and $\Delta (\textrm{M}_{23})$ are 2-connected. If $G = \textrm{PSL}_3(q)$, where $q= t^a \ne 4$, then $\Delta (G)$ has vertex set $\{t\} \cup \pi _0$, where $\pi _0 = \pi ((q-1)(q+1)(q^2+q+1))$; the set $\pi _0$ induces a complete subgraph of $\Delta (G)$, while the vertex t is adjacent only to the primes in $\pi _1 = \pi ((q+1)(q^2+q+1))$; so, all the vertices in $\pi _1$ are complete vertices of $\Delta (G)$ and, since $|\pi _1| \ge 2$, $\Delta (G)$ is 2-connected. If $G = \textrm{PSU}_3(q^2)$, where $q= t^a >2$, then $\Delta (G)$ has vertex set $\{t\} \cup \pi _0$, where $\pi _0 = \pi ((q-1)(q+1)(q^2-q+1))$; the set $\pi _0$ induces a complete subgraph of $\Delta (G)$, while the vertex t is adjacent only to the primes in $\pi _1 = \pi ((q+1)(q^2-q+1))$; again, all the vertices in $\pi _1$ are complete vertices of $\Delta (G)$ and, since $|\pi _1| \ge 2$, $\Delta (G)$ is 2-connected. Finally, if $G = \textrm{Sz}(q)$, where $q= 2^a \ge 8$ and a is odd, then by Lemma 3.3 all the vertices in $\pi _1= \pi (q-1)$ are complete vertices of $\Delta (G)$. Hence, $\Delta (G)$ is not 2-connected if and only if $2^a-1$ is a prime power: as it is well known (see for instance [25, Proposition 3.1]), this implies that both $2^a-1$ and a are prime numbers. This proves (b). Finally, (c) is Theorem 2.1 of [22].$\square$

Fig. 4

Degree graphs of $\textrm{J}_1$, $\mathrm{M_{11}}$, $\mathrm{{PSL}}_3(4)$

We recall that the character degree graphs of $\textrm{M}_{11}$, $\textrm{J}_1$ and $\textrm{PSL}_3(4)$ are as follows [5].

Recall that, for a and n integers larger than 1, a prime divisor q of $a^n-1$ is called a primitive prime divisor if q does not divide $a^b -1$ for all $1 \le b <n$. In this case, n is the order of a modulo q, so n divides $q-1$. It is known ([25, Theorem 6.2]) that $a^n - 1$ always has primitive prime divisors except when $n = 2$ and $a= 2^c -1$ for some integer c, or when $n=6$ and $a= 2$.

We will make use of the following well-known facts about linear groups.

Lemma 3.5

Let t be a prime number and $a \ge 2$ an integer. Let p be a primitive prime divisor of $t^a -1$ and let X be a subgroup of $G = \textrm{GL}_a(t)$ such that $|X| = p$. Then $\textbf{C}_G(X)$ is a cyclic group of order $t^a -1$.

Proof

Let V be the natural module for G. We observe that, as p does not divide $t^b -1$ for every positive integer $b <a$, the subgroup X acts irreducibly on V. Hence, by Schur’s lemma, the ring $\mathbb {K} = \mathrm{{End}}_{\mathbb {F}_t[X]}(V)$ of the $\mathbb {F}_t[X]$-endomorphisms of V is a finite field and, since $\textbf{C}_G(X)$ is contained in the multiplicative group of $\mathbb {K}$, it follows that $\textbf{C}_G(X)$ is cyclic. By [16, II.7.3] G contains a cyclic subgroup C of order $t^{a} - 1$ (a Singer cycle) and $\textbf{C}_G(C) = C$; so, C is a maximal cyclic subgroup of G. Observing that the p-part of |G| coincides with the p-part of |C|, we can assume that X is a subgroup of C. Hence $C \subseteq \textbf{C}_G(X)$ and, since $\textbf{C}_G(X)$ is cyclic, we conclude that $\textbf{C}_G(X) = C$.$\square$

Lemma 3.6

For a positive integer a and a prime t, let $G = \textrm{GL}_{2a}(t)$ and let $K \le L \le G$ be such that $L \cong \textrm{GL}_{2}(t^a)$ and $K \cong \textrm{SL}_{2}(t^a)$. Then $\textbf{C}_G(K) = \textbf{Z}(L)$ is a cyclic group of order $t^a -1$.

Proof

Let C be a Singer cycle of L, so, $|C| = t^{2a} - 1$ and C is a maximal cyclic subgroup of G. Assume first that there exists a primitive prime divisor p of $t^{2a}-1$. Hence, p divides |K| and we consider a subgroup $X \le K \cap C$ with $|X| = p$. As $C \le \textbf{C}_G(X)$, by Lemma 3.5 we conclude that $\textbf{C}_G(X) = C$. Thus, $\textbf{C}_G(K) \le \textbf{C}_G(X) \le L$ and it is well known that $\textbf{C}_G(K) = \textbf{C}_L(K) = \textbf{Z}(L)$ is cyclic of order $t^a -1$.

If there is no primitive prime divisor of $t^{2a}-1$, then either $a=1$ and we are done as $L = G$, or $t^{2a} = 2^6$ and we can argue as above with a cyclic subgroup X of K such that $|X| = 9$.$\square$

As another important reference, we recall the characterization of the non-solvable groups whose character degree graph is disconnected [22].

Theorem 3.7

([22, Theorem 4.1 and Theorem 6.3]) Let G be a non-solvable group such that $\Delta (G)$ is disconnected. Then $\Delta (G)$ has either two or three connected components and:

• (I) $\Delta (G)$ has two connected components if and only if there exist normal subgroups $N\subseteq K$ of G such that, setting $C/N=\textbf{C}_{G/N}(K/N)$, the following conditions hold.

  • (a) $K/N\cong \textrm{PSL}_2(t^a)$, where t is a prime with $t^a\ge 4$.

  • (b) G/K is abelian.

  • (c) If $t^a\ne 4$, then t does not divide |G/CK|.

  • (d) If $N\ne 1$, then either $K\cong \textrm{SL}_2(t^a)$ or there exists a minimal normal subgroup L of G, $L \le K$, such that $K/L\cong \textrm{SL}_2(t^a)$ and L is isomorphic to the natural module for K/L.

  • (e) If $t=2$ or $t^a=5$, then either $CK\ne G$ or $N\ne 1$.

  • (f) If $t=2$ and K is an in (d) in the case $K\not \cong \textrm{SL}_2(t^a)$, then every non-principal character in $\textrm{Irr}(L)$ extends to its inertia subgroup in G.

• (II) $\Delta (G)$ has three connected components if and only if $G \cong \textrm{SL}_2(2^a) \times A$, where $a \ge 2$ and A is an abelian group.

Proposition 3.8

Let G be a non-solvable group such that $\Delta (G)$ is disconnected and let R be the solvable radical of G. Then G/R is an almost simple group with socle isomorphic to $\textrm{PSL}_2(t^a)$, where t is a prime and $t^a \ge 4$, and $\textrm{V}(G) = \pi (G/R)$.

Proof

By Theorem 3.7, all conclusions are clear if $\Delta (G)$ has three connected components. So, we can assume that $\Delta (G)$ has two connected components and we adopt the notation (and conclusions) of Part (I) of Theorem 3.7. Let R be the solvable radical of G. By (I)(a), (b) and (d), it follows that $C = R$, $N = K \cap R$ and that G/R is an almost simple group with socle $KR/R \cong K/N \cong \textrm{PSL}_2(t^a)$, where t is a prime and $t^a \ge 4$. Also, clearly $\pi (G/R) = \textrm{V}(G/R) \subseteq \textrm{V}(G)$. For the converse inclusion, let u be a prime such that $u \not \in \pi (G/R)$; so, $u \ne 2$, $u \ne t$ and $u \not \in \pi (t^{2a}-1)$ and hence u does not divide |K|. We will prove that $u \not \in \textrm{V}(G)$. Let U be a Sylow u-subgroup of G and observe that $U \le R$. As R/N is abelian, being isomorphic to a subgroup of G/K, UN/N is an abelian normal subgroup of G/N. Moreover, as N/L is a central subgroup (of order dividing $2 \ne u$) of G/L, UL/L is an abelian normal subgroup of G/L. If $L = 1$, then $u \not \in \textrm{V}(G)$. So, we can assume that L is the natural module for $K/L \cong \textrm{SL}_2(t^a)$. Since $[K, UL] \le K \cap UL$ and |K| is coprime to u, $[K, UL] \le L \le \textbf{C}_G(L)$. Setting $\overline{G} = G/\textbf{C}_G(L)$, we have $\overline{U} \le \textbf{C}_{\overline{G}}(\overline{K})$ and, as $\overline{G}$ can be seen as a subgroup of $\textrm{GL}_{2a}(t)$ and $\overline{K} \cong \textrm{SL}_2(t^a)$, by Lemma 3.6 and the coprimality of u and $t^a-1$ we deduce that $\overline{U} = 1$, so that $U \le \textbf{C}_G(L)$. Hence $UL = U \times L$ and again U is a normal abelian Sylow u-subgroup of G, so $u \not \in \textrm{V}(G)$.$\square$

The following result will come into play later on.

Theorem 3.9

Let G be an almost simple group with socle S, and let $\delta = \pi (G) - \pi (S)$. If $\delta \ne \emptyset$, then S is a simple group of Lie type, and every vertex in $\delta$ is adjacent to every other vertex of $\Delta (G)$ that is not the characteristic of S.

Proof

Assume $\delta \ne \emptyset$ and let $p \in \delta$. Since p divides $|\mathrm{{Aut}}(S)|$ but p does not divide |S|, by the classification of the finite simple groups we deduce that S is a simple group of Lie type in characteristic, say, t. By Theorem 2.7 of [27], p is adjacent in $\Delta (G)$ to every vertex $q\in \pi (S)$ such that $q\ne t$. Moreover, G/S has a normal (in fact, central) and cyclic Hall $\delta$-subgroup D/S ([27, Lemma 2.10]); so, by Schur–Zassenhaus theorem, G has a cyclic Hall $\delta$-subgroup A and by Lemma 2.6 of [27], A has a regular orbit on $\textrm{Irr}(S)$. Hence, by Clifford correspondence, there is a $\chi \in \textrm{Irr}(G)$ such that |A| divides $\chi (1)$ and we conclude that, in particular, the subgraph of $\Delta (G)$ induced by $\delta$ is a clique.$\square$

We remark that the set $\delta$ in the statement of Theorem 3.9 is empty for the simple groups of Lie type of double characteristic.

In the course of our analysis, we will also make use of special types of actions of groups on modules (see [4]).

Definition 3.10

Let H and V be finite groups, and assume that H acts by automorphisms on V. Given a prime number q, we say that the pair (H, V) satisfies the condition $\mathcal {N}_q$ if q divides $|H: \textbf{C}_H(V)|$ and, for every non-trivial $v\in V$, there exists a Sylow q-subgroup Q of H such that $Q\trianglelefteq \textbf{C}_H(v)$.

If (H, V) satisfies $\mathcal {N}_q$, then V turns out to be an elementary abelian r-group for a suitable prime r, and V is in fact an irreducible module for H over the field $\mathbb {F}_r$ with r elements (see Lemma 4 of [32]). We also remark that if (H, V) satisfies $\mathcal {N}_q$, then the centralizers in V of distinct Sylow q-subgroups of H have trivial intersection.

Lemma 3.11

Let t, q, r be prime numbers, let $H = \textrm{SL}_2(t^a)$ (with $t^a \ge 4$) and let V be an $\mathbb {F}_r[H]$-module. Then (H, V) satisfies $\mathcal {N}_q$ if and only if either $t^a = 5$ and V is the natural module for $H/\textbf{C}_H(V) \cong \textrm{SL}_2(4)$ or $\textbf{C}_H(V) = 1$, i.e. V is faithful, and one of the following holds.

• 1) $t = q = r$ and V is the natural $\mathbb {F}_r[H]$-module (so $|V| = t^{2a}$);

• 2) $q = r = 3$ and $(t^a, |V|) \in \{(5, 3^4), (13, 3^6)\}$.

Proof

First, we consider the “only if” part of the statement. If $t \ne 2 \ne q$, this is Proposition 13 of [4], while for $t = 2$ and q odd it follows from Lemma 3.3 of [1]. We can therefore assume $q = 2$, thus also $r = 2$ by Part (2) of Proposition 8 of [4]. Next, we suppose that t is odd, and we prove that $t^a = 5$ and that V is isomorphic to the natural module for $H/\textbf{C}_H(V) \cong \textrm{SL}_2(4)$. Observe that, by the condition $\mathcal {N}_2$, the kernel $\textbf{C}_H(V)$ of the action is the cyclic subgroup $\textbf{Z}(H)$ of order 2. Let T be a Sylow t-subgroup of H. If there exists a non-trivial element $x \in T$ such that $\textbf{C}_V(x) \ne 1$, then x normalizes a Sylow 2-subgroup of H by the condition $\mathcal {N}_2$: in view of the structure of the subgroups of $\textrm{PSL}_2(t^a)$ ([16, Hauptsatz II.8.27]), this can happen only if $t= 3$.

Let us first assume $t \ne 3$. Hence, T acts fixed-point freely on V and, as T is elementary abelian, it follows that $a= 1$. Let Q be a Sylow 2-subgroup of H. It is well known that Q is a generalized quaternion group (since H has a unique involution) and it easily follows that $\textbf{N}_H(Q) = Q$ if $t^2 \equiv 1 \pmod {16}$ and, recalling that $H/\textbf{Z}(H)$ has subgroups isomorphic to $A_4$ as $t \ne 2$ ([16, Hauptsatz II.8.27]), that $\textbf{N}_H(Q) \cong \textrm{SL}_2(3)$ if $t^2 \not \equiv 1 \pmod {16}$. Now, if p is an odd divisor of $t-1$, then H has a Frobenius subgroup TP, with kernel T and P cyclic of order p. By Theorem 15.16 of [17], $\textbf{C}_V(P)$ is non-trivial and hence, again by the condition $\mathcal {N}_2$, P normalizes a Sylow 2-subgroup of H. It follows that either $t-1 = 2^k \cdot 3$, with $k \le 2$, or $t-1 = 2^k$, $k \ge 2$. The condition $\mathcal {N}_2$ implies that the set $V^{\#}$ of the non-trivial elements of V is a disjoint union of the sets $\textbf{C}_V(Q) - \{1 \}$, where Q varies in the set of the Sylow 2-subgroups of H. Hence, writing $|V| = 2^d$, $|\textbf{C}_V(Q)|= 2^b$ and denoting by $n_2(H)$ the number of Sylow 2-subgroups of H, we have

$$\begin{aligned} n_2(H) = \frac{2^d-1}{2^b -1} = 1 + 2^b + 2^{2b} + \cdots + 2^{(\frac{d}{b} -1)b}. \end{aligned}$$

(1)

If $t = 7$, then $n_2(H) = 21$ and hence $d= 6$ (and $b= 2$), which is impossible as H has no irreducible module of dimension 6 over $\mathbb {F}_2$. If $t = 13$, then $n_2(H) = 91$, which has no binary expansion of the form (1). Hence, $t = 2^k +1$, with $k \ge 2$, and $n_2(H) = t(t+1)/2 = 1 + 2^{k-1} + 2^k + 2^{2k-1}$. By (1), it follows that $k= 2$ and $t = 5$, so $d = 4$ (and $b = 1$). Of the two H-module of dimension 4 over $\mathbb {F}_2$, the only one that satisfies $\mathcal {N}_2$ is the natural modules for $H/\textbf{C}_H(V) \cong \textrm{SL}_2(4)$.

On the other hand, assume $t = 3$; so $a \ge 2$ and a Sylow 3-subgroup of H, being non-cyclic, cannot act fixed-point freely on V. Since the normalizer of a Sylow 3-subgroup of H acts transitively on its subgroups of order 3, all the subgroups of order 3 of H are conjugate in H. It follows that each of them has a non-trivial centralizer in V and hence, by the condition $\mathcal {N}_2$ and the discussion above, we deduce that a is odd and that $\textbf{C}_H(v) \cong \textrm{SL}_2(3)$ for every non-trivial $v \in V$. In particular, all the H-orbits of non-trivial vectors of V have the same size (i.e. H acts $\frac{1}{2}$-transitively on V). Hence, recalling that H is non-solvable and that the orbit sizes are odd by the condition $\mathcal {N}_2$, Theorem 6 of [15] yields that H acts transitively on the non-trivial elements of V. So, using the classification of the doubly transitive affine permutation groups (see Appendix 1 of [23]) and recalling that $t \ne q$ (as $t= 3$ and $q= 2$), we deduce that the only possiblity is $H \cong \textrm{SL}_2(9)$ and $|V| = 2^4$; but in this case, for any non-trivial $v \in V$, $\textbf{C}_H(v) \cong S_4$, a contradiction.

So, we are left with the case $t = q = r = 2$. In this situation, equation (1) gives $2^d - 1 = (2^a +1)(2^b -1) = 2^{a+b} +2^b - 2^a - 1$ and hence $a = b$ and $d = 2a$. By Lemma 3.12 of [28], we conclude again that V is the natural $\mathbb {F}_2[H]$-module.

Conversely, it is easily checked that each isomorphism type of the modules described in the statement (there are two conjugacy classes both of subgroups isomorphic to $\textrm{SL}_2(5)$ in $\textrm{GL}_4(3)$ and of subgroups isomorphic to $\textrm{SL}_2(13)$ in $\textrm{GL}_6(3)$) satisfies the condition $\mathcal {N}_q$.$\square$

Remark 3.12

We observe that if $H = \textrm{PSL}_2(t^a)$ and V is an $\mathbb {F}_r [H]$-module such that (H, V) satisfies the condition $\mathcal {N}_q$, then, seeing V in a natural way as a module for $K = \textrm{SL}_2(t^a)$ (with $\textbf{Z}(K)$ in the kernel of the action), (K, V) satisfies $\mathcal {N}_q$ too. In fact, $|K:\textbf{C}_K(v)| = |H:\textbf{C}_H(v)|$ for every $v \in V$ and $\textbf{C}_K(v)$ contains a Sylow q-subgroup of K as a normal subgroup, for every non-trivial $v \in V$. We hence conclude that Lemma 3.11 describes also all possible module actions of $\textrm{PSL}_2(t^a)$ that satisfy the condition $\mathcal {N}_q$, for any prime q.

Lemma 3.13

Let K be a quasi-simple group and let V be a finite and faithful K-module such that, for a prime q, (K, V) satisfies the condition $\mathcal {N}_q$. Then $K/\textbf{Z}(K) \not \cong J_1, \mathrm{{M}}_{11}, \textrm{PSL}_3(4)$. Moreover, if $K/\textbf{Z}(K) \cong \textrm{Sz}(2^a)$, then $q \ne 2$.

Proof

Write $|V| = r^d$, where r is a prime, and for a Sylow q-subgroup Q of K let $|\textbf{C}_V(Q)| = r^b$. Since (K, V) satisfies the condition $\mathcal {N}_q$, Proposition 2.3(b,c) of [7] yields that b is a proper divisor of d and, setting $c = d/b$, $(r^d - 1)/(r^b -1) = 1 + r^b + r^{2b} + \cdots + r^{(c -1)b}$ coincides with the number $n_q(K)$ of the Sylow q-subgroups of K. Moreover, Theorem 2.5 of [7] implies that r divides |K|. A check of the r-adic representations of $n_q(K)$, for every choice of prime divisors r, q of |K|, excludes the cases $K/\textbf{Z}(K) \cong J_1, M_{11}, \textrm{PSL}_3(4)$.

Finally, working by contradiction we assume that $K/\textbf{Z}(K) \cong \textrm{Sz}(2^a)$ for an odd integer $a \ge 3$ and that (K, V) satisfies the condition $\mathcal {N}_2$. Then $r=2$ by [7, Proposition 2.3(a)] and, as $n_2(K) = 2^{2a}+1$, we deduce that $b = 2a$ and that $d = 4a$. The Schur multiplier of $\textrm{Sz}(2^a)$ is a 2-group for $a = 3$, and it is trivial for $a \ge 5$ ([2, Theorems 1 and 2]). Hence, as the action of K on V is faithful and satisfies the condition $\mathcal {N}_2$, we conclude that in any case $\textbf{Z}(K) = 1$. By the structure of the absolutely irreducible modules for the Suzuki simple groups on fields of characteristic 2 ([26, Lemma 1]), we deduce that V is (any Galois conjugate of) the natural $\mathbb {F}_{2^a}[K]$-module seen as $\mathbb {F}_2[K]$-module, and hence $|\textbf{C}_V(S)|= 2^a$ and $b= a$, a contradiction.$\square$

Next, we give an improvement of Proposition 3.2 of [1].

Proposition 3.14

Let H be a non-solvable group and let V be a finite and faithful H-module. If (H, V) satisfies the condition $\mathcal {N}_q$ for some prime q, then the solvable radical of H is cyclic.

Proof

We work by induction on |V|. By Lemma 4 of [32] we know that V is an irreducible module; write $|V| = r^a$, where r is a prime and $a \ge 2$. By Proposition 3.2 of [1], we can assume that $r = q$. Let R be the solvable radical of H and let Q be a Sylow q-subgroup of H.

We consider first the case $a = 2$. Then we can see H as a subgroup of $\textrm{GL}_2(q)$ and $H_0 = H \cap \textrm{SL}_2(q)$ is non-solvable; moreover, $(H_0, V)$ satisfies $\mathcal {N}_q$. If $H_0$ is a proper (non-solvable) subgroup of $\textrm{SL}_2(q)$, then the classification of the subgroups of $\textrm{SL}_2(q)$ yields $H_0 \cong A_5 \cong \textrm{SL}_2(4)$: Lemma 3.11 yields now that $|V| = 2^4$, not our case because we are assuming $|V|=r^2$. Hence, $\textrm{SL}_2(q)=H_0$ and therefore $R \le \textbf{C}_{\textrm{GL}_2(q)}(H_0) \le \textbf{Z}(\textrm{GL}_2(q))$ is cyclic.

Next, we assume that $|V| = 2^6$. So, by Lemma 3.1 of  [1], H has a normal subgroup isomorphic to $\textrm{SL}_2(8)$. Since $\textrm{GL}_6(2)$ has a unique conjugacy class of maximal subgroups having a section isomorphic to $\textrm{SL}_2(8)$, and they are isomorphic to $\textrm{GL}_2(8) : C_3 = (C_7 \times \textrm{SL}_2(8)):C_3$, we conclude that also in this case R is cyclic.

We can hence assume that $|V| = q^a \ne q^2, 2^6$; so, there exists a primitive prime divisor t of $q^a -1$ (recall also that a divides $t-1$). Let T be a Sylow t-subgroup of H. Since (H, V) satisfies the condition $\mathcal {N}_q$, then $(|V|-1)/(|\textbf{C}_V(Q)|-1) = |\textrm{Syl}_q(H)|$ divides |H|, thus $T \ne 1$. We also observe that t does not divide |R|. In fact, if $T_0 = T \cap R \ne 1$, then $\textbf{Z}(T_0)$, a normal abelian subgroup of $\textbf{N}_H(T_0)$, acts irreducibly on V. Hence, by [25, Theorem 2.1], $\textbf{N}_H(T_0)$ is solvable, which is a contradiction as $H = R \textbf{N}_H(T_0)$ by the Frattini argument.

For every prime divisor p of the order of R, there exists a T-invariant Sylow p-subgroup P of R and by Lemma 6 of [4] we get $[P, T] = 1$ if $p \ne 2$. It follows that $R = \textbf{C}_R(T) D$, where D is a T-invariant Sylow 2-subgroup of R. Write $E = [R, T]$; then $E = [\textbf{C}_R(T) D, T] = [D,T] \le D$ is a normal 2-subgroup of R. So, $E \le \textbf{F}(R) \le \textbf{F}(H)$. We observe that $\textbf{C}_H(T) \le \textbf{C}_{\textrm{GL}_a(q)}(T)$ is cyclic by Lemma 3.5.

It is enough to prove that E is cyclic: in this case, in fact, T centralizes E (as $\textrm{Aut}(E)$ is a 2-group and $t \ne 2$) and then by coprimality $[R, T] = [R, T, T] = [E, T] =1$, so $R \le \textbf{C}_H(T)$ is cyclic.

Working by contradiction, we assume that E is non-cyclic. If A is a characteristic abelian subgroup of E, then V is an irreducible AT-module (because t is a primitive prime divisor of $q^a-1$); moreover, the restriction of V to A is homogeneous, since otherwise it would have at least t homogeneous components, yielding the contradiction $a\ge t>a$; thus, A is cyclic. As a consequence, T centralizes every characteristic abelian subgroup of E. Since $[E,T]=E$, [3, 24.7] yields that E is an extraspecial 2-group and $\textbf{Z}(E) = \textbf{C}_E(T)$. Write $|E| = 2^{2n +1}$. By applying [25, Corollary 2.6] to an irreducible constituent of the homogeneous module $V_E$, we see that $2^n$ divides the dimension a of V over $\mathbb {F}_q$ and then $2^n +1 \le a +1 \le t$. On the other hand, |T| divides $2^n \pm 1$ by [16, Satz V.17.13] and we deduce that $t = 2^n+1 = a+1$. Also, by [25, Corollary 2.6], V is an absolutely irreducible E-module. As $a > 2$, then $n \ge 2$ and there exists a non-central involution y in E. Let $Y = \textbf{C}_H(y)$ and $U = \textbf{C}_V(y)$. We remark that $q \ne 2$, as E acts faithfully and irreducibly on V. Hence, it follows that $|U| = |V|^{1/2}$. In fact, if $\phi$ is the Brauer character corresponding to V, then $\phi \in \textrm{Irr}(E)$, $\phi (1) = 2^n$ and $\phi (y) = 0$. So, $\dim _{\mathbb {F}_q}(U) = [\phi _{\langle y \rangle }, 1_{\langle y \rangle }] = \phi (1)/2 = a/2$.

Now, if $\textbf{C}_H(U)$ contains a Sylow q-subgroup of H, that (up to conjugation) we can assume to be Q, then $U = \textbf{C}_V(Q)$. In fact, $U \le \textbf{C}_V(Q)$ and $|\textbf{C}_V(Q)| \le |V|^{1/2}$, because the condition $\mathcal {N}_q$ implies that the centralizers in V of two distinct Sylow q-subgroups of H have trivial intersection. So, $\textbf{C}_V(\langle y \rangle ) = \textbf{C}_V(Q)$ and, in particular, y normalizes Q because of the condition $\mathcal {N}_q$. As $y \in \textbf{O}_2(R) \trianglelefteq H$, it follows that $[y, Q] \le \textbf{O}_2(R) \cap Q = 1$ and hence by Thompson’s $A\times B$ Lemma ([3, 24.2]), we deduce that y acts trivially on V, a contradiction.

Hence, q divides $|H: \textbf{C}_H(U)|$ and, since $q \ne 2$ and $\langle y \rangle \le \textbf{O}_2(R) \trianglelefteq H$, [7, Lemma 2.4] yields that (Y, U) satisfies the condition $\mathcal {N}_q$, as well. Set $\overline{Y} = Y/\textbf{C}_Y(U)$. If $\overline{Y}$ is solvable then, recalling that $a\ne 2$, Proposition 9 in [4] ensures that G is a group of semilinear maps on V; now, $\textbf{F}(\overline{Y})$ is cyclic by Lemma 6.4 and Corollary 6.6 of [25]. If $\overline{Y}$ is non-solvable, then we by induction get that $\textbf{F}(\overline{Y})$ is cyclic. Now, $\textbf{C}_E(\langle y \rangle ) = \langle y \rangle \times E_0$, where $E_0$ is an extraspecial group of order $2^{2(n-1)+1}$. We observe that $E_0 \le E \cap Y \le \textbf{F}(H) \cap Y \le \textbf{F}(Y)$ and that $\textbf{C}_{E_0}(U) = 1$, as $\textbf{C}_{E_0}(U)$ is a normal subgroup of $E_0$ and it intersects trivially $\textbf{Z}(E_0) = \textbf{Z}(E) = \langle z \rangle$, because z acts as the inversion on V. So $E_0 \cong \overline{E_0} \le \textbf{F}(\overline{Y})$, which is cyclic, the final contradiction. $\square$

We now derive a first set of consequences of the assumption that $\Delta (G)$ has connectivity degree 1, in the case that the group G has a non-abelian minimal normal subgroup (case that, of course, includes all almost simple groups).

Proposition 3.15

Let G be a group which has a non-abelian minimal normal subgroup M. If $\Delta (G)$ is connected and has a cut-vertex p, then the following conditions are satisfied.

• (a) $\textrm{V}(G)=\pi (G/\textbf{C}_G(M))\cup \textrm{V}(\textbf{C}_G(M))$.

• (b) $\textrm{V}(\textbf{C}_G(M))\subseteq \{p\}$, and $R(G)=\textbf{C}_G(M)$. Furthermore, if $\textrm{V}(\textbf{C}_G(M))= \{p\}$, then p is a complete vertex of $\Delta (G)$.

• (c) M is a simple group.

• (d) $\Delta (M)$ is either disconnected or it is connected with cut-vertex p.

• (e) M is isomorphic to one of the groups of the following list:

  $$\begin{aligned} \mathcal {L} = \{\mathrm{{PSL}}_2(t^a)~(\text {with }\;t^a \ge 4),~ \mathrm{{Sz}}(2^a)~(\text { with }\;a \ge 3,~ a\text { odd}),~\mathrm{{PSL}}_3(4),~\mathrm{{M}}_{11},~\mathrm{{J}}_1\}. \end{aligned}$$

Proof

Setting $C=\textbf{C}_G(M)$, we first prove that $\textrm{V}(G)=\pi (G/C)\cup \textrm{V}(C)$. Certainly $\pi (G/C)\cup \textrm{V}(C) \subseteq \textrm{V}(G)$. If $q\in \textrm{V}(G) - \pi (G/C)$, then C contains a Sylow q-subgroup Q of G. Now, if q does not belong to $\textrm{V}(C)$, then Q is normal in C (thus, in G) and abelian, which yields the contradiction $q\not \in \textrm{V}(G)$. This proves (a).

Next, we show that for every choice of $q \in \pi (G/C)$ and $r \in \textrm{V}(C)$, the vertices q and r are adjacent in $\Delta (G)$. Observe in fact that, in view of [7, Proposition 2.10(b)], for every $q \in \pi (G/C)$ there exists $\theta \in \textrm{Irr}(M)$ such that q divides the degree of every $\chi \in \textrm{Irr}(G|\theta )$. Thus, if $\phi \in \textrm{Irr}(C)$ is such that r divides $\phi (1)$, then any irreducible character of G lying over $\theta \times \phi \in \textrm{Irr}(MC)$ has a degree divisible by qr, as claimed.

Recalling that $\pi (G/C) = \textrm{V}(G/C)$ contains at least three elements (as G/C has a non-abelian composition factor), we claim that the previous paragraph forces $\textrm{V}(C) \subseteq \{p\}$. To see this, assume that $\textrm{V}(C)-\{p\}$ contains a prime r; let $q \in \pi (G/C)-\{p\}$, and choose two distinct primes s and u in $\textrm{V}(G)-\{p\}$. If one of them lies in $\pi (G/C)$ and the other in $\textrm{V}(C)$, then we know that s, u are adjacent in $\Delta (G)$; on the other hand, if both lie in $\pi (G/C)$ or $\textrm{V}(C)$, then either $s-r-u$ or $s-q-u$ is a path in $\Delta (G)$. This contradicts the fact that $\Delta (G) - p$ is disconnected, so $\textrm{V}(C) \subseteq \{p\}$. We also observe that, if $\textrm{V}(C) = \{p\}$, then by the previous paragraph p is a complete vertex of $\Delta (G)$. Finally, since $\textrm{V}(C) \subseteq \{p\}$, Proposition 3.1 yields that C has an abelian normal p-complement, and hence $C \subseteq R(G)$. As the other inclusion is clear, we get $C=R(G)$ and (b) is proved.

Let us now show that M is simple. Assuming the contrary, Proposition 2.10(c) of [7] yields that $\pi (G/C)$ is a clique of $\Delta (G)$, against the fact that $\Delta (G)-p$ is not connected. This proves (c).

In order to prove (d) and (e), we set $\overline{G} = G/C$. Recalling that $\Delta (\overline{G})$ is a subgraph of $\Delta (G)$ and that $\textrm{V}(G) = \pi (\overline{G}) \cup \{ p\}$, it is clear that if p does not divide $|\overline{G}|$, then $\Delta (\overline{G})$ is disconnected. Since $\overline{G}$ is an almost simple group with socle isomorphic to M, by Theorem 3.7 it follows that $M\cong \mathrm{{PSL}}_2(t^a)$ for $t^a\ge 4$ and hence $\Delta (M)$ is disconnected, giving us both (d) and (e). So, we may assume $p\in \pi (\overline{G})$ and hence $\textrm{V}(G) = \pi (\overline{G})$. If $\pi (M) = \pi (\overline{G})$, then $\Delta (M)$ is a subgraph of $\Delta (G)$ with the same vertex set, so $\Delta (M)$ is either disconnected or it is connected with cut-vertex p, hence (d) and (e) follow by Part (b) of Theorem 3.4. If $\pi (\overline{G})-\pi (M)$ is non-empty, then Theorem 3.9 ensures that M is a simple group of Lie type (in characteristic t, say), and that every prime in $\pi (\overline{G})-\pi (M)$ is adjacent in $\Delta (G)$ to every other vertex different from t. In particular, $\Delta (G) - t$ is a connected graph and hence $p \ne t$. Now, if $\Delta (M)$ is disconnected, then $M\cong \mathrm{{PSL}}_2(t^a)$ for $t^a\ge 4$ by Part (c) of Theorem 3.4. If $\Delta (M)$ is connected, then necessarily $p \in \pi (M)$ and p is the only vertex adjacent to t in $\Delta (G)$. It follows that $\Delta (M)$ is connected with cut-vertex p, and hence by Part (b) of Theorem 3.4, M is isomorphic to one of the simple groups in the list $\mathcal {L}$. The proof of (d) and (e) is now complete.$\square$

Next, we state a result that is going to be of fundamental importance for the rest of our work.

Theorem 3.16

Let G be a non-solvable group such that $\Delta (G)$ is connected and it has a cut-vertex p. Then, setting $R=R(G)$, we have that G/R is an almost simple group such that $\textrm{V}(G)=\pi (G/R)\cup \{p\}$. Furthermore, the socle X/R of G/R is such that $\Delta (X/R)$ is either disconnected or connected with cut-vertex p, and X/R is isomorphic to one of the simple groups in the list $\mathcal {L}$ of Proposition 3.15.

Proof

We will prove that if G is a non-solvable group such that $\Delta (G)$ is either disconnected or connected with cut-vertex p, then G/R is an almost simple group with socle $X/R \in \mathcal {L}$ such that $\Delta (X/R)$ is either disconnected or connected with cut-vertex p, and that either $\textrm{V}(G) = \pi (G/R)$ or $\textrm{V}(G)=\pi (G/R)\cup \{p\}$ (respectively). Assuming that the statement is false, let G be a counterexample having minimal order. We observe that, by Proposition 3.8, $\Delta (G)$ is connected and we denote by p a cut-vertex of $\Delta (G)$. By Proposition 3.15, we see that G does not have any non-abelian minimal normal subgroup. We remark that the choice of G implies that, for every solvable normal subgroup N of G, the set $\textrm{V}(G)$ is strictly larger than $\textrm{V}(G/N)\cup \{p\}$. In fact, assuming the contrary, as $\Delta (G/N)$ is a subgraph of $\Delta (G)$, we get that $\Delta (G/N)$ is either disconnected or connected with cut-vertex p. Now, by the minimality of G we have that $G/R\cong (G/N)/(R/N)$ is an almost simple group whose socle $X/R\in \mathcal {L}$ is such that $\Delta (X/R)$ is either disconnected or connected with cut-vertex p, and $\textrm{V}(G/N)\cup \{p\} \subseteq \textrm{V}(G/R)\cup \{p\}$; so, G would not be a counterexample.

Moreover, we claim that the generalized Fitting subgroup $\textbf{F}^*(G)$ of G and the Fitting subgroup $\textbf{F}(G)$ of G coincide. In fact, let $\textbf{E}(G)$ denote the subgroup generated by all the components of G. Arguing by contradiction, assume $\textbf{E}(G)\ne 1$: as G does not have any non-abelian minimal normal subgroups, we have $Z=\textbf{Z}(\textbf{E}(G))\ne 1$. Now, as observed in the previous paragraph, there exists a prime $q\in \textrm{V}(G)-\textrm{V}(G/Z)$; so, if $Q\in \textrm{Syl}_q(G)$, then QZ is a normal subgroup of G and QZ/Z is abelian. Note that q does not divide $|\textbf{E}(G)/Z|$, because $\pi (\textbf{E}(G)/Z)=\textrm{V}(\textbf{E}(G)/Z)\subseteq \textrm{V}(G/Z)$. Since QZ is solvable, it centralizes $\textbf{E}(G)$, and so Z is central in QZ. Therefore Q is normal in G, and now we must have $Q\cap Z\ne 1$, as otherwise $Q\cong QZ/Z$ would be an abelian normal Sylow q-subgroup of G, against $q \in \textrm{V}(G)$. The conclusion is that $\textbf{E}(G)$ has a non-trivial central Sylow q-subgroup, a contradiction.

Next, we claim that the Frattini subgroup $\varvec{\varPhi }(G)$ of G is trivial. Assume the contrary, and consider a minimal normal subgroup M of G such that $M \le \varvec{\varPhi }(G)$. If $q\in \textrm{V}(G)-\textrm{V}(G/M)$, then G/M has an abelian normal Sylow q-subgroup, but the fact that $\textbf{F}(G/M)=\textbf{F}(G)/M$ yields that G has a normal Sylow q-subgroup Q as well. Since Q cannot be abelian, then $Q\cap M\ne 1$, so $M\subseteq Q$; in fact we have $M=Q'$, and we see that q is uniquely determined by M. In other words, $\textrm{V}(G)-\textrm{V}(G/M)=\{q\}$ and, as observed in the first paragraph, $q\ne p$. Now, by our assumptions, the graph $\Delta (G) - p$ is disconnected, and we denote by $\pi$ the connected component of q in this subgraph. Let L be a q-complement of G, and consider any non-principal $\lambda \in \textrm{Irr}(M)$. By Theorem 13.31 of [17], and by the fact that $M\subseteq \textbf{Z}(Q)$, there exists $\psi \in \textrm{Irr}(Q|\lambda )$ such that the inertia subgroup $I_L(\psi )$ coincides with $I_L(\lambda )$; moreover, by coprimality, $\psi$ has an extension to $I_G(\psi )=QI_L(\psi )=QI_L(\lambda )$. Note that, clearly, $\psi (1)$ is divisible by q. Now, let $t\in \textrm{V}(G) - \pi$, $t\ne p$. In particular, q and t are not adjacent in $\Delta (G)$ and hence Gallagher’s theorem and Clifford correspondence yield that $I_L(\lambda )$ contains a Sylow t-subgroup of L as a normal subgroup (and this Sylow subgroup is also abelian). On one hand, this implies that $\textbf{C}_L(M)$ (which is contained in $I_L(\lambda )$) has an abelian normal Sylow t-subgroup. On the other hand, [7, Theorem 2.5] ensures that $L/\textbf{C}_L(M)$ is a group of semilinear maps on M, so it is solvable. Hence, L, and therefore $G=QL$, is t-solvable. We conclude that the connected component $\pi$ of $\Delta (G)-p$ contains all the prime divisors of any non-solvable chief factor of G. In particular, it contains a prime different from q and this implies that $\Delta (G/M)$ is either disconnected or connected with cut-vertex p. By the minimality of G, and since $R(G/M) = R/M$, we have that $G/R \cong (G/M)/(R/M)$ is an almost simple group with socle $X/R \in \mathcal {L}$ and that $\textrm{V}(G/M) = \pi (G/R) \cup \{p\}$. Writing $\pi (G/R) = \pi (X/R) \cup \sigma$, with $\sigma \cap \pi (X/R) = \emptyset$, by Theorem 3.9, we see that if $\sigma \ne \emptyset$, then X/R is a simple group of Lie type of characteristic (say) r and that all primes in $\sigma$ are adjacent to every prime in $\pi (X/R)$, except possibly to r, in $\Delta (G/R)$ and hence in $\Delta (G)$. Since, as observed above, every prime divisor of |X/R| lies in $\pi$, we deduce that $\textrm{V}(G/R)$ is contained in the connected component $\pi$ of q in $\Delta (G)-p$ and hence, recalling that $\textrm{V}(G) - \{q\} = \textrm{V}(G/M) = \pi (G/R) \cup \{p\}$, $\Delta (G) - p$ would be connected, a contradiction. Hence, $\varvec{\varPhi }(G)=1$.

So, $F = \textbf{F}^*(G) = \textbf{F}(G)$ is a direct product $M_1\times \cdots \times M_k$ of (abelian) minimal normal subgroups of G. Since $F=\textbf{C}_G(F)=\bigcap _{i=1}^k\textbf{C}_G(M_i)$, the factor group G/F embeds in the direct product of the $G/\textbf{C}_G(M_i)$, and we deduce that there exists a minimal normal subgroup M of G such that $G/\textbf{C}_G(M)$ is non-solvable. Since M is abelian and $\varvec{\varPhi }(G) = 1$, M has a complement $H \cong G/M$ in G. Let $\overline{G} = G/\textbf{C}_H(M)$. Let $\pi _0 = \textrm{V}(G) - (\textrm{V}(G/M) \cup \{p\})$, $q \in \pi _0$ and Q a Sylow q-subgroup of G. As QM/M is an abelian normal subgroup of G/M, we observe that q does not divide |M|, as otherwise $M = Q' \le \varvec{\varPhi }(Q) \le \varvec{\varPhi }(G) = 1$, a contradiction. So, Q is abelian, and we can assume $Q \le H$; also, we have $[QM, QM] = [M, Q] \trianglelefteq G$ and it follows that $[M, Q] = M$. Denoting by $\widehat{M}$ the dual group of M, we then get $[\widehat{M}, Q] = \widehat{M}$: in particular, q divides $|H: I_H(\mu )|$ for every non-trivial $\mu \in \widehat{M}$. Let $s \in \textrm{V}(G)$ be a prime that is not adjacent to q in $\Delta (G)$ (recall that, q being different from p, such an s certainly exists). Then, as $\mu$ extends to $I_G(\mu ) = M I_H(\mu )$, Gallagher’s theorem and Clifford correspondence imply that $I_H(\mu )$ contains a Sylow s-subgroup of H as a normal subgroup, and this Sylow s-subgroup is also abelian, for every non-trivial $\mu \in \widehat{M}$. Note that s divides $|\overline{H}|$, since otherwise a Sylow s-subgroup of H would be contained in $\textbf{C}_H(M)$, and it would easily follow that G has an abelian normal Sylow s-subgroup, against the fact that $s\in \textrm{V}(G)$.

Let $\pi$ be the connected component of $\Delta (G) - p$ that contains q. Since by assumption $\Delta (G) - p$ is disconnected, the set $\delta = \textrm{V}(G) -(\pi \cup \{p\})$ is non-empty. By the previous paragraph, $\pi _0 \subseteq \pi$ and $(\overline{H}, \widehat{M})$ satisfies $\mathcal {N}_s$ for every $s \in \delta$. As $\delta \ne \emptyset$, Proposition 3.14 yields that the solvable radical $\overline{Y}$ of $\overline{H}$ is cyclic. Let $\overline{X} /\overline{Y}$ be a minimal normal subgroup of $\overline{H} / \overline{Y}$; then $\overline{X} / \overline{Y} \cong S^k$, where S is a non-abelian simple group. If $\pi (S) - \{p\} \subseteq \delta$, then (since $\overline{H}$ has abelian Hall $\delta$-subgroups) S has an abelian p-complement, so there exists a non-trivial element x of S such that $|S:\textbf{C}_S(x)|$ is a power of the prime p, and this is not possible by Burnside’s theorem ([17, Theorem 3.9]). So, the connected component $\pi$ of $\Delta (G) -p$ intersects non-trivially $\pi (S)$ and, since $\pi (S) \subseteq \textrm{V}(G/M)$, it follows that $\Delta (G/M)$ is either disconnected or connected with cut-vertex p. By the minimality of G, we have that $H \cong G/M$ has a unique non-solvable composition factor $S \in \mathcal {L}$, and that $\Delta (S)$ is either disconnected or connected with cut-vertex p. Hence, $\overline{X}/\overline{Y} \cong S$; observe also that $\Delta (S)$ is a subgraph of $\Delta (G)$. As $\overline{Y}$ is cyclic, $\overline{Y} \le \textbf{Z}(\overline{X})$ and then $\overline{K} = \overline{X}'$ is a quasi-simple group ([3, (31.1)]). Now, if q divides $|\overline{K}|$, then ($\overline{K}$ being perfect) it divides $|\overline{K}/\textbf{Z}(\overline{K})|$ as well, hence it divides |S| and it is therefore a vertex of $\Delta (G/M)$, not our case. Thus, recalling that $\overline{Q}$ is a normal subgroup of $\overline{H}$, we deduce that $\overline{Q}$ centralizes $\overline{K}\trianglelefteq \overline{H}$; moreover, we have that $(\overline{K}, \widehat{M})$ satisfies $\mathcal {N}_s$ for every $s \in \delta \cap \pi (S)$. But we know that S lies in $\mathcal {L}$, whence Lemma 3.13 yields that either $S \cong \textrm{PSL}_2(t^a)$ or $S \cong \textrm{Sz}(2^a)$.

In the former case, we get either $\overline{K} = S$ or $\overline{K} \cong \textrm{SL}_2(t^a)$. Recall that $(\overline{K},\widehat{M})$ satisfies $\mathcal {N}_s$ for every $s\in \delta$: so, by Lemma 3.11 and Remark 3.12, as $\widehat{M}$ is a faithful $\overline{K}$-module, either ($s = t$ and) $|\widehat{M}| = t^{2a}$, or ($s= 3$ and) $|\widehat{M}| = 3^4$ with $\overline{K} \cong \textrm{SL}_2(5)$, or finally ($s= 3$ and) $|\widehat{M}| = 3^6$ with $\overline{K} \cong \textrm{SL}_2(13)$. If $|\widehat{M}| = t^{2a}$, then we can see $\overline{H}$ as a subgroup of $\textrm{GL}_{2a}(t)$ and, by Lemma 3.6, $|\textbf{C}_{\overline{H}}(\overline{K})|$ divides $|\overline{K}|$. Since $\overline{Q} \le \textbf{C}_{\overline{H}}(\overline{K})$ has order coprime to $|\overline{K}|$, we get a contradiction as $\overline{Q} \cong Q \ne 1$. If $|\widehat{M}| = 3^4$, then $\overline{K} \cong \textrm{SL}_2(5)$ can be seen as a subgroup of $\overline{L} = \textrm{GL}_4(3)$; one computes that then $|\textbf{C}_{\overline{L}}(\overline{K})| = 8$, which is not possible since $\overline{Q} \le \textbf{C}_{\overline{L}}(\overline{K})$. If $|\widehat{M}| = 3^6$, then we see $\overline{K} \cong \textrm{SL}_2(13)$ as a subgroup of $\overline{L} = \textrm{GL}_6(3)$; one computes that $\textbf{C}_{\overline{L}}(\overline{K}) = \textbf{Z}(\overline{L})$, of order 2, and this is again impossible as $\overline{Q} \le \textbf{C}_{\overline{L}}(\overline{K})$.

On the other hand, if $S \cong \textrm{Sz}(2^a)$, then by the structure of the degree graph of the Suzuki groups and the fact that $\Delta (S)$ is connected with cut-vertex p, we deduce that $2^a-1 = p$ and that $\delta \cap \pi (S)$ is either $\{2\}$ or $\pi (2^{2a}+1)$. The first possibility is ruled out by Lemma 3.13 and the second one is excluded because S does not have abelian $\pi (2^{2a}+1)$-Hall subgroups. This is the final contradiction that completes the proof.$\square$

4 The Main Result

We are now ready to prove the main result of this paper.

Theorem 4.1

Let G be a non-solvable group with no composition factors isomorphic to $\textrm{PSL}_2(t^a)$ (t prime, $t^a\ge 4$), let R and K be, respectively, the solvable radical and the solvable residual of G, and let p be a prime number. Then the graph $\Delta (G)$ is connected and has cut-vertex p if and only if one of the following holds.

• (a) $K \cong \mathrm{{Sz}}(2^a)$, $a\ge 3$ is a prime, $p=2^a-1$ and $\textrm{V}(G/K)\subseteq \{p\}$.

• (b) $K \cong \mathrm{{PSL}}_3(4)$, $|G:KR|\in \{1,3\}$, $p=5$ and $\textrm{V}(G/K)\subseteq \{5\}$.

• (c) $K \cong \mathrm{{M}}_{11}$, $G=K\times R$, $p=5$ and $\textrm{V}(R)\subseteq \{5\}$.

• (d) $K \cong \mathrm{{J}}_1$, $G=K\times R$, $p=2$ and $\textrm{V}(R)\subseteq \{ 2\}$.

Moreover, p is the unique cut-vertex of $\Delta (G)$ and $\Delta (G) - p$ has two complete connected components. In all cases except case (d), one of the connected components of $\Delta (G) - p$ has size 1 and, except case (d) when R is abelian, p is a complete vertex of $\Delta (G)$.

Proof

By Theorem 3.16, we know that G/R is an almost simple group; we denote by X/R its socle. As $X/R \not \cong \mathrm{{PSL}}_2(t^a)$ by our assumptions, X/R is isomorphic to a simple group in the following list:

$$\begin{aligned} \mathcal {L}_0 = \{\mathrm{{Sz}}(2^a)~(a \ge 3, \;a \text { odd}),~\mathrm{{PSL}}_3(4),~\mathrm{{M}}_{11},~\mathrm{{J}}_1\}. \end{aligned}$$

Moreover, since the degree graphs of the groups in $\mathcal {L}_0$ are connected (see Theorem 3.4), by Theorem 3.16, we also have that p is a cut-vertex of $\Delta (X/R)$.

We observe that $KR = X$, because KR certainly contains X, and X contains KR, as $K/K\cap X \cong KX/X$ is solvable, thus $X\supseteq K$. Now, setting $L = K \cap R$, we see that $K/L \cong X/R$. We will first show that $L = 1$: working by contradiction, we assume that $L \ne 1$. Let $L/L_0$ be a chief factor of K (possibly $L_0=1$) and consider a non-principal character $\lambda \in \textrm{Irr}(L/L_0)$. If $\lambda$ is K-invariant, then $\textrm{ker}(\lambda )/L_0$ is a proper K-invariant subgroup of $L/L_0$. Hence, $\textrm{ker}(\lambda ) = L_0$ and $\lambda$ is a faithful and K-invariant linear character of $L/L_0$. It follows that $L/L_0$ is cyclic and $L/L_0 \le \textbf{Z}(K/L_0)$. Since $K/L_0$ is a perfect group, by Theorem 11.19 of [17], it follows that $L/L_0$ is isomorphic to a subgroup of the Schur multiplier $\mathrm{{M}}(K/L)$. In particular, we deduce that no non-principal $\lambda \in \textrm{Irr}(L/L_0)$ can be K-invariant if $\mathrm{{M}}(K/L) = 1$. We will now derive a contradiction, by separately considering the various possibilities for the simple group K/L.

$K/L \cong \mathrm{{Sz}}(q)$ (where $q = 2^a$ and $a \ge {3}$ is an odd integer). By Lemma 3.3 and Theorem 3.4, we know that $2^a-1 = p$ and that 2 is only adjacent to p in $\Delta (K/L)$. Let $\lambda \in \textrm{Irr}(L/L_0)$. Assuming that $\lambda$ is K-invariant, since the Schur multiplier of $\textrm{Sz}(2^a)$ is trivial for $a \ge 5$ ([2, Theorem 1]), then $a=3$, $p = 7$ and $\mathrm{{M}}(K/L) \cong C_2\times C_2$ ([2, Theorem 2]). As one can check in [5], a perfect central extension of $\textrm{Sz}(8)$ by a subgroup of order 2 has irreducible characters of degree 40, and this is a contradiction. Therefore, $I_K(\lambda )/L$ is a proper subgroup of K/L, and hence it is contained in a maximal subgroup, of K/L. We recall that the maximal subgroups of $\mathrm{{Sz}}(q)$ are isomorphic to one of the following groups (see, for instance, [31, Theorem 4.1]).

• (a) Frobenius groups $Q\rtimes C_{q-1}$, where $Q\in \textrm{Syl}_2(\text {Sz}(q))$;

• (b) Suzuki simple groups $\mathrm{{Sz}}(q_0)$, where $q= q_0^r$, r is a prime and $q_0 \ge 8$;

• (c) Dihedral groups $D_{2(q-1)}$;

• (d) $C_{f_{+}}\rtimes C_4$, where $f_{+} = q +\sqrt{2q}+1$.

• (e) $C_{f_{-}}\rtimes C_4$, where $f_{-} = q -\sqrt{2q}+1$.

Since 2 is only adjacent to p in $\Delta (K/L)$, by Clifford correspondence the index $|K:I_K(\lambda )|$ must be either odd or coprime to $q^2+1$, and hence the unique possibility for $I_K(\lambda )/L$ is to be contained in a Frobenius group $Q \rtimes C_{q-1}$ (case (a) above) and that $I_K(\lambda )/L$ contains a Sylow 2-subgroup Q of K/L. This is true for every non-trivial $\lambda$ in the dual group V of $L/L_0$, and hence (K/L, V) verifies the condition $\mathcal {N}_2$; but this is impossible by Lemma 3.13.

$K/L \cong \textrm{PSL}_3(4)$. Recall that $\Delta (K/L)$, which is a subgraph of $\Delta (G)$, is a connected graph whose vertex set is $\{2,3,5,7\}$ and it has cut-vertex 5 (See Fig. 4); moreover, in $\Delta (K/L)$, the vertex 5 is the only neighbour of 2. Since we have $\textrm{V}(G) = \pi (K/L)\cup \{p\}$ by Theorem 3.16, the disconnectedness of $\Delta (G)-p$ forces $p=5$. Hence, 2 is adjacent only to 5 in $\Delta (G)$ as well. Assume first that there exists a non-principal $\lambda \in \textrm{Irr}(L/L_0)$ which is K-invariant. As the Schur multiplier of $\text {PSL}_3(4)$ is isomorphic to $C_4\times C_4 \times C_3$ [5], by the above discussion we deduce that $L/L_0$ is a cyclic central subgroup of $K/L_0$, and that $|L/L_0|$ is either 2 or 3. One can check in [5] that in the first case $K/L_0$ has an irreducible character of degree 28, while in the second case $K/L_0$ has an irreducible character of degree 84, giving a contradiction in both cases. So we may assume that $I_K(\lambda )<K$, and hence $I_K(\lambda )/L$ is contained in a maximal subgroup H/L of K/L. The maximal subgroups of $\text {PSL}_3(4)$ are isomorphic to $(C_2)^4\rtimes A_5$, $A_6$, $\text {PSL}_3(2)$, and $(C_3)^2 \rtimes Q_8$ [5] and, since 2 is only adjacent to 5 in $\Delta (G)$, it follows that H/L is isomorphic to $(C_2)^4\rtimes A_5$. Moreover, $I_K(\lambda )/L$ is forced to contain a Sylow 2-subgroup of K/L: in other words, the action of K/L on the dual group of $L/L_0$ satisfies condition $\mathcal {N}_2$. However, this is impossible by Lemma 3.13, and the desired conclusion is achieved in this case.

$K/L \cong \textrm{M}_{11}$. By Theorem 3.16 and the structure of $\Delta (\textrm{M}_{11})$ (see Fig. 4), we know that $p = 5$ is a cut-vertex of both $\Delta (G)$ and $\Delta (K/L)$, that $\textrm{V}(G) = \{2,3,5,11\}$ and that 3 is adjacent only to 5 in $\Delta (G)$. As $K/L \cong M_{11}$ has trivial Schur multiplier [5], then K/L acts faithfully and irreducibly on the dual group V of $L/L_0$ and, since K/L cannot have any regular orbit on V (as otherwise $\Delta (G)$ would be a complete graph) by [18, Theorem 2.3] and [12, Theorem 1.1], we deduce that V is either a 10-dimensional $\mathbb {F}_q[K/L]$-module, with $q \in \{2, 3\}$, or V is a 5-dimensional $\mathbb {F}_3[K/L]$-module. In the first case, one computes (via GAP [13]) that there is a K/L-orbit in V whose length is divisible by all the prime divisors of K/L, so by Clifford theory $\Delta (G)$ is a complete graph, a contradiction. On the other hand, there are two isomorphism types of 5-dimensional irreducible $\mathbb {F}_3[K/L]$-modules. One of them has a K/L-orbit of size $132 = 2^2\cdot 3\cdot 11$, so by Clifford theory 3 and 11 would be adjacent in $\Delta (G)$, a contradiction. The second one, which we keep denoting as V, has non-trivial orbit sizes 22 and 220, is self-dual and the second cohomology group $H^2(K/L, V)$ is trivial. One checks again via GAP [13] that the semidirect product $H = V \rtimes K/L$ has an irreducible character of degree $660 = 2^2\cdot 3 \cdot 5 \cdot 11$ and, since H is isomorphic to a normal section of G, it follows that $\Delta (G)$ is a complete graph, a contradiction.

$K/L \cong \textrm{J}_1$. By Theorem 3.16 and the structure of $\Delta (\textrm{J}_{1})$ (see Fig. 4), we know that $p = 2$ is a cut-vertex of both $\Delta (G)$ and $\Delta (K/L)$, and that $\textrm{V}(G) = \pi (K/L) = \{2,3,5,7,11, 19 \}$. As $K/L \cong \mathrm{{J}}_{1}$ has trivial Schur multiplier [5], then K/L acts faithfully and irreducibly on the dual group V of $L/L_0$. Again Theorem 2.3 of [18] and Theorem 1.1 of [12] ensure that either K/L has a regular orbit on V or V is the 20-dimensional $\mathbb {F}_2[K/L]$-module. One checks via GAP [13] that in the last case there is a K/L-orbit in V of size $2^2\cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 19$. Hence, in any case, by Clifford theory $\Delta (G)$ is a complete graph, a contradiction.

Our conclusion so far is that $L = 1$, and hence that K is a minimal normal subgroup of G. We will conclude the proof of the claims (a)–(d) by again considering separately the possibilities for $K \in \mathcal {L}_0$. By Theorem 3.4, $\Delta (K)$ is connected and, by Theorem 3.16, p is a cut-vertex of both $\Delta (G)$ and $\Delta (K)$. Let $C = \textbf{C}_G(K)$. As $R \cap K = 1$, we have $R \le C$ and, since G/R is almost simple, we deduce that $R = C$.

If $K \cong \mathrm{{Sz}}(2^a)$, where $a\ne 1$ is an odd positive integer then, by Lemma 3.3, we know that the vertex 2 is only adjacent in $\Delta (K)$ to the prime divisors of $2^a-1$. It follows that $2^a-1$ is a power of the prime p, so $2^a - 1 = p$ is a Mersenne prime by Proposition 3.1 of [25], and hence a is a prime number. Let $\theta$ be the Steinberg character of the socle $X/R \cong K$ of G/R; so $\theta (1)$ is a power of 2 and $\theta$ has an extension $\psi$ to G/R. Seeing $\psi$ as an irreducible character of G by inflation, then $\psi$ is an extension of the character $\theta _0\in \textrm{Irr}(K)$ that corresponds to $\theta$ in the natural isomorphism between X/R and K. By Gallagher’s theorem we get $\textrm{Irr}(G\,|\, \theta _0)= \{\psi \gamma \,|\, \gamma \in \textrm{Irr}(G/K)\}$, and hence 2 is adjacent in $\Delta (G)$ to every prime in $\textrm{V}(G/K)$; this forces $\textrm{V}(G/K)\subseteq \{p\}$ and (a) is proved.

If $K \cong \textrm{PSL}_3(4)$ then, by Theorem 3.16, $\textrm{V}(G) = \pi (K) = \{2, 3, 5, 7\}$ and, as p is a cut-vertex of both $\Delta (G)$ and $\Delta (K)$, then $p=5$ (see Fig. 4) and $\Delta (G) = \Delta (K)$. The outer automorphism group of $\textrm{PSL}_3(4)$ is isomorphic to $C_2\times S_3$ and all almost simple extensions of $\textrm{PSL}_3(4)$ by a subgroup of order 2 have an irreducible character of degree divisible by 6 [5]. It follows that |G : KR| is odd, and hence $|G:KR|\in \{1,3\}$. As in the previous paragraph, the Steinberg character $\theta _0$ of K has an extension $\psi$ to G, and then by Gallagher’s theorem $\textrm{Irr}(G\,|\,\theta _0)= \{\psi \gamma \,|\,\gamma \in \textrm{Irr}(G/K)\}$. Hence, 2 is adjacent to every prime in $\textrm{V}(G/K)$, which forces $\textrm{V}(G/K)\subseteq \{5\}$ and (b) is proved.

If $K \cong \textrm{M}_{11}$ or $K \cong \textrm{J}_{1}$, then $G = K \times R$ because the outer automorphism group of K is trivial. Hence, $\Delta (G) = \Delta (K) *\Delta (R)$ is the join of the degree graphs of K and R and, since G has cut-vertex p, recalling the graphs of $\textrm{M}_{11}$ and $\textrm{J}_1$ (see Fig. 4) it follows that $\textrm{V}(R) \subseteq \{ p \}$. If $K \cong \textrm{M}_{11}$, then $p =5$ is a complete vertex of $\Delta (G) = \Delta (K)$. If $K \cong \textrm{J}_1$, then $p =2$ and either $\Delta (G) = \Delta (K)$, or $\Delta (G)$ is obtained from $\Delta (K)$ by adding an edge between 2 and 11. So, also (c) and (d) are proved and the proof of the ‘only if’ part of the statement is complete.

Conversely, assume that one of the conditions (a), (b), (c) or (d) holds. Since K is a non-abelian simple group and G/K is solvable, $\textbf{C}_G(K)$ (which is isomorphic to a subgroup of G/K) is solvable as well and hence, as the solvable radical R of G is contained in $\textbf{C}_G(K)$, we see that $R = \textbf{C}_G(K)$. Moreover, G/KR is isomorphic to a subgroup of the outer automorphism group of K.

Assume first (a), so $K \cong \mathrm{{Sz}}(2^a)$ where $p = 2^a-1$ is a prime, $a \ge 3$ is a prime and $\textrm{V}(G/K)\subseteq \{p\}$. The outer automorphism group of a Suzuki simple group consists only of field automorphisms [5], so G/KR is either trivial or of order a. Recalling that p is a complete vertex of $\Delta (K)$, if $G = K \times R$ then $\Delta (G) = \Delta (K)$ and p is both a complete vertex and the unique cut-vertex of $\Delta (G)$. So, we can assume that $|G/KR| = a$, and by Theorem 1.1 of [14], we have that a is adjacent in $\Delta (G/R)$ and hence in $\Delta (G)$ to every other vertex in $\pi (K) - \{ 2 \}$ (by the way, one can easily check that $a \in \pi (K)$ only when $a = 5$). Hence, $\Delta (G) - 2$ is a complete graph. If $\chi \in \textrm{Irr}(G)$ has even degree, then $\chi$ lies above the Steinberg character $\theta$ of K, because a is odd and $\textrm{V}(R) \subseteq \textrm{V}(G/K)\subseteq \{p\}$. Since, by the same argument used above, $\theta$ is G-invariant and extends to G, by Gallagher’s theorem $\chi (1) = \theta (1) \beta (1)$ for some $\beta \in \textrm{Irr}(G/K)$. Hence, 2 is adjacent only to p in $\Delta (G)$, and therefore p is a cut-vertex of $\Delta (G)$. Moreover, also in this case p is a complete vertex of $\Delta (G)$.

Assume now (b), so $K \cong \mathrm{{PSL}}_3(4)$, $|G:KR|\in \{1,3\}$ and $\textrm{V}(G/K)\subseteq \{5\}$. If $G = K \times R$, then $\Delta (G) = \Delta (K)$ as $\textrm{V}(R) \subseteq \{ 5\}$ and 5 is a complete vertex of $\Delta (K)$, thus we are done. So, we can assume $|G: KR|=3$. If $\chi \in \textrm{Irr}(G)$ has even degree, then as in the previous paragraph we deduce that $\chi$ lies over the Steinberg character $\theta$ of K and that $\chi (1) = \theta (1)\beta (1)$ for some $\beta \in \textrm{Irr}(G/K)$. Therefore, 2 is only adjacent to 5 in $\Delta (G)$, and hence again $\Delta (G) = \Delta (K)$. So, 5 is a both a complete vertex and the only cut-vertex of $\Delta (G)$.

Similarly, assuming (c) (i.e. $K \cong \mathrm{{M}}_{11}$), $G=K\times R$ and $\textrm{V}(R)\subseteq \{5\}$, we have that $\Delta (G) = \Delta (K)$ and all assertions follow.

If we have (d), so $K \cong \mathrm{{J}}_1$, $G=K\times R$ and $\textrm{V}(R)\subseteq \{ 2\}$, then either $\Delta (G) = \Delta (K)$ or $\Delta (G)$ is obtained from $\Delta (K)$ by adding the edge $\{2, 11\}$ (so 2 is a complete vertex of $\Delta (G)$ in this case). It follows that 2 is the only cut-vertex of $\Delta (G)$, and it is a complete vertex if and only if R is non-abelian.

Finally, the degree graphs of the relevant groups are displayed in Fig. 1 (cases (a–d)), and all the remaining assertions of the statement follow at once.$\square$

5 A Proof of Theorem C

In this concluding section we prove Theorem C, that gives a characterization of the non-solvable groups whose degree graph is disconnected and has a cut-vertex.

We recall first some features of the degree graphs of the almost simple groups with socle isomorphic to $\textrm{PSL}_2(t^a)$.

Lemma 5.1

Let G be an almost simple group with socle $S \cong \textrm{PSL}_2(t^a)$, where t is a prime and $t^a \ge 4$.

• (a) If q is a prime divisor of |G/S|, then q is adjacent in $\Delta (G)$ to every prime in $\pi (S) - \{ t\}$.

• (b) Assume $t^a > 5$. If t divides |G : S|, then $\Delta (G)$ is connected, while if t does not divide |G : S|, then t is an isolated vertex of $\Delta (G)$.

Proof

Claim (a) follows from Theorem A of [30], and (b) is Theorem 2.7 of [22].$\square$

Proof of Theorem C

Let us first assume that $\Delta (G)$ is a disconnected graph and that it has a cut-vertex p. We recall that, by the main theorem of [24], $\Delta (G)$ has at most three connected components. If $\Delta (G)$ has three connected components then, by Theorem 3.7, $G=\text {SL}_2(2^a) \times A$, where A is an abelian group and a is an integer larger than 1. In this situation, the three connected components of $\Delta (G)$ are complete graphs with vertex sets $\{2\}$, $\pi (2^a+1)$ and $\pi (2^a-1)$, and this is against the existence of a cut-vertex in $\Delta (G)$. Thus, we deduce that $\Delta (G)$ has two connected components. By Theorem 3.7, G/K is an abelian group and there is a normal subgroup $N \le K$ of G such that $K/N\cong \textrm{PSL}_2(t^a)$ with $t^a\ge 4$; by Proposition 3.8, $\textrm{V}(G) = \pi (G/R)$. Moreover, if $N>1$, then either $K\cong \textrm{SL}_2(t^a)$ or there exists a minimal normal subgroup L of G, $L \le N$, such that $K/L\cong \textrm{SL}_2(t^a)$ and L is isomorphic to the natural module for K/L. In the last case, as the natural module for $\textrm{SL}_2(t^a)$ is self-dual, the stabilizer of any non-trivial irreducible character of L is a Sylow t-subgroup of K, and hence Clifford theory and Lemma 5.1 yield that $\Delta (G) - t$ is a complete graph, which is again impossible by the assumption of the existence of a cut-vertex in $\Delta (G)$. Hence, either $N= 1$ and $K \cong \textrm{PSL}_2(t^a)$ or $|N| = 2$ and $K\cong \textrm{SL}_2(t^a)$. Let now C be a subgroup of G such that $C/N = \textbf{C}_{G/N}(K/N)$. Clearly, $R \subseteq C$; more precisely, $R \subseteq \textbf{C}_G(K)$, because $[K, R] \subseteq N$, so $[K, R, K] = 1 = [R,K, K]$ and hence, recalling that K is a perfect group, by the Three Subgroups lemma, $[K, R] = [K, K, R] = 1$. Conversely, as K/N is the only non-solvable composition factor of G, C is a solvable normal subgroup of G, so $C \subseteq R$ and hence $C = R$. Therefore, Theorem 3.7 yields that if $t^a > 5$, then t does not divide |G : KR|. If $t \ne 2$, then by Lemma 3.2 and Lemma 5.1, the assumption that p is a cut-vertex of $\Delta (G)$ yields that |G : KR| is necessarily a power of p and that $p=2$. Moreover, again by the assumption that $p = 2$ is a cut-vertex of $\Delta (G)$, none of $t^a+1$ and $t^a-1$ can be a power of 2, and hence by [25, Proposition 3.1], $t^a \ne 9$ and $t^a$ is neither a Fermat nor a Mersenne prime. (In particular, $t^a \ne 5$.) If $t=2$ and $t^a \ne 4$, then Lemma 3.2 implies that $G \ne KR$ and, together with Lemma 5.1, that $|G:KR|\ne 1$ is a power of $p\ne 2$. Finally, if $t^a= 4$, then K is isomorphic to $\textrm{SL}_2(4)$ and $\textrm{V}(G) = \pi (G/R) = \{2,3,5\}$ and, since $\Delta (G)$ is disconnected, $\Delta (G)$ cannot have any cut-vertex.

Conversely, we assume that either $K \cong \textrm{PSL}_2(t^a)$ or $K \cong \textrm{SL}_2(t^a)$ (where t is a prime and $t^a\ge 4$), G/K is abelian, $|G:KR| = p^b$ (with $b \ge 0$), and that either (a) or (b) holds. Suppose first that $t=2$. Let $\chi$ be an irreducible character of G such that $\chi (1)$ is even and let $\psi$ be an irreducible constituent of $\chi _{K \times R}$. Then $\psi = \alpha \times \beta$, where $\alpha \in \textrm{Irr}(K)$ and $\beta \in \textrm{Irr}(R)$; note that $\psi (1)$ is even as |G : KR| is odd. Since R (which is isomorphic to a subgroup of G/K) is abelian, we see that $\alpha (1)$ is even and hence $\alpha$ is the Steinberg character of K; in particular, $\alpha$ is G-invariant and $\alpha (1) = 2^a$. As G/K is abelian, also $\beta$ is G-invariant and hence $\psi$ is G-invariant. Now, G/KR is cyclic because it is isomorphic to a subgroup of the outer automorphism group of K; hence, by Corollary 11.22 of [17], $\psi$ extends to G and, by Gallagher’s theorem, $\chi (1)$ is a power of 2. We deduce that 2 is an isolated vertex of $\Delta (G)$ and, in particular, $\Delta (G)$ is disconnected. Moreover, by part (a) of Lemma 5.1 the vertex p is adjacent in $\Delta (G)$ to all the vertices in $\textrm{V}(G) - \{2, p\}$, so p is a cut-vertex of $\Delta (G)$.

Finally, we assume that t is odd. We observe that, by the same argument we used above, $R/N = \textbf{C}_{G/N}(K/N)$; hence, by Theorem 3.7, $\Delta (G)$ is disconnected. Moreover, by Lemma 3.2 and the fact that $\Delta (K)$ is a subgraph of $\Delta (G)$, $p=2$ is adjacent in $\Delta (G)$ to all vertices of $\textrm{V}(G) - \{ 2, t\}$. Let us now assume, working by contradiction, that there is a character $\chi \in \textrm{Irr}(G)$ such that qs divides $\chi (1)$ for some odd primes $q\in \pi (t^a-1)$ and $s\in \pi (t^a+1)$. Let $\theta \in \textrm{Irr}(KR)$ be an irreducible constituent of $\chi _{KR}$. Since |G : M| is power of 2, then qs necessarily divides $\theta (1)$. Observe that N, being a cyclic group of order at most 2, is central in G and hence $KR = KD \times H$, where $D\in \textrm{Syl}_2(R)$ and H is the abelian 2-complement of R. It follows that qs divides the degree of any irreducible constituent $\alpha$ of $\theta _K$, and this is a contradiction by Lemma 3.2. Hence, no vertex of $\pi (t^a-1) - \{ 2\}$ is adjacent to any vertex of $\pi (t^a+1) - \{ 2\}$ and we conclude that $\Delta (G) = \Delta (K)$. Finally, by (a) both $\pi (t^a-1) -\{2\}$ and $\pi (t^a+1) -\{2\}$ are non-empty sets of vertices of $\Delta (G)$ and hence 2 is a cut-vertex of $\Delta (G)$. The proof is complete.$\square$