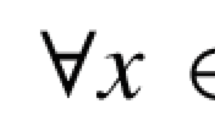Local and Global Canonical Forms for Differential-Algebraic Equations with Symmetries

Abstract

Linear time-varying differential-algebraic equations with symmetries are studied. The structures that we address are self-adjoint and skew-adjoint systems. Local and global canonical forms under congruence are presented and used to classify the geometric properties of the flow associated with the differential equation as symplectic or generalized orthogonal flow. As applications, the results are applied to the analysis of dissipative Hamiltonian systems arising from circuit simulation and incompressible flow.

1 Introduction

We study regular linear variable coefficient differential-algebraic equations (DAEs)

$$ E(t) \dot{x} =A(t) x+f(t),\quad E,A\in C(\mathbb{I}, \mathbb{R}^{n,n}),~f\in C(\mathbb{I},\mathbb{R}^{n})\text{ sufficiently smooth}, $$

(1)

which additionally possess certain symmetries, in particular self-adjoint and skew-adjoint structures. Here $\mathbb {I}\subseteq \mathbb {R}$ is a compact non-trivial time interval and $C^{k}(\mathbb {I},\mathbb {R}^{n,n})$ with $k\in {\mathbb {N}}_{0}\cup \{\infty \}$ denotes the set of k times continuously differentiable functions from $\mathbb {I}$ into the set of real n × n matrices $\mathbb {R}^{n,n}$. In the case k = 0 we drop the superscript. A function is said to be sufficiently smooth if k is sufficiently large such that all needed derivatives exist.

The discussed classes of DAEs with symmetries are defined as follows.

Definition 1.1

The DAE (1) and its associated pair (E,A) of matrix functions are called self-adjoint if

$$ E^{T}=-E,\quad A^{T}=A+\dot{E} $$

(2)

as equality of functions.

Definition 1.2

The DAE (1) and its associated pair (E,A) of matrix functions are called skew-adjoint if

$$ E^{T}=E,\quad A^{T}=-A-\dot{E} $$

(3)

as equality of functions.

Systems with these types of symmetries arise in the modeling of physical systems, e.g., by a (generalized) Hamiltonian formalism or in optimal control problems leading to a self-adjoint structure or by so-called dissipative Hamiltonian systems leading to a skew-adjoint structure.

Our main motivation to study differential-algebraic equations with self-adjoint and skew-adjoint pairs arises from multi-physics, multi-scale models that are coupling different physical domains that may include mechanical, mechatronic, fluidic, thermic, hydraulic, pneumatic, elastic, plastic, or electric components, see e.g. [1, 2, 11, 19, 38, 39].

An important class of problems where multi-physics and multi-scale modeling arises is the human cariovascular system, where model hierarchies of detailed models for the blood flow in large vessels, modeled via the Navier–Stokes equations, and reduced or surrogate models for the capillary vessels, modeled via electrical network equations, are coupled together to improve computational efficiency, while at the same time achieving a desired simulation accuracy, see [13, 14, 32, 33, 35]. Due to the physical background, after space discretization and linearization along a solution, as well as ignoring dissipation terms, all the components arising in this application can be expressed as DAE systems with symmetries.

Motivated by classical bond graph theory, see [31, 42], and to deal with general multi-physics and multi-scale coupling, in recent years the framework of port-Hamiltonian systems has become an important modeling paradigm, see [3, 15, 20, 28, 30, 43, 44] or the recent survey [29], that encodes underlying physical principles directly into the algebraic structure of the coefficient matrices and in the geometric structure associated with the flow of the dynamical system. This leads to a remarkably flexible modeling approach, which has also been extended to include algebraic constraints, so that the resulting model is a port-Hamiltonian differential-algebraic equation (pHDAE), [3, 28, 45]. Such systems allow for automated modeling in a modularized network based fashion, and they are ideal for building model hierarchies of very fine models for numerical simulation and reduced or surrogate models for control and optimization. This makes them particularly suited also for large networks, such as power, gas, or district heating networks where such model hierarchies are used to adapt the simulation and optimization techniques to user needs, [9, 18, 28].

Since in this paper we will mainly discuss linear time-varying DAE systems with symmetries, we introduce the structure of pHDAEs for this case as in [3], see [28] for the more general nonlinear framework. Linear time-varying DAE systems arise when general nonlinear DAE systems are linearized along non-stationary solutions [6] and the study of this class is essential for the understanding of the general nonlinear DAEs, see [22]. For nonlinear pHDAE with non-quadratic Hamiltonian systems also a local approximation of the Hamiltonian by a quadratic Hamiltonian is typical.

Linear time-varying pHDAE systems with quadratic Hamiltonian have the form

$$ \begin{array}{@{}rcl@{}} E(t)\dot{x} + E(t)K(t)x &=& (J(t)-R(t))x + (G(t)-P(t))u, \end{array} $$

(4a)

$$ \begin{array}{@{}rcl@{}} y &=& (G(t)+P(t))^{T} x + (S(t)-N(t))u, \end{array} $$

(4b)

with state x, input u, output y and coefficients $E\in C^{1}(\mathbb {I},\mathbb {R}^{n,n})$, $J,R,K \in C(\mathbb {I},\mathbb {R}^{n,n})$, $G,P\in C(\mathbb {I},\mathbb {R}^{n, m})$, $S,N\in C(\mathbb {I},\mathbb {R}^{m, m})$, S = S^T,N = −N^T. As energy function we employ a quadratic Hamiltonian

$$ \mathcal{H} \colon \mathbb{I} \times \mathbb{R}^{n}\to \mathbb{R},\qquad (t,x) \mapsto \frac{1}{2}x^{H} E(t)x, $$

where E(t) is the local Hessian of the Hamiltonian when linearizing around a nonstationary solution and the pair of coefficients (E,J − EK) is skew-adjoint, while the matrix function associated with dissipation of energy

$$ \mathcal{W} = \begin{bmatrix} R & P\\ P^{T} & S \end{bmatrix} $$

is pointwise positive semidefinite. Furthermore, typically one also has that E is pointwise positive semidefinite as well. If the system does not have an output equation and the input is considered as an inhomogeneity then this is called a dissipative Hamiltonian DAE (dHDAE).

The underlying skew-adjoint structure arises if the dissipation term R is neglected, i.e., if $\mathcal {W}=0$ in (4). Typically the problems with dissipation can be considered as a perturbed symmetry structure and a dissipative term can be treated separately as a by-product in simulation methods (Fig. 1).

Fig. 1

Circuit example

To illustrate applications for dHDAEs and DAEs with symmetries consider the following simple examples, for further applications see [3, 28, 45, 46] or the recent survey [29].

Example 1.3

Consider the pHDAE formulation of an electrical circuit from [28]. Denoting by V_i the voltages and by I_i the currents, where L > 0 models an inductor, C₁,C₂ > 0 capacitors, R_G,R_L,R_R > 0 resistances, and E_G a controlled voltage source, one obtains a pHDAE

$$ \begin{array}{@{}rcl@{}} E\dot{x} &=& (J-R) x + G u, \\ y &=& G^{T} x, \end{array} $$

with $x=\begin {bmatrix} I &V_{1}&V_{2}&I_{G}&I_{R} \end {bmatrix}^{T}$, u = E_G, y = I_G, E = diag(L,C₁,C₂,0,0),

$$ G=\begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \\ 0 \end{bmatrix},\quad J = \begin{bmatrix} 0 & -1 & 1 & 0 & 0 \\ 1 & 0 & 0 & -1 & 0 \\ -1 & 0 & 0 & 0 & -1 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \end{bmatrix}, \quad R = \begin{bmatrix} R_{L} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & R_{G} & 0 \\ 0 & 0 & 0 & 0 & R_{R} \end{bmatrix}. $$

The quadratic Hamiltonian, describing the energy stored in the inductor and the two capacitors, is given by

$$ \mathcal{H}(I,V_{1},V_{2}) = \frac{1}{2}LI^{2} + \frac{1}{2}C_{1}{V_{1}^{2}} + \frac{1}{2}C_{2}{V_{2}^{2}}. $$

If the generator is shut down (i.e. E_G = 0), then the system approaches an equilibrium solution for which $\frac {d}{dt} {\mathscr{H}}(x)=0$, so that I = I_G = I_R = 0 and thus x = 0 in the equilibrium. Without the damping by the resistances (i.e. setting R_L = R_G = R_R = 0) this is a skew-adjoint DAE.

Example 1.4

A classical example of a partial differential equation which, after proper space discretization leads to a pHDAE, see e.g. [12, 34], are the incompressible or nearly incompressible Navier–Stokes equations describing the flow of a Newtonian fluid in a domain Ω,

$$ \begin{array}{@{}rcl@{}} \partial_{t}{v} &=& \nu {{\varDelta}} v - (v\cdot\nabla) v - \nabla p + f \qquad \text{in } {{\varOmega}} \times \mathbb{T} ,\\ 0 &=& \nabla^{T} v \qquad \text{in } {{\varOmega}} \times \mathbb{T}, \end{array} $$

together with suitable initial and boundary conditions, see e.g. [41]. When one linearizes around a prescribed vector field $v_{\infty }$, then one obtains the linearized Navier–Stokes equations, and if $v_{\infty }$ is constant in space and the term $(v_{\infty }\cdot \nabla ) v$ is neglected then one obtains the Stokes equation.

Performing a finite element discretization in space, see for instance [26], a Galerkin projection leads to a dHDAE of the form

$$ \begin{bmatrix} M & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} \dot{v} \\ \dot{p} \end{bmatrix} = \begin{bmatrix} A_{S}(t)-A_{H}(t) & -B\\ B^{T} & -C \end{bmatrix} \begin{bmatrix} v\\ p \end{bmatrix} + \begin{bmatrix} f(t)\\ 0 \end{bmatrix}, $$

(5)

where M = M^T > 0 is the mass matrix, $A_{S}=-{A_{S}^{T}}$, $A_{H}={A_{H}^{T}}\geq 0$ are skew-symmetric and symmetric part of the discretized and linearized convection-diffusion operator, B is the discretized gradient operator, B^T is the discretized divergence operator, which we assume to be normalized so that it is of full row rank, and C = C^T > 0 is a stabilization term of small norm that is needed for some finite element spaces, see e.g. [4, 34, 36, 37]. Here v and p denote the discretized velocity and pressure, respectively, and f is a forcing term. Without the damping (i.e. for A_H = 0 and C = 0) we again have a skew-adjoint DAE.

The class of problems with self-adjoint structure arises most prominently in the context of constrained generalized Hamiltonian systems and in optimal control problems, where the operators associated with the optimality conditions have this structure.

Example 1.5

In [23] the optimality conditions were derived for the linear-quadratic optimal control problem of minimizing a cost functional

$$ \mathcal{J}(x,u)=\frac{1}{2} x(t_{f})^{T} M_{f} x(t_{f})+\frac{1}{2} {\int}_{t_{0}}^{t_{f}}\left( x^{T} W x +x^{T} S u +u^{T} S^{T} x +u^{T} R u\right) dt, $$

subject to the DAE constraint

$$ E \dot{x}= A x+ B u + f,\quad x(t_{0})={x_{0}}\in\mathbb{R}^{n}, $$

with $E,A,W\in C(\mathbb {I},\mathbb {R}^{n,n})$, $B \in C(\mathbb {I},\mathbb {R}^{n,m})$, $S \in C(\mathbb {I},\mathbb {R}^{n,m})$, $R \in C(\mathbb {I},\mathbb {R}^{m,m})$, $f \in C(\mathbb {I},\mathbb {R}^{n})$ and $M_{e} \in \mathbb {R}^{n,n}$, where R = R^T, W = W^T and $M_{f}={M_{f}^{T}}$.

After some appropriate reformulation (via some index reduction process) and under some smoothness conditions, the optimality condition is given by a boundary value problem

$$ \left[\begin{array}{ccc} 0 & E & 0\\ -E^{T} & 0 & 0\\ 0 & 0 & 0 \end{array}\right] \frac{d}{dt} \left[\begin{array}{c} \lambda \\ x \\ u \end{array}\right] = \left[\begin{array}{ccc} 0 & A & B\\ A^{T}+\frac{d}{dt} E^{T} & W & S\\ B^{T} & S^{T} & R \end{array}\right] \left[\begin{array}{c} \lambda \\ x \\ u \end{array}\right] + \left[\begin{array}{c} f\\ 0 \\ 0 \end{array}\right], $$

with boundary conditions x(t₀) = x₀, E(t_f)^Tλ(t_f) − M_fx(t_f) = 0. The associated pair of coefficient functions obviously is a a self-adjoint pair, see [25].

Example 1.6

Linear multibody systems with linear holonomic constraints, see [16, 27], take the form

$$ \begin{array}{@{}rcl@{}} M \dot{p} & =& -W q -G^{T} \lambda,\\ \dot{q} & = & p,\\ 0 & =&G q, \end{array} $$

where $p,q \in C^{1}(\mathbb {I}, \mathbb {R}^{n})$, $W,M\in \mathbb {R}^{n,n}$ with W = W^T, M = M^T, and $G\in \mathbb {R}^{m,n}$. If the mass matrix is positive definite, i.e. M > 0, then we can multiply the second equation by − M and the constraint by − 1 to obtain, after switching the first and second equation,

$$ \left[\begin{array}{ccc} 0 & M & 0 \\ -M & 0 & 0 \\ 0 & 0 & 0 \end{array}\right] \left[\begin{array}{c} \dot{q} \\ \dot{p} \\ \dot{\lambda} \end{array}\right] = \left[\begin{array}{ccc} -W & 0 & -G^{T} \\ 0 & -M & 0 \\ -G & 0 & 0 \end{array}\right] \left[\begin{array}{c} q \\ p \\ \lambda \end{array}\right], $$

which has the structure of a self-adjoint DAE.

If W > 0 then we can also multiply the second equation of the constrained Hamiltonian system by W to obtain

$$ \left[\begin{array}{ccc} W & 0 & 0 \\ 0 & M & 0 \\ 0 & 0 & 0 \end{array}\right] \left[\begin{array}{c} \dot{q} \\ \dot{p} \\ \dot{\lambda} \end{array}\right] = \left[\begin{array}{ccc} 0 & W & 0 \\ -W & 0 & -G^{T} \\ 0 & G & 0 \end{array}\right] \left[\begin{array}{c} q \\ p \\ \lambda \end{array}\right] $$

which now has the structure of a skew-adjoint DAE.

Remark 1.7

It should be noted that if in a self-adjoint system $E \dot {x}=A x+f$, both E and A are constant in time and invertible, then by multiplication with E^− 1 and a change of variables z = Ax we get a system $A^{-1} \dot {z} = E^{-1} z+ E^{-1} f$ that is skew-adjoint. A similar construction has also been proposed for dissipative Hamiltonian systems in [10].

Having illustrated the importance of DAEs with symmetries, in this paper we present canonical forms for DAEs (1) with self-adjoint and skew-adjoint structure and show the consequences for the resulting flows.

The paper is organized as follows. In Section 2 we recall some results for general DAEs. In Section 3 we discuss local and global canonical forms for self-adjoint and in Section 4 for skew-adjoint DAEs.

2 Preliminaries

Linear time-varying DAE systems have been extensively discussed, see [22] for a detailed analytical and numerical treatment. In this section we recall some basic concepts from the general theory of DAEs. Our first concept is that of regularity for DAEs that is concerned with the existence of solutions at least for sufficiently smooth inhomogeneity (surjectivity) and uniqueness of the solution in the cases where the initial condition x(t₀) = x₀ allows for a solution (injectivity).

Definition 2.1

The pair (E,A) and the corresponding DAE (1) are called regular if

• 1. the DAE (1) is solvable for every sufficiently smooth f,

• 2. the solution is unique for every $t_{0}\in \mathbb {I}$ and every $x_{0}\in \mathbb {R}^{n}$ allowing for a solution of the DAE with x(t₀) = x₀,

• 3. the solution depends smoothly on f, t₀, and x₀.

The most important technique for the analysis of general linear DAEs is the construction of suitable local and global canonical forms under global equivalence. Since we will refer to these results and some techniques from their derivation, we include here the necessary material from the general (square) case.

We start with (global) equivalence which refers to time-dependent scaling of the DAE and changes of basis.

Definition 2.2

Two pairs (E_i,A_i), $E_{i},A_{i}\in C(\mathbb {I},\mathbb {R}^{n,n})$, i = 1,2, of matrix functions are called (globally) equivalent if there exist pointwise nonsingular matrix functions $P\in C(\mathbb {I},\mathbb {R}^{n,n})$ and $Q\in C^{1}(\mathbb {I},\mathbb {R}^{n,n})$ such that

$$ E_{2} = PE_{1}Q, \quad A_{2} = PA_{1}Q - PE_{1} \dot{Q} $$

as equality of functions. We write $(E_{1},A_{1}) \sim (E_{2},A_{2})$.

It is easy to see that the relation defined in Definition 2.2 indeed is an equivalence relation, [22].

The derivation of canonical forms then relies on the following property of matrix functions on intervals, see [7, 22].

Theorem 2.3

Let $E\in C^{k}(\mathbb {I},\mathbb {R}^{m,n})$, $k\in {\mathbb {N}}_{0} \cup \{\infty \}$, with rankE(t) = r for all $t\in \mathbb {I}$. Then there exist pointwise orthogonal functions $U\in C^{k}(\mathbb {I},\mathbb {R}^{m,m})$ and $V\in C^{k}(\mathbb {I},\mathbb {R}^{n,n})$ such that

$$ U^{T}EV = \begin{bmatrix} {{\varSigma}}&0\\ 0&0 \end{bmatrix} $$

with pointwise nonsingular ${{\varSigma }}\in C^{k}(\mathbb {I},\mathbb {R}^{r,r})$.

We then have the following result on a local canonical form, i.e., a canonical form that requires the restriction to certain subintervals, see [22, Sections 3.1 and 3.3]. In the following, non-specified blocks of matrices or matrix functions are denoted by ∗.

Theorem 2.4

Let (E,A) be regular with $E,A\in C(\mathbb {I},\mathbb {R}^{n,n})$ sufficiently smooth. Then there exist pairwise disjoint open intervals $\mathbb {I}_{j}$, $j\in {\mathbb {N}}$, with

$$ \overline{\bigcup_{j\in{\mathbb{N}}}\mathbb{I}_{j}}=\mathbb{I} $$

(6)

such that on every $\mathbb {I}_{j}$ one has

$$ (E,A)\sim \left( \left[\begin{array}{cc} I_{d}&W\\ 0&G \end{array}\right], \left[\begin{array}{cc} 0&0\\ 0&I_{a} \end{array}\right]\right), $$

where G is structurally nilpotent according to

$$ G=\left[\begin{array}{cccc} 0&\ast&\cdots&\ast\\ &\ddots&\ddots&\vdots\\ &&\ddots&\ast\\ &&&0 \end{array}\right]. $$

Furthermore, the size d of the differential part and the size a of the algebraic part are the same for every interval.

A restriction to subintervals is necessary to obtain the structural nilpotent form of G, which requires constant rank assumptions. This phenomenon occurs naturally for example in robotics when position constraints have a singularity due to two robot arms forming a straight line, see e.g. [8], and no structural nilpotent G exists globally.

A global canonical form, i.e., a canonical form that does not require the restriction to certain subintervals, was given in [5]. We state this result here in a version for real-valued problems omitting the last step of the proof which would require complex-valued transformations. We include the proof for later reference.

Theorem 2.5

Let (E,A) be regular with $E,A\in C(\mathbb {I},\mathbb {R}^{n,n})$ sufficiently smooth. Then we have

$$ (E,A)\sim\left( \left[\begin{array}{cc} I_{d}&E_{12}\\ 0&E_{22} \end{array}\right], \left[\begin{array}{cc} 0&A_{12}\\ 0&A_{22} \end{array}\right]\right), $$

(7)

where

$$ E_{22}(t)\dot{x}_{2}=A_{22}(t)x_{2}+f_{2}(t) $$

is uniquely solvable for every sufficiently smooth f₂ without specifying initial conditions.

Proof

If the homogeneous equation

$$ E(t)\dot{x}=A(t)x $$

has only the trivial solution, then the first block in (7) is missing (i.e., d = 0) and the claim holds trivially by assumption. In any case, the solution space is finite dimensional, since otherwise we could not select a unique solution by prescribing initial conditions.

Let therefore d≠ 0 and let {ϕ₁,…,ϕ_d} be a basis of the solution space. Setting Φ = [ϕ₁ ⋯ ϕ_d], we have

$$ \text{rank} {{\varPhi}}(t)=d\quad\text{ for all }t\in\mathbb{I}, $$

since, if we had rankΦ(t) < d for some $t_{0}\in \mathbb {I}$, then there would exist coefficients $\alpha _{1},\ldots ,\alpha _{d}\in \mathbb {R}$, not all being zero, with

$$ \alpha_{1}\phi_{1}(t_{0})+\cdots+\alpha_{d}\phi_{d}(t_{0})=0 $$

and α₁ϕ₁ + ⋯ + α_dϕ_d would be a nontrivial solution of the homogeneous initial value problem.

Hence, by Theorem 2.3 there exists a smooth, pointwise nonsingular matrix function U with

$$ U^{H}{{\varPhi}}= \left[\begin{array}{c} I_{d}\\ 0 \end{array}\right]. $$

Defining

$$ {{\varPhi}}^{\prime}=U \left[\begin{array}{c} 0\\ I_{a} \end{array}\right] $$

yields a pointwise nonsingular matrix function $Q=[{{\varPhi }}~~{{\varPhi }}^{\prime }]$. Since $E\dot {{\varPhi }}=A{{\varPhi }}$, we obtain

$$ (E,A)\sim ([E{{\varPhi}}~~E{{\varPhi}}^{\prime}], [A{{\varPhi}}~~A{{\varPhi}}^{\prime}] - [E\dot{{\varPhi}}~~E\dot{{\varPhi}}^{\prime}]) = ([E_{1}~~E_{2}],[0~~A_{2}]). $$

In this relation, E₁ has full column rank d. To see this, suppose that $\text {rank} E_{1}(\hat {t})<d$ for some $\hat {t}\in \mathbb {I}$. Then there would exist a vector w≠ 0 with

$$ E_{1}(\hat{t})w=0. $$

Defining in this situation

$$ f(t)=\left\{\begin{array}{ll} \frac{1}{t-\hat{t}}E_{1}(t)w&\quad\text{for }t\ne \hat{t},\\ \frac{d}{dt}(E_{1}(t)w)&\quad\text{for } t= \hat{t}, \end{array}\right. $$

we would obtain a smooth inhomogeneity f. The function x given by

$$ x(t)=\left[\begin{array}{c} \log(\vert t-\hat{t}\vert)w\\ 0 \end{array}\right] $$

would then solve

$$ {[E_{1}(t)~~E_{2}(t)]}\dot{x}=[0~~A_{2}(t)]x+f(t) $$

on $\mathbb {I}\setminus \{\hat {t}\}$ in contradiction to the assumption of unique solvability, which includes by definition that solutions are defined on the entire interval $\mathbb {I}$.

Hence, since E₁ has full column rank, there exists a smooth, pointwise nonsingular matrix function P with

$$ PE_{1}=\left[\begin{array}{c} I_{d}\\ 0 \end{array}\right], $$

and thus

$$ (E,A) \sim \left( \left[\begin{array}{cc} I_{d}&E_{12}\\ 0&E_{22} \end{array}\right], \left[\begin{array}{cc} 0&A_{12}\\ 0&A_{22} \end{array}\right]\right). $$

The equation

$$ E_{22}(t)\dot{x}_{2}=A_{22}(t)x_{2} $$

only admits the trivial solution. To see this, suppose that x₂≠ 0 is a nontrivial solution and x₁ a solution of the ODE

$$ \dot{x}_{1}+E_{12}(t)\dot{x}_{2}(t)=A_{22}(t)x_{2}(t). $$

Then we obtain

$$ {[E_{1}(t)~~E_{2}(t)]} \left[\begin{array}{c} \dot{x}_{1}(t)\\ \dot{x}_{2}(t) \end{array}\right]= [0~~A_{2}(t)] \left[\begin{array}{c} x_{1}(t)\\ x_{2}(t) \end{array}\right]. $$

Since x₂≠ 0, transforming back gives

$$ E(t)Q(t) \left[\begin{array}{c} \dot{x}_{1}(t)\\ \dot{x}_{2}(t) \end{array}\right] = (A(t)Q(t)-E(t)\dot{Q}(t)) \left[\begin{array}{c} x_{1}(t)\\ x_{2}(t) \end{array}\right] $$

or $E(t)\dot {x}(t)=A(t)x(t)$ with

$$ x=Q\left[\begin{array}{c} x_{1}\\ x_{2} \end{array}\right] \ne0,\quad x\not\in\text{span}\{\phi_{1},\ldots,\phi_{d}\}. $$

But this contradicts the construction of ϕ₁,…,ϕ_d, and hence (7) holds. □

In the presence of symmetries, we of course want to maintain these properties, which requires to restrict the allowed equivalence transformations. We will make use of the following notions and properties.

Definition 2.6

Two pairs (E_i,A_i), $E_{i},A_{i}\in C(\mathbb {I},\mathbb {R}^{n,n})$, i = 1,2, of matrix functions are called congruent if there exist a pointwise nonsingular matrix function $Q\in C^{1}(\mathbb {I},\mathbb {R}^{n,n})$ such that

$$ E_{2}=Q^{T}E_{1}Q,\quad A_{2}=Q^{T}A_{1}Q-Q^{T}E_{1}\dot{Q} $$

as equality of functions. We write (E₁,A₁) ≡ (E₂,A₂).

Again, it is easy to see that the relation defined in Definition 2.6 indeed is an equivalence relation, see [25].

The following result then modifies Theorem 2.3 provided some symmetry property holds.

Theorem 2.7

Let $E\in C^{k}(\mathbb {I},\mathbb {R}^{n,n})$, $k\in {\mathbb {N}}_{0}\cup \{\infty \}$, with rankE(t) = r for all $t\in \mathbb {I}$ and let kernelE(t)^T = kernelE(t) for all $t\in \mathbb {I}$. Then there exist a pointwise orthogonal function $Q\in C^{k}(\mathbb {I},\mathbb {R}^{n,n})$ such that

$$ Q^{T}EQ= \begin{bmatrix} {{\varSigma}}&0\\ 0&0 \end{bmatrix} $$

with pointwise nonsingular ${{\varSigma }}\in C^{k}(\mathbb {I},\mathbb {R}^{r,r})$.

Proof

With Q = V from Theorem 2.3, the pointwise property kernelE^T = kernelE allows to choose U = Q^T. □

In the next two sections we will employ these preliminary results to derive canonical forms for self-adjoint and skew-adjoint DAEs.

3 Canonical Forms for Self-Adjoint Pairs of Matrix Functions

In this section we study canonical forms under congruence for self-adjoint DAEs. We survey, modify, and extend previous results from [25]. We first recall that congruence preserves the self-adjoint structure.

Lemma 3.1

Consider two pairs of matrix functions (E,A) and $(\widetilde {E},\widetilde {A})$ that are congruent and let (E,A) be self-adjoint. Then $(\widetilde {E},\widetilde {A})$ is self-adjoint as well.

For self-adjoint pairs the following local canonical form under pointwise orthogonal congruence transformations is due to [25] stated here for the special case of a regular pair of matrix functions.

Theorem 3.2

Let (E,A) be regular with $E,A\in C(\mathbb {I},\mathbb {R}^{n,n})$ sufficiently smooth and let (E,A) be skew-adjoint. Then there exist pairwise disjoint open intervals $\mathbb {I}_{j}$, $j\in {\mathbb {N}}$, with (6) such that on every $\mathbb {I}_{j}$ there exists a pointwise orthogonal $Q\in C(\mathbb {I},\mathbb {R}^{n,n})$ with

where

and Δ,Σ₂₂,Γ₁,…,Γ_w are pointwise nonsingular. Furthermore,

$$ {{\varDelta}}^{T} = -{{\varDelta}},\quad {{\varSigma}}_{11}^{T} = {{\varSigma}}_{11}+\dot{{\varDelta}}, \quad {{\varSigma}}_{21}^{T} = {{\varSigma}}_{12},\quad{{\varSigma}}_{22}^{T} = {{\varSigma}}_{22},\quad A_{41}^{T}=A_{14}+\dot{E}_{14}. $$

Theorem 3.2 can be further refined by allowing for a restricted class of non-orthogonal transformations, see again [25].

Theorem 3.3

Let (E,A) be regular with $E,A\in C(\mathbb {I},\mathbb {R}^{n,n})$ sufficiently smooth and let (E,A) be skew-adjoint. Then there exist pairwise disjoint open intervals $\mathbb {I}_{j}$, $j\in {\mathbb {N}}$, with (6) such that on every $\mathbb {I}_{j}$ there exists a pointwise nonsingular $Q\in C(\mathbb {I},\mathbb {R}^{n,n})$ with

(8)

where

and Σ₂₂ pointwise nonsingular. Furthermore,

$$ J=\left[\begin{array}{cc} 0&I_{p}\\ -I_{p}&0 \end{array}\right],\quad C^{T}=C,\quad {{\varSigma}}_{22}^{T}={{\varSigma}}_{22},\quad A_{41}^{T}=A_{14}+\dot{E}_{14}. $$

By successively resolving the algebraic equations in the fourth, third and first row of the DAE with solution $[{x}_{1}^{T} ~~ {x}_{2}^{T} ~~ {x}_{3}^{T} ~~ {x}_{4}^{T}]^{T}$ and inhomogeneity $[{f}_{1}^{T} ~~ {f}_{2}^{T} ~~ {f}_{3}^{T} ~~ {f}_{4}^{T}]^{T}$ associated with (8), we can directly solve for x₁ in terms of linear combinations of derivatives of f₄, for x₃ in terms of x₁ and f₃, and for x₄ in terms of linear combinations of derivatives of f₁ and all other components. The only dynamic behavior related to (8) is described by the second block row. Inserting x₁ obtained from the last block row and calling the updated inhomogeneity $\widetilde {f}_{2}$, the associated ODE reads

$$ \dot{x}_{2}=J^{-1}C(t)x_{2}+J^{-1}\widetilde{f}_{2}(t). $$

(9)

The matrix function M = J^− 1C satisfies M^TJ − JM = 0 and lies therefore pointwise in the Lie algebra of Hamiltonian matrices, see e.g. [17]. Thus, the flow corresponding to (9) defined by

$$ \dot{{\varPhi}}_{2}=J^{-1}C(t) {{\varPhi}}_{2},\quad {{\varPhi}}_{2}(t_{0})= I $$

satisfies ${{{\varPhi }}_{2}^{T}} J {{\varPhi }}_{2} =J$, see e.g. [16], and is therefore symplectic.

In [25], also a global canonical form for self-adjoint DAEs and the associated pairs (E,A) was derived. The following modified result differs in the assumptions, and, moreover, the resulting canonical form is more refined.

Theorem 3.4

Let (E,A) be regular with $E,A\in C(\mathbb {I},\mathbb {R}^{n,n})$ sufficiently smooth and let (E,A) be self-adjoint. Then we have

$$ (E,A)\equiv\left( \left[\begin{array}{ccc} 0&I_{p}&0\\ -I_{p}&0&0\\ 0&0&E_{33} \end{array}\right], \left[\begin{array}{ccc} 0&0&0\\ 0&A_{22}&A_{23}\\ 0&A_{32}&A_{33} \end{array}\right]\right), $$

(10)

where

$$ E_{33}(t)\dot{x}_{3}=A_{33}(t)x_{3}+f_{3}(t), $$

(11)

is uniquely solvable for every sufficiently smooth f₃ without specifying initial conditions. Furthermore,

$$ E_{33}^{T}=-E_{33},\quad A_{22}^{T}=A_{22},\quad A_{32}^{T}=A_{23},\quad A_{33}^{T}=A_{33}+\dot{E}_{33}. $$

(12)

Proof

According to Theorem 3.3, the size d of the differential part is given by d = 2p. This implies that the solution space of the homogeneous equation

$$ E(t)\dot{x}=A(t)x $$

is of dimension 2p. If p = 0, then the first two blocks are missing and the claim holds trivially by assumption.

Let therefore p≠ 0 and let {ϕ₁,…,ϕ_2p} be a basis of the solution space. Setting Φ = [ϕ₁ ⋯ ϕ_2p], we have

$$ \text{rank} {{\varPhi}}(t)=2p\quad\text{ for all }t\in\mathbb{I} $$

as in the general case of Theorem 2.5.

Hence, by Theorem 2.3 there exists a smooth, pointwise nonsingular matrix function U with

$$ U^{H}{{\varPhi}}=\left[\begin{array}{c} I_{2p}\\ 0 \end{array}\right]. $$

Defining

$$ {{\varPhi}}^{\prime}=U\left[\begin{array}{c} 0\\ I_{a} \end{array}\right] $$

with a = n − 2p yields a pointwise nonsingular matrix function $Q=[{{\varPhi }}~~{{\varPhi }}^{\prime }]$. Since $E\dot {{\varPhi }}=A{{\varPhi }}$, we obtain

$$ (\widetilde{E},\widetilde{A})=(Q^{T}EQ,Q^{T}AQ-Q^{T}E\dot{Q}) $$

with

$$ \begin{array}{@{}rcl@{}} \widetilde{E}&=&\left[\begin{array}{cc} {{\varPhi}}^{T}E{{\varPhi}}&{{\varPhi}}^{T}E{{\varPhi}}^{\prime}\\ {{\varPhi}}^{{\prime}T}E{{\varPhi}}&{{\varPhi}}^{{\prime}T}E{{\varPhi}}^{\prime} \end{array}\right] = \left[\begin{array}{cc} \widetilde{E}_{11}&\widetilde{E}_{12}\\ -\widetilde{E}_{12}^{T}&\widetilde{E}_{22} \end{array}\right],\\ \widetilde{A} &=& \left[\begin{array}{cc} {{\varPhi}}^{T}(A{{\varPhi}}-E\dot{{\varPhi}})&{{\varPhi}}^{T}(A{{\varPhi}}^{\prime}-E\dot{{\varPhi}}^{\prime})\\ {{\varPhi}}^{{\prime}T}(A{{\varPhi}}-E\dot{{\varPhi}})&{{\varPhi}}^{{\prime}T}(A{{\varPhi}}^{\prime}-E\dot{{\varPhi}}^{\prime}) \end{array}\right] = \left[\begin{array}{cc} 0&\widetilde{A}_{12}\\ 0&\widetilde{A}_{22} \end{array}\right]. \end{array} $$

To simplify the notation, we omit now and later at similar instances the tildes thus re-using the same notation for possibly different quantities and write

$$ (E,A)\equiv\left( \left[\begin{array}{cc} E_{11}&E_{12}\\ -E_{12}^{T}&E_{22} \end{array}\right], \left[\begin{array}{cc} 0&A_{12}\\ 0&A_{22} \end{array}\right]\right). $$

As in the general case, we can conclude that

$$ \text{rank}\left[\begin{array}{c} E_{11}\\ -E_{12}^{T} \end{array}\right]=2p. $$

Since self-adjointness is conserved, we additionally have

$$ E_{11}^{T}=-E_{11},\quad E_{22}^{T}=-E_{22},\quad 0=\dot{E}_{11},\quad 0=A_{12}+\dot{E}_{12},\quad A_{22}^{T}=A_{22}+\dot{E}_{22}. $$

In particular, E₁₁ is constant and skew-symmetric. Hence, see [25], there exists an orthogonal symplectic matrix $U\in \mathbb {R}^{2p,2p}$ with

$$ \begin{array}{@{}rcl@{}} \widetilde{E} &=& \left[\begin{array}{cc} U^{T}&0\\ 0&I_{a} \end{array}\right] \left[\begin{array}{cc} E_{11}&E_{12}\\ -E_{12}^{T}&E_{22} \end{array}\right] \left[\begin{array}{cc} U&0\\ 0&I_{a} \end{array}\right]= \left[\begin{array}{ccc} 0&\widetilde{E}_{12}&\widetilde{E}_{13}\\ -\widetilde{E}_{12}^{T}&\widetilde{E}_{22}&\widetilde{E}_{23}\\ -\widetilde{E}_{13}^{T}&-\widetilde{E}_{23}^{T}&\widetilde{E}_{33} \end{array}\right],\\ \widetilde{A} &=& \left[\begin{array}{cc} U^{T}&0\\ 0&I_{a} \end{array}\right] \left[\begin{array}{cc} 0&A_{12}\\ 0&A_{22} \end{array}\right] \left[\begin{array}{cc} U&0\\ 0&I_{a} \end{array}\right]= \left[\begin{array}{ccc} 0&0&\widetilde{A}_{13}\\ 0&0&\widetilde{A}_{23}\\ 0&0&\widetilde{A}_{33} \end{array}\right], \end{array} $$

where $\widetilde {E}_{12}\in \mathbb {R}^{p,p}$.

Omitting again the tildes, we write

$$ (E,A)\equiv\left( \left[\begin{array}{ccc} 0&E_{12}&E_{13}\\ -E_{12}^{T}&E_{22}&E_{23}\\ -E_{13}^{T}&-E_{23}^{T}&E_{33} \end{array}\right], \left[\begin{array}{ccc} 0&0&A_{13}\\ 0&0&A_{23}\\ 0&0&A_{33} \end{array}\right]\right). $$

Conservation of self-adjointness and full rank of the leading block yields

$$ E_{22}^{T}=-E_{22},\quad E_{33}^{T}=-E_{33},\quad 0=\dot{E}_{12},\quad 0=\dot{E}_{22},\quad\text{rank}[E_{12}~~E_{13}]=p. $$

Hence, there exists a smooth, pointwise nonsingular matrix function V with

$$ {[E_{12}~~E_{13}]V=[I_{p}~~0]} $$

leading to

$$ \begin{array}{@{}rcl@{}} \widetilde{E} &=& \left[\begin{array}{cc} I_{p}&0\\ 0&V^{T} \end{array}\right] \left[\begin{array}{ccc} 0&E_{12}&E_{13}\\ -E_{12}^{T}&E_{22}&E_{23}\\ -E_{13}^{T}&-E_{23}^{T}&E_{33} \end{array}\right] \left[\begin{array}{cc} I_{p}&0\\ 0&V \end{array}\right] = \left[\begin{array}{ccc} 0&I_{p}&0\\ -I_{p}&\widetilde{E}_{22}&\widetilde{E}_{23}\\ 0&-\widetilde{E}_{23}^{T}&\widetilde{E}_{33} \end{array}\right],\\ \widetilde{A} &=& \left[\begin{array}{cc} I_{p}&0\\ 0&V^{T} \end{array}\right] \left[\begin{array}{ccc} 0&0&\widetilde{A}_{13}\\ 0&0&\widetilde{A}_{23}\\ 0&0&\widetilde{A}_{33} \end{array}\right] \left[\begin{array}{cc} I_{p}&0\\ 0&V \end{array}\right]- \left[\begin{array}{cc} I_{p}&0\\ 0&V^{T} \end{array}\right] \left[\begin{array}{ccc} 0&E_{12}&E_{13}\\ -E_{12}^{T}&E_{22}&E_{23}\\ -E_{13}^{T}&-E_{23}^{T}&E_{33} \end{array}\right] \left[\begin{array}{cc} 0&0\\ 0&\dot{V} \end{array}\right]\\ &=& \left[\begin{array}{ccc} 0&\widetilde{A}_{12}&\widetilde{A}_{13}\\ 0&\widetilde{A}_{22}&\widetilde{A}_{23}\\ 0&\widetilde{A}_{32}&\widetilde{A}_{33} \end{array}\right]. \end{array} $$

Omitting the tildes again, we write

$$ (E,A)\equiv \left( \left[\begin{array}{ccc} 0&I_{p}&0\\ -I_{p}&E_{22}&E_{23}\\ 0&-E_{23}^{T}&E_{33} \end{array}\right], \left[\begin{array}{ccc} 0&A_{12}&A_{13}\\ 0&A_{22}&A_{23}\\ 0&A_{32}&A_{33} \end{array}\right]\right). $$

Conservation of self-adjointness yields

$$ E_{22}^{T}=-E_{22},\quad E_{33}^{T}=-E_{33},\quad 0=A_{12},\quad 0=A_{13}. $$

Finally, after a congruence transformation with,

$$ \left[\begin{array}{ccc} I_{p}&\frac{1}{2}E_{22}&E_{23}\\ 0&I_{p}&0\\ 0&0&I_{a} \end{array}\right], $$

we arrive at

$$ \begin{array}{@{}rcl@{}} \widetilde{E} &=& \left[\begin{array}{ccc} I_{p}&0&0\\ -\frac{1}{2}E_{22}&I_{p}&0\\ E_{23}^{T}&0&I_{a} \end{array}\right] \left[\begin{array}{ccc} 0&I_{p}&0\\ -I_{p}&E_{22}&E_{23}\\ 0&-E_{23}^{T}&E_{33} \end{array}\right] \left[\begin{array}{ccc} I_{p}&\frac{1}{2}E_{22}&E_{23}\\ 0&I_{p}&0\\ 0&0&I_{a} \end{array}\right] = \left[\begin{array}{ccc} 0&I_{p}&0\\ -I_{p}&0&0\\ 0&0&\widetilde{E}_{33} \end{array}\right],\\ \widetilde{A} &=& \left[\begin{array}{ccc} I_{p}&0&0\\ -\frac{1}{2}E_{22}&I_{p}&0\\ E_{23}^{T}&0&I_{a} \end{array}\right] \left[\begin{array}{ccc} 0&A_{12}&A_{13}\\ 0&A_{22}&A_{23}\\ 0&A_{32}&A_{33} \end{array}\right] \left[\begin{array}{ccc} I_{p}&\frac{1}{2}E_{22}&E_{23}\\ 0&I_{p}&0\\ 0&0&I_{a} \end{array}\right]\\ && - \left[\begin{array}{ccc} I_{p}&0&0\\ -\frac{1}{2}E_{22}&I_{p}&0\\ E_{23}^{T}&0&I_{a} \end{array}\right] \left[\begin{array}{ccc} 0&I_{p}&0\\ -I_{p}&E_{22}&E_{23}\\ 0&-E_{23}^{T}&E_{33} \end{array}\right] \left[\begin{array}{ccc} 0&\frac{1}{2}\dot{E}_{22}&\dot{E}_{23}\\ 0&0&0\\ 0&0&0 \end{array}\right] = \left[\begin{array}{ccc} 0&0&0\\ 0&\widetilde{A}_{22}&\widetilde{A}_{23}\\ 0&\widetilde{A}_{32}&\widetilde{A}_{33} \end{array}\right]. \end{array} $$

Omitting again the tildes then yields

$$ (E,A)\equiv \left( \left[\begin{array}{ccc} 0&I_{p}&0\\ -I_{p}&0&0\\ 0&0&E_{33} \end{array}\right], \left[\begin{array}{ccc} 0&0&0\\ 0&A_{22}&A_{23}\\ 0&A_{32}&A_{33} \end{array}\right]\right) $$

which is just (10), where (11) follows along the same lines as in the general case and (12) follows by the conservation of self-adjointness. □

Theorem 3.4 shows that the symmetry defined by the self-adjoint structure under some weak assumptions leads to the geometric property that the flow associated with the dynamic part of the DAE transformed to global canonical form is symplectic, i.e. this property of classical Hamiltonian systems is lifted to the DAE case via the self-adjoint structure. In the next section we show that an analogous property holds for skew-adjoint DAEs.

4 Canonical Forms for Skew-Adjoint Pairs of Matrix Functions

While the self-adjoint structure had been analyzed for DAEs already in [25], the skew-adjoint structure and its importance for energy based modeling has only recently been observed in [3, 40], where also local canonical forms under constant rank assumptions have been studied. In this section we show that also global canonical forms under congruence can be derived for skew-adjoint DAEs. These then again imply the geometric properties of an underlying flow.

Lemma 4.1

Consider two pairs of matrix functions (E,A) and $(\widetilde {E},\widetilde {A})$ that are congruent and let (E,A) be skew-adjoint. Then $(\widetilde {E},\widetilde {A})$ is skew-adjoint as well.

Proof

The proof is analogous to that of Lemma 3.1 presented in [25]. □

The following result on a local canonical form under pointwise orthogonal congruence transformations is due to [40].

Theorem 4.2

Let (E,A) be regular with $E,A\in C(\mathbb {I},\mathbb {R}^{n,n})$ sufficiently smooth and let (E,A) be skew-adjoint. Then there exist pairwise disjoint open intervals $\mathbb {I}_{j}$, $j\in {\mathbb {N}}$, with (6) such that on every $\mathbb {I}_{j}$ there exists a pointwise orthogonal $Q\in C(\mathbb {I},\mathbb {R}^{n,n})$ with

where

and Δ,Σ₂₂,Γ₁,…,Γ_w are pointwise nonsingular. Furthermore,

$$ {{\varDelta}}^{T}={{\varDelta}},\quad{{\varSigma}}_{11}^{T}=-{{\varSigma}}_{11}-\dot{{\varDelta}},\quad {{\varSigma}}_{21}^{T}=-{{\varSigma}}_{12},\quad{{\varSigma}}_{22}^{T}=-{{\varSigma}}_{22},\quad A_{41}^{T}=-A_{14}-\dot{E}_{14}. $$

Theorem 3.2 can be further refined by allowing for a restricted class of non-orthogonal transformations, which yields the following local canonical form which, using a recent result of [21], is more refined than that in [40].

Theorem 4.3

Let (E,A) be regular with $E,A\in C(\mathbb {I},\mathbb {R}^{n,n})$ sufficiently smooth and let (E,A) be skew-adjoint. Then there exist pairwise disjoint open intervals $\mathbb {I}_{j}$, $j\in {\mathbb {N}}$, with (6) such that on every $\mathbb {I}_{j}$ there exists a pointwise nonsingular $Q\in C(\mathbb {I},\mathbb {R}^{n,n})$ with

(13)

where

and Σ₂₂ pointwise nonsingular. Furthermore,

$$ S=\left[\begin{array}{cc} I_{p}&0\\ 0&-I_{q} \end{array}\right],\quad J^{T}=-J,\quad {{\varSigma}}_{22}^{T}=-{{\varSigma}}_{22},\quad A_{41}^{T}=-A_{14}-\dot{E}_{14}. $$

Proof

Compared with the result in [40], to obtain the stated local canonical form we need a smooth version of Sylvester’s law of inertia, which is proved in [21]. In particular, this result shows the existence of a smooth transformation W with W^T ΔW = S, where Δ is pointwise nonsingular and symmetric. □

By successively resolving the algebraic equations in the fourth, third and first row of the DAE with solution $[{x}_{1}^{T} ~~ {x}_{2}^{T} ~~ {x}_{3}^{T} ~~ {x}_{4}^{T}]^{T}$ and inhomogeneity $[{f}_{1}^{T} ~~ {f}_{2}^{T} ~~ {f}_{3}^{T} ~~ {f}_{4}^{T}]^{T}$ associated with (8), we can directly solve for x₁ in terms of linear combinations of derivatives of f₄, for x₃ in terms of x₁ and f₃, and for x₄ in terms of linear combinations of derivatives of f₁ and all other components. The only dynamic behavior related to (8) is described by the second block row. Inserting x₁ obtained from the last block row and calling the updated inhomogeneity $\widetilde {f}_{2}$, the associated ODE reads

$$ \dot{x}_{2}=S^{-1}J(t)x_{2}+S^{-1}\widetilde{f}_{2}(t). $$

(14)

The matrix function M = S^− 1J has the property that SM is skew-symmetric, i.e., that (SM)^T = −(SM) or M^TS + SM = 0, and lies therefore pointwise in the Lie algebra belonging to the quadratic Lie group

$$ O(p,q)=\{{{\varPhi}}\in\mathbb{R}^{n,n}~|~{{\varPhi}}^{T}S{{\varPhi}}=S\}, $$

the so-called generalized orthogonal group with inertia(p,q,0), see e.g. [17], implying that the flow belonging to (14) lies in O(p,q). Observe the special case p = 0 or q = 0 where the flow is then orthogonal.

We also obtain a global canonical form.

Theorem 4.4

Let (E,A) be regular with $E,A\in C(\mathbb {I},\mathbb {R}^{n,n})$ sufficiently smooth and let (E,A) be skew-adjoint. Then we have

$$ (E,A)\equiv\left( \left[\begin{array}{ccc} I_{p}&0&0\\ 0&-I_{q}&0\\ 0&0&E_{33} \end{array}\right], \left[\begin{array}{ccc} 0&0&0\\ 0&0&0\\ 0&0&A_{33} \end{array}\right]\right), $$

(15)

where

$$ E_{33}(t)\dot{x}_{3}=A_{33}(t)x_{3}+f_{3}(t) $$

(16)

is uniquely solvable for every sufficiently smooth f₃ without specifying initial conditions. Furthermore,

$$ E_{33}^{T}=E_{33},\quad A_{33}^{T}=-A_{33}-\dot{E}_{33}. $$

(17)

Proof

According to Theorem 4.3, the size d of the differential part is given by d = p + q. This implies that the solution space of the homogeneous equation

$$ E(t)\dot{x}=A(t)x $$

is of dimension p + q. If p + q = 0, then the first two blocks are missing and the claim holds trivially by assumption.

Let therefore p + q≠ 0 and let {ϕ₁,…,ϕ_p+q} be a basis of the solution space. Setting Φ = [ϕ₁ ⋯ ϕ_p+q], we have

$$ \text{rank} {{\varPhi}}(t)=p+q\quad\text{ for all }t\in\mathbb{I} $$

as in the general case of Theorem 2.5.

Hence, by Theorem 2.3 there exists a smooth, pointwise nonsingular matrix function U with

$$ U^{H}{{\varPhi}}= \left[\begin{array}{c} I_{p+q}\\ 0 \end{array}\right]. $$

Defining

$$ {{\varPhi}}^{\prime}=U \left[\begin{array}{c} 0\\ I_{a} \end{array}\right] $$

with a = n − (p + q) yields a pointwise nonsingular matrix function $Q=[{{\varPhi }}~~{{\varPhi }}^{\prime }]$. Since $E\dot {{\varPhi }}=A{{\varPhi }}$, we obtain

$$ (\widetilde{E},\widetilde{A})=(Q^{T}EQ,Q^{T}AQ-Q^{T}E\dot{Q}) $$

with

$$ \begin{array}{@{}rcl@{}} \widetilde{E} &=& \left[\begin{array}{cc} {{\varPhi}}^{T}E{{\varPhi}}&{{\varPhi}}^{T}E{{\varPhi}}^{\prime}\\ {{\varPhi}}^{{\prime}T}E{{\varPhi}}&{{\varPhi}}^{{\prime}T}E{{\varPhi}}^{\prime} \end{array}\right] = \left[\begin{array}{cc} \widetilde{E}_{11}&\widetilde{E}_{12}\\ \widetilde{E}_{12}^{T}&\widetilde{E}_{22} \end{array}\right],\\ \widetilde{A} &=& \left[\begin{array}{cc} {{\varPhi}}^{T}(A{{\varPhi}}-E\dot{{\varPhi}})&{{\varPhi}}^{T}(A{{\varPhi}}^{\prime}-E\dot{{\varPhi}}^{\prime})\\ {{\varPhi}}^{{\prime}T}(A{{\varPhi}}-E\dot{{\varPhi}})&{{\varPhi}}^{{\prime}T}(A{{\varPhi}}^{\prime}-E\dot{{\varPhi}}^{\prime}) \end{array}\right] = \left[\begin{array}{cc} 0&\widetilde{A}_{12}\\ 0&\widetilde{A}_{22} \end{array}\right]. \end{array} $$

As in the proof of Theorem 3.4, we omit now and later at similar instances the tildes thus re-using the same notation for possibly different quantities and write

$$ (E,A)\equiv\left( \left[\begin{array}{cc} E_{11}&E_{12}\\ E_{12}^{T}&E_{22} \end{array}\right], \left[\begin{array}{cc} 0&A_{12}\\ 0&A_{22} \end{array}\right]\right). $$

As in the general case, we can conclude that

$$ \text{rank} \left[\begin{array}{c} E_{11}\\ E_{12}^{T} \end{array}\right]=p+q. $$

Since skew-adjointness is conserved, we additionally have

$$ E_{11}^{T}=E_{11},\quad E_{22}^{T}=E_{22},\quad 0=\dot{E}_{11},\quad 0=-A_{12}-\dot{E}_{12},\quad A_{22}^{T}=-A_{22}-\dot{E}_{22}. $$

In particular, E₁₁ is constant and symmetric. Moreover, in the following we will show that E₁₁ is nonsingular.

Due to Sylvester’s law of inertia, there is a nonsingular matrix $U\in \mathbb {R}^{d,d}$, d = p + q + r, with

$$ \begin{array}{@{}rcl@{}} \widetilde{E} &=& \left[\begin{array}{cc} U^{T}&0\\ 0&I_{a} \end{array}\right] \left[\begin{array}{cc} E_{11}&E_{12}\\ E_{12}^{T}&E_{22} \end{array}\right] \left[\begin{array}{cc} U&0\\ 0&I_{a} \end{array}\right] = \left[\begin{array}{ccc} S&0&\widetilde{E}_{13}\\ 0&0&\widetilde{E}_{23}\\ \widetilde{E}_{13}^{T}&\widetilde{E}_{23}^{T}&\widetilde{E}_{33} \end{array}\right],\\ \widetilde{A} &=& \left[\begin{array}{cc} U^{T}&0\\ 0&I_{a} \end{array}\right] \left[\begin{array}{cc} 0&A_{12}\\ 0&A_{22} \end{array}\right] \left[\begin{array}{cc} U&0\\ 0&I_{a} \end{array}\right] = \left[\begin{array}{ccc} 0&0&\widetilde{A}_{13}\\ 0&0&\widetilde{A}_{23}\\ 0&0&\widetilde{A}_{33} \end{array}\right], \end{array} $$

where S = diag(I_p,−I_q).

Omitting again the tildes, we write

$$ (E,A)\equiv \left( \left[\begin{array}{ccc} S&0&E_{13}\\ 0&0&E_{23}\\ E_{13}^{T}&E_{23}^{T}&E_{33} \end{array}\right], \left[\begin{array}{ccc} 0&0&A_{13}\\ 0&0&A_{23}\\ 0&0&A_{33} \end{array}\right]\right). $$

Conservation of skew-adjointness and full rank of the leading block yields

$$ E_{33}=E_{33}^{T},\quad 0=-A_{13}-\dot{E}_{13},\quad 0=-A_{23}-\dot{E}_{23},\quad A_{33}^{T}=-A_{33}-\dot{E}_{33},\quad\text{rank} E_{23}=r. $$

Hence, there exists a smooth, pointwise nonsingular matrix function V with

$$ E_{23}V=[I_{r}~~0] $$

leading to

$$ \begin{array}{@{}rcl@{}} \widetilde{E} &=& \left[\begin{array}{ccc} I_{p+q}&0&0\\ 0&I_{r}&0\\ 0&0&V^{T} \end{array}\right] \left[\begin{array}{ccc} S&0&E_{13}\\ 0&0&E_{23}\\ E_{13}^{T}&E_{23}^{T}&E_{33} \end{array}\right] \left[\begin{array}{ccc} I_{p+q}&0&0\\ 0&I_{r}&0\\ 0&0&V \end{array}\right] = \left[\begin{array}{cccc} S&0&\widetilde{E}_{13}&\widetilde{E}_{14}\\ 0&0&I_{r}&0\\ \widetilde{E}_{13}^{T}&I_{r}&\widetilde{E}_{33}&\widetilde{E}_{34}\\ \widetilde{E}_{14}^{T}&0&\widetilde{E}_{34}^{T}&\widetilde{E}_{44} \end{array}\right],\\ \widetilde{A} &=& \left[\begin{array}{ccc} I_{p+q}&0&0\\ 0&I_{r}&0\\ 0&0&V^{T} \end{array}\right] \left[\begin{array}{ccc} 0&0&A_{13}\\ 0&0&A_{23}\\ 0&0&A_{33} \end{array}\right] \left[\begin{array}{ccc} I_{p+q}&0&0\\ 0&I_{r}&0\\ 0&0&V \end{array}\right]\\ && -\left[\begin{array}{ccc} I_{p+q}&0&0\\ 0&I_{r}&0\\ 0&0&V^{T} \end{array}\right] \left[\begin{array}{ccc} S&0&E_{13}\\ 0&0&E_{23}\\ E_{13}^{T}&E_{23}^{T}&E_{33} \end{array}\right] \left[\begin{array}{ccc} 0&0&0\\ 0&0&0\\ 0&0&\dot{V} \end{array}\right] = \left[\begin{array}{cccc} 0&0&\widetilde{A}_{13}&\widetilde{A}_{14}\\ 0&0&\widetilde{A}_{23}&\widetilde{A}_{24}\\ 0&0&\widetilde{A}_{33}&\widetilde{A}_{34}\\ 0&0&\widetilde{A}_{43}&\widetilde{A}_{44} \end{array}\right]. \end{array} $$

Omitting again the tildes, we write

$$ (E,A)\equiv\left( \left[\begin{array}{cccc} S&0&E_{13}&E_{14}\\ 0&0&I_{r}&0\\ E_{13}^{T}&I_{r}&E_{33}&E_{34}\\ E_{14}^{T}&0&E_{34}^{T}&E_{44} \end{array}\right], \left[\begin{array}{cccc} 0&0&A_{13}&A_{14}\\ 0&0&A_{23}&A_{24}\\ 0&0&A_{33}&A_{34}\\ 0&0&A_{43}&A_{44} \end{array}\right]\right). $$

Conservation of self-adjointness yields

$$ E_{33}^{T}=E_{33},\quad E_{44}^{T}=E_{44},\quad 0=-A_{13}-\dot{E}_{13},\quad 0=-A_{14}-\dot{E}_{14},\quad 0=A_{23},\quad 0=A_{24}, $$

and

$$ A_{33}^{T}=-A_{33}-\dot{E}_{33},\quad A_{43}^{T}=-A_{34}-\dot{E}_{34},\quad A_{44}^{T}=-A_{44}-\dot{E}_{44}. $$

Finally, after a congruence transformation with,

$$ \left[\begin{array}{cccc} I_{p+q}&0&-S^{-1}E_{13}&-S^{-1}E_{14}\\ 0&I_{r}&0&0\\ 0&0&I_{r}&0\\ 0&0&0&I_{a} \end{array}\right], $$

we arrive at

$$ \begin{array}{@{}rcl@{}} \widetilde{E} &=& \left[\begin{array}{cccc} I_{p+q}&0&0&0\\ 0&I_{r}&0&0\\ -E_{13}^{T}S^{-1}&0&I_{r}&0\\ -E_{14}^{T}S^{-1}&0&0&I_{a} \end{array}\right] \left[\begin{array}{cccc} S&0&E_{13}&E_{14}\\ 0&0&I_{r}&0\\ E_{13}^{T}&I_{r}&E_{33}&E_{34}\\ E_{14}^{T}&0&E_{34}^{T}&E_{44} \end{array}\right] \left[\begin{array}{cccc} I_{p+q}&0&-S^{-1}E_{13}&-S^{-1}E_{14}\\ 0&I_{r}&0&0\\ 0&0&I_{r}&0\\ 0&0&0&I_{a} \end{array}\right]\\ &=& \left[\begin{array}{cccc} S&0&0&0\\ 0&0&I_{r}&0\\ 0&I_{r}&\widetilde{E}_{33}&\widetilde{E}_{34}\\ 0&0&\widetilde{E}_{34}^{T}&\widetilde{E}_{44} \end{array}\right],\\ \widetilde{A} &=& \left[\begin{array}{cccc} I_{p+q}&0&0&0\\ 0&I_{r}&0&0\\ -E_{13}^{T}S^{-1}&0&I_{r}&0\\ -E_{14}^{T}S^{-1}&0&0&I_{a} \end{array}\right] \left[\begin{array}{cccc} 0&0&A_{13}&A_{14}\\ 0&0&A_{23}&A_{24}\\ 0&0&A_{33}&A_{34}\\ 0&0&A_{43}&A_{44} \end{array}\right] \left[\begin{array}{cccc} I_{p+q}&0&-S^{-1}E_{13}&-S^{-1}E_{14}\\ 0&I_{r}&0&0\\ 0&0&I_{r}&0\\ 0&0&0&I_{a} \end{array}\right]\\ && - \left[\begin{array}{cccc} I_{p+q}&0&0&0\\ 0&I_{r}&0&0\\ -E_{13}^{T}S^{-1}&0&I_{r}&0\\ -E_{14}^{T}S^{-1}&0&0&I_{a} \end{array}\right] \left[\begin{array}{cccc} S&0&E_{13}&E_{14}\\ 0&0&I_{r}&0\\ E_{13}^{T}&I_{r}&E_{33}&E_{34}\\ E_{14}^{T}&0&E_{34}^{T}&E_{44} \end{array}\right] \left[\begin{array}{cccc} 0&0&-S^{-1}\dot{E}_{13}&-S^{-1}\dot{E}_{14}\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0 \end{array}\right]\\ &=& \left[\begin{array}{cccc} 0&0&0&0\\ 0&0&0&0\\ 0&0&\widetilde{A}_{33}&\widetilde{A}_{34}\\ 0&0&\widetilde{A}_{43}&\widetilde{A}_{44} \end{array}\right]. \end{array} $$

The corresponding homogeneous DAE $\widetilde {E}\dot {\widetilde {x}}=\widetilde {A}{\widetilde {x}}$ has the form

$$ \begin{array}{@{}rcl@{}} S\dot{\widetilde{x}}_{1} &=& 0,\\ \dot{\widetilde{x}}_{3} &=& 0,\\ \dot{\widetilde{x}}_{2} + \widetilde{E}_{33} \dot{\widetilde{x}}_{3} + \widetilde{E}_{34} \dot{\widetilde{x}}_{4} &=& \widetilde{A}_{33} {\widetilde{x}}_{3} + \widetilde{A}_{34} {\widetilde{x}}_{4},\\ \widetilde{E}_{34}^{T} \dot{\widetilde{x}}_{3} + \widetilde{E}_{44} \dot{\widetilde{x}}_{4} &=& \widetilde{A}_{43} {\widetilde{x}}_{3} + \widetilde{A}_{44} {\widetilde{x}}_{4}. \end{array} $$

If we take ${\widetilde {x}}_{1}$ and ${\widetilde {x}}_{3}$ as solutions of the first two equations, the fourth equation must determine ${\widetilde {x}}_{4}$, possibly imposing a suitable initial condition. Finally, the third equation then fixes ${\widetilde {x}}_{2}$ using a suitable initial condition. Hence the dimension of the solution space is at least p + q + 2r. But the dimension was assumed to be p + q implying that r = 0.

Omitting the tildes again, skipping the second and third block row and column, which are of zero dimension, and renumbering the indices gives

$$ (E,A) \equiv \left( \left[\begin{array}{ccc} I_{p}&0&0\\ 0&-I_{q}&0\\ 0&0&E_{33} \end{array}\right], \left[\begin{array}{ccc} 0&0&0\\ 0&0&0\\ 0&0&A_{33} \end{array}\right]\right) $$

which is just (15), where (16) follows along the same lines as in the general case and (17) follows by the conservation of skew-adjointness. □

The presented canonical forms have some direct consequences in the case that E is pointwise positive semidefinite.

Corollary 4.5

Let (E,A) be regular with $E,A\in C(\mathbb {I},\mathbb {R}^{n,n})$ sufficiently smooth and let (E,A) be skew-adjoint with E pointwise positive semidefinite. Then in the canonical form (13) E₄₁ = 0 and the flow associated with the dynamical part of the system is orthogonal.

Proof

Since Q^TEQ is positive semidefinite for positive semidefinite E, it follows that the blocks in positions (1,3), (3,1), (4,1) and (1,4) of (13) are zero and that S is pointwise positive definite. Thus q = 0 and the flow corresponding to (14) is orthogonal. □

Remark 4.6

Corollary 4.5 immediately implies also an upper bound on the so-called differentiation index of the DAE, see [22], which is at most two. This follows directly from (13), since with E₄₁ = 0 at most one differentiation of the inhomogeneity is needed.

Remark 4.7

The construction of the local and global canonical forms is possible, but not really practical computationally. As in the procedure for general DAE systems it is more practical to use derivative arrays to filter out a subsystem that consists of separated algebraic and differential equations, where the consistency of the initial value can be checked and where it can be assured that the constraints are preserved in the numerical procedure, see [22]. For skew- and self-adjoint systems this is possible as well, see the recent paper [24].

To illustrate the canonical forms we discuss two examples.

Example 4.8

Consider the circuit in Example 1.3. In this case the construction of the local and global form is extremely simple. Reordering the rows and columns in the order second, third, first, fourth, and fifth, we obtain the skew-adjoint system in canonical form

If u is given and the resistive terms are neglected, i.e. R_L,R_G,R_R = 0, then this is skew-adjoint DAE, in which the last two equations can be solved as V₂ = 0 and V₁ = −u and from the first two equations we get $I_{G}=-C_{1} \dot {V}_{1}= C_{1} \dot {u}$ and $I_{R}=-C_{2} \dot {V}_{2}=0$ and the dynamic equation is

$$ L \dot{I} =-V_{2} =0, $$

which has the orthogonal flow I = 1.

Example 4.9

Consider the linear time-varying DAE (5) in Example 1.4 with A_H = 0 and C = 0. This corresponds to the situation that dissipation due to friction is negligible and that no artificial stabilization term in the space discretization is used. Performing a full rank decomposition

$$ U^{T} B = \left[\begin{array}{c} B_{1} \\ 0 \end{array}\right], $$

with B₁ nonsingular (which corresponds to the partitioning of the velocity into the parts that have divergence zero and nonzero), and applying a congruence transformation with

$$ \left[\begin{array}{cc} U & 0 \\ 0 & I \end{array}\right] $$

yields a transformed system

$$ \left[\begin{array}{ccc} M_{11} & M_{12} & 0 \\ M_{21} & M_{22} & 0 \\ 0 & 0 & 0 \end{array}\right] \left[\begin{array}{c} \dot{v}_{1} \\ \dot{v}_{2} \\ \dot{p} \end{array}\right] = \left[\begin{array}{ccc} J_{11}(t) & J_{12}(t) & -B_{1} \\ J_{21}(t) & J_{22}(t) & 0 \\ {B_{1}^{T}} & 0 & 0 \end{array}\right] \left[\begin{array}{c} v_{1} \\ v_{2} \\ p \end{array}\right] + \left[\begin{array}{c} f_{1}(t) \\ f_{2}(t) \\ 0 \end{array}\right]. $$

The third equation yields v₁ = 0 and the first equation gives

$$ p= B_{1}^{-1} (J_{12}(t) v_{2} -M_{12} \dot{v}_{2}+f_{1}(t)), $$

while the underlying dynamics of the system is described by the skew-adjoint DAE

$$ M_{22} \dot{v}_{2} = J_{22}(t) v_{2} +f_{2}(t) $$

with constant $M_{22}=M_{22}^{T}>0$ and pointwise skew-symmetric J₂₂. After a change of basis with the positive definite square root $M_{22}^{1/2}$ of M₂₂ according to $\tilde {v}_{2}= M_{22}^{1/2}v_{2}$ and scaling the equation by its inverse $M_{22}^{-1/2}$, we obtain an ODE system

$$ \dot{\tilde{v}}_{2} =\tilde{J}_{22}(t) \tilde{v}_{2}+ \tilde{f}_{2}(t), $$

with pointwise skew-symmetric $\tilde {J}_{22}$, which has an orthogonal flow.

5 Conclusions

We have derived local and global canonical forms under congruence transformations for self-adjoint and skew-adjoint systems of linear variable coefficient differential-algebraic equations. The associated flows for the dynamical part of the system are shown to be symplectic or in the generalized orthogonal groups. The results are illustrated at the hand of examples from electrical network and flow simulation.