Numerical Approximation of Poisson Problems in Long Domains

Abstract

In this paper, we consider the Poisson equation on a “long” domain which is the Cartesian product of a one-dimensional long interval with a (d − 1)-dimensional domain. The right-hand side is assumed to have a rank-1 tensor structure. We will present and compare methods to construct approximations of the solution which have tensor structure and the computational effort is governed by only solving elliptic problems on lower-dimensional domains. A zero-th order tensor approximation is derived by using tools from asymptotic analysis (method 1). The resulting approximation is an elementary tensor and, hence has a fixed error which turns out to be very close to the best possible approximation of zero-th order. This approximation can be used as a starting guess for the derivation of higher-order tensor approximations by a greedy-type method (method 2). Numerical experiments show that this method is converging towards the exact solution. Method 3 is based on the derivation of a tensor approximation via exponential sums applied to discretized differential operators and their inverses. It can be proved that this method converges exponentially with respect to the tensor rank. We present numerical experiments which compare the performance and sensitivity of these three methods.

Introduction

In this paper, we consider elliptic partial differential equations on domains which are the Cartesian product of a “long” interval I_ℓ = (−ℓ,ℓ) with a (d − 1)-dimensional domain ω, the cross section - a typical application is the modelling of a flow in long cylinders. We will investigate and compare methods which reduce the problem on the original d-dimensional domain to a problem on the cross section of the domain. Such type of dimension reduction methods have important practical applications in fluid and continuum mechanics in order to reduce the computational complexity. We refer, e.g., to [27] for different kinds of application. As a model problem we consider the Poisson equation with homogeneous Dirichlet boundary conditions and a right-hand side which is an elementary tensor; i.e., the product of a univariate function (on the long interval) and a (d − 1)-variate function on the cross section. Such problems have been studied by using asymptotic analysis, see., e.g., [9]. Our first approximation (method 1) is based on this technique and approximates the solution by an elementary tensor where the function on the cross section is the solution of a Poisson-problem on the cross section and the corresponding univariate function is determined afterwards as the best approximation in the Sobolev space ${H_{0}^{1}}$ on the long interval. In Lemma 2 below, it is shown that this approximation converges exponentially with respect to the length of the cylinder for any subdomain $I_{\ell _{0}}\times \omega$ for fixed ℓ₀ < ℓ. However, for fixed ℓ this is a one-term approximation with a fixed error.

Method 2 uses the result of method 1 as the initial guess for an iterative procedure which results in a greedy-type method. Recursively, one assumes that a rank-k tensor approximation of the solution has already been derived and then starts an iteration to compute the k + 1 term: a) one chooses an univariate function on I_ℓ as an initial guess for this iteration and determines the function on the cross section as the best approximation in ${H_{0}^{1}}$ of the cross-section. In step b) the iteration is flipped and one fixes the new function on the cross section and determines the corresponding best approximation in ${H_{0}^{1}}$ of the interval. Steps a) and b) are iterated until a stopping criterion is reached and this gives the k + 1 term in the tensor approximation. In the literature this approach is also known as Proper Generalized Decomposition (PGD) [7]. We have performed numerical experiments which are reported in Section 4 which show that this method leads to a convergent approximation also for fixed ℓ as the tensor rank of the approximation increases. However, it turns out that this method is quite sensitive and requires that the inner iteration a), b) leads to an accurate approximation of the (k + 1) term in order to ensure that the outer iteration is converging. This greedy algorithm has similarities with alternating least squares (ALS) methods which would alternatingly optimize the low-rank factors of the approximate solution. While the greedy method has the advantage that it can be combined with method 1 in a natural fashion, the numerical experiments which we have performed indicate that the convergence speed can slow down as the number of outer iterations increases. This is well known and there are various strategies to accelerate the convergence speed such as Galerkin projection or one half-step of ALS on the low-rank factors. The former is discussed in [19], the latter in the context of PGD applied to uncertainty quantification. If the structure allows to conveniently perform one half-step or even a full step of ALS, the convergence gets substantially accelerated. We have considered here the original greedy method because its popularity related to its straightforward implementation; it is well suited when only a moderate approximation accuracy of the Poisson problem is required.

Method 3 is based on a different approach which employs numerical tensor calculus (see [14]). First one defines an exponential sum approximation of the function 1/x. Since the differential operator −Δ is of tensor form, the exponential sum, applied to the inverse of a discretisation of the Laplacian by a matrix which must preserve the tensor format, directly leads to a tensor approximation of the solution u. We emphasize that the explicit computation of the inverse of the discretisation matrix can be avoided by using the hierarchical format for their representation (see [15]). An advantage of this method is that a full theory is available which applies to our application and allows us to choose the tensor rank via an a priori error estimate. It also can be shown that the tensor approximation converges exponentially with respect to the tensor rank (see [14]).

The goal of this paper is to compare three popular approaches for the numerical approximation of Poisson problems in domains of the form I_ℓ × ω and to assess their performance with respect to the length ℓ via numerical experiments. These methods exhibit different computational complexities and our results can be used to determine a suitable method given a desired accuracy range. For an in-depth theoretical analysis of the presented methods we refer to the existing literature.

There exist various other approaches in the literature such as DMRG [24], AMEN [10], and QTT [17, 18, 23], and hierarchical local model reduction by domain decomposition [26] which also have in principle the potential to solve Poisson-type problems on long domains. We also mention here that the discretized equation (see eq. (19)) takes the form of a Sylvester matrix equation. The numerical solution of Sylvester equations has been discussed at length in the literature; see, e.g., [28]. In particular, an ADI method or rational Krylov subspace method with optimally chosen shifts (which constructs the rational approximation directly and not via exponential sums) will be more efficient than methods 2 and 3. We have chosen the proposed method 1-3 for a systematic comparison since they were developed in different areas of mathematics and all three are very popular. In the conclusions, we will summarize the behaviour of these methods depending on the kind of application and the accuracy requirements.

The paper is structured as follows. In Section 2 we formulate the problem on the long product domain and introduce the assumptions on the tensor format of the right-hand side. The three different methods for constructing a tensor approximation of the solution are presented in Section 3. The results of numerical experiments are presented in Section 4 where the convergence and sensitivity of the different methods is investigated and compared. For the experiments we consider first the case that the cross section is the one-dimensional unit interval and then the more complicated case that the cross section is an L-shaped polygonal domain. Finally, in the concluding section we summarize the results and give an outlook.

Setting

Let ω be an open, bounded and connected Lipschitz domain in $\mathbb {R}^{d-1}$, d ≥ 1. In the following we consider Poisson problems on domains of the form

$$ {{\varOmega}}_{\ell}:=I_{\ell}\times\omega\quad\text{with}\quad I_{\ell}:=(-\ell,\ell), $$

where ℓ is large. We are interested in Dirichlet boundary value problems of the form

$$ \begin{array}{@{}rcl@{}} -{{\varDelta}} u_{\ell} & =& F\quad\text{ in }{{\varOmega}}_{\ell},\\ u_{\ell} & =& 0\quad\text{ on }\partial{{\varOmega}}_{\ell} \end{array} $$

(1)

with weak formulation

$$ \left\{\begin{array}{l} \text{find }u_{\ell}\in {H_{0}^{1}}({{\varOmega}}_{\ell})\text{ s.t. }\\ (\nabla u_{\ell},\nabla v)_{L_{2}({{\varOmega}}_{\ell})}=(F,v)_{L_{2}({{\varOmega}}_{\ell})}\quad\forall v\in {H_{0}^{1}}({{\varOmega}}_{\ell}). \end{array}\right. $$

Specifically we are interested in right-hand sides f which have a tensor structure of the form F = 1 ⊗ f or more generally $F={\sum }_{k=0}^{n} g_{k}\otimes f_{k}$, $n\in \mathbb {N}$, where g_k is a univariate function and f, f_k are functions which depend only on the (d − 1)-dimensional variable $x^{\prime }\in \omega$. Here, we use the standard tensor notation $(g\otimes f)(x) = g(x_{1})f(x^{\prime })$ with $x^{\prime }= (x_{k})_{k=2}^{d}$. In this paper, we will present and compare methods to approximate u_ℓ in tensor form.

We consider a right-hand side of the form

$$ F=1\otimes f\qquad\text{for some }f\in L^{2}(\omega) $$

(2)

and derive a first approximation of u_ℓ as the solution of the (d − 1)-dimensional problem on ω:

$$ \begin{array}{@{}rcl@{}} -{{\varDelta}}^{\prime}u_{\infty}(x^{\prime})& =& f(x^{\prime})\quad\text{ in }\omega,\\ u_{\infty} & =& 0\qquad~~\text{ on }\partial\omega \end{array} $$

(3)

with weak form

$$ \left\{\begin{array}{l} \text{find }u_{\infty}\in {H_{0}^{1}}(\omega)\text{ s.t. }\\ (\nabla^{\prime}u_{\infty},\nabla^{\prime}v)_{L_{2}(\omega)}=(f,v)_{L_{2}(\omega)}\quad\forall v\in {H_{0}^{1}}(\omega). \end{array}\right. $$

Numerical Approximation

In this section we derive three different methods to approximate problem (1). In all three methods we exploit the special structure of the domain Ω_ℓ and the right-hand side F. Our goal is to reduce the original d-dimensional problem on Ω_ℓ to one or more (d − 1)-dimensional problems on ω. Compared to standard methods like finite elements methods or finite difference methods, which solve the equations on Ω_ℓ, this strategy can significantly reduce the computational cost since ℓ is considered large and the discretisation in the x₁ direction can be avoided.

Method 1: A One-term Approximation Based on an Asymptotic Analysis of Problem (1)

Although the right-hand side F in (1) is independent of x₁, it is easy to see that this is not the case for the solution u_ℓ, i.e., due to the homogeneous Dirichlet boundary conditions it is clear that u_ℓ depends on x₁. However, if ℓ is large one can expect that u_ℓ is approximately constant with respect to x₁ in a subdomain ${{\varOmega }}_{\ell _{0}}$, where 0 < ℓ₀ ≪ ℓ and thus converges locally to a function independent of x₁ for $\ell \rightarrow \infty$. The asymptotic behaviour of the solution u_ℓ when $\ell \rightarrow \infty$ has been investigated in [8]. It can be shown that

$$ u_{\ell}\longrightarrow1\otimes u_{\infty}\qquad\text{in }{{\varOmega}}_{\ell_{0}}, $$

where $u_{\infty }$ is the solution of (3), with an exponential rate of convergence. More precisely, the following theorem holds:

Theorem 1

There exist constants c,α > 0 independent of ℓ s.t.

$$ {\int}_{{{\varOmega}}_{\ell/2}}|\nabla(u_{\ell}-1\otimes u_{\infty})|^{2}dx \leq c\mathrm{e}^{-\alpha\ell}\|f\|_{2,\omega}^{2}, $$

where ∥⋅∥_2,ω refers to the L²(ω)-norm.

For a proof we refer to [8, Theorem 6.6].

Theorem 1 shows that $1\otimes u_{\infty }$ is a good approximation of u_ℓ in Ω_ℓ/2 when ℓ is large. This motivates to seek approximations of u_ℓ in Ω_ℓ which are of the form

$$ u_{\ell}\approx u_{\ell}^{M_{1}}:=\psi_{\ell}\otimes u_{\infty}, $$

where $\psi _{\ell }\in {H_{0}^{1}}(-\ell ,\ell )$. Here, we choose ψ_ℓ to be the solution of the following best approximation problem: Given $u_{\ell }\in {H_{0}^{1}}({{\varOmega }}_{\ell })$ and $u_{\infty }\in {H_{0}^{1}}(\omega )$, find $\psi \in {H_{0}^{1}}(-\ell ,\ell )$ s.t.

$$ \|\nabla(u_{\ell}-\psi\otimes u_{\infty})\|_{2} = \underset{\theta\in {H_{0}^{1}}(-\ell,\ell)}{\inf}\|\nabla(u_{\ell}-\theta\otimes u_{\infty})\|_{2}. $$

(4)

In order to solve problem (4) we define the functional

$$ J(u_{\ell},u_{\infty})(\theta):=\|\nabla(u_{\ell}-\theta\otimes u_{\infty})\|_{2}^{2} $$

and consider the variational problem of minimizing it with respect to $\theta \in {H_{0}^{1}}(-\ell ,\ell )$.

A simple computation shows that this is equivalent to finding $\tilde {\theta }\in {H_{0}^{1}}(I_{\ell })$ such that

$$ \left. \begin{array}{ll} &\left( \nabla\left( \theta\otimes u_{\infty}\right),\nabla\left( \tilde{\theta}\otimes u_{\infty}\right)\right)_{2}=\left( \nabla u_{\ell},\nabla\left( \tilde{\theta}\otimes u_{\infty}\right)\right)_{2}\\ \Longleftrightarrow \quad& \left( \left( \begin{array}{c} \theta^{\prime}\otimes u_{\infty}\\ \theta\otimes\nabla^{\prime}u_{\infty} \end{array}\right), \left( \begin{array}{c} \tilde{\theta}^{\prime}\otimes u_{\infty}\\ \tilde{\theta}\otimes\nabla^{\prime}u_{\infty} \end{array}\right)\right)_{2}=\left( -{{\varDelta}} u_{\ell},\tilde{\theta}\otimes u_{\infty}\right)_{2}\\ \Longleftrightarrow \quad& {\alpha}_{\infty}^{2}\left( \theta^{\prime},\tilde{\theta}^{\prime}\right)_{2,I_{\ell}}+\beta_{\infty}^{2}\left( \theta,\tilde{\theta}\right)_{2,I_{\ell}}=\left( 1\otimes f,\tilde{\theta}\otimes u_{\infty}\right)_{2}\\ \Longleftrightarrow\quad & {\alpha}_{\infty}^{2}\left( \theta^{\prime},\tilde{\theta}^{\prime}\right)_{2,I_{\ell}}+\beta_{\infty}^{2}\left( \theta,\tilde{\theta}\right)_{2,I_{\ell}}=\left( 1\otimes\left( -{{\varDelta}}^{\prime}u_{\infty}\right),\tilde{\theta}\otimes u_{\infty}\right)_{2}\\ \Longleftrightarrow\quad& {\alpha}_{\infty}^{2}\left( \theta^{\prime},\tilde{\theta}^{\prime}\right)_{2,I_{\ell}}+\beta_{\infty}^{2}\left( \theta,\tilde{\theta}\right)_{2,I_{\ell}}={\beta}_{\infty}^{2}{\int}_{I_{\ell}}\tilde{\theta}. \end{array} \right\} \quad\forall\tilde{\theta}\in {H_{0}^{1}}\left( I_{\ell}\right) $$

with

$$ \alpha_{\infty}:=\|u_{\infty}\|_{2,\omega},\quad \beta_{\infty}:=\|\nabla^{\prime}u_{\infty}\|_{2,\omega}. $$

The strong form of the resulting equation is

$$ \begin{array}{@{}rcl@{}} -\alpha_{\infty}^{2}\theta^{\prime\prime}+\beta_{\infty}^{2}\theta &=&\beta_{\infty}^{2}\quad\text{ on }(-\ell,\ell),\\ \theta(-\ell)=\theta(\ell) & =& 0. \end{array} $$

The solution of this one-dimensional boundary value problem is given by

$$ \theta(x_{1}) := 1-\frac{\cosh\left( \frac{\beta_{\infty}}{\alpha_{\infty}}x_{1}\right)}{\cosh\left( \frac{\beta_{\infty}}{\alpha_{\infty}}\ell\right)}. $$

This shows that an approximation of our original problem (1) is given by

$$ u_{\ell}^{M_{1}}:=\psi_{\ell}(\lambda_{\infty},\cdot) \otimes u_{\infty},\quad\text{ with }\psi_{\ell}(a,x_{1}):=1-\frac{\cosh(ax_{1})}{\cosh(a\ell)} $$

(5)

and

$$ \lambda_{\infty}=\frac{\beta_{\infty}}{\alpha_{\infty}}=\frac{\sqrt{(f,u_{\infty})_{2,\omega}}}{\alpha_{\infty}}. $$

Note that ψ_ℓ(a,⋅) satisfies

$$ -\psi_{\ell}^{\prime\prime}(a,\cdot)+a^{2}\psi_{\ell}(a,\cdot) = a^{2}\quad\text{ and }\quad\psi_{\ell}(\pm\ell) = 0. $$

(6)

In Section 4 we report on various numerical experiments that show the approximation properties of this rather simple one-term approximation.

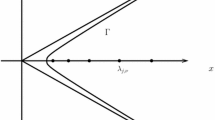
Figure 1 shows a plot of $\psi _{\ell }(\lambda _{\infty },\cdot )$ for ℓ = 20 and $\lambda _{\infty }=2$. Since ψ_ℓ approaches 1 with an exponential rate as x₁ moves away from ± ℓ towards the origin, an analogous result to Theorem 1 can be shown for ${u}_{\ell }^{M_{1}}$.

Fig. 1

Plot of $\psi _{\ell }(\lambda _{\infty },\cdot )$ for ℓ = 20 and $\lambda _{\infty }=2$

Lemma 2

There exist constants $c,\tilde {c}>0$ independent of ℓ such that, for δ_ℓ < ℓ,

$$ \|\nabla(u_{\ell}-\psi_{\ell}(\lambda_{\infty},\cdot) \otimes u_{\infty})\|_{2,{{\varOmega}}_{\ell-\delta_{\ell}}}^{2} \leq C_{\omega,\delta_{\ell}}^{(1)}\|u_{\infty}\|_{2,\omega}^{2}+C_{\omega,\delta_{\ell}}^{(2)}\|\nabla^{\prime}u_{\infty}\|_{2,\omega}^{2}, $$

(7)

with

$$ C_{\omega,\delta_{\ell}}^{(1)}:=4\mathrm{e}^{-2\lambda_{1}\delta_{\ell}},\qquad C_{\omega,\delta_{\ell}}^{(2)}:=4\left( \frac{1}{\lambda_{1}}\mathrm{e}^{-2\lambda_{1}\delta_{\ell}}+6(\ell-\delta_{\ell}) \mathrm{e}^{-2\lambda_{1}\ell}\right) $$

and

$$ \lambda_{1}:=\underset{v\in {H_{0}^{1}}(\omega)\backslash\{0\}}{\inf}\frac{\|\nabla^{\prime}v\|_{2,\omega}}{\|v\|_{2,\omega}}. $$

(8)

The right-hand side in (7) goes to 0 with an exponential rate of convergence if δ_ℓ is bounded from below when $\ell \rightarrow \infty$.

Proof

For i = 1,2,…, let w_i be the i-th eigenfunction of $-{{\varDelta }}^{\prime }$, i.e., $w_{i}\in {H_{0}^{1}}(\omega )$ is a solution of

$$ (\nabla^{\prime}w_{i},\nabla^{\prime}v)_{2,\omega}={{\lambda}_{i}^{2}}(w_{i},v)_{2,\omega}\qquad\forall v\in {H_{0}^{1}}(\omega) $$

(9)

and we normalize the eigenfunctions such that (w_i,w_j)_2,ω = δ_i,j and order them such that (λ_i)_i is increasing monotonously. Furthermore let $u_{\ell ,i}\in {{H}_{0}^{1}}({{\varOmega }}_{\ell })$ be the solution of

$$ (\nabla u_{\ell,i},\nabla v)_{2}={{\lambda}_{i}^{2}}(1\otimes w_{i},v)_{2}\qquad\forall v\in {{H}_{0}^{1}}({{\varOmega}}_{\ell}). $$

Then one concludes from (6) and (9) that

$$ u_{\ell,i}=\psi_{\ell}(\lambda_{i},\cdot) \otimes w_{i}. $$

If f ∈ L²(ω) it holds

$$ f=\sum\limits_{i=1}^{\infty}(f,w_{i})_{2,\omega}w_{i}. $$

This shows that the solutions of (3) and (1) can be expressed as

$$ \begin{array}{@{}rcl@{}} u_{\infty} & =& \sum\limits_{i=1}^{\infty}\frac{(f,w_{i})_{2,\omega}}{{\lambda_{i}^{2}}}w_{i},\\ u_{\ell} & =& \sum\limits_{i=1}^{\infty}\frac{(f,w_{i})_{2,\omega}}{{{\lambda}_{i}^{2}}}u_{\ell,i}=\sum\limits_{i=1}^{\infty}\frac{(f,w_{i})_{2,\omega}}{\lambda_{i}}\psi_{\ell}(\lambda_{i},\cdot) \otimes w_{i}. \end{array} $$

With ψ_ℓ as in (5) we get

$$ u_{\ell}-\psi_{\ell}(\lambda_{\infty},\cdot)\otimes u_{\infty} = \sum\limits_{i=1}^{\infty}\frac{(f,w_{i})_{2,\omega}}{{\lambda_{i}^{2}}}\phi_{\ell,i}\otimes w_{i},\qquad \phi_{\ell,i} (x_{1}):=\frac{\cosh(\lambda_{\infty}x_{1})}{\cosh(\lambda_{\infty}\ell)}-\frac{\cosh(\lambda_{i}x_{1})}{\cosh(\lambda_{i}\ell)}. $$

Let δ_ℓ < ℓ. Then, since ${\int \limits }_{\omega }w_{i}w_{j}dx^{\prime }=\delta _{i,j}$, we get

$$ \begin{array}{@{}rcl@{}} |\nabla(u_{\ell}-\psi_{\ell}(\lambda_{\infty},\cdot)\otimes u_{\infty}) |_{2,{{\varOmega}}_{\ell-\delta_{\ell}}}^{2} &=& {\int}_{-\ell+\delta_{\ell}}^{\ell-\delta_{\ell}}{\int}_{\omega}|\nabla(u_{\ell}-\psi_{\ell}(\lambda_{\infty},\cdot) \otimes u_{\infty})|^{2}dx\\ &=&\sum\limits_{i=1}^{\infty}\frac{(f,w_{i})^{2}}{{{\lambda}_{i}^{4}}}{\int}_{-\ell + \delta_{\ell}}^{\ell-\delta_{\ell}}\left( (\phi_{\ell,i}^{\prime})^{2}+{\lambda_{i}^{2}}\phi_{\ell,i}^{2}\right). \end{array} $$

(10)

One has for any α > 0

$$ \begin{array}{@{}rcl@{}} {\int}_{-\ell+\delta_{\ell}}^{\ell-\delta_{\ell}}\left( \frac{\cosh(\alpha x_{1})}{\cosh(\alpha\ell)}\right)^{2}dx_{1} & =& 2{\int}_{0}^{\ell-\delta_{\ell}}\left( \frac{\cosh(\alpha x_{1})}{\cosh(\alpha\ell)}\right)^{2}dx_{1}\\ & =& \frac{1}{2}{\int}_{0}^{\ell-\delta_{\ell}}\frac{\mathrm{e}^{2\alpha x_{1}}+2+\mathrm{e}^{-2\alpha x_{1}}}{\cosh(\alpha\ell)^{2}}dx_{1}\\ &\leq& 2{\int}_{0}^{\ell-\delta_{\ell}}\frac{\operatorname{e}^{2\alpha x_{1}}+3}{\mathrm{e}^{2\alpha\ell}}dx_{1}\\ &\leq& \frac{1}{\alpha}\mathrm{e}^{-2\alpha\delta_{\ell}}+6(\ell -\delta_{\ell})\mathrm{e}^{-2\alpha\ell} \end{array} $$

and similarly

$$ {\int}_{-\ell+\delta_{\ell}}^{\ell-\delta_{\ell}}\left( \frac{\sinh(\alpha x_{1})}{\cosh(\alpha\ell)}\right)^{2}dx_{1} \leq \frac{1}{\alpha}\mathrm{e}^{-2\alpha\delta_{\ell}}. $$

Since λ₁ ≤ λ_i for all $i\in \mathbb {N}$ and

$$ \lambda_{1}=\underset{v\in {H_{0}^{1}}(\omega)\backslash\{0\}}{\inf}\frac{\|\nabla^{\prime}v\|_{2,\omega}}{\|v\|_{2,\omega}} \leq \frac{\|\nabla^{\prime}u_{\infty}\|_{2,\omega}}{\|u_{\infty}\|_{2,\omega}}=\lambda_{\infty}, $$

we get

$$ {\int}_{-\ell+\delta_{\ell}}^{\ell-\delta_{\ell}}\left( {\phi}_{\ell,i}^{\prime}\right)^{2} \leq 2\mathrm{e}^{-2\lambda_{\infty}\delta_{\ell}}+ 2\mathrm{e}^{-2\lambda_{1}\delta_{\ell}} \leq 4\mathrm{e}^{-2\lambda_{1}\delta_{\ell}}={C}_{\omega,\delta_{\ell}}^{(1)} $$

(11)

and

$$ \begin{array}{@{}rcl@{}} {\int}_{-\ell+\delta_{\ell}}^{\ell-\delta_{\ell}}\phi_{\ell,i}^{2} & \leq & 2{\int}_{-\ell+\delta_{\ell}}^{\ell-\delta_{\ell}}\left( \left\vert \frac{\cosh(\lambda_{\infty}x_{1})}{\cosh(\lambda_{\infty}\ell)}\right\vert^{2} + \left\vert \frac{\cosh(\lambda_{i}x_{1})}{\cosh(\lambda_{i}\ell)}\right\vert^{2}\right) \\ &\leq& 2\left( \frac{1}{\lambda_{\infty}}\mathrm{e}^{-2\lambda_{\infty}\delta_{\ell}}+\frac{1}{\lambda_{i}}\mathrm{e}^{-2\lambda_{i}\delta_{\ell}} + 6(\ell-\delta_{\ell}) \mathrm{e}^{-2\lambda_{\infty}\ell} + 6(\ell-\delta_{\ell})\mathrm{e}^{-2\lambda_{i}\ell}\right) \\ &\leq& 4\left( \frac{1}{\lambda_{1}}\mathrm{e}^{-2\lambda_{1}\delta_{\ell}}+6(\ell-\delta_{\ell}) \mathrm{e}^{-2\lambda_{1}\ell}\right) = C_{\omega,\delta_{\ell}}^{(2)}. \end{array} $$

(12)

We employ the estimates (11) and (12) in (10) and obtain

$$ \begin{array}{@{}rcl@{}} \|\nabla(u_{\ell}-\psi_{\ell}(\lambda_{\infty},\cdot) \otimes u_{\infty})\|_{2,{{\varOmega}}_{\ell-\delta_{\ell}}}^{2} & \leq& {C}_{\omega,\delta_{\ell}}^{(1)}\sum\limits_{i=1}^{\infty}\frac{(f,w_{i})_{2,\omega}^{2}}{{\lambda_{i}^{4}}}+{C}_{\omega,\delta_{\ell}}^{(2)}\sum\limits_{i=1}^{\infty}\frac{(f,w_{i})_{2,\omega}^{2}}{{\lambda_{i}^{2}}}\\ &=& C_{\omega,\delta_{\ell}}^{(1)}\|u_{\infty}\|_{2,\omega}^{2}+C_{\omega,\delta_{\ell}}^{(2)}\|\nabla^{\prime}u_{\infty}\|_{2,\omega}^{2}, \end{array} $$

which shows the assertion. □

Lemma 2 suggests that one cannot expect convergence of the approximation $\psi _{\ell }(\lambda _{\infty },\cdot ) \otimes u_{\infty }$ on the whole domain Ω_ℓ. Indeed it can be shown that, in general, $\|\nabla (u_{\ell }-\psi _{\ell }(\lambda _{\infty },\cdot )\otimes u_{\infty }) \|_{2,{{\varOmega }}_{\ell }}\nrightarrow 0$ as $\ell \rightarrow \infty$. Setting δ_ℓ = 0 in Lemma 2 shows that the error on Ω_ℓ can be estimated as follows:

Corollary 3

It holds

$$ \|\nabla(u_{\ell}-\psi_{\ell}(\lambda_{\infty},\cdot)\otimes u_{\infty})\|_{2,{{\varOmega}}_{\ell}}^{2} \leq 4\left( \|u_{\infty}\|_{2,\omega}^{2} + 6\ell\mathrm{e}^{-2\lambda_{1}\ell}\|\nabla^{\prime}u_{\infty}\|_{2,\omega}^{2}\right), $$

where λ₁ is as in (8).

Method 2: An Alternating Least Squares Type Iteration

Method 1 can be interpreted as a 2-step algorithm to obtain an approximation $u^{M_{1}}_{\ell }$ of u_ℓ.

• Step 1: Solve (3) in order to obtain an approximation of the form $1\otimes u_{\infty }$ which is non-conforming, i.e., does not belong to ${{H}_{0}^{1}}({{\varOmega }}_{\ell })$.

• Step 2: Using $u_{\infty }$, find a function ψ_ℓ that satisfies (4) in order to obtain the conforming approximation $u_{\ell }^{M_{1}}:=\psi _{\ell }(\lambda _{\infty },\cdot )\otimes u_{\infty }\in {{H}_{0}^{1}}({{\varOmega }}_{\ell })$.

In this section we extend this idea and seek approximations of the form

$$ {u}_{\ell,m}^{M_{2}}=\sum\limits_{j=0}^{m}p^{(j)}\otimes q^{(j)} $$

(13)

by iteratively solving least squares problems similar to (4). We denote by

$$ \text{ Res}_{m}=u_{\ell}-u_{\ell,m}^{M_{2}}=u_{\ell}-\sum\limits_{j=0}^{m}p^{(j)}\otimes q^{(j)} $$

the residual of the approximation and suggest the following iteration to obtain $u_{\ell ,m}^{M_{2}}$:

• m = 0: Set $q^{(0)}=u_{\infty }$ and $p^{(0)}=\psi _{\ell }(\lambda _{\infty },\cdot )$.

• m > 0: Find $q^{(m)}\in {{H}_{0}^{1}}(\omega )$ s.t.

  $$ q^{(m)}=\underset{q\in {{H}_{0}^{1}}(\omega)}{{\arg\min}}\|\nabla\left( \text{Res}_{m-1}-p^{(m-1)}\otimes q\right)\|_{2}. $$

  (14)

  Then, given q^(m), find $p^{(m)}\in {{H}_{0}^{1}}(I_{\ell })$ s.t.

  $$ p^{(m)}=\underset{p\in {{H}_{0}^{1}}(I_{\ell})}{{\arg\min}}\|\nabla\left( \text{Res}_{m-1}-p\otimes q^{(m)}\right)\|_{2}. $$

  (15)

  Iterate (14) and (15) until a stopping criterion is reached (inner iteration). Then set Res_m = Res_m− 1 − p^(m) ⊗ q^(m).

The algorithm exhibits properties of a greedy algorithm. It is easy to see that in each step of the (outer) iteration the error decreases or stays constant. We focus here on its accuracy in comparison with the two other methods via numerical experiments. We emphasize that for tensors of order at least 3, convergence can be shown for the (inner) iteration (see [11, 25, 29, 30]). This limit, however, is not a global minimum in general. The outer iteration can be shown to converge as well against the true solution u_ℓ under the condition that we find the best rank-1 approximation in the inner iteration (see [12]).

The idea of computing approximations in the separated form (13) by iteratively enriching the current solution with rank-1 terms is known in the literature as Proper Generalized Decomposition (PGD). The PGD has been applied to various problems in computational mechanics (e.g. [1, 4, 5, 21]), computational rheology [6], quantum chemistry (e.g. [2, 3]) and others.

An extensive review of the method can be found in [7]. For an error and convergence analysis of the (outer) iteration in the case of the Poisson equation we also refer to [20], where a similar (but not identical) approach as ours is considered.

In each step of the (outer) iteration above we need to solve at least two minimization problems (14) and (15). In the following we derive the strong formulations of these problems.

Resolution of (14)

As before an investigation of the functional

$$ J(q^{(m)}):=\|\nabla(\text{Res}_{m-1}-p^{(m-1)}\otimes q^{(m)})\|_{2}^{2} $$

shows that q^(m) needs to satisfy

$$ \begin{array}{@{}rcl@{}} \left( \nabla\left( p^{(m-1)}\otimes q^{(m)}\right),\nabla\left( p^{(m-1)}\otimes q\right)\right)_{2}\!& = &\! \left( \nabla\text{Res}_{m-1},\nabla\left( p^{(m-1)}\otimes q\right)\right)_{2}\\ \Longleftrightarrow\quad p_{0,m-1}\left( -{{\varDelta}}^{\prime}q^{(m)},q\right)_{2,\omega}+ p_{1,m-1}\left( q^{(m)},q\right)_{2,\omega} &=& \left( -{{\varDelta}}\text{Res}_{m-1},p^{(m-1)}\otimes q\right)_{2} \end{array} $$

for all $q\in {H_{0}^{1}}(\omega )$, where

$$ p_{0,m-1}:=\|p^{(m-1)}\|_{2,I_{\ell}}^{2},\quad p_{1,m-1}:=\|\left( p^{(m-1)}\right)^{\prime}\|_{2,I_{\ell}}^{2}. $$

For the right-hand side we obtain

$$ \begin{array}{@{}rcl@{}} &&\left( -{{\varDelta}}\text{Res}_{m-1},p^{(m-1)}\otimes q\right)_{2}= \left( -{{\varDelta}}\left( u_{\ell}-\sum\limits_{j=0}^{m-1}p^{(j)}\otimes q^{(j)}\right),p^{(m-1)}\otimes q\right)_{2}\\ &&\qquad=\left( 1\otimes f,p^{(m-1)}\otimes q\right)_{2} + \left( \sum\limits_{j=0}^{m-1}\left( p^{(j)}\right)^{\prime\prime}\otimes q^{(j)} + p^{(j)}\otimes{{\varDelta}}^{\prime}q^{(j)},p^{(m-1)}\otimes q\right)_{2}\\ &&\qquad=\tilde{p}_{m-1}(f,q)_{2,\omega}+\sum\limits_{j=0}^{m-1}\left( \tilde{p}_{2,j,m-1}\left( q^{(j)},q\right)_{2,\omega}+\tilde{p}_{0,j,m-1}\left( {{\varDelta}}^{\prime}q^{(j)},q\right)_{2,\omega}\right), \end{array} $$

where

$$ \tilde{p}_{m-1}:={\int}_{-\ell}^{\ell}p^{(m-1)},\quad \tilde{p}_{2,j,m-1}:=\left( \left( p^{(j)}\right)^{\prime\prime},p^{(m-1)}\right)_{2,I_{\ell}},\quad\tilde{p}_{0,j,m-1}:=\left( p^{(j)},p^{(m-1)}\right)_{2,I_{\ell}}. $$

In order to compute (14) we therefore have to solve in ω

$$ -p_{0,m-1}{{\varDelta}}^{\prime}q^{(m)}+p_{1,m-1}q^{(m)}=\tilde{p}_{m-1}f+\sum\limits_{j=0}^{m-1}\left( \tilde{p}_{2,j,m-1}q^{(j)}+\tilde{p}_{0,j,m-1}{{\varDelta}}^{\prime}q^{(j)}\right). $$

(16)

Resolution of (15)

Setting the derivative of the functional

$$ J(p^{(m)}):=\|\nabla(\text{Res}_{m-1}-p^{(m)}\otimes q^{(m)})\|_{2}^{2} $$

to zero, shows that p^(m) needs to satisfy

$$ \begin{array}{@{}rcl@{}} \left( \nabla\left( p^{(m)}\otimes q^{(m)}\right),\nabla\left( p\otimes q^{(m)}\right)\right)_{2} & = & \left( \nabla\text{Res}_{m},\nabla\left( p\otimes q^{(m)}\right)\right)_{2}\\ \Longleftrightarrow\quad-q_{0,m}\left( \left( p^{(m)}\right)^{\prime\prime},p\right)_{2,I_{\ell}} + q_{1,m}\left( p^{(m)},p\right)_{2,I_{\ell}} & = & \left( -{{\varDelta}}\text{Res}_{m},p\otimes q^{(m)}\right)_{2} \end{array} $$

for all $p\in {{H}_{0}^{1}}(-\ell ,\ell )$, where

$$ q_{0,m}=\|q^{(m)}\|_{2,\omega}^{2},\quad q_{1,m}=\|\nabla^{\prime}q^{(m)}\|_{2,\omega}^{2}. $$

For the right-hand side we obtain

$$ \begin{array}{@{}rcl@{}} &&\left( -{{\varDelta}}\text{Res}_{m-1},p\otimes q^{(m)}\right)_{2}= \left( -{{\varDelta}}\left( u_{\ell}-\sum\limits_{j=0}^{m-1}p^{(j)}\otimes q^{(j)}\right),p\otimes q^{(m)}\right)_{2}\\ &&\qquad=\left( 1\otimes f,p\otimes q^{(m)}\right)_{2} +\left( \sum\limits_{j=0}^{m-1}\left( \left( p^{(j)}\right)^{\prime\prime}\otimes q^{(j)} + p^{(j)}\otimes{{\varDelta}}^{\prime}q^{(j)}\right),p\otimes q^{(m)}\right)_{2}\\ &&\qquad=\tilde{q}_{m}{\int}_{-\ell}^{\ell}p+\sum\limits_{j=0}^{m-1}\left( \tilde{q}_{0,j,m}\left( \left( p^{(j)}\right)^{\prime\prime},p\right)_{2,I_{\ell}}+\tilde{q}_{2,j,m}\left( p^{(j)},p\right)_{2,I_{\ell}}\right), \end{array} $$

where

$$ \tilde{q}_{m}:=\left( f,q^{(m)}\right)_{2,\omega},\quad\tilde{q}_{2,j,m}:=\left( {{\varDelta}}^{\prime}q^{(j)},q^{(m)}\right)_{2,\omega},\quad\tilde{q}_{0,j,m}:=\left( q^{(j)},q^{(m)}\right)_{2,\omega}. $$

In order to obtain the solution of (15) we therefore have to solve in I_ℓ

$$ -q_{0,m}\left( p^{(m)}\right)^{\prime\prime}+q_{1,m}p^{(m)}=\tilde{q}_{m}+\sum\limits_{j=0}^{m-1}\left( \tilde{q}_{2,j,m}p^{(j)}+\tilde{q}_{0,j,m}\left( p^{(j)}\right)^{\prime\prime}\right). $$

(17)

Remark 4

The constants p_1,m− 1, $\tilde {p}_{2,j,m-1}$, q_1,m and $\tilde {q}_{2,j,m}$ involve derivatives and Laplace-operators. Note that after solving (16) and (17) for q^(m) and p^(m), discrete versions of ${{\varDelta }}^{\prime }q^{(m)}$ and $(p^{(m)})^{\prime \prime }$ can be easily obtained via the same equations. Furthermore, since

$$ q_{1,m}=\|\nabla^{\prime}q^{(m)}\|_{2,\omega}^{2}=\left( -{{\varDelta}}^{\prime}q^{(m)},q^{(m)}\right)_{2,\omega}=-\tilde{q}_{2,m,m} $$

and

$$ p_{1,m-1}=\|\left( p^{(m-1)}\right)^{\prime}\|_{2,I_{\ell}}^{2} = \left( -\left( p^{(m-1)}\right)^{\prime\prime},p^{(m-1)}\right)_{2,I_{\ell}}=-\tilde{p}_{2,m-1,m-1} $$

a numerical computation of the gradients can be avoided.

Method 3: Exploiting the Tensor Product Structure of the Operator

In this section we exploit the tensor product structure of the Laplace operator and the domain Ω_ℓ. Recall that

$$ {{\varOmega}}_{\ell}=I_{\ell}\times\omega. $$

Note that we do not assume that ω has a tensor product structure. Furthermore the Laplace operator in our original problem (1) can be written as

$$ -{{\varDelta}}=-{\partial_{1}^{2}}-{{\varDelta}}^{\prime}. $$

(18)

We discretize (1) with F as in (2) on a mesh $\mathcal {G}$, e.g., by finite elements or finite differences on a tensor mesh, i.e., each mesh cell has the form (x_i− 1,x_i) × τ_j, where τ_j is an element of the mesh for ω. The essential assumption is that the system matrix for the discrete version of −Δ in (18) is of the tensor form

$$ A=A_{1}\otimes M^{\prime}+M_{1}\otimes A^{\prime}. $$

(19)

If we discretize with a finite difference scheme on an equidistant grid for I_ℓ with step size h, then A₁ is the tridiagonal matrix h^− 2tridiag[− 1,2,− 1] and M₁ is the identity matrix. A finite element discretisation with piecewise linear elements leads as well to A₁ = h^− 2tridiag[− 1,2,− 1], while $M_{x_{1}}=\text {tridiag}[1/6,2/3,1/6]$. It can be shown that the inverse of the matrix A can be efficiently approximated with a sum of matrix exponentials. More precisely the following Theorem holds which is proved in [14, Proposition 9.34].

Theorem 5

Let M^(j), A^(j) be positive definite matrices with $\lambda _{\min \limits }^{(j)}$ and $\lambda _{\max \limits }^{(j)}$ being the extreme eigenvalues of the generalized eigenvalue problem A^(j)x = λM^(j)x and set

$$ \begin{array}{@{}rcl@{}} A &= & A^{(1)}\otimes M^{(2)}\otimes\cdots\otimes M^{(n)}+M^{(1)}\otimes A^{(2)}\otimes\cdots\otimes M^{(n)}+\cdots\\ &&+M^{(1)}\otimes\cdots\otimes M^{(n-1)}\otimes A^{(n)}. \end{array} $$

Then A^− 1 can be approximated by

$$ B:=\left( \sum\limits_{\nu=1}^{r}a_{\nu,[a,b]}\otimes_{j=1}^{n}{\exp}\left( -\alpha_{\nu,[a,b]} \left( M^{(j)}\right)^{-1}A^{(j)}\right)\right) \left( \otimes_{j=1}^{n}\left( M^{(j)}\right)^{-1}\right), $$

where the coefficients a_ν,α_ν > 0 are such that

$$ \begin{array}{@{}rcl@{}} \varepsilon\left( \frac{1}{x},[a,b],r\right) & :=& \|\frac{1}{x}-\sum\limits_{\nu=1}^{r}a_{\nu,[a,b]}\mathrm{e}^{-\alpha_{\nu,[a,b]}x}\|_{[a,b]}\\ & =& \inf\left\{\|\frac{1}{x}-\sum\limits_{\nu=1}^{r}b_{\nu}\mathrm{e}^{-\beta_{\nu}x}\|_{[a,b],\infty}: ~b_{\nu},\beta_{\nu}\in\mathbb{R}\right\} \end{array} $$

with $a:={\sum }_{j=1}^{n}\lambda _{\min \limits }^{(j)}$ and $b:={\sum }_{j=1}^{n}{\lambda }_{\max \limits }^{(j)}$. The error can be estimated by

$$ \|A^{-1}-B\|_{2}\leq\varepsilon\left( \frac{1}{x},[a,b],r\right)\|M^{-1}\|_{2}, $$

where $M=\otimes _{j=1}^{n}M^{(j)}$.

Theorem 5 shows how the inverse of matrices of the form (19) can be approximated by sums of matrix exponentials. It is based on the approximability of the function 1/x by sums of exponentials in the interval [a,b]. We refer to [14, 16] for details how to choose r and the coefficients a_ν,[a,b], α_ν,[a,b] in order to reach a given error tolerance $\varepsilon \left (\frac {1}{x},[a,b],r\right )$. Note that the interval [a,b] where 1/x needs to be approximated depends on the matrices A^(j) and M^(j). Thus, if A changes a and b need to be recomputed which in turn has an influence on the optimal choice of the parameters a_ν,[a,b] and α_ν,[a,b].

Numerical methods based on Theorem 5 can only be efficient if the occurring matrix exponential can be evaluated at low cost. In our setting we will need to compute the matrices $\exp \big (-\alpha _{\nu ,[a,b]}{M}_{1}^{-1}A_{1}\big )$ and $\exp \big (-\alpha _{\nu ,[a,b]}(M^{\prime })^{-1}A^{\prime }\big )$. The evaluation of the first matrix will typically be simpler. In the case where a finite difference scheme is employed and A₁ is a tridiagonal Toeplitz matrix while M₁ is the identity, the matrix exponential can be computed by diagonalizing A₁, e.g., A₁ = SD₁S^− 1, and using $\exp \big (-\alpha _{\nu ,[a,b]}{M}_{1}^{-1}A_{1}\big )=S\exp \big (-\alpha _{\nu ,[a,b]}D_{1}\big )S^{-1}$. The computation of exponentials for general matrices is more involved. We refer to [22] for an overview of different numerical methods. Here, we will make use of the Dunford–Cauchy integral (see [15]). For a matrix $\tilde {M}$ we can write

$$ {\exp}(-\tilde{M}) = \frac{1}{2\pi\mathrm{i}}\oint_{\mathcal{C}}(\zeta I-\tilde{M})^{-1}\mathrm{e}^{-\zeta}d\zeta $$

for a contour $\mathcal {C}=\partial D$ which encircles all eigenvalues of $\tilde {M}$. We assume here that $\tilde {M}$ is positive definite. Then the spectrum of $\tilde {M}$ satisfies $\sigma (\tilde {M})\subset (0,\|M\|]$ and the following (infinite) parabola

$$ \left\{\zeta(s)=x(s)+\mathrm{i}y(s):x(s):=s^{2},~y(s):=-s\quad\text{for }s\in\mathbb{R}\right\} $$

can be used as integration curve $\mathcal {C}$. The substitution $\zeta \rightarrow s^{2}-\mathrm {i}s$ then leads to

$$ {\exp}(-\tilde{M}) = {\int}_{-\infty}^{\infty}\underbrace{\left( \frac{1}{2\pi\mathrm{i}}(s^{2}-\mathrm{i}s)I-\tilde{M}\right)^{-1}\mathrm{e}^{-s^{2}+\mathrm{i}s}(2s-\mathrm{i})}_{=:G(s)}ds. $$

(20)

The integrand decays exponentially for $s\rightarrow \pm \infty$. Therefore (20) can be efficiently approximated by sinc quadrature, i.e.,

$$ {\exp}(-\tilde{M}) = {\int}_{-\infty}^{\infty}G(s)ds\approx\mathfrak{h}\sum\limits_{\nu=-N}^{N}G(\nu\mathfrak{h}), $$

(21)

where $\mathfrak {h}>0$ and should be chosen s.t. $\mathfrak {h}=\mathcal {O}\left ((N+1)^{-2/3}\right )$. We refer to [15] for an introduction to sinc quadrature and for error estimates for the approximation in (21). The parameters $\mathfrak {h}$ and N in our implementation have been chosen such that quadrature errors become negligible compared to the overall discretisation error. For practical computations, the halving rule (see [15, §14.2.2.2]) could be faster while the Dunford–Schwartz representation with sinc quadrature is more suited for an error analysis.

Numerical Experiments

The Case of a Planar Cylinder

In this subsection we apply the methods derived in Section 3 to a simple model problem in two dimensions. We consider the planar cylinder

$$ {{\varOmega}}_{\ell}^{2D}=I_{\ell}\times(-1,1) $$

and solve (1) for different right-hand sides F = 1 ⊗ f (see (2)) and different lengths ℓ. The reduced problem (3) on ω = (− 1,1) is solved using a standard finite difference scheme with a mesh width of h = 10^− 2. We compare the approximations of (1) to a reference solution $u_{2D,\ell }^{\text {ref}}$ that is computed using a finite difference method on a sufficiently refined two-dimensional grid (mesh width h = 10^− 2).

In Table 1 we state the $L^{2}({{\varOmega }}_{\ell }^{2D})$-errors of the approximations $u_{2D,\ell }^{M_{1}}$ for various values of ℓ and right-hand sides f. Having in mind that $u_{2D,\ell }^{M_{1}}$ is a rather simple one-term approximation that only requires the solution of one (d − 1)-dimensional problem (plus some postprocessing), the accuracy of the approximation is satisfactory especially for larger values of ℓ.

Table 1 Relative $L^{2}({{\varOmega }}_{\ell }^{2D})$-errors of the approximations $u_{2D,\ell }^{M_{1}}$ for different values of ℓ and f

Figure 2 shows the pointwise, absolute error $\left |{u}_{2D,\ell }^{M_{1}}-{u}_{2D,\ell }^{\text {ref}}\right |$ in Ω_ℓ for ℓ = 10 and $f(x^{\prime })=\tanh (4x^{\prime }+1)$. As expected the accuracy of the approximation is very high in the interior of the planar cylinder (away from ± ℓ).

Fig. 2

Absolute error $\left |u_{2D,\ell }^{M_{1}}-u_{2D,\ell }^{\text {ref}}\right |$ for ℓ = 10 and $f(x^{\prime })=\tanh (4x^{\prime }+1)$

Lemma 2 (and Fig. 2) suggests that the approximation in the interior of the cylinder is significantly better than on the whole domain Ω_ℓ. Indeed, if the region of interest is only a subdomain ${{\varOmega }}_{\ell _{0}}\subset {{\varOmega }}_{\ell }$, where ℓ₀ < ℓ, the error decreases exponentially as $\ell _{0}\rightarrow 0$. Figure 3 shows the relative error $\|u_{2D,\ell }^{M_{1}}-u_{2D,\ell }^{\text {ref}}\|_{L^{2}({{\varOmega }}_{\ell _{0}})}/\|u_{2D,\ell }^{\text {ref}}\|_{L^{2}({{\varOmega }}_{\ell _{0}})}$ with respect to ℓ₀ for ℓ = 20,50 and the right-hand side $f(x^{\prime })=\tanh (4x^{\prime }+1)$. We can see that the exponential convergence sets in almost immediately as l₀ moves away from ℓ.

Fig. 3

Relative L²-errors of the approximation $u_{2D,\ell }^{M_{1}}$ in ${{\varOmega }}_{\ell _{0}}$ for $f(x^{\prime })=\tanh (4x^{\prime }+1)$

To conclude, method 1 can be used in applications where

• only a limited approximation accuracy is required,

• a good starting point for more accurate methods is needed,

• the region of interest is a subdomain ${{\varOmega }}_{\ell _{0}}$ of Ω_ℓ with ℓ₀ < ℓ.

In method 2 we use ${u}_{2D,\ell }^{M_{1}}$ as starting value of the iteration which is then successively refined by approximating the residual in each step with a series of L² best approximations. In Table 2 we state the relative errors of this approach in the case $f(x^{\prime })=\tanh (4x^{\prime }+1)$ for different values of ℓ and iteration steps. We can see that five iterations are sufficient to reduce the error of the initial approximation ${u}_{2D,\ell }^{M_{1}}$ by a factor 100 for all considered values of ℓ. However, in this case more iterations do not lead to significantly better results and the convergence seems to flatten. One explanation for this is that the residuals are increasingly difficult to approximate with each step of the iteration. After a few iterations a one-term approximation of these residuals of the form p^(m) ⊗ q^(m) therefore is not sufficiently accurate which leads to reduced decay of the error in the overall scheme.

Table 2 Relative L²-errors of the approximations $u_{2D,\ell ,m}^{M_{2}}$ for different values of ℓ and iterations m. We used $f(x^{\prime })=\tanh (4x^{\prime }+1)$ throughout

Note that in the case ℓ = 1, Ω_ℓ cannot be considered as a “long” domain. Therefore, the initial approximation ${u}_{2D,\ell }^{M_{1}}$ only exhibits a low accuracy. Nevertheless the error of ${u}_{2D,\ell ,m}^{M_{2}}$ decays quickly as m increases and reaches a similar level of accuracy as for larger ℓ. This shows that method 2 can be used for more general domains than considered here (e.g. [13]).

In Table 3 we show the relative errors of the approximations ${u}_{2D,\ell ,r}^{M_{3}}$ for $f(x^{\prime })=\tanh (4x^{\prime }+1)$ and different values of ℓ and r. As the theory predicts the error decays exponentially in r and is governed by the approximability of the function 1/x by exponential sums. Note that in this two-dimensional example the arising matrix exponentials could be computed via diagonalization of the involved finite difference matrices. An approximation of the Dunford–Cauchy integral was not necessary in this case.

Table 3 Relative L²-errors of the approximations $u_{2D,\ell ,r}^{M_{3}}$ for different values of ℓ and r. We used $f(x^{\prime })=\tanh (4x^{\prime }+1)$ throughout

A Three-dimensional Domain with a Non-rectangular Cross Section

In this section we consider the three-dimensional domain

$$ {{\varOmega}}_{\ell}=(-\ell,\ell)\times\underbrace{\left[(0,2)\times(0,1)\cup (0,1)\times(1,2)\right]}_{=\omega}, $$

where ω is an “L-shaped” domain (see Fig. 4). As before we solve problem (1) for different right-hand sides f and different values of ℓ. The reduced problem (3) on ω is solved using a standard 2D finite difference scheme. As 3D reference solution we use an accurate approximation using method 3, i.e., ${u}_{3D,\ell ,r}^{M_{3}}$ for r = 30, which is known to converge exponentially in r. The reduced problem and the reference solution are computed with a mesh width of 0.02.

Fig. 4

Plot of domain Ω_ℓ and cross-section ω

Table 4 shows the relative errors of the approximations $u_{3D,\ell }^{M_{1}}$ for different values of ℓ and right-hand sides f. As the theory predicts we cannot observe an exponentially decreasing error as ℓ gets large, since we measure the error on the whole domain Ω_ℓ and not only a subdomain ${{\varOmega }}_{\ell -\delta _{\ell }}$. As before we only have to solve one two-dimensional problem on ω in order to obtain the approximation ${u}_{3D,\ell }^{M_{1}}$.

Table 4 Relative L²-errors of the approximations $u_{3D,\ell }^{M_{1}}$ for different values of ℓ and f

In Table 5 we show the relative errors of the approximations ${u}_{3D,\ell ,m}^{M_{2}}$ for $f(x^{\prime })=\tanh (x_{2}x_{3})$ and different values of ℓ and m (number of iterations). As in the 2D case this method significantly improves the initial approximation ${u}_{3D,\ell ,1}^{M_{2}}={u}_{3D,\ell }^{M_{1}}$ using the alternating least squares type iteration. However, also here we observe that the convergence slows down when a certain accuracy is reached. We remark that a good starting point for the iteration is crucial for this method. In all our experiments ${u}_{3D,\ell }^{M_{1}}$ was a good choice which leads to a convergence behaviour similar to the ones in Table 5. Other choices often did not lead to satisfactory results.

Table 5 Relative L²-errors of the approximations $u_{3D,\ell ,m}^{M_{2}}$ for different values of ℓ and iterations m. We used $f(x^{\prime })=\tanh (x_{2}x_{3})$ throughout

In Table 6 we show the relative errors of the approximations $u_{3D,\ell ,r}^{M_{3}}$ again for $f(x^{\prime })=\tanh (x_{2}x_{3})$ and different values of ℓ and r. As before the error decays exponentially with respect to r. The arising matrix exponentials $\exp (-\alpha _{\nu ,[a,b]}A_{x^{\prime }})$ in these experiments were computed using the sinc quadrature approximation (21). The number of quadrature points N was chosen such that the corresponding quadrature error had an negligible effect on the overall approximation.

Table 6 Relative L²-errors of the approximations $u_{3D,\ell ,r}^{M_{3}}$ for different values of ℓ and r. We used $f(x^{\prime })=\tanh (x_{2}x_{3})$ throughout

Conclusion

We have compared three different methods for constructing tensor approximations to the solution of a Poisson equation on a long product domain for a right-hand side which is an elementary tensor.

The construction of a one-term tensor approximation is based on asymptotic analysis. The approximation converges exponentially (on a fixed subdomain) as the length of the cylinder goes to infinity. However, the error is fixed for fixed length since the approximation consists of only one term. The cost for computing this approximation is very low—it consists of solving a Poisson-type problem on the cross section and a cheap post-processing step to find the univariate function in the one-term tensor approximation.

The greedy-type method uses this elementary tensor and generates step-by-step a rank-k approximation. The computation of the m-th term in the tensor approximation itself requires an inner iteration. If one is interested in only a moderate accuracy (but improved accuracy compared to the initial approximation) this method is still relatively cheap and significantly improves the accuracy. However, the theory for this application is not fully developed and the definition of a good stopping criterion is based on heuristics and experiments.

Finally the approximation which is based on exponential sums is the method of choice among these three methods if a higher accuracy is required. A well developed a priori error analysis allows us to choose the tensor rank in the approximation in a very economic way. Since the method is converging exponentially with respect to the tensor rank, the method is also very efficient (but more expensive than the first two methods for the very first terms in the tensor representation). However, its implementation requires the realization of inverses of discretisation matrices in a sparse ${\mathscr{H}}$-matrix format and a contour quadrature approximation of the Cauchy–Dunford integral by sinc quadrature by using a non-trivial parametrisation of the contour.

We expect that these methods can be further developed and an error analysis which takes into account all error sources (contour quadrature, discretisation, iteration error, asymptotics with respect to the length of the cylinder, ${\mathscr{H}}$-matrix approximation) seems to be feasible. Also the methods are interesting in the context of a-posteriori error analysis to estimate the error due to the truncation of the tensor representation at a cost which is proportional to the solution of problems on the cross sections. We further expect that more general product domains of the form $\times _{m=1}^{d}\omega _{m}$ for some $\omega _{m}\in \mathbb {R}^{d_{m}}$ with dimensions 1 ≤ d_m ≤ d such that ${\sum }_{m=1}^{d}d_{m}=d$ and domains with outlets can be handled by our methods since also in this case zero-th order tensor approximation can be derived by asymptotic analysis (see [9]).