Bounds on the Objective Value of Feasible Roundings

Abstract

For mixed-integer linear and nonlinear optimization problems we study the objective value of feasible points which are constructed by the feasible rounding approaches from Neumann et al. (Comput. Optim. Appl. 72, 309–337, 2019; J. Optim. Theory Appl. 184, 433–465, 2020). We provide a-priori bounds on the deviation of such objective values from the optimal value and apply them to explain and quantify the positive effect of finer grids of integer feasible points on the performance of the feasible rounding approaches. Computational results for large scale knapsack problems illustrate our theoretical findings.

1 Introduction

In this paper we study the quality of feasible points of mixed-integer linear and nonlinear optimization problems (MILPs and MINLPs, resp.) as they are constructed by the feasible rounding approaches from [19, 20]. These approaches are based on a property of the feasible set which we call granularity and which states that a certain inner parallel set of the continuously relaxed feasible set is nonempty. The main effect of granularity is that it relaxes the difficulties imposed by the integrality conditions and hence, under suitable assumptions, provides a setting in which feasible points of MINLPs may be generated at low computational cost.

Our present analysis is motivated by the successful application of this algorithmic approach to mixed-integer linear and nonlinear problems in [19] and [20], respectively. In these papers computational studies of problems from the MIPLIB and MINLPLib libraries show that granularity may be expected and exploited in various real world applications. Moreover, the practical performance is observed to improve for optimization problems with finer grids of integer feasible points, that is, with ‘more integer feasible points relative to the size of the continuously relaxed feasible set’. This positive effect does not only refer to the applicability of the granularity concept, but also to the quality of the generated feasible points in terms of their objective values.

In fact, in applications a small deviation of this objective value from the minimal value may lead to the decision to accept the feasible point as ‘close enough to optimal’. Otherwise, a feasible point with low objective value may be used to initialize an appropriate branch-and-cut method with a small upper bound on the optimal value, or to start a local search heuristic there (cf., e.g., [4]).

The remainder of this article is structured as follows. Section 2 recalls some preliminaries from [19, 20], such as the main construction needed for the definition of granularity, an explicit description of a subset of the appearing inner parallel set, and enlargement ideas which promote the performance of the resulting feasible rounding approach. Section 3 provides a-priori bounds on the deviation of the objective value of the generated feasible point from the optimal value, before Section 4 applies these bounds to explain and quantify the positive effect of fine integer grids on the performance of the feasible rounding approach. In Section 5 we illustrate our theoretical findings by computational results for large scale knapsack problems, and some conclusions and final remarks end the article in Section 6.

2 Preliminaries

We study mixed-integer nonlinear optimization problems of the form

$$ MINLP:\qquad \min\limits_{(x,y)\in\mathbb{R}^{n}\times \mathbb{Z}^{m}} f(x,y) \quad\text{s.t.}\quad g_{i}(x,y) \le 0,~ i\in I,~ (x,y) \in D $$

with real-valued functions f, g_i, i ∈ I, defined on $\mathbb {R}^{n}\times \mathbb {R}^{m}$, a finite index set I = {1,…,q}, $q\in \mathbb {N}$, and a nonempty polyhedral set

$$ D = \{(x,y)\in\mathbb{R}^{n}\times\mathbb{R}^{m}~|~ Ax+By\le b\} $$

with some (p,n)-matrix A, (p,m)-matrix B and $b\in \mathbb {R}^{p}$, $p\in \mathbb {N}$.

To verify granularity of a given problem MINLP we will impose additional Lipschitz assumptions for the functions f, g_i, i ∈ I, on the set D, and to state the a-priori bounds on objective values we shall further require convexity of the functions f, g_i, i ∈ I. However, these additional assumptions will only be introduced where necessary, since the granularity concept also covers various nonlinear instances which, in particular, go beyond the case of mixed-integer convex optimization problems (MICPs). On the other hand, we shall specify our general results to mixed-integer linear optimization problems (MILPs) when appropriate (cf. Example 2 and Corollary 1) and, in particular, we will illustrate them in Section 5 along some MILP. Note that the presented results are novel not only for MINLPs, but also for MILPs. While the purely integer case (n = 0) is included in our analysis, we will assume m,p > 0 throughout this article.

2.1 Granularity

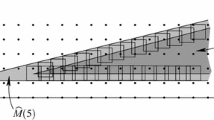
In the following let us recall some constructions which were presented in [19, 20] for the case of mixed-integer linear optimization problems (MILPs) and mixed-integer nonlinear optimization problems (MINLPs), respectively. We shall denote the feasible set of the NLP relaxation $\widehat {MINLP}$ of MINLP by

$$ \widehat M = \{(x,y)\in\mathbb{R}^{n}\times\mathbb{R}^{m}~|~ (x,y)\in D,~ g(x,y)\le0\}, $$

where g denotes the vector of functions g_i, i ∈ I. Moreover, for any point $(x,y)\in \mathbb {R}^{n}\times \mathbb {R}^{m}$ we call $(\check x,\check y)$ a rounding if

$$ \check x= x\quad\text{ and }\quad\check y\in \mathbb{Z}^{m},\quad |\check y_{j}- y_{j}| \le \tfrac{1}2,~j=1,\ldots,m, $$

hold, that is, y is rounded componentwise to a point in the mesh $\mathbb {Z}^{m}$, and x remains unchanged. Note that a rounding does not have to be unique.

With the sets

$$ B_{\infty}\left( 0,\tfrac{1}{2}\right) := \{y\in\mathbb{R}^{m}~|~ \|y\|_{\infty}\le\tfrac{1}{2}\}\quad\text{ and }\quad K := \{0\}\times B_{\infty}\left( 0,\tfrac12\right) $$

any rounding of (x,y) obviously satisfies

$$ (\check x,\check y) \in \left( (x,y)+K\right)\cap\left( \mathbb{R}^{n}\times \mathbb{Z}^{m}\right). $$

(1)

The central object of our technique is the inner parallel set of $\widehat M$ with respect to K,

$$ \widehat M^{-} := \{(x,y)\in\mathbb{R}^{n}\times\mathbb{R}^{m}~|~ (x,y)+K\subseteq\widehat M\}. $$

Any rounding of any point $(x,y)\in \widehat M^{-}$ must lie in the feasible set M of MINLP since in view of (1) it satisfies

$$ (\check x,\check y) \in \left( (x,y)+K\right)\cap\left( \mathbb{R}^{n}\times \mathbb{Z}^{m}\right) \subseteq \widehat M\cap\left( \mathbb{R}^{n}\times \mathbb{Z}^{m}\right) = M. $$

Hence, if the inner parallel set $\widehat M^{-}$ is nonempty, then also M is nonempty. Of course, this observation is only useful if the inner parallel set is nonempty, which gives rise to the following definition.

Definition 1

We call the set Mgranular if the inner parallel set $\widehat M^{-}$ of $\widehat M$ is nonempty. Moreover, we call a problem MINLP granular if its feasible set M is granular.

We remark that [19, 20] provide several examples for granular problems in the linear as well as in the nonlinear case.

In the terminology of Definition 1 our above observation states that any granular problem MINLP is consistent. Firstly, this gives rise to a feasibility test for MINLPs and, secondly, for any granular MINLP one may aim at the explicit computation of some feasible point. For a discussion of the former aspect we refer to [19, 20] and rather focus on the latter in the present paper.

To this end we need to compute at least a subset T⁻ of $\widehat M^{-}$ explicitly which, like the set $\widehat M^{-}$, is not restricted by integrality constraints. The general idea of the feasible rounding approaches from [19, 20] is to minimize f over T⁻ and round any optimal point to a point in M. This employment of the objective function f aims at obtaining a feasible point with a reasonably good objective value. In Section 3 we shall quantify how ‘bad’ this objective value may be in the worst case.

2.2 A Functional Description for the Inner Parallel Set

To obtain a functional description of some set $T^{-}\subseteq \widehat M^{-}$ observe that with the abbreviation

$$ G := \{(x,y)\in\mathbb{R}^{n}\times\mathbb{R}^{m}~|~ g(x,y)\le0\} $$

we may write $\widehat M=D\cap G$ and that the inner parallel set of $\widehat M$ thus satisfies $\widehat M^{-}=D^{-}\cap G^{-}$. From [25, Lemma 2.3] we know the closed form expression for the inner parallel set of D,

$$ D^{-}=\{(x,y)\in\mathbb{R}^{n}\times\mathbb{R}^{m}~|~ Ax+By+\|\upbeta\|_{1}/2\le b\}, $$

(2)

where ${\upbeta }_{i}^{\intercal }$, i = 1,…,p, denote the rows of the matrix B and, by a slight abuse of notation, ∥β∥₁ stands for the vector $(\|{\upbeta }_{1}\|_{1},\ldots ,\|{\upbeta }_{p}\|_{1})^{\intercal }$.

Moreover, the definition of the set G⁻ yields its semi-infinite description

$$ \begin{array}{@{}rcl@{}} G^{-}&=&\{(x,y)\in\mathbb{R}^{n}\times\mathbb{R}^{m}~|~ (x,y)+K\subseteq G\}\\ &=&\{(x,y)\in\mathbb{R}^{n}\times\mathbb{R}^{m}~|~ g(x,y+\eta)\le 0~~\forall \eta\in B_{\infty}(0,\tfrac12)\}. \end{array} $$

For the derivation of some algorithmically tractable inner approximation of G⁻ we employ global Lipschitz conditions with respect to y uniformly in x for the functions g_i, i ∈ I, on the set D. This distinction between the roles of x and y is caused by the definition of inner parallel sets, whose geometric construction only depends on the discrete variable y.

In fact, for any $x\in \mathbb {R}^{n}$ we define the set $D(x) := \{y\in \mathbb {R}^{m}~|~(x,y)\in D\}$ and denote by $\text {pr}_{x}D := \{x\in \mathbb {R}^{n}~|~D(x)\neq \emptyset \}$ the parallel projection of D to the ‘x-space’ $\mathbb {R}^{n}$. Then the functions g_i, i ∈ I, are assumed to satisfy Lipschitz conditions with respect to the $\ell _{\infty }$-norm on the fibers {x}× D(x), independently of the choice of x ∈pr_xD.

Assumption 1

For all i ∈ I there exists some $L^{i}_{\infty }\ge 0$ such that for all x ∈pr_xD and all y¹,y² ∈ D(x) we have

$$ |g_{i}(x,y^{1})-g_{i}(x,y^{2})| \le L^{i}_{\infty}\|(x,y^{1})-(x,y^{2})\|_{\infty} = L^{i}_{\infty}\|y^{1}-y^{2}\|_{\infty}. $$

Some problem classes for which the Lipschitz constants from Assumption 1 can be calculated are discussed in [20]. In particular, if the set D is bounded and the functions g_i, i ∈ I, are continuously differentiable with respect to y, one may choose

$$ L^{i}_{\infty}=\max_{(x,y)\in D}\|\nabla_{y}g_{i}(x,y)\|_{1},\quad i\in I, $$

which allows to compute such Lipschitz constants for many test instances from the MINLPLib [20].

Under Assumption 1, and with $L_{\infty }$ denoting the vector of Lipschitz constants $L^{i}_{\infty }$, i ∈ I, one may define the set

$$ T^{-} := \left\{(x,y)\in D^{-}~|~ g(x,y)+L_{\infty}/2\le 0\right\} $$

and show the desired inclusion $T^{-}\subseteq \widehat M^{-}$ [20]. Recall that thus any rounding $(\check x,\check y)$ of any point (x,y) ∈ T⁻ lies in M.

2.3 Enlargements

We point out that it may depend on the geometry of the relaxed feasible set $\widehat M$ whether the feasible set M of MINLP is granular or not. In particular, for MINLPs with binary variables the standard formulation of $\widehat M$ would usually lead to an empty inner parallel set $\widehat M^{-}$ [19, 20]. On the other hand, the set $\widehat M$ may often be replaced by a set $\widetilde M$ in such a way that the corresponding new inner parallel set $\widetilde M^{-}$ is larger than $\widehat M^{-}$, without losing the property that any rounding of any of its elements lies in M. This admits to exploit granularity also for many MINLPs with binary variables [19, 20].

The main idea for the construction of such enlargements is a preprocessing step for the functional description of MINLP. It first enlarges the relaxed feasible set $\widehat M$ of M to some set $\widetilde M\supseteq \widehat M$ for which the feasible set M of MINLP can still be written as

$$ M = \widetilde M \cap (\mathbb{R}^{n}\times \mathbb{Z}^{m}). $$

(3)

Then we call the inner parallel set

$$ \widetilde M^{-} = \{(x,y)\in\mathbb{R}^{n}\times\mathbb{R}^{m}~|~ (x,y)+K\subseteq\widetilde M\} $$

of $\widetilde M$ an enlarged inner parallel set of $\widehat M$ since the relation $\widehat M\subseteq \widetilde M$ implies $\widehat M^{-}\subseteq \widetilde M^{-}$. Depending on the functional description of $\widetilde M$ and, in particular, the appearing Lipschitz constants, the inner approximation $\widetilde T^{-}$ of $\widetilde M^{-}$ may then be larger than T⁻.

While there are several options for the construction of enlargements of the set $\widehat M$ [20], in the following let us focus on those resulting from constant additive relaxations Ax + By ≤ b + σ and g(x,y) ≤ τ of its constraints with appropriately chosen vectors σ,τ ≥ 0. Note that this approach maintains algorithmically attractive properties like the polyhedrality of D and differentiability or convexity of the functions g_i, i ∈ I. We set

$$ D_{\sigma} := \{(x,y)\in\mathbb{R}^{n}\times\mathbb{R}^{m}~|~ Ax+By\le b+\sigma\} $$

as well as

$$ G_{\tau} := \{(x,y)\in\mathbb{R}^{n}\times\mathbb{R}^{m}~|~ g(x,y)\le\tau\}. $$

Clearly, for each ρ := (σ,τ) ≥ 0 the set

$$ \widehat M_{\rho}:=D_{\sigma}\cap G_{\tau} $$

(4)

satisfies $\widehat M\subseteq \widehat M_{\rho }$. If we denote the appropriate choices of ρ for (3) by

$$ R := \{\rho\in\mathbb{R}^{p}\times\mathbb{R}^{q}~|~ \rho\ge0,~M=\widehat M_{\rho}\cap(\mathbb{R}^{n}\times \mathbb{Z}^{m})\} $$

then for each ρ ∈ R any rounding of any element of $\widehat M_{\rho }^{-}$ lies in M. Furthermore, we have $\widehat M^{-}\subseteq \widehat M^{-}_{\rho }$, so that $\widehat M^{-}_{\rho }$ is more likely to be nonempty than $\widehat M^{-}$. In fact, after preprocessing $\widehat M$ to $\widehat M_{\rho }$ for some ρ ∈ R, according to Definition 1 the set M and the problem MINLP are granular and, thus, consistent if the enlarged inner parallel set $\widehat M^{-}_{\rho }$ is nonempty. Note that due to (4) we may write $\widehat M^{-}_{\rho }=D_{\sigma }^{-}\cap G_{\tau }^{-}$ with

$$ D_{\sigma}^{-} = \{(x,y)\in\mathbb{R}^{n}\times\mathbb{R}^{m}~|~ Ax+By+\|\upbeta\|_{1}/2\le b+\sigma\}. $$

Moreover,

$$ T^{-}_{\rho} = \{(x,y)\in D^{-}_{\sigma}~|~ g(x,y)+L_{\infty}/2\le\tau\} $$

is an inner approximation of $\widehat M^{-}_{\rho }$, where the entries of the vector $L_{\infty }$ are Lipschitz constants of the functions g_i(x,y) − τ_i, i ∈ I, on D_σ in the sense of Assumption 1. Observe that, while these Lipschitz constants do not depend on τ, they may well depend on σ. This leads to the undesirable issue that for ρ ∈ R, despite the inclusion $\widehat M^{-}\subseteq \widehat M^{-}_{\rho }$, the corresponding inner approximations T⁻ and $T_{\rho }^{-}$ do not necessarily satisfy $T^{-}\subseteq T_{\rho }^{-}$. In the present paper we do not further discuss this problem, but refer to [20] for its treatment by the alternative concept of pseudo-granularity.

As a consequence, here we shall study the following version of the feasible rounding approach by shrink-optimize-round (FRA-SOR) [19, 20]: For a given problem MINLP compute enlargement parameters ρ = (σ,τ) ∈ R and corresponding Lipschitz constants of the functions g_i(x,y) − τ_i, i ∈ I, on D_σ in the sense of Assumption 1. Then compute an optimal point $(x^{s}_{\rho },y^{s}_{\rho })$ of f over $T^{-}_{\rho }$, that is, of the problem

$$ \begin{array}{@{}rcl@{}} P^{s}_{\rho}:\quad \min\limits_{(x,y)\in\mathbb{R}^{n}\times\mathbb{R}^{m}} f(x,y)\quad \text{ s.t. }~Ax+By+\|\upbeta\|_{1}/2&\le& b+\sigma,\\ g(x,y)+L^{\sigma}_{\infty}/2 &\le& \tau, \end{array} $$

and round it to $(\check x^{s}_{\rho },\check y^{s}_{\rho })\in M$.

Due to rounding effects as well as due to the necessary modifications on the transition from M to $T_{\rho }^{-}$, the generated point $(\check x^{s}_{\rho },\check y^{s}_{\rho })$ cannot be expected to be optimal for MINLP. Yet, in the next section we shall show that one can use the close relation of the sets $T_{\rho }^{-}$ and $\widehat M_{\rho }$ to derive an upper bound on the objective value of $(\check x^{s}_{\rho },\check y^{s}_{\rho })$ that merely depends on the problem data.

3 Bounds on the Objective Value

Since any point $(\check x^{s}_{\rho },\check y^{s}_{\rho })$ generated by FRA-SOR is feasible for MINLP, its objective value $\check v^{s}_{\rho }:=f(\check x^{s}_{\rho },\check y^{s}_{\rho })$ exceeds the optimal value v of MINLP. Unfortunately, simple examples illustrate that the gap between $\check v^{s}_{\rho }$ and v may actually be arbitrarily large [20]. The main aim of this section is to state an upper bound for the gap $\check v^{s}_{\rho }-v$ in terms of the problem data.

As v is unknown, we bound it in terms of the optimal value $\widehat v$ of the continuously relaxed problem $\widehat {MINLP}$ by

$$ 0 \le \check v^{s}_{\rho} - v \le \check v^{s}_{\rho}-\widehat v. $$

(5)

This bound may be computed explicitly. In fact, after the solution of $P^{s}_{\rho }$, in addition only the relaxed problem $\widehat {MINLP}$ has to be solved. Note that in this bound we propose to use the optimal value $\widehat v$ of f over $\widehat M$ without any enlargement constructions, rather than the optimal value of f over $\widehat M_{\rho }$, since this leads to a tighter bound.

While such an a-posteriori bound can be achieved at low computational cost under suitable assumptions, it is not useful for investigations with regard to the dependence of the achieved objective value on the problem data. Hence, next we shall derive an a-priori bound for $\check v^{s}_{\rho }-v$ which does not depend on the solution of some auxiliary optimization problem, but merely on the data of MINLP.

In particular, in Section 4 we will be interested in the behavior of $(\check v^{s}_{\rho }-v)/|v|$ for different degrees of integer grid fineness in MINLP, as this will not only confirm but also quantify the empirically observed fact from [19, 20] that finer grids lead to smaller relative deviations between $\check v^{s}_{\rho }$ and v.

For the derivation of the main results in this section let us temporarily ignore the possibility of enlargements by some ρ ∈ R, but consider the original problem corresponding to ρ = 0. For our analysis we will assume T⁻≠∅, since otherwise FRA-SOR does not provide a point $(\check x^{s},\check y^{s})$. Subsequently

$$ \text{dist}\big((\widehat x,\widehat y),T^{-}\big) := \inf_{(x,y)\in T^{-}}\|(x,y)-(\widehat x,\widehat y)\| $$

(6)

shall denote the distance of some point $(\widehat x,\widehat y) \in \mathbb {R}^{n}\times \mathbb {R}^{m}$ to the set T⁻ with respect to some norm ∥⋅∥ on $\mathbb {R}^{n}\times \mathbb {R}^{m}$. In addition to the uniform Lipschitz continuity of the functions g_i, i ∈ I, with respect to the $\ell _{\infty }$-norm from Assumption 1, in the following we will also need Lipschitz continuity of f with respect to the norm from (6).

Assumption 2

There exists some L^f ≥ 0 such that for all (x¹,y¹), (x²,y²) ∈ D we have

$$ |f(x^{1},y^{1})-f(x^{2},y^{2})| \le L^{f}\|(x^{1},y^{1})-(x^{2},y^{2})\|. $$

Furthermore, in the following $L^{f}_{\infty }\ge 0$ will denote a Lipschitz constant with respect to y uniformly in x for f on D with respect to the $\ell _{\infty }$-norm. Under Assumption 2 a possible, but not necessarily tight, choice is $L^{f}_{\infty }:=\kappa L^{f}$ with some norm constant κ > 0 such that for all $(x,y)\in \mathbb {R}^{n}\times \mathbb {R}^{m}$ we have $\|(x,y)\|\le \kappa \|(x,y)\|_{\infty }$. In particular, the existence of $L^{f}_{\infty }$ follows from Assumption 2. However, the following example indicates a better choice for linear objective functions.

Example 1

For a linear objective function $f(x,y)=c^{\intercal } x+d^{\intercal } y$ the best possible Lipschitz constant on $\mathbb {R}^{n}\times \mathbb {R}^{m}$, that is, the Lipschitz modulus

$$ \sup\limits_{(x^{1},y^{1})\neq(x^{2},y^{2})}\frac{|f(x^{1},y^{1})-f(x^{2},y^{2})|}{\|(x^{1},y^{1})-(x^{2},y^{2})\|}, $$

is easily seen to coincide with the dual norm of (c,d), so that we may set

$$ L^{f} := \|(c,d)\|^{\star} := \max\{c^{\intercal} x+d^{\intercal} y~|~\|(x,y)\|\le 1\}. $$

Moreover, we may choose

$$ L^{f}_{\infty} := \|d\|^{\star}_{\infty} = \|d\|_{1}. $$

Lemma 1

Let Assumptions 1 and 2 hold, let $(\widehat x^{\star },\widehat y^{\star })$ denote any optimal point of $\widehat {MINLP}$, and let $(\check x^{s},\check y^{s})$ denote any rounding of any optimal point (x^s,y^s) of P^s. Then the value $\check v^{s}=f(\check x^{s},\check y^{s})$ satisfies

$$ 0 \le \check v^{s}-v \le L^{f}_{\infty}/2+L^{f}\text{dist}\big((\widehat x^{\star},\widehat y^{\star}),T^{-}\big). $$

Proof

As above, the first inequality stems from the feasibility of $(\check x^{s},\check y^{s})$ for MINLP. For the proof of the second inequality note that, with any projection (x^π,y^π) of $(\widehat x^{\star },\widehat y^{\star })$ onto the set T⁻ with respect to ∥⋅∥, the upper bound $\check v^{s}-\widehat v$ of $\check v^{s}-v$ from (5) may be written as

$$ \check v^{s}-\widehat v = \left( f(\check x^{s},\check y^{s})-f(x^{s},y^{s})\right) +\left( f(x^{s},y^{s})-f(x^{\pi},y^{\pi})\right) + \left( f(x^{\pi},y^{\pi})-f(\widehat x^{\star},\widehat y^{\star})\right). $$

Due to $\check x^{s}=x^{s}$, the first term satisfies

$$ f(\check x^{s},\check y^{s})-f(x^{s},y^{s}) \le L^{f}_{\infty}\|(x^{s},\check y^{s})-(x^{s},y^{s})\|_{\infty} = L^{f}_{\infty}\|\check y^{s}-y^{s}\|_{\infty} \le L^{f}_{\infty}/2. $$

Since (x^s,y^s) is an optimal point of P^s, while (x^π,y^π) is a feasible point, for the second term we obtain

$$ f(x^{s},y^{s})-f(x^{\pi},y^{\pi}) \le 0. $$

Finally, as the distance is the optimal value of the corresponding projection problem, the third term can be bounded by

$$ f(x^{\pi},y^{\pi})-f(\widehat x^{\star},\widehat y^{\star}) \le L^{f}\|(x^{\pi},y^{\pi})-(\widehat x^{\star},\widehat y^{\star})\| = L^{f}\text{dist}\big((\widehat x^{\star},\widehat y^{\star}),T^{-}\big), $$

and the assertion is shown. □

It remains to bound the expression $\text {dist}((\widehat x^{\star },\widehat y^{\star }),T^{-})$ from the upper bound in Lemma 1 in terms of the problem data. To this end, we will employ a global error bound for the system of inequalities describing T⁻. For the statement of this global error bound we construct the penalty function

$$ \|(Ax+By-b+\|\upbeta\|_{1}/2)^{+},(g(x,y)+L_{\infty}/2)^{+}\|_{\infty} $$

of the set T⁻ where $a^{+}:=(\max \limits \{0,a_{1}\},\ldots ,\max \limits \{0,a_{N}\})^{\intercal }$ denotes the componentwise positive-part operator for vectors $a\in \mathbb {R}^{N}$. A global error bound relates the geometric distance to the (consistent) set T⁻ with the evaluation of its penalty function by stating the existence of a constant γ > 0 such that for all $(\widehat x,\widehat y)\in \mathbb {R}^{n}\times \mathbb {R}^{m}$ we have

$$ \text{dist}\big((\widehat x,\widehat y),T^{-}\big) \le \gamma\|(A\widehat x+B\widehat y-b+\|\upbeta\|_{1}/2)^{+},(g(\widehat x,\widehat y)+L_{\infty}/2)^{+}\|_{\infty}. $$

(7)

As Hoffman showed the existence of such a bound for any linear system of inequalities in his seminal work [9], γ is also called a Hoffman constant, and the error bound (7) is known as a Hoffman error bound. Short proofs of this result for the polyhedral case can be found in [7, 11]. For global error bounds of broader problem classes see, for example, [1, 6, 12,13,14,15,16,17,18, 24], and [2, 3, 22] for surveys. These references also contain sufficient conditions for the existence of global error bounds. To cite an early result for the nonlinear case from [24], if for convex functions g_i, i ∈ I, the set T⁻ is bounded and satisfies Slater’s condition, then a global error bound holds.

The next result simplifies the error bound (7) for points $(\widehat x,\widehat y)\in \widehat M$. It was used analogously in [26, Theorem 3.3] and follows from the subadditivity of the max operator, the monotonicity of the $\ell _{\infty }$-norm, as well as $(A\widehat x+B\widehat y-b)^{+}=0$ and $g^{+}(\widehat x,\widehat y)=0$ for any $(\widehat x,\widehat y)\in \widehat M$. Furthermore, we use that the appearing term $\|(\|\upbeta \|_{1})\|_{\infty }$ coincides with the maximal absolute row sum $\|B\|_{\infty }$ of the matrix B.

Lemma 2

Let Assumption 1 hold, and let the error bound (7) hold with some γ > 0. Then all $(\widehat x,\widehat y)\in \widehat M$ satisfy

$$ \text{dist}\big((\widehat x,\widehat y),T^{-}\big) \le \gamma \max\{\|B\|_{\infty},\|L_{\infty}\|_{\infty}\}/2. $$

The combination of Lemma 1 and Lemma 2 yields the main result of this section.

Theorem 3

Let Assumptions 1 and 2 hold, and let the error bound (7) hold with some γ > 0. Then the objective value $\check v^{s}$ of any rounding of any optimal point of P^s satisfies

$$ 0 \le \check v^{s}-v \le \left( L^{f}_{\infty}+L^{f}\gamma\max\{\|B\|_{\infty},\|L_{\infty}\|_{\infty}\}\right)/2. $$

Example 2

For a mixed-integer linear problem MILP the nonlinear function g is absent (i.e., q = 0), and f has the form from Example 1. Furthermore, from [9] it is known that for polyhedral constraints a global error bound always holds so that this assumption may be dropped from Theorem 3. In view of Example 1 this results in the a-priori bound

$$ 0 \le \check v^{s}-v \le \left( \|d\|_{1}+\|(c,d)\|^{\star}\gamma\|B\|_{\infty}\right)/2. $$

The result of Theorem 3 remains valid for any enlargement vector ρ ∈ R with minor modifications. In fact, if γ satisfies the error bound estimate

$$ \text{dist}\big((\widehat x,\widehat y),T^{-}_{\rho}\big) \le \gamma\|(A\widehat x+B\widehat y-b-\sigma+\|\upbeta\|_{1}/2)^{+},(g(\widehat x,\widehat y)-\tau+L_{\infty}/2)^{+}\|_{\infty} $$

instead of (7), then also the objective value $\check v^{s}_{\rho }$ of any rounding of any optimal point of $P^{s}_{\rho }$ satisfies the estimates from Theorem 3. We remark that for the proof of this result Lemma 1 needs to consider an optimal point $(\widehat x^{\star }_{\rho },\widehat y^{\star }_{\rho })$ of $\widehat {MINLP}_{\rho }$.

4 The Effect of the Integer Grid Fineness on the Objective Value

As mentioned before, we are particularly interested in a-priori bounds which explain the behavior of $(\check v^{s}_{\rho }-v)/|v|$ for different degrees of integer grid fineness in MINLP. To motivate our subsequent model for this effect, let us start by considering the purely integer linear problem

$$ ILP_{t}:\qquad\min\limits_{y\in\mathbb{Z}^{m}} d^{\intercal} y\quad\text{s.t.}\quad By\le b+t\bar b $$

with a parameter t > 0 and a fixed vector $\bar b>0$ which perturb the right-hand side vector b. Increasing values of t increase the number of feasible integer points and, in relation to the relaxed feasible sets $\widehat M(t)$, the grid becomes finer.

For increasing values of t we wish to analyze the quality of the feasible point generated by FRA-SOR for ILP_t, that is, the deviation of its objective value $\check {v}^{s}_{t}$ from v_t. However, since also |v_t| increases with t, instead of the absolute deviation we consider the behavior of the relative deviation $(\check {v}^{s}_{t}-v_{t})/|v_{t}|$.

To make such an analysis also applicable to nonlinear constraints, let us focus on the relative effect of the integer grid fineness on the objective value. This may be modeled by a parameter h > 0 which scales the variables (x,y) to (hx,hy) and leads to the parametric problem

$$ MINLP_{h}:\qquad \min\limits_{(x,y)\in\mathbb{R}^{n}\times\mathbb{Z}^{m}} f(hx,hy) \quad\text{s.t.}\quad g(hx,hy) \le 0,\quad (hx,hy) \in D $$

with optimal value v_h. The above effect for increasing t is now translated to decreasing h > 0 and, due to $hy\in h\mathbb {Z}^{m}$, for h ↘ 0 the grid $h\mathbb {Z}^{m}$ indeed becomes finer. A similar construction is mentioned in [25], but there it is neither used explicitly, nor does [25] provide bounds on the objective values of feasible points.

To apply the results on a-priori bounds from Section 3 to MINLP_h, for simplicity let us again ignore enlargement constructions, and let us define the functions f^h(x,y) := f(hx,hy) and g^h(x,y) := g(hx,hy) as well as the matrices A^h := hA and B^h := hB. We may then rewrite MINLP_h as

$$ \min\limits_{(x,y)\in\mathbb{R}^{n}\times\mathbb{Z}^{m}} f^{h}(x,y) \quad\text{s.t.}\quad A^{h}x+B^{h}y\le b,\quad g^{h}(x,y) \le 0, $$

and the application of FRA-SOR consists in rounding an optimal point $(\widehat {x}^{s}_{h},\widehat {y}^{s}_{h})$ of

$$ {P^{s}_{h}}: \min_{(x,y)\in\mathbb{R}^{n}\times\mathbb{R}^{m}} f^{h}(x,y)\quad\text{s.t.}\quad A^{h}x+B^{h}y+\|{\upbeta}^{h}\|_{1}/2\le b,\quad g^{h}(x,y)+L^{h}_{\infty}/2 \le 0, $$

to $(\check {x}^{s}_{h},\check {y}^{s}_{h})$ with objective value $\check {v}^{s}_{h}:=f^{h}(\check {x}^{s}_{h},\check {y}^{s}_{h})$. Here, the vector ∥β^h∥₁ coincides with h∥β∥₁, and for each i ∈ I the i-th entry of the vector $L^{h}_{\infty }$ denotes the Lipschitz constant of ${g^{h}_{i}}$ on $\mathbb {R}^{n}\times \mathbb {R}^{m}$ with respect to y and uniformly in x. It is easily seen to coincide with $hL^{i}_{\infty }$, if the functions g_i, i ∈ I, satisfy Assumption 1 with Lipschitz constants $L^{i}_{\infty }$, i ∈ I.

In this notation, the above mentioned empirical observation from [19, 20] is that the relative bound $(\check {v}^{s}_{h}-v_{h})/|v_{h} |$ seems to tend to zero for h ↘ 0. In the remainder of this section we shall prove this conjecture and quantify the corresponding rate of decrease.

In the subsequent result we will use that the optimal value $\widehat v$ of the continuously relaxed problem $\widehat {MINLP}_{h}$ does not depend on h, since in the relaxed problem the substitution of (hx,hy) by (x,y) is just a (scaling) transformation of coordinates. We will also assume $\widehat v>0$, which may always be attained by adding a suitable constant to the objective function f.

Furthermore, we shall use the set

$$ \widetilde T^{-}_{h}:=\{(x,y)\in\mathbb{R}^{n}\times\mathbb{R}^{m}~|~ Ax+By+h\|\upbeta\|_{1}/2\le b,~g(x,y)+hL_{\infty}/2\le0\} $$

and assume that it satisfies the error bound

$$ \text{dist}\big((\widehat x,\widehat y),\widetilde T^{-}_{h}\big) \le \gamma_{h}\|(A\widehat x+B\widehat y-b+h\|\upbeta\|_{1}/2)^{+},(g(\widehat x,\widehat y)+hL_{\infty}/2)^{+}\|_{\infty} $$

(8)

for all $(\widehat x,\widehat y)\in \mathbb {R}^{n}\times \mathbb {R}^{m}$ with the Hoffman constant γ_h > 0.

Lemma 3

Let $\widehat v>0$, let f and g satisfy Assumptions 2 and 1, respectively, for h > 0 let $\widetilde T^{-}_{h}$ be nonempty, and let the error bound (8) hold with some γ_h > 0. Then the objective value $\check {v}^{s}_{h}$ of any rounding of any optimal point of ${P^{s}_{h}}$ satisfies

$$ 0 \le \frac{\check{v}^{s}_{h}-v_{h}}{v_{h}} \le h\frac{L^{f}_{\infty}+L^{f}\gamma_{h} \max\{\|B\|_{\infty},\|L_{\infty}\|_{\infty}\}}{2\widehat v}. $$

(9)

Proof

Since the denominator v_h is bounded below by the optimal value $\widehat v>0$ of the continuous relaxation, we obtain

$$ 0 \le \frac{\check{v}^{s}_{h}-v_{h}}{v_{h}} \le \frac{\check{v}^{s}_{h}-v_{h}}{\widehat v}. $$

Moreover, the numerator $\check {v}^{s}_{h}-v_{h}$ may be bounded above by applying Theorem 3 to the problem MINLP_h. In fact, it is easy to see that Assumption 2 for f with the Lipschitz constant L^f implies that f^h satisfies Assumption 2 with the Lipschitz constant hL^f. Analogously, $hL^{f}_{\infty }$ and $hL^{i}_{\infty }$ are Lipschitz constants with respect to y uniformly in x for f^h and ${g_{i}^{h}}$, i ∈ I, respectively, with respect to the $\ell _{\infty }$-norm.

Since a point (x,y) lies in

$$ \begin{array}{@{}rcl@{}} T^{-}_{h}&:=&\{(x,y)\in\mathbb{R}^{n}\times\mathbb{R}^{m}~|~ A^{h}x+B^{h}y+h\|\upbeta\|_{1}/2\le b,~g^{h}(x,y)+hL_{\infty}/2\le0\}\\ &=&\{(x,y)\in\mathbb{R}^{n}\times\mathbb{R}^{m}~|~ A(hx)+B(hy)+h\|\upbeta\|_{1}/2\le b,~g(hx,hy)+hL_{\infty}/2\le0\} \end{array} $$

if and only if (ξ,η) := (hx,hy) lies in $\widetilde T^{-}_{h}$, the assumption $\widetilde T^{-}_{h}\neq \emptyset$ implies that also $T^{-}_{h}$ is nonempty. Furthermore, as an error bound for the set $T^{-}_{h}$ we obtain for all $(\widehat x,\widehat y)\in \mathbb {R}^{n}\times \mathbb {R}^{m}$

$$ \begin{array}{@{}rcl@{}} \text{dist}\left( (\widehat x,\widehat y),T^{-}_{h}\right)&=&\inf_{(x,y)\in T^{-}_{h}}\|(x,y)-(\widehat x,\widehat y)\|=\inf_{(hx,hy)\in \widetilde T^{-}_{h}}\|(x,y)-(\widehat x,\widehat y)\|\\ &=&\inf_{(\xi,\eta)\in \widetilde T^{-}_{h}}\|(\xi,\eta)/h-(\widehat x,\widehat y)\|=\inf_{(\xi,\eta)\in \widetilde T^{-}_{h}}\left\|(\xi,\eta)-(h\widehat x,h\widehat y)\right\|/h\\ &=&\text{dist}\left( (h\widehat x,h\widehat y),\widetilde T^{-}_{h}\right)/h\\ &\le&\gamma_{h}\|(A(h\widehat x)+B(h\widehat y)-b+h\|\upbeta\|_{1}/2)^{+},(g(h\widehat x,h\widehat y)+hL_{\infty}/2)^{+}\|_{\infty}/h\\ &=&\gamma_{h}\|(A^{h}\widehat x+B^{h}\widehat y-b+h\|\upbeta\|_{1}/2)^{+},(g^{h}(\widehat x,\widehat y)+hL_{\infty}/2)^{+}\|_{\infty}/h, \end{array} $$

that is, γ_h/h serves as a Hoffman constant for the system of inequalities describing $T^{-}_{h}$. Theorem 3 thus yields

$$ \begin{array}{@{}rcl@{}} \check{v}^{s}_{h}-v_{h}&\le& \left( (hL^{f}_{\infty})+(hL^{f})(\gamma_{h}/h) \max\{h\|B\|_{\infty},\|(hL_{\infty})\|_{\infty}\}\right)/2\\ &=&h\left( (L^{f}_{\infty})+L^{f}\gamma_{h} \max\{\|B\|_{\infty},\|L_{\infty}\|_{\infty}\}\right)/2. \end{array} $$

The combination of the estimates for the numerator and the denominator now yields the assertion. □

Theorem 4

Let $\widehat v>0$, let f and g satisfy Assumptions 2 and 1, respectively, let the functions g_i, i ∈ I, be convex on $\mathbb {R}^{n}\times \mathbb {R}^{m}$, and let the set $\widehat M=\{(x,y)\in \mathbb {R}^{n}\times \mathbb {R}^{m}~|~Ax+By\le b,~g(x,y)\le 0\}$ be bounded and satisfy Slater’s condition. Then for all sufficiently small h > 0 the set $T^{-}_{h}$ is nonempty, the error bound (8) holds with some γ_h > 0, the relative bound $(\check {v}^{s}_{h}-v_{h})/v_{h}$ satisfies the relations (9), and it tends to zero at least linearly with h ↘ 0.

Proof

By Slater’s condition for the set $\widehat M$ there is a point $(\bar x,\bar y)$ with $A\bar x+B\bar y<b$ and $g(\bar x,\bar y)<0$. Then for all sufficiently small h > 0 the point $(\bar x,\bar y)$ is also a Slater point of $\widetilde T^{-}_{h}$. Firstly, this implies that also $T^{-}_{h}$ is nonempty for these h. Secondly, since $\widetilde T^{-}_{h}$ is bounded as a subset of the bounded set $\widehat M$, by [24] the error bound (8) holds with some γ_h > 0. The relations (9) thus follow from Lemma 3. Finally, the linear decrease of the relative bounds with h ↘ 0 is due to the fact that the Hoffman constants γ_h remain bounded for all sufficiently small h > 0. This is shown in [21] for convex problems under mild assumptions and may be applied to the present setting along the lines of the proof of [26, Corollary 3.6]. □

We point out that the assumptions of Theorem 4 may be significantly relaxed in the MILP case from Example 2. Then not only Assumptions 2 and 1 hold with L^f = ∥(c,d)∥^⋆ and $L_{\infty }=\|\upbeta \|_{1}$ as well as $L^{f}_{\infty }=\|d\|_{1}$, but from [9] it is also known that for polyhedral constraints the error bound (8) is satisfied without further assumptions, and that the corresponding Hoffman constant γ may even be chosen independently of the right-hand side vector and, thus, in our case independently of h. Altogether, this shows the following result.

Corollary 1

For an MILP let $\widehat v>0$, and let the set $\widehat M=\{(x,y)\in \mathbb {R}^{n}\times \mathbb {R}^{m}~|~Ax+By\le b\}$ satisfy Slater’s condition. Then for all sufficiently small h > 0 the set $T^{-}_{h}$ is nonempty, the error bound (8) holds with some γ > 0, the relative bound $(\check {v}^{s}_{h}-v_{h})/v_{h}$ satisfies the relations

$$ 0 \le \frac{\check{v}^{s}_{h}-v_{h}}{v_{h}} \le h\frac{\|d\|_{1}+\|(c,d)\|^{\star}\gamma \|B\|_{\infty}}{2\widehat v} $$

and, thus, it tends to zero at least linearly with h ↘ 0.

5 An Application to Bounded Knapsack Problems

The following computational study comprises results for the bounded knapsack problem which was introduced in [5] and is known to be an NP-hard MILP (cf. [10, pp. 483–491]). In its original formulation, which is also called the 0-1 knapsack problem, all decision variables are binary. The bounded knapsack problem (BKP) is a generalization of the 0-1 knapsack problem where it is possible to pick more than one piece per item, that is, the integer decision variables may not be binary. A possible numerical approach to bounded knapsack problems is to transform them into equivalent 0-1 knapsack problems for which solution techniques exist that perform very well in practical applications. In contrast to this approach we exploit granularity of the BKP and obtain very good feasible points by applying FRA-SOR to test instances of the bounded knapsack problem.

In the bounded knapsack problem we have $m\in \mathbb {N}$ item types and denote the value and weight of item j ∈{1,…,m} by v_j and w_j, respectively. Further, there are at most $b_{j}\in \mathbb {N}$ units of item j available and the capacity of the knapsack is given by c > 0. By maximizing the total value of all items in the knapsack we arrive at the purely integer optimization problem

$$ BKP:\qquad\max_{y\in\mathbb{Z}^{m}} v^{\intercal} y\quad\text{s.t.}\quad w^{\intercal} y\le c,~0\le y\le b. $$

In order to obtain hard test examples of the BKP we create so-called strongly correlated instances (cf. [23] for an analogous treatment in the context of 0-1 knapsack problems), that is, the weights w_j are uniformly distributed in the interval [1,10000] and we have v_j = w_j + 1000. Furthermore, b_j, j ∈{1,…,m}, is uniformly distributed within the set {0,…,U} for an integer upper bound $U\in \mathbb {N}$ and, in order to avoid trivial solutions, we set $c=\delta w^{\intercal } b$ for some δ ∈ (0,1).

Note that the integer grid fineness of the BKP is controlled by the randomly chosen data b and w as well as δ ∈ (0,1). The expected value of b is (U/2)e, where e denotes the all ones vector. At least for a fixed vector of weights w the expected value of c then is $\delta (U/2)w^{\intercal } e$. For the expected test instances the parameter U thus plays the role of the parameter t from the problem ILP_t in Section 4 and controls the grid fineness.

According to (2) the inner parallel set of $D=\{y\in \mathbb {R}^{m}~|~w^{\intercal } y\le c,~0\le y\le b\}$ is

$$ T^{-}=D^{-}=\{y\in\mathbb{R}^{m}~|~w^{\intercal} y\le c-\tfrac12\|w\|_{1},~-y\le-\tfrac12 e,~y\le b-\tfrac12 e\}. $$

Using the enlargement technique from Section 2.3 with $\sigma =(0,\frac 12 e,\frac 12 e)$ yields the enlarged inner parallel set

$$ T^{-}_{\sigma} := \{y\in\mathbb{R}^{m}~|~ w^{\intercal} y\le c-\tfrac12\|w\|_{1},~ 0\le y\le b\}. $$

We see that $T^{-}_{\sigma }$ is nonempty if and only if $c-\frac {1}{2}\|w\|_{1}\ge 0$ holds. For our specific choice of c the latter is equivalent to

$$ w^{\intercal}(\delta b-\tfrac12 e) \ge 0. $$

In particular, $T^{-}_{\sigma }$ may be empty for small values of δ and b_j, j ∈{1,…,m}. In the remainder of this section we set δ = 1/3 and use different values of U ≥ 5. Then the expected values of the terms δb_j − 1/2, j = 1,…,m, exceed 1/3, so that the enlarged inner parallel sets may be expected to be nonempty.

In fact, the enlarged inner parallel set $T^{-}_{\sigma }$ turns out to be nonempty in all created test instances, so that all test problems are granular in the sense of Definition 1. In particular, no further enlargement of the inner parallel set is necessary.

FRA-SOR is implemented in MATLAB R2016b and the arising optimization problem is solved with Gurobi 7 [8], which we also use for a comparison. All tests are run on a personal computer with two cores à 2.3 GHz and 8 GB RAM.

In Table 1 we consider the relative optimality gap $(\widehat {v}-\check {v}^{s}_{\sigma })/\widehat {v}$ of FRA-SOR applied to different instances of the BKP. The results seem to indicate that the optimality gap is independent of the problem size m. However, we see a strong dependency of the optimality gap on the upper bound U. This is caused by the fact that U controls the expected grid fineness, which plays a crucial role in the error bound obtained for FRA-SOR.

Table 1 Relative optimality gap of FRA-SOR for different choices of U and m

Note that the error bound given in Example 2 actually bounds the absolute optimality gap, and that this bound decreases linearly with finer grids. Thus, for the current setting this result predicts a hyperbolic decrease of the relative optimality gap with increasing values of U. This is confirmed by Fig. 1.

Fig. 1

Relative optimality gap for m = 1000 and different choices of U

As mentioned above, solving the BKP to optimality is an NP-hard optimization problem. Instead, for nonempty enlarged inner parallel sets the main effort of our feasible rounding approach consists of solving a continuous linear optimization problem which can be done in polynomial time. This fact is demonstrated in Table 2 and Fig. 2 where we see that especially for the larger test instances FRA-SOR is able to find very good feasible points in reasonable time. Their relative optimality gaps (cf. Table 1) are of order 10^− 3, that is, the additional time that Gurobi needs to identify a global optimal point only yields a marginal benefit.

Table 2 Computing time in seconds for FRA-SOR (left) and Gurobi (right) for different choices of U and m

Fig. 2

Computing time in seconds for an optimal point by Gurobi and a feasible point by FRA-SOR for U = 1000 and different choices of m

6 Conclusions

This article assesses the quality of a point generated by a feasible rounding approach for mixed-integer nonlinear optimization problems. To this end, its optimality gap is estimated by a-posteriori as well as a-priori bounds, and the latter are shown to decrease at least linearly with increasing integer grid fineness.

The bounded knapsack problem illustrates our findings computationally. Detailed numerical results for the application of the feasible rounding approach to problems from the MIPLIB and MINLPLib libraries, which motivated the current research, are reported in [19, 20].