1 Introduction and motivation

Gearboxes and rotating components are widespread in various applications all over the world. By discussing the effect of the sensor position and the impact of the vibration transfer from the gear contact across the shaft and the bearing, the sensor position’s importance will be evaluated. Therefore, measurements at the gear and on the housing have been performed in parallel. Typically, acceleration sensors are positioned on the housing close to the bearing. With this position, an often-used system has been established in the last decades for the structural health monitoring of rotating machinery [1,2,3,4]. The sensor is located in a comparingly easy accessible position. It does not take complex cabling out of the gearbox from the rotating shaft, passing sealing, and getting into contact with splashing oil, as presented by the modification of a gear test rig in previous work [5]. Additionally, expensive slip rings are not necessary.

However, at this measurement setup, a high signal-to-noise ratio is required for the reliable detection of frequencies of interest when investigating the rotation-related frequencies reliable because of the damping by the bearing with its time-varying stiffness. Bearing frequencies must be considered when monitoring shaft imbalances or the loaded tooth contact of gears. This problem gets even worse when damage occurs. Damage can have a particular frequency based on the pass-by-frequency of the fault location in the loaded contact. But, also, a change of frequencies is possible because of the time-varying stiffness between fault and sensor. Then, the location detection of the damage is complex. In addition, the bearing frequencies can in theory mask damage on the rotating components because of the higher signal amplitude caused by the shorter transfer path to the sensor. The vibration transmission behavior also varies due to time-varying stiffness and direction-dependent vibration transmission behavior [6]. Practical applications show that condition monitoring based on monitoring at the gearbox housing is nevertheless working.

Consequently, this work aims to evaluate the influence of the sensor position on monitoring rotating machinery. In this case, a gear test rig is considered, where similar specified sensors are applied on the gear and the housing close to the bearing. New technologies like wireless data transfer and energy can lead to widespread monitoring of rotating machinery with the placement of the sensor on the rotating part of the machinery. Thus, the costs and effort to take for integration can be lowered by the current innovation in technology and offering new possibilities of sensor placement for research and industrial applications.

Chapter 2 gives an overview of the hardware for the measurement, while Chap. 3 presents and discusses the experimental data. In Chap. 4, the conclusion and outlook on future progress are explained.

2 Measurement setup

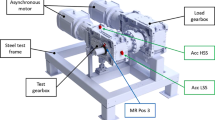
An FZG back-to-back gear test rig has been modified for the experimental test setup. The modification progress is described in previous work [5]. The test rig offers sensing positions on the housing already presented by Sendlbeck [1]. The sensor positions on the housing are displayed in Fig. 1.

Fig. 1
figure 1

Positions of the sensors on the housing. (Left: gear wheel shaft, right gear pinion shaft)

Full size image

To achieve sufficient results of the acceleration measurement at this position, an analysis of the housing structure with ANSYS Workbench has been performed to check the location of the sensors on the housing. Figures 2 and 3 show the results based on the input of bearing forces caused by the loads applied on the test rig. It can be seen that high acceleration at the excitation of the gear mesh frequency (GMF) appears at the locations close to the bearing. Due to the helical gears, different vibration levels occur at the four positions of the bearing. Furthermore, forces and vibrations in axial directions need to be taken into account [7].

Fig. 2
figure 2

Simulated absolute vibration level in all three axes of the gearbox housing at the front side of the gearbox housing at the gear mesh frequency excitation at the speed of 500 rpm [7]

Full size image
Fig. 3
figure 3

Simulated absolute vibration level in all three axes of the gearbox housing at the back side of the gearbox housing at the gear mesh frequency excitation at the speed of 500 rpm [7]

Full size image

The measurement position on the shaft by the sensor ring has been presented by Goetz [8, 9] and the design has been modified to fit the different test rig dimensions. This system is shown in Fig. 4. Here, vibration sensors at the pinion gear of type BK4518 [8] and BK4519 [9] from Brüel&Kjaer are selected. With these sensors and the assembly, measurement in circumferential and radial direction is possible due to the different positioning. The two sensors that are measuring in the same absolute direction are highlighted in Fig. 4. Note that there is an axial gap between the gears because of the axial displacement caused by the application of 500 Nm and the missing second bearing at the front of the housing in order to take the Picture of the assembled sensor ring.

Fig. 4
figure 4

Sensors in assembled state at the sensor ring which is screwed axially to the pinion gear

Full size image

For a good comparison of the results of all sensors, identical sensors with the same sensitivity are equipped. The sensitivity is 10 mV/g, and the maximal acceleration is up to ±500g [8, 9]. To be able to compare all signals, a National Instruments PXI-8110 DAQ-System [10] with Brüel&Kjaer Condition Amplifier of Type 2693 [11] and National Instruments BNC-2090A connector [12] have been used, acquiring all sensor data with a selected sampling rate of 100 kHz continuously. The analogous signals are transferred from the rotating sensors with a slip ring. Shielded coaxial cables are used on the complete signal line to avoid signal disturbance from external effects.

3 Experimental results

In this chapter, the experimental results are presented. It should be noted that the test rig is operated with tapered roller bearings of type FAG 32310‑A [13] to mount the shaft with helical gears. The axial preload is set to 10 µm for proper operation to manage temperature-based deflections. The gears are connected to the shaft with a conical interference fit, resulting in a high stiffness between gear and shaft. This allows that the influence of the bearing stiffness on the vibration transmission can be adequately evaluated.

The following selected results are used to display the effect of the sensor position on the measurement. The load on the test setup has been 500 Nm to achieve a sufficient signal-to-noise ratio of the gear meshing. Rotational speeds from 100 to 1200 rpm with an increment of 100 rpm at the pinion shaft are tested. Between each step, the rotational speed of the pinion gear shaft was increased slowly. Ten seconds after reaching each target speed the measurement was started to achieve a stationary state at the measurement with constant speed. At every speed, a measurement of 45 s was made to compensate for the small speed variation caused by the motor of the test rig.

3.1 Measurement results in the time domain

In Fig. 5 the signal from the sensor measuring on the gear in the radial direction is displayed in blue. In Fig. 6 the sensor signal on the housing close to the bearing of the shaft, is shown in orange, at 200 rpm rotation speed of the pinion shaft. The sensors on the housing also measure in the radial direction. The figures showing the raw signal which can be translated by the datasheet of the sensors: 10 mV ~ 1g [8, 9].

Fig. 5
figure 5

Signal of the on the rotating gear measuring in the radial direction in the time domain at 200 rpm

Full size image
Fig. 6
figure 6

Signal of the on the housing measuring in the radial direction in the time domain at 200 rpm

Full size image

There is less difference between the signals because of low excitation at low speeds. A more significant difference appears at higher speeds because of higher excitation of the rotating parts, as displayed in Fig. 7 below, when higher speed is applied.

Fig. 7
figure 7

Comparison of signals in the time domain at 1200 rpm

Full size image

The mean signal level over the whole measurement time of 45 s between the sensors for each speed has been compared to evaluate this effect. In Fig. 8, this difference is presented for the different speed levels. Therefore, the mean absolute value of the sensors on the sensor ring (average of both sensors) is compared to the mean total value of the sensor located close to the pinion shaft of the housing. Below the calculation of the y‑axis value Fig. 8 for each speed level described. Each data point in the time domain of acceleration corresponds to a dedicated acceleration at a certain time. So, here the mean vibration level at different positions at the gearbox is been investigated.

  1. 1.

    Calculation of the mean value of each sensors x acceleration vector y with \(45*10^{5}\) datapoints in the time domain (TMV)

$$\text{TMV}\left(x\right)=\frac{\sum \left(\textit{absolute}\,\textit{values}\left(y\left(x\right)\right)\right)}{\textit{number of datapoints}}$$
  1. 2.

    Averaging the TMVs of sensor 1 (S1) and sensor 2 (S2) at the sensor ring (SR)

$$\text{TMV}\left(SR\right)=\frac{\text{TMV}\left(S1\right)+\text{TMV}\left(S2\right)}{2}$$
  1. 3.

    Calculating the y‑axis value of Fig. 8 by the comparison of the TMVs at different measurement positions: sensors at sensor ring (SR) vs. housing sensor (HS)

$$yP8=\left[\frac{\text{TMV}\left(SR\right)}{\text{TMV}\left(HS\right)}-1\right]*100{\%}$$
Fig. 8
figure 8

Difference of mean absolute value over 45 s sampling time in the domain between signal on the gear and signal on the housing at different measurement positions on different speed levels

Full size image

Figure 8 shows that the difference is two times higher at 100 rpm and seven times higher at 1000 rpm. In consequence, rotating sensors can better capture the higher vibration level at rising speeds in the time domain.

3.2 Measurement results of the sensors in the frequency domain

Besides evaluations on the time domain, the frequency domain has also been considered. The results are showing that single frequencies can be easily detected on the signals of the rotating sensor by selecting filters compared to the signal on the housing, because of the higher signal level in the frequency domain. This can be achieved by applying a high-pass filter. When the signal of the frequencies of interest is higher, a more robust selection of the filter properties under changing conditions like varying speed, load or other factors is possible. At the rotating sensor the frequencies of the higher harmonics of the fundamental frequencies are measurable, while the signal-to-noise of these frequencies at the sensor signal of the housing sensor is worse cause only frequencies with highest acceleration level can be detected.

3.3 Comparison of the resolution of the peak frequency

To show this effect and the effect on the different speed levels, the average value of the peak frequency of both sensors on the sensor ring is compared to the value of the peak frequency of the sensor on the housing at the pinion shaft in Fig. 9. It has to be noted that the frequency of the peak value at the different sensors was in all cases similar and there was no frequency drift between the different sensor positions. Below the calculation of the ratio between the peak values of the fast fourier transformed signal is explained.

  1. 1.

    Fast fourier transform of each sensors x data vector y in the frequency domain (FV)

$$FV\left(x\right)=fft(y\left(x\right))$$
  1. 2.

    Identifying the peak value in sensors x spectrum FV (PV)

$$PV\left(x\right)=peak(\textit{absolute}\,\textit{value}\left(FV\left(x\right)\right))$$
  1. 3.

    Averaging the peak values PV(S1) and PV(S2) at the sensor ring (SR)

$$PV\left(SR\right)=\frac{PV\left(S1\right)+\left(PVS2\right)}{2}$$
  1. 4.

    Calculation of the y‑axis value of Fig. 9 by the comparison of the peak values PV (x) of sensors at sensor ring and housing sensor

$$yP9=\frac{PV\left(SR\right)}{PV\left(HS\right)}$$
Fig. 9
figure 9

Relative value between different measurement positions on the signal level of the peak frequency in the frequency domain at different speeds

Full size image

It can be seen that, especially at low speeds, there is a higher difference between the peak value in the frequency domain between the signal of the rotating sensors at the gear and the housing. So, the comparingly low excitation can be better detected by the rotating acceleration sensors. This effect can also be seen in the trend when comparing the peak value to the average value in the frequency domain for different sensors. The mean value over all speeds is 88.83. Figure 10 displays the difference between the peak and average values in the frequency domain for the rotating sensor measuring in the circumferential direction. Figure 11 shows the difference between the peak and average values in the frequency domain for the rotating sensor measuring in the radial direction. It can be seen that the value especially at low speeds below 500 rpm is higher. Figure 12 displays the difference between the peak and average values in the frequency domain for the housing sensor measuring in radial direction. The absolute value of the peak frequency is significantly higher in the frequency domain when applying comparable sensors on the housing and at the gear. Figure 13 shows then that at higher speeds the value of the peak frequency is rising compared to the average value in the frequency domain because of higher excitation level which can be better transferred to the sensor on the housing. But even at high loads, the relative value between peak and average is much higher at the rotating sensors then at the housing sensor. At 900 rpm, the mean value of the rotating sensors is still more than five times higher. This indicates again, that a measurement at low excitation levels is better suited with rotating sensors close to the source of excitation. So, a sensing on the gear enables sufficient results for low and higher speed levels compared to sensors placed onto housing which need a certain excitation in order to fulfill proper resolution on the frequencies of interest. Below the calculation of each y‑axis value is explained:

  1. 1.

    Fast fourier transform of each sensors x data vector y in the frequency domain (FV)

$$FV\left(x\right)=fft(y\left(x\right))$$
  1. 2.

    Identifying the peak value in sensors x spectrum FV (PV)

$$PV\left(x\right)=peak(\textit{absolute}\,\textit{value}\left(FV\left(x\right)\right))$$
  1. 3.

    Identifying the mean value in sensors x spectrum FV (PV)

$$MV\left(x\right)=\frac{\sum \textit{absolute}\,\textit{values}\left(FV\left(x\right)\right)}{\textit{number of datapoints}}$$
  1. 4.

    Calculation of the y‑axis value of Fig. 9 by the comparison of the peak values PV (x) of each sensor x and its mean value MV (x)

$$yP101112=\frac{PV\left(x\right)}{MV\left(x\right)}$$
Fig. 10
figure 10

Difference between the peak value and average value in the frequency domain for the rotating sensor measuring in the circumferential direction. (Speed on the x‑axis)

Full size image
Fig. 11
figure 11

Difference between the peak value and average value in the frequency domain for the rotating sensor measuring in the radial direction. (Speed on the x‑axis)

Full size image
Fig. 12
figure 12

Difference between the peak value and average value in the frequency domain for the housing sensor measuring in the radial direction. (Speed on the x‑axis)

Full size image
Fig. 13
figure 13

SIZA Prototype with inserted microelectronics before fitting and sealing with silicone and glue

Full size image

3.4 Conclusions on sensorintegration on the rotating element

The results of this experiment indicate that the resolution between the signal level of the peak of vibration frequencies compared to the mean values is better when sensing the rotating element. This effect will be used in the sensor-integrating gear wheel (german: “sensorintegrierendes Zahnrad” SIZA). The prototype is depicted below.

The SIZA used as described in previous work [5] has the similar setup as the sensor ring but with different accelerometers of type ADXL 1005 [14]. The integration of the accelerometer is shown in Fig. 14.

Fig. 14
figure 14

Insert of customized accelerometer board with ADXL1005 accelerometer

Full size image

Future investigations will show lower-graded sensors inside the gear using capacitive sensing compared to the setup with high-resolution piezoelectric sensors. Because of the measurement position, cheaper, lower-graded sensors are possible. Further progress will show the tradeoff between integration with cheaper electronics compared to high-resolution electronics, which are placed at a distance from the source of excitation.

4 Conclusion and outlook

Based on specific parameters, this paper shows a first overview of the effect of different sensor positions in and on the gearbox. In all scenarios at different speeds, the results show a significantly higher signal amplitude at the measurement of the rotation element. This effect increases at low speed when the excitation level is low. With these sensors, a better resolution of frequencies with lower amplitude, like higher harmonics, is possible. In the future, gears with damages will be tested where other damage-related frequencies appear, and the effect of the measurement position will be investigated. Additionally, major influences like bearing preload, torque, and rotational speed will be examined to show the influence of the transfer path in more detail. Here, measurement in the axial direction can also be planned to investigate this vibration transfer.

Based on the results it can be stated that an integration of sensors at or in the gear helps to analyze lower excitation levels than with often used measurement positions at the housing. For a detailed analysis of the vibration transfer besides the bearings, tolerances and the test rig’s assembly have to be considered for more information on the vibration transfer. Based on the data investigations on the frequency- and direction-depending damping of the bearing can be achieved as is already stated in bearing-specific sources.