1 Introduction

In wet-running multi-plate clutches (short: wet clutches), load-independent drag losses occur in the disengaged state and under differential speed due to fluid shearing. In particular, if several clutches in a drivetrain are disengaged at the same time, their drag losses can represent a considerable percentage of the total loss [1]. Results of various investigations show that the drag losses of wet clutches can be reduced by an optimized clutch design and optimized operating conditions [2,3,4,5,6]. Consequently, determining the drag torque in the early development phase is of high importance. Currently, the drag torque can be determined accurately and reliably by means of costly and time-consuming measurements on a suitable test rig. Alternatively, drag losses can be precisely calculated with computing-intensive CFD (computational fluid dynamics) models, while analytical calculation models allow only a rough, but non-time-consuming estimation.

1.1 Drag loss behavior

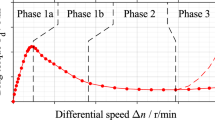
The drag loss behavior of wet clutches has been frequently investigated in prior studies from the 1970s [7, 8] until today [4, 9]. Usually, the authors describe the drag loss behavior by the change of the drag torque with respect to the differential speed (see Fig. 1). The curve can be divided into three characteristic phases ([10]; see Fig. 1). For a more detailed specification, individual phases are often further subdivided ([3, 4, 11, 12]; see Fig. 1). Further characteristics are the power loss and the dissipated energy with respect to the differential speed [6, 13].

Fig. 1
figure 1

Characteristic drag torque curve and its classification, based on [4, 10]

Full size image

In these experimental and theoretical studies, various parameters influencing the drag torque were identified. The main influencing parameters are the plate size, number of gaps, oil viscosity, feeding flow rate in the case of injection lubrication, oil level in the case of dip lubrication, clearance, groove pattern, differential speed, and operating mode [4,5,6, 13,14,15,16,17,18,19,20]. However, the design of the carriers also has a crucial influence on the drag losses [13]. Further, the distribution of the total clearance and the material properties of the friction lining affect the drag loss behavior [12, 21]. The characteristic drag torque curve is comparable for injection lubrication and dip lubrication, although the effects acting in the gaps are different [4, 22]. At a low differential speed, the drag torque increases approximately linearly until a maximum is reached (Phase 1a, see Fig. 1). In the case of the widely used injection lubrication, the gap is completely filled with oil in this phase, resulting in a single-phase flow. As the differential speed increases, the conveying effect of the clutch also increases. As the conveyable flow rate exceeds the feeding flow rate, air is sucked into the gap and a two-phase flow is formed. The reduced oil-wetted surface and the lower viscosity of the oil-air mixture cause the drag torque to continuously decrease (Phase 1b, see Fig. 1) until a quasi-steady drag torque is reached (Phase 2, see Fig. 1). At very high speed, a re-increase of the drag torque (Phase 3, see Fig. 1) may occur as a result of plate tumbling or plate movement [13, 23,24,25,26].

1.2 Calculation methods

Methods for calculating the drag torque of wet clutches are the current state of research. Basically, existing models are either based on analytical or numerical calculation methods. The numerical CFD simulation represents a modern tool to calculate the drag torque and has therefore been used in various research studies [9, 11, 20, 27,28,29,30,31,32,33]. CFD simulations can be performed in the early development phase, do not require prototype parts or even series parts, and enable targeted optimization of the clutch design and the operating parameters. The CFD simulation provides the consideration of the real groove geometry and a high level of detail in modeling the fluid behavior [2, 27]. Also, the design of the carriers can be considered [11, 34]. Thus, the CFD simulation enables modeling of the entire clutch system. Consequently, a very high depth of the model can be realized, which in turn commonly results in a high accuracy of the calculations [11, 27]. A decisive step in model development is the final validation of the simulation model by means of complex experiments. A high correspondence of simulation and measurement can be achieved with a high-resolution 3D CFD model [27]. To model the heterogenous phase distribution in the two-phase flow, the Volume of Fluid (VOF) model [35] is commonly used [11, 27,28,29,30,31]. However, the simulations usually require high computational resources [2, 11]. To obtain results in acceptable time, simplifications are often made with respect to clutch geometry and fluid behavior [11, 36, 37]. For instance, mixture models [36] and cavitation models [12, 37, 38] solve the two-phase flow region by considering a viscosity of the oil-air mixture. With a cavitation model, the drag torque at a specific differential speed can be calculated in about 1.5 hrs on a workstation with 32 cores, while the more computing-intensive Volume of Fluid model leads to about 8 hrs of computation [11]. The CFD models usually consider only one gap with a constant clearance [11, 34, 37]. Thus, the time-dependent variation of the clearance is not considered.

Analytical models [22, 39,40,41,42,43,44,45,46,47] represent a further option to estimate the drag losses. The analytical models presented in the literature are typically based on the Navier-Stokes equations, often assuming major simplifications. Cited models usually assume, among other things, a laminar, incompressible, and steady flow in the gap and neglect gravity and the axial flow component. Generally, analytical models have a lower model depth compared to numerical models. For example, the groove geometry is commonly not considered. Therefore, analytical models are not universally applicable, especially regarding the groove pattern. The groove area or the groove volume are often used to determine correction factors [39, 43]. In addition, existing analytical models cannot be used to calculate the drag losses of the entire clutch system. The model parameters are typically limited to the number of gaps, plate size, oil viscosity, differential speed, clearance, and feeding flow rate [39,40,41, 43]. Further, analytical models usually allow only the calculation of the drag torque caused by fluid shearing in the gap. However, it is known from experimental investigations that the design of the carriers can considerably influence the drag loss behavior [13]. In the case of non-grooved plates, analytical models [39,40,41, 43] show good correspondence with the measurement in the region of single-phase flow [2]. However, the simplified modeling of the complex two-phase flow partly causes major deviations between experiment and calculation [2]. In the case of grooved plates, however, satisfactory results cannot be achieved generally [2]. Analytical models require low computational resources and thus allow a non-time-consuming estimation of the drag torque. However, due to various simplifications and limitations in the model building, the achievable accuracy is low [2].

1.3 Aim of the study

The aim of the study therefore was to develop a methodology that can be used to build a data-driven model for the prediction of the drag losses of wet clutches with low computational effort and, at the same time, with sufficient accuracy under consideration of a high number of influencing parameters. Today, data-driven modeling is widely used in different fields of engineering and science [48]. Figure 2 shows the classification of the data-driven model in terms of computational effort and accuracy or model depth compared to existing models.

Fig. 2
figure 2

Classification of the data-driven model compared to existing analytical models and CFD models

Full size image

2 Methodology

The developed methodology covers all relevant steps from data generation to the validated prediction model as well as its usage. The main- and sub-steps of the methodology are visualized in Fig. 3. In the modeling, we do not consider the re-increase of the drag torque in Phase 3.

Fig. 3
figure 3

Methodology to build a data-driven model for the prediction of the drag losses of wet clutches

Full size image

2.1 Step 1: Data generation

The developed methodology uses drag torque measurements performed on a drivetrain test rig or component test rig. For drag torque measurements, the SAE No. 2 component test rig [49] was already applied in various investigations [3, 5, 14, 20, 39, 50]. Further investigations applied test rigs with a similar set-up and function principle [6, 51,52,53]. With test rigs of this design, one can consider the influence of the interaction and axial movement of the plates of the clutch pack on the drag loss behavior. Single-disk test rigs are usually used for the verification and validation of analytical and numerical calculation models [44, 54,55,56]. As a result of the different test rig concepts, different test procedures are sometimes selected for the experimental studies [6, 12]. In this paper, only the generation and processing of experimental data is described. Also, data from systematic CFD simulations can be processed within the methodology to develop a surrogate model, e.g. The experimental investigations require series parts or at least prototype parts. If there are no series parts available, especially SLA (stereolithography) is a suitable additive manufacturing process to generate prototype parts out of epoxy resin [18, 57].

2.1.1 Drag torque test rig

In this paper, we describe in detail the set-up and functionality of the LK‑4 drag torque test rig [6]. The LK‑4 drag torque test rig was developed at the Gear Research Center (FZG) of the Technical University of Munich to investigate the drag loss behavior of wet clutches. Figure 4 shows the set-up of the LK‑4 test rig. The test rig is designed only for drag torque measurements, which means that the clutch cannot be engaged on this test rig. Compared to single-disk test rigs, the LK‑4 drag torque test rig enables investigations to be carried out on a full clutch pack. As in real usage, the plates are mounted in the respective carriers. Both carriers can be driven independently of each other. This allows investigations to be carried out in both brake and clutch operating mode.

Fig. 4
figure 4

Graphical display (isometric view (top) and detail (bottom)) of the LK‑4 drag torque test rig, based on [6]

Full size image

The outer carrier (1) is connected to the hollow shaft (2). The inner carrier (3) is connected to the full shaft (5) via the measuring shaft (4). The torque measurement is based on the strain measurement principle. For this purpose, strain gauges are applied to the measuring shaft. Due to the arrangement of the measuring shaft between the inner carrier and the full shaft, the measuring signal is free from systematic errors such as loss torques due to seals or bearings. The hollow or full shaft is driven separately by a speed-controlled asynchronous machine (not shown) via a V-ribbed belt (6).

The clutch pack (7) is placed between the spacer ring (8) and the closing cover (9). The total clearance of the clutch pack is set by the position of the closing cover. Depending on the clearance to be set, a spacer ring (10) is used to position the closing cover.

The speeds of the two carriers are recorded by means of inductive incremental encoders (11 and 12). The torque signal is transferred via a telemetry system (13) from the rotating full shaft. All measurement signals are processed and visualized in the measurement program (FZGLab, Technical University of Munich, DE). The test rig is controlled by a PLC (programmable logic controller).

For investigations with injection lubrication, the tempered oil is injected via an oil nozzle (14) in radial direction. Immediately before the oil enters the nozzle, the feeding flow rate and the temperature are measured. Depending on the design of the carriers, the oil commonly enters the gaps through slots in the inner carrier and leaves through slots in the outer carrier.

For investigations with dip lubrication, the oil nozzle is replaced by a distribution disk. Here, an oil sump with a defined level is set in the housing (15). To ensure a constant oil temperature, the sump is permanently supplied with tempered oil. The oil is tempered to the feeding temperature in an external oil unit. The oil sump temperature is measured at one position [4].

The operating limits of the LK‑4 drag torque test rig are given in the publication of Groetsch et al. [11].

2.1.2 Test procedure

For the experimental determination of the steady drag torque, the stepwise adjustment of the differential speed has proven to be reliable [4, 6, 11, 17, 58] and is therefore used in the presented methodology.

Here, the speed of the carriers is increased synchronously in steps up to a maximum speed and then reduced again to zero. The step size and step duration are selected depending on the test phase and usually range from 25 to 150 rpm and from 30 to 120 s, respectively. For investigations in brake operating mode, one of both carriers is stationary, while in clutch operating mode both carriers rotate at any given speed ratio relative to each other. Figure 5 shows an example of a test procedure for a brake operating mode with a rotating inner carrier and increasing as well as decreasing speed steps. The resulting drag torque Td as well as the oil injection temperature ϑ are also shown in Fig. 5. The differential speed between the clutch plates in this operating mode is equal to the absolute speed of the inner carrier nIC. Depending on the objective of the investigation, the test procedure can also contain only increasing or decreasing speed steps [4, 6, 12, 59]. In the case of only increasing speed steps, the test is completed after the maximum speed has been reached. In the case of only decreasing speed steps, the two carriers are each first accelerated to a specific maximum speed. Their speed is then reduced stepwise. The maximum speed, step sizes, and step durations mainly depend on the plate size, the operating conditions, and the test phase. The test duration depends on the parameters mentioned above and usually ranges between 45 and 90 min [4, 6]. After mounting the plates, the total clearance is commonly not evenly distributed among the gaps. It should be considered that an uneven distribution of the total clearance leads to a higher drag torque [21, 59, 60]. In order to minimize this specific influence on the drag torque, we suggest to perform a speed ramp after each mounting to force a more even distribution of the clearance.

Fig. 5
figure 5

Example of test procedure and measured data for the brake operating mode with a rotating inner carrier and injection lubrication. (Note: The marked time interval is shown in Fig. 6)

Full size image

Depending on the test rig concept, an additional torque caused by the acceleration of the clutch components can be avoided by the stepwise speed adjustment. Furthermore, compared to a continuous speed ramp [12, 61], influences of transient effects due to a speed change are prevented.

2.1.3 Evaluation methodology

We adapt the evaluation methodology according to Draexl et al. [6] to evaluate the tests performed. The evaluation methodology basically transforms the drag torque measured over time into the mean shear stress over the speed difference of the outer and inner carrier.

Due to the temperature controlling of the external oil unit, the oil injection temperature varies around its set point. Depending on the operating conditions, the temperature variation can reach approximately ± 2 K [11]. This temperature variation, in turn, affects the drag torque due to the associated change of the oil viscosity. Therefore, we extend the evaluation methodology of Draexl et al. [6] to compensate for the abovementioned temperature variation. We correct the measured drag torque curve according to Eq. 1 by means of the ratio of the actual viscosity and the target viscosity. We calculate both viscosity values for the actual and target temperature according to DIN 51563 [62] and DIN 51757 [63]. Hence, the corrected drag torque is related to the constant set temperature and is therefore free from variations induced by temperature changes.

$$T_{\mathrm{d,corr}}\left(t\right)=T_{\mathrm{d}}\left(t\right)\cdot \frac{\mu (\vartheta (t))}{\mu (\vartheta _{\mathrm{tgt}})}$$
(1)

Compensation of temperature variations is only performed for evaluations of tests with injection lubrication, since in this case the feeding temperature is known from the measurements. In the case of dip lubrication, the compensation is not applied. In this case, the temperature variations caused by the external oil unit have a negligible influence on the drag torque because of the different test set-up and oil supply [4]. Further, it is challenging to measure a representative actual temperature of the oil in the gaps. Using the temperature of the surrounding oil in the housing is also not appropriate due to layering effects in the oil sump.

The shearing of the oil in the gap causes an increase in temperature and consequently a decrease in viscosity [2, 5]. This decrease in viscosity due to the temperature increase is not considered in the evaluation. Each drag torque measurement is corrected and referenced to the target injection temperature.

The mean drag torque is determined for each differential speed step from the temperature-compensated drag torque curve. We do not consider the first 70% of the step length in the averaging. In this way, amongst others, transient effects that occur during and immediately after the speed changes can be excluded. In Fig. 6, the time intervals used for the evaluation are marked and correspond to the last 30% of the step length in each case.

Fig. 6
figure 6

Exemplary time interval of corrected drag torque (red), speed of inner carrier (green), and oil temperature (black). The shaded areas mark the last 30% of the points measured at each speed step

Full size image

In order to compare different plate sizes and numbers of gaps, the drag torque is related to the mean diameter and the total friction surface according to Eq. 2 [6]. This gives the mean shear stress acting on the plates.

$$\tau _{\mathrm{m}}=\frac{2\cdot T_{\mathrm{d}}}{d_{\mathrm{m}}\cdot N\cdot A}=\frac{2\cdot T_{\mathrm{d}}}{{d_{\mathrm{m}}}^{3}\cdot \pi \cdot N}\cdot \frac{\left(d_{\mathrm{o}}/d_{\mathrm{i}}+1\right)}{\left(d_{\mathrm{o}}/d_{\mathrm{i}}-1\right)}$$
(2)

The mean shear stress will be referred to only as shear stress in the following for ease of reading in this paper.

Figure 7 shows the evaluated test from Fig. 5 for the increasing speed steps.

Fig. 7
figure 7

Evaluated test from Fig. 5 for the increasing speed steps

Full size image

The graphical visualization of the shear stress curve (see Fig. 7) provides detailed information on the drag loss behavior of the clutches investigated. However, the graphical visualization of the results is not suitable for a more comprehensive evaluation, and especially to quantitatively compare the effects of the influencing parameters on drag loss behavior. Hence, characterizing parameters are often evaluated, which describe the drag loss behavior comprehensively and still allow easy comparability [4, 6, 11]. The determination of the characteristic parameters is part of Step 2.

In data-driven modeling, data quality is of high importance. Erroneous or biased data may lead to erroneous models [48].

2.1.4 Design of experiments

The geometry and operating parameters investigated in the test series represent the model parameters in the subsequent built model and thus specify the model depth. In general, a higher model depth requires more extensive test series [64]. The range of validity of the model is specified by the maximum distances between the levels of the test parameters. In the case that the influencing parameters are not known initially, they can be identified by means of prior screening tests [65].

We note that the final choice of the experimental design mainly depends on the expected effects and the number of parameters to be investigated. Using a two-level factorial design, for example, a linear model can be determined [64]. For the detection of curvature effects, the test plan needs to be augmented to at least a three-level design [66]. However, in the case of a high number of influencing parameters, this may be unfeasible [66]. Fractional factorial designs like the central composite design or the Box-Behnken design require only a fraction of the tests of a full factorial design [66]. Both designs can be used to detect quadratic effects [66]. For more complex models, space-filling designs like Latin hypercubes offer an evenly distribution of the test points on the design space in order to gather as much information as possible [64, 66, 67]. However, in the case of drag torque measurements it is not always possible to set the test parameters at any desired value. In particular, geometry parameters can normally only be varied between specific variants. Therefore, the application of space-filling designs is not always feasible in terms of experimental drag loss testing. With abovementioned designs, the test plan is determined before the measurements are performed. Consequently, the test plan cannot adapt to effects that are identified during the testing [64].

In contrast, adaptive sequential sampling, also known as active learning, chooses the location of the next test point based on previously observed behavior [64, 68]. With adaptive sampling, a targeted testing and model building can be carried out. However, the continuous interaction of experimental testing and model building may not always be suitable in the case of drag loss investigations. With adaptive sampling, usually non-parametric models can be determined [64].

2.2 Step 2: Evaluation of characteristic drag loss values

The machine learning algorithms require continuous numerical targets to solve the given regression problem. Therefore, we define characteristic points of the shear stress curve, which can be used to quantify the drag loss behavior. We identified the maximum (transition from Phase 1a to Phase 1b) and the beginning of the quasi-steady Phase 2 (transition from Phase 1b to Phase 2) as robust and representative characteristic points of the shear stress curve. As an example, the characteristic points are shown in Fig. 8. Each characteristic point is described by a shear stress value and a differential speed value. This results in four characteristic values. We also define an approximation function to model the full drag torque curve based on the characteristic values.

Fig. 8
figure 8

Characteristic points of the shear stress curve: Maximum (×) at τm,max and ∆nmax as well as the beginning of Phase 2 (+) at τm,1–2 and ∆n1–2

Full size image

We validate and evaluate the methods to determine the characteristic values and the approximation function using a test dataset. The test dataset originates from the research project FVA 671 II [16] and includes 254 measurements.

2.2.1 Maximum shear stress

The characteristic value τm,max can be easily determined as the maximum value of the shear stress curve (see Fig. 9a, b). For the determination of the characteristic value ∆nmax, we considered two different methods. At the first method (Method 1; index g, global), we evaluate the differential speed ∆nmax,g associated with the global maximum shear stress τm,max (see Fig. 9a–d). When performing the test, the size of the speed steps is usually adjusted depending on the plate size and the test parameters. As a consequence, and generally because of the stepwise test procedure, there is a systematic variance of the characteristic value ∆nmax across the dataset. This induced variance could be reduced by a smaller size of the speed steps in the region of the maximum shear stress leading to a finer resolution of the shear stress curve in this region. Considerably longer test runtimes would be the consequence.

Fig. 9
figure 9

Determination of the maximum using two different methods for shear stress curves with definite (a) and plateau-like (b) maxima; Details of the two maxima (c, d); Difference between both methods for all measurements of the test dataset (e)

Full size image

As the exemplary measurement in Fig. 9d further shows, the maximum may also form a plateau. In such cases, the evaluation of the global maximum does not provide robust and representative results for the characteristic value ∆nmax. To prevent this, we determine the characteristic value ∆nmax as follows (Method 2; index c, centroid): For the area enclosed between the shear stress curve and a horizontal boundary line at 80% of the maximum shear stress τm,max (see red shaded area in Fig. 9a–d), we determine the centroid thereof and use the x‑coordinate as ∆nmax,c. For curves with a definite maximum (see Fig. 9a, c), the characteristic value ∆nmax is not significantly corrected. In contrast, for plateau-like maxima (see Fig. 9b, d) there is a significant correction of the characteristic value ∆nmax. We applied both methods on the test dataset. Figure 9e illustrates the difference between both methods. Lastly, the characteristic value ∆nmax is determined according to Method 2.

The maximum torque respectively the maximum shear stress is used as a characteristic in various investigations [5, 6, 13]. But here the global maximum is used.

2.2.2 Modeling of shear stress curve in phase 1a

To model the shear stress curve in Phase 1a, we use the characteristic maximum and the zero point as support points for the approximation function. According to Newton’s law of viscosity and for completely filled gaps, the shear stress increases linearly with the differential speed. This behavior can be commonly observed in the lower differential speed region of Phase 1a [4, 6, 12]. However, a further increase of the differential speed closer to the maximum shear stress often shows a degressive behavior [4, 6, 12]. Consequently, the approximation of Phase 1a by a linear function is not suitable. Therefore, we choose a quadratic function to approximate Phase 1a, with the vertex at the maximum shear stress τm,max and crossing zero. The approximation is shown in Fig. 10a, b.

Fig. 10
figure 10

Approximation of Phase 1a using a quadratic function for two exemplary shown shear stress curves (a, b); Distribution of coefficient of determination R2 for all measurements of the test dataset (c)

Full size image

Figure 10c quantifies the quality of approximation for all measurements of the test dataset. For about 90% of all measurements, a coefficient of determination R2 of more than 0.9 can be shown. The high quality of approximation supports the choice of the quadratic function.

2.2.3 Modeling of shear stress curve in phase 1b and phase 2 and beginning of steady phase

The characteristic drop of the shear stress in Phase 1b and the subsequent quasi-steady state in Phase 2 are interpolated by a Gaussian function (also Gaussian bell curve) according to Eq. 3. For interpolation, we only use the section ∆n ≥ a2 (to the right of the maximum). The interpolation is shown in Fig. 11a, b.

$$\tau _{\mathrm{m}}\left(\Updelta n| \Updelta n\geq a_{2}\right)=a_{1}\cdot e^{-{\left(\frac{\Updelta n-a_{2}}{a_{3}}\right)^{2}}}+a_{4}$$
(3)
Fig. 11
figure 11

Iteration step k = 1 to determine the transition from Phase 1b to Phase 2 using an interpolation function shown for shear stress curves with constant (a) and decreasing (b) Phase 2; Distribution of the coefficient of determination R2 of the interpolation for all measurements of the test dataset (c)

Full size image

We determine the characteristic transition point to the steady shear stress zone iteratively in two steps. The interpolation is constrained by three boundary conditions (BC) according to Eq. 4. In the first iteration step (index k = 1), we set the horizontal asymptote of the interpolation function to the local minimum of Phase 2 (see BC I). The peak of the interpolation function has to be located in the previously determined maximum (see BC II). The interpolation function is bounded by the maximum and the asymptote (see BC III) in vertical direction. Thus, only the coefficient \({a}_{3}^{\left(1\right)}\) is fitted in the interpolation.

$$\text{BC I}\colon {a}_{4}^{\left(1\right)}=\tau _{\mathrm{m,min}}$$
(4a)
$$\text{BC II}\colon {a}_{2}^{\left(1\right)}=\Updelta n_{ \mathrm{max,c}}$$
(4b)
$$\text{BC III}\colon {a}_{1}^{\left(1\right)}=\tau _{\mathrm{m,max} }-\tau _{\mathrm{m,min} }$$
(4c)

Figure 11c quantifies the quality of approximation for all measurements of the test dataset. For about 92% of all measurements, a coefficient of determination R2 of more than 0.95 can be found. About 97% of all measurements achieve a coefficient of determination R2 of more than 0.9. The high quality of approximation demonstrates the suitability of the Gaussian function to model Phase 1b and Phase 2.

The transition from Phase 1b to Phase 2 is defined as a point on the determined interpolation function according to Eq. 5. After the first iteration step, the transition is described by the characteristic values \({\Updelta n}_{1-2}^{\left(1\right)}\) and \({\tau }_{\mathrm{m,}1-2}^{\left(1\right)}\).

$${\tau }_{\mathrm{m,}1-2}^{\left(k\right)}=0.05\cdot {a}_{1}^{\left(k\right)}+{a}_{4}^{\left(k\right)}$$
(5a)
$${\tau }_{\mathrm{m,}1-2}^{\left(k\right)}={a}_{1}^{\left(k\right)}\cdot e^{-{\left(\frac{{\Updelta n}_{1-2}^{\left(k\right)}-{a}_{2}^{\left(k\right)}}{{a}_{3}^{\left(k\right)}}\right)^{2}}}+{a}_{4}^{\left(k\right)}$$
(5b)

Figure 11a, b shows the determination of the transition from Phase 1b to Phase 2.

The shear stress may continue to decrease slightly (see Fig. 11b) or increase again in Phase 2 [3]. Also, variations around a quasi-steady value can be observed. Consequently, the local minimum shear stress τm,min of Phase 2 neither serves as a robust boundary condition (see BC I and BC III) according to Eq. 4 nor represents a robust parameter to determine the characteristic values \({\Updelta n}_{1-2}^{\left(1\right)}\) and \({\tau }_{\mathrm{m,}1-2}^{\left(1\right)}\) according to Eq. 5.

We use the characteristic value \({\Updelta n}_{1-2}^{\left(1\right)}\) as the starting point of Phase 2 to calculate the average of the shear stress values \(\tau _{\mathrm{m,min,avg}}\) in this phase. In the second iteration step (index k = 2), we use the more robust average \(\tau _{\mathrm{m,min,avg}}\) for the boundary conditions according to Eq. 6 (see BC I and BC III). BC II is not affected.

$$\text{BC I}\colon {a}_{4}^{\left(2\right)}=\tau _{\mathrm{m,min,avg}}$$
(6a)
$$\text{BC II}\colon {a}_{2}^{\left(2\right)}=\Updelta n_{\mathrm{max,c}}$$
(6b)
$$\text{BC III}\colon {a}_{1}^{\left(2\right)}=\tau _{\mathrm{m,max} }-\tau _{\mathrm{m,min,avg}}$$
(6c)

The more robust boundary conditions show up in a higher quality of approximation of the interpolation function, see Fig. 12d. For all measurements of the test dataset, a coefficient of determination R2 of more than 0.9 can be found. Almost 97% of all measurements achieve a coefficient of determination R2 of more than 0.95.

Fig. 12
figure 12

Iteration step k = 2 to determine the transition from Phase 1b to Phase 2 using an interpolation function shown for shear stress curves with constant (a) and decreasing (b) Phase 2; Detail of the transition (c); Distribution of coefficient of determination R2 of the interpolation for all measurements of the test dataset (d)

Full size image

The characteristic values \({\Updelta n}_{1-2}^{\left(2\right)}\) and \({\tau }_{\mathrm{m,}1-2}^{\left(2\right)}\) are calculated according to Eq. 5 using the boundary conditions of the second iteration step. The characteristic values are shown in Fig. 12a, b and in detail in Fig. 12c.

2.2.4 Approximation of shear stress curve

The shear stress curve is finally approximated by a quadratic function in Phase 1a and a Gaussian function in Phase 1b and Phase 2, see Fig. 13a, b. Figure 13c proves the high quality of approximation of the combined function.

Fig. 13
figure 13

Approximation of a full shear stress curve using a quadratic function (Phase 1a) and Gaussian function (Phase 1b and Phase 2) as well as finally used characteristic values shown for two exemplary shear stress curves (a, b); Distribution of coefficient of determination R2 for all measurements of the test dataset (c)

Full size image

For about 90% of all measurements, a coefficient of determination R2 of more than 0.95 can be demonstrated. About 98% of all measurements achieve a coefficient of determination R2 of more than 0.9. This result illustrates the suitability of the identified approximation function to model the shear stress curve.

To complete Step 2, the characteristic values for each measurement in the dataset have to be evaluated.

2.3 Step 3: Data analysis and preparation

The structure of the dataset used to build the model is basically known from the design of the experiments in Step 1. When combining multiple datasets from several investigations, we recommend analyzing the structure of the total dataset to identify any missing data. Furthermore, in Step 3 the input and output parameters of the model are defined. Depending on the subject area, the input parameters are also named features or independent variables. For the output parameters, the terms targets or dependent variables are common. The investigated influencing parameters represent the features for the model training. As targets, the four characteristic values are used. Each data sample of the dataset is described by a set of features and the targets.

2.4 Step 4: Data-driven modeling

The aim of Step 4 is to determine the relationships between the influencing parameters (input) and their dependent characteristic values (output) through supervised machine learning algorithms. Based on the modeling of the underlying causal relationships in the given dataset, predictions for unknown target values can then be calculated. Even if fundamental relationships are already known from various experimental and theoretical investigations, the mathematical relationships between the influencing parameters and the characteristic values are usually unknown. In many common algorithms, such as linear regression, the mathematical form of the model is defined [69]. Such algorithms can considerably limit the prediction performance of the model when making incorrect assumptions. After examination of the suitability of different algorithms, we recommend the symbolic regression and the Gaussian process regression to build the model, mainly because they are easy to interpret and highly flexible at the same time. We note, however, that the final choice of algorithm depends, among other things, on the size and structure of the dataset, the general complexity of the correlations, the number of features, or the variance of the targets.

With symbolic regression, a mathematical function is searched to describe the relationships using genetic programming [70]. At initialization of the algorithm, a set of mathematical operations and functions has to be defined. This gives the opportunity to bring in prior knowledge. In the subsequent selection and evolution steps, the best function is determined in an evolutionary process until a stopping criterion is reached. A key advantage of the symbolic regression is the easy interpretability of the result function. However, the comparatively long training time may be a disadvantage. In addition, the random choice of the first generation of the model population may affect the outcome. For a detailed explanation of the symbolic regression and genetic programming, we refer to the corresponding literature [70, 71]. If implementing in Python, we recommend to use package gplearn [72].

We consider the non-parametric models of the Gaussian process regression as the most suitable. Gaussian process regression can also include expert knowledge in model building through the selection and specification of kernel functions. In addition, the variance of drag torque from repeated measurements can be considered when training the model. A major advantage of the Gaussian process regression is the specification of the prediction uncertainty in terms of a confidence interval. This allows simultaneously checking if the model is based on sufficient data for the current prediction. For a detailed explanation of the Gaussian process regression, we refer to corresponding literature [69, 73,74,75,76]. If implementing in Python, we recommend to use package GPflow [77] or GPy [78].

The validation of the prediction models uses measurements. When running the tests, combinations of test parameters are selected which are not represented in the training dataset.

2.5 Step 5: Prediction of characteristic drag loss values

Using the models, the characteristic values are predicted. For both shear stress characteristic values, the back calculation to the drag torque is performed according to Eq. 2. Figure 14 shows an example of typical input parameters and the output parameters of the model.

Fig. 14
figure 14

Example of typical input parameters and output parameters of the prediction model and approximated drag torque curve

Full size image

2.6 Step 6: Approximation of drag loss behavior

The approximation function defined in Step 2 is used to model the entire drag torque curve. The approximation function is composed of a quadratic function (Phase 1a) and a Gaussian function (Phase 1b and Phase 2). The coefficients of the approximation function are given by the characteristic values. Figure 14 shows the approximation of the drag torque curve based on the characteristic points.

3 Limitations und outlook

In the presented methodology, one can only use measurements that show the characteristic drag loss behavior (see Fig. 7). Drag torque curves, which differ from this, cannot be processed. So far, the model is limited to the prediction of drag losses caused by the shearing of the oil. In the current modeling, we do not consider the re-increase of the drag torque due to plate tumbling at very high speeds. The occurrence and onset of plate tumbling, for example, could be modeled using classification and regression algorithms. This would extend the scope of application of the prediction model to very high speeds. For user-friendly handling, we suggest embedding the model into a graphical user interface. It is also possible to use the prediction model as a block in a full powertrain simulation. As part of a further development of the presented methodology, further characteristic values should also be considered, such as the maximum power loss or the dissipated energy [6, 13]. At the current state, the model predicts four characteristic values related to the drag loss behavior. Based on the predictions, we approximate the shear stress curve. Alternatively, to predict the shear stress curve directly, each curve would first have to be discretized. Figure 15 shows an example of the discretization.

Fig. 15
figure 15

Exemplary discretization of a shear stress curve into 21 equidistant intervals

Full size image

A model is then trained for each of the discrete differential speeds. The interpolated shear stress values are used as targets. While the presented methodology requires only four models, this approach requires considerably more models to be trained, depending on the discretization. However, a disadvantage of this approach is that the models are not coupled and may predict a non-monotonic drag torque behavior in the respective phases.

4 Conclusion

This paper describes a methodology for data-driven modeling and prediction of drag losses of wet clutches. As input, we use drag torque measurements obtained from systematic investigations on the influence of various geometry and operating parameters on drag loss behavior. Supervised machine learning algorithms are used to determine the relationships between the influencing parameters and characteristic values of the drag loss behavior. The main time effort is required for preparing (collecting, cleaning, analyzing, visualizing) the data [79]. This requires a suitable test rig and at least prototype parts. The test effort depends in particular on the desired model depth. As complementary investigations showed, a high prediction accuracy can be achieved with flexible and powerful regression models. We recommend the symbolic regression and Gaussian process regression to build the models mainly because they are easy to interpret and highly flexible. Since the model is based on drag torque measurements performed on complete clutch systems, it allows practice-oriented predictions to be made. A major advantage of the presented methodology is that all different types of influencing parameters can be considered in the model building, irrespective of the complexity of their effect. For instance, even the influences of the material properties of the friction lining, a complex groove geometry, and an uneven distribution of the total clearance can be modeled without restrictions. With an adequate dataset, a high model depth can be realized. Only training the model usually requires increased computing power, depending on the chosen machine learning algorithm. The drag torque predictions require low computational effort. Through the data-driven modeling, a high model accuracy can be achieved, irrespective of the complexity of the flow and physical effects acting. The achievable model accuracy eventually depends on the quality of the drag torque measurements.

5 Nomenclature

The nomenclature is shown in Table 1.

Table 1 Nomenclature
Full size table

6 Indices

The indices are shown in Table 2.

Table 2 Indices
Full size table