1 Introduction

The growth in wind power generation has maintained its rapid pace, as almost 94 GW of capacity were added in 2021 with a year-over-year growth of 12% [1]. In this growing industry, wind turbine manufacturers are competing to capture the greatest market share by developing reliable and cost-effective wind turbine systems [2, 3]. They strive for successful and rapid prototype testing to ensure the desired product reliability and a faster time to market. These objectives have led to significant advances toward the development of several full-scale nacelle testing facilities around the world [4]. Table 1 lists some of the typical tests that can be conducted on a nacelle test bench. These facilities have become an attractive method for testing, as they offer system-level testing capabilities for the complete nacelle with the goal of applying realistic loads that the nacelle will experience in field operation in a controlled and repeatable environment.

Table 1 Typical mechanical and electrical tests conducted on a nacelle testing bench [5]
Full size table

However, the fast-growing trend of wind turbine size and operational capacity has increased the demands on the existing nacelle testing facilities. Many of them are already (or will soon be) too small to provide the required set of operational loads for the growing demands of larger wind turbines. As wind turbine technology is evolving, the existing testing methods also need to adapt correspondingly. There has been a trend for establishing larger test benches with increased load application capabilities to accommodate the demands of larger wind turbines [5]. However, this continuous trend of constructing bigger nacelle test benches for larger wind turbines might not be a sustainable solution. Furthermore, accessing the established nacelle test facilities is already financially difficult for smaller manufacturers of wind turbines and currently only possible for the bigger ones [6]. Constructing even larger test benches with possibly higher test costs may leave very few wind turbine manufacturers with the financial means to utilize these facilities in their development process.

Therefore, innovations are needed to enhance the functionality of the existing nacelle test benches and maximize their use. Scaled testing offers a potential solution, as it is a widely used approach across several industries for resolving difficulties related to test capacity and specimen size. Efforts are being made in the INNTERESTING research project [7] to explore the innovative use of scaled tests to resolve the abovementioned challenges in wind turbine system testing. This project proposes an innovative testing approach where advanced simulation techniques are combined with scaled tests of drivetrain components. The models are developed and validated using scaled test results and then used to simulate the full-scale component response without requiring full-scale tests. However, the successful demonstration and the application scope for this approach are yet to be seen.

Another possible solution lies in the use of virtual testing, which has already seen application in almost every major industrial sector including the automotive [8,9,10,11], railway [12,13,14], and aerospace [15, 16] industries. Virtual testing forms a fundamental part of the development process in these industries, with the aim of either reducing the number of physical tests or pushing past the limits of physical testing. Although virtual testing of wind turbine drivetrains is rather new when compared with other industrial sectors, it has nevertheless demonstrated promising potential in several recent research studies [17,18,19,20,21,22,23,24,25,26,27]. The VirtGondel research project [28] at Fraunhofer IWES aims to advance the application of virtual testing further. The project proposes an innovative hybrid testing approach utilizing the virtual test bench model in combination with full-scale physical tests, which allows load ranges beyond the test bench capacity to be investigated. Unlike scaled testing, this approach removes the uncertainties that are inherent to a physical scaling of the test specimen.

This contribution presents this hybrid testing approach for emulating the full load response of a nacelle device under test (DUT). The detailed methodology will be explained in Sect. 2. The high-fidelity model is described in Sect. 3 along with the required model fidelity. Case studies performed to demonstrate the proposed hybrid testing methodology are presented in Sect. 4, followed by further discussion of the presented methodology in Sect. 5. The conclusion can be found in Sect. 6.

2 Hybrid nacelle test methodology

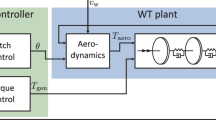
The proposed hybrid testing methodology for wind turbine nacelles is elaborated in Fig. 1 (represented inside the blue box). First, full-scale physical tests are conducted on a nacelle test bench at partial loads that are achievable within the load application capability of the test bench. Alongside these tests, virtual testing is performed for the same load regime. The measured DUT response at partial loads obtained from physical tests is compared against simulation results from virtual tests, and the virtual model is adapted as necessary to achieve the desired accuracy. Afterward, the validated virtual model is used to simulate the response of the DUT under full loads beyond the testing limits of the test bench.

Fig. 1
figure 1

Workflow for the evaluation of the hybrid nacelle testing procedure

Full size image

Nacelle tests on a 5 MW GE Cypress platform conducted at the DyNaLab facility of Fraunhofer IWES were used to demonstrate the proposed hybrid testing method. The nacelle features a multi-stage geared high-speed drivetrain with three point suspension topology. The main shaft is connected with the test bench load application system (LAS) via a hub adapter. The entire nacelle system rests on the tower adapter at the yaw bearing interface. During testing, the yaw system is locked to restrict the nacelle motion in the yaw direction. From the list of nacelle tests mentioned in Table 1, the parasitic load tests have been chosen. The DyNaLab offers electrical and mechanical tests for a wind turbine nacelle of up to 10 MW power with the capability to apply up to 20 MNm bending moments and 2 MN forces at the hub interface. The virtual model of the nacelle is validated using only the partial load response obtained during the physical testing of the 5 MW nacelle. In this way, the capability of the validated virtual model to simulate the full load response can be evaluated using the available measurements from the physical tests conducted at full loads as shown in Fig. 1 (represented inside the gray dashed box).

3 Model description

A high-fidelity multibody simulation (MBS) model of the test setup was developed in Adams [29]. The model serves as a virtual twin of the physical test setup, as it includes all the relevant components of the test bench load application system and the nacelle drivetrain to reproduce the functionality and response of the actual physical system. Fig. 2 shows the entire virtual testing setup and the measurement locations for the DUT response of interest. The test bench flange adapters, coupling, and drive shaft are modeled as flexible bodies created by modal reduction of their respective finite element (FE) models using Craig-Bampton component mode synthesis [30]. Further details of the test bench LAS model have been elaborated in [31]. The MBS model of the nacelle drivetrain was developed such that it fulfills the NREL recommendations for drive train MBS model fidelity [32]. However, some enhancements have been made with regard to bearing stiffness. Instead of using bushing elements with a constant stiffness matrix, nonlinear force elements were used with spline functions to represent the bearing movements for wider ranges of applied load correctly. Table 2 summarizes the implemented modeling approach for the global system model.

Fig. 2
figure 2

Virtual test bench model for the hybrid test concept and the measurement locations

Full size image

Fig. 2 also shows the three measurement locations for the evaluation of the desired DUT response, which were implemented during the physical testing of the DUT. The first one is the relative displacement between the main shaft and the bedplate. This is measured in the physical system using three laser sensors for the measurement of the relative displacements in axial (X), yaw (Y), and pitch (Z) directions. The second one is the relative displacement between the gearbox housing and the gearbox support structure. Multiple laser sensors are installed between these two components to measure the gearbox housing deflections relative to the support structure in axial, yaw, and pitch directions. The simulation model delivers the relative displacements at the same locations to provide a one-to-one match with the physical measurements. Lastly, the bedplate deformations are measured using strain gauges installed at a location of interest. These are directly compared with the modal strains extracted from the bedplate flexible body at the same location where the strain gauge is installed.

Table 2 Implemented modeling approach for the virtual model
Full size table

4 Case studies

To demonstrate the proposed hybrid testing methodology, parasitic load tests have been carried out in which the LAS system of the test bench applies the following unidirectional loads on the drivetrain:

  • Pitch forces

  • Yaw forces

  • Axial forces

  • Pitch moments

  • Yaw moments

In each of these tests, loads are applied individually at the hub interface with a stepped profile of increasing amplitude. As discussed in Sect. 2, model validation and tuning using the results from partial load tests is a fundamental part of the proposed hybrid testing approach. However, performing the necessary tuning of model parameters to improve the error of a particular system response should not be detrimental to the remaining ones, since model parameters are very likely to have an influence on multiple system responses. It is vital to identify the influence of model parameters on the DUT responses first. Therefore, a sensitivity study is conducted by changing model parameters individually and comparing the changes in the response of interest. The findings are used as a reference during the model validation at partial loads for each of the unidirectional load cases.

4.1 Sensitivity study

The model parameters under study are the main bearing stiffness, the yaw bearing stiffness, the stiffness of the yaw lock system, the stiffness of the planet carrier bearing (stage 1), and the elastomer stiffness of the bolted connections between the gearbox housing flange and the gearbox support structure. These parameters are independently changed by a fixed percentage while keeping the remaining parameters unchanged. The results of the sensitivity study are plotted in Figs. 3–5. The exact values of percentage change in response due to the parameter change are not shown for reasons of confidentiality. Instead, the percentage change is plotted in the vertical axis as a qualitative sensitivity measure with an upper limit (high) representing larger differences in response due to parameter change and a lower limit (low) representing no noticeable differences in response. Several interdependencies can be observed between some model parameters and the drivetrain response.

Fig. 3
figure 3

Model sensitivity for axial loads

Full size image
Fig. 4
figure 4

Model sensitivity for yaw loads

Full size image
Fig. 5
figure 5

Model sensitivity for pitch loads

Full size image

It is important to mention that, even though the main shaft is directly connected to the hub adapter, the displacement measurements of the two components have a key difference: the hub displacement measures the global movement of the hub relative to the stationary reference point on the ground, while the main shaft displacement is the relative motion between the main shaft and the bedplate. The stiffness of the main bearing has a direct influence on the displacement of the main shaft and the hub. It also has a noticeable effect on the strain readings at the strain gauge location on the bedplate for the pitch loads. The yaw bearing shows a higher influence on the hub displacement for the pitch loads as well as a noticeable effect on the bedplate strain readings and the main shaft displacement. The stiffness of the yaw locks strongly influences the hub displacements in the yaw direction and has some noticeable influence in the pitch direction. The gearbox elastomer stiffness has a stronger influence on the gearbox housing deflection for axial loads and shows some noticeable influence on several system responses for pitch loads. The bearing stiffness of the first stage planet carrier shows noticeable influence on the main shaft displacement and hub displacement for the pitch load case. These findings are used as a reference for the parameter tuning and model validation under partial loads.

4.2 Response under pitch forces

Fig. 6 shows the results for applied pitch loads. The DUT response corresponding to the partial loads and full load regions is separated by a vertical dashed line. The measured response at partial loads (i.e., below 60% load range) is used for model tuning with the objective of minimizing the error. This tuned model then simulates the response for extrapolated full loads (i.e., above 60% load range) shown on the right side of the vertical dashed line. The measured responses for all load ranges are also plotted for evaluation purposes. The relative error of the main shaft vertical displacement, although high in the 20–40% load regions, remains below 7% in the 60% load region and reduces significantly in the full load region. The reason for the higher relative error in the lower load regions could be linked to the higher nonlinearity in the stiffness of the main bearing at lower loads, due to which minor deviation of the modeled nonlinear stiffness curve from the real behavior can lead to higher uncertainties in response. The gearbox tangential deflection shows sufficient correlation with the measured results with the relative error remaining below 15% in the full load region. The simulated bedplate strain, although having a higher relative error in the partial load region, shows good correlation with the measured strain in the full load region with less than 3% relative error. The strain sensors installed on the bedplate also captured the oscillations corresponding to the main shaft rotation frequency. This is the reason for the noticeable oscillations in the bedplate strain measurements. These oscillations are not visible in the displacement measurements as those signals included filtering.

Fig. 6
figure 6

Load profile of the applied pitch forces at the hub interface and the corresponding drivetrain response

Full size image

4.3 Response under yaw forces

Fig. 7 shows the case of yaw loads applied at the hub interface and the corresponding drivetrain response. The main shaft displacement in the yaw direction and gearbox radial deflection show a slight error in the partial load region but good agreement of the full load displacement response with the relative error remaining below 7%. However, the bedplate strain shows higher differences with a maximum relative error of 20% in the full load range.

Fig. 7
figure 7

Load profile of the applied yaw forces at the hub interface for hybrid testing and the corresponding drivetrain response

Full size image

4.4 Response under axial forces

For the axial load case, the main shaft axial displacement and the bedplate strain are compared and plotted in Fig. 8. Due to the type of drivetrain topology, axial deflections of the gearbox housing did not occur in the discussed load regime and, therefore, are not included for this load case. The main shaft displacement results show good correlation with the measured values, with errors remaining below 4% in all load regions. The simulated bedplate strain follows the measured strain trajectory with a maximum relative error of 20% in the full load range.

Fig. 8
figure 8

Load profile of the applied axial forces at the hub interface for hybrid testing and the corresponding drivetrain response

Full size image

4.5 Response under pitch moments

Fig. 9 shows the case for applied pitch moments and the corresponding response. Very good agreement can be observed for the main shaft pitch displacement with the maximum relative error below 7% in full load response. The relative error in gearbox tangential deflection remains mostly very low until 75% load levels and below 12% in the full load range. The bedplate strain shows very good agreement in the partial load region with the error building up in the full load region but remaining just above 15%.

Fig. 9
figure 9

Load profile of the applied pitch moment at the hub interface for hybrid testing and the corresponding drivetrain response

Full size image

4.6 Response under yaw moments

The drivetrain response under yaw moments is shown in Fig. 10. The main shaft displacement remains in good agreement with the measured results, with the relative error less than 5% in partial loads. However, the error gradually increases at higher loads with a maximum relative error of 11% at full load. The bedplate strain response shows a good match with measured strains, with less than 5% relative error at partial loads and a maximum relative error of 8% in the full load region. The gearbox radial deflection, although having a higher relative error in the partial load range, shows satisfactory results at full loads with a maximum relative error of around 11%.

Fig. 10
figure 10

Load profile of the applied yaw moment at the hub interface for hybrid testing and the corresponding drivetrain response

Full size image

5 Discussion

The proposed hybrid testing approach presented in this contribution aims to enhance the existing nacelle testing methods by combining the simulations with the experimental measurements. The results from the demonstrated load cases are promising, as the proposed hybrid test methodology was able to predict the full load drivetrain response under parasitic loads for most of the considered load cases. Table 3 summarizes the uncertainty in predicting the full load response of all the considered load cases. The bedplate strain showed a higher error in some load cases, which can be due to multiple reasons such as insufficient selected modes during flexible body generation, oversimplified interface definition (e.g., fixed joints instead of bolted connection with pretension) in the regions near the strain sensor, uncertainty in material definition (elastic modulus), or insufficient mesh density. Another possible solution for removing such errors is the integration of better validation criteria such as the incorporation of the rate of increase in error. These aspects will be investigated further in future work. It is also vital to identify the correlation between model parameters and the system response as well as possible nonlinearity in the system. The presented work considered nonlinear bearing stiffness, which showed good results for predicting the main shaft displacements at full loads. Only the parasitic load tests were considered in the presented work. Future work will incorporate this approach for more types of nacelle tests as listed in Table 1.

The combined used of physical and simulative testing methods has been witnessed in almost every major industrial sector. Its implementation in the wind industry has significant potential, as it can help with the discovery of solutions to some of the challenges facing nacelle testing. The presented work is an attempt at advancing the use of hybrid testing methodology for wind turbine nacelles. This procedure achieves the actual test results covering most of the important aspects for design evaluation as well as obtaining the full load response backed up by validated models. The conducted physical tests, although in partial load regime, give important insights into the relevant system behavior and foster confidence in the validity of simulation models. These measurements are vital for developing reliable virtual models, as simulation models often require tuning and validation. The validated virtual model covers the full load response with potentially lower uncertainties compared with a virtual model which has not been validated. This method allows combination of the advantages of both realms (physical and virtual) of nacelle testing. Furthermore, the use of validated simulation models not only provides insights into the full load response, but can also reduce the number of physical tests required, which can reduce the test costs.

Table 3 Summary of percentage errors between simulated and measured response in different load regions
Full size table

6 Conclusion

This contribution presented a hybrid testing method for nacelle testing which aims to predict the full load response of a wind turbine nacelle. The proposed approach utilized a high-fidelity virtual model of the nacelle and the test bench, which was validated by using measurements via physical nacelle testing conducted only at partial loads. Different parasitic load cases were considered as case studies for the demonstration of the proposed methodology. The results have shown that the virtual model after being validated using partial load measurements has performed well in predicting the full load response of the drivetrain. Possible solutions for the errors observed in some of the predicted responses have been discussed. This approach utilizes the existing tools and methods for predicting load response beyond the testing capacity of the nacelle test bench. Following further improvements, this method of hybrid nacelle testing not only has potential for resolving some of the challenges facing existing test benches for testing larger wind turbines, but might even help reduce the cost of conducting nacelle tests.