Improvements to gearbox acoustics via thrust collars

Abstract

Thrust collars relieve the gearbox housing of the axial force and tilting moments generated by helical gears. The different transfer path also reduces the vibration excitation of the housing due to meshing, which could lead to improved acoustics. This paper presents measurements of noise level reduction of an experimental gearbox. A gearbox dynamics simulation model is used to investigate the effects resulting from the inclusion of thrust collars.

Zusammenfassung

Druckkämme entlasten das Getriebegehäuse von der Axialkraft und dem Kippmoment der Schrägverzahnung. Der veränderte Übertragungspfad verringert ebenfalls die Schwingungsanregung des Gehäuses durch den Verzahnungseingriff, was verbesserte akustische Eigenschaften bedeuten könnte. In diesem Aufsatz wird über Messungen der reduzierten Schallabstrahlung eines Versuchsgetriebes berichtet. Ein Getriebedynamiksimulationsmodell wird eingesetzt, um die Effekte zu untersuchen, welche aus der Nutzung von Druckkammlagerungen resultieren.

Thrust collars conduct axial thrust between rotating parallel shafts in gearboxes. They are made from disks mounted next to the pinion, whose cone-shaped running tracks interact with likewise cone-shaped tracks on the sides of the bull gear (see Fig. 1). The conical shape leads to a convergent gap which permits hydrodynamic lubrication. Thrust collars are a standard element of integrally geared compressors, where they conduct the compresssor thrust from the high speed to the low speed shaft, where it can be absorbed in more efficient low-speed instead of high-speed thrust bearings. Due to the low slip of the lubricated thrust collar contact that lies close to the pitch circle of the gears, thrust collar power loss is low, which leads to a more efficient complete package than without the inclusion of thrust collars.

Fig. 1

Thrust collar application in a helical gearbox with indicated axial force path and exaggerated cone angle $\delta$

Besides integrally geared compressors, thrust collars have been proven for compensating the axial thrust of helical gears. The gears’ axial thrust produces a tilting moment which at marked helix angles can become problematic especially at high gear ratios (large lever) or when mounting the gears directly on roller bearings, as is practiced in epicyclic gearboxes. Sources [23] and [11] provide examples of series applications due to said motivations.

Shortening the path of the gears’ axial force has the additional advantage of reducing the vibrational excitation of the gearbox housing resulting from meshing excitation. On top of that, the thrust collars’ oil film is a damping element that could possibly attenuate coupled degrees of freedom as well. This leads to the hypothesis that utilizing thrust collars in helical gearboxes could be a suitable approach to reducing gearbox noise.

Heß performed experiments using an experimental gearbox whose focus lay in the changing of an adjusted bearing assembly of tapered roller bearings to a fixed/free assembly of spherical roller bearings and in [16] published reports of acceleration measurements of the bearing covers recorded as a sideline that were on average 4.4 dB lower when using thrust collars.

As these experiments had a different primary objective, many parameters relevant to gearbox acoustics were changed at once. Therefore beneficial acoustic properties due to the thrust collars can not be inferred with certainty.

Texas A&M University and Hanwha Power Systems/Techwin performed the most extensive studies on dynamics of gearboxes equipped with thrust collars to date [2, 3, 12, 19]. They analyzed thrust collar-induced transfer of vibration from the low speed to the high speed shaft and vibration caused by thrust collar runout. They were prompted by sub-synchronous vibration observed in integrally geared compressors that at times had amplitudes exceeding specification limits that could be interpreted as a sign of imminent rotordynamic instability. Their multiple models are close to the interior model described below yet not entirely suitable for acoustic analyses.

This paper presents results from further experiments performed on a modifiable gearbox with relevant parameters held constant. A simple computational model is introduced and validated for studying the effect of thrust collars on gearbox acoustics that fundamentally follows the standard procedures for simulating machine dynamics.

1 Experiments

1.1 Experimental gearbox

In Heß’ previous experiments, inbetween the measurements with and without acting thrust collar, thrust collars and changeable bull gear tracks were removed, which changed stiffness and mass and thus vibrational properties of the system. Furthermore the bearings were swapped. Besides the influence of the bearing type, it is known that the clearance between bearing seat and outer ring has a dominant impact on gearbox acoustics (e.g. [15]).

To combat these issues, in the present experiments, the thrust collars were kept mounted on the shafts for the configuration without thrust collars and instead only pushed back axially for a small distance in order to prevent the forming of an acting hydrodynamic oil film while not changing masses and stiffness in a significant manner. The shims are marked in green in Fig. 3. The bearings were not swapped between experiments. Instead, a bearing on the high-speed side that works as a non-locating bearing in the configuration with thrust collars was converted to a locating bearing for the configuration without thrust collars by inserting split rings (marked red in Fig. 3). A photograph of the gearbox is shown in Fig. 2.

Fig. 2

Photo of the experimental gearbox

Fig. 3

Experimental gearbox in two configurations

The limited suitability of the experimental gearbox for exploring acoustic effects needs to be noted, as the walls are unrealistically thick. The thickness is advantageous when many different bearing types need to be mounted in one seat by adding spacer rings. An additional impediment lies is the acrylic observation window spanning the entire topside of the gearbox that permits easy viewing of lubricant distribution but does not provide much soundproofing regarding airborne sound emitted directly from the gears.

Measurements for both configurations with and without thrust collar respectively are performed at four combinations of speed and torque. The adjustability of torque is limited by the employed hydrodynamic brake especially at low speeds.

A significant distance of the operating points from large momentary shifts in sum power level was ensured to not have the results be affected by shifting resonances.

In order to rule out outliers, measurements at all operating points are performed three times each. After measuring at the four operating points once, the gearbox is converted to the other configuration, whereupon it is converted back for the repeat measurement.

Accelerometers were used to record vibration in the orthogonal direction on all four bearing covers. Acceleration levels were calculated using the reference level 1 µm $\text{s}^{-2}$ [4].

The radiated sound power level was determined via a sound intensity measurement according to [6].

The results are shown in Figs. 4 and 5. Whiskers denote the range from measured minima to maxima. The bars for the acceleration level process measurements from all four bearing caps. Mean values, maxima, and minima of all measurements in the configuration with thrust collars are lower than in the one without thrust collars. The mean difference is shown above the respective bars. It is lower than, but still close to Heß’ initial results.

Fig. 4

Measured difference in acceleration level

Fig. 5

Measured difference in sound power level

The reduction in sound power level is lower than the reduction in acceleration level, yet considerable especially for such thick walls.

2 Theoretical Model

A theoretical model is introduced in order to further investigate dynamics of thrust collar-equipped gearboxes and to gain a better understanding of hard to measure internal parameters. As vibration excitation of plates in out-of-plane direction and bending modes leads to much greater noise emission than in-plane excitation of the same force amplitude, the analysis has to include a calculation of sound emission and can not stop at comparing bearing forces or energy spectra.

The proposed analysis thus consists of two separate partial models of the gearbox. The first one models the propagation of structure-borne sound in the interior composed of shafts, gears, bearings and thrust collars. The second one models the propagation of airborne sound radiated from the gearbox housing. As the considered housing stiffness is some orders of magnitude greater than the bearing stiffness (based on the introduced experimental gearbox), the housing does not have a significant influence on the vibration of the interior; thus a one-way coupling by imposing the calculated forces and moments from the interior model to the bearing seats of the exterior model suffices.

2.1 Interior model

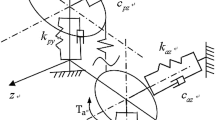
The model of the interior is shown in Fig. 6. For brevity it is reduced to the simplest shaft geometry possible. For modeling the more complex shaft geometriy of the experimental gearbox with varying diameters, additional elements need to be used.

Fig. 6

Interior model

Three translational and three rotational degress of freedom are employed. In the following calculations they are ordered $x_{i},y_{i},z_{i},\phi_{i},\psi_{i},\theta_{i}$.

For clarity, springs and dampers in Fig. 6 are shown as simplified one-dimensional elements. In general they operate in arbitrary directions.

Element numbers are shown in the center of an element, node numbers in circles on the edges of elements.

The shafts are modeled as four cylindrical Timoshenko beam elements with elements 2 and 3 as well as 6 and 7 representing the gears and the rest representing the free sections of the shafts. The stiffness matrix $\mathbf{K}_{\mathrm{S}_{i}}$ of a Timoshenko beam element with 12 degrees of freedom utilizing cubic shape functions as well as the mass $\mathbf{M}_{\mathrm{S}_{i}}$ and gyroscopic matrix $\mathbf{G}_{\mathrm{S}_{i}}$ can be taken from literature (e.g. [7]).

The insertion of a thrust collar leads to changes in roller bearing load. As the bearing stiffness is load dependent, a physical model concerning the load-displacement relationship of ball bearings [10] is first employed in calculating the static equilibrium of the torque-loaded system and then the $6\times 6$ tangent stiffness matrix of the bearings $\mathbf{K}_{\mathrm{B}_{i}}$ is calculated for the following dynamic analysis by numerical differentiation. For the configuration with thrust collars, bearings 1‑3 are non-locating bearings while bearing 4 is locating, whereas in the thrust collar-less configuration, bearing 1 is locating as well. Ball bearing damping is set as the midpoint of the relation $c=(0.25\dots 2.5)\times 10^{-5}\,\text{s}\cdot k$ from [7] for main-diagonal translational degrees of freedom; rotational and coupling degrees of freedom are modeled without damping:

$$\mathbf{C}_{\mathrm{B}_{i}}=1.375\times 10^{-5}\,\text{s}\cdot\text{diag}(k_{xx_{i}},k_{yy_{i}},k_{zz_{i}},0,0,0)$$

(1)

This empirical relation between bearing stiffness and damping also agrees well with measurements by the author reported in [15].

Thrust collar stiffness $\mathbf{K}_{\mathrm{TC}}$ is modeled as a connection between nodes 2 and 7 in directions $z$ and $\psi$:

The damping matrix $\mathbf{C}_{\mathrm{TC}}$ is built analogously by multiplying by $c_{\mathrm{TC}}$ instead of $k_{\mathrm{TC}}$.

When comparing gearboxes with and without thrust collar, solely the spring-damper-element should be switched on and off. As was noted in the experimental section, changing mass and shaft stiffness could lead to significant changes in system dynamics, yet only the connection of pinion and bull gear is a defining feature whereas system inertia could much easier be tuned by other means.

The gearing is modeled by connecting nodes 3 and 8 with a spring and damper in the plane of action normal to the gear tooth surfaces. The model is taken in modified form from [20]. The matrix for the vectorial mapping of spring and damper is built as follows:

$$\begin{aligned}\mathbf{V}=\end{aligned}$$

(3)

$$\begin{aligned}\displaystyle\begin{bmatrix}\mathrm{c}^{2}\beta\text{s}^{2}\alpha_{t}&\mathrm{c}^{2}\beta\text{s}\alpha_{t}\mathrm{c}\alpha_{t}&-\mathrm{c}\beta\text{s}\beta\text{s}\alpha_{t}&\mathrm{c}\beta\text{s}\beta s^{2}\alpha_{t}&\mathrm{c}\beta\text{s}\beta\mathrm{c}\alpha_{t}\text{s}\alpha_{t}&\mathrm{c}^{2}\beta\text{s}\alpha_{t}\\ &\mathrm{c}^{2}\beta\mathrm{c}^{2}\alpha_{t}&-\mathrm{c}\beta\text{s}\beta\mathrm{c}\alpha&\mathrm{c}\beta\text{s}\beta\mathrm{c}\alpha_{t}\text{s}\alpha_{t}&\mathrm{c}\beta\text{s}\beta\mathrm{c}^{2}\alpha_{t}&\mathrm{c}^{2}\beta\mathrm{c}\alpha_{t}\\ &&\text{s}^{2}\beta&-\text{s}^{2}\beta\text{s}\alpha_{t}&-\text{s}^{2}\beta\mathrm{c}\alpha_{t}&-\text{s}\beta\mathrm{c}\beta\\ &&&\text{s}^{2}\beta\text{s}^{2}\alpha_{t}&\text{s}^{2}\beta\text{s}\alpha_{t}\mathrm{c}\alpha_{t}&\text{s}\beta\mathrm{c}\beta\text{s}\alpha_{t}\\ &\textit{sym.}&&&\text{s}^{2}\beta\mathrm{c}^{2}\alpha_{t}&\text{s}\beta\mathrm{c}\beta\mathrm{c}\alpha_{t}\\ &&&&&\mathrm{c}^{2}\beta\end{bmatrix}\end{aligned}$$

($\text{s}\equiv\sin$, $\mathrm{c}\equiv\cos$)As the rotational degrees of freedom in matrix $\mathbf{V}$ are treated as translational ones (arc length) for compactness, they need to be multiplied by matrices $\mathbf{R}_{1}=\begin{bmatrix}\mathbf{1}_{6\times 3}&\frac{d_{1}}{2}\cdot\mathbf{1}_{6\times 3}\end{bmatrix}$ and $\mathbf{R}_{2}=\begin{bmatrix}\mathbf{1}_{6\times 3}&-\frac{d_{2}}{2}\cdot\mathbf{1}_{6\times 3}\end{bmatrix}$ for incorporation into the proposed model using angles and moments (element-wise multiplication / Hadamard product $\circ$):

$$\mathbf{K}_{G}=k_{G}\cdot\begin{bmatrix}\mathbf{V}\circ\mathbf{R}_{1}\circ\mathbf{R}_{1}^{\intercal}&-\mathbf{V}\circ\mathbf{R}_{2}\circ\mathbf{R}_{1}^{\intercal}\\ -\mathbf{V}\circ\mathbf{R}_{1}\circ\mathbf{R}_{2}^{\intercal}&\mathbf{V}\circ\mathbf{R}_{2}\circ\mathbf{R}_{2}^{\intercal}\end{bmatrix}$$

(4)

(Damping analogously using $\mathbf{C}_{G}$ and $c_{G}$ instead of $\mathbf{K}_{G}$ and $k_{G}$.)

The assembly of global stiffness matrix $\mathbf{K}$ is shown in Eq. 5 with matrix indices of one single digit denominating bearings or shafts respectively and longer indices identifying regions of matrices. Entries for $\mathbf{K}_{\mathrm{TC}}$ are omitted for studying the configuration without thrust collars. Damping matrix $\mathbf{C}$ is assembled analogously with corresponding partial matrices $\mathbf{C}_{xx}$ instead of $\mathbf{K}_{xx}$. The assembly of global mass matrix $\mathbf{M}$ is shown in Eq. 6; gyroscopic matrix $\mathbf{G}$ is built analogously by using partial matrices $\mathbf{G}_{xx}$ instead of $\mathbf{M}_{xx}$ and additionally dividing entries for the low-speed shaft by the gear ratio $u$.

As the focus of this study lies not in the modeling of parametric excitation from changing meshing stiffness and transmission error but in the analysis of the transfer path, the former is modeled by a simplified substitute. It was first shown by [18] that instead of rigorously modeling the nonlinear time-harmonic meshing phenomena, keeping the calculation linear time-invariant by utilizing a constant average mesh stiffness and displacement-driven excitation can be a reasonably accurate but much less computationally intensive alternative. The probability of missing drastic changes in dynamics due to parametric instabilities is rather low for helical gears compared to spur gears [14]. In order to compare bearing forces and moments and their phase shift, the analysis is carried out in the frequency domain with a single-frequency sinusoidal excitation. This truncation of a Fourier series representation of the transmission error achieves a further simplification – albeit an easily removable one. For comparing transmission properties, the amplitude can be chosen arbitrarily with the constraint of being small so as not to infringe on assumptions of linearizations. The excitation frequency amounts to the meshing frequency.

The dynamic system is written as a descriptor state-space model:

$$\underbrace{\begin{bmatrix}\textbf{I}&\textbf{0}\\ \textbf{0}&\textbf{M}\end{bmatrix}}_{\textbf{E}}\underbrace{\begin{Bmatrix}\dot{\textbf{q}}\\ \ddot{\textbf{q}}\end{Bmatrix}}_{\dot{\textbf{x}}}=\underbrace{\begin{bmatrix}\textbf{0}&\textbf{I}\\ -\textbf{K}&-\textbf{C}-\Omega\mathbf{G}\end{bmatrix}}_{\textbf{A}}\underbrace{\begin{Bmatrix}\textbf{q}\\ \dot{\textbf{q}}\end{Bmatrix}}_{\textbf{x}}+\textbf{B}\textbf{u}$$

(7)

$$\mathbf{y}=\mathbf{C}_{\mathrm{ss}}\mathbf{x}$$

(8)

The rotational frequency $\Omega$ is assumed to be a fraction of the excitation frequency $f$:

$$\Omega=\frac{f}{z_{1}}$$

(9)

with $z_{1}$ being the pinion’s number of theeth. For validation (following section), with the gearbox being externally excited and at a standstill, this relation is omitted and $\Omega$ is set to zero.

Apart from validation with external torsional excitation, the system is excited by applying a sinusoidally time-varying transmission error $e(t)$ at the gear mesh interface. Vectors $\mathbf{e}_{1,2}$ are used for calculating the components of the excitation in the direction of the gear spring-damper element:

$$\displaystyle\mathbf{e}_{1}=-\begin{bmatrix}\mathrm{c}\beta\text{s}\alpha_{t}&\mathrm{c}\beta\mathrm{c}\alpha_{t}&-\text{s}\beta&\frac{d_{1}}{2}\text{s}\beta\text{s}\alpha_{t}&\frac{d_{1}}{2}\text{s}\beta\mathrm{c}\alpha_{t}&\frac{d_{1}}{2}\mathrm{c}\alpha_{t}\end{bmatrix}^{\intercal}$$

(10)

$$\displaystyle\mathbf{e}_{2}=-\begin{bmatrix}-\mathrm{c}\beta\text{s}\alpha_{t}&-\mathrm{c}\beta\mathrm{c}\alpha_{t}&\text{s}\beta&\frac{d_{2}}{2}\text{s}\beta\text{s}\alpha_{t}&\frac{d_{2}}{2}\text{s}\beta\mathrm{c}\alpha_{t}&\frac{d_{2}}{2}\mathrm{c}\alpha_{t}\end{bmatrix}^{\intercal}$$

(11)

The exciting force vector $\mathbf{F}$ is nonzero at the indicated entries:

$$\displaystyle\mathbf{F}_{13-18}=\hat{e}\cdot(k_{G}+\mathrm{i}c_{G})\cdot\mathbf{e}_{1}$$

(12)

$$\displaystyle\mathbf{F}_{43-48}=\hat{e}\cdot(k_{G}+\mathrm{i}c_{G})\cdot\mathbf{e}_{2}$$

(13)

utilizing complex number notation with the complex number $\mathrm{i}$ for writing sinusoidal functions as phasors.The input matrix $\mathbf{B}$ is built as follows:

$$\mathbf{B}=\begin{bmatrix}\mathbf{0}&\mathbf{F}\end{bmatrix}^{\intercal}$$

(14)

In order to obtain a vector $\mathbf{y}$ of the bearing forces and moments, the state vector $\mathbf{x}$ is multiplied with output matrix $\mathbf{C}_{\mathrm{ss}}$ (Eq. 8)

$$\mathbf{C}_{\mathrm{ss}}=\mathbf{Q}\cdot\begin{bmatrix}\mathbf{K}_{\mathrm{B}}\mathbf{C}_{\mathrm{B}}\end{bmatrix}$$

(15)

$\mathbf{K}_{\mathrm{B}}$ and $\mathbf{C}_{\mathrm{B}}$ are the assembled total stiffness or damping matrices respectively according to Eq. 5 that contain only entries for the bearings. $\mathbf{Q}$ is a logic matrix for eliminating rows:

$$\mathbf{Q}=\begin{bmatrix}\mathbf{Q}_{\mathrm{B1}}\mathbf{Q}_{\mathrm{B2}}\mathbf{Q}_{\mathrm{B3}}\mathbf{Q}_{\mathrm{B4}}\end{bmatrix}^{\intercal}$$

(16)

with the entries

$$q_{\mathrm{Bi}_{j,6\cdot(n_{\mathrm{Bi}}-1)+j}}=1\qquad j=1,\dots,5$$

(17)

and the rest zero.

2.2 Sound radiation simulation

A parametric 3d model of the gearbox housing is set up in the commercial finite element program Ansys Workbench 19.1. In a first step, wall vibration due to the imposed bearing loads is calculated in the module “Harmonic Response”. In a subsequent step, these vibrations are employed as a boundary condition in the module “Harmonic Acoustics” for calculating the sound power level on the exterior surface of a control volume (enveloping cube of air, semi-transparent in Fig. 12).

The bearing forces and moments are modeled as loads on a remote point connected to the respective bearing bores.

Whereas material damping is ignored for the previously described interior model due to viscous oil film damping being much more significant, wall vibration is modeled including Rayleigh damping as there are no other damping mechanisms present in this subsystem. The damping coefficients are obtained from analyzing decaying acceleration levels following a hammer impact on the real gearbox. The impulse response is decomposed using wavelet transforms which allows the calculation of damping ratios for each frequency which can be used for fitting Rayleigh factors [21]. This dissipation mechanism also incorporates acoustic radiation damping.

A full two-way coupling between structure and acoustics is generally not needed for heavy structures vibrating in air [1]. The coupling strength can be judged by relating acoustic and mechanical impedances $Z_{\mathrm{A}}$ and $Z_{\mathrm{M}}$. The criterion provided in [1] can be used to assess coupling strength:

$$\begin{aligned}\displaystyle\lambda&\displaystyle=\frac{Z_{\mathrm{A}}}{Z_{\mathrm{M}}}=\frac{\rho_{\mathrm{A}}c_{\mathrm{A}}}{\rho_{\mathrm{M}}h\omega}\\ \displaystyle&\displaystyle=\frac{1.2\,\text{kg}\,\text{m}^{-3}\cdot 343\,\text{m}\,\text{s}^{-1}}{7800\,\text{kg}\,\text{m}^{-3}\cdot 60\,\text{m}\text{m}\cdot(2\pi\cdot 50\,\,\text{s}^{-1})}\\ \displaystyle&\displaystyle=2.8\times 10^{-3}\ll 1\end{aligned}$$

(18)

As the ratio of impedances $\lambda$ is much smaller than 1, a one-way coupling is adequate.

3 Validation

In order to reduce uncertainty, for validation purposes the experimental gearbox is excited by a known single-frequency sinusoidal load supplied by a shaker instead of meshing gears. Meeting experimental results from running tests would be especially difficult due to the machine bed of the experimental gearbox being quite flexible and thus transmitting structure-borne sound emitted from the motor and hydrodynamic brake. This further excitation of the gearbox housing stays constant between different configurations, but would need to be modeled in order to predict the absolute vibration level in a running test.

3.1 Values used for calculation

Variables are listed in Table 1. Average gear mesh stiffness is calculated according to Weber and Banaschek [22] using the implementation described in [9]. Gear damping is estimated from results from [8] for low speeds. The Lehr damping factor $\zeta$ employed in that source is approximately converted to viscous damping using the relation $c=2\zeta\sqrt{k\cdot m}$.

Table 1 Experimental gearbox

Thrust collar stiffness is calculated via FEM. Agreement of this method compared with experiments was demonstrated in [17]. In [13] dynamic coefficients were measured on a thrust collar test rig. This test rig represents an integrally geared compressor which means that loads are low and speeds are high compared to e.g. vehicle gearboxes or the experimental gearbox used in this article. Measured stiffness was in the order of $10^{9}$–$10^{10}$ N $\text{m}^{-1}$, damping was $10^{3}$–$10^{4}$ Ns $\text{m}^{-1}$.

From this, a thrust collar damping of $10^{2}$ Ns $\text{m}^{-1}$ is estimated for the experimental gearbox by calculating a ratio of stiffness and damping values as has been previously described for ball bearing damping.

As all viscous damping coefficients are estimates from literature and none could be measured independently due to an insufficient test setup, only rough agreement between simulation and measurement is expected. Better – but not any more legitimate – results could be achieved by tuning these initial estimates.

3.2 Interior model

For validating the interior model and the coupling of bearing forces and gearbox housing vibration, the experimental transmission is statically loaded by attaching weights to a lever. Dynamic excitation is provided by a shaker attached to said lever. This configuration is shown in Fig. 7. Measurements of bearing cap acceleration responses at the respective exciting frequencies are compared to simulation results. Due to the similar thicknesses of the gearbox wall and the machine bed of this specific test rig, the machine bed and its spring suspension need to be included in the simulation. In order to primarily conduct vibration from shaker to gearbox housing via the shafts and not via the machine bed, the lever bearing and shaker are mounted on a structure isolated from the machine bed. The exciting torque is determined using a torque sensor. As the shaker is not powerful enough to provide adequate excitation at high frequencies, only a limited frequency range is sweeped. For the best signal quality possible, the highest possible exciting torque at each frequency is used. For analysis, the accleration is thus normalized for applied dynamic torque which varies significantly. The result (Fig. 9) is quite satisfying considering the large number of poorly known variables. Resonance frequencies are shifted, amplitudes are mostly in the correct order of magnitude.

Fig. 7

Photo of the experimental transmission loaded via levers

Fig. 8

Model used for validating housing vibration calculations due to dynamic bearing forces from interior model

Fig. 9

Comparison of measured and simulated bearing cap acceleration normalized for dynamic torque

3.3 Sound radiation

As the sound emission levels attainable by exciting the transmission mounted on the heavy machine bed using the small-sized shaker are low, the sound radiation simulation is validated separately by analyzing measurements performed in an anechoic chamber with direct force excitation of the standalone gearbox housing (Fig. 10). The gearbox housing is mounted on soft springs (5 N $\text{mm}^{-1}$) in order to provide a suspension with known properties. The exciting force is applied as a point load to the center of the gearbox floor. The exciting force is measured via strain gauges applied to the exciting rod. The applied maximum possible force amplitude does not vary as irregularly as the aforementioned torque does, so no normalization is applied. It decreases approximately linearly from minimum to maximum frequency from 6.8 to 4.8 N. As the shaker radiates sound as well, its accelerations are recorded and following time integration used to apply velocities to the according faces in the simulation model. For validation, sound pressure levels at the respective exciting frequencies are compared at a set position (center of gearbox in horizontal direction, 500 mm higher than top gearbox cover in vertical direction). Measurements are performed at reference frequencies according to [5].

Fig. 10

Gearbox housing in an anechoic chamber. The microphone distance is reduced for the photo

Results are shown in Fig. 12. Apart from the lowest frequency, differences in sound pressure level are less than 3 dB.

Fig. 11

Model used for sound radiation simulation validation. The enveloping cube of air is semi-transparent

Fig. 12

Comparison of measured and simulated sound pressure levels

The above-described validation results for both subsystems do not suggest a gross error in modeling. A better match via more precisely-determined parameters, validation in a greater frequency range and validation of the whole running system would be worthwile but would require a more tailored test rig.

4 Analysis

4.1 Bearing force

For explorative calculations a simplified version of the experimental gearbox is used where the shaft is made up of the minimum number of segments as shown in Fig. 6 with the mean shaft diameter from Table 1 as an end-to-end diameter. This is done for space reasons in order to avoid printing detailed blueprints for reproducibility.

Calculated differences in bearing force amplitude levels are shown in Fig. 13. Negative levels mean lower force levels in the configuration with a thrust collar than in the configuration without one. As resonance frequencies are shifted by changes to the dynamic system, there are peaks in the difference levels resulting from resonances being hit in only one system at a time. It is assumed that systems could be tuned to some extent freely in order to shift resonances out of critical frequency ranges in operation. Therefore the focus of this analysis lies not on the difference in peak amplitudes caused by resonances but on averaged overall behaviour.

Fig. 13

Comparison of bearing force amplitudes in the base configuration gearbox with and without thrust collar. Negative force amplitude difference levels $\Delta L_{F}$ mean lower force levels in the configuration with a thrust collar than in the configuration without one

It can be seen from the sharp changes at the ordinate of some bearing force/moment differences, that static bearing force/moment differences can not be used to asses dynamic differences. Where both configurations have a locating bearing (bearing 4), axial force Fz is only close to zero for low frequencies for the configuration with a thrust collar. At higher frequencies, the difference between both configurations decreases. The reduction in axial bearing force at the second locating bearing for the configuration without a thrust collar cannot be shown as a difference level (division by zero). It can further be found that the average difference level is positive for some components at some bearings and negative for others. Thus the impact on acoustics cannot be gauged from only interpreting bearing force levels.

When using a constant bearing stiffness instead of the detailed load-dependent model, resonance frequencies mostly stay constant between the two configurations. Average differences in bearing force amplitude levels are positive for some components and negative for others as well.

4.2 Housing vibration

The computer model of the experimental gearbox housing is fixed at its feet for this vibration simulation and the following acoustic simulation (instead of the soft spring suspension used for validation). Acceleration difference levels in large frequency ranges have different signs at different bearings (Fig. 14) which means that the impact on acoustics cannot be gauged from housing vibration and thus needs to be analyzed in a sound radiation simulation.

Fig. 14

Simulated acceleration difference levels. Negative difference levels mean lower acceleration levels in the configuration with a thrust collar than in the configuration without one

4.3 Sound radiation

As sound radiation simulations are highly resource intensive, it would be unfeasible to examine a complete frequency sweep. Instead, in order to exclude the influence of shifting resonances, only midpoints of frequency ranges that lie further than 10 Hz away from a shifting phase response in any degree of freedom of the bearing seats are considered. For automated elimination, a threshold of 1° $\text{Hz}^{-1}$ is used for the phase gradient. These filtered frequencies include cases with different signs of acceleration difference levels.

Simulation results are shown in Fig. 15. At all considered frequencies the sound pressure difference level is negative, which means lower noise emissions for the configuration with a thrust collar. Difference levels are greater than in the running test, which can probably be explained by three factors: First, although no large changes in sound pressure level were observed at neighboring frequencies to the test frequencies, the selection of running speeds could not be made using the rather aggressive method of discarding frequencies on the basis of phase shifts, which also excludes minor effects of resonances not apparent from examining just the measured sound pressure levels. Second, sound pressure levels were measured as a compound of meshing excitation and further excitation from motor and brake conducted via the machine bed. This further constant excitation is not included in the simulation model. Third, the experimental gearbox has a comparatively sound-permeable acrylic top cover, which leads to sound radiated directly from the gears being included in the measurement as well.

Fig. 15

Simulated sound pressure difference levels at frequencies well clear of resonances. Negative difference levels mean lower sound pressure levels in the configuration with a thrust collar than in the configuration without one

5 Conclusions

The hypotheses that Heß’ experimental results were solely the result of better load-bearing behavior of the gears due to lower tilting angles or due to different transmission properties of the differently-loaded bearings – mechanisms that can be achieved by simpler means – could be disproved by not modeling the former and suppressing the latter for a short analysis. The implemented model instead aids in recognizing that the use of thrust collars leads to changes in gearbox acoustics due to the altered vibration excitation at the bearing seats. Further analysis is needed in order to obtain sufficient insight for targeted optimization. Possibly thrust collars can merely be used for attenuating noise in a specific frequency range while being counter-productive in others.

In order to model more realistic vehicle gearboxes with much thinner walls and possibly higher gains, bearing seat stiffness needs to be included in the analysis of the interior.

For efficient analysis, the sound radiation simulation needs to be replaced by less resource-intensive substitute models, e.g. analytical plate vibration models. This would allow the simulation of a large number of different operating points whose power levels could then be used for an averaged overall comparison over the whole operating range without the need for filtering out single evaluation points for possible interference of resonances.

Further experimental validation is crucial. This requires a much revised test rig in order to be able to measure partial influences and influences of different variables.

The potential of thrust collars for acoustic improvements is high as this modification to the transfer path could be used as an additional measure on top of already established ones.

Nomenclature can be found in Tab. 2.

Appendix

 

Table 2 Nomenclature