1 Introduction

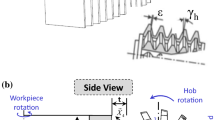
Gear hobbing is an established gear manufacturing process and is widely used in the wind power, automotive, aerospace and general engineering applications [1]. For the evaluation of the tool load and the interpretation of the wear behavior, uncut chip geometries such as the maximum uncut chip thickness are often used [2,3,4,5]. Due to the complexity of the hobbing kinematics and chip formation, numerical penetration calculation software such as SPARTApro [3, 4], FRS/MAT [5] or HOB3D [6] have to be used for the determination of the uncut chip geometries. The disadvantage of the geometric approach is the insufficient description of the contact conditions between tool and workpiece. Material properties, cutting speed, cutting edge shape as well as the (effective) rake and clearance angles have no influence on the uncut chip geometry.

To take physical properties into account, researchers have extended the penetration calculation by empirical and analytical models. On the one hand, cutting force models have been developed to predict the resulting force components for the hobbing process [7, 8]. The forces are calculated based on the uncut chip thickness from the penetration calculation and empirical coefficients determined in machining trials. On the other hand, models for the prediction of cutting forces and mean rake face temperatures using an analytical formulation of the orthogonal cut have been reported [9, 10].

For a detailed analysis of the thermomechanical load in the gear hobbing process, Finite Element Analysis (FEA) was applied in recent studies. Bouzakis et al. used the FE software Deform 3D to analyze the chip formation [11, 12], the cutting forces [12] as well as the tool stresses [13]. Liu et al. studied the thermomechanical load of a cutting engagement for rack and pinion milling [14], while Dong et al. analyzed the tool wear [15]. Karpuscheski et al. reported on the influence of different tool profiles on the cutting temperature in individual generating positions using the FE software AdvantEdge [16, 17]. Due to the high computational time required for the simulation, the aforementioned FE simulations were usually limited to the interaction of only one tooth with the workpiece material. To evaluate the load collective of the entire process, all generating positions would have to be simulated, which would exponentially increase the required simulation time. For an efficient analysis of the full hobbing process, a method is required which allows the analyzation of the thermomechanical tool load for all generating positions within a reasonable simulation time.

The aim of this work is to predict the thermomechanical tool load in gear hobbing by means of a multiscale model. The model combines the uncut chip geometries from a geometric penetration calculation (macro scale) with thermomechanical load and state variables from FE simulations of the orthogonal cut (micro scale). Cutting speed, uncut chip thickness and rake angle are varied within a defined parameter space in FE simulations using Abaqus/CAE. Cutting forces and rake face temperatures are obtained from the simulation based on the workpiece material behavior as well as the contact conditions at the tool/chip interface. Functional relationships between the obtained thermomechanical quantities and the variation parameters are deducted. The hobbing process is then simulated by means of the geometric penetration calculation SPARTApro and the uncut chip geometries are determined for each generating position. To calculate the cutting force and temperature profile, the determined approximate equations are solved at every discrete point of the cutting edge for each generating position based on the local uncut chip geometries. The result is a multiscale model for describing the thermomechanical tool load in each generating position.

2 Analysis of the thermomechanical load in the linear-orthogonal cut

2.1 Setup and conditions of the simulation

The simulation was carried out by means of a thermomechanically coupled, explicit FE model of the linear-orthogonal cut using the Coupled Eulerian-Lagrangian (CEL) formulation in Abaqus/CAE 6.14‑6, Fig. 1. Similar models have been used by other researchers who validated the suitability of such a model to represent the orthogonal cut [18,19,20].

Fig. 1
figure 1

FE model of the linear-orthogonal cut and parameter space

Full size image

The workpiece material domain was discretized by the Eulerian formulation using EC3D8RT elements, while the stationary tool was meshed using C3D8RT elements with Lagrangian formulation. The smallest edge length was lE = 6 µm for the Eulerian domain and lE = 2 µm for the tool. The chip is formed by the continuous flow of the material through the Eulerian domain against the tool. Due to the fixed mesh, this method is insensitive to large deformations and no distortion of the elements occur [21].

Case-hardening steel 18CrNiMo7‑6 was used as workpiece material and tungsten carbide as cutting substrate. The mechanical and thermal properties of the respective materials used for the simulation are shown in Table 1.

Table 1 Mechanical and thermal properties of cutting and workpiece material at 20 °C
Full size table

The thermomechanical workpiece material behavior was described according to the Johnson-Cook (JC) constitutive material law, Eq. 1 [22] :

$$\sigma _{F}\left(\epsilon ,\dot{\epsilon },\vartheta \right)=\left(A+B\cdot \epsilon ^{n}\right)\cdot \left(1+C\cdot ln\dot{\frac{\epsilon }{\dot{\epsilon _{0}}}}\right)\cdot \left(1-\left[\frac{\vartheta -\vartheta _{0}}{\vartheta _{m}-\vartheta _{0}}\right]^{m}\right)$$
(1)

where σF is the flow stress, ϵ the equivalent plastic strain, \(\dot{\epsilon }\) the plastic strain rate, \(\dot{\epsilon }_{0}\) the reference strain rate, ϑ the current temperature and ϑm melting temperature. A, B, C, n and m are material constants determined in experiments at or below the transition temperature ϑ0. The constants are shown for a soft state case-hardening steel 18CrNiMo7‑6 as a typical steel grade for gears in Table 2. The material constants were validated by Abouridouane et al. for an FE simulation of the orthogonal cut [18]. The simulations were performed using the same simulation environment and FE formulation as in the present case. It can therefore be assumed that the material model is also valid for the present case.

Table 2 JC parameters for case-hardened steel 18CrNiMo7‑6 [18]
Full size table

The friction at the tool/chip interface was described by the Couloumb friction law at a constant coefficient of friction of μ = 0.4. The fraction of plastic work converted into heat was considered by a Quinney-Taylor coefficient of β = 0.9 and the thermal contact by a contact heat transfer coefficient of ht = 104 W / (m2 ⋅ °C) [21, 23].

The uncut chip thickness was varied in the range of 0.01 ≤ hcu ≤ 0.25 mm, the cutting speed in the range of 50 ≤ vc ≤ 400 m/min and the rake angle by γ = 0° ± 4°, Fig. 1. The chosen ranges represent common values for gear hobbing of small to medium sized gears made of case-hardening steel. The parameter combination vc = 200 m/min, hcu = 0.1 mm and γ = 0° was used as reference. Since the simulation can be evaluated at different time increments, the uncut chip length was kept constant at lcu = 30 mm. The cutting edge radius and the uncut chip width were rβ = 20 µm and bcu = 0.02 mm. The clearance angle was α = 10°. The evaluation of the cutting force Fc was performed at the tool reference point (RP) in x-direction and the evaluation of the temperature ϑ along the rake face at different time increments of the simulation.

2.2 Modeling of the cutting force

In the simulation, the cutting force Fc corresponds to the force component acting on the tool in x-direction. The force was averaged over 200 time increments and divided by the uncut chip width bcu = 0.02 mm to form the specific cutting force \(F_{c}^{'}\).

The specific cutting force \(F_{c}^{'}\) decreased with increasing cutting speed vc due to thermal softening of the workpiece material, Fig. 2. With increasing uncut chip thickness hcu, a linear increase of the cutting force can be observed as a result of the increasing uncut chip cross section. A negative rake angle resulted in a higher specific cutting force than a positive rake angle, which can be attributed to an increasing plastic deformation with decreasing rake angle. The observed effects are in accordance with acknowledged machining theory such as Merchants shear plane theory [24].

Fig. 2
figure 2

Influence of the variation parameter on the specific cutting force

Full size image

Based on the simulations, a regression model for the specific force was parameterized following the basic Kienzle model by assuming a steady-state process [25]. The influence of the uncut chip thickness and the cutting speed is described as a power function and the influence of the rake angle as an exponential function. The modeled specific cutting force \(F_{c,\mathrm{mdl}}^{'}\) matches the simulated specific cutting force \(F_{c,\mathrm{sim}}^{'}\) with a coefficient of determination of R2 = 0.9894.

2.3 Modeling of the temperature distribution on the rake face

In contrast to the cutting force, the temperature was not determined as an average value of all time increments, but as a function of time and rake face position. The recorded temperature profile starts at x = 0, which was defined as the location where the curvature of the cutting edge radius changes into the straight line of the rake face, Fig. 3. The temperature profile over the curvature of the cutting edge radius was not considered.

Fig. 3
figure 3

Course of temperature along the rake face and over time

Full size image

Most of the power consumed in machining is converted into heat. The power Pc required for metal cutting is given by Eq. 2:

$$P_{c}=F_{c}\cdot v_{c}$$
(2)

where Fc is the cutting force and vc the cutting speed. The conversion of power into heat occurs in two principal regions of plastic deformation: The primary shear zone (PSZ) and the secondary shear zone (SSZ). The resulting temperature at the tool/chip interface is then given by the heating of the material passing through the heat sources at the shear zones. Starting with an initial temperature ϑγ,x0 at x = 0 mm, the temperature increases almost linearly until reaching a maximum value and then decreases towards an asymptotic limit of ϑγ,0. The maximum temperature ϑγ,max at the tool/chip interface occurs where the material leaves the SSZ at xϑγ,max. [26].

In the area of the temperature rise, the chip and the tool are in contact. The temperature drops as the contact between chip and tool breaks. Compared to the cutting force, the temperature requires more time to change into a steady state. This transient behavior must be taken into account when modeling the temperature, since the temperature is otherwise overestimated at the beginning of the cut.

Temperature profiles as a function of the variation parameters are shown in Fig. 4. The influence of the rake angle γ was not considered in this case, as only a minor influence of the rake angle on the temperature profile was found in initial simulations. Instead, the time dependency of the temperature was taken into account. An increase in the cutting speed led to a quantitative increase in the temperature due to a higher power consumption in the cutting process which is converted into heat. For a cutting speed of vc = 50 m/min and an uncut chip thickness of hcu = 0.1 mm, the maximum temperature ϑγ,max was present directly at the cutting edge at x = 0 mm. At cutting speeds of vc > 150 m/min, the position of the maximum temperature was shifted towards the rake face. When cutting at low speeds, sliding contact between tool and chip may be dominant at the tool/chip interface, while at higher cutting speeds, a flow-zone is observed where the chip is seized to the rake face [27]. Depending on the contact conditions at the tool/chip interface, the mode of heat generation and the temperature distribution can differ. Essentially, at low cutting speeds, the rate of heat generation due to plastic deformation in the PSZ is higher than the rate of heat generation in the SSZ due to friction and thus no further increase in temperature occurs at the tool/chip interface.

An increase in the uncut chip thickness led to an increase in the temperature, as well as to an increase in the distance between the position of the maximum temperature and the cutting edge. The higher temperatures can be attributed to the increasing cutting force (cf. Fig. 2), that is required for the machining of larger cross-sections, and therefore to a higher energy which is converted into heat. The extension of the heated area further from the edge is due the increase in the contact length between tool and chip. With increasing cutting time the temperature increases and approaches a stationary state.

Fig. 4
figure 4

Comparison of modeled and simulated temperature profiles

Full size image

Approximate equations for calculating the temperature ϑγ,x0 at x = 0 mm, the maximum temperature ϑγ.max and the position of the maximum temperature xϑγ,max were developed, Fig. 4. For the calculation of the complete profile, the temperature between ϑγ,x0 and ϑγ.max, is approximated linearly, while the temperature drop is modeled using a power law. For the latter, it was assumed that the curve tends toward the ambient temperature.

For the calculation of the maximum temperature, the restriction was established that its location always occurs in distance to the cutting edge and is not affected by the cutting speed. Consequently, the location solely depends on the uncut chip thickness. This reduced the modeling effort while providing good agreement for most observations. The shortcoming of this approach is apparent at a cutting speed of vc = 50 m/min. At this cutting speed, the maximum temperature was almost exclusively reached at the cutting edge, which led to incorrect values in the calculation. Since usual cutting speeds for hobbing soft state case-hardening steels are vc > 150 m/min, the deviation at low cutting speeds can be regarded as negligible. Further deviations were observed for small uncut chip thicknesses of hcu < rβ and small time increments τ < 2 ms. These deviations could become more relevant if high cutting speeds are used in the machining of small-module gears. Here, the model must be further optimized in the future.

3 Coupling of the approximate equations with the penetration calculation

The hobbing process was calculated with the manufacturing simulation SPARTApro based on a geometric penetration calculation. SPARTApro is an established simulation method for gear hobbing and has been used in various research activities [2,3,4]. The software abstracts the workpiece into a defined number of parallel planes, which are penetrated by the tool profile during the simulation of the machine kinematics, Fig. 5. The intersections between the tool envelope body and the workpiece planes represent discrete uncut chip cross-sections over the tool rotation angle. The uncut chip cross-sections have defined uncut chip thicknesses and widths along the cutting edge. The locally and temporally known uncut chip geometries are used as input variables for the equations developed in Sect. 2.

Fig. 5
figure 5

Procedure for scaling the cutting force and temperature to the macro scale

Full size image

The calculation of the resulting cutting force on the macro level was performed according to the established method of discrete addition of the forces along the cutting edge over all individual cross-section elements at a certain point of time [7, 8]. In the calculation, the local cutting speed vc,lok at the cutting edge point must also be taken into account. The resulting cutting force is calculated for each point in time or tool rotation angle of the cut, resulting in a continuous force curve over the cutting engagement.

3.1 Calculation of the temperature for variable uncut chip thickness profile

In contrast to the cutting force, the prediction of the temperature at each cross-section element is more complex. On the one hand, the individual cutting time at each point of the cutting edge must be taken into account. On the other hand, the temperature varies across the rake face. Additionally, a variable uncut chip thickness profile and the transient behavior at the beginning of the cut must be considered.

For a typical uncut chip geometry, the procedure for temperature calculation is shown schematically in Fig. 6. The ordinate describes the tool profile on which the individual cutting edge increments xp are located. The profile is divided into a leading (LF) and a trailing flank (TF). The abscissa indicates the cutting time t and the start of cut for each point of the cutting edge. The points of the cutting edge come into contact with the material at different times. This is taken into account by the time variable τ, which represents the individual cutting time at the respective cutting edge position. The uncut chip thickness hcu at time t at a point xp of the cutting edge can be derived from the color scale.

Fig. 6
figure 6

Calculation of temperature with variable chip thickness profile

Full size image

In a representative cross-section A‑A (xp = 0 mm), the cut starts at time τ0 and ends at τend. To calculate the cutting force at any time τ, the chip thickness hcu(τ), calculated by the penetration calculation, is used. This approach is valid because the force transitions to a steady state almost instantaneously (cf. Fig. 3). The temperature, however, is subject to a stronger time dependence. If an arbitrary chip thickness is passed to the model at time τ, it is assumed that this chip thickness has been present since the beginning of the cut. The use of the chip thickness hcu(τ) at time τ would therefore lead to a larger uncut chip cross-section A(τ) than the actual uncut chip cross-section Acu(τ). Since the uncut chip cross-section is proportional to the work done, the energy consumption and consequently the resulting temperature would be overestimated. For this reason, the mean chip thickness hcu,m(τ), averaged from τ0 to τ, is used. The model still assumes that the transferred chip thickness is present since the beginning of the cut. In this case, however, the area of the uncut chip cross-section is equal to the area of Acu(τ). Therefore, the energy supplied to the system is comparable.

To verify whether the mean uncut chip thickness hcu,m(τ) can be used for the discrete calculation of the temperature, an FE model with triangular uncut chip thickness profile was setup, (Fig. 6 top right). The boundary conditions as well as the material and contact model were used analogously to the FE model of the linear-orthogonal cut described in Sect. 2.1. The result of the simulation is compared to the calculated temperature profiles (Fig. 6 bottom right). It is evident that both a calculation with hcu(τ) and with hcu,m(τ) follow the qualitative course of the simulated temperature. The temperature profile calculated with the mean uncut chip thickness hcu,m(τ) also shows a quantitative agreement with the simulated temperature curve. Towards the end of the cut, however, the calculated temperature does not drop as fast as in the simulation. In this case, better agreements with the first approach are observed.

Since the second approach adequately describes the temperature curve both qualitatively and quantitatively until shortly before the end of the cut is reached, it is used in all further considerations. To describe the rapid temperature drop towards the end of the cut, the temperature values are numerically reduced to ambient temperature by means of a decay function.

3.2 Calculation of the temperature on the macro scale

Analogous to the cutting force, the rake face temperature was calculated at explicit time increments t based on discrete cross-section elements of the cutting edge. The local cutting speed vc.lok, the cutting time τ at which the cutting edge element is in contact and the mean uncut chip thickness hcu,m(τ) serve as input variables. The temperature profile along the rake face was determined according to the procedure described in Sect. 2.3. For this purpose, the assumption was made that no interactions with neighboring cutting elements occur. Effects due to unfavorable chip formation at curved areas are also not considered by the model.

Fig. 7 shows the temperature calculation for an exemplary gear case with a normal module of mn2 = 2.557 mm for a representative generating position. The rake face temperature is analyzed at five different time increments. At t1 = 5.8 ms, the trailing flank (TF) is in contact with the workpiece. The average temperature at this time is ϑγ,1 ≈ 400 °C. At t2 = 8.3 ms, a larger area of the trailing flank as well as the tool tip are involved in the cutting process. After t3 = 10.8 ms, the maximum uncut chip thickness is reached at the tip, resulting in temperatures of approximately ϑγ,3 = 740 °C in this region. The maximum temperature of ϑγ,4 = 750 °C is calculated in the region of the tip radius of the trailing flank at t4 = 11.5 ms. The magnification of the corresponding area shows that the maximum value does not occur directly at the cutting edge, but at a distance to it. On the one hand, the fact that the highest temperature occurs at this point is due to the high average chip thicknesses machined with this cutting edge element. On the other hand, the additional long contact time of the element with the workpiece leads to a higher temperature. Cutting edge elements with higher chip thicknesses but short contact times exhibit lower temperature values. At t5 = 14.6 ms, only the leading flank is in contact. Due to the low uncut chip thicknesses and comparatively short contact times, only low temperatures are present.

Fig. 7
figure 7

Calculation of temperature distribution on the rake face

Full size image

It can be concluded that the model is capable of calculating the temperature profile on the rake face with spatial and time resolution. As the thermal load strongly influences the tool wear, the knowledge of the temperature profile is extremely useful for tool wear predictions and process optimization. Compared to an FE simulation, the developed model requires significantly shorter calculation times (minutes instead of days) and can therefore be used to calculate the temperature profile for all generating positions in the hobbing process efficiently. By its nature, the model is only valid for the configured parameter range. In addition, as the chip formation is not actually simulated, deviations between the modeled temperature profile and by FE simulated profile are to be expected. For further considerations, load collectives can be derived on the basis of the model, which describe the frequency of the occurring temperature values at critical points of the cutting edge or the rake face.

4 Validation of the multiscale model

For validation of the model, two methods were pursued: First, the calculation of the cutting force was verified in machining trials by means of the fly-cutting process. Second, the temperature distribution was compared to an FE simulation of a full engagement of a single hob tooth.

4.1 Verification of the cutting force calculation in machining trials

The calculation of the cutting force was verified by using force and torque measurements in the fly-cutting trial, Fig. 8. The fly-cutting trial represents an established analogy process to gear hobbing, where a single hob tooth reproduces all the generating positions of the corresponding hob by means of a continuous shift process [28]. The trials were carried out on a Liebherr LC180 gear hobbing machine. The cutting force Fc and the torque Mv were measured with a rotating multi-component dynamometer Kistler RCD 9171A, which was mounted between the tool and the main bearing. In the process, reaction forces occur at both the main and the counter bearing of the tool shaft, whereas the resulting torque around the tool axis is absorbed only by the main bearing. Investigations by Klocke et al. also revealed interfering signals in the range of cutting forces during force measurements in the fly-cutting trial [29]. For this reason, the validation was carried out exclusively on the basis of the torque measurement.

Fig. 8
figure 8

Setup of the fly-cutting trial and design of experiments

Full size image

Gear and tool geometry were the same as for the simulation. All trials were carried out in climb cut at dry cutting conditions. The cutting speed vc and the feed rate fa were varied. The resulting maximum uncut chip thickness hcu,max,Hoff was calculated according to Hoffmeister [3] from the feed rate fa and is specified in Fig. 8. The workpiece material was a case-hardening steel 20MnCr5. A detailed characterization of the material can be found in a recent study of Troß et al., where the exact same material batch was used for tool wear investigations [28]. The material used for the trials does not fully correspond to the case-hardened steel 18CrNiMo7‑6 on which the simulations are based. However, both materials have a comparable ferritic-pearlitic material structure, cf. [18, 28], and mechanical and thermal properties, cf. [30, 31]. Therefore, this comparison is considered sufficient. The tools used were separated from a WC-Co K30 carbide hob with an AlCrN coating.

The maximum torque of each test point was then calculated and compared to the maximum measured torque. The results are shown in Fig. 9. The calculated maximum torque Mv,max is in good agreement with the measured torque for all test points. A maximum deviation of approx. 4% was observed. The results confirm that based on FE simulations of the orthogonal cut, the cutting force can be reproduced. Despite that the material model deviates from the test material, a good agreement between model and simulation was achieved. In order to optimize the model, the material and contact laws for the material used in the machining trial must be parameterized in future experiments.

Fig. 9
figure 9

Comparison of measured and calculated maximum torque

Full size image

4.2 Verification of the temperature calculation by FE simulation

Due to the limited accessibility of the cutting zone in the fly-cutting trial, the verification of the temperature calculation was performed using an FE simulation of a full tooth engagement for the previously considered gear case, Fig. 10. The model was created in Abaqus/CAE with thermomechanically coupled Eulerian-Lagrangian (CEL) formulation. All workpiece and cutting material parameters as well as contact conditions were chosen as for the orthogonal cut simulation (cf. Sect. 2.1). The tool rotates on its axis with a rotational speed n0 and is simultaneously shifted along its axis at a tangential speed vt. The translational motion reproduces the helix of the hob, while the rotational motion generates the cutting speed vc. An ideal cutting edge with rβ = 0 µm was assumed, as a cutting edge radius drastically increased the simulation time. The tip clearance angle was αan = 10° and the tip and flank rake angle were γan = γfn = 0°.

At the beginning of the simulation, a part of the stationary Eulerian domain is assigned to the material in the form of the gap to be machined. The gap geometry of the considered generating position was extracted from the previously used penetration calculation SPARTApro and transferred to Abaqus/CAE in STEP file format. The relative position of the tool at the beginning of the cut was also taken from the penetration calculation. As the tool comes into contact with the material during the cutting movement, a chip is formed based on the implemented material and contact laws.

Fig. 10
figure 10

Setup of FE simulation of full cutting engagement

Full size image

A disadvantage of the CEL method is that the Eulerian domain and not the workpiece gap has to be meshed. This limits a local adjustment of the mesh resolution in the area of chip formation. Almost the entire Eulerian domain has to be meshed with the same resolution. With the considered element length of lE = 40 µm, approximately 4 × 107 elements would result for the Eulerian domain with uniform meshing. By partitioning, the number of elements were reduced to about 2 × 107 elements, which, however, still places high demands on the required computing power. The simulation was performed on 48 cores (Intel Xeon Platinum 8160 “SkyLake” 2.1 GHz) and required about two weeks of computing time. A resolution comparable to the simulation of the orthogonal cut with a smallest edge length of lE = 6 µm could not be reasonably realized with this method.

The comparison between the model and the FE simulation is shown in Fig. 11. For a representative generating position, temperatures at t = 4.2 ms and t = 4.9 ms as well as the course of the cutting force Fc over the tool engagement are compared. Comparable maximum temperatures were obtained in the simulation, however, deviations regarding the temperature distribution can be observed. The stressed area of the rake face simulated by FE is larger than the one predicted by the model. In the simulation, a large portion of the rake face exhibits temperatures around ϑγ = 400 °C. In the model, the temperature drops shortly after the cutting edge. The reason for this may be found in the chip formation, which deviates from the linear orthogonal cut. Since the chip cannot roll up unhindered, a larger area of the rake face is in contact with the chip. However, for the evaluation of the tool load only the maximum values are initially of interest. While the maximum temperature values are in good agreement, the position of the occurring maxima must still be verified in further investigations.

Fig. 11
figure 11

Comparison of model and FE simulation

Full size image

A significant difference can be observed in the comparison of the simulated and the modeled cutting force Fc. The simulated force exceeds the modeled value up to 70%. In addition, the data points of the simulated cutting force show a strong scattering for t > 3 ms. The reason for this can be found in the resolution of the Eulerian domain. During the tool engagement, small uncut chip thicknesses of hcu < 40 µm are present on the tool flanks (cf. also Fig. 7). Since the uncut chip thicknesses are smaller than the selected resolution of lE = 40 µm, the forces are overestimated. In the area of the tool tip, a minor influence is to be expected, since uncut chip thicknesses of hcu > 100 µm predominate. As the cutting force significantly influences the resulting temperature, a reliable comparison of the rake face temperature is only possible if the simulated and modeled force agree. Therefore, the simulation must be further optimized in this respect. Finally, simulation and model have to be validated in machining trials.

5 Summary

A multiscale approach on how to describe the thermomechanical tool load in gear hobbing was presented. At the micro scale, FE simulations of the orthogonal cut were used to analyze the interaction of the cutting edge with the workpiece material. Equations for calculating the specific cutting force \(F_{c}^{'}\) and the local rake face temperature ϑγ were derived. The deducted equations indicated good agreement with the simulation results. For the calculation of the temperature profile, deviations were observed for uncut chip thicknesses of hcu < rβ and for a cutting speed of vc = 50 m/min cut. For the present case, these deviations were negligible with regard to the focused gear size and the cutting speed range relevant for the material group. Depending on the application, further optimization may be required. For future investigations, additional parameters, such as the cutting edge radius or the coefficient of friction are to be included in the model consideration.

The macro scale was calculated with the geometric penetration calculation SPARTApro. This allowed a spatially and temporally resolved determination of the uncut chip geometries for each generating position. The uncut chip geometries were used as input variables for the derived approximate equations, which were solved at each point of the cutting edge for each generating position. The scaling of the cutting force was performed according to the established procedure of discrete addition of the forces along the cutting edge over all individual cross-section elements.

For the calculation of the temperature, an approach to consider a variable chip thickness profile by means of the mean uncut chip thickness hcu,m(τ) was presented. Based on this, the temperature distribution on the rake face of a hob tooth in one generating position was calculated.

The verification of the calculated cutting force was carried out using torque measurements in the fly-cutting trials. A comparison of calculation and experiment showed good agreement. Since a material model deviating from the test material was used, further optimization potential is to be expected here.

Due to the limited accessibility of the cutting zone, the temperature distribution could not be verified in the fly-cutting trial. The model was therefore compared to an FE simulation of a full engagement of a hob tooth. Although CEL formulation is well-suited for the orthogonal cut, limitations in simulating a full tooth engagement were apparent. Even with a relatively large element size of lE = 40 µm, a great number of 2 × 107 elements were required for meshing the Eulerian domain. Since uncut chip thicknesses smaller than the applied element size are present on the tool flanks, forces up to 70% higher than calculated by the model were simulated. As the force significantly influences the resulting temperature, a reliable comparison of the rake face temperature was only possible to a limited extent. In future investigations, the FE model of the full tooth engagement must be further optimized.