1 Introduction

A major focus in the development of gear boxes is the optimization of the gears. The aim is to increase the transferable power as well as the efficiency and load capacity of those components. At the same time, the demands on the design process are growing in terms of development time and financial effort. The use of simulation tools can shorten the design process and significantly reduce the need for costly gear tests.

BECAL is a comprehensive simulation tool for the tooth contact analysis (TCA) of bevel, hypoid, beveloid and cylindrical gears, developed at the IMM (TU Dresden) in cooperation with the Institute of Geometry at the Faculty of Mathematics (TU Dresden). It allows the calculation of local stress on the tooth flank as well as in the tooth root. Derived from this, the local load capacity regarding flank and root can be determined. In addition, this simulation tool enables the consideration of the efficiency as well as an analysis of the acoustic excitation in the tooth mesh. The BECAL calculation process is shown in Fig. 1 [1].

Fig. 1
figure 1

BECAL calculation process

Full size image

The flank and root geometry of the gear is provided by a manufacturing simulation, a geometry import or measurement data. The geometry is thus represented by a discrete 3D point cloud. However, in order to perform the stress calculation, it is necessary to determine the coordinates, normals and curvatures for each of these points. In addition, for tooth stiffness determination and tooth root stress calculation (BEM method [1, 2] or FEA method [3]), it is necessary to identify arbitrary points in the tooth root.

To do this, the discrete data points are transformed into a mathematically closed surface representation. At present, this is an approximation with Bézier tensor product surfaces. Depending on the tooth geometry, this surface representation can result in significant deviations between the approximated surface and the given points. Especially local modifications, such as tip and root relief or local flank damage (e.g. micro pitting, wear) can be insufficiently represented with this approach.

Thus, surface deviations can have a direct impact on the calculation of flank and root stresses. For example, the curvature on the flank has a significant influence on the Hertzian pressure, which in turn is the basis for the load capacity against pitting and micro pitting. The same occurs with the representation of the root geometry, which can have an effect on the root stress and, accordingly, on the tooth root capacity. Finally, such deviations are compensated for by an increased safety factor in the gear design, which means that the potential of the gears cannot be completely utilized.

In this context, this paper focuses on the surface representation with non-uniform rational B‑spline surfaces (NURBS) with the aim of significantly improving the approximation of the flank and root geometry. For this purpose, both the Bézier and NURBS approach are compared based on their mathematical properties. Furthermore, the results of the representation accuracy, the local stress for flank and root, and the local load capacity are used to demonstrate the potential of the alternative NURBS approach for an improved gear design process.

2 Gear geometry representation in the tooth contact analysis

There are several simulation tools for the tooth contact analysis (TCA), which differ in the range of available gear types and in the degree of complexity and thus in the computational effort and time required. In the following section, two additional tools are presented to give a classification of the BECAL TCA.

RIKOR, developed at the FZG (TU Munich), is a TCA program for the calculation of spur, helical and double helical gears. It is able to consider tooth flank modifications but also to determine shaft deformations and bearing deflections of the surrounding system and to take these into account in the tooth contact simulation. The geometry of the cylindrical gears is described purely analytically from the involute profile according to DIN 3960. Hence, the determination of the contact distances in the tooth mesh, which is necessary for the further stiffness and stress calculation, is also conducted analytically and therefore requires less computing time. However, by using the theoretical geometry from DIN 3960, the actual geometry resulting from the manufacturing process cannot be taken into account. Furthermore, the geometry of bevel and hypoid gears cannot be calculated with this analytical approach due to the multiply curved flank and root geometry [4].

ZaKo3D, developed at the WZL (RWTH Aachen University), is another TCA tool that is comparable to BECAL in terms of manufacturing simulation and calculation of stiffness and stress, but has a significant difference in the representation of flank and root geometry. Since in BECAL the flank surface is approximated in a manner that the contact distance between the flanks in the mesh can be determined analytically, the contact analysis is accurate and very fast [1, 5]. In contrast, ZaKo3D uses an interpolation algorithm based on Bézier surfaces or a triangulated mesh to achieve the highest accuracy with respect to the output data from the manufacturing simulation. Both approaches make it necessary to determine the contact distances with numerical algorithms, such as the Newton scheme. The advantage of the interpolation lies in the consideration of detailed manufacturing-related micro geometric flank deviations, such as feed marks and profile section deviations. However, this detailed flank description requires a high computational effort [6, 7].

In summary, BECAL offers a compromise between a sufficiently accurate description of the flank geometry (including the manufacturing process) and a high computational speed. For this reason, the surface approximation concept will be pursued. In order to increase the surface accuracy, the use of an alternative surface approach with NURBS is further investigated.

3 Approximation of flank and root geometry

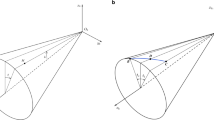
For the approximation of the tooth geometry in BECAL, both, the flank and the root geometry are represented with separate surface descriptions by Bézier tensor product surfaces. For the purpose of surface approximation, the target points, e.g. as provided by the manufacturing simulation, must first be parameterized. In BECAL, the parameterization is based on spherical coordinates, as shown in Fig. 2. Furthermore, the parameters are limited to a range \(\mathbb{R}\in [0,1]\) to fit the polynomial surface representation. The approximation, which determines the Bézier surface coefficients, is done by solving a linear minimization problem (least square fit) [1, 5].

Fig. 2
figure 2

Parameterization of the flank geometry (a) and root geometry (b)

Full size image

To describe the flank surface X, the spherical coordinates R and θ are used as parameters for the representation of φ according to

$$\varphi =X\left(R,\theta \right)$$
(1)

shown in Fig. 2. This form of surface mapping has a major advantage: In order to determine the contact distances in the load-free tooth contact simulation, the tooth is divided into spherical sections along the face width. Based on this, the contact line and the contact distances along this line are calculated. Thus, the representation as defined in Eq. 1 has the benefit that the spherical sections as well as the contact distances can be determined directly and precisely. This avoids the use of complex contact determination algorithms and therefore enables high processing speeds [1, 5, 8].

The description of the root surface is also based on spherical coordinates. In contrast to the flank, an additional parameter u is introduced. This parameter is needed to describe the potentially strongly curved root geometry. The representation of the root surface is defined as

$$\left[\begin{array}{c} \varphi \\ \theta \end{array}\right]=X\left(R,u\right)$$
(2)

Following the flank description, spherical sections can also be calculated with a constant R along the u parameter, which is direct and fast [1].

4 Comparison of the Bézier and NURBS surface approach

To understand the differences between Bézier and NURBS surfaces and the resulting advantages of NURBS, their mathematical description is explained and contrasted, and possibilities for approximation with these approaches are shown.

4.1 Bézier surfaces

Bézier surfaces result from the tensor product of two Bézier curves and are following the equation

$$X\left(t,s\right)=\sum _{i}^{n}\sum _{j}^{m}b_{ij}\cdot B_{in}\left(t\right)\cdot B_{jm}\left(s\right).$$
(3)

The Bernstein polynomials Bin(t), Bjm(s) are used as basis functions. Here n and m define the polynomial degree of the Bernstein polynomials along the parameters t  and s. This results in \([n+1\times m+1]\) Bézier points bij, which define a bidirectional net of control points [9,10,11]. Fig. 3 shows the control net and the resulting Bézier surface for a polynomial degree \(n=m=4\).

Fig. 3
figure 3

Bézier surface with polynomial degree \(n=m=4\)

Full size image

The Bernstein polynomials Bin(t) form a basis system of linearly independent functions, which are calculated according to Eq. 4.

$$B_{in}\left(t\right)=\left(\begin{array}{c} n\\ i \end{array}\right)\cdot \left(1-t\right)^{n-i}\cdot t^{i},i=0,1,\ldots ,n$$
(4)

Corresponding to the polynomial degree n, the basis system is defined with \([n+1]\) functions on the range t in [0, 1]. Fig. 4 shows the system of Bernstein polynomials for degree \(n=4\).

Fig. 4
figure 4

Basis system of Bernstein polynomials for degree \(n=4\)

Full size image

The function values of the Bernstein polynomials Bin(t), Bjm(s) determine the influence of the corresponding Bézier point bij along the parameters t and s. Due to the nature of the Bernstein polynomials, which have a function value greater than 0 on the range t, s in (0,1), the location of a single Bézier point influences the shape of the entire surface. In addition, the number of Bézier points is directly coupled to the polynomial degree [9,10,11].

4.2 Non uniform rational b-spline surfaces (NURBS)

NURBS surfaces are a general form of the rational B‑spline surfaces as described in Eq. 5

$$X\left(t,s\right)=\frac{\sum _{i}^{n}\sum _{j}^{m}N_{ik}\left(t\right)N_{jl}\left(s\right)\cdot w_{ij}\cdot d_{ij}}{\sum _{i}^{n}\sum _{j}^{m}N_{ik}\left(t\right)N_{jl}\left(s\right)\cdot w_{ij}}$$
(5)

Here the function X(t,s) describes a surface of order k and l along the parameters t and s. The \([n\times m]\) De Boor points dij represent the control net over the surface. In addition, a rational denominator is added to the function of the surface. Here, the weights \(w_{ij}(> 0)\) represent additional design parameters. The basis functions Nik(t) form a linearly independent basis system of functions analogous to Bernstein polynomials (acc. Eq. 4). These are piecewise defined (segmented) polynomials of order k (polynomial degree \(k-1\)) and their properties are similar to the Bernstein polynomials’ properties. The basis functions are described as follows:

$$k=1\quad N_{i1}\left(t\right)=\left\{\begin{array}{cc} 1 & \textit{where}\,t_{i}\leq t< t_{i+1}\\ 0 & \textit{otherwise} \end{array}\right.,$$
(6)
$$k> 1\quad N_{ik}\left(t\right)=\frac{t-t_{i}}{t_{i+k-1}-t_{i}}N_{i,k-1}\left(t\right)+\frac{t_{i+k}-t}{t_{i+k}-t_{i+1}}N_{i+1,k-1}\left(t\right).$$
(7)

Equation 7 represents a recursive function. In contrast to Bernstein polynomials, basis functions are based on a knot vector τ, with the knots ti. These must be provided in ascending order. Its defined as:

$$\tau =\left\{t_{0},t_{1},t_{2},\ldots ,t_{n+k}\right\},\ t_{i}\leq t_{i+1}.$$
(8)

Depending on the distribution of the knots in the knot vector, uniform rational b‑splines have equidistantly distributed knots, while NURBS contain arbitrarily distributed knots. The knots may occur multiple times in the knot vector. If the first knot \(t_{0}=0\) and the last knot \(t_{\left(n+k\right)}=1\) occur k-times in the knot vector, the basis functions are \(N_{0k}(0)=N_{n-1,k}(1)=1\) (see Fig. 5). This is especially relevant for the description of surfaces, since, in this case the boundary points of the control net thus lie on the surface. If the interior knots occur l-times, the differentiability of the surface at the point along parameter t reduces to \(C^{k-1-l}\). Basis functions of order \(k=4\) with single interior knots are therefore continuously differentiable at most three times, which is, for instance relevant for the computation of curvatures [9, 10].

Fig. 5
figure 5

Basis functions, \(k=4\), \(n=6\), \(\tau =\{0,0,0,0,0.25,0.5,1,1,1,1\}\)

Full size image

Examples for basis functions are shown in Figs. 5 and 6. The bars shown above the functions indicate the range \(N_{ik}(t)> 0\) for the corresponding basis function. The basis functions in both Figures differ regarding the knot vector.

Fig. 6
figure 6

Basis functions, \(k=4\), \(n=6\), \(\tau =\{0,0,0,0,0.25,0.25,1,1,1,1\}\)

Full size image

In summary, compared to the Bernstein polynomials, the basis functions are defined in segments, which can be specifically influenced via the knot vector. Transferred to a rational B‑spline surface, this means that the control points (De Boor points) have only a local influence on the surface. Furthermore, the surface order or the polynomial degree is independent of the number of De Boor points, as long as \(n\geq k-1\). Additionally, the influence of single control points can be controlled by the weights wij. Thus, compared to the Bézier representation, NURBS surfaces have a much larger degree of freedom for modeling surfaces, which satisfies the requirement of an accurate representation of complex shapes.

4.3 Approximation algorithms

To represent the surfaces with the mentioned approaches, the corresponding control points and weights have to be determined. By means of the surface approximation, these parameters are calculated on the basis of a given set of points. Hence, it is required to represent the given points accurately, i.e. to minimize the deviations. There are various mathematical methods for solving this minimization problem. The most common method is the least square fit [10], which is used in BECAL for the surface approximation with Bézier surfaces [1, 5].

When approximating with NURBS surfaces, the weights wij (acc. Eq. 5) must be determined in addition to the De Boor points. When using the least square fit method, there is a possibility that the weights become negative values. This would mean that the denominator of the approximation function becomes \(X(t_{i},s_{i})=0\) for certain parameters and consequently the surface has a singularity at that point. Therefore, negative weights must be unconditionally avoided. For this purpose, Elsässer [12] developed a method with the advantage that no nonlinear optimization problems occur. The minimization problem follows

$$\overline{F}=F+\lambda G\rightarrow min$$
(9)

Here, F describes the distance function in Eq. 10, G represents the control term as defined in Eq. 11.

$$F=\sum _{i}^{N}\overline{X}^{2}\left(t_{i},s_{i}\right)-\left(\left(\overline{X}\left(t_{i},s_{i}\right)\cdot P_{i}\right)\right)^{2},\textit{where}\ \overline{X}=\left[\begin{array}{c} \sum \sum N_{ik}\left(t\right)N_{jl}\left(s\right)\cdot w_{ij}\\ \sum \sum N_{ik}\left(t\right)N_{jl}\left(s\right)\cdot w_{ij}\cdot d_{ij} \end{array}\right]$$
(10)
$$G=\sum _{i}^{N}\left(\sum _{j}^{n}\sum _{l}^{m}w_{j}N_{ik}\left(t_{i}\right)N_{jl}\left(s_{i}\right)-1\right)^{2}$$
(11)

The factor λ controls the influence of the control term. It is first estimated in order to determine the weights wij and to check whether these are negative. If there are negative weights, λ is increased and the weights are determined again. This process is carried out until positive weights are obtained.

5 Potential of the NURBS surface approach in the TCA

Finally, both surface approaches are used in the BECAL TCA and compared with respect to their influence on the results of stress, load capacity and acoustic excitation. Therefore, two different gear types (acc. Fig. 7) are analyzed. The first example shows a hypoid gear set with a linear tip relief and a spherical root relief on the drive side of the pinion. The second example describes a forged differential gear characterized by a strongly curved tooth root geometry.

Fig. 7
figure 7

Tooth geometry examples; tip and root relief (a); strongly curved root geometry (b)

Full size image

The flank deviation and stress results of the first example are summarized in Fig. 8. As shown in the upper left figure, the flank deviations of the Bézier surface range from −5.45 µm to 3.3 µm with a root mean square value of 1.42 µm. The difference in curvature, especially at the tooth tip at the transition from the involute profile to the linear tip relief, causes the Bézier surface to oscillate. This results in two local maxima of Hertzian stress along the tooth profile.

Fig. 8
figure 8

Comparison of local deviation and stress results; hypoid gear with tip and root relief

Full size image

In contrast, the NURBS surface has an overall deviation of 2.35 µm, which is strongly concentrated on the transition line at the tooth tip. In addition, the surface is less oscillating, resulting in flank deviations of less than 0.1 µm for the most of the flank. The root mean square value is 0.21 µm. Thus, a more realistic pressure distribution can be achieved with the NURBS surface, while the maximum of the Hertzian stress is located at the tip. Table 1 lists the minima and maxima of stress and load capacity.

Table 1 Comparison of stress and load capacity results; hypoid gear with tip and root relief
Full size table

It is apparent that the maximum Hertzian stress is underestimated with the Bézier surface. Accordingly, the safeties calculated for the flank, especially for pitting and micro pitting, are too high compared to the results obtained with the NURBS surface. Contrary to expectations, the tip relief does not result in lower stress at the tooth tip in this example. This can be explained by the high total contact ratio of \(\varepsilon _{\gamma }> 2.5\), which leads to a smooth pressure distribution along the path of contact and thus to a low transmission error. Hence, the common effect of tip relief, to reduce the transmission error, is not given. Instead, it leads to a limitation of the contact pattern and therefore to an increase of the contact stress. However, the higher accuracy of the approximation surface allows for more detailed design of the micro geometry, such as applying higher profile crowning or using a spherical relief to reduce the stress at the tip.

Another important criterion for the gear design, is the acoustic excitation. In Fig. 9 the excitation spectrum for the transmission error under load is shown. By comparing Bézier and NURBS, two different spectra can be obtained. In particular, the first three harmonics differ significantly in the level of excitation, resulting in calculated volume levels of 94.3 dB (Bézier) and 89.5 dB (NURBS).

Fig. 9
figure 9

Comparison of acoustic results; hypoid gear with tip and root relief

Full size image

The results for the second example are shown in Fig. 10 and Table 2. The calculation of the root tensile stress is performed using FEM influence vectors according to [13]. Similar to the results from the first example, the deviations at the tooth root can be reduced by a factor of 3.7 by means of root mean square. Accordingly, Bézier gives deviations in the range of −78.9 µm to 114.24 µm, while the NURBS surface only shows deviations in the range of −43.08 µm to 24.52 µm. It can be seen that both surfaces are primarily oscillating at the transition from the toe to the straight midsection and from there to the heel. However, unlike for the flank surface, these deviations have no significant influence on the tensile stress in the tooth root and thus on the safety against tooth root fracture.

Fig. 10
figure 10

Comparison of local deviation and stress results; forged differential gear with a strongly curved root geometry

Full size image
Table 2 Comparison of stress and load capacity results; forged differential gear with a strongly curved root geometry
Full size table

6 Summary

For the tooth contact simulation in BECAL, it is necessary to transfer the point cloud-based tooth geometry into a mathematical description. This is performed by an approximation of the target points, which, in contrast to an interpolation, enables an efficient and fast TCA. In order to improve the mapping accuracy of the flank and root geometry, only the use of a higher-order approach compared to the presently used Bézier tensor product surfaces must be considered.

For this purpose, NURBS and Bézier surfaces are analyzed and compared with each other. The comparison concludes that NURBS provide a significantly higher degree of freedom to describe complex surfaces. In particular, this results from the independence of polynomial degree and number of control points as well as the additional weights.

Finally, two different gear geometries are used to demonstrate that NURBS surfaces can improve the mapping accuracy by a factor greater than 3. In particular, the flank representation shows a significant influence on the pressure distribution as well as the results of the flank load capacity. Since the correct curvature is primarily relevant here, deviations in the range of a few microns already lead to a false statement regarding the flank load capacity and acoustic excitation. In comparison, deviations of the geometry in the tooth root are found to be less relevant for the calculation of the tooth root load capacity.