1 Introduction

The planetary load sharing behaviour can be described by the mesh load factor Kγ according to ISO 6336‑1 [15] and is calculated based on the individual normal tooth forces of each mesh. Besides gear errors (quality) and assembly deviations, the load sharing is also influenced by the stiffness or rigidity of shafts, housing and bearings, the number of planets and the operating conditions [23]. Different standards and classifications such as AGMA 6123-C16 [1], BS EN 61400‑4 [3], DNVGL-CG-0036 [7] and the “Guideline for the Certification of Wind Turbines” [8] give a rough estimation of Kγ for different applications, but merely based on the number of planets. Only in AGMA 6123-B06 [1] a distinction into four basic grades of requirements regarding the operational speed range is provided.

Against this background, numerous theoretical and experimental investigations of the planetary load sharing behaviour and its influencing parameters were carried out. 2D or 3D lumped-parameter models with different degrees of freedom form the more simplified simulation models [4, 9, 14, 17, 20, 24], whereas more complex hybrid models combine analytical approaches for describing the tooth contact and finite element calculations for the overall deformations of the gearbox components [16, 19, 22]. Kahraman [17] investigates the influence of assembly deviations and manufacturing errors on the dynamic load sharing behaviour of a planetary spur gearbox with four planets to establish basic design guidelines. Using a floating sun gear significantly improves the dynamic load share. Manufacturing errors, such as run-out errors, or assembly variations, such as tangential planet position errors, affect the load sharing substantially. Those results correspond well with the work of Ren et al. [24] (herringbone planetary gear set), Iglesias et al. [14] (spur planetary gear set) as well as Leque and Kahraman [20] (helical planetary gear set). Besides gear errors and assembly variations, the number of planets and the load have an essential influence [20, 22, 25]. While higher loads improve the load share between the different planet gears due to higher elastic deformations, a higher number of planets results in a higher sensitivity regarding errors. Through more complex models with full finite element calculations, Kahraman and Vijayakar [19] (spur planetary gear set), James and Harris [16] and Ligata et al. [22] (both helical planetary gear sets) analysed the influence of the stiffness and deformation of the central members of a planetary gearbox and attest an improved load share by stiffness reduction. Hidaka, Terauchi et al. perform several experimental studies on a spur gear planetary gear set to characterize the static and dynamic load sharing behaviour. The results are presented in a series of reports [11,12,13] and coincide with Cunliffe [4] and Hayashi [10]. At high rotational speeds and for low loads the load sharing behaviour is influenced significantly by the dynamic system behaviour of the planetary gear system, whereas the dynamic load share for low speeds with sufficient distance to resonance areas corresponds well with the static one. Further experiments are conducted by Ligata et al. [21, 22] and Boguski et al. [2] to analyse in detail the influence of manufacturing errors and ring gear stiffness on the quasi-static load sharing of different planetary gear set configurations. The experimental data is often used to validate simulation models. The results show good compliance and confirm the calculated results [16, 18, 25]. In the previous works, the load sharing behaviour of spur and helical planetary gears is extensively studied, but double-helical gears are rarely addressed [24]. Due to the combination of low mesh excitation with avoiding axial forces, double-helical planetary gear sets are used in modern high-performance and high-speed applications and form essential drive trains. In this study, the load sharing behaviour of such a double-helical planetary gear set is experimentally investigated under static and dynamic operation conditions to evaluate the influence of speeds under consideration of the vibration characteristics of the system.

2 Test specimen

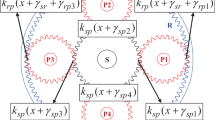
This study uses a five-planet double-helical planetary gear set, which is shown in Fig. 1. Table 1 lists the basic design parameters of the test gears. The sun and planets are manufactured as double-helical gears, while the ring gear consists of two internal helical gears with opposite helical angles.

Fig. 1
figure 1

5‑planet double- helical planetary gear set

Full size image
Table 1 Gear data of the test gear set
Full size table

The stagger angle γs, which defines the relative angular position of the two gear halves with respect to each other, is set to zero. The sun gear is the input and the carrier the output shaft, as the ring gear is fixed to the housing. Sun and planet gears are case hardened, while the ring gear is nitrated. After the heat treatment, all gears are ground and super-finished to achieve very precise flank geometries with a high surface quality. One of the five planet gears shows slightly poorer gear qualities compared to the other ones (see Table 1: max. values for planet 2, min. values for other planets) but is still within the desired tolerances. Standard flank modifications (tip relieves and crowning) are used to ensure a uniform contact pressure distribution in all gear meshes. The planet gears are equally spaced and mounted with two cylindrical roller element bearings on the planet pins. To avoid undesired influences due to mass unbalances the parts with high rotational speeds (e.g. sun shaft and sun gear wheel) are balanced according to DIN ISO 21940-11 [5] to grade 2 and the assembled carrier to grade 6.3. For the experiments in this study, no additional planet position errors or gear errors are applied. The planet pin hole errors in the carrier resulting from the manufacturing process are determined by a 3D measurement. The maximum pin hole position error in tangential direction is 64.6 μm and in radial direction 31.5 μm. Compared to the maximum amount of tip relief at the planet gear with 26 μm, this position error is not completely negligible.

3 Test rig and test matrix

The planetary test gearbox was designed to fit into the back-to-back planetary gearbox test rig at the Gear Research Centre (FZG) of the Technical University of Munich. The test rig is shown in Fig. 2 and a detailed description of the principle function and measurement devices can be found in [26]. Two identical gearboxes are mounted in the test gearbox and slave gearbox housing, respectively. Both gearboxes are connected by the carrier and sun shaft. The ring gear of the test gearbox is fixed to the housing, while the ring gear of the slave gearbox can be twisted automatically by jackscrew hoist gears to preload the planetary gearboxes. A maximum torque of 15000 Nm at the carrier shaft can be applied. The electrical drive motor is attached with couplings to the sun shaft and provides a maximum rotational speed of 8000 rpm. The planetary gearbox in the test housing is equipped with most of the sensors, thus is the main subject of this study.

Fig. 2
figure 2

Back-to-back planetary gearbox test rig

Full size image

The static load share tests are performed with a constant single input (sun) speed of 150 rpm at eight discrete carrier shaft torque levels between 1500 and 15000 Nm. The dynamic load share tests are performed during speed ramp-ups from 0 to 6800 rpm sun speed at all eight torque levels to obtain load share data over the complete operational range.

4 Instrumentation, data collection and sensor calibration

The planet load sharing behaviour is obtained by continously monitoring the tangential bending strains at each planet pin. These bending strains are caused by the combined tangential mesh forces of each planet gear with the sun and ring gear respectively. For this purpose one strain gauge (HBM type 1‑LY41-6/1000) with 1000 Ω resistance is mounted in the middle of each planet pin at the location of maximum bending due to the mesh forces, which are transmitted by two cylindrical roller element bearings to each planet pin. One planet pin is equipped with an additional strain gauge, that measures the strain in radial direction as a result of the centrifugal forces at higher rotational speeds. For the measurement positions a groove is machined into the outer surface of the planet pin to provide sufficient room and protect the strain gauge from the inner races of the cylindrical roller element bearings during assembly. The depth of the groove is limited to the absolutely necessary minimum to ensure sufficient distance to the neutral axis for the bending strain measurement. An exemplary planet pin with two strain gauges for measuring the tangetial and radial strains is shown in Fig. 3.

Fig. 3
figure 3

Exemplary planet pin with 2 strain gauges for measuring tangential and radial strains due to mesh forces and CF loads

Full size image

Since the ring gear is fixed to the housing, the planet carrier acts as the output shaft and rotates. For measuring the strains an inductive telemetry is used. The sensor cables are led through several bores to the rotor of the telemetry on the carrier shaft. There, each strain gauge is interconnected to a Wheatstone quarter bridge and the bridge voltage is digitized and contactlessly transmitted to the stationary data acquisition system. All measurement data is collected and stored by an NI PXIe-8880 system (mounted in a NI PXIe-1085 chassis). Additionally, angular positions of sun and carrier shaft are measured by an optical absolute angular position sensor system, consisting of a RESOLUT readhead and a RESA ring, manufactured by Renishaw. During each test run the strain data is recorded with a sample rate of 30 kHz. Due to the manual application process of the strain gauges and the differences between the sensors of one charge, all strain gauges have to be calibrated to be able to measure even small differences in the load sharing. For this purpose a planet pin calibration device is designed, which is illustrated in Fig. 4.

Fig. 4
figure 4

Overview of planet pin calibration device

Full size image

The planet pin is mounted exactly in the same way as in the planet carrier and is then manually loaded with a jackscrew hoist gear up to 20 kN. The strain is measured with the same inductive telemetry which is also used during the tests to avoid errors due to differences in the amplifiers and data acquisition system. The loading and unloading process is performed several consecutive times and the data is used to generate a linear regression line for the correlation of force and strain. An additional laser distance sensor is used to check the reliability of the loading and unloading process by measureing the deflection. Fig. 5 shows an exemplary result of a planet pin strain gauge calibration.

Fig. 5
figure 5

Exemplary result of a planet pin calibration. Applied force range from −20 to 20 kN and averaging of five consecutive test procedures

Full size image

Before a test run starts, the test rig is heated up to 40 °C. Tooth mass temperatures of sun and ring gear as well as the oil inlet temperatures are monitored to ensure all components have the same temperature. This procedure is important because all strain gauges at the pins are not compensated against temperature-induced elongation in the quarter bride circuit. After heating up, the strain data is recorded under no-load condition to obtain a zero-torque offset point for all strain gauges. This is essential, because even under no-load, the planet pins are bent due to small assembly deviations of the carrier. After that, the torque level is applied to the back-to-back test rig configuration and the drive motor accelerates the rig according to the speed requirement with a speed rate of 30 rpm/s. The stationary speed is generally kept for 90 s, whereas the maximum speed during a speed ramp-up is just kept for 5 s. During all test runs the two separate oil systems, respectively for test and slave gearbox, controlled the oil inlet temperature to 40 °C with an accuracy of ± 2 °C.

5 Data evaluation and computation of load sharing

The recorded strain data of all five sensors is used to calculate the load share of the double-helical planetary test gearbox. In a first step the raw data is filtered to exclude data transmission errors of the telemetry. The zero-torque offset value, derived from the tests under no-load condition, is used to correct the time data of each sensor channel and eliminate the influence of the assembly process of the carrier. Subsequently the results of the planet pin calibration are applied to calculate the planet pin tangential forces FP,n(t) based on the measured tangential strain εP,n(t) for each planet n according to Eq. 1, where m denotes the gradient of the linear regression.

$$F_{P,n}(t)=m\cdot \varepsilon _{P,n}(t)$$
(1)

The forces FP,n(t) are summed up to find the total pin force such that the percentage represented by a gauge of this total force value represents the load carried by that planet n. Mathematically, the mesh load factor Kγ,n(t) of the n-th planet is defined as

$$K_{\gamma ,n}\left(t\right)=\frac{F_{P,n}\left(t\right)}{\sum _{i=1}^{N}F_{P,i}\left(t\right)}$$
(2)

The average value of Kγ,n(t) over the test time of 90 s is chosen to represent the mean portion of load carried by planet n. Fig. 6 displays a 0.125 s segment of a load share test at 4000 rpm input speed and 10000 Nm load. It includes the planet pin calibration based forces for all five planets (normalized to the overall maximum planet pin force) as well as the carrier angular position. Due to the high sampling rate of 30 kHz the impact of the gear mesh is also clearly visible. The planet pin forces fluctuate about 1.5 kN during a carrier rotation as a resulting combination of manufacturing deviations, the gear mesh and system dynamics. This peak-to-peak band (see Fig. 6) is used to define the range of load share variation and characterize the influence of the dynamic system behaviour of the gear set.

Fig. 6
figure 6

Exemplary segment of load sharing test at 4000 rpm sun speed and 10000 Nm carrier torque (partial load). Planet pin forces normalized to maximum overall planet pin force

Full size image

6 Results

In the first step, the quasi-static load share at 150 rpm input speed and a variation of torque from 1500 to 15000 Nm is evaluated as a reference for the tests under higher rotational speeds. Fig. 7 shows the load share according to Eq. 2 for all five planets. The errorbar denotes the maximum peak-to-peak value during the test run.

Fig. 7
figure 7

Static load share at 150 rpm input speed. Average value (dots), maximum peak-to-peak load share value (error bar)

Full size image

The static load share behaviour is well comparable to earlier experimental and simulative results of spur or helical planetary gearboxes [2, 21]. Under low load, the individual gear meshes are slightly loaded and the deflections of gearbox components are minor. Thus manufacturing and assembly deviations dominate the load sharing behaviour, resulting in higher average load sharing factors (dots in Fig. 7) as well as maximum peak-to-peak value (error bar in Fig. 7). With increasing load, the elastic deflections grow and balance the manufacturing deviations and errors, hence yielding to smaller load sharing factors and reduced peak-to-peak values. Planet 1 carries the highest load over the complete torque range. The maximum of 25.2% is reached at 1500 Nm and drops to 23.0% at 15000 Nm. The difference between the load share values of all five planets at quasi-static conditions and full load are quite small, since the gear quality (see Table 1) as well as the manufacturing erros of the carrier are small. A remaining slightly unequal load sharing under maximum load is plausible, since planet carrier, ring gear, and housing of the test rig are very stiff. Results for the dynamic load share behaviour is displayed in Fig. 8 for a speed ramp-up to 6800 rpm input speed and 1500 Nm load. The load share factors are calculated for each time point respectivley. For better visibility only the average value (dotted line) and the envelope of maximum values of peak-to-peak load share factors (solid line) are shown for each planet, since the envelope is arragned symmetrically around the mean average value. Up to an input speed of around 5000 rpm, the average as well as the the envelope values indicate no significant changes in the load sharing.

Fig. 8
figure 8

Dynamic load share during speed ramp-up from 500 to 6800 rpm at 1500 Nm load torque. Average value (dotted line), envelope of maximum peak-to-peak value (solid line)

Full size image

For higher speeds from 6000 to 6800 rpm, the maximum and minimum peak-to-peak values start to grow exponentially, and the gradient of the average values also indicates an increase. Considering the order-diagram of an acceleration sensor measuring the structure-borne noise at the fixed ring gear in radial direction (see Fig. 9, measurement details described in [26]), an increase of the structure-borne noise level of the 1st, 2nd, 3rd and 4th mesh order is recognizable in the same speed range (6000 to 6800 rpm). Furthermore, hyperbolas, representing eigenfrequencies, are indicating possible resonance areas slightly above 6800 rpm for the 1st and 3rd mesh order with increased vibration amplitudes in the gear mesh. Another indicator for increased excitation in planetary gearboxes is the ovalization of the sun orbit. Fig. 10 illustrates the the sun orbit of the test gearbox for five carrier rotations at 150 rpm and 6800 rpm respectively (measurement method described in [26]). The measured values are normalized to the maximum sun orbit value. At high rotational speeds the amplitudes of the orbit are significantly increased (cantilevered bearing support), leading to higher reaction forces in the gear mesh and thus, increased amplitudes of the dynamic load share factor. Similar to the static load sharing behaviour, the dynamic load sharing improves significantly with higher loads. Fig. 11 displays the dynamic load share factor during a speed ramp-up from 500 to 6800 rpm at full load (15000 Nm). The average load share factors as well as the maximum peak-to-peak envelope is minimized and can be assumed to be constant over the complete speedrange, even in the critical speed range of 6000 to 6800 rpm.

Fig. 9
figure 9

Order-diagram of radial structure-borne noise at the ring gear during seep ramp-up to 6800 rpm and 1500 Nm load torque

Full size image
Fig. 10
figure 10

Sun orbit measurement at 1500 Nm load torque, normalized to the maximum measured orbit value. Quasi-static conditions (150 rpm input speed) and dynamic conditions (6800 rpm input speed)

Full size image
Fig. 11
figure 11

Dynamic load share during speed ramp-up from 500 to 6800 rpm at 15000 Nm load torque (full load). Average value (dotted line), envelope of maximum peak-to-peak value (solid line)

Full size image

7 Conclusion

In this study the dynamic load sharing behavior of a five planet double-helical planetary gear set was investigated experimentally on a back-to-back test rig. A high-frequency strain measurement at the planet pins was used to calculate the load share factors based on the bending strains. Comparing the load share under high rotational speeds with quasi-static conditions, the following conclusions and design recommendations can be drawn:

  • The load share factors determined under quasi-static condition are applicable for a wide operational range of speed and torque. Dynamic effects on the load sharing behaviour have to be considered only at very high speeds (also depending on the ressonance area of the gear meshes).

  • Although high-precision gears and components are used in this study, the results show relative large differences in load sharing under low load when comparing the individual planets. Thus, including the tolerance chain into the design process is recommended.

  • At high speeds and low loads, the load sharing behaviour is significantly influenced by the vibration behavior of the drive train. Resonance areas can lead to increased load share values and amplitudes. The operational range of the planetary gearbox should be checked for such ressonance areas (tooth numbers and masses) to avoid them during continous operation.

  • Not only the gear mesh affects the load share under high rotational speeds, but also the movement of the sun. This coincides with previous experiments in the literature [12]. A tradeoff between the adjustability of the sun to improve the load sharing for lower speeds and a reasonable bearing arrangement for high speeds is necessary.

Since these experiments are based on high precision gears and gearbox components, further investigations have to consider typical manufacturing and assembly errors, such as planet position errors or excentricities.