1 Introduction

Over the last 10 years, new registrations of passenger cars increased by approx. 21% in Germany for the segment above 100 kW (see Fig. 1). The trend is not restricted to Germany but is also apparent worldwide. A second trend is that more and more lightweight passenger cars are being constructed, for example with the aim of improving CO2 figures and to satisfy EU regulations. To ensure increased performance, the gearbox and powertrain have to be made more robust, which, however, increases the weight of common gearboxes. The two trends would therefore appear contradictory.

Fig. 1
figure 1

New registrations of passenger cars in Germany in 2009 and 2018 divided into performance categories based on the data of [1, 2]

Full size image

To achieve both goals, gears in gearboxes can be shot-peened. The high compressive residual stresses introduced by the shot-peening process have the effect of increasing the tooth root load carrying capacity, because the strain maximum is no longer at the surface but below it. The research findings presented in [3,4,5] show that the tooth root load carrying capacity of (duo-)shot-peened gears can be increased by up to 48% compared to unpeened gears. The consequence of this is that a higher torque can be transmitted. In some cases, it is also possible to make the gearbox smaller. This reduces not only the weight of the gearbox but also that of the car as a whole. However, there is one drawback. As the strain maximum is below the surface, the crack initiation is often no longer at the surface but below it, for example, at a non-metallic inclusion.

Experimental tests are typically carried out to determine the tooth root bending strength of gears. A limiting number of 3 million (see [6]) or 6 million (see [7]) load cycles, respectively, is usually chosen for pulsator testing. For most gear materials, this range is considered the beginning of the long-life strength range. However, research has shown that with shot-peened gears, tooth root fracture damage still occurs at such non-metallic inclusions in and above the very high cycle fatigue range. This means that a further reduction in load carrying capacity is expected at higher load cycles, something which is not covered in the reference fatigue tests. The question is whether there is a significant decrease in bending load carrying capacity and, also, if pulsating tests at higher load cycles—or even tests on the FZG back-to-back test rig—are necessary to determine a proper endurance fatigue limit of shot-peened gears. This paper investigates these questions.

2 Current state of knowledge

2.1 Non-metallic inclusions

In the event of a crack initiation below the surface, common shot-peened gears made from case-carburized MnCr- or CrNiMo-alloyed steels (e.g. 20MnCr5 or 18CrNiMo7-6) fail at typical main inclusions of two types: oblong manganese sulfides in MnCr-alloyed steels and spherical or oblong aluminum oxides in CrNiMo-alloyed steels (see Fig. 2; [8, 9]).

Fig. 2
figure 2

Typical non-metallic inclusions in gear steels. a Oblong manganese sulfide in MnCr-alloyed steel. b Oblong aluminum oxide in CrNiMo-alloyed steel. c Spherical aluminum oxide in CrNiMo-alloyed steel

Full size image

Each material characterization is always done at random but should, of course, be representative of the steel batch. In industrial practice, six samples are usually inspected to determine the degree of cleanliness, for instance according to ISO 4967 [10], DIN 50602 [11] or SEP 1571 [12]. However, the distribution of non-metallic inclusions differs slightly, even within each individual steel batch. With the development of increasingly clean steels, it is becoming increasingly difficult to reliably determine the degree of cleanliness and the size and distribution of non-metallic inclusions. Murakami [13], for example, confirms that determination of the inspection plane affects the size and number of inclusions determined, see Fig. 3.

Fig. 3
figure 3

Influence of inspection plane on apparent inclusion size [13]

Full size image

Melander et al. [14] demonstrate the influence of inclusion content on the fatigue strength of bearing steels and derive distribution functions for the inclusion densities. The assumption is that fewer and smaller inclusions reduce the probability of crack initiation at an inclusion and increase the fatigue strength. Tridello et al. [15, 16] also made use of this assumption. In several publications, a number of authors [17,18,19,20,21] derive competing distribution functions for different inclusion types. These distribution functions remain the subject of current research. To sum up, it is evident that the fatigue strength of shot-peened gears depends on the size and distribution of inclusions.

2.2 Classic S-N curves

In addition to the classic S‑N curve known as the Palmgren-Miner original, there are also the Palmgren-Miner modified (or Haibach) approach and the Palmgren-Miner elementary approach (see Fig. 4). Standardized approaches for gears, such as ISO 6336, generally assume a classic S‑N curve with either a constant endurance limit (Palmgren-Miner original) or a decreasing endurance limit (Palmgren-Miner modified) for a higher number of load cycles. Crack initiation is always assumed to take place at the surface.

Fig. 4
figure 4

Classic S‑N curves for the high cycle fatigue range (acc. to [22] (translated))

Full size image

2.3 Experimental results in and above the very high cycle fatigue regime

The literature shows that in the very high cycle fatigue range of shot-peened specimens, crack initiation is often below the surface at non-metallic inclusions and, therefore, the fatigue strength decreases. This is documented for standard specimens (for example rotating bending, tension-compression and thin-walled tube specimens) and gears, among others.

2.3.1 Standard specimens

Fig. 5 shows an example stepwise S‑N curve for rotating bending specimens from Murakami et al. [23]. Failures with shot-peened standard specimens are also documented for between 107 and 109 load cycles, for example in studies by Toyoda et al. [24], Bathias et al. [25], Nakajima et al. [26], Thumser et al. [27], Sun et al. [28], Tridello et al. [16, 29, 30], Sandaiji and Tamura [31], and Nambu and Egami [32].

Fig. 5
figure 5

Comparison of S‑N data between rotating bending and tension-compression [23]

Full size image

Wang et al. [33] and Tallerico and Cameron [34] even describe such failures for up to 1010 load cycles. Sakai [35] reviews studies on the VHCF of metallic materials for machine structural use, and summarizes and presents further investigations and their S‑N curves. Fatigue failures in the VHCF range have also been documented for bearing steels [36], nitrocarburated specimens [37], austempered ductile iron (ADI) [38], dual-phase steels [39] and welded joints [40].

2.3.2 Gears

In the case of shot-peened gears, studies by Stenico [42] (based on [43]) and Bretl [41] (based on [44] , published internationally in [45]), among others, display similar characteristics to those documented for standard specimens. The test results produced by Bretl [41] show foremost failures due to subsurface crack initiation at non-metallic inclusions up to 108 load cycles (see Fig. 6). Not only is a decrease in the endurance fatigue life evident, it also seems that even with up to 108 load cycles, there is still no endurance fatigue limit for shot-peened gears.

Fig. 6
figure 6

Summary of results of various shot-peen tests reported in [41] (translated); (y-axis: ratio of nominal tooth root stress σF0 for each test point and nominal tooth root stress for 50% failure probability at a load cycle limit of 6 million σF0∞_6Mio for each variant)

Full size image

2.4 Modified S-N curves in the VHCF range

Nishijima and Kanazawa [46] show that even when shot-peened gears display increased bending strength in the high cycle fatigue range, a decrease in bending strength must be assumed at a higher number of load cycles. This results in a stepwise S‑N-curve, as in Fig. 7b, unlike with the traditional concept shown in Fig. 7a or Fig. 4. The first part of the modified S‑N curve represents the range comprising finite life and surface fatigue limit with crack initiation at the surface. The second part shows internal fatigue with an internal fatigue limit, which is defined by crack initiation below the surface at non-metallic inclusions.

Fig. 7
figure 7

Two S‑N curve concepts according to Nishijima and Kanazawa [46]. a Traditional concept of an S‑N curve. b The concept of a twofold S‑N curve

Full size image

Bathias presents a concept of a gigacycle fatigue S‑N curve in [47], see Fig. 8. The author states that “only the exploration of the life range between 106 and 1010 cycles will create a safer approach to modeling …” the S‑N curve above the high cycle fatigue range. In [37], S‑N curves are composed of only one inclined line and one horizontal line (fatigue limit) for nitrocarburized and post-oxidated standard specimens (see Fig. 9). The failures from inclusions were up to approximately 106 load cycles.

Fig. 8
figure 8

Concept of a gigacycle fatigue S‑N curve acc. to [47]

Full size image
Fig. 9
figure 9

S‑N curve for nitrocarburized and post-oxidated specimen [37]

Full size image

Murakami et al. [48] define no second infinite fatigue limit for internal inclusions in the very high cycle fatigue range, even above 109 load cycles (see Fig. 10). This approach is also used by Mughrabi in [49, 50]. Murakami et al. state that “the transition from short to superlong fatigue life appears as a horizontal step in the S‑N curve” and that the mechanism of fatigue fracture at superlong fatigue life has not yet been clarified.

Fig. 10
figure 10

Typical S‑N curve for high strength steels [48]

Full size image

2.5 S-N curves based on stochastic distributions

The S‑N curve is generally based on a certain stochastic distribution in the infinite and finite fatigue ranges. On account of this, Nakamura et al. [51] derived a probability density and distribution functions of the fatigue strength in the gigacycle fatigue range of the test results of [35], see Fig. 11. Paolino et al. also presented a stepwise S‑N curve in [52], based on a numerically estimated statistical distribution, with regard to the transition between high cycle fatigue (HCF) and very high cycle fatigue (VHCF), see Fig. 12. They derived mathematical correlations based on the experimental results.

Fig. 11
figure 11

Probability density and distribution functions of fatigue strength in the giga cycle fatigue range [35]

Full size image
Fig. 12
figure 12

Schematic diagram of a statistical Duplex S‑N curve with fatigue limit [52]

Full size image

2.6 Summary of the current state of knowledge

With case-carburized, shot-peened gears, crack initiation in and above the high cycle fatigue range typically occurs below the surface at non-metallic inclusions, due to the high compressive residual stresses introduced by the shot-peening process. This characteristic is influenced by the size and distribution of the inclusion. There are various competing techniques for determining an S‑N curve above the high-cycle fatigue range. However, the experimental results of standard specimens and gears indicate that even at up to 1010 load cycles, no internal infinite or endurance fatigue limit can be assumed.

3 Systematic investigations of the bending fatigue strength of case-carburized, shot-peened gears in the VHCF range

3.1 Material variants, test gears and test rigs

The results of the experiment presented are based on research project [8] and the work done by Schurer [9]. The experimental results were published in part in [53], while a model approach considering the influence of non-metallic inclusions on the tooth root bending fatigue strength on the basis of these experimental results was published in [54, 55]. This project was conducted at the Gear Research Center (FZG) of the Technical University of Munich (TUM) in cooperation with steel producers, transmission manufacturers, automobile manufacturers, etc. For more information about the steel batches and their chemical compositions, degree of cleanliness, production routes and raw bar material diameters, see [55]. All steel batches displayed a high degree of cleanliness according to ISO 4967 method A [14] among others, and the chemical compositions of all variants were in accordance with the specifications in [56]. Table 1 provides a brief overview.

Table 1 Overview of material variants investigated, gear sizes, and test rigs used
Full size table

Extensive experiments were conducted to study fatigue behavior in gear tooth roots, especially in the very high cycle fatigue range. The tests were carried out on pulsator test rigs (normal module of 1.5 mm, 5 mm and 10 mm) with additional tests being carried out on FZG back-to-back test rigs with a center distance of a = 91.5 mm [57] (normal module of 1.5 mm (except V9)). The test rigs are shown in Fig. 13. In the pulsator test rig, the test gear is fixed between two clamps to cover a certain number of teeth, and two gear teeth are loaded by applying a pulsating bending force. The FZG back-to-back test rig operates according to a recirculating power loop principle to supply a fixed torque to a pair of test gears in the test gearbox [58].

Fig. 13
figure 13

Test rigs used for investigations on the tooth root bending strength. a FZG back-to-back test rig (center distance a = 91.5 mm) [57]. b Pulsator test rig [8]

Full size image

3.2 Experimental results

When performing tooth root bending studies, the limiting number of load cycles for tests conducted on the pulsating test rig is commonly either 3 million (pursuant to ISO 6336‑5 [6]) or 6 million (pursuant to FVA directive 563 I [7]). The limiting number of load cycles using the FZG back-to-back test rig to determine tooth root load carrying capacity is generally set to 10 million (see [43, 59]). As shown in Sect. 2, no endurance fatigue limit can be assumed for shot-peened gears up to this number of load cycles. In the extensive experimental investigations on which this paper is based, the limiting numbers of load cycles were therefore set to:

  • Pulsator test rig:

    • Normal module mn = 1.5 mm: 15 · 106 load cycles

    • Normal module mn = 5 mm: 10 · 106 load cycles

    • Normal module mn = 10 mm: 10 · 106 load cycles

  • FZG back-to-back test rig: 30 · 106 load cycles

For some test points, the limiting number of load cycles was increased up to 60 million load cycles on the pulsator test rig and to 50 million load cycles on the FZG back-to-back test rig (see Figs. 14 and 15). For the sake of clarity, overlapping test points of passed specimens were shifted towards a higher number of load cycles.

Fig. 14
figure 14

Overview of experimental results on the pulsator test rig (overlapping test points of passed specimens are shifted towards a higher number of load cycles). a mn = 1.5 mm. b mn = 5 mm. c mn = 10 mm

Full size image
Fig. 15
figure 15

Overview of all experimental results on the FZG back-to-back test rig (overlapping test points of passed specimens are shifted towards a higher number of load cycles)

Full size image

Non-metallic inclusions are statistically distributed in a material and to cause a failure, a critical non-metallic inclusion must be present at a critical distance from the surface. In the pulsating tests, the gears were clamped over two teeth for each test point, whereas on the FZG back-to-back test rig, all 59 teeth of the pinion meshed with the wheel. This leads to a higher failure probability on the FZG back-to-back test rig because of the higher volume of material investigated and the greater probability of non-metallic inclusions appearing.

Regarding the results of pulsating tests for the 1.5 mm gear module, Fig. 14 shows that most of the fractures initiated below the surface occurred up to 15 million load cycles. Above 15 million load cycles, no more failures occurred across all load levels. The 5 mm gear size shows a similar trend, with one late fracture just before 30 million load cycles. The 10 mm test gear module shows one fracture at a non-metallic inclusion near 10 million load cycles.

Considering the tests performed on the FZG back-to-back test rig, the pattern is basically the same. Almost all fracture damage occurred above 10 million load cycles, at times reaching 45 million load cycles. Tests at load levels of 170 and 150 Nm were halted after reaching a limiting number of load cycles 50 million.

To sum up, a further decrease in bending fatigue strength is apparent on the pulsator test rig above the standard limiting number of load cycles for all three gear sizes investigated. A further decrease can also be expected above the extended limiting number of load cycles. In addition, it can be assumed that on the FZG back-to-back test rig, fracture damage initiated at non-metallic inclusions from below the surface still occur above 50 million load cycles and the bending fatigue strength therefore begins to decrease again.

4 Discussion

For unpeened and most shot-blasted specimens, crack initiation occurs at the surface, and no significant decrease in endurance limit is expected at a higher number of load cycles (classic S‑N curve—Palmgren-Miner original). However, as can be seen in Sect. 2, the transition from the high to the very high cycle fatigue range can be very different in shot-peened specimens with primarily fisheye failures. First, the start point and incline of the second step vary from material to material. Furthermore, for the range above 30 million load cycles, the progression of the curve has not yet been verified for the bending strength of case-carburized, shot-peened gears with a crack initiation from below the surface at a non-metallic inclusion (fisheye failure). Fig. 16 presents some probable curve progressions beyond 30 million load cycles in the very high cycle fatigue range up to 108 load cycles. It could be that the progression for the presented experimental data resembles the schematic stepwise S‑N curve with an internal fatigue strength such as (1). However, other progressions are also possible, such as (2) (different incline), (3) (internal fatigue limit at higher load cycles) and (4) (no internal fatigue limit).

Fig. 16
figure 16

Probable curve progressions beyond 30 million load cycles in the very high cycle fatigue range for shot-peened specimens with primarily fisheye failures

Full size image

So far, none of the approaches presented in Sect. 2 exactly match the experimental data basis of case-carburized, shot-peened gears with fisheye failures. Further experiments should be performed to investigate the range between 30 and 100 million load cycles in particular.

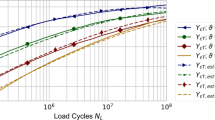
An initial estimation of a fatigue endurance limit for up to 15 million load cycles (pulsator tests) and 30 million load cycles (FZG back-to-back tests) is given in Fig. 17. The estimated S‑N curve of the pulsating tests (see Fig. 17a) shows the first part of the stepwise S‑N curve for surface fatigue up to the normal limiting number of load cycles. As the number of load cycles increases, the crack mechanism changes from fractures initiated from the surface to fractures initiated from below the surface at non-metallic inclusions. This is the range of the second step of the stepwise S‑N curve. However, it cannot be determined how strong the decrease in bending fatigue strength will be or what incline the second limited lifetime has until the internal endurance fatigue limit is reached. Of course, the limiting number of load cycles can be increased on the pulsating test rig, but it is not certain, based on the distribution function, whether critical non-metallic inclusions are at a critical depth.

Fig. 17
figure 17

Estimated stepwise S‑N curves for a failure probability of approximately 50% in the experimental results. a Results of pulsating test. b Results with FZG back-to-back test rig

Full size image

The first part of the stepwise S‑N curve is also visible on the FZG back-to-back test rig; see Fig. 17b. However, based on the lower number of load cycles and the non-metallic inclusion distribution, the results from the pulsator test rig show a higher estimated fatigue limit than that of the FZG back-to-back test rig. Therefore, to determine the bending fatigue strength for even higher numbers of load cycles it makes sense to use the FZG back-to-back test rig to examine a higher material volume.

5 Conclusion

The research findings reveal that no bending fatigue limit can be expected for shot-peened gears, even up to 50 million or 60 million load cycles, respectively. It was shown that the limiting number of load cycles should be increased to determine of the bending fatigue of shot-peened gears. Furthermore, no value could be assigned for a limiting number of load cycles that is sufficient for determining the endurance fatigue limit. The limiting number of load cycles on the pulsating test rig should be increased, but it is not certain if critical non-metallic inclusions are always present at a critical depth based on the distribution function. Based on the lower number of load cycles and the distribution of non-metallic inclusions, the pulsator test rig shows a higher estimated fatigue limit than that determined in the FZG back-to-back test rig. Therefore, in further investigations, it seems appropriate to conduct the test on the FZG back-to-back test rig, due to the large number of meshing teeth in this test rig and to increase the number of load cycles to determine the bending fatigue strength to even higher load cycles. So far, none of the approaches presented in Sect. 2 exactly match the experimental data basis. Further investigations into gears should concentrate in particular on the range between 30 and 100 million load cycles.