1 Introduction

Freewheel clutches are frictionally engaged clutches with a long history of usage [1, 2]. Depending on the application, freewheel clutches are available as sprag clutches, overrunning clutches, or retaining clutches. They all share the working principle of being connected by friction. Freewheel clutches are designed to transmit torque; the torque leads to tangential and radial forces in the contacts between the rollers and the rings. In contrast to rolling bearings, freewheel clutches are not designed to transmit axial loads, which exist in most technical applications. Therefore, rolling bearings often accompany freewheel clutches and handle the additional axial loads. Without the support of the rolling bearings, the freewheel clutch can lose its friction connection due to slippage and, with that, its ability to transmit torque.

This publication focuses on overrunning clutches and their application in drive trains. Degrees of non-uniformity cause other components like gears, belt systems, synchronizer rings, and rolling bearings to vibrate within the production-related axial clearance range. The overrunning clutch faces unwanted, additional axial loads that provoke a loss of friction connection in the Hertzian contact area. Sliding friction occurs and so the overrunning clutch loses its function abruptly. The hitherto valid design criterion [1] is

$$\tan \left(\alpha \right)=\frac{F_{t}}{F_{n}}\leq \mu$$
(1)

If this criterion is fulfilled, the friction connection in the Hertzian contact area is guaranteed. It states that the tangent of the clamping angle α must be smaller than the Hertzian contact zone’s friction coefficient µ. The clamping angle α in turn is equal to the quotient of the tangential force Ft, which results from the circumferential torque T, and the normal force Fn, which acts in radial direction.

The design criterion (Eq. 1) does not take axial loads into account. Thus, it does not meet the load requirements of today’s drive train applications. This publication presents an improved design criterion. The hitherto valid design criterion (Eq. 1) is the basis of the improved design criterion but corrected using current experimental research. Overrunning clutches are presented as an application example. The improved design criterion bases on physical principles; therefore, it is of interest for other Hertzian contact based friction connections.

2 Working principle of overrunning clutches

Fig. 1 shows the components of overrunning clutches and the forces that act within an overrunning clutch based on the contact of one roller, the rings, and the spring. Fig. 2 illustrates the two main operation modes—freewheeling and locking. The operation mode depends on the angular velocity differences and the moving direction of the clutch’s components. The overrunning clutch operates in locking mode if

  • the outer ring moves counterclockwise (ccw.) with a higher angular velocity than the inner ring;

  • the inner ring moves clockwise (cw.) with a higher angular velocity than the outer ring.

Fig. 1
figure 1

a Equilibrium of forces at Hertzian contact level, b friction cone [3]

Full size image
Fig. 2
figure 2

Freewheel clutch operation modes

Full size image

The roller is clamped in the narrowed gap between the inner and outer ring, creating a frictional connection between the rings. The overrunning clutch transmits torque. It freewheels if

  • the outer ring moves clockwise (cw.) with a higher angular velocity than the inner ring;

  • the inner ring moves counterclockwise (ccw.) with a higher angular velocity than the outer ring.

The overrunning clutch does not transmit torque if it operates in freewheeling mode. In this operation mode the roller is in contact with the spring and rotates freely otherwise. The spring’s task is to push the roller into the narrowing gap and thus shorten the needed time to change the operation mode from freewheel clutching to locking.

3 Freewheel clutch design—state of the art

Amongst others, [1, 3,4,5,6,7,8,9,10] and [11] discuss different aspects of overrunning clutch and freewheel clutch design. Each of these publications focuses on a specific design aspect.

All publications share the common understanding of the underlying basic physical principle, i.e. the friction connection in the Hertzian contact area. For example, [12,13,14,15,16,17,18, 20] and [21] discuss topics like contact mechanics, friction, stick-slip, and surface design that are not specific to freewheel clutches but relevant for freewheel clutch design.

This publication does not focus on the mathematical design approach of an appropriate friction connection. The above-mentioned publications provide this knowledge. It aims at the general understanding of the chosen approach to develop an improved freewheel clutch design criterion. Therefore, the design equations are presented in a way that is simplified accordingly. Fig. 1 shows the equilibrium of forces at the Hertzian inner and outer ring contacts. This means that:

$$F_{t}=F_{t,i}=F_{t,o}\cdot F_{n}=F_{n,i}=F_{n,o}\cdot \alpha _{t,i}=\alpha _{t,o}$$
(2)

Taking all z rollers into consideration leads to a transmittable torque of:

$$T=T_{i}=T_{o}=z\cdot X\cdot F_{t,i}=z\cdot r_{\text{OR},i}\cdot F_{t,o}$$
(3)

One of the most important freewheel clutch design parameters is the clamping angle α, which is composed of two parts: The freewheel clutch’s assumed rigid contact geometry and the elastic load-/deformation relation.

The solely geometry-based part suffices as a design approximation. It does not include forces that are derived from the initiated torque and is given by

$$\cos (\alpha ) = \cos\left(\alpha _{0}\right)=\sqrt{\frac{r_{\text{RO}}+X}{2\cdot \left(r_{\text{OR},i}-r_{\text{RO}}\right)}},$$
(4)

where α0 is the clamping angle at the initial position (Fig. 3).

Fig. 3
figure 3

Clamping angle change during operation [8]

Full size image

The Freewheel clutch material is not rigid but elastic. Thus, the overall deformation is the sum of

  • the forces that occur in locking mode and cause a deformation of the contacting components (inner ring, outer ring, and rollers);

  • the stiffness of the shaft and the hub;

  • the Hertzian contact pressure at the inner and outer ring contacts, which causes a flattening of the contacting surfaces.

With increasing loads, the roller moves further into the narrowing gap that appears to expand, Fig. 3. Starting at the initial position 0, the roller’s centre moves with a distance s. The clamping angle at position 1 can be calculated according to Eq. 5, and the resulting distance s as shown in Eq. 6:

$$\alpha _{1} = \frac{1}{2} \cos^{-1} \left(\frac{X-f_{\text{RO,IR}}-u_{\text{RO,IR}}+r_{\text{RO}}} {r_{\text{OR}}-f_{\text{RO,OR}}-u_{\text{RO,OR}}+r_{\text{RO}}}\right)$$
(5)
$$s=\left(r_{\text{OR}}+f_{\text{RO,OR}}+u_{\text{RO,OR}}-r_{RO}\right)\cdot \left(2\cdot \alpha _{1}-2\cdot \alpha _{01}\right)$$
(6)

Depending on the torque, the inner ring twists relatively to the outer ring with a torsion angle φ [8]. The dependency between the torque and the angle φ is the Freewheel clutch’s torsional spring characteristic. The angle φ can be measured or calculated (Eq. 7); it acts as an evaluation parameter for the test rig validation in Sect. 6.

$$\varphi =\frac{s}{r_{\text{OR}}}+\frac{s}{X}$$
(7)

The geometric portion of the clamping angle α causes loads in the clamping contact. That, in turn, influences the elastic load-/deformation relation contribution to α. This interdependence causes the necessity to calculate the freewheel clutch’s load behavior iteratively (i.e. Newton-Raphson approach), Fig. 4.

Fig. 4
figure 4

Iterative calculation of load behavior [8]

Full size image

4 Research background, methodology and approach

Sect. 1 introduces overrunning clutches, their applications in drivetrains, and the requirements they need to meet. Axial loads add to the forces that originate from the transmitted torque. Sect. 2 describes the state of the art of overrunning clutch design. A result is that the current design criterion given in Eq. 1 does not take axial loads in the overrunning clutch design into consideration. Thus, in order to achieve a reliable design of frictionally engaged freewheel clutches, the existing design criterion needs to be refined based on (Eq. 1) and the information presented in Sect. 2.

Accordingly, Sect. 4 discusses the derivation of an improved design criterion based on an analytical approach and on experiments with a newly developed dedicated test rig.

Sect. 5 provides information about the test rig, its design concept, the measurement concept, the test series boundary conditions, the validation of the test rig suitability, and measurement results. Sect. 6 deals with the validation of the improved design criterion by cross-checking it against experimental evidence from Sect. 5.

5 Derivation of an improved design criterion

If Eq. 1 is fulfilled, the friction connection at the Hertzian contacts is intact and the freewheel clutch transmits torque. Fig. 1 illustrates the hitherto valid design criterion (Eq. 1) graphically. It indicates that this criterion is only valid for a two-dimensional load case and not for three-dimensional load cases which are caused by the additional axial load.

Based on the state of the art, the improved design criterion uses

  • all three dimensions of the friction cone

  • the friction coefficient µ in the Hertzian contact as a design criterion.

The numerator of Eq. 1 is expanded to

$$\tan \left(\alpha \right)=\frac{\sqrt{{F_{t}}^{2}+{F_{\text{ax}}}^{2}}}{F_{n}}\leq \mu$$
(8)

Including Eq. 3 and rearranging Eq. 1 to get the normal force Fn leads to

$$\sqrt{ \left( \frac{F_{\text{ax}}^{2} \cdot r_{\text{OR},i}^{2}} {T^{2}} + 1 \right) \cdot \tan (\alpha )^{2}} < \mu$$
(9)

Or, in short

$$\mu _{\mathrm{req}}< \mu$$
(10)

It states that each load case requires an adequately amounted friction coefficient µreq to be able to transmit torque without failure due to slippage. µreq depends on the applied loads, the contact geometry, the design of the clamping angle α and material properties, amongst other parameters. In Eq. 10 the currently available friction coefficient µ is the counterpart to the required friction coefficient µreq.

The improved design criterion states that the freewheel clutch transmits torque, based on frictional engagement, if the currently available friction coefficient µ is greater than the required friction coefficient µreq that the load case demands. µ can be measured or estimated by literature review. Regarding the friction cone illustration (Fig. 1) it means that if the resulting force remains within the friction cone, the friction connection is guaranteed. As soon as the resulting force exceeds the friction cone, the inequality Eq. 10 is no longer fulfilled. The friction connection in the Hertzian contacts is lost, the freewheel clutch slips.

6 Experimental investigations

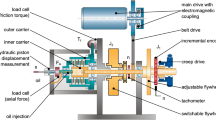
The improved design criterion is based on experimental investigations. Fig. 5 presents a photograph of the specially designed freewheel clutch test rig, while Fig. 6 shows a cross section of the test rig that contains the freewheel clutch. The objective of the rig was to investigate the dynamic behavior and lifetime performance of freewheel clutches by performing test series with different combinations of static and dynamic loads.

Fig. 5
figure 5

Photograph of freewheel clutch test rig

Full size image
Fig. 6
figure 6

Cross section of freewheel clutch test rig [3]

Full size image

The installed measurement equipment allows to measure the axial load and displacement, the torque near the freewheel clutch’s inner ring as well as at the servo motors, and the torsion angles at the inner and outer ring.

The realized concept is the result of a systematic design approach. At first, the basic requirements were established:

  • definition of test specimen (freewheel clutch A and B)

  • axial and radial load application

  • load cases that include varying combinations of static and dynamic loads (Fig. 7)

  • maximum test frequency for dynamic load cases (30 Hz)

  • maximum axial load (3 kN)

  • maximum torque (26 Nm)

  • maximum axial displacement at freewheel clutch inner ring (3 mm) switching component (inner ring)

  • axial load application to component (inner ring)

  • maximum torsion angle φ (± 10°)

  • measured parameters (torque, axial load, axial distance, torsion angle at the inner as well as the outer ring)

Fig. 7
figure 7

Load cases [3]

Full size image

Most relevant were the decisions about how to apply and synchronize the loads and how to develop a control loop. In case of the axial load application, several working principles were investigated: pneumatic muscles, hydraulic actuators, piezo-electric actuators and shakers. Ultimately, pneumatic muscles were identified as the best choice to fulfill the competing requirements of acceptable costs and sufficient magnitude and frequency of axial loads and displacements, the more, as a compressed-air system was readily available with little effort. In terms of the torque application, the requirements restricted the possible options to hydraulic rotary actuators, torque motors and servomotors.

Hydraulic rotary actuators turned out not to reach the required frequencies. As torque motors were rejected due to their high costs and excessive space requirements, servomotors remained as the best solution. A control loop was created that included the pneumatic muscles as well as both servomotors and the measurement equipment. The synchronization of the control loop posed a challenge as it had to be particularly precise to be able to perform the required load cases (Fig. 7).

The capabilities of the test rig were validated by measuring the torsion angles φ and comparing them with computational predictions (i.e. following the approach in Fig. 4), resulting in a close match, Fig. 8. Fig. 7 and Table 1 summarize the load cases as well as the test series boundary conditions:

  • load case one: both loads are stationary. Torque is applied first. After reaching its set point it is kept constant. Afterwards, axial load is applied and increased continuously.

  • load case two: the torque is stationary and the axial load is alternating. The procedure resembles that of load case one. The frequency of the axial load modulation is kept constant whereas the amplitude is increased continuously.

  • load case three: both loads are transient and applied simultaneously. Their modulation frequencies are identical. The torque amplitude is kept constant whereas the axial load amplitude is increased continuously.

Fig. 8
figure 8

Test rig validation based on freewheel clutch A’s torsion angle φ [3]

Full size image
Table 1 Test series boundary conditions [3]
Full size table

The test runs are terminated when the friction connection is lost, indicated by gross slip of the freewheel clutches. It is recognizable in the measured data as a sudden torque reduction. At this point the design criterion according to Eq. 1 is not fulfilled anymore. A full factorial test design was chosen to ensure an unbiased interpretation of the resulting data. The overall number of test runs amounts to 500 per investigated freewheel clutch (Table 1).

FVA2 reference oil was chosen as lubricant, a mineral, paraffin solvent refined oil that does not contain additives. This excludes the potential additive influence on the freewheel clutch’s slip behavior. Table 2 lists FVA2’s characteristic properties. Fig. 9 summarizes the test results of load case 1 with freewheel clutch A.

Table 2 Lubricant properties of FVA2 reference oil [19]
Full size table
Fig. 9
figure 9

Freewheel clutch A, load case 1, result overview [3]

Full size image

The results show that the freewheel clutch can endure some amount of additional stationary axial load without losing the friction connection due to gross sliding. The freewheel clutch slips at a certain threshold value of further increased axial load. This behavior was observed at all test runs, regardless of the load case or tested freewheel clutch (A, B). There was a clear distinction between non-slipping and slipping freewheel clutch operating conditions. This observation served as a basis for the development of the improved design criterion that allows to include superimposed axial loads.

7 Validation of improved design criterion by cross-checking against experimental evidence

Applying the improved design criterion to the test rig results (Fig. 9) leads to Fig. 10. It demonstrates that three categories exist that describe the frictional engagement status in the Hertzian contacts and thereby the freewheel clutch’s failure probability due to slippage. At an average of

  • \(\frac{\mu }{\mu _{\text{req}}}< 0.8\), freewheel clutch A most likely loses the friction connection

  • \(0.8\leq \frac{\mu }{\mu _{\text{req}}}< 1.0\), freewheel clutch A partially loses the friction connection

  • \(\frac{\mu }{\mu _{\text{req}}}\geq 1.0\), freewheel clutch A very rarely loses the friction connection.

Fig. 10
figure 10

Freewheel clutch A, load case 1, application of improved design criterion [3]

Full size image

These observations lead to an abstracted “traffic light” slippage prediction model that is based on the improved design criterion (Eq. 10):

  • Green symbolizes the condition in which the freewheel clutch functions reliably with low risk of failure due to slippage.

  • Yellow symbolizes the condition in which a function loss due to slippage is unlikely, yet not impossible.

  • Red symbolizes the condition in which the freewheel clutch will certainly lose its function due to slippage.

This model visualizes the improved design criterion. It enables the freewheel clutch designer and user to estimate the freewheel clutch’s failure probability due to slippage. A prove for its applicability to other freewheel clutches is presented in Fig. 11, by the example of freewheel type B. Fig. 12 shows that freewheel clutch B’s slippage behavior resembles the one of freewheel clutch A. The improved design criterion and its visualization in the form of the traffic light model are, within the investigated dimensions, usable for other freewheel clutches too. As the improved design criterion bases on a physical operating principle, it may be applicable to other Hertzian friction connections too.

Fig. 11
figure 11

Freewheel clutch A & B, load case 1, observed slippage due to friction loss [3]

Full size image
Fig. 12
figure 12

Freewheel clutch B, load case 1, application of improved design criterion [3]

Full size image

8 Conclusion

Freewheel clutches are frictionally engaged, directional clutches. A loss of the friction connection on contact level due to gross slip is equivalent to a function loss of the freewheel clutch. The hitherto valid design criterion included the forces that result from the applied torque T. It was not possible to consider additional static or dynamic axial loads as well. This publication presents an improved design criterion that allows a function loss prognosis including axial loads.

At first, the improved design criterion was derived analytically, based on the state of the art freewheel clutch design criterion (Sect. 2). To prove its validity experimentally, a dedicated test rig was built (Sect. 3) and employed for an appropriately designed set of measurements which demonstrated its proper functioning. Subsequently, a full factorial test plan was carried out with two test specimens (freewheel clutch A and B). The improved design criterion was applied and found to be suitable for both test specimen; thereby, its validity was clearly confirmed (Sect. 6).