Introduction

Chemometrics can be defined as “the chemical discipline that uses mathematical and statistical methods, (a) to design or select optimal measurement procedures and experiments, and (b) to provide maximum chemical information by analyzing chemical data” [1]. The term chemometrics was introduced in 1972 by Svante Wold, professor of Organic Chemistry at Umeå University, Sweden, and Bruce R. Kowalski, professor of Analytical Chemistry at University of Washington, Seattle, USA. In chemistry, it is similar to the previous econometrics and biometrics terms for economic and biological sciences, respectively.

The foundation of the International Chemometrics Society in 1974 has led to the first description of this discipline. In the following years, some journals devoted special sections to papers on chemometrics (Analytical Chemistry, Analytica Chimica Acta, Talanta, Applied Spectroscopy, ….). In the 1980s, new journals were founded to cover this field: Journal of Chemometrics (Wiley), Chemometrics and Intelligent Laboratory Systems (Elsevier), and Journal of Chemical Information and Modeling (ACS publications).

Several important books/monographs on chemometrics were also first published in the 1980s, including the first edition of Malinowski and Howery's Factor Analysis in Chemistry [2], Sharaf et al.’s Chemometrics [3]; Massart et al. Chemometrics: a textbook [4]; and Multivariate Calibration by Martens and Naes [5]. More recently, a reference work (in 4 volumes) has been published (two editions at the moment) [6].

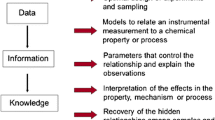
Nowadays, even with the contribution of many authors in recent years, application of chemometrics to electrochemistry, in general, and electroanalytical chemistry, in particular, is still relatively scarce as compared with what happens in spectroscopy and, more recently, in image analysis. We guess this is the consequence of the intimate link between mathematics and electrochemistry, where the essential body of knowledge concerns: (i) proper physico-chemical pictures of the electrochemical processes and the corresponding joint transport phenomena, (ii) the analytical or numerical solutions of these mathematical formulations (outlined according to the corresponding models), and hopefully (iii) the proper physico-chemical interpretation of the electroanalytical data. This approach is usually designated as hard modeling, and it is the common approach used in electrochemical investigations and found in literature. However, in many cases, the postulation of a theoretical physico-chemical model is very difficult because the electrode process (including accompanying chemical reactions), the transport phenomena process, or both of them are rather involved. In such cases, the lack of a hard model makes of the highest interest whatever another type of approach.

The global alternative approach can come from chemometrics, and it is based on extracting results and/or identify models from numerical and statistical analysis of the data, instead of fitting an assumed a priori theoretical model to the experimental data. This new approach is denoted as soft-modeling to distinguish it clearly from the classical approach [11,12,13].

Nowadays, chemometrics is applied in the field of electroanalysis for different purposes: experimental design, signal processing, exploratory data analysis, and, especially, calibration [11, 13, 14]. Methods intended for the evaluation of linear data such as principal component analysis (PCA) or partial least squares (PLS) calibration can be applied to many electrochemical data, provided that a few additional components can account for slight deviations from linearity. In the most extreme situations, non-linear methods such as artificial neural networks (ANN) or support vector machine (SVM) can be an alternative. But, independently of the chemometric method employed, it must be emphasized that the inherent characteristics of electroanalytical data must be considered for a sound interpretation of the results.

As compared to spectra, electroanalytical signals have clear drawbacks, as the poorer reproducibility, their strong dependence on measuring parameters, the matrix effects or the usual deviations from linearity, but they also have advantages, like the well-defined shape (peaks and sigmoids that can be easily adjusted by parametric functions). Anyway, some of the most recent analytical applications of the electrochemical techniques and methods are intimately related to chemometric methods, and their development would not be possible without chemometrics.

University teaching of chemometrics and electrochemistry

In the departments/faculties of chemistry, the teaching of chemometrics is usually under the responsibility of the analytical chemistry unit/section/department. Thus, in practice, it is more related to the foundations of analytical chemistry and instrumental analysis, especially the optical techniques, than to other subdisciplines as, for instance, electrochemistry. Because of that, chemometrics is usually not mentioned in the courses of electrochemistry.

Chemometrics has dedicated subjects in many Spanish universities at both Degree and M.Sci. levels, usually as an optional subject. This is the case of the Degree of Chemistry at the University of Barcelona, where there is the optional subject “chemometrics” of 3 ECTS, which is among the most appreciated by the students in the surveys. Half of its time (15 h) is devoted to theory class introducing the fundamentals of the most usual chemometric techniques: principal component analysis (PCA), principal component regression (PCR), partial least squares (PLS), soft independent modeling of class analogy (SIMCA), and partial least squares discriminant analysis (PLS-DA). The other half of the time (6 sessions of 2 h) is carried out in the computer classroom applying the techniques above to numerical examples. For this purpose, the commercial software PLS-Toolbox [7], by Eigenvector Research, is used. This is a Matlab-based [8] toolbox with a really user-friendly interface. PLS_Toolbox can operate in the same way as other Matlab toolboxes or compiled together with Matlab into a compact version named SOLO. Besides the computer sessions, the students work in groups using their own computers to deal with more complex sets of data. Although most of the examples are from spectroscopic origin, in the last years, some electrochemical data have also been introduced.

In the following, we will describe very briefly some applications published by our research team that can be mentioned when teaching electrochemistry or electroanalysis to illustrate for the students the convenience of a sound knowledge of chemometrics to extract a maximum of information from electrochemical data.

Selected applications

The fist application is the use of a voltammetric electronic tongue for the quantification of aminothiols [15]. Electronic tongues are arrays of sensors having insufficient selectivity to work stand-alone in the determination of one or more analytes [16]. However, if they have cross-response towards a group of analytes, they can be grouped into an electronic tongue. Cross-response means mixed sensitivity (understanding sensitivity as the slope of the calibration plot). For instance, sensor 1 has sensitivities of 10 and 30 towards analytes A and B, respectively, whereas sensor 2 has sensitivities of 40 and 25 towards the same analytes).

In the example of ref. [15], we have three sensors based on commercial screen-printed electrodes (SPE) of different composition: carbon nanofibers (CNF), carbon (C), and gold cured at low temperature (AuBT). Figure 1a-c show the differential pulse voltammograms (DPV) obtained for different mixtures of three aminothiols: cysteine (Cys), homocysteine (hCys), and glutathione (GSH). These individual voltammograms are not able to distinguish among all three substances. However, the combination of these data into a row-wise augmented matrix, after a preliminary baseline correction and normalization (Fig. 1d), improves the overall selectivity. Then, the application of three individual partial least squares (PLS-1) calibration models allows a reasonable quantification of all three aminothiols, as shown by Fig. 2.

Fig. 1
figure 1

Differential pulse voltammograms (DPV) obtained from mixtures of cysteine (Cys), homocysteine (hCys), and glutathione (GSH) with an electronic tongue integrated by three commercial screen-printed electrodes of carbon nanofibers, CNF a, carbon, C b and gold cured at low temperature, AuBT c. In d, it is shown the augmented data matrix, row-wise constructed with the voltammograms of individual sensors a–c previously baseline-corrected and normalized. The analysis of pure solutions of the aminothiols shows that their oxidation signals appear at increasing peak potentials in the order Cys, hCys, and GSH, and this is the order of the peaks (from left to right) observed in the graphs of the mixtures. Reproduced from [15] with permission

Full size image
Fig. 2
figure 2

Predicted versus experimental concentrations of cysteine a, homocysteine b, and glutathione c obtained with three individual PLS-1 models adjusted to the data shown in Fig. 1d. Calibration and external validation values are denoted with solid and empty circles, respectively. Reproduced from [15] with permission

Full size image

The second example is the application of multivariate curve resolution by alternating least squares (MCR-ALS) to a set of differential pulse (DP) voltammograms and circular dichroism (CD) data obtained for the system Cd2+—Cys-Gly peptide. The augmented data matrix is shown in Fig. 3. The application of MCR-ALS with a set of restrictions imposed to keep the physico-chemical meaning of the solution produces the pure signals (Fig. 4a) and the concentration profiles (Fig. 4b) of the different substances involved in the complexation equilibria. This information allows one to propose binding mechanisms such as this shown in Fig. 5.

Fig. 3
figure 3

Augmented data matrix containing normalized DP voltammograms and CD spectra measured at different ratios of Cd2+ and the peptide Cys-Gly at pH 7.5 in the presence of KNO3 0.01 mol L−1 and PIPES buffer 1·10−3 mol L−1. Reproduced from [17] with permission

Full size image
Fig. 4
figure 4

Normalized pure signals (voltammograms and spectra) a and concentration profiles b obtained for the different species involved in the binding of Cd2+ by the peptide Cys-Gly. The species are Cys-Gly (1), Cd2+-ion (2), Cd(Cys-Gly)2 (3), and Cd2(Cys-Gly)2 (4). Reproduced from [17] with permission

Full size image
Fig. 5
figure 5

Proposed structures for the complexes on the basis of the results shown in Fig. 4. Reproduced from [17] with permission

Full size image

The third example is the use of liquid chromatography (HPLC) with amperometric detection (AD) to discriminate among three varieties of white whine (Albariño, Verdejo, and Chardonnay). This is a typical case of chromatographic fingerprinting for the discrimination of samples, but with the electrochemical view in the detection. Figure 6 shows typical chromatograms of the three wine varieties, which do not have a characteristic compound to discriminate them, but a characteristic pattern of the multiple peaks conforming the chromatographic profile in this selected time window of 25 min.

Fig. 6
figure 6

Typical HPLC-AD chromatograms of the three wine varieties considered (Albariño, Verdejo, and Chardonnay) using a SeQuant ZIC-pHILIC column with a mobile phase of 0.05% (v/v) TFA: ACN (19:81) and a flow rate of 1 mL min−1. AD was carried out with a screen-printed gold electrode at a fixed potential of + 1.00 V vs. Ag/AgCl (3 mol L−1 KCl) reference electrode. Reproduced from [18] with permission

Full size image

In this work, wine samples were distributed among a calibration set (4 Albariño, 4 Verdejo, and 4 Chardonnay) and a validation set (2 Albariño, 2 Verdejo, 2 Chardonnay, and 1 Albariño/Chardonnay), and a PLS-DA model was built. The resulting 3D scores plot is shown in Fig. 7. In the plot of Fig. 7a (latent variables LV1, LV3, and LV4), Verdejo samples can be easily distinguished, whereas in the plot of Fig. 7b (with LV2, LV3, and LV4) allows the discrimination between Albariño and Chardonnay samples.

Fig. 7
figure 7

3D-scores plots obtained after PLS-DA models built from white wine HPLC-AD signals. Latent variables 1, 3, and 4 A or 2, 3, and 4 B are considered. Calibration (cal) and validation (val) sets are represented by filled and empty symbols, respectively. Reproduced from [18] with permission

Full size image

Conclusions

Electrochemists cannot restrict their data management strategies to the combination of deterministic equations about (electro)chemical equilibrium, adsorption, kinetics, and mass transport. Contemporary science and technology are exploring systems of increasing complexity and generating huge amounts of data coming from different measuring devices. Fortunately, electrochemical sensors are an important part of such devices and chemometric tools can be very useful to extract the valuable information hidden there. This is why we believe that at the university level, the courses of electrochemistry should incorporate some chemometric contents and the courses on chemometrics should include some examples of the multivariate analysis of electrochemical data.