Abstract
Dynamic EIS (dEIS) is the joint use of cyclic voltammetry and electrochemical impedance spectroscopy. A method is planned for data evaluation which involves transformations yielding potential program invariant forms of certain characteristic functions. This way of calculation is illustrated by the analysis of two archetypes of electrochemical kinetics. A future task is to develop the related theories and to perform demonstration experiments aimed at establishing dEIS as a robust, general-purpose technique for characterizing electrochemical systems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
There are two extremes of doing research. One is the work of pioneers—breaking the ground, finding the tools, setting the rules, and showing the directions for the followers. The other is the job of the consolidators: re-doing experiments to confirm (or disprove) the existence of phenomena and/or to provide reliable data, testing or falsifying parts of theories, and re-formulating concepts to make the theories concise, that is, to make disciplines well-established. Pioneering is unpredictable, consolidation is a never-ending task.
The need for consolidation comes not only from new phenomena and materials but also from technical advancement. This is so also when classical electrochemical methods are considered. These methods, as summarized in a widely used, excellent textbook [1], obtained their mature forms before the era of digital data acquisition—in the age of flatbed recorders. At that time, evaluation of the charts was done by comparing coordinates of characteristic points (e.g., peak location and height) with the related equations. Nowadays, data acquisition methods and computational facilities allow us to include all (or at least many) data points into the analysis instead of a few characteristic points only and to perform complex analyses utilizing the information carried by the entire measured curve. Accordingly, the theory on electrochemical kinetics—the subject of which are charge transfer processes affected also by adsorption and transport from/to the interface—should be re-shaped, enabling one to extract as much information as possible from measured data. This is, certainly, a task to deal with also in the future. One possible way is outlined here.
The current state
A couple of classical, basic electrochemical measurement techniques exist based on measurement of potential E, and current j, as a function of time t (or frequency ω). Some of them, like cyclic voltammetry, CV, are performed in a broad potential range, while others—collectively called electrochemical impedance (or immittance) spectroscopy, EIS—usually in a narrow one.
The two methods, CV and EIS, are typically used for different purposes: with CV, we learn the qualitative features (e.g., what kind of reactions take place and what is the order-of-magnitude of currents), whereas EIS is used to get quantitative information on some known properties (e.g., what is the exact rate of a reaction). Just as the old scientist-classifying joke (about “impedance transformers” and “potential sweepers”) implies, electrochemists are rarely familiar with both methods; the textbooks teach us the two methods separately and few if any connection is shown between the results of the two types of measurements. This is so, even though there exist some variants of CV and EIS which include some element of the other method (e.g., AC voltammetry or EIS measured sequentially on stepwise set potentials or harmonic analysis with large amplitude perturbations).
There are two links connecting the two methods: one is the experimental method of dynamic EIS (dEIS), and the other is a theoretical one: the potential program invariant (PPI) representation of the measured j(t) vs E(t) voltammetry data.
dEIS is a combination of CV and EIS: it is their simultaneous use. During dEIS measurements, the potential is scanned just like in the case of the classical CV; however, it is also perturbed by a small amplitude, periodic, noise-like voltage. This way, audio-frequency impedance spectra can be measured continuously as the potential is varied. dEIS is apparently a complicated method; yet, it does not require sophisticated instruments, only a commercially available data acquisition system, some modifications on the potentiostat plus the software. Such instruments have been developed at many places among them in our laboratory, for various applications which are beyond the present scope. Note that the implementation of dEIS to potentiostats will be an important (and probably profitable) task of instrument manufacturers.
One difference between CV (or in general: the j(t) vs E(t) voltammetry) and EIS is to be emphasized here: EIS has a standardized output in the sense that it produces spectra that are independent on the actual form of potential or current perturbation by which they have been measured. In contrast, the results of voltammetry measurements do depend on the E(t) function (scan rates and turning potentials). However, appropriate transformations may yield functions which have lost their connection with the potential program by which they have been measured—that is, they result in PPI functions. The classical example for such a transform is the semi-integrated form of cyclic voltammograms of reversible redox couples, as demonstrated five decades ago [2]. This is the archetype of the PPI representation of voltammograms taken in a broad potential range.
In principle, the same electric properties of a system can be determined either by a set of CVs taken with multiple scan rates or from EIS measured in broad frequency range at multiple potentials. In this sense, the methods CV and EIS are equivalents, and hence, in the ideal case, one should be able to transform a set of CVs to another set of EIS and vice versa. In the same vein, from dEIS measurements, both results (i.e., CV and EIS) should yield the same physical-chemical quantities as from complete sets of separate CVs or EIS. There exist numerous CV and EIS theories; however, only a few treat the two methods simultaneously with the aim of exploring the connections between them. A future task is to elaborate such theories. Two simple textbook cases might serve as an illustration.
Two examples of PPI representations
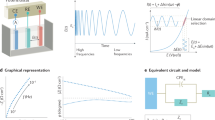
In the first example, we consider the diffusion-controlled charge transfer reaction with infinite reaction rates taking on a noble metal electrode of planar geometry. The CV of this “reversible system” is the well-known curve with asymmetric peaks and big hysteresis; this curve does depend on the scan parameters such as the scan rate (see Fig. 1a). However, applying a convolution procedure on the current-time curve, one can get the so-called semi-integrated form, Mrev, so that the Mrev vs E curve becomes hysteresis free and scan rate independent, i.e., a PPI function. The derivative dMrev/dE vs E, per se, is also PPI. If the same system is investigated by impedance measurements, one obtains spectra which can be analyzed in terms of a Randles circuit, with zero charge transfer resistance. The coefficient of the Warburg admittance, σW,rev, exhibits a potential dependence which is just the same as that of dMrev/dE vs E obtained from the CVs, as it has been shown theoretically [3] and experimentally (Fig. 1b, [4]). To conclude, there is a PPI function, Mrev, which appears in the theories of both CV and EIS in the context of charge transfer of reversible redox systems. Mrev and dMrev/dE are the PPI function of large- and small-signal (“global” and “local”) responses.
Evaluation of CVs and EIS to yield the same PPI functions for a reversible redox system. a CVs at scan rates as indicated (solid lines). Impedance spectra have been measured at the dots. b Warburg admittance coefficient, σ, vs IR-corrected potential, EIRc, as evaluated from dEIS. The solid lines are the dM/dEIRc curves
The second example concerns the same system but with finite charge transfer rates. The CV of this “quasi-reversible system” is similar to that of a reversible one, but the peak-separation is scan rate dependent (see Fig. 2a). By the methods described in ref. [5], one can transform the set of CVs to two PPI functions: jinf, which characterizes charge transfer alone, and Mrev, which is a property of the diffusional flux (see Fig. 2b.) For analyzing EIS of the same system, the equivalent circuit is a full Randles circuit. In the case of dEIS, the charge transfer resistance and the Warburg admittance coefficient depend on the scan rate. However, with a transformation described in ref. [6], one can get rid of the scan rate dependences and get PPI functions djinf/dE and the σW,rev. = dMrev/dE.
Outlook
Development and testing of such theories are in progress, for various electrochemical situations. Just as other theories and methods, they are by no means universal. Rather they are elements of a toolbox, just like the equivalent circuit elements are in impedance analysis. Nevertheless, these theories will yield three great advances over the existing ones:
-
1.
Whereas the conventional voltammetry methods yield curves which depend both on electrochemical properties of the system and measurement parameters, the PPI functions depend on the former only. In this sense, they are the appropriate representations of the physical-chemical properties.
-
2.
PPI functions are usually calculated by integral transforms; hence, these theories allow us to determine physical-chemical quantities from many data points rather than from single or a few ones (from peak heights, peak distances, etc.). Such procedures improve measurement accuracy and robustness in general.
-
3.
Finally, dEIS theories involving PPI functions are expected to carry the same information in a much more concise way than the present (CV and EIS) ones known from textbooks.
The new theories are expected to consolidate the background of dEIS evaluations and to improve the accuracy of the results. This will, in turn, open new routes for the pioneers of electrochemistry.
References
Bard AJ, Faulkner LR (2001) Electrochemical Methods. Wiley, New York 1980
Oldham KB (1972) A signal-independent electroanalytical method. Anal Chem 44(1):196–198
Pajkossy T (1997) Potential program invariant representation of voltammetric measurement results of reversible redox couples. J Electroanal Chem 422(1-2):13–19
Pajkossy T, Mészáros G (2020) Connection of CVs and impedance spectra of reversible redox systems, as used for the validation of a dynamic electrochemical impedance spectrum measurement system. J Solid State Electrochem. https://doi.org/10.1007/s10008-020-04661-8
Pajkossy T, Vesztergom S (2019) Analysis of voltammograms of quasi-reversible redox systems: transformation to potential program invariant form. Electrochim Acta 297:1121–1129
Pajkossy T (2019) Dynamic electrochemical impedance spectroscopy of quasi-reversible redox systems. Properties of the Faradaic impedance, and relations to those of voltammograms. Electrochim Acta 308:410
Funding
Open access funding provided by Research Centre for Natural Sciences. Financial assistance of the National Research, Technology and Innovation Office of through the project OTKA-NN-112034 is acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pajkossy, T. Voltammetry coupled with impedance spectroscopy. J Solid State Electrochem 24, 2157–2159 (2020). https://doi.org/10.1007/s10008-020-04689-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10008-020-04689-w