Abstract
Kelvin probe-based contact potential measurements were conducted with in situ electrochemical hydrogen loading of a Pd membrane with a thickness of 100 μm. The theoretical basis of diffusion coefficient calculation based on measured response time of potential drop, arising from hydrogen arriving at the detection side of the Pd membrane, was discussed. In situ hydrogen loading was also utilized for insertion of different amounts of hydrogen into the Pd sample while monitoring the resulting contact potential difference changes. Measurement of contact potential difference at different final values of hydrogen concentration in the Pd membrane was performed at various atmospheric conditions, focusing in this work on increasing relative humidity (4 to 85% rH). Moreover, the effect of humidity changes on hydrogen effusion kinetics at room temperature and low oxygen content (<1%) was studied.

ᅟ
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Research on hydrogen is gaining more and more importance within the last decades. Especially in surface science and material science, much progress concerning hydrogen uptake and diffusion in metals has been achieved [1]. In addition, development of new techniques for hydrogen sensing as well as precise calibration procedures for hydrogen analysers is an ongoing process still relevant for scientific investigation of hydrogen-related topics [2].
Hydrogen is known to be a promising energy carrier for the future. Therefore, production, storage, release and transport are crucial topics to improve the transformation of chemical energy “in” hydrogen to mechanical energy to be used for mobile transport [3]. One main topic of course is hydrogen storage, which can be carried out either in gaseous or in liquid state or solid by physisorption of hydrogen on materials with a high specific surface area, as well as hydrogen intercalation in hydrides and metals. [4]. Hydrogen intercalation as hydride in host materials is a promising field; recently, sodium borohydride has been proposed having good reversible capacities for hydrogen storage [5]. Also, theoretical calculations concerning the influence of Al, Nb or Ti doping of magnesium-boron-hydride on the diffusion path of hydrogen atoms through these materials have been performed. The results indicate that doping weakens the B–H bond with Nb showing the best effect [6]. Remarkable improvement of hydrogen absorption kinetics and thus absorption speed has been shown for accumulative roll bonded (ARB) Mg-LaNi5 soot hybrid materials. Therefore, intimate mixing of the components along with a fine microstructure and increased defect density in the hybrid are found to be key parameters for hydrogen absorption properties [7]. Along with this, a variety of systems has been studied ranging from metals [8] to organic materials like carbon nanotubes [9, 10].
From early state of chemical engineering hydrogen embrittlement (HE) is a known problem [11, 12] in metal industry, which had to be faced already in 1911 during the development of ammonia synthesis by Haber and Bosch. The first attempt to overcome problems due to cracking because of reaction of hydrogen with carbon in the steel at high pressures was performed by coating the inner wall of the reactor with pure iron and drilling narrow holes in the outer steel wall, so that hydrogen could diffuse through the iron and leaf the reactor without causing damage [13]. Up to now, HE is already widely investigated [14, 15]; nevertheless, it is still a problem for the performance of materials in construction causing severe damages because of delayed fracture [16]. Challenges in characterizing the microstructure because of varying phases and/or compositional gradients, especially for alloyed steel, still have to be overcome. Quantification and assessment of trap site interactions with absorbed hydrogen play an important role for investigations [17]. According to Akiyama et al. [18], diffusible hydrogen has been found to be the main contribution to HE. Determination of the amount of hydrogen from atmospheric corrosion contributing to HE is not straightforward because of changing environmental conditions as well as corrosion behaviour with time.
Hydrogen evolution during cold rolling process in metal industry has impact on the surface structure of the working roll. Potentiodynamic investigation reveals a stationary situation established between the destruction and repassivation of the role material. It has been shown that galvanic coupling of the roll with the product causes pressure-supported atomic hydrogen adsorption into the rolls decreasing their lifetime [19].
Technical relevance for hydrogenation and dehydrogenation via catalytic reactions has supported Pd membranes being permselective for hydrogen. Compact palladium composite membranes are used in packed bed catalysts for hydrogen separation in gas-phase dehydrogenation reactions [20].
Various techniques for detection of hydrogen evolution, uptake and diffusion have been established contributing to deeper understanding of the topic. Standard methods for hydrogen detection in metals are the Devanathan-Stachurski cell, which provides information about the diffusion constants of hydrogen in metals and density of trap sites [21, 22] or thermodesorption technique [23].
Along with other methods recently, Kelvin probe (KP) gains more interest for detecting hydrogen in metals. Due to its sensitivity to changes in surface morphology, oxidation states and crystal structure of the outer layers of the material, KP can be employed for qualitative and quantitative hydrogen detection via measurement of changes in the surface Volta potential distribution. The first research on Pd surfaces showed a decreased Volta potential and hence a decreased work function on the surface (exit side) of hydrogen-loaded Pd. Interpretation of the results led to the assumption that formation of electrochemical equilibrium between reduced residual oxygen and hydrogen oxidation takes place. Changes in the surface potential were related to an increasing amount of diffused hydrogen [24]. However, further studies showed a logarithmic correlation between the amount of hydrogen and the measured surface Volta potential. The latter dependency is only valid in the case that a thin layer of electrolyte (e.g. water) is adsorbed on the surface [25].
Because of the good absorption behaviour and high diffusion rate of hydrogen in palladium, it is commonly used for model studies on metal hydrogen systems for almost a century now [26]. In this case, also the production route of the investigated Pd surface makes a difference in the hydrogen uptake and diffusion behaviour. Pd thin films can be either electroless deposited, electrochemically deposited or prepared by physical vapour deposition, which shows varying performance for calibration of the hydrogen sensors by impedance spectroscopy [27]. The absorption of hydrogen by occupying vacancies causes several changes in the material. Depending on the way of absorption, e.g. at interstitial sites or traps, different amount of energy is needed to liberate the hydrogen and desorb it from the material. Electronic properties during hydrogen uptake as well as phase transition from PdH α-phase to β-phase can both be recorded by KP [28].
Analysis of hydrogen diffusion in steel tends to be more complex. The procedure of loading steel samples with hydrogen is presented elsewhere [29]. Investigating the surface of iron which is naturally oxidized shows a decrease of surface Volta potential as soon as hydrogen reaches the surface. This change leads to a lowering in work function and occurs due to reduction of Fe3+ to Fe2+ changing the Fermi level position, which is defined by the ratio of Fe2+/Fe3+ at the oxide surface [30]. Depending on the atmosphere on the exit side, various possible situations may be observed. Atmospheric oxygen, for instance, will reoxidize the Fe2+ to Fe3+ [29] according to the scheme proposed elsewhere [30, 31]. Due to complex structure and composition of oxides, reproducibility is not easily achieved. To overcome this obstacle, samples are coated with a thin layer of Pd which drains the hydrogen from the steel/oxide sample. Traps deliver new hydrogen atoms from regions deeper in the sample.
As mentioned before, hydrogen on the surface of a material is very active. Previous studies focussing on silver show that there is a dependency on the surface microstructure of Ag2O concerning the ability to reduce hydrogen. It was shown that the surface to volume ratio of the Ag2O crystals as well as the facet-dependent activity of the morphologies plays a role in the oxide reduction process via differences in the contact area size [32].
A detailed study on hydrogen detection in and on the surface of metals by KP can be found in the literature [33]. The present study focuses on using the interaction of Pd and hydrogen for semiquantitative determination of hydrogen concentration within the metal.
Materials and methods
An 80 × 10-mm-sized piece of palladium foil (Goodfellow, as rolled, 99.5%) with 0.1-mm thickness was used as a sample. Before usage, the Pd foil was cleaned ultrasonically in acetone, ethanol and deionized water. For KP measurements with in situ electrochemical hydrogen loading, the sample was mounted into a specially designed 3D printed cell (Fig. 1) described elsewhere [34]. As electrolyte, 0.1-M NaOH solution, which was deaerated by Ar bubbling for at least 2 h prior to measurement, was used. During the KP measurement, the electrolyte flow rate was adjusted to 75 cm3 s−1, which was large enough to rapidly entrain possibly formed gas bubbles at working or counter electrode.
KP measurements were performed with a system from Wicinski & Wicinski GbR with a 300-μm-diameter Cr–Ni probe tip build into an in-house developed chamber and transfer system. Tip-sample distance was kept constant automatically to 110 μm. KP sample chamber atmosphere was varied in terms of relative humidity (rH), whereas oxygen content and temperature (23 ± 1.0 °C) were kept constant. During the measurements, the KP chamber was constantly flushed with nitrogen (5.0, Linde, Austria). The oxygen concentration in the KP chamber was monitored with an oxygen sensor with a lower detection limit of 1%. As the chamber, which is gastight except for a gas outlet backpressure valve, is constantly flushed with nitrogen, it can be assumed that the real oxygen concentration is much lower than 1%. In order to enable comparison to electrochemical potentials, the system was calibrated before measurement by probing an electrochemical system with known potential, which was in this case the liquid surface of a saturated CuSO4 solution in a Cu crucible [35].
For electrochemical hydrogen loading, an IVIUM CompactStat potentiostat in floating mode was employed. Hydrogen permeation measurement with KP hydrogen detection at the exit side was performed galvanostatically at 1 mA cm−2. For cyclic voltammetric study of hydrogen insertion behaviour, a triangular potential waveform was applied for 3 cycles with a scan rate of 10 mV s−1 between −0.9 and 0.6 V versus (standard hydrogen electrode (SHE)). For hydrogen detection measurements at varying humidity conditions, potentiostatic pulses at −0.7 V (SHE) with durations of 5, 15, 30, 50, 75, 105, 140 and 180 s were applied. All electrochemical measurements were performed in a three-electrode setup comprising a Hg/HgO/0.1 M NaOH-microreference electrode as well as a gold counter electrode. Between hydrogen loading intervals, electrochemical unloading was performed by applying a potential of −0.1 V (SHE) to the entry side of the sample.
Results and discussion
Measurement basics and principles
As the experiments performed in this work are based on hydrogen diffusion through a palladium foil, it is essential to know the hydrogen diffusion kinetics in the studied material. Therefore, a hydrogen permeation measurement was performed by in situ hydrogen loading while detecting hydrogen arriving at the exit side of the sample with KP. Hydrogen loading was conducted in the same way as in electrochemical hydrogen permeation experiments according to Devanathan and Stachurski [21], involving sufficiently cathodic polarization of a metal sample in order to force hydrogen uptake. In alkaline solution, absorption of hydrogen can be described with two different mechanisms, in which the hydrogen uptake is proceeding in one (direct absorption, Eq. 1) or two (indirect absorption, Eq. 2) steps. The indirect mechanism contains adsorption of hydrogen followed by absorption into the Pd sample (Eq. 3) [36].
When hydrogen reaches the absorbed state, it will diffuse driven by concentration gradients by jumping from one interstitial position to the next. In case of Pd, hydrogen occupies mostly octahedral sites in the metal lattice [37]. Generally, hydrogen uptake leads to expansion of the crystal lattice, causing mechanical stresses, which in turn cause changes in work function of the metal [38, 39]. In case of Pd, deformation of the metal lattice gets even more pronounced when the hydrogen-rich β-PdH phase is formed [40]. Regarding the diffusional process of hydrogen in a metal lattice, trapping phenomena have to be considered, which can be divided into two types according to their ability to trap hydrogen reversibly, like grain boundaries and dislocations or, irreversibly, like precipitates [41]. In this context, the presence of β-PdH in the metal in combination with the less hydrogen-rich α-phase can cause reversible trapping of hydrogen atoms [42, 43].
In case of electrochemical permeation methods, the exit side of the metal membrane is anodically polarized (see Eq. 4) and the resulting oxidation current is measured to quantify arriving hydrogen.
If no electrochemical oxidation of hydrogen is possible, as it is the case for permeation experiments measured by KP, hydrogen removal from the Pd is solely based on the recombination of two adsorbed hydrogen atoms and subsequent desorption (Eq. 5), which is endothermic in case of Pd [37, 44, 45] or the reaction with oxygen resulting in water formation [46].
As the hydrogen removal from the sample is much slower compared to the electrochemical oxidation performed in electrochemical permeation experiments, hydrogen concentration at the hydrogen exit side of the sample deviates from zero. Therefore, evaluation of hydrogen diffusion coefficient in case of KP detection is different from the Devanathan-Stachurski method.
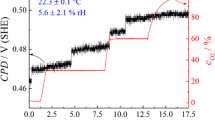
Sensitivity of the KP in terms of hydrogen determination was proven to be comparatively high; a hydrogen loading pulse of 60 s with 1 mA cm−2, as shown in Fig. 2, is sufficient to cause a sharp drop in measured contact potential difference (CPD) in the moment of hydrogen arrival at the exit side of the sample. From the onset time of this CPD drop, the hydrogen diffusion coefficient (D) can be calculated. Figure 2b depicts the CPD transient measured for a longer hydrogen loading pulse, again with 1 mA cm−2. Hydrogen loading was maintained until a stable CPD reading was obtained in order to visualize formation of the β-PdH phase. Reaching of a mixed α-/β-PdH phase can be also detected in the height information obtained from the automatic height control system of the used KP system. The increase in height is a direct consequence of the volume expansion accompanying the β-PdH phase formation. After exceeding the maximum α-PdH concentration, a stable CPD of 0.006 V (SHE) was measured. This value is limiting the range, in which Pd can be used for hydrogen quantification. As Evers et al. [25] and Lee et al. [47] have demonstrated, correlation between work function or electrode potential and hydrogen concentration in the material is only observable in the less hydrogen containing α-PdH phase.
Calculation of the diffusion coefficient D is based on Fick’s second law describing the non-stationary diffusion [48, 49], which in one direction (x) reads
C is the concentration of diffusing substance, which diffuses in x-direction. The solution for the diffusion equation for x > 0, where x = 0 is defined as the hydrogen entry side of the sample and x = L is the corresponding exit side, with the initial condition C t = 0,x > 0 = C 0 and the boundary condition C t > 0,x = 0 = C H,x = 0 gives the following:
The concentration distribution (Fig. 2) can be approximated by the following:
The penetration depth is therefore defined as follows:
In our case, x pen is limited by the thickness (L = 0.01 cm) of the membrane and the time t corresponds to the onset or response time (t onset) of the measured KP potential drop. Therefore, solution of D gives, for the case of materials with very low hydrogen trap density,
This value is in good agreement to previously published results [21, 34, 42, 50, 51].
After finishing hydrogen loading for determination of diffusion coefficient, point measurement of CPD was continued until a return of the potential almost to the initial value of 0.575 V (SHE) was observed. Increase in potential, which describes removal of hydrogen from the Pd sample, is slow due to conditions inhibiting the reaction of absorbed hydrogen and consecutive removal from the foil. In contrast to electrochemical unloading of hydrogen, where an anodic potential is applied to the sample, enabling fast reaction kinetics, removal of hydrogen has to occur by recombination of adsorbed hydrogen followed by desorption as molecular hydrogen (Fig. 3) or by reaction with atmospheric oxygen at the hydrogen exit side of the sample [29]. Additional to the effusion of hydrogen into the atmosphere on the exit side of the sample probed by the KP, hydrogen can diffuse back to the entry side of the sample, where a loss of hydrogen into the electrolyte is highly probable. Kirchheim and coworkers showed in several publications that the loss of hydrogen in molecular state into the electrolyte is highly dependent on mobility and activity of hydrogen in the electrolyte [52–54]. In order to decrease the hydrogen mobility in the electrolyte, a highly viscous electrolyte was used, which is, however, not suited for the herein presented flow cell setup.
An interesting aspect found in results presented in Fig. 2 is that the potential is not reaching its starting value, even after very long recovering times. This aspect was already reported in literature [33] and can be on the one hand due to hydrogen trapping phenomena as well as irreversible deformations of the metal lattice.
As preparation for electrochemical hydrogen loading of the Pd sample, a suitable potential has to be chosen. For this purpose, a cyclic voltammogram of Pd in 0.1-M NaOH solution was recorded (Fig. 4) at the same electrolyte flow rate as for all other experiments described in this work. Maintenance of flow rate is essential, as convectional changes were reported to affect hydrogen entry into the metal sample [55] significantly. The shape of the recorded cyclic voltammogram (CV) is slightly different from other published results [36, 56, 57], which can be due to electrolyte convection. Nevertheless, a cathodic peak resulting from hydrogen adsorption, absorption and hydrogen evolution as indicated in Fig. 3 can be identified. At less cathodic potentials, reduction of Pd oxide (−0.09 V (SHE)), previously formed at potentials above 0.1 V (SHE), is visible.
Combined with results from a previous work [34], a potential of −0.7 V (SHE) was chosen for hydrogen loading of the Pd sample, which is positioned in the hydrogen adsorption and absorption region as depicted in Fig. 3. At lower potentials, hydrogen evolution reaction (HER) occurs dominating the hydrogen ingress with formation of a mixed α-,β-PdH phase at the entry side of the Pd membrane. Even though the used flow cell allows for polarizations at lower potentials going along with hydrogen evolution as shown in [34], those cathodic potentials are not considered for hydrogen loading as formation of β-PdH phase has to be avoided [25, 47].
In order to achieve various amounts of hydrogen in the Pd sample, as mentioned earlier, several loading cycles were conducted by applying a constant potential of −0.7 V (SHE) with pulse durations between 5 and 180 s. The corresponding current transients (j) measured during these potentiostatic H-loading cycles are presented in Fig. 5. From integration of the obtained current transients, the amount of inserted hydrogen can be calculated as shown representatively in the inset of Fig. 5 for hydrogen loading pulse of 75-s duration. The calculation is based on Faraday’s laws [58]:
Q H describes the amount of charge per square centimetre, which can be correlated to the amount of hydrogen inserted (n H). Finally, by dividing the obtained n H by the thickness of the sample (L), one obtains the hydrogen concentration per volume (c H,coulometric):
At −0.7 V (SHE), the hydrogen evolution is assumed to be negligible, enabling calculation of the inserted amount of hydrogen from integration of the measured insertion current during cathodic polarization. However, part of the hydrogen, which was inserted into the Pd membrane, will be lost into the electrolyte, especially after finishing cathodic polarization. Therefore, the calculated amount of hydrogen (Eqs. 11 and 12) is an approximation, reflecting the amount of hydrogen in the Pd membrane without giving the exact value. Determination of the real hydrogen concentration is, for the system used, only accessible via numerical simulation, taking into account loss of hydrogen into the electrolyte and effusion of hydrogen into the KP chamber atmosphere next to diffusion rates of hydrogen in Pd. The loss of hydrogen into the KP chamber atmosphere as well as the loss into the electrolyte is dependent not only on the hydrogen concentration in the Pd, but also on the composition of the electrolyte and the atmosphere, respectively.
Hydrogen detection and humidity influence
In order to avoid systematic measurement errors due to changes in the sample material, which is in our case Pd, occurring during variation of KP measurement atmosphere, CPD was recorded (Fig. 6) for at least 45 min at each adjusted value of relative humidity (rH). Variation of potential in a humidity range between <1 and 60% is less than 30 mV; between <1% and the maximum of 90%, the potential deviation from the original value at lowest humidity is 42 mV. This variation in potential can be attributed to contributions of capacitance changes between tip and sample, which are affecting the measured CPD as shown in the inset of Fig. 6. This measurement was performed by probing the liquid surface of a CuSO4 solution in a Cu crucible, which is also used for correlating the CPD to electrochemical potentials. In this case, no adsorption effects on solid surfaces have to be considered, in contrast to the capacitance changes induced by variation in rH. Therefore, the CPD changes measured later during hydrogen loading are fully induced by interaction of the Pd sample with the inserted hydrogen and not with the measurement atmosphere. It should be considered that the humidity directly above the liquid surface of the copper sulphate solution is probably higher compared to the overall humidity in the KP chamber.
Figure 7 shows the CPD measurement with in situ hydrogen insertion on a freshly prepared Pd sample and indicates the increasing hydrogen loading pulse durations, starting from 5 s at −0.7 V (SHE) up to 180 s at the lowest possible oxygen concentration and humidity level adjustable for long-term measurements in the KP setup. After hydrogen reaches the exit side of the membrane, a clear drop in potential is measured by the KP, in a similar manner as it was shown for the hydrogen permeation transient in Fig. 2. With increasing loading time corresponding to higher amounts of hydrogen inserted into the material, lower CPD values are observed. Shortly after finishing the hydrogen loading process, an increase of CPD is measured. The return of the CPD to its starting value is due to conditions measured in, very slowly, which was already discussed related to Fig. 2. Removal of hydrogen from the Pd sample is therefore only depending on desorption of molecular hydrogen or reaction with oxygen in the measurement atmosphere, which was kept as low as possible in this first measurement. Another possibility to force hydrogen removal is to apply a sufficiently anodic potential to the entry side of the Pd membrane to allow oxidation of hydrogen. This was performed by polarizing the membrane shortly before the subsequent loading cycle is started to a potential of −0.1 V (SHE). The resulting oxidation current was in a range of picoampere per square centimetre. Polarization at higher anodic potentials than −0.1 V (SHE) was not possible, as formation of palladium oxide is expected to occur. Therefore, the low levels of measured oxidation current can be interpreted as an electrochemically non-measurable amount of hydrogen remaining in the sample. In order to allow CPD measurement with different amounts of hydrogen loaded into the Pd within a reasonable time frame, recovery intervals between H-loading of several hours were not considered as meaningful. Therefore, consecutive loading cycles were started when CPD reached about 50 to 60% of the former potential value, tolerating the fact that hydrogen remaining inside the material inserted in the previous loading cycle may still contribute to the drop in CPD. However, due to the logarithmical dependency of the CPD on the hydrogen concentration in the material, resulting in relatively large CPD changes corresponding to a small amount of hydrogen, residual hydrogen amounts remaining in the sample from the previous loading can be neglected compared to the amount of hydrogen, which is inserted in the subsequent cycle. In this manner, duration (t n) of hydrogen loading pulse duration was not increased linearly but cubically as follows:
with x being the number of the loading cycle.
As also previously described in context of Figs. 2b and 4 and shown by the group of Rohwerder [25], calibration of the KP potential in dependence of the hydrogen concentration in Pd is limited by the formation of β-PdH x , which occurs above a concentration of x = 0.02 [37]. Formation of a mixed α,β-PdH x phase is indicated by a plateau in CPD and measured in this work giving a value of about 0.006 V (SHE) [25]. Therefore, the measured CPD should not fall below this potential value during hydrogen loading cycles.
In a similar manner as presented in Fig. 7, the hydrogen loading procedure was repeated for varying humidity conditions, but constant temperature and oxygen content. The results for 10% rH, 25% rH, 50% rH and 85% rH are depicted in Fig. 8. Shape of the curves is comparable as well as the potential range fluctuating between 200 and 450 mV according to alternation of the loading and recovering cycles. The fluctuation in humidity for all cases was about ±1% rH, except for the measurement with highest humidity content (85% rH) exhibiting a deviation of ±5% rH from the set value, because adjustment and stabilization of humidity values above 80% rH over a long time period are already at the limit of the system. Comparing the CPD transient presented in Fig. 7 with the subsequently measured transients, shown in Fig. 8, a steady decrease of CPD reached during hydrogen unloading pulses can be observed for the first measured transient. For all subsequently measured transients (Fig. 8), the potential almost reaches the starting value between the hydrogen loading pulses. Therefore, the very first hydrogen loading/unloading experiment is characterized by an irreversible hydrogen absorption causing persistent changes in the material’s structure.
Potential minima were evaluated from the recorded CPD transients, and corresponding hydrogen concentrations were obtained from integration of the loading current, allowing the calculation of linear regression curves for every single humidity setting.
Results are summarized in Fig. 9 in which the obtained CPD minima are plotted versus the logarithm of the approximated hydrogen concentration determined from integration of cathodic current measured on the entry side (c H,coulometric). The measured data values were fitted by linear regression, and resulting parameters are listed in Table 1. The linear fit for the freshly prepared sample (4% rH (1)) shows a different behaviour compared to all other subsequent calibration experiments. This manifests not only in a much higher slope of the curve, but also in a less cathodic starting potential of 0.6 V, compared to 0.4–0.5 V (SHE), resulting in a larger potential range over the entire measurement. Therefore, the measurement at lowest humidity was repeated subsequently to the other measurements (4% rH (2)). Interestingly, the slope of this curve matches those of all other curves revealing an irreversible process happening during the first loading cycle. This finding corresponds to the work of Evers et al. [33] mentioning a deviating behaviour of freshly prepared Pd samples. It has to be emphasized that after the first loading/unloading procedure, the initial potential was not reached anymore, leading to a lower starting value in CPD for the next loading/unloading experiment at increased rH. Therefore, we can assume that even there was no formation of a mixed α,β-PdH x phase at the surface, which is probed by the surface-sensitive KP technique, there might be formation of this phase mixture within the sample. This can be accompanied by filling of other trap sites like various kinds of dislocations due to the manufacturing procedure of the foil used. Therefore, the absolute potentials for all the subsequent measurements at higher humidity are shifted and should not be taken as absolute values.
Linear fitting curves revealing dependency of measured absolute CPD values on logarithm of coulometrically determined hydrogen concentration (c H,coulometric in mol cm−3) in Pd, obtained for different humidity values. Measurement points marked with squares (4% rH (1)) represent data from freshly prepared Pd specimen, while all other values were acquired in consecutive measurements on the same Pd sample
Another aspect is the loss of hydrogen into the electrolyte as well as into the chamber atmosphere, which was already mentioned earlier. This loss will occur in higher rates when the hydrogen concentration in the Pd is higher. This may lead to a systematic influence of the determined slopes as it causes a weaker drop in CPD for the longest hydrogen loading pulses.
In order to enable evaluation of the quality of the linear regression, it is useful to consider the correlation coefficient of the linear fit (see Table 1). Especially for humidity values of 25 and 50% rH, linearity of experimental data is poor resulting in low values of R 2. Thus, it seems beneficial to use low humidity for hydrogen determination. On the other hand, our experiments show that also for the highest achievable humidity of 85% rH, a reasonable R 2 can be achieved. Regarding the slope of the curves for samples which were already hydrogen loaded in a previous experiment, the values of k (see Table 1) are in the range of −0.061 to −0.076 V per decade. Theoretically, a value of −0.059 V is expected because of Nernstian behaviour:
Electrochemical potential E corresponds to CPD measured by means of KP, a(H+) is the activity of protons in the water layer on the exit side of the sample, whereas a(Hab) describes the activity of hydrogen within the sample. Assuming that after the first loading cycle, the concentration of H+ in the nanoscopic water layer remains constant, which was also observed by Evers et al. [25], the CPD only depends on the concentration of hydrogen dissolved in the Pd (Hab).
The slopes of the linear regressions determined at different levels of relative humidity seem to scatter around an average value of approximately 69 mV per decade. There is no clear influence of the relative humidity observable.
Based on the assumption that environmental conditions influence the removal of hydrogen from the sample, additional evaluation of the CPD transients during the recovery intervals was performed. For this purpose, the increase of CPD after finishing of hydrogen loading was approximated by linear regressions for each loading/unloading cycle. The averaged slopes of these regressions versus the humidity are depicted in Fig. 10.
For humidity values up to 50% rH, the slopes are nearly constant at 0.140 mV s−1 revealing similar unloading speed. Regarding the highest measured humidity conditions, a deceleration in hydrogen removal kinetics can be observed with a value of 0.055 mV s−1. Increasing humidity in the measurement atmosphere leads to an increase in water layer thickness on the sample surface [59–61]. Therefore, for high humidity values, dilution effects may influence the proton concentration in the water layer. This influence is negligible for the calibration because only the maximum hydrogen concentration resulting in a minimum of CPD is considered neglecting mostly the surface reaction kinetics. Changes in proton concentration are only minimal contributing to the value of CPD, governed by the drastic change in Hab. The situation is different for the case of a naturally occurring removal of hydrogen from the metal sample. As no active hydrogen unloading was performed as it is done, for instance, by applying a sufficiently anodic potential to the exit side or by heating up the sample, the removal of hydrogen is based on the recombination of adsorbed hydrogen followed by desorption as molecule or by reaction with oxygen. The kinetics of these processes is therefore affecting the slope of the recovery curves measured by KP. As the oxygen content and temperature were kept constant during the experiment, changes in kinetics are only related to variation of rH. As reported by Hu et al. [59] and Freund et al. [62], water surface coverage and thickness of the water layer are highly dependent on the rH. These two parameters are in turn affected by the hydrophilicity as well as structural qualities like lattice constants and texture of the surface [60]. In case of Pd(100), formation of stable water droplets could be verified by molecular dynamic simulations. Hu et al. [59] defined three different regions for wetting of mica. In a similar manner, stepwise increase of humidity, as it was performed in this study, will also influence the coverage and thickness of the water layer on Pd. According to previous studies by Freund et al. [62] on the water coverage of noble metals such as gold, above 55% rH, the surface was covered with a continuous water film. Below this value, droplets could be observed. For the present investigation, a similar behaviour can be assumed for the studied Pd sample. Therefore, it is explainable why an increase in rH can cause a change in surface kinetics as it was observed for rise from 50 to 85% rH. However, the observed change in surface kinetics is of minor importance for KP detection of hydrogen due to the large KP tip size compared to the size of water droplets, which is in the nanometre range, but might therefore have a strong effect on SKPFM measurements [63].
Further investigations concerning variations in the oxygen content in measurement atmosphere are expected as oxygen can act as a direct reaction partner for hydrogen facilitating its removal from the Pd sample.
Conclusions
Variation of contact potential difference (CPD) measured by KP depending on the amount of hydrogen absorbed in Pd was performed at distinct rH settings ranging from 4 to 85%. Humidity changes have minor effect on the slope of linear fitting curves, but quality of the curves was reduced by adjustment of elevated humidity values (10, 25, 50% rH). However, for the largest set rH of 85%, quality of linear regression enhanced, going along with deceleration of kinetics of natural removal of hydrogen from Pd, a fact which complicates semiquantitative measurement procedure. Therefore, experiments at low humidity values (<10% rH) are recommended for hydrogen detection in Pd.
Consecutive hydrogen loading into the Pd membrane and subsequent effusion of hydrogen into the sample environment lead to irreversible changes in the structure of the Pd sample. These changes lead to misleading absolute CPD values and can be due to filling of trap sites within the Pd metal lattice during the first hydrogen loading pulses. Moreover, the formation of a mixed α,β-PdH x phase is limiting the range, in which Pd could be used as calibration material for hydrogen quantification as the potential dependency on the logarithm of hydrogen concentration is lost. From these findings, the following consequences can be deduced:
-
In order to reduce irreversible trapping of hydrogen in the Pd membrane, the sample should offer a minimum number of possible trap sites. Trap site density in cold-rolled Pd should be reduced, e.g. by annealing.
-
The limitation due to the formation of the β-PdH x phase could be overcome by using a different material, which should have similar advantages like Pd as being resistant to environmental influences like oxidation by atmospheric oxygen as Pd or increase in rH, having a high hydrogen diffusion coefficient and being able to absorb a large amount of hydrogen, but which has at least an extended α-phase region compared to Pd.
References
Oriani RA (1970) The diffusion and trapping of hydrogen in steel. Acta Metall Mater 18:147–157
Merzlikin SV, Mingers AM, Kurz D, Hassel AW (2014) An electrochemical calibration unit for hydrogen analysers. Talanta 125:257–264
Schlapbach L, Züttel A (2001) Hydrogen-storage materials for mobile applications. Nature 414:353–358
Züttel A (2003) Materials for hydrogen storage. Mater Today 6:24–33
Xueping Z, Jiaojiao Z, Shenglin L, Xuanhui Q, Ping L, Yanbei G, Weihua L (2015) A new solid material for hydrogen storage. Int J Hydrog Energy 40:10502–10507
Sun N, Xu B, Zhao S, Sun Z, Li X, Meng L (2015) Influences of Al, Ti and Nb doping on the structure and hydrogen storage property of Mg(BH4)2(001) surface—a theoretical study. Int J Hydrog Energy 40:10516–10526
Faisal M, Gupta A, Shervani S, Balani K, Subrahmanyam A (2015) Enhanced hydrogen storage in accumulative roll bonded Mg-based hybrid. Int J Hydrog Energy 40:11498–11505
Kwon H, Yoo J-H, Cho S-W (2015) Hydrogen absorption/desorption property of (La,Ce,Pr)(Ni,Mn,Al)5 alloys. Int J Hydrogennnn 40:11902–11907
Bacsa R, Laurent C, Morishima R, Suzuki H, Le Lay M (2004) Hydrogen storage in high surface area carbon nanotubes produced by catalytic chemical vapor deposition. J Phys Chem B 108:12718–12723
Züttel A, Sudan P, Mauron P, Kiyobayashi T, Emmenegger C, Schlapbach L (2002) Hydrogen storage in carbon nanostructures. Int J Hydrogennnn 27:203–212
Gest RJ, Troiano AR (1974) Stress corrosion and hydrogen embrittlement in an aluminum alloy. Corrosion 30:274–279
Djukic MB, Sijacki Zeravcic V, Bakic GM, Sedmak A, Rajicic B (2015) Hydrogen damage of steels. Eng Fail Anal 58:485–498
Travis AS, Schröter HG, Homburg E, Morris PJT (1998) Determinants in the evolution of the European Chemical Industry, 1900–1939. Springer, Dordrecht
Song J, Curtin WA (2011) A nanoscale mechanism of hydrogen embrittlement in metals. Acta Mater 59:1557–1569
Herlach D, Kottler C, Wider T, Maier K (2000) Hydrogen embrittlement of metals. Physica B 289-290:443–446
Katano G, Ueyama K, Mori M (2001) Observation of hydrogen distribution in high-strength steel. J Mater Sci 36:2277–2286
Frappart S, Oudriss A, Feaugas X, Creus J, Bouhattate J, Thébault F, Delattre L, Marchebois H (2011) Hydrogen trapping in martensitic steel investigated using electrochemical permeation and thermal desorption spectroscopy. Scripta Mater 65:859–862
Akiyama E, Li S, Shinohara T, Zhang Z, Tsuzaki K (2011) Hydrogen entry into Fe and high strength steels under simulated atmospheric corrosion. Electrochim Acta 56:1799–1805
Merzlikin SV, Wildau M, Steinhoff K, Hassel AW (2014) Prove of hydrogen formation through direct potential measurements in the rolling slit during cold rolling. Metall Res Technol 111:25–35
Dittmeyer R, Höllein V, Daub K (2001) Membrane reactors for hydrogenation and dehydrogenation processes based on supported palladium. J Mol Catal A Chem 173:135–184
Devanathan MAV, Stachurski Z (1962) The adsorption and diffusion of electrolytic hydrogen in palladium. P Roy Soc A-Math Phy 270:90–102
Devanathan MAV, Stachurski Z (1964) The mechanism of hydrogen evolution on iron in acid solutions by determination of permeation rates. J Electrochem Soc 111:619–623
Nagumo M, Nakamura M, Takai K (2001) Hydrogen thermal desorption relevant to delayed-fracture susceptibility of high-strength steels. Metall and Mat Trans A 32:339–347
Senöz C, Evers S, Stratmann M, Rohwerder M (2011) Scanning Kelvin probe as a highly sensitive tool for detecting hydrogen permeation with high local resolution. Electrochem Commun 13:1542–1545
Evers S, Rohwerder M (2012) The hydrogen electrode in the “dry”: a Kelvin probe approach to measuring hydrogen in metals. Electrochem Commun 24:85–88
Maeland A, Flanagan TB (1966) The hydrogen-palladium system. Platinum Metals Rev 10:20–23
Walkner S, Schimo G, Mardare AI, Hassel AW (2015) Palladium thin films for hydrogen sensing in aqueous electrolytes. Phys Stat Sol A 212:1273–1280
Yang T-h, S-i P (1996) Hydrogen absorption and diffusion into and in palladium: AC-impedance analysis under impermeable boundary conditions. Electrochim Acta 41:843–848
Williams G, McMurray HN, Newman RC (2013) Surface oxide reduction by hydrogen permeation through iron foil detected using a scanning Kelvin probe. Electrochem Commun 27:144–147
Krasemann M, Streckel H, Hoffmann K, Grabke HJ, Stratmann M (1998) In: Natishan PM (ed) Detection of hydrogen ingress into iron oxide and iron oxy-hydroxide layers by the Kelvin probe, Electrochemical Society, Pennington
Stratmann M, Hoffmann K (1989) In situ Möβbauer spectroscopic study of reactions within rust layers. Corros Sci 29:1329–1352
Schimo G, Kreuzer AM, Hassel AW (2015) Morphology and size effects on the reduction of silver oxide by hydrogen. Phys Stat Sol A 212:1202–1209
Evers S, Senöz C, Rohwerder M (2013) Hydrogen detection in metals: a review and introduction of a Kelvin probe approach. Sci Technol Adv Mater 14:014201 (12pp)
Schimo G, Burgstaller W, Hassel AW (2015) Potentiodynamic hydrogen permeation on palladium-Kelvin probe compared to 3D printed microelectrochemical cell. Electrochem Commun 60:208–211
Rohwerder M, Turcu F (2007) High-resolution Kelvin probe microscopy in corrosion science: scanning Kelvin probe force microscopy (SKPFM) versus classical scanning Kelvin probe (SKP). Electrochim Acta 53:290–299
Gabrielli C, Grand PP, Lasia A, Perrot H (2004) Investigation of hydrogen adsorption-absorption into thin palladium films: I. Theory. J Electrochem Soc 151:A1925
Manchester FD, San-Martin A, Pitre JM (1994) The H-Pd (hydrogen-palladium) system. J Phase Equilib 15:62–83
Zoltowski P (1999) Effects of self-induced mechanical stress in hydrogen sorption by metals, by EIS. Electrochim Acta 44:4415–4429
Nazarov AP, Thierry D (2007) Application of Volta potential mapping to determine metal surface defects. Electrochim Acta 52:7689–7696
Oriani RA (1967) In: Staehle RW, Fouty SC van de Roogen WR (ed) Hydrogen in metals, Houston
Pressouyre GM (1979) A classification of hydrogen traps in steel. MTA 10:1571–1573
Yang T-h, S-i P, Yoon Y-G (1997) Hydrogen transport through Pd electrode: current transient analysis. Electrochim Acta 42:1701–1708
S-i P, Yang T-h (1998) Theoretical analysis of hydrogen transport through an electrode at the coexistence of two hydrogen-poor and -rich phases based upon the concept of hydrogen trapping. J Electroanal Chem 441:183–189
Flanagan TB, Luo W, Clewley JD (1991) Calorimetric enthalpies of absorption and desorption of protium and deuterium by palladium. J L-Common Met 172-174:42–55
Jewell L, Davis B (2006) Review of absorption and adsorption in the hydrogen–palladium system. Appl Cata A 310:1–15
Pauer G, Kratzer M, Winkler A (2005) Reaction and desorption kinetics of H2 and H2O on activated and non-activated palladium surfaces. Vacuum 80:81–86
Lee J-W, S-i P (2005) Anomalous behaviour of hydrogen extraction from hydride-forming metals and alloys under impermeable boundary conditions. Electrochim Acta 50:1777–1805
Beek WJ, Muttzall KMK, van Heuven JW (1999) Transport phenomena. Wiley, New York
Crank J (1975) The mathematics of diffusion. Clarendon Press, Oxford
Zoltowski P, Makowska E (2001) Diffusion coefficient of hydrogen in α-phase palladium and palladium-platinum alloy. Phys Chem Chem Phys 3:2935–2942
Lim C, S-i P (1994) Impedance analysis of hydrogen absorption reaction on Pd membrane electrode in 0.1 M LiOH solution under permeable boundary conditions. Electrochim Acta 39:363–373
Kirchheim R (1988) Hydrogen solubility and diffusivity in defective and amorphous metals. Prog Mater Sci 32:261–325
Kirchheim R (1980) Electrochemical methods for measuring diffusivities of hydrogen in palladium and palladium alloys. J Electrochem Soc 127:2419
Mütschele T, Kirchheim R (1987) Hydrogen as a probe for the average thickness of a grain boundary. Scripta Metall 21:1101–1104
Fushimi K, Jin M, Nakanishi T, Hasegawa Y, Kawano T, Kimura M (2014) Convection-dependent hydrogen permeation into a carbon steel sheet. ECS Electrochem Lett 3:C21–C23
Martin MH, Lasia A (2008) Study of the hydrogen absorption in Pd in alkaline solution. Electrochim Acta 53:6317–6322
Bolza’n AE (1995) Phenomenological aspects related to the electrochemical behaviour of smooth palladium electrodes in alkaline solutions. J Electroanal Chem 380:127–138
Hamann CH, Vielstich W (2005) Elektrochemie. Wiley, Weinheim
Hu J, Xiang X-D, Ogletree DF, Salmeron M (1995) Imaging the condensation and evaporation of molecularly thin films of water with nanometer resolution. Science 268:267–269
Xu Z, Gao Y, Wang C, Fang H (2015) Nanoscale hydrophilicity on metal surfaces at room temperature: coupling lattice constants and crystal faces. J Phys Chem C 119:20409–20415
Frankel GS, Stratmann M, Rohwerder M, Michalik A, Maier B, Dora J, Wicinski M (2007) Potential control under thin aqueous layers using a Kelvin probe. Corros Sci 49:2021–2036
Freund J, Halbritter J, Hürber JKH (1999) How dry are dried samples? Water adsorption measured by STM. Microsc Res Tech 44:327–338
Wicinski M, Burgstaller W, Hassel AW (2016) Lateral resolution in scanning Kelvin probe microscopy. Corros Sci 104:1–8
Acknowledgments
Open access funding provided by Johannes Kepler University Linz. The financial support within the Comet Programme given by the Austrian Government via FFG (Austrian Research Foundation Agency) and by the Government of Lower Austria and Upper Austria is gratefully acknowledged. The financial support by the Austrian Federal Ministry of Science, Research and Economy and the National Foundation for Research, Technology and Development through the Christian Doppler Laboratory for Combinatorial Oxide Chemistry (COMBOX) is gratefully acknowledged. The authors thank the voestalpine for the support as well as Andrei I. Mardare and Christian M. Siket for many helpful discussions.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
ESM 1
(PDF 370 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Burgstaller, W., Schimo, G. & Hassel, A.W. Challenges in hydrogen quantification using Kelvin probe technique at different levels of relative humidity. J Solid State Electrochem 21, 1785–1796 (2017). https://doi.org/10.1007/s10008-017-3541-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10008-017-3541-3