Electrochemical oscillations and bistability during anodic dissolution of vanadium electrode in acidic media—part II. The model

Abstract

Following our experimental results on the oscillatory and bistable vanadium electrooxidation in phosphoric acid medium (Gorzkowski et al., 2011), we constructed a theoretical model of the V/H₃PO₄ passivation/dissolution system which allowed us to reproduce the basic dynamic instabilities observed. In this model, the formation of the negative resistance (N-NDR) region was ascribed to the potential-dependent formation/destruction of the inhibitive V₂O₅ layer on the electrode surface. The dynamic system was defined in terms of two variables: electrode potential and surface concentration of VO ⁺₂ species. Both relaxation oscillations and bistability for conditions similar to the experimental ones were obtained in numerical calculations and a theoretical bifurcation diagram was constructed. The analysis of the system’s dynamics in terms of nullclines allowed us to detect directly unattainable unstable steady states associated with both the oscillatory and bistable regimes.

Introduction

In a previous paper [1], we described the oscillations and bistability reported during the anodic oxidation of vanadium in various aqueous acidic media: H₃PO₄, H₂SO₄, HNO₃, HClO₄, and CF₃COOH. The complexity of these systems is caused, among others, by the relatively fast electrodissolution process, being a source of temporal drift of its characteristics. This makes systematic experimental studies of this process rather difficult. Nevertheless, the dynamic instabilities accompanying the vanadium electrodissolution in various acidic media have not been intensively studied so far, except for primary reports for the occurrence of the oscillations [2], followed by our recent experimental studies [1]. In the case of such complicated systems, theoretical modeling, focused on the properties essential for the onset of dynamic instabilities, is a convenient tool for understanding of the core oscillatory mechanism and its quantitative analysis. The construction of our model and its quantitative parameters refer to the properties of the V/H₃PO₄ system, most intensively studied by us. We also compare the results of our analysis with the characteristics of the electrodissolution of vanadium electrode in other acidic media studied.

The model of V electrodissolution in H₃PO₄

Electrochemical characteristics of the system

Significant parts of the construction of our model follow the approach of Koper and Sluyters to the simulation of the oscillations accompanied with active/passive transition of the solid electrodes [3], which we adapt and extend for the specific features of the V/H₃PO₄ system. The results of our calculations for H₃PO₄ medium are compared with our experimental results.

The first point which has to be clarified in the construction of our model is the choice of vanadium species that are involved in electrochemical processes exhibiting dynamic instabilities [4]. The surface of metallic vanadium undergoes spontaneous chemical oxidation in contact with oxygen from the air and in oxygenated aqueous solutions, yielding a layer of V₂O₃. Under electrochemical conditions, depending on the electrode potential imposed during the anodic polarization, various vanadium(I), vanadium(II), vanadium(III), vanadium(IV), and vanadium(V) species are formed, with the potential-dependent relative proportions. In our case, since the dynamic instabilities of interest occur at relatively positive potentials, compared to V(IV)/V(V) standard potential, it is not necessary to consider all these possible states, but it is a reasonable simplification to limit the model construction to the metallic vanadium and its compounds at the fifth oxidation states. This thermodynamic reasoning is additionally corroborated by the following direct experimental observations. Already at potentials less positive for ca. 0.3 V than the onset of the oscillations, the trail of blue soluble species of V(IV), entering the solution adjacent to vanadium surface, vanishes. The greenish precipitate which forms at similar potentials is a mixed-valence V(IV)/V(V) compound. Thus, at even more positive potentials where oscillations exist, the assumption of predominantly present V(V) oxidation state is reasonable. Accordingly, for model purposes, we assumed the scheme of electrochemical processes shown in Fig. 1.

Fig. 1

Simplified scheme of electrooxidation processes of vanadium anode in phosphate media, limited to steps essential for modeling of the dynamic instabilities

This scheme describes the typical I–E characteristics of the vanadium anodically polarized to a sufficiently positive potentials, at which the metallic vanadium is oxidized, yielding two kinds of species: soluble VO ⁺₂ species and adsorbed layer of V₂O₅. If the solubility product K _so of the [VO ⁺₂ ][H₂PO ⁻₄ ] salt is reached, VO ⁺₂ ions form a (most probably porous) precipitate with H₂PO ⁻₄ .

The potential-independent chemical equilibrium of the formation/dissolution of this precipitate leads to the formation of the anodic limiting current on the I–E characteristics of vanadium electrodissolution. On the other hand, the compact layer of adsorbed V₂O₅ (see Fig. 2) inhibits the electron transfer, and the increasing coverage of this compound with increasing positive potential is a source of an N-shaped negative differential resistance (N-NDR) in the I–E characteristics. Thus, the potential-dependent adsorption/desorption of V₂O₅, expressed in terms of a pH-dependent redox equilibrium between V₂O₅ and V:

$$ {\text{2V}} + {5}{{\text{H}}_{{2}}}{\text{O}}\begin{array}{*{20}{c}} {\xrightarrow{{{{\text{k}}_{{2}}}}}} \\ {\xleftarrow{{{\text{k}}_{{{ - 2}}}}}{}} \\ \end{array} {{\text{V}}_{{2}}}{{\text{O}}_{{5}}} + {10}{{\text{H}}^{ + }} + {10}{e^{{ - }}} $$

(1)

is considered a principal source of instabilities in the modeled system. In other words, the purely chemical dissolution of V₂O₅ with H⁺ ions was assumed as negligible.

Fig. 2

Schematic composition of the V/solution interface. Potential-dependent oxidation of vanadium leads to a compact, inhibitory layer of V₂O₅, followed by a porous layer of the [VO ⁺₂ ][H₂PO ⁻₄ ] salt

In conclusion, the shape of the I–E (or I–U) dependence, where U is the external voltage and E means the interfacial potential drop at the working electrode, in the potential region of interest is determined by the following three factors, of the role increasing with positive potential: (1) the exponential increase of the rate of anodic oxidation of V(0) to VO ⁺₂ , (2) the precipitation of [VO ⁺₂ ][H₂PO ⁻₄ ] species, the solubility of which decides the limiting value of this current, and (3) the parallel formation of the inhibitive adsorption layer of V₂O₅ that gives rise to the region of the negative differential resistance (NDR).

The rate constants k ₂ and k ₋₂ of V₂O₅ electrochemical formation and destruction, respectively, depend on the electrode potential in the following way:

$$ {k_2}(E) = k_2^0{e^{{\frac{{{\beta_{\text{n}}}F}}{{RT}}\left( {E - E_2^0} \right)}}} $$

(2)

$$ {k_{{ - 2}}}(E) = k_{{ - 2}}^0{e^{{ - \frac{{{\alpha_{\text{n}}}F}}{{RT}}\left( {E - E_2^0} \right)}}}{\left[ {{{\text{H}}^{ + }}} \right]^{{10}}} $$

(3)

where it was assumed that the stoichiometric coefficient of [H⁺] ions in the reduction of V₂O₅ can be transferred to a rate law. Also, a smaller exponent, perhaps even more realistic, could be assumed, but this factor is not crucial for the model system dynamics due to only small variations of [H⁺] (see below).

The interpretation of the Tafel slope for the n-electron process is not as straightforward as for the one-electron process and depends on whether the same step controls the rate of the reaction in the anodic and cathodic direction [5, 6]. Therefore, for simplification, it was assumed that the kinetics of (relatively slow) V(IV) $\begin{array}{*{20}{c}} \to \\ \leftarrow \\ \end{array}$V(V) process determines the overall rate of process (1) and, accordingly, the symmetry factor β _n is equal to β for this one-electron processes, determined before as equal to 0.36 [7]. In turn, α _n was, in this model, assumed as equal to 1− β _n. This means that, as in homogeneous kinetics, for a multistep (here, n-electron) process, its overall equilibrium constant will not be expressed as the ratio of rate constants of the rate determining forward and backward processes. The choice of value of β _n is one of the factors that affect the concordance of the experimental and simulated dependences, including the course of dynamic instabilities, but for the determination of qualitative types of behaviors, typical of nonlinear dynamics, are not crucial, contrary to classical electrochemistry, oriented on the exact determination of all thermodynamic and kinetic parameters. Here, Eqs. 1–3 are in fact a way of introducing to the model the potential-dependent electrode coverage of the inhibiting species which explains the N-NDR region on the I–E curve, when the potential is changed in either anodic or cathodic direction.

Analogous assumption was made in the definition of the anodic faradaic current:

$$ {I_{\text{f}}} = nFA{f_{\text{R}}}{k_1}(E) \times T(E) \times S\left( {{C_{{{\text{VO}}_{{2}}^{ + }}}}} \right) $$

(4)

where k ₁(E) is the potential-dependent rate constant of the slowest step V(IV)– > V(V) electrode process:

$$ {k_1}(E) = k_1^0{e^{{\frac{{{\beta_{\text{n}}}F}}{{RT}}\left( {E - E_1^0} \right)}}} $$

(5)

The backward (electroreduction) reaction was, in this case, neglected as considered negligible at the positive potentials considered. Furthermore, the term f _R denotes the roughness factor of the V electrode, which is necessary since the product Af _R of this factor and of the geometrical electrode surface (A) is the real electrode surface area available for the electron transfer. In turn, T(E) = 1−θ(E) (where θ is the electrode coverage of V₂O₅) is the fraction of the electrode surface free of the inhibitory layer of adsorbed V₂O₅ where the anodic oxidation of V(0) can occur. Thus, at places covered with V₂O₅, the anodic process is assumed to be completely inhibited. Finally, quantity S, as in the Koper’s and Sluyters’ approach [3], describes the limitation of the vanadium electrodissolution through the solubility product K _so of the porous layer of the [VO ⁺₂ ][H₂PO ⁻₄ ] salt:

$$ S = 1 - \frac{{{C_{{{\text{VO}}_2^{ + }}}}}}{{{C_{{{ \max }}}}}} $$

(6)

with the maximum concentration of VO ⁺₂ species, C _max, defined by the solubility product:

$$ {K_{\text{so}}} = {C_{{\max }}}\left[ {{{\text{H}}_{{2}}}{\text{PO}}_{{4}}^{{ - }}} \right] $$

(7)

Thus, if initially there are no VO ⁺₂ ions at the interface, the ones that are formed freely diffuse and migrate towards the bulk of the solution. If, for a given H₂PO ⁻₄ concentration the solubility product is reached, the probability of such transport decreases to zero. The quantity S varies thus from zero to 1. The other symbols in Eq. 4 have their usual significance.

According to the above dependences, among ionic forms of phosphoric acid, only H₂PO ⁻₄ is considered as the species present in substantial amount. Since the acid–base equilibria establish quickly, compared to other processes, the concentration of H₂PO ⁻₄ ions can be considered as always equal to an equilibrium value and related to the concentration of H⁺ ions and H₃PO₄ molecules through the first dissociation constant K _a:

$$ {K_{\text{a}}} = \frac{{\left[ {{{\text{H}}^{ + }}} \right]{ }\left[ {{{\text{H}}_{{2}}}{\text{PO}}_{{4}}^{{ - }}} \right]}}{{\left[ {{{\text{H}}_{{3}}}{\text{P}}{{\text{O}}_{{4}}}} \right]}} $$

(8)

Since H₃PO₄ is present in excess, compared to the amount consumed in chemical reactions at the electrode, its equilibrium concentration [H₃PO₄] at the electrode surface can be considered as practically constant and thus also equal to the bulk value, approximated by equilibrium concentration, for a given total concentration of H₃PO₄.

It is important to note that in the model constructed by Koper and Sluyters [3], the dynamics of H⁺ ions, originating from strong acid and transported through migration and diffusion, was important for obtaining the realistic oscillatory solutions. However, in our case, the local concentration of [H⁺] was quickly regulated also by fast dissociation/protonation of only partly dissociated H₃PO₄/H₂PO ⁻₄ species. In consequence, the local [H⁺] dynamics appeared to be relatively weak and its inclusion to the model did not generate substantially different results. Therefore, our model does not contain the equation for d[H⁺]/dt dynamics.

Furthermore, the local concentrations of all ions in the solution (outside the double layer) have to meet the electroneutrality condition:

$$ {C_{{{\text{VO}}_{{2}}^{ + }}}} + \left[ {{{\text{H}}^{ + }}} \right] = \left[ {{{\text{H}}_{{2}}}{\text{PO}}_{{_{{4}}}}^{{ - }}} \right] $$

(9)

which, combined with Eq. 7 yields the following dependence for [H₂PO ⁻₄ ]:

$$ \left[ {{{\text{H}}_{{2}}}{\text{PO}}_{{4}}^{{ - }}} \right] = \frac{{{C_{{{\text{VO}}_{{2}}^{ + }}}} + \sqrt {{{{\left( {{C_{{{\text{VO}}_{{2}}^{ + }}}}} \right)}^{{2}}} + {4}{K_{\text{a}}}\left[ {{{\text{H}}_{{3}}}{\text{P}}{{\text{O}}_{{4}}}} \right]}} }}{{2}} $$

(10)

Definition of the dynamic system

The dynamic system is defined in terms of two dynamic variables which are sufficient to model the oscillatory behavior: the electrode potential E and the surface concentration of VO ⁺₂ ions. In principle, the dynamics of electrode coverage (θ) of the inhibitive V₂O₅ layer could also be considered, but as our numerical experiments showed, such an extension of the dynamic system does not produce qualitatively different oscillatory regimes (e.g., complex oscillations). In consequence, we applied the steady-state approximation to the dθ/dt dynamics, determined by the stoichiometry of Eq. 1:

$$ \frac{{{\text{d}}\theta }}{{{\text{d}}t}} = {k_2}(E)\left( {1 - \theta } \right) - {k_{{ - 2}}}(E)\theta {\left[ {{{\text{H}}^{ + }}} \right]^{{10}}} $$

(11)

Putting dθ/dt = 0 yields the following steady-state coverage, adapting instantaneously to the given electrode potential:

$$ {\theta_{\text{SS}}} = \frac{1}{{1 + \frac{{k_{{ - 2}}^0}}{{k_2^0}}{e^{{\frac{F}{{RT}}\left( {E - E_2^0} \right)}}}{{\left[ {{{\text{H}}^{ + }}} \right]}^{{10}}}}} $$

(12)

where, as explained above, the ratio of the rate constants k ₂ and k ₋₂ does not correspond to the equilibrium constant of the overall 5e process but refers only to the rate-determining step V(IV) $\begin{array}{*{20}{c}} \to \\ \leftarrow \\ \end{array}$V(V) in the process (1).Further construction of the model is based on the charge conservation principle for the typical equivalent circuit (Fig. 3) with the total current splitted into the faradaic and capacitive components:

$$ {I_{\text{tot}}} = {I_{\text{f}}} + {I_{\text{c}}} = {I_{\text{f}}} + A{f_{\text{R}}}{C_{\text{d}}}\frac{{{\text{d}}E}}{{{\text{d}}t}} $$

(13)

where the faradaic current that is given by Eq. 4 and C _d in the equation for the capacitive current is the differential double layer capacitance per unit area, assumed further for simplicity as a constant, potential-independent value. Since the model reproduces the system’s dynamics under dc conditions, Z _f in Fig. 3 means the zero-frequency impedance of the process.

Fig. 3

Equivalent circuit for the anodic dissolution of V in H₃PO₄ medium. Total current I _tot splits into the capacitive component (I _c), flowing through the double layer of capacitance C _d, and the faradaic component (I _f), flowing through the element of impedance Z _f. The interfacial potential drop at the working electrode E is smaller than the external voltage U for the ohmic drop I _tot R _s

A combination of Eqs. 4, 6, 12, and 13 yields the following dependence for the dynamics of the electrode potential which is the first of two equations defining the dynamic system considered:

$$ \frac{{{\text{d}}E}}{{{\text{d}}t}} = \frac{{U - E}}{{{f_{\text{R}}}A{C_{\text{d}}}{R_{\text{S}}}}} - \frac{{nF{k_1}(E)\left( {1 - \theta } \right) \times \left( {1 - \frac{{{C_{{{\text{VO}}_{{_{{2}}}}^{ + }}}}}}{{{C_{{\max }}}}}} \right)}}{{{C_{\text{d}}}}} $$

(14)

The second equation describes the temporal dynamics of the surface concentration of VO ⁺₂ ions as a consequence of their production due to metallic vanadium electrooxidation and the diffusion and migration towards the bulk of the solution. The basis for its derivation is the Nernst approximation of the linear diffusion layer of thickness δ , illustrated by Fig. 4. In terms of this scheme, the shaded area denotes the change, in time step dt, of the amount of soluble vanadium species in the diffusion layer, associated with the change of its surface concentration from C ₁ to C ₂, i.e., equal to the area of the triangle: ½(C ₂−C ₁)δ . In further treatment of this problem, it is important to realize that the volume of the diffusion layer is practically equal to Aδ, while the electron transfer occurs at the electrode surface of an effective area f _R A. Taking into account this condition, one derives the following equation for the dynamics of the surface concentration of VO ⁺₂ ions:

$$ \frac{{{\text{d}}{C_{{{\text{VO}}_{{2}}^{ + }}}}}}{{{\text{d}}t}} = \frac{{2{f_{\text{R}}}{k_1}(E) \times \left( {1 - \theta } \right) \times \left( {1 - \frac{{{C_{{{\text{VO}}_{{2}}^{ + }}}}}}{{{C_{{\max }}}}}} \right)}}{\delta } - \frac{{2D{C_{{{\text{VO}}_{{2}}^{ + }}}}}}{{{\delta^2}}} - {t_{{{\text{VO}}_{{2}}^{ + }}}}\frac{{2n{f_{\text{R}}}{k_1}(E) \times \left( {1 - \theta } \right) \times \left( {1 - \frac{{{C_{{{\text{VO}}_{{2}}^{ + }}}}}}{{{C_{{\max }}}}}} \right)}}{{z\delta }} $$

(15)

in which D is the diffusion coefficient of the VO ⁺₂ ions, while their transference number is given by:

$$ {t_{{{\text{VO}}_{{2}}^{ + }}}} = \frac{{{\lambda_{{{\text{VO}}_{{2}}^{ + }}}}{C_{{{\text{VO}}_{{2}}^{ + }}}}}}{{{\lambda_{{{\text{VO}}_{{2}}^{ + }}}}{C_{{{\text{VO}}_{{2}}^{ + }}}} + {\lambda_{{{{\text{H}}^{ + }}}}}\left[ {{{\text{H}}^{ + }}} \right] + {\lambda_{{{{\text{H}}_{{2}}}{\text{PO}}_{{4}}^{{ - }}}}}\left[ {{{\text{H}}_{{2}}}{\text{PO}}_{{4}}^{{ - }}} \right]}} $$

(16)

Fig. 4

Two model-linearized concentration profiles of vanadium species VO ⁺₂ formed during the anodic electrodissolution of metallic vanadium and distributed in the Nernst diffusion layer of thickness δ

In Eq. 16, λ _i 's are the molar conductivities of the respective ions and z (equal here to 1) is electric charge, expressed in the units of the elementary charge.

In conclusion, Eqs. 14 and 15 define the dynamic system considered.

The thickness of diffusion layer was calculated using Eq. 17 [5]:

$$ \delta = 1.61 \times {D^{{\frac{1}{3}}}}{r^{{ - \frac{1}{2}}}}{\nu^{{\frac{1}{6}}}} $$

(17)

where D is the diffusion coefficient, r is the rotation rate (rad s⁻¹), and ν is the kinematic viscosity of the solution.

Results of the modelings

Calculations made in terms of the above model require numerical values of all parameters, some of them being unknown and thus treated as the adjustable values, like standard rate constants k ⁰₁ , k ⁰₂ , k ⁰₋₂ , formal potentials E ⁰₁ , E ⁰₂ , solubility product K _so of [VO ⁺₂ ][H₂PO ⁻₄ ], as well as the roughness factor f _R. These unknown values were chosen so that the modeled and experimental dependences are possibly similar to each other within a reasonable computational time.

The validity of general construction of our model was confirmed by the fact that, in our numerical calculations, we were able to reproduce both oscillatory and bistable courses of the vanadium electrooxidation for physically reliable parameters and conditions similar to those existing in our experiments [1]. A representative comparison of experimental and simulated oscillatory courses is collected in Fig. 5. All of the theoretical dependences were obtained for the conditions of the rotating disk electrode, which allowed us to assume the appropriate constant thickness of the Nernst diffusion layer, treated as a fixed parameter in every simulation. The simulations also reproduced the definitely relaxation nature of most oscillations, indicating a significant difference between the time scales of the dynamics of the electrode potential and the surface concentration of vanadium species. Furthermore, as in real experiments, an increase in the disk rotation speed favored the transition to bistable behavior. A representative comparison of experimental and theoretical bistable dependences is shown in Fig. 6.

Fig. 5

Comparison of the experimental (left: a-1, b-1, c-1) and corresponding simulated (right: a-2, b-2, c-2) oscillatory modes of the vanadium electrooxidation in phosphate media. Experimental conditions: vanadium electrode (1-mm-diameter vanadium wire, embedded in Teflon), temperature T = 0 °C, scan rate v = 10 mV s⁻¹. Parameters of the model: C(H₃PO₄) = 2×10³ mol m⁻³, f _R = 5, T = 273 K, C _d = 0.2 Fm⁻², A = 7.86×10⁻⁷ m², R _S = 180 Ω, E ⁰₁  = 0.768 V, k ₁ = 8×10⁻⁵ mol m⁻² s⁻¹, E ⁰₂  = 1.168 V, k ⁰₋₂ /k ⁰₂  = 1×10⁻²⁰ mol⁻¹⁰ m³⁰ , K _so = 5.5×10⁴ mol⁻²m⁶ , scan rate v = 2 mV s⁻¹. The zero rotation speed of the disk electrode in the experiment (a-1) was in the model calculations (a-2) approximated by low (100 rpm) rotation speed

Fig. 6

Comparison of the experimental (left: a-1, b-1, c-1) and simulated (right: a-2, b-2, c-2) bistable modes of the vanadium electrooxidation in phosphate media. Experimental conditions: vanadium electrode (1-mm-diameter vanadium wire, embedded in Teflon), temperature T = 0 °C, scan rate v = 10 mV s⁻¹. Parameters of the model: C(H₃PO₄) =2×10³ mol m⁻³, f _R = 5, T = 273 K, C _d = 0.2 F m⁻², A = 7.86×10⁻⁷ m², R _s = 180 Ω, E ⁰₁  = 0.768 V, k ₁ = 8×10⁻⁵ mol m⁻² s⁻¹, E ⁰₂  = 1.168 V, k ⁰₋₂ /k ⁰₂  = 1×10⁻²⁰ mol⁻¹⁰ m³⁰, K _sol = 5.5×10⁴ mol⁻² m⁶ , scan rate v = 2 mV s⁻¹. Rotation speed of the vanadium disk electrode shown in respective diagrams

Systematic numerical calculations performed for varying bifurcation parameters, external voltage U and the rotation speed of the disk electrode, allowed us to construct the theoretical bifurcation diagrams. Figure 7 compares such diagrams with the experimental ones. One notices that the general “fish-like” shape is exhibited by all diagrams. The concordance is not only morphological since, for a given serial resistance used in the experiment, one obtains a similar theoretical bifurcation diagram.

Fig. 7

Theoretical bifurcation diagram (1) corresponding to the model system (Eqs. 14 and 15), compared with the experimental ones (2, 3) taken from Fig. 13 in [1], recorded for T = 0 °C

One can conclude that our two-variable model is sufficient for basic model characteristics of the V/H₃PO₄ dynamical system, with respect to periodic oscillations. Since it is also more convenient for the purposes of stability analysis than any higher-dimensional case, we shall limit our further considerations to the phase space defined by Eqs. 14 and 15.

Before such analysis is performed, it is still interesting to compare the essential morphology of our simulated dependences with the typical oscillatory courses recorded for various acids, different from the phosphoric one [1]. One then concludes that the results for H₃PO₄ include morphological elements specific for other acids. For small rotation rates and large external resistances, the simulations resemble the oscillatory behavior reported for HClO₄ during the reverse scan. Furthermore, the qualitative concordance was even better than for H₃PO₄ since in both the experiments and the simulations the oscillations occurred only on the branch of the I–E dependence exhibiting a negative slope under dc conditions. Such similarities are not surprising: the differences between these systems should be of rather quantitative than qualitative nature since the essential passivation/dissolution mechanism of instabilities should be full of analogies, and the mathematical core of the model should be also the same or very similar. However, such comparison indicates also that the V/H₃PO₄ system can be considered as the most complex dynamical system that we have studied [1] as it reveals the oscillations on both the negative and positive branches, in line with the negative resistance partly hidden under dc conditions. One can suppose that these differences are due to various composition and structure (porosity) of sparingly soluble vanadium compounds, formed in contact with various acidic media.

Stability analysis

A standard and powerful technique of nonlinear dynamics is the linear stability analysis of steady states [8]. However, it refers not to the original but to the linearized equations. Therefore, in order to study our original nonlinear model system, we used the nullclines [9] of Eqs. 14 and 15, i.e., dependences C vs. E derived from Eqs. 14 and 15 each independently set to zero. Accordingly, the intersection of nullclines, corresponding to the simultaneous meeting of the conditions, dE/dt = dC/dt = 0, determines the possible steady state(s) of the system, for given control parameters. The advantage of nullcline-based analysis is that it conveys the nonlinear information about the system’s dynamics around the respective steady state. The nullclines and the phase trajectories of our dynamic system were plotted with the use of XPP-AUT v. 5.99 software [10].

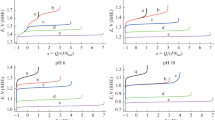
Figure 8 shows the representative collection of nullclines of Eqs. 14 and 15 plotted for two values of Nernst diffusion layer thickness δ (determined by the disk rotation speed) and two external voltages U. Since the external voltage exists only in Eq. 14, and the diffusion layer thickness only in Equation 15, the course of each of the nullclines in the E–C space depends solely either on U or on δ . In turn, Fig. 9 shows the exemplary pair of those nullclines with the corresponding phase trajectory (stable limit cycle) superimposed. The course of this trajectory confirms that the electrode potential E is a fast variable compared to the surface concentration, the dynamic characteristics of which are typical of the N-NDR systems (i.e., system with N-shaped region of negative differential resistance, analyzed by Koper [11]; see also [12] for review of NDR types). As for relaxation oscillations, the phase trajectory consists of almost horizontal sections, meaning almost instantaneous adjustments to E-nullcline, followed by slow travel along and close to this nullcline. The system travels so up to the point of the maximum (or minimum) of E-nullcline, where the concentration change makes the system apart from the E-nullcline, causing acceleration and sudden jump of the electrode potential to another branch of E-nullcline, as shown in Fig. 9. In an analogous way, the stability of any steady state (ss) may be easily deduced: it is stable for E _ss values lower (higher) than for local maximum (minimum) or unstable if E _ss is placed between the local maximum and the local minimum of E-nullcline.

Fig. 8

Exemplary nullclines for the dynamic system (Eqs. 14 and 15), constructed for two rotation speeds and two external voltages U. The direction of the arrows denotes the sign of appropriate derivatives dE/dt and dC/dt

Fig. 9

Exemplary pair (1, 2) of nullclines (for U = 1.368 V, rotation speed = 500 rpm) and the corresponding phase trajectory (3) for a system exhibiting relaxation oscillations. The system quickly adjusts to the E-nullcline and travels along it towards the C-nullcline. Between the local maximum and minimum, the branch of the E-nullcline is unstable and the system jumps to a stable branch

Using such diagnosis of stability of steady states, it is instructive to correlate their parameters with various dynamic regimes. Figure 10 shows, constructed in this way, the bifurcation diagram, which collects the stable and unstable steady states and stable oscillations, for constant (moderate) speed rotation rate and increasing values of external voltage U. For low values of U, the system is monostable. Upon increasing U, the single, stable steady state loses its stability at ca. 1.32 V, and the oscillations set in, with the amplitude covering the distance between the minimum and maximum of the E-nullclines. The diagram shows that, within the oscillatory region, one to three unstable steady states can coexist. At U close to 1.39 V, the oscillations cease and the system returns to monostable behavior. Figure 11 shows, as an example, how three unstable steady states are detected through the course of nullclines which, due to opposite curvatures, intersect three times. Upon variation of U, the E-nullcline would move without changing its shape, but the number of its intersections with C-nullcline would change.

Fig. 10

Theoretical bifurcation diagram with U as bifurcation parameter for rotation speed 500 rpm, constructed based on the course of nullclines. The imposed external voltage U is denoted by line 1. Steady states 2 are stable while steady states 3, lying between the maximum (4) and minimum (5) of E-nullcline, are unstable. Oscillations, of the amplitude defined by the distance between lines 4 and 5, occur when no steady state is stable for a given external voltage U

Fig. 11

a The course of nullclines and of the phase trajectory for the case of three unstable steady states (rotating speed 500 rpm, U = 1.325 V). b Magnified section of a showing the phase trajectory leaving the E-nullcline at point 4 and passing by the unstable steady state. c The difference between nullclines

Figure 12 illustrates the bistable regime for higher rotation speed, when only bistability is observed. Then, the nullclines intersect before the local maximum and after local minimum. A system traveling slowly along E-nullcline towards C-nullcline reaches the intersection and sets into this stable steady state. Between the two possible steady states, the unstable saddle point is observed.

Fig. 12

Nullclines and phase trajectories for a bistable system (U = 1.468 V; rotation speed =2,500 rpm). “Low-current” (“high-current”) means trajectories tending to low-current (high-current) stable steady state

Figure 13 shows these characteristics for varying U. The two (“upper” and “lower”) branches of stable steady states partly overlap, giving rise to a bistable behavior for U between ca. 1.44 and 1.51 V. The fold of steady states is completed by unstable steady states.

Fig. 13

Theoretical bifurcation diagram with U as bifurcation parameter for rotation speed 2,500 rpm, constructed based on the course for nullclines. The imposed external voltage U is denoted by line 1. Steady states 2 are stable while steady states 3, lying between the maximum (4) and minimum (5) of E-nullcline, are unstable. In the region where upper and lower branches of stable steady states (2) coexist, the system exhibits bistability

Summary and conclusions

Following our experimental results on the oscillatory and bistable vanadium electrooxidation in phosphoric acid medium [1], we constructed a theoretical model of the V/H₃PO₄ passivation/dissolution system which allowed us to reproduce the basic dynamic instabilities observed. In this model, the formation of the negative resistance (N-NDR) region was ascribed to the potential-dependent formation/destruction of the V₂O₅ layer on the electrode surface which, in the places free of that adsorbate, dissolved anodically with the formation of VO ⁺₂ ions that could produce porous precipitate with H₂PO ⁻₄ ions, when the solubility product was exceeded. The electrochemical dynamic system considered was defined in terms of two variables: electrode potential and surface concentration of VO ⁺₂ species. In spite of various simplifications, theoretical bifurcation diagrams were reasonably concordant with the experimental ones. In addition, we described the system’s dynamics in terms of nullclines, the analysis of which allowed us to detect directly inaccessible unstable steady states associated with both the oscillatory and bistable regimes.