Introduction

Nonlinear dynamic instabilities, including oscillatory and bistable behavior, remain the subject of intensive studies in both homogeneous [1] and heterogeneous systems [2–4]. Concerning the latter ones, the oscillatory dissolution of solid electrodes was reported as early as in 1828 by Fechner [5]. Since that time, oscillatory phenomena were found for many electrodissolution reactions of solid electrodes. The electrodissolution of iron in various media (mainly aqueous H2SO4) was studied most intensively, both experimentally and theoretically (cf. e.g., [6–16]). Other thoroughly studied oscillatory electrodissolution systems include, among others, copper in phosphoric acid [17–21], copper in chloride media [22, 23], and nickel in sulfuric acid [24, 25]. While early studies involved classical electrochemical characteristics of those processes, the more recent ones also include the analysis of these phenomena in terms of standard techniques of nonlinear dynamics. Accordingly, the theories of instabilities in such systems, exhibiting transition between the active and the passive states of solid electrodes, evolved from the description of the chemical processes at the electrode/electrolyte interface (cf. e.g., [6]) to the models that define the characteristics of the entire electric circuit responsible for the onset of the oscillations [26], including the cooperation between the negative polarization resistance of the charge-transfer process and the ohmic potential drops. Such models cannot always explain all the dynamic features of the system, but in the case of electrodissolution processes it is quite understandable; contrary to processes occurring at mercury electrodes, the composition of the passive or porous layers formed at the solid electrode surface is usually so complex that it is very difficult, if not impossible, to describe precisely the state of the electrode/electrolyte interface, which therefore is represented by its simplified structure in the model.

A survey of literature shows that oscillatory electrodissolution of vanadium electrodes so far attracted relatively little attention of the researchers. The papers, only recently published, reported the oscillations of the vanadium oxidation current in phosphate media [27, 28] as a phenomenon that rather unexpectedly occurred during the research oriented on the preparative electrosynthesis of phosphate–vanadium compounds. At the potentials positive enough for the onset of the oscillations, it was reported the formation, on the electrode surface, of green precipitate, being a hydrated salt of V(IV) and V(V) of an empirical formula H0.2VOPO4 × 2.33 H2O [27].

In view of these findings, it seems justified to undertake the first systematic studies of the dynamic instabilities associated with vanadium dissolution in various media. In this paper, we describe experimental studies of this process occurring in the phosphoric acid medium (for which oscillations were first reported [27, 28]) and, for comparison, also for other acids: nitric, sulfuric, perchloric, and trifluoroacetic. In the next part of the work, we present the numerical model that enabled us to reproduce basic scenarios of dynamical instabilities in the studied system.

Experimental

All electrochemical measurements were carried out in a conventional three-electrode cell. Various constructions of the working electrode, made from 99.7% vanadium (Sigma-Aldrich) were used. For the measurements with the stationary vanadium electrode, the V wire (1 mm in diameter) was immersed into the electrolyte solution into the depth of 1 mm in order to form the convex meniscus of the fluid, ensuring its constant and reproducible contact with the electrode. For the measurements with rotating disk electrode (mod. 636, ser. 01103, manufactured by Pine Instrument Company, USA), either the vanadium rod (with a diameter of 2.7 or 6.0 mm) or the vanadium wire (1 mm diameter) was used. Prior to the experiment, vanadium surface was polished in a series of wet sandings, with the grit size ranging from 400 to 2,500, followed by rinsing of the electrode with triply distilled water, additionally deionized using Millipore filter. As the counter-electrode, either the platinum or vanadium wire was used. As the reference electrode, either the saturated calomel electrode (SCE) or the mercury–mercury(I) sulfate electrode (connected to the studied solution with a salt bridge with a glass frit) was used. Potentiodynamic and potentiostatic chronoamperometric experiments were made with the CHI 660b workstation (CH Instruments, Inc., USA).

The dynamic electrochemical impedance measurements were performed using a home-made setup assembled at the Department of Electrochemistry, Corrosion and Materials Engineering of Gdańsk University of Technology (Poland). National Instruments Ltd. PCI-6120 digital–analog card was used for both ac signal generation and measurements of the voltage and current response. A KGLstat v. 2.1 potentiostat was used as a current–voltage converter. The perturbation signal was a package of the voltage sinusoids of a frequency within the range of 140 kHz to 7 Hz. The sampling frequency was 400 kHz and the width of the analyzing window was equal to 10 ms. All measurements were carried out in a thermostated electrochemical cell, with the temperature of external water jacket controlled by the ultrathermostat MLW type MK70.

The solutions of acids were prepared using p.a. 85% phosphoric acid (Chempur), p.a. 95% sulfuric(VI) acid (Chempur), p.a. 65% nitric acid (POCh), p.a. 70% perchloric acid (POCh), 99.2% trifluoroacetic acid (Reachim), p.a. 100% acetic acid (POCh), and p.a. 36% hydrochloric acid (Chempur). Triply distilled water deionized using Millipore filter was used for preparing these solutions. The samples had not been deareated since dissolved oxygen did not undergo electrode processes within the studied potential range and thus did not interfere with the vanadium electrooxidation.

The SEM images were taken with a LEO 435 VP microscope (Germany), controlled by the manufacturer commercial software via a PC.

Results and discussion

Preliminary experiments have indicated that for the phosphoric acid concentrations ensuring the onset of oscillations (ca. 1 mol dm−3), the vanadium electrode never underwent so strong passivation, as for example the iron electrode in H2SO4 or Cu in H3PO4. Therefore, the electrooxidation current density of vanadium, even at its minimum, was for at least several orders of magnitude higher than for Cu/H3PO4 under similar conditions. In consequence, the vanadium wire or rod was dissolving relatively quickly. This made the long-time measurements difficult because even during short-time measurements, the current exhibited certain undesirable drift both beyond and inside the region of the dynamical instabilities. Furthermore, in the case of vanadium wire embedded in Teflon case, it was necessary to remove occasionally the layer of Teflon in order to restore the contact of deeply etched electrode with the H3PO4 solution. For all these reasons, the experimental possibilities of the precise analysis of the dynamic instabilities in the system studied were limited, as all the regimes were rather quasi-steady state, even if rotating disk vanadium electrode was used. Stronger passivation was observed only for relatively high H3PO4 concentrations (from 6 M to 15 M), but the oscillations were then completely suppressed.

Microscopic images, made under ex situ conditions immediately after emerging the electrode from the solution, have shown that the dissolution of vanadium was accompanied with a gradual decrease in the roughness of the surface (Fig. 1). These images will justify the moderate value of the surface roughness factor of the electrode, assumed by us further in the construction of the numerical model reproducing the oscillations (see part II).

Fig. 1
figure 1

a–c SEM images showing variation of the roughness of the surface of vanadium electrode prior to the measurement (a), after electrodissolution experiment stopped inside the oscillation region (b), and after completion of a full, single linear potential scan (c); the corresponding potentials and associated dynamic regimes are indicated in the enclosed I–U dependence (d)

Full size image

Oscillations at the stationary vanadium electrode in H3PO4 medium

Preliminary experiments involving the vanadium wire, contacting the meniscus of the 2 M H3PO4 electrolyte, confirmed the typical sequence of phenomena, observed under potentiodynamic conditions: with increasing positive potential, the anodic current of vanadium dissolution increased up to a maximum value, followed by the decrease in current and the onset of oscillations on the I–E dependence with negative slope, i.e., to the region of a negative differential resistance (NDR), more precisely N-NDR, meaning the shape of the I–E curve resembles the letter N. These oscillations persisted at more positive potentials also when the current started to increase again, but eventually they ceased. Repeating this potentiodynamic experiment also shows the permanent drift of the system’s characteristics as a function of time (Fig. 2).

Fig. 2
figure 2

a Typical potentiodynamic (v = 10 mV s−1) I–U curves recorded for the sequence of anodic polarizations of the stationary vanadium electrode (ϕ = 1 mm) in 2 M H3PO4 (T = 23 °C). b Enlarged part of (a), revealing the shape of the oscillations. U means the externally applied voltage (vs. the Hg|Hg2SO4|0.1 M H2SO4 electrode), not corrected for the ohmic potential drop in the solution

Full size image

Based on earlier studies of Albahadily and Schell [19–21] for the Cu/H3PO4 system, one could expect that the decrease in temperature (to −17 °C), causing the increase of the fluid viscosity, will result in prolonged lifetime and better reproducibility of the oscillations also for the V/H3PO4 system. Our experiments have shown that for temperatures ranging from 36 °C to 0 °C, the tendency to enhance the lifetime of the oscillations was indeed observed (Fig. 3a–c), with the birth of these oscillations starting from the small amplitude ones, suggesting the supercritical Hopf bifurcation. Surprisingly, the decrease of temperature to −6 °C caused a more complex dynamic behavior in which prolonged gradual increase of the oscillation amplitude occurred with slowly increasing voltage U and was further followed by the sequence of small- and high-amplitude oscillations, suggesting the occurrence of period-doubling bifurcation (Fig. 3d). Following the small amplitude oscillations, the significant sudden increase of their amplitude (resembling the so-called canard explosion) and certain elongation of its period are observed for a certain range of U. Eventually high amplitude oscillations decay rather abruptly, similarly as e.g. in the case of potentiodynamic (v = 10 mV s−1) Ni electrodissolution in 1 M H2SO4 [25], when the homoclinic (saddle-loop) bifurcation [29] occurs. However, this bifurcation manifests itself also through the increasing period of oscillations upon approaching the bifurcation point, which dependence we did not clearly notice in our numerous experiments, perhaps due to permanent drift of the system’s characteristics. In consequence, we cannot ascribe the decay of oscillations unambiguously to this type of bifurcation. In conclusion, for the V/H3PO4 system, contrary to Cu/H3PO4, there is an optimum, intermediate temperature range for which oscillations are relatively simple, presumably due to different kinetics of formation and structural properties of the solid phase(s) that in both cases form at the electrode surface and undergo dissolution.

Fig. 3
figure 3

Potentiodynamic (v = 10 mV s−1) I–U curves of the anodic dissolution of stationary vanadium electrode (ϕ = 1 mm) in 2 M H3PO4 at different temperatures: a T = 36 °C, b T = 10 °C, c T = 0 °C, and d T = −6 °C

Full size image

Oscillations and bistability at the rotating disk vanadium electrode in H3PO4 medium

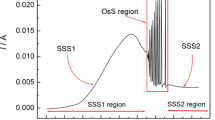
Stabilization of hydrodynamic conditions for the vanadium electrodissolution, achieved for the rotating vanadium disk electrode, allowed us to approach the steady-state regimes closer than for the stationary electrodes. For experimental conditions, similar to those for the stationary vanadium electrode, we observed sustained oscillations exhibiting, however, also certain drift in their characteristics. More important was the possibility to record the bistable behavior. As mentioned above, based on earlier literature results [28] at relatively high concentrations of H3PO4, the oscillations could not be observed, presumably due to more advanced formation and stabilization of solid precipitate on the electrode surface. However, just under such conditions, even for 14.7 M H3PO4 we discovered the bistability in the electrodissolution of vanadium (Fig. 4a). In turn, Fig. 4b and c shows the effect of temperature and of disk rotation rate, respectively, on the region of this bistability. For lower concentrations of H3PO4, with increasing disk rotation rate, we observed transition between the oscillations and bistability, according to the experimental stability diagram shown in Fig. 5. This diagram was constructed based on the potentiodynamic experiments (v = 10 mV s−1), but similar results were obtained for the potentiostatic (U = const) studies. The shape of this stability diagram is typical for the systems in which the region of a negative differential resistance attains a shape of N letter, i.e., for the N-NDR oscillators studied under potentiostatic conditions.

Fig. 4
figure 4

a Bistability in the anodic dissolution of the rotating vanadium disk electrode (ϕ = 6 mm; 3,000 rpm) in 14.7 M H3PO4 (T = 23°C; v = 10 mV s−1). b Effect of temperature on the bistable region. c Effect of disk rotation rate on the bistable region (T = −15 °C, v = 10 mV s−1). Note that the variations of current are caused also by the continuous change of the effective surface area of the electrode (surface roughness)

Full size image
Fig. 5
figure 5

Stability diagram for the anodic dissolution of the rotating vanadium disk electrode in 2 M H3PO4 at T = 0 °C

Full size image

Effect of external serial resistance

The dynamic phenomena described above were reported under potentiostatic (U = const) conditions without external resistor in the circuit. One may suppose that, as for other NDR systems, the ohmic potential drops participate in the coupling leading to bistability and oscillations, but the own resistance of the electrochemical system is sufficient to meet the conditions for the loss of stability. In order to establish more evidently the role of ohmic drops, we performed the series of experiments in which the additional, adjustable serial resistance was inserted in the circuit of the working electrode. The composition of the solution (2 M H3PO4) and the rotation rate of the vanadium disk electrode (2,000 rpm) remained unchanged while the resistance R s was increased. For the applied vanadium disk (ϕ = 1 mm) embedded in Teflon casing, with scan rate v = 10 mV s−1 and solution temperature T = 22 °C, the general tendencies were the following: for relatively low R s, of the order of 100 Ω, the oscillatory region exhibited shifting to more anodic voltages, with simultaneous widening of the range of U in which it occurred; for relatively high R s (1–5 kΩ), only bistability was observed (Fig. 6). This tendency, analogous to those observed for other N-NDR oscillators, confirms the role of ohmic potential drops in the dynamic instabilities of the V/H3PO4 system.

Fig. 6
figure 6

Effect of added serial resistance (indicated in the figures) on the I–U potentiodynamic curves of the electrodissolution of vanadium electrode (ϕ = 1 mm/Teflon; 2,000 rpm) in a 2 mol dm−3 H3PO4 solution (T = 22°C; v = 10 mV s−1)

Full size image

Impedance characteristics of the V/H3PO4 system

At present stage of understanding of the electrochemical oscillators, it is clear that impedance measurements can be a source of valuable information on the detailed mechanism of the oscillations and even allow to place the studied system in the respective group, following, e.g., the classification suggested by Strasser et al. [30]. However, for the V/H3PO4 system, the characteristics of which undergo permanent drift due to rather high rate of vanadium dissolution, even in the region of (partial) passivation, typical impedance measurements supply data of limited reliability. Therefore, we used the novel technique introduced and developed by the group of Darowicki et al. [31–34] in which the impedance spectrum can be collected also for the non-steady state, i.e., in this case drifting, but non-oscillatory state. The essential principle of the method is the following: applied potential is modified with perturbation signal, which is a package of sinusoidal voltage signals with amplitude equal for all components but different frequencies and phase angles. A comparison between decomposed current and voltage signal allows one to calculate the instantaneous impedance, in the appropriately chosen Gaussian window of time, using the short-time Fourier transform.

In Fig. 7, we present the collection of impedance spectra recorded for the V/2 M H3PO4 system, in the absence of external resistance, for three voltages U (1.27 V, 1.35 V, and 1.42 V), compared with the potentiodynamic I–U curve, obtained simultaneously for the same sample, so the ohmic potential drop in the solution was the same in both cases. The comparison presented in Fig. 7 shows that the vanadium electrodissolution has even more complex characteristics than it could be supposed only from dc measurements: the impedance spectra enter the region of negative real impedance at the potentials where the I–E slope of the dc dependence (zero frequency) at the same voltage is positive. This immediately suggests the presence of a hidden negative resistance under dc conditions for the studied sample. However, it does not mean that the system studied by us can be unambiguously classified as the HN-NDR (Hidden N-NDR) type oscillator in which, according to idea developed originally by Koper and Sluyters [35], the negative impedance is caused by the relatively fast process that under dc conditions is masked (hidden) by the slower process of a positive impedance. This is because the following problems have to be taken into account. First, the spectrum does not reveal the whole shape expected for such a case, i.e., the loop beginning and ending with the positive real impedance, for both zero and infinite frequencies, with the negative real impedance manifesting itself only for its intermediate regions. This is because of unsuccessful attempts to measure the impedance for ac frequencies lower than those indicated in Fig. 7. Second, if the electrochemical dynamical system belongs to the HN-NDR class, the oscillatory behavior should be observed also under galvanostatic conditions. However, our numerous efforts to record such dynamics under polarization with anodic current resulted only in the shift of the vanadium electrode potential to very positive values, at which the electrode surface was irreversibly blocked by the solid products of its dissolution. Third, the bifurcation diagram shown in Fig. 5 has a shape typical for the N-NDR and not for the HN-NDR oscillator, the latter one predicting oscillations also for increasing serial resistance (cf. e.g., figure 19 in [4]). Nevertheless, we do not exclude completely the formation of the HN-NDR system since we found the I–E characteristics of V/H3PO4 system quite sensitive to various factors. It is apparently not possible to prepare two samples and make measurements under practically identical conditions. Thus, in some experiments, the N-NDR region may not be hidden while in other ones partly hidden by the anodic current increasing at more positive potentials. This only reveals the complexity and serious electrochemical instability of the V/H3PO4 system.

Fig. 7
figure 7

a Impedance spectra (Nyquist plots) of the electrodissolution of vanadium in 2 M H3PO, compared with b potentiodynamic I–U response recorded simultaneously for the same sample. For the indicated three voltages, the slope of the dc I–U curve is positive, while the Nyquist spectra enter the region of the negative real impedance, thus suggesting the existence of the hidden negative impedance under dc conditions. The voltage is expressed vs. the saturated calomel electrode. In (a), ac angular frequencies (ω, rad·s−1) are shown

Full size image

Comparative studies of vanadium electrodissolution in other acidic media

Since the characteristics of the dynamic instabilities in the vanadium electrodissolution process should depend, among others, on the solubility and structural properties of the passive layer formed during the anodization, including its eventual pitting corrosion, it seems reasonable to study the effect of replacing the phosphoric acid with several other acids. For this comparison, we selected the nitric, sulfuric, perchloric, and trifluoroacetic acids.

Figure 8 shows the exemplary dynamic instabilities recorded for these acidic media, using the rotating vanadium disk electrode, while Fig. 9 collects the corresponding stability diagrams. Other conditions are specified in the caption to particular figure. This comparison shows similar shape of the bifurcation diagrams for the V/H3PO4 and V/H2SO4 systems (Fig. 9a), although in the latter case the entire diagram is shifted towards lower voltages and higher rotation speeds, presumably due to the different solution resistance. Also, V/H2SO4 appears to be a simpler dynamical system as the oscillations occur only within the N-NDR region of the I–U dependence and do not enter the positive I–U slope. In turn, V/HNO3 system (Fig. 9b) produces irregular and highly irreproducible dynamic instabilities, observed also at very positive potentials. The specific feature of this system is, however, the occurrence of oscillations inside the region of bistability (i.e., the hysteresis involves either the steady-state or oscillatory regime). The borders of dynamic behaviors around U = ca. 1.5 V are drawn out due to high irreproducibility of the dynamic behaviors in this region.

Fig. 8
figure 8

Exemplary voltammetric curves of electrodissolution of rotating vanadium electrode (1-mm-diameter vanadium wire, embedded in Teflon) in various acidic media. Temperature T = 0 °C, scan rate v = 10 mV s−1. Rotation speed and type of acid are shown in the insets, in the respective figures. Concentration of every acid equals to 2 mol dm−3, except for CF3COOH (0.5 mol dm−3)

Full size image
Fig. 9
figure 9

Bifurcation diagrams of electrodissolution of vanadium electrode in various acidic media, for the experimental conditions specified in the caption to Fig. 8

Full size image

The next studied system, V/HClO4 (Fig. 9c), shows another type of bistability—during the forward scan (in the anodic direction), only a sudden drop of anodic current at the potential close to 1.2 V was observed, while during the reversed cathodic scan, the oscillations were observed for a wide range of rotation speed. In this case, the current returns to relatively high values only at U of ca. 0.8 V.

Finally, the V/CF3COOH system (Fig. 9d) shows current oscillations on both forward and reverse scans, but in different range of potentials: in the reverse scan, those oscillations appear with a delay, i.e., at less anodic potentials. Although the causes of this hysteresis are not clear, it is possible that at least one of them is the continuous drift of the system’s characteristics (electrode surface state) during the slow scan cyclic voltammetric experiment.

We were not able to found analogous instabilities during electrodissolution of vanadium in hydrochloric acid and in acetic acid. In the first case, this can be ascribed to relatively high solubility of chloride salts of vanadium or to halide attack on vanadium oxide film, causing its fast pitting corrosion. In the latter case, acetic acid, as a weak electrolyte, causes high solution resistance and ensures only low acidity which factors may not create sufficient conditions for the onset of instabilities.

Conclusions

To summarize our experimental studies, we conclude that the electrodissolution of vanadium in H3PO4 and other acids reveals rather complex dynamics, but the permanent drift of the state of V electrodes makes the clear diagnosis and strict description of all reported dynamic instabilities rather difficult. Such difficulties do not qualify the systems studied as the ones particularly useful for the purposes of testing various mechanisms of electrochemical oscillations. It is also difficult to judge whether any of those systems may constitute a new type of electrochemical oscillator. Nevertheless, their complexity makes them a challenging subject for numerical modelings that should indicate the essential mechanism of oscillations and reproduce, if not all, at least some of the reported instabilities. Such modeling is described in the second part of our paper.