Introduction

Due to the central role of phosphates in biochemistry, mechanisms of reactions of organophosphorus compounds were subjects of intensive studies, with the existence of free metaphosphate being a subject of controversy both in chemistry and in biochemistry for many years [1]. One of the examples of this problem was the mechanism of the thiol-thione rearrangement of monothiophosphate skeleton [2] illustrated by Scheme 1 (atom numbering used throughout the text indicated as subscripts):

scheme 1

Scheme 1

Two alternative mechanisms have been proposed as illustrated in Fig. 1. In the upper pathway, the P-S bond dissociates heterolytically to form (intimate) ion pair that recombines via the formation of the P-O bond [3]. In the lower pathway, an internal nucleophilic attack of the oxygen atom on the adjacent phosphorus atom with the formation of a cyclic transition state (or an intermediate) is assumed [4].

Fig. 1
figure 1

Assumed alternative mechanisms of organic monothiophosphate isomerization (see text for details)

Full size image

The problem has been approached with many experimental techniques, one of them being measurements of kinetic isotope effects (KIEs [5]) [6, 7]. We have measured kinetic isotope effects of sulfur [8] and phosphoryl oxygens [8, 9] for the reaction carried out in 1-methylnaphthalene, benzonitrile, and propylene carbonate. Based on these measurements and simple modeling, a switch in the mechanism upon change from non-polar to polar solvents has been postulated. However, quantum-chemical modeling of this reaction was then not possible and even with the advent of early ab initio and semiempirical methodology calculations of systems containing phosphorus atoms were scarce and became available only recently.

With the availability of modern density functionals, it is now possible to address the mechanism of the above reaction theoretically. In order to decide on the theory level, a survey of published data has been carried out. Results of older theoretical approaches have been representatively evaluated in the extensive benchmark of calculations on hydrolysis of organophosphorus compounds that has been published in 2010 [10]. Over 50 functionals expressed in Pople’s or Dunning’s basis sets have been compared with the reference calculations carried out at the CCSD(T)/CBS//B3LYP/6-311++G(2d,2p) theory level. Overall, MPWB1K/6-311+G(2d,2p) calculations [11,12,13,14] were found to perform the best. Notably, due to the time when the benchmark was compiled, no functionals that include a correction for dispersion have been evaluated. Since then, an extensive review of theoretical approaches to hydrolysis of biological phosphates has been published recently [15]. This contribution concentrates, however, on methodological aspects of calculations while employing only SMD/M06-2X/6311+G9d,p)//SMD/M06-2X/6-31+G(d) level of theory. Some other (non-exhaustive) recent examples of using different theory levels in modeling properties and reactivity of phosphorus-containing molecules include DFTB3/3OB in structure determination [16, 17], B3LYP & MP3 with 6-311G(d,p) basis set in conformational analysis [18], B3LYP/cc-pVTZ/TIP3P and B3LYP-D3/def2-SVP(D) in studies of anharmonicity of phosphate ions in water [19, 20], M06-2X, M06L and PBE with 6-31+G(d,p) in lipophilicity calculations [21] ωB97/6-311+G(3df,2p)//M06-2X/6-311+G(d,p) in investigations of the reaction with OH radical [22], MP3/6-311++G(2d,2p)//B3LYP/6−31+G(d) in hydrolysis of pesticides [23], PM3/MM, BLYP/6-31G(d)/MM, B3LYP/6-31G*/MM and COSMO/B3LYP/6-31G(d) in hydrolysis of monoesters [24], B3LYP/6–311+G(d,p) and M06-2X/6–311+G(d,p) in gas-phase decomposition [25], B3LYP/6-311+G(d,p) in metathiophosphate di- and polymerization [26], M06-2X/6-311+G(3df,2p) and B2PLYP/6311+G(3df,2p)//(IEFPCM) /M06-2X/6-311+G(d,p) in oxidation [27], PBE-D3/PAW in non-aqueous degradation [28], M06-2X/6–31G(d,p) and BLYP-D3/aug-cc-pVTZ in binding to an enzyme [29], and B97D/6-31+G(d)/AMBER [30], B3LYP/6-31G(d) [31] and PBE0-D3/def2-TZVP [32] in enzymatic catalysis.

In this contribution, we have approached modeling of the alternative pathways of the isomerization of bis(5,5-dimethyl-2-oxo-1,2,4-dioxaphosphorinanyl) sulfide using contemporary computational tools. Based on the examples given above, a density functional augmented by dispersion correction, namely ωB97xD [33], expressed in a triple-zeta, 6-311++G(d) [34], basis set has been chosen. This theory level, augmented by continuum solvent model, allowed for analysis of both alternative pathways and associated kinetic isotope effects.

Methods

All calculations were performed using Gaussian16 package [35] and visualized with GaussView6 program [36]. All calculations were first carried out using ωB97xD functional expressed in the def2-SVPP basis set [37]. Harmonic frequencies were calculated to validate optimization to stationary points. IRC protocol [38] was employed for the confirmation that the transition states corresponded to studied reactions. The solvent was represented by the PCM model [39]. The reaction in 1-methylnaphthalene has been modeled in the gas phase, and using parameters for p-xylene. For the reaction in benzonitrile, the parameters for this solvent were employed. Since, however, parameters for propylene carbonate are not available, we have used these for water, which provides the high extreme on the polarity scale to ensure the polarity of the solvent larger than that under experimental conditions. Subsequently, stationary points were re-optimized at the PCM(aq)/ωB97xD/6-311++G(d) level of theory and harmonic frequencies obtained at this theory level were used in calculations of isotope effects by means of our own Isoeff2017 program [40].

Results and discussion

Selection of the theory level

Two trends can be seen from the examples discussed in the Introduction; firstly, there is a shift from the robust B3LYP functional [41, 42] to those that take into account dispersion, and secondly, the majority of calculations have been performed with a triple-zeta basis set. Our failures in finding the transition state for the dissociative pathway at the B3LYP/6-31+G(d) and ωB97xD/def2-SVPP levels of theory are in line with the observation that the basis set of the triple-zeta quality is necessary for reactions that involve reactions at the phosphorus center. We have, therefore, decided to employ ωB97xD functional, which we found performing very well for other systems [43]. The decision on the basis set has been made on the basis of charge distribution in phosphathioate anion that we have studied experimentally. Our 31P-NMR results indicate that there is little charge delocalization in this anion with the extra electron localized mostly on the sulfur atom [44]. Many theory levels and charge partitioning schemes fail to correctly distribute electron density in agreement with this observation [45]. We have, therefore, evaluated a number of basis sets taking into consideration Műlliken partial atomic charges on sulfur and exocyclic oxygen. The results are collected in Table 1. The results obtained with the 6-311++G basis set are in the best agreement with the experimental observation while the increase of polarization of the basis set leads to opposite charge distribution. Since our goal has been studies of reaction mechanisms, the polarization functions needed to be employed. We have, therefore, resorted to the 6-311++G(d) basis set. APT partial atomic charges, while generally larger in absolute values, led qualitatively to the same results (data not shown). Furthermore, in order to facilitate calculations, we have decided to use “cheaper” Ahlrichs def2-SVPP basis set that preserves the trend of this charge distribution, for initial scans, IRCs, and optimizations and to resort to ωB97xD/6-311++G(d) level only for final calculations.

Table 1 Partial atomic charges (a.u.) on exocyclic oxygen atom and sulfur atom in 5,5-dimethyl-1,3,2-dioxaphosphorinane-2-oxo-2-thio anion calculated with ωB97xD functional and different basis sets
Full size table

Isomerization mechanisms

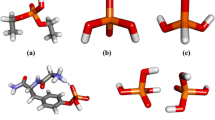
We have identified three pathways leading from the symmetrical thiopyrophosphate 1 to the asymmetrical product 2. The corresponding transition state structures are illustrated in Fig. 2 and the main structural data collected in Table 2.

Fig. 2
figure 2

Transition state structures obtained for the dissociative mechanism (left) and two associative mechanisms (middle and right). For clarity, parts remote to the reaction center are rendered as wireframes

Full size image
Table 2 Main geometric and energetic parameters (kcal/mol) of the reactants and transition state structures at the ωB97xD/6-311++G(d)/PCM(aq) level of theory. Atom numbering follows the Scheme in the Introduction
Full size table

Reported in Table 2, bond orders were obtained from the Pauling equation: [46].

$$ {r}_n={r}_1-c\bullet \ln \left(\mathrm{n}\right) $$
(1)

where r is the bond length and n is the bond order. Indices n and 1 correspond to n-order and single bond, respectively. Coefficients c for P-S and P-O bonds were evaluated on the basis of averaged bond lengths for single and double bonds in reactants.

The three localized transition state structures are characterized by different charge distribution; in the TSd structure, practically full charge separation between dissociating fragments is observed. The breaking P1-S distance is nearly 4.5 Å. However, from the last line of Table 2, it is apparent that the dissociative mechanism can be excluded from further considerations as the formation of the ion pair that recombines to the product is energetically too demanding. The TSi1 transition state structure shows moderate P1-S bond breaking that is concertedly compensated by the significant shortening of the P1-O4 distance. The charge distribution between the two fragments stays, however, neutral as in both reactants. Transition state structure TSi2 resembles geometrically TSi1, with main distinctions being a rotation of the P1SP3O4 plane by about 90° and the formation of the P1-O4 bond being even more advanced. The charge on the \( SP3(O4){\displaystyle \begin{array}{c}/\\ {}\backslash \end{array}} \) fragment is positive in accordance with the synchronous breaking of the P3-S bond and formation of the P1-O4 bond and building the negative charge on the O5, although surprisingly, this is not paralleled by the elongation of the P1-O5 bond. Attempts to localize a cyclic intermediate failed at all considered theory levels indicating that such structure is not a stationary point. The concerted mechanism proceeding via TSi2 requires less energy than the one characterized by the TSi1. In fact, the calculated Gibbs free energy of activation of 29.3 kcal/mol is in excellent agreement with the experimentally determined enthalpy of activation of 29.9±1.3 kcal/mol [47].

Isotope effects

Isotope effects for reaction channels proceeding via all three transition states are collected in Table 3. For direct comparison with the experimental data, we have calculated isotope effects of sulfur-36, and oxygen-18 averaged over both exocyclic positions.

Table 3 Calculated and experimental kinetic isotope effects at 404 K
Full size table

As can be seen, kinetic isotope effects obtained from TSi1 do not agree with the experimental data; the oxygen KIE is substantially larger while sulfur KIE substantially smaller than values obtained experimentally. The results obtained for the pathway proceeding via TSi2 on the other hand agree very well with the experimental data. We thus conclude that the reaction proceeds via cyclic albeit non-synchronous transition state: the P-S bond breaking is advanced by some 70% while the formation of the new P-O bond is advanced only to some 30% (taking into account bond orders).

The above findings leave unsolved one observation, namely the decrease of sulfur KIE in the polar solvent; k32/k36, in propylene carbonate, has been found equal to 1.0210±0.0014. Our calculations indicate that the increase of polarity of the solvent leads to an increase of the isotope effect, as illustrated in Table 4, which does not agree with this experimental observation.

Table 4 Dependence of the calculated sulfur KIE for the reaction proceeding via TSi2 on the polarity of the solvent at ωB97xD/def2-SVPP/PCM theory level
Full size table

Alternative mechanisms

In the search for the explanation of this discrepancy, we have considered a few alternative mechanisms suggested in the literature. The possibility of bimolecular reaction between two molecules of monothiopyrophosphate [48] has been excluded since it is hard even to construct a model of reactants due to steric effects. It is, however, known that it is very hard to obtain and store propylene carbonate without traces of water. Thus, another alternative mechanistic option that has been considered is a reaction between phosphathioate anion and symmetrical reactant illustrated by Scheme 2:

scheme 2

Scheme 2

Small amounts of the anion could result from tracer amounts of water in propylene carbonate which can hydrolyze the reactant 1. In fact, the energetic cost of this hydrolysis has been found to be about 16.5 kcal/mol when hydroxyl ion is considered as the nucleophile. The 36S-KIE for this reaction is small (1.0065). The reaction between phosphathioate anion and reactant 1 is also feasible under studied conditions; calculated Gibbs free energy of activation equals to 25.7 kcal/mol. Again, sulfur KIEs for this reaction are much smaller than the isotope effect calculated for the unimolecular reaction (1.0097 for the sulfur atom in the leaving group and 0.9989 for the sulfur atom in the incoming group). Thus, small participation of this reaction channel in the formation of the product 2 can explain the observed decrease of the sulfur isotope effect.

Conclusions

A few general conclusions arise from the studies presented herein. The most important is the mechanistic finding that, opposite to previous interpretation, the mechanism of unimolecular thiol-thione isomerization of organic monothiopyrophosphates proceed via a cyclic transition state with the P-S bond breaking much more advanced than the formation of the new P-O bond. The lower value of the sulfur kinetic isotope effect observed in a polar solvent, propylene carbonate, most probably results from the participation of side bimolecular reaction of the reactant with phosphathiolate anion and is not the result of the change in the mechanism of the unimolecular reaction. It should be kept in mind that continuum solvent models neglect direct interactions of solvent molecules with the reactants. Due to molecular size of all solvents of interest, however, studies with explicit solvation are prohibitively time-consuming. We have, therefore, studied possibility of direct interactions between ionic fragments formed in the dissociative pathway and a single molecule of benzonitrile or propylene carbonate (data not shown) and found them to be energetically disfavored. In the studied system, interactions of 1-methylnaphtalene with reactants is rather unlikely.

A somewhat surprising observation has been made that atomic partial charge localization does not correlate directly with bond lengths. More studies are required to investigate this phenomenon in terms of the theory level used, especially the basis set, for other phosphorus–sulfur- and phosphorus–oxygen-containing organophosphorus compounds.

Results obtained using cheaper B3LYP/6-31+G(d) and ωB97xD/Def2-SVPP theory levels are very similar to those obtained with ωB97xD/6-311++G(d) for energetics and kinetic isotope effects. However, only at the triple-zeta level of the basis set it was possible to localize the transition state for the dissociative pathway.