Introduction

Common madder (Rubiae tinctorum L.) is a plant commonly found in southern and southeastern Europe, in the Mediterranean area, and in central Asia [1]. The herb contains many polyphenol derivatives such as flavonoids and anthraquinones [1–3]. Several years ago its medicinal usefulness was discovered and the root of madder is used for the kidney and bladder stone treatment [1, 3, 4]. The observed activity is due to the presence of polyphenols and polyphenol glycosides which dissolve calcium oxalate, the foremost compound in kidney stones [5]. It was recognized that carbohydrates and polyphenols serve as ligands of the calcium cation with a multiple coordination number. Three frequent coordination numbers, mainly 6, 7 and 8 were observed, but less common numbers (5, 9, 10) are also possible. The high numbers correspond to the second coordination sphere and are possible due to small ligand-ligand repulsions [6]. In general, the bidentate binding is common for these ions [7–9] and carboxylates form complexes with calcium in such a fashion [7]. Polyphenols, such as curcumin, tannic acid and (+)−catechin, control the intercellular calcium transport due to complexation of ions [10]. Different mechanisms were observed for different ligands involved in these processes [11]. Flavonoids, as the most frequent antioxidants, possess ability of chelating of divalent metal [12]. The reports regarding Ca2+− sugar complexes are widely present in the literature. The formation of metal-carbohydrate structures requires an appropriate steric arrangement of at least three hydroxyl groups. According to the general rule: pyranoses in a chair conformation with axial-equatorial-axial (ax-eq-ax) or with 1,3,5 triaxial (ax-ax-ax) hydroxyl groups or furanoses with three adjacent hydroxyl groups in the cis-cis arrangement are the best coordinating ligands [13, 14]. Furthermore, the preferred configuration of binding depends of the size of cation (e.g., for the ionic radius smaller than 80 pm the ax-ax-ax arrangement is preferred). However, it is still not known which of the metal-carbohydrate complex constitutes the most stable moiety. The spectroscopic studies for D-glucuronate, epi-inositol, and L-arabinose were performed in order to characterize the structure of sugar after the Ca2+ complexation. The observations lead to the following conclusions [14–18] (i) the hydrogen-bonding network of the free sugar is preserved upon the metalation (ii) all groups of its or sugar derivatives containing oxygen and water molecules are involved in the metal-ligand bonding (iii) usually the α-anomer of calcium complexes crystallizes (iv) the most common coordination number amounts to eight. The above findings indicate the strong complexing properties of sugar and polyphenols and suggest that the glycosylation of polyphenols can increase their calcium binding ability. Our studies confirm these conclusions [4, 19]. The analysis of different fractions of the extract of Humulus lupus L. has indicated that fractions richer in glycoside compounds possess better calcium oxalate dissolving properties [19]. Moreover, studies on synthetic glycosides have shown that anthraquinone glycosides form stronger complexes compared to that of lone anthraquinones [4]. In the above experiment glycosyl compounds were analyzed as dissolving media of calcium oxalate and inhibitors of the crystals formation. In all studied cases, the sample of glycoside had shown two times higher efficiency compared to one of lone aglycon [4]. Additionally investigatios, we have also characterized the complexation of Ca2+ by alizarine, one of the most popular anthraquinone, by applying NMR and theoretical DFT studies. The results indicated that the metal cation is attached to two hydroxyl groups in the bidentate mode [20]. The studies presented in this work supplement the investigation of Ca2+−ligand complexes for carbohydrate and alizarine glucoside ligands.

Computational details

The calculations presented here were performed applying the density functional theory (DFT) formalism [21]. The approach is based on the hybrid exchange-correlation functional proposed by Becke, Lee, Yang and Parr (B3LYP) [22]. The studies applied the standard Pople’s 6-31G(d,p) atomic basis set [23, 24]. Thermodynamic properties of studied complexes were calculated taking into account the ideal gas, rigid rotor, and harmonic oscillator approximations [25]. The atomic charges were divided within the Mulliken population scheme [26]. The interaction energies were calculated according to the expression

$$ \varDelta {E_{{\operatorname{int}}}}={E_{AB }}-\left( {{E_A}+{E_B}} \right), $$

including the correction for the basis set superposition error [27]. The computations were carried out using the GAUSSIAN 09 suite of codes [28].

The starting geometries

Because of the large number of potential conformers of glucose the proper selection of starting structures is critical. The formal number of conformers (2900) may be reduced considering the stereochemistry [29]. The further reduction can be achived taking into account the fact that in the aqueous solution of D-glucose preferably adopts the chair 4C1 conformation [30, 31]. However some additional structures have to be considered, since the coordination of metal may lead to energetically preferred complexes not favored in the case of non-interacting glucose. Our selection is based on the carefull work of Salpin and Tortajada [30] which reports the conformational study for the [Pb(D-glucose)−H]+ cation. Twenty structures, out of 31 presented in their work, were adopted in the present study. The number of conformers is further reduced due to the fact that some of the original conformers differ only by the place of deprotonation. The selected structures of glucose and alizarin constitute the reasonable starting point for designing the glycoside of alizarin. Sixty one structures were derived applying these geometries. The nomenclature applied in this work is the same as one developed in the paper [30], where the name of particular complex contains the anomer type (α or β which are identified here as “a” or “b”), the type of conformer, the position of the hydroxymethyl group (gg, gt, tg) and labels of glucose (Table 1) or glucoside (Table 2) atoms coordinating calcium. Additionally, some structures are characterized by the dihedral angle F-C1-O2-C2’ (in parenthesis).

Table 1 The number of contacts (N), relative interaction energy (ΔΔEint), relative enthalpy (ΔH) and relative free enthalpy of the complex formation (ΔG) for glucose-Ca2+ cation and the Mulliken atomic charge on the Ca center. Energy in kcal mol−1, atomic charge in electron. The lowest interaction energy of −178.0 kcal mol−1 in the β-glucose-Ca2+ complex in OS2 and CEFA sequence constitutes the reference level
Full size table
Table 2 The Ca-oxygen distances in glucose-Ca2+complexes. Distances in angstrom
Full size table

Complexes with the Ca2+ cation

Glucose

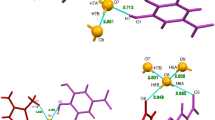
Two arrangements of hydroxyl groups: axial-equatorial-axial (ax-eq-ax) or axial-axial-axial (ax-ax-ax) are possible for carbohydrates. Since interactions are influenced by the volume of cation, because the Ca2+ size is greater than 80 pm (114 pm), the preffered arrangement results as ax-eq-ax [32–35]. In glucose five possible sites were indicated for the cation coordination [34]. The preferred locations of metal are those where interactions occur with oxygen atoms A, E (hydroxyl groups) and oxygen F included in the ring (Fig. 1).

Fig. 1
figure 1

Schematic representation of glucoside including glucose (with A-F letters designating oxygen atoms) and alizarin (O1, O2, O9, O10 for the oxygen atoms) fragments

Full size image

For the case of glucose the results may be divided into three groups according to the number of coordination contacts (four (IV), three (III) and two (II)). Only one isomer exists with calcium coordinated by four oxygen atoms (Fig. 2). The similar structure was observed for sodium as a metal cation [35]. Such a complex is the energetically most stable with the glucose-Ca2+ interaction energy of −178.0 kcal mol−1. The III-coordinate complexes are significantly weaker (Table 1), with the smallest relative interaction energy of 17.9 kcal mol−1. The α-anomer always coordinates calcium via F oxygen, whereas β-anomers possess the same sequence of oxygens mainly E, F, A. With the single exception, the interaction energy for boat and skew (or twisted boat) conformations is higher comparing to chair conformations. However due to the hydroxyl anomeric group located on the same side as the hydroxymethyl group the lower interaction energy is observed for the β-anomer. Such an arrangement allows for the more efficient interactions between components of complex. The smallest interaction energies characterize II-coordinate complexes. The difference within this group ranges from 34.5 to 54.0 kcal mol−1. In contrast to III-coordinate complexes α-anomers interact stronger. All II-coordinate conformers prefer chair conformations.

Fig. 2
figure 2

The structure of the most stable a glucose-Ca2+ b glucoside of alizarin-Ca2+ complexes

Full size image

The number of contacts constitutes the main parameter characterizing thermodynamics of studied complexes. Since interactions are dominated by the electrostatic term, and in the first order approximation interactions may be considered as additive. Each new Ca2+−O contact contributes roughly 20 kcal mol−1 to the total interaction energy. The consecutive inclusion of contacts influences the atomic charge on the calcium atom and in consequence lowers the interaction. The atomic charge on metal, due to the electron charge transfer from oxygen, decreases by approximately 0.05 electron, leading to the observable energetical effect. However the effect is too small to change the order between isomers grouped according to the number of contacts. The relative enthalpy and free enthalpy values, compared to interaction energy, include additionally the effect of the ring modification due to the conformation change as well as ring organization (Table 1). The contributions are also approximately additive. The inclusion of ring effects always increases the stabilization of isomers (compared to the IV-contact structure). The interaction energy values are in close relation with metal-oxygen distances. The shortest distances characterize the II-contacts complexes, while the most stable complex IV-contacts possesses the longest Ca2+−O bonds (Table 2).

Glycoside

In glycoside, due to new bonds formed between glucose and alizarin, the number of active oxygen centers for the Ca2+ coordination is significantly higher. Additionally, the alizarine fragment with the complex corresponds to the tautomer with carbonyl group in the O1 position (Fig. 1). The isomers may be devided into two groups characterized by V and IV coordinating oxygens. As expected, V-coordinate structures are more stable compared to those with four O-Ca contacts. The lowest interaction energy (−233.0 kcal mol−1) was obtained for the OS2 conformation of β-anomer. The same trend was also observed in glucose. The geometry of glycone in this glucoside and interactions between calcium ion and oxygen atoms in glycone are similar to that observed in the most stable glucose-Ca2+ complex (Fig. 2).

The glucoside-Ca2+ complexes are characterized by an additional Ca-O bond corresponding to the carbonyl group of alizarin fragment (Fig. 2). The additivity of interactions is again visible and the number of contacts, in analogy to glucose, constitutes the main factor controlling the stability. The four coordinate complexes are systematically less stable. The results indicate that carbonyl oxygen contributes the most to the overall energy stabilization. The difference between ΔΔEint and ΔH (Table 3) is positive or negative indicating that the structure of the energetically lowest total energy is characterized by skeleton (conformer) which is not energetically the most preferred. The atomic charge on the calcium cation is lower for moieties of V-contacts compared to that of IV-contact. The small difference between ΔH and ΔG indicate little influence of entropy of the studied processes. The computations including the solvent effect (CPCM model) suggest that general conclusions for glycoside do not change.

Table 3 The number of contacts O-Ca2+ (N), relative interaction energy (ΔΔEint), relative enthalpy (ΔH), and relative free enthalpy (ΔG) for glucoside complexes, the atomic charge on Ca and the C = O∙∙∙∙Ca2+ distance. Energy in kcal mol−1, atomic Mulliken charge in electron, distance in angstrom. The reference lowest interaction energy amounts to −233.0 kcal mol−1
Full size table

Conclusions

The presented theoretical studies confirm the experimental findings [19] indicating that glucose and its alizarin glycoside can form complexes with the calcium cation. The results show that the stronger interaction energy correlates with the higher coordination number. For both, glucose and glycoside the largest interaction was observed for β-anomer in the skew-boat conformation. It suggests that the interaction with a metal cation can enforce the conformational conversion. The conformational changes in the glycone part contribute to stabilization energy. The results suggest that the OS2 conformation constitutes the preferred structure for glucose and glucoside complexes. The interaction energy depends on distances between calcium and oxygen, the shortest distances are observed for carbonyl oxygen. The increasing number of O-Ca2+ contact decreases the single contact contribution but the overall interaction energy increases. These findings suggest that the coordination number constitutes the main factor controlling the total energy.