Introduction

Armchair-type SWCNTs, along with zigzag and chiral carbon nanotube structures [1–6], are important for both basic science studies and practical applications (e.g., in modern material science). Single-wall carbon nanotubes are frequently referred to as one-dimensional structures due to their nanoscale dimensions and quantum properties. Typical SWCNT diameters are from 0.4 to 4 nm, and their lengths range from 100 nm to several micrometers. Their unique mechanical, electro-optical and physicochemical properties make them potentially promising building blocks, components, and molecular devices in both engineering and nanomedicine [2, 7, 8]. The presence of flexible SWCNT additives with significant tensile strength to a typical polymer matrix allows the fabrication of materials with enhanced mechanical properties. However, due to the “smooth” surfaces of SWCNTs, their “anchoring” to and interactions with the surrounding matrix are relatively poor.

The rational design of advanced composite materials requires some kind of interaction between the SWCNTs and the surrounding matrix. Anchoring hydrophobic pristine SWCNTs, used as an additive, becomes much easier when various substituents are introduced (e.g., through end, side, and end-side functionalization of SWCNT), preferably with polar functional groups. On the other hand, acids are used to clean and remove the remains of the metal catalyst applied to the raw carbon nanotube material during the process of SWCNT synthesis. As result, partial damage, chemical oxidation, and the introduction of both –OH and –COOH substituents occur in the purified material [9].

It is known that pristine SWCNTs are long tubes with high length/diameter ratios, and that their surfaces consist of neighboring carbon hexagons (or, more formally, rolled graphene planes); these surfaces are closed at their ends by hemispheres made from carbon pentagons and hexagons. On the other hand, the deviation from planarity (and the instability of the ideally planar benzene-like ring) of the rolled graphene plane decreases as the tube diameter increases, so the tips or ends of the tubes are more reactive (unstable). This means that the tips of SWCNTs are more prone to damage and scission during acid cleaning of the raw material. As a consequence, SWCNTs that are functionalized at their ends (rims) by COOH or OH groups are formed [10, 11]. More chemically reactive media are able to covalently functionalize the surfaces of SWCNTs (mainly at surface defects and by disrupting aromatic ring bond systems). Two types of SWCNT functionalization—sidewall and end functionalization—are known and have been studied experimentally and theoretically [10–15].

The functionalization of pristine SWCNTs dramatically changes their chemical, electronic and transport properties [16]. The initially relatively chemically inert SWCNTs, after functionalization with –OH and –COOH, can form chemical links with more complex reagents such as aminoacids, DNA components, various drugs, and can be dissolved in common solvents. Unfortunately, experimentally derived information on the molecular structures of SWCNTs (from X-ray, SEM, TEM, IR, Raman spectroscopy, etc.) are incomplete, and severe limitations exist [10, 15, 17].

Theoretical calculations [18] are only able to produce results with high chemical accuracy (±1 kcal mol−1) for very small and simple molecular systems. Such calculations are performed at a very high level of theoretical sophistication [coupled clusters with singles, doublets and perturbative treatment of triple excitations—CCSD(T)], and using very large basis sets. In order to gain valuable insights into systems containing several or more atoms, several theoretical approximations must be made.

Accurate theoretical calculations are very expensive, and a common practice is to “cut” a small piece of a larger structure and saturate the dangling bonds with hydrogen atoms, and often to ignore intermolecular interactions (H-bonds or van der Waals), the presence of solvent, etc. The RHF method does not take into account electron correlation and is not recommended for systems with multiple bonds (aromatic rings) and lone electron pairs (OH). DFT takes into account electron correlation to some extent, and is comparable in terms of computational expense to the former method. B3LYP is the most popular and versatile density functional, and was deliberately used in our studies [19]. Thus, among the current trends, density functional theory (DFT) is one of the best compromises between accuracy and computational expense. Other approaches, including semi-empirical molecular modeling, are cheaper but less reliable. The results obtained from these theoretical tools must therefore be compared with experimental data and the results of accurate ab initio calculations.

In materials science, molecular modeling—in particular at the density functional theory level (DFT)—of structures and energies [18] provides a fairly efficient and inexpensive way of supporting future laboratory studies. For example, Morokuma and coworkers [20] studied the structures and Raman spectra of model pristine and oxidized SWCNTs, and Leszczynski and coworkers [21] conducted calculations of hydrogen atoms that were chemisorbed by armchair SWCNTs. Basiuk [22] reported on the higher reactivity of carboxylic groups toward methanol exhibited by armchair vs. zigzag functionalized SWCNTs. Denis [23] reported on the stability and the electronic properties of SH-functionalized SWCNTs. Recently, Hashemi and coworkers [24] studied the influence of end OH substitution on armchair SWCNT diameter and the subsequent atomic charges in detail. Unfortunately, they used an inferior Hartree–Fock method instead of density functional theory, which incorporates some amount of electron correlation and enables results of comparable quality to those obtained with post-HF methods (e.g., MP2 or better) to be obtained. In addition, they used a very small and unreliable basis set (STO-3G).

Raman spectroscopy is often used in studies of SWCNTs, and, in particular, the low-frequency radial breathing mode (RBM) at about 140–400 cm−1 is inversely correlated with nanotube diameter [3, 25–27].

In our recent paper, we reported on end-substituted zigzag SWCNTs with OH groups, and calculated the respective hydroxylation energies [19]. From one to nine OH substituents were considered, and the functionalized SWCNT obtained, their geometries and their energetics were analyzed.

In this paper, we report the results of our study of the structures of three models of pristine armchair (5,5) SWCNTs 3.7, 8.8, and 16.0 Å in length that were optimized at the level of B3LYP/3-21G or better, and their corresponding end-functionalized structures. From one to ten OH groups were added at one end of the nanotube, and the hydroxylation energies were calculated and compared with previously reported zigzag SWCNTs and selected small molecular systems (phenanthrene and picene). The RBM fragment of the measured Raman spectra of pristine SWCNTs was used as the reference for the theoretically predicted wavenumbers.

The paper provides insights into the OH functionalization of armchair single-wall carbon nanotubes, and indicates the possibility of functionalizing one end of the tube with 1–10 OH substituents.

Computational methods

All calculations were performed using the Gaussian 03 [28] and 09 [29] programs. Reliable B3LYP density functional and basis sets of a relatively small size (3-21G and 6-31G*) were selected, enabling fairly large-scale calculations to be performed. To facilitate these fairly large-scale calculations, we selected a model of an armchair (5,5) SWCNT with a diameter of about 6.9 Å (similar to a previously reported zigzag (9,0) SWCNT with a diameter of 7.1 Å). Full structure optimization of the unsubstituted and OH-modified SWCNTs was performed. IR and Raman harmonic frequencies were calculated. All positive frequencies indicated the ground-state structure of the optimized system. The energy of the formation of one OH group (ΔE in kcal mol−1) at the edge of the nanotube, which was initially terminated with H atoms, was calculated by considering the hypothetical reaction [19]

$$ {\text{SWCNT-H}} + \frac{1}{2} \,{{\text{O}}_{{2}}} \to {\text{SWCNT-OH}} + \Delta{E}. $$
(1)

The energies required to add subsequent groups were assumed to be calculated as follows:

$$ \Delta E = \left( {{E_{{\text{SWCNT}{{(\text{OH})}_{{n - 1}}}}}} + \frac{1}{2}{E_{{{{\text{O}}_2}}}}} \right) - {E_{{\text{SWCNT}{{(\text{OH})}_n}}}}, $$
(2)

where n = 1, 2 …10. There are many paths to go from one to ten hydroxyl groups on the rim of the tube, corresponding to “full hydroxylation.” The addition of a subsequent OH group close to the previous one would be energetically favored due to the formation of H-bonding. Therefore, we continued to replace neighboring hydrogen atoms at the nanotube rim in the calculations, leading to the estimation of the hydroxylation energy from Eq. 2.

We also considered the hydroxylation energies for model systems (picene and phenanthrene) with fully optimized planar and curved structures, cut from the SWCNTs. Despite the large energy loss due to delocalization upon ring bending (about 123 kcal mol−1 for picene calculated at B3LYP/6-31G* level), the corresponding hydroxylation energies were similar (31.7 and 36.6 kcal mol−1 for curved and planar picene models). Thus, in the subsequent text, we prefer to focus on the results obtained for fully optimized (planar) structures.

Raman measurements

A purified commercial sample of a mixture of HiPco SWCNTs [30] was used for the Raman studies. The HiPco samples were high-purity SWCNTs produced using a gas-phase CVD (chemical vapor deposition) process in the so-called HiPco process.

Micro-Raman spectra with resolution of 1 cm−1 were measured with a Dilor (Lille, France) XY 800 spectrometer at room temperature using the 514.5 nm line from an Ar laser (Spectra Physics, model 2017). More details on the experimental methods used are described in our previous work [31].

Results and discussion

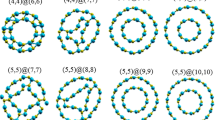
In Fig. 1, selected ideal armchair SWCNTs with three different lengths (3.7, 8.8, and 16.0 Å) are shown, all with a diameter of 6.9 Å. A similar diameter has been reported previously for model armchair SWCNTs [6, 32]. The free dangling bonds on carbon atoms are saturated with hydrogen atoms, and the corresponding molecules are labeled armchair structures A, B, and C, respectively. It is worth noticing that the corresponding zigzag tubes are significantly shorter (2.8, 7.1, and 13.5 Å).

Fig. 1
figure 1

Schematic structures (side views) and dimensions (in Å) of B3LYP/3-21 G optimized ideal armchair (5,5) SWCNTs with one (structure A), three (structure B) and six (structure C) strings of attached hexagon rings

Full size image

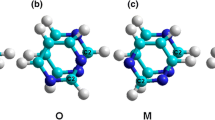
Substitution of the hydrogen atoms at one end of the SWCNT with 1–10 hydroxyl groups led to stable OH-functionalized structures. Unlike the zigzag SWCNT [19], the currently analyzed armchair has several possibilities for the arrangement of substituents at the rim. For example, there are three possible functionalization patterns for two neighboring OH groups (Fig. 2). Thus, two substituents can be positioned in two neighboring benzene rings and form a larger ring due to H-bond stabilization (seven-membered structure I), or they can be positioned ortho on the same benzene ring, forming a smaller H-bonding ring (five-membered structure II), or they can be positioned relatively far from each other on two neighboring benzene rings (structure III). The latter case is unfavorable for the formation of H-bonding. Obviously, separating the OH substituents by a significant distance will also exclude the formation of H-bonding and so, for simplicity, this situation will not be considered here. To summarize the possible H-bond structures, Table 1 provides the geometric parameters of structures I and II. According to Desiraju [33], the formation of the O–H…O bonds shown in Fig. 2 indicates fairly strong stabilization of the rings formed (Table 1).

Fig. 2
figure 2

Schematic definitions of various localizations of two substituents on an armchair (5,5) SWCNT rim. H-bonding leads to the formation of seven- and five-membered rings

Full size image
Table 1 Geometric parameters of OH bonds formed (see Fig. 2 for definitions of structures I and II)
Full size table

Three neighboring OH substituents would form adjacent larger and smaller H-bond rings (due to symmetry, the opposite case is equivalent). However, four, six and eight adjacent OH groups lead to more complex situations. Thus, for H-bonding between four substituents, three rings are formed (seven-, five-, seven- or five-, seven-, five-membered). We will arbitrarily designate the structures in which larger or smaller H-rings prevail as “L” and “S,” respectively. These structures contain two, four, six, and eight OH substituents, respectively. In addition, the label “L” corresponds to cases with equal numbers of five- and seven-membered rings where the latter rings were initially formed. Similarly, the initial formation of five-membered rings would lead to structures labeled “S.” These structures contain three, five, seven, and ten OH groups, respectively. Table 2 summarizes the number of possible variants of OH-functionalized armchair SWCNTs as a function of substituent number.

Table 2 Classification of OH-functionalized armchair structures
Full size table

Figure 3 shows B3LYP/3-21G OH-functionalized armchair nanotubes (structures C and B) with ten, four and five substituents, respectively. The calculated diameters of structures A, B and C with one end completely substituted (ten OH groups) are 7.22, 7.23, and 7.20 Å, respectively—slightly larger than the corresponding unsubstituted analogs (6.94, 6.98, and 6.93 Å). Similar diameters for pristine and end-OH-substituted armchair (5,5) SWCNTs were calculated by Hashemi and coworkers [24]. We can speculate that this small increase in diameter is caused by steric destabilization and structural rearrangement, which leads to the formation of a chain of consecutive hydrogen bonds upon the addition of 10 OH groups. It is also clear that a kind of funnel-shaped deformation occurs upon end functionalization with OH groups (Fig. 3a). The last OH group in Fig. 3b, which belongs to five-membered ring, is nearly collinear with the tube radius and is significantly less tilted in Fig. 3c. In the latter case, the last OH substituent forms a seven-membered ring. The two different patterns shown in Fig. 3b and c illustrate general geometric differences at the rims of multiply substituted armchair (5,5) SWCNTs (see also Table 2). As reported previously [24], the change in SWCNT diameter prompted by OH functionalization would change the atomic charge distribution, thus changing the reactivity of the side of the nanotube toward electrophilic and nucleophilic attack. As a result, the reactivities of functionalized and pristine SWCNTs would differ. However, we would not discuss this issue in the present study.

Fig. 3
figure 3

Side and top views of OH-functionalized armchair nanotubes: a C140H10(OH)10 with ten OH substituents, b C80H16(OH)4 with four OH substituents, and c C80H15(OH)5 with five OH substituents. All tubes show a funnel-type deformation at the rim

Full size image

As seen in Figs. 2 and 3, when one to several OH groups are attached one by one to the nanotube rim, the last substituent is tilted outwards (i.e., it protrudes outwards), and thus resembles the zigzag SWCNT [19]. The tilt angle is larger when two OH groups are attached to the same benzene ring (ortho substitution; see Figs. 2, 3).

Two types of C–C bonds are present on the “surface” of an armchair SWCNT: those perpendicular to and those tilted at some angle with respect to the tube axis (Fig. 4). Their lengths oscillate according to their positions with respect to the axis and rim. This behavior is similar to that reported previously by Zhou and coworkers [6] and Tanaka and coworkers [34]. It is evident from Fig. 4 that a model formed from three strips of carbon hexagon rings (structure B) reproduces the C–C bond lengths of larger (longer) CNTs fairly well.

Fig. 4
figure 4

The dependence of the length of the C–C bond on its position within structures A, B, and C. Selected bonds that are directed perpendicularly, and at an angle to the nanotube axis, are marked in bold

Full size image

The structures of armchair SWCNTs differ from those of zigzag ones, and their rims show different shapes. In the latter, each hydrogen atom is attached to a different hexagon (benzene) ring [19]. In the former, every two hydrogen atoms are at ortho positions on one hexagon ring. Thus, in principle, up to nine substituents—each of them attached to a different ring—could functionalize a rim of zigzag SWCNTs. Similarly, for armchair SWCNTs, one could expect ten substituents “sitting” on five hexagon rings.

To gain some insight into the energetics and substitution pattern at the nanotube rim, we will consider two smaller models first: phenanthrene and its derivative picene, as shown in Fig. 5a and b, as well as their singly and doubly substituted structures, which resemble the functionalization patterns at the SWCNT rim. Obviously, these model compounds are planar, their structures are fully optimized and do not take into account the curvature of the SWCNT. On the other hand, such models do provide some semi-quantitative information about the geometry and energetics of H-bonds formed. The other solution would be artificial bending of their structures, which we prefer to avoid. Such bending would make these models unbalanced (nanotubes with small diameters form saturated and balanced geometrical structures).

Fig. 5
figure 5

a Phenanthrene and its mono- and disubstituted OH derivatives. b Picene and its disubstituted OH derivatives

Full size image

The hydroxylation energies per single OH group for phenanthrene and picene, calculated at the B3LYP/3-21 G and 6-31G* levels, are given in Table 3. The energies calculated using a larger and more flexible basis set (6-31G*) are about 10% smaller, but the absolute trends are reproduced by the 3-21G basis set and are similar to those previously calculated for zigzag SWCNTs [19]. It is worth mentioning that adding two OH groups that form a seven-membered H-bonding pattern to phenanthrene causes a distortion (twisting) of the initially planar molecule due to the formation of H-bonds, and is energetically less favorable than the five-membered motif in which the planarity of all aromatic rings is preserved. A similar situation is observed for picene (Table 3), for which molecular planarity is even more significant.

Table 3 B3LYP-calculated hydroxylation energies for the model molecules (in kcal mol−1 per substitution)
Full size table

Replacing the first hydrogen atom with an OH group in an armchair SWCNT requires a considerable amount of energy (about 37 kcal mol−1 for structures A and B when calculated at the B3LYP/3-21G level), but adding the next group requires only slightly more energy (about 4 kcal mol−1, see Fig. 6). However, in the case of the zigzag structure, significantly more energy is required [19]. We can assume that the destabilization of the armchair nanotube rim is efficiently compensated for by the formation of a hydrogen bond that stabilizes the structure. As result, upon adding 2–9 OH groups, we observe roughly the same energy cost (a kind of plateau is formed; see Fig. 6). However, closing a loop of substituents requires more energy. Besides, adding substituents to a shorter nanotube (structure A, Fig. 6a) produces a less scattered energy pattern than adding them to a longer nanotube (structure B, Fig. 6b). This kind of energy pattern also supports the importance of H-bond formation. In addition, in contrast to planar model molecules (see Fig. 6 for picene), the initial shape of a SWCNT is curved, and no energy is needed for the molecular plane twisting required to produce efficient H-bonding. Picene was taken as a very crude model of an armchair SWCNT, and for the corresponding S structure we placed 1–4 OH groups at carbons 5, 6, 7 and 8, respectively. In a similar manner, OH substituents were placed at carbons 1, 14, 13, and 12 for structure L. We want to stress that in Fig. 6, the differences in energy according to Eq. 2, or the relative values, are shown. Thus, each point n shows the amount of energy needed to introduce one OH group into a structure containing (n − 1) OH substituents. Note that for ten OH groups, there is only one structure (and total energy), but there will be two different numbers due to the different energies of the L and S structures containing nine OH substituents.

Fig. 6
figure 6

Dependence of the hydroxylation energy for structures A and B of armchair SWCNTs (in kcal mol−1 per single OH group, calculated at the B3LYP/3-21G level) on the number of substituents for L/S functionalization (to improve visualization, the data points are connected). The energy values represent relative energies according to Eq. 2. Results for picene are included for comparison

Full size image

We also examined the effect of the basis set size on the absolute value of hydroxylation energy. It is evident from Fig. 7 that the absolute value of hydroxylation energy per single OH group calculated using the larger basis set (6-31G*) is about 5–8 kcal mol−1 lower than that obtained using the 3-21G basis set. Obviously, the ΔE values obtained with the smaller basis set (3-21G) differ, and are generally considered less accurate (and describe the energy landscape more roughly), but the overall qualitative pattern observed for both basis sets is the same. The above result is very important, as it shows that reliable calculations can be conducted on larger molecular systems.

Fig. 7
figure 7

Dependence of the B3LYP-predicted absolute hydroxylation energy for armchair SWCNT OH functionalization (structure B, in kcal mol−1 per single OH group) on the number of OH groups added, when small and medium-sized basis sets (3-21 G and 6-31 G*) are employed for the calculations. The data points are connected in order to improve visualization

Full size image

Figure 8a and b compare the hydroxylation energies calculated via B3LYP/3-21G per OH substituent for zigzag [19] and armchair SWCNTs. L and S H-bonding patterns were considered for armchair functionalization, and both are notably below the corresponding zigzag energies. As mentioned before, the scatter in the energy difference (ΔE) for armchair SWCNTs is due to the formation of structures I or II (see Fig. 2).

Fig. 8
figure 8

Comparison of the absolute hydroxylation energies for zigzag [19] and armchair SWCNT OH functionalization (in kcal mol−1 per single OH group) predicted using B3LYP/3-21G. SWCNTs of different lengths were selected, and both L and S patterns of H-bonding were considered. The data points are connected in order to improve visualization

Full size image

In the last stage of our study, we checked the quality of our DFT calculations by comparing those results with some experimental results. A comparison of DFT-calculated and measured Raman spectra of SWCNTs provides an indirect test of the proposed theoretical strategy, including structural and vibrational studies of models A, B and C. Thus, below we briefly analyze the selected harmonic vibrations and compare them with measured Raman spectra of pristine SWCNTs.

The most characteristic feature of the Raman spectra of SWCNTs is a collective skeleton vibration called the radial breathing mode (RBM), which is assumed to be inversely proportional to their radius [3, 25–27, 35]. This kind of vibrational mode originates from the symmetric movement of all carbon atoms along the radius, and can be visualized as a form of tube breathing. Thus, Fig. 9 presents a fragment of the Raman spectrum of a commercial sample containing SWCNTs with different diameters (d), showing several peaks in the RBM region. The commercial HiPco sample is a mixture of SWCNTs with different diameters (and lengths), and it is apparent that the contents of the tubes (as characterized by their diameters) are reflected in the fitted intensities (dotted lines in Fig. 9). The most intense peaks are 3 and 1. On the other hand, peak intensities systematically decrease, forming a long tail toward higher wavelengths.

Fig. 9
figure 9

Raman spectrum of purified SWCNTs in the RBM region. Individual peaks correspond to nanotubes with different diameters

Full size image

Several empirical formulae for estimating the radius of an SWCNT from its observed RBM have been reported [3, 25–27, 35]. For example,

$$ \nu \left( {\text{RBM}} \right) = {A}/{\text{d}}, $$
(3)

where A = 227, was suggested in [36]. For small-diameter SWCNTs (<1.4 nm), a slightly different formula was reported [26]:

$$ \nu \left( {\text{RBM}} \right) = {A}/{\text{d}} + {15}, $$
(4)

where A = 219.

The estimated SWCNT diameters determined from the positions of the peaks (Raman frequencies) in Fig. 9 are gathered in Table 4. The SWCNT diameters were calculated according to Eq. 3.

Table 4 SWCNT diameters (d) estimated from the Raman radial breathing mode (RBM; in cm−1) for peaks observed in Fig. 9
Full size table

We now discuss in detail the RBM position calculated at the B3LYP/6-31G* level for initial structure B (a medium-length SWCNT without any OH groups) and its derivatives containing one, two and ten OH substituents. The frequencies of this characteristic vibration are 318.06, 318.50, 319.26, and 344.27 cm−1 for structure B and its derivatives, respectively, and their Raman activities are 26.03, 16.36, 12.58 and 110.61 A4/AMU. According to Eq. 3, for our pristine SWCNT (0.69 nm in diameter), we should observe a Raman peak at 329 cm−1 (see Table 4). Thus, the DFT-calculated position of this vibration is fairly accurate, and differs by only 11 cm−1 from the empirical results. Similar agreement between the RBM values obtained from B3LYP calculations for zigzag (9,0) SWCNTs [19] and estimated from Eq. 3 is evident from Table 4. It is worth noting that, starting from 1.05 nm, as the carbon nanotubes decrease in diameter their contributions become fairly small. Thus, our experimental RBM pattern cannot prove the presence of nanotubes with diameters of about 0.7 nm, as used in our molecular modeling.

Also, the observed Raman spectrum in Fig. 9 originates from a sample of pristine SWCNTs. On the other hand, on the basis of our DFT calculations presented above, it is evident that the positions of RBM peaks should not shift significantly upon hydroxylation. This can be explained by the fact that the presence of OH groups at the ends of (long) nanotubes only distorts the rim geometry; their presence does not affect the rest of the tube (the interior part further from the end).

We also note that upon increasing the number of substitutions, the intensity of the RBM in the experimental Raman spectrum initially decreases due to a decrease in symmetry. However, full substitution (with ten OH groups) produces significantly more intense vibrations than the pristine nanotube.

Conclusions

The present density functional theory studies using B3LYP/3-21G and B3LYP/6-31G* calculations indicate that it is possible to OH functionalize one end of an armchair SWCNT with 1–10 substituents. The hydroxylation energy per OH group is about 10 kcal mol−1 lower than for a zigzag SWCNT. This result suggests a significantly higher reactivity toward OH functionalization of armchair vs. zigzag SWCNTs. Functionalization with ten OH groups increases the rim diameter from 6.9 (in pristine CNT) to 7.2 Å, and shifts the RBM mode from 318 to 344 cm−1. The intensity of this diagnostic Raman vibration increases about fivefold.