Abstract
We investigate algebraic multigrid (AMG) methods for the linear systems arising from the discretization of Navier–Stokes equations via the finite pointset method. In the segregated approach, three pressure systems and one velocity system need to be solved. In the coupled approach, one of the pressure systems is coupled with the velocity system, leading to a coupled velocity-pressure saddle point system. The discretization of the differential operators used in FPM leads to non-symmetric matrices that do not have the M-matrix property. Even though the theoretical framework for many AMG methods requires these properties, our AMG methods can be successfully applied to these matrices and show a robust and scalable convergence when compared to a BiCGStab(2) solver.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the past years, meshfree methods have gained an increasing popularity in computational science and engineering, as they offer a number of advantages over mesh-based methods. For instance, the time-consuming and not completely automatable generation of meshes is avoided. This is especially beneficial in transient simulations, where the computational domain may change from time step to time step, for example due to geometry movement, free surface evolution in multi-phase flow simulations, or topology changes. Mesh-based techniques need to re-mesh in such situations, while meshfree methods that do not rely on a fixed connectivity structure can naturally adapt themselves to the new situation.
The finite pointset method (FPM) [7] is a meshfree method for the approximation of continuum mechanics equations. It employs a moving point cloud to discretize the partial differential equations using generalized finite differences (GFDM). The points are mass-less, so they may be deleted or inserted as needed to resolve the computational domain to the desired accuracy, while the differential operators are set up using an automated differentiation procedure. However, the resulting linear systems may be very ill-conditioned. A thorough description of FPM including the latest developments can be found in [17].
Algebraic multigrid (AMG) methods provide robust and scalable linear solvers for a wide class of problems. They are in principle a natural choice for meshfree discretizations since the intrinsic “multigrid” hierarchy is constructed automatically. However many AMG heuristics assume that the system matrix is a symmetric M-matrix (or at least is not “too far” from one, i.e. negative off-diagonal entries should dominate the positive ones). The matrices produced by FPM do not fall within this category. They are non-symmetric even for self-adjoint operators, and the automatic differentiation mechanism produces mixed-signed matrix rows. Furthermore, FPM not only discretizes scalar elliptic PDEs, but also systems of elliptic equations or even saddle point systems.
Several approaches have been proposed [14] to construct FPM stencils such that the resulting matrices at least possess the M-matrix property. These approaches introduce strong restrictions on the point cloud geometry of boundary conditions. Thus, in general, the resulting linear systems are not M-matrices and the linear solver must be applicable to non-M-matrices.
In Sect. 2, we give an introduction to FPM. In Sect. 3, we briefly recapitulate the algebraic multigrid method and describe our AMG techniques to solve the matrices produced by FPM, while we demonstrate their applicability in Sect. 4. Finally, we give some remarks in Sect. 5.
2 The finite pointset method
In this section, we introduce the finite pointset method. In particular, we focus on the derivation of the linear systems that need to be solved. We refer to [7] for a more detailed description, especially for all aspects not mentioned here such as the point cloud management.
2.1 Equations to be solved
The fluid flow is modeled by three conservation equations, which describe the relation between the velocity \(\mathbf {v} = (u, v, w)^T\), the pressure p, and the temperature T. Let
denote the material derivative, which models the change of a physical property along the trajectory of a fluid particle. As the material derivative is “naturally” represented by FPM’s discretization technique, we will employ this operator wherever a time derivative is involved. For the scope of this paper, we restrict ourselves to the case of incompressible fluids. In particular, we have constant density along the path of a fluid particle \((\frac{d}{dt} \rho = 0)\).
The three conservation equations are:
-
The conservation of momentum, which is given by
$$\begin{aligned} \frac{d}{dt} \left( \rho \mathbf {v} \right) = \left( \nabla ^T S \right) ^T - \nabla p + \rho g \end{aligned}$$(2)where \(\rho \) denotes the density, S is the stress tensor (see below), and g contains the external body forces.
-
The conservation of mass, which is enforced by the continuity equation
$$\begin{aligned} \nabla ^T \cdot \rho \mathbf {v} = 0 \end{aligned}$$(3) -
The conservation of energy, which is controlled by the temperature equation
$$\begin{aligned} \begin{aligned} ( \rho c_V ) \frac{d}{dt} T ={}&\nabla ^T ( S \cdot \mathbf {v} )- ( \nabla ^T S ) \cdot \mathbf {v} \\&- p (\nabla ^T \mathbf {v}) + \nabla ^T ( k \nabla T ) + q \end{aligned} \end{aligned}$$(4)where T denotes the temperature, k the heat conductivity, and \(c_v\) the heat capacity.
Within the scope of this paper, we limit ourselves to the case of viscous stress tensors,
where \(\eta \) denotes the viscosity of the fluid, and
is the strain rate tensor. Equation (2) hence can be re-written as
Before we turn ourselves to the discretized counterparts of the Eqs. (2) and (3), we first describe the FPM discretization technique.
2.2 Organization of the point cloud
For each phase (water, air, oil, etc.) a separate point cloud \(\mathcal {P} = \left\{ \mathbf {x_i} \right\} \) is defined. The density of the point cloud is determined by the smoothing length \(h = h(\mathbf {x}, t)\), which can be given as a function of space and time (but is constant per phase in most applications). Via this parameter, the resolution of the discretized problems is steered.
In order to discretize the differential operators, the computational domain needs to be covered by balls of radius \(r_{\text {hole}} \cdot h\) around each point. However, points may not be too close to each other, i.e. they have to keep a minimum distance of \(r_{\text {min}} \cdot h\). Typical values of \(r_{\text {hole}}=0.45\) and \(r_{\text {min}} \in [0.1,0.2]\). This leads to a point cloud where between 20 and 50 points can be found within each ball of radius h (independent of h). The boundaries of the domain are also filled with points, see Sect. 2.5.
2.3 Construction of differential operators
The differential operators are discretized using generalized finite differences defined via the points \(\mathbf {x}_i\), \(i=1,\ldots ,N\) of the cloud. The method is very similar to the Moving Least Squares method (MLS) by Lancaster and Salkauskas [8]. For each physical quantity f, we identify its value at the point \(\mathbf {x}_i\),
and let the derivatives be approximated by sums of the form
where \(*\) denotes the desired derivative, e.g. \(*=0\) (function evaluation), \(*=x\) (first derivative in x-direction), \(*=\varDelta \) (Laplacian). \(N_i\) is the neighborhood of point \(\mathbf {x}_i\) consisting of the nearest points \(\mathbf {x}_j\) within a ball of radius h around \(\mathbf {x}_i\). The set \(N_i\) must be large enough such that all derivatives needed for the PDE’s discretization can be set up, we usually have \(\vert N_i \vert = 40\) for second order PDEs. Note that the relation \(j \in N_i\) is not symmetric.
The coefficients \(c^{*}_{ij}\) need to be independent of f to avoid expensive computations, thus, we compute them such that they exactly reproduce the considered differential operator for monomials up to a certain (typically: second) order.
We therefore define, for each point \(\mathbf {x}_i\), a set of M discrete test vectors \( \left( k^m_i \right) _{m=1}^M\), where each \(k^m_i = \left( k^m_{i,j} \right) _{j \in N_i}\) represents the discretization of a test function (monomial) within the neighborhood \(N_i\), while \(b_{i,m}^{*}\) contains the value of its derivative \(*\) at the point \(\mathbf {x}_i\). In this terms, the requirements of exact differentiation for the test functions translates to
or, in matrix form,
where the m-th row of \(K^T_i\) consists of the entries \(\left( k^m_{i,j} \right) _{j \in N_i}\), and the vectors \(b_i^{*}\) and \(c^{*}_i\) are given by \(b_i^{*} = \left( b_{i,m}^{*} \right) _{m=1}^M\) and \(c^{*}_i = \left( c_{ij}^{*} \right) _{j \in N_i}\). Furthermore, the distance of the points should be taken into account. To this end, we introduce a weight function,
where the distance function \(r_{i,j}\) is given by
We group, for each i, the weights into a diagonal matrix
where \(w_{i,j} = w(r_{i,j}) = w(r(\mathbf {x}_i,\mathbf {x}_j))\). With the aid of the matrices \(K_i\) and \(W_i\), we formulate the conditions for \(c_i^{*}\) in a least-squares sense, i.e.
We solve these small least-squares systems for each point \(\mathbf {x}_i\) directly and construct the discretized differential operator (9).
Note that at the boundary we can use the same ideas as in the interior of the domain: For Dirichlet boundaries, we set the central stencil value \(c_{ii} ^\text {D} = 1\) and the other stencil values to 0. For Neumann boundary conditions, we need to compute the normal based on the neighbors that are also boundary points and then solve a least squares problem in order to find a discretization of the normal derivative. See [17] for more details on boundary conditions.
2.4 FPM discretization of the conservation laws
In this section, we describe the implicit Euler time stepping scheme used to solve the partial differential equations introduced in Sect. 2.1. We present two different methods: First, the segregated approach, where the velocity is computed using a Chorin projection-like ansatz, and the coupled approach, where a divergence-free velocity field is computed directly by the solution of a saddle point system.
The finite pointset method employs a Lagrangian approach, i.e. the points move with the velocity field \(\mathbf {v}\). This allows us to approximate material derivative of the velocity at the i-th point by
where the superscript n is used to indicate a quantity at a specific time step n.
We integrate the momentum equation (7) for each particle \(\mathbf {x}_i\) and obtain
where \(\frac{d\epsilon }{dt}\big \vert _{n+1}\) denotes the evaluation of the strain rate tensor at time step \(n+1\). In the following, we omit the point coordinates \((\mathbf {x}^n_i)\).
From (6), we know that \(\frac{d\epsilon }{dt}\) only depends on \(\mathbf {v}\) and its derivatives, hence we define
(For example, for incompressible flow with constant viscosity, we have \(\varPsi _{\eta } (\mathbf {v}) = \nabla ^T \left( \eta \nabla \mathbf {v} \right) \).)
We now re-organize (18) such that all terms referring to time step \(n+1\) move to the left hand side, while the terms depending on time step n are on the right hand side. At this point, in the segregated approach we need to replace \(p^{n+1}\) by an intermediate pressure \(\hat{p}\). In consequence, we only solve for a velocity predictor \(\hat{\mathbf {v}}^{n+1}\) here,
The spatial discretization of this equation yields a sparse linear system of equations \(\mathbf {A} \hat{\mathbf {v}}^{n+1}_h = \mathbf {f}_h\). The velocity solution \(\hat{\mathbf {v}}^{n+1}\) of (20) does not yet satisfy the continuity equation for incompressible fluids,
and also does not take into account the pressure at the new time step \(p^{n+1}\).
To this end, let us reconsider (20) and replace \(\hat{p}\) by the corrected pressure \(p^{n+1} = \hat{p} + p_{\text {corr}}\) as well as the predicted velocity \(\hat{\mathbf {v}}\) by the corrected velocity \(v^{n+1}\),
Subtracting (20) from (22) and taking the divergence yields
We assume that we can neglect the viscous term
if the time step is small enough. In addition, for incompressible flow we require \(\nabla ^T \mathbf {v}^{n+1} = 0\). It remains to solve the Poisson equation
and use the gradient of the pressure correction \(p_{\text {corr}}^{n+1}\) to update the velocity field.
A drawback of the segregated approach is the lack of accuracy in the case of low Reynolds numbers, i.e. when the magnitude of the term \(\varPsi _{\eta } ( \mathbf {v}^{n+1} - \hat{\mathbf {v}}^{n+1} )\) would require time steps that are too small to allow for an effective simulation, see e.g. [18] and the references therein for a detailed discussion. An option to overcome this problem is to solve for velocity and correction pressure in one single linear solve (coupled approach). The correction pressure then serves as a Lagrangian multiplier, i.e. we solve the saddle point system
or, in matrix form,
The virtual time step \(\varDelta t_{\text {virt}}\) is chosen as a fraction of the time step \(\varDelta t\). Theoretically, the best possible value is \(\varDelta t_{\text {virt}} = 0\), but smaller values make the linear system harder to solve.
While the coupled approach is more generally applicable than the segregated approach, it also takes more computational efforts. In Sect. 4.2 we give an example where the segregated approach fails, while the coupled approach produces a valid solution.
Regardless whether approach is used, we need an intermediate pressure \(\hat{p}\). To this end, we take the divergence of the momentum equation (2),
and split the pressure into two parts \(p^{n+1} = p^{n+1}_{\text {hyd}} + p^{n+1}_{\text {dyn}}\). First, we formulate the equation for the hydrostatic pressure \(p^{n+1}_{\text {hyd}}\),
which can be computed without knowing the new velocity \(\mathbf {v}^{n+1}\). In contrast, to update the dynamic pressure via
the updated velocity \(\mathbf {v}^{n+1}\) is needed. Hence, in (20) we use \(\hat{p} = p_{\text {hyd}}^{n+1} + p_{\text {dyn}}^n\), i.e. we use the dynamic pressure from the previous time step and the hydrostatic pressure of the current time step.
The discrete form of (29), (30) and (24) lead to scalar linear systems of the form \(D p_h = f_h\). If the same boundary conditions are enforced, the matrices are equal within a time step.
Finally, the new temperature \(T^{n+1}\) needs to be determined. As for velocity and pressure, we use an implicit scheme,
The right hand side \(\hat{q}\) only depends on quantities known at this stage. For the left hand side, we introduce \(I_T - \varTheta _T = (\rho c_V ) - \varDelta t \nabla ^T \cdot ( k \nabla )\) and obtain the heat equation
To conclude this section, we recapitulate the equations we need to solve in every time step,
-
1.
Compute the hydrostatic pressure \(p^{n+1}_{\text {hyd}}\) according to (29),
-
2.
Set \(\hat{p} = p^{n+1}_{\text {hyd}} + p^{n}_{\text {dyn}}\) and compute the new velocity field \(\mathbf {v}^{n+1}\) as well as the correction pressure \(p^{n+1}_{\text {corr}}\),
-
either by the segregated approach: First compute the velocity predictor (20), then solve the Poisson equation (24),
-
or by the coupled approach: Solve the saddle point system (27).
In both cases, use the gradient of \(p^{n+1}_{\text {corr}}\) to correct the velocity.
-
-
3.
Compute the dynamic pressure \(p^{n+1}_{\text {dyn}}\) according to (30).
-
4.
Update the temperature using (32).
Now that the velocity and pressure values are known, we use the velocity field to move the point cloud, re-organize it where necessary and start the next time step. Note that we do not need to solve a non-linear equation in the whole solution process, the non-linearity is absorbed in the splitting of the pressure (the right hand side of (30) depends non-linearly on the velocity). Instead, we need to solve three (segregated) or two (coupled) scalar Poisson-like equations as well as a three-dimensional elliptic system (segregated) or a four-dimensional saddle point system (coupled). In practice, the temperature equation as well as the vectorial velocity equation in the segregated approach can be solved easily using an one-level method like BiCGStab(2) [15]. In the next section, we hence focus on the solution of the Poisson-like pressure equations and the saddle point systems using AMG.
2.5 Matrix properties
The matrices constructed by the finite pointset method differ in several aspects from more common finite difference, finite volume, or finite element discretization. First, as already pointed out in [14], this discretization leads to non-symmetric matrices even for symmetric operators like the Laplacian as the point neighborhood relation is not symmetric, see Sect. 2.3. In addition, FPM employs a row-wise scaling of the matrix such that the diagonals are normalized to one.
Furthermore, the least-squares approach generally does not guarantee that all off-diagonal matrix entries are non-positive. Suchde [17, section 2.5.5] describes a method to improve the diagonal dominance of the matrix, which in turn makes positive off-diagonal coefficients less likely, but still it is not guaranteed that no positive off-diagonal coefficients occur. This means that not only will the matrix be non-symmetric, but it also will not have the M-matrix property. Both symmetry and the M-matrix property are building blocks of most AMG convergence theories, although there has also been work on convergence theories for non-symmetric M-matrices, e.g. [10, 11].
To the best of the authors’ knowledge, there is no method to overcome the non-symmetry of the matrix. The M-matrix property on the other hand can be ensured by using the method described in [14], which uses a linear minimization approach instead of the least-squares approach presented in Sect. 2.3. This method ensures the M-matrix property, and, in addition it yields minimal stencils, i.e. stencils that have a minimal number of entries among all consistent stencils. The numerical results in [14] show that the improvements in performance of the considered AMG algorithm mostly are a consequence of the increased sparsity of the matrix, rather than a consequence of the M-matrix property. Since the linear minimization approach needs additional work in the point cloud organization and is not as general applicable as the least-squares approach in terms of boundary conditions and conditions on the point cloud, we based this work on the least-squares approach.
The boundary conditions of the partial differential equations are not eliminated from the system. For each boundary point \(\mathbf {x}_i\) and its associated degrees of freedom, the matrix row represents the respective boundary condition discretized using the techniques described in Sect. 2.3.
3 AMG for FPM
3.1 Algebraic multigrid
In this section, we briefly recapitulate the basic Ruge–Stüben AMG algorithm [16]. Suppose the linear system is given as
where \(A \in \mathbb {R}^{N \times N}\), and \(u, v \in \mathbb {R}^N\).
The key AMG idea is to automatically construct a multigrid hierarchy, that is, a hierarchy of coarse grids \(\varOmega _l\), interpolation operators \(I_l\), and coarse grid operators \(A_l\) based on the fine grid matrix \(A_1 = A\) and the initial “grid” (index set) \(\varOmega _1=\{1,\ldots ,N\}\).
In any multigrid method, the coarse grid correction must reduce the error components not efficiently damped by the smoother \(M_l\). Common choices for the smoother are Jacobi, Gauss–Seidel, or (S)SOR relaxation. For symmetric positive definite M-matrices \(A_l\), the smooth error (i.e. the error components e that remain after a few iterations, \(M_l e \approx e\)) can be characterized using the matrix \(A_l\): A smooth error only varies slightly along large off-diagonal negative couplings \(a_{ij}\). We hence define, for each index \(i \in \varOmega _l\), the set \(\mathcal {S}_i\) of strong couplings by identifying all i for which the negative respective matrix coupling \(a_{ij}\) exceeds a certain threshold,
The strong couplings define the edges of a graph whose nodes are given by \(\varOmega _l\). We then determine a maximal independent set (the coarse grid points) \(\mathcal {C}_l \subset \varOmega _l\) such that each fine grid point \(i \in \mathcal {F}_l = \varOmega _l {\setminus } \mathcal {C}_l\) is strongly connected to at least one coarse grid point \(j \in \mathcal {C}_l\). Then, we build the interpolation operator \(I_l\) row by row using standard interpolation, such that each value at point \(i \in \mathcal {F}_l\) is interpolated from the values at (directly or indirectly) strongly connected coarse grid points around i. The resulting interpolation row is truncated to avoid large stencils: All entries that are smaller (by absolute value) than a factor \(\epsilon _{tr}\) of the largest entry are dropped and the interpolation row is re-scaled such that its row sum remains unchanged.
The set \(C_l\) serves as coarse mesh \(\varOmega _{l+1}\), while the coarse level matrix is computed by the Galerkin product,
with \(I_l^T\) being the restriction operator.
We apply this procedure recursively until the size of the matrix is reasonable small for direct solution. Then, we can start the usual V-cycle.
-
1.
Smooth the error by applying \(\nu _1\) iterations of a relaxation operator \(M_l\) to the current approximation \(u_l ^n\):
$$\begin{aligned} \tilde{u}_l ^n = M_l^{\nu _1} u_l ^n \end{aligned}$$(36) -
2.
Compute and restrict the residual to the coarse level:
$$\begin{aligned} r_{l+1} = I_l^T \left( f_l - A_l \tilde{u}_l ^n \right) \end{aligned}$$(37) -
3.
Solve the coarse level equation either recursively or directly:
$$\begin{aligned} e_{l+1} = A_{l+1} ^{-1} r_{l+1} \end{aligned}$$(38) -
4.
Interpolate the computed correction back to the fine level:
$$\begin{aligned} e_l = I_l e_{l+1} \end{aligned}$$(39) -
5.
Apply the correction and another \(\nu _2\) iterations of the relaxation:
$$\begin{aligned} u_l ^{n+1} = u_l^{\nu _2} \left( \tilde{u}_l ^n + e_l \right) \end{aligned}$$(40) -
6.
Continue with step 1 until the approximation \(u_l ^{n+1}\) fulfills a specified termination criterion.
3.2 AMG for the Poisson equations in FPM
For the Poisson equations (29), (26), and (30), we employ standard AMG coarsening as well as standard interpolation. To improve the performance of our AMG method, we use an aggressive coarsening technique on the first level. Aggressive coarsening reduces the number of coarse level points by extending the definition of strong couplings to long-range strong couplings, that is, each fine grid point \(i \in \mathcal {F}_l\) is not required to be directly coupled to a coarse grid point \(j \in \mathcal {C}_l\), but, in the graph of strong connections, has one a path of at most length 2 to a coarse grid point. Interpolation (the so-called multi-pass interpolation) then also follows these paths, see [16, Section 7.1.2] for details.
In our numerical experiments, the non-symmetry of the problem as well as the positive couplings did not produce any difficulties here. We need however take care of the decomposition of the linear system into disconnected subsystems: The point cloud may disintegrate into smaller sub-clouds, not only due to the discrete geometry (separate isolated domains), but also resulting from splashes that move away from the main part of the fluid. In particular, the modeling of these splashes may involve all-Neumann boundary conditions, which leads to singular linear systems. As the splashes are small (typically \(<100\) points), we employ a direct linear solver here that produces a solution perpendicular to the constant kernel vector.
As the two (or three) pressure systems computed in each time step share the same matrix if the boundary conditions are not changed, the AMG setup can be re-used.
3.3 AMG for coupled velocity-pressure equations
For the coupled saddle point systems, standard AMG techniques cannot be applied directly. The resulting matrix
is neither definite nor diagonally dominant. Thus, the usual relaxation schemes (Jacobi, Gauss–Seidel) cannot be used. Instead, we employ an inexact Uzawa scheme [13]
Here, \(\hat{\mathbf {A}}\) denotes the diagonal of \(\mathbf {A}\) scaled such that \(\hat{\mathbf {A}} - \mathbf {A}\) is positive definite. The diagonal matrix \(\hat{S}\) is formed such that \(\hat{S} - C \hat{\mathbf {A}}^{-1} B -D\) is positive definite.
There are many approaches to AMG for systems of equations, see [2] for an overview. We employ unknown-based AMG[12] to construct coarse grids and interpolation operators for the three velocity components as well as the pressure component separately . Let us decompose \(\mathcal {K}\) by the velocity components u, v, w, and the pressure p,
where each block \(X_{yz}\) describes the connections between the (scalar) unknowns y and z. Now, for each of the unknowns u, v, w, and p, we use the corresponding diagonal block \(A_{uu}\), \(A_{vv}\), \(A_{ww}\), \(D_{pp} = D\) and obtain interpolation operators \(I_u\), \(I_v\), \(I_w\), and \(I_p\), respectively, so that the overall interpolation operator takes the block-diagonal form
In the case of non-constant viscosity \(\eta \), the off-diagonal velocity matrix blocks \(A_{xy}\), \(x \ne y\) can also contain significant non-zero entries. In this case, simple unknown-based AMG might not be sufficient and a pre-processing of the matrix on the finest level is needed: We use the alternate-block-factorization idea [1]. To this end, let us re-order the matrix \(\mathcal {K}\) by the discretization points,
where each small matrix \(\tilde{K} \in \mathbb {R}^{4 \times 4}\) represents the couplings between point i and point j,
We scale \(\mathcal {K}\) from the left using a block diagonal matrix, where each diagonal block takes the form
Hence, all cross-velocity couplings inside a point are eliminated. We obtain (now re-ordering the system back by unknowns) the linear system
Now, we apply unknown-based AMG to the block-scaled matrix \(\mathcal {\bar{K}}\). (Note that the off-diagonal blocks \(\bar{A}_{xy}, x \ne y\), are not necessarily empty but are ignored for coarse grid and interpolation construction.)
In the case of small virtual time steps (\(\varDelta t_{\text {virt}} < 0.1 \varDelta t\)), the approach described above is not sufficient. In this case, the entries of D become relatively small and it is no longer possible to ignore the sub-matrices B and C in the AMG setup. To take these into account, we use the saddle point AMG method introduced in [9]. The propagation of the respective errors \(\mathbf {e_v}\) and \(e_p\) of the velocity and the pressure during each Uzawa iteration step (42)–(44) is expressed by
An efficient AMG method needs to reduce the error components that cannot be quickly damped by the smoother. The rightmost factor in Eq. (51) suggests that the error propagation of the Uzawa method is, at least partly, described by a Jacobi-like iteration using the matrix
This heuristically motivates us to use the matrices \(\mathbf {A}\) and \(C \hat{\mathbf {A}}^{-1} B + D\) to build the coarse spaces and interpolation operators for velocity and pressure, respectively. As B represents the gradient operator, and C the divergence operator, the approximate Schur complement \(C \hat{\mathbf {A}}^{-1} B\) – like D – has the characteristics of a discretized Poisson operator and hence can be used to build the coarse grid and interpolation for the pressure. For the velocity components, as before we use the diagonal blocks \(A_{uu}\), \(A_{vv}\), and \(A_{ww}\) (or \(\bar{A}_{uu}\), \(\bar{A}_{vv}\), and \(\bar{A}_{ww}\) if the alternate block factorization is employed on the first level) to construct the coarse grids and interpolation operators for each of the velocity components. Again, we obtain an interpolation operator of the form (46).
We can optionally enhance the quality of the interpolation by an additional stabilization factor. To this end, let us sort the velocity variables (regardless whether they belong to u, v, or w) by coarse and fine grid points
and, correspondingly, re-write \(\mathcal {K}\),
as well as (46),
Now, we compute the F-stabilized interpolation by [9]
This interpolation operator is no longer block-diagonal and requires more memory than (46). Its advantage is the increased stability, i.e. the coarse grid operator
satisfies an inf-sup-condition if the fine grid operator \(\mathcal {K}\) satisfies one, see Lemma 4.6 in [9] for details. In contrast, if we just use the block diagonal interpolation operator (46), the coarse grid matrix may even become singular depending on the interplay between the coarse velocity and pressure spaces.
4 Numerical results
The following benchmarks were carried out on compute nodes with Intel(R) Xeon(R) E5-2660 processors running at 2.20 GHz and 16 GB of memory. We used the SAMG library developed at Fraunhofer SCAI, which implements a number of AMG components. We used the FPM implementation developed at Fraunhofer ITWM. This implementation uses a BiCGStab(2) solver by default, hence this serves as baseline for our experiments. Note that the matrices generated by the FPM discretization are normalized, i.e. scaled such that their diagonal entries equal one, so no additional Jacobi preconditioning is employed. For the scalar pressure systems, in our AMG experiments we use a V(1, 1) cycle with Gauss–Seidel (or, in the parallel case, hybrid Jacobi/Gauss–Seidel) smoothing as a preconditioner for a classical BiCGStab method. In case of the coupled velocity-pressure equations, we use Uzawa smoothing (42)–(44) on every level and use AMG as a preconditioner for GMRES(30) unless stated otherwise. The iteration is stopped if the \(l^1\) norm of the residual vector r satisfies
where s is a scaling vector provided by FPM. It is chosen so that the scaled residual represents a measure for the error reduction in the gradient of the function that is being solved for rather than the values of the function themselves. It also accounts for jumping coefficients in the physical properties of the model, e.g. jumping thermal diffusivity at material interfaces. As a result, the error is reduced evenly across the whole domain, even in very heterogeneous situations.
We employ classical Ruge–Stüben coarsening and standard interpolation on all levels, except on the first (finest) level, where aggressive coarsening and multi-pass interpolation are used (see Sect. 3.2). We truncate the interpolation at \(\epsilon _{tr} =0.2\) to avoid too large interpolation stencils. In both the segregated and the coupled approach we ignore all positive couplings and use \(\alpha = 0.25\) in the definition of strong couplings (34) for scalar (pressure) systems. We terminate the coarsening if the number variables drops below \(100 \cdot \sqrt{np}\), where np denotes the number of processes, and use a direct solver on the coarsest level.
4.1 Coarsening compared to finite differences
The stencils produced by FPM’s discretization technique are quite denser than those produced by usual FD, FE, or FV discretizations of Poisson-like problems. We investigate the impact of this property by comparing a 9-point finite difference discretization of a Laplacian equation on a unit 3D cube with Dirichlet boundary conditions to the hydrostatic pressure system (29) on the same cube discretized using FPM. For the finite differences stencil case, we use a random right hand side for the linear system and for the FPM cube we use the right hand side induced by gravity in the hydrostatic pressure system. In both cases, we reduce the residual by 8 orders of magnitude. For the finite differences discretization, we choose a \(40\times 40 \times 40\)-grid, leading to exactly 64k matrix rows. For the generalized finite difference method (GFDM) used in FPM, we cannot prescribe an exact number of points / matrix rows. We choose a smoothing length of \(h=0.07\) to obtain \(\approx \,\hbox {67k}\) points.
Tables 1 and 2 show that the effect of the aggressive coarsening strategy is very similar in both discretizations: The setup time and the time per cycle is reduced at the cost of some extra cycles. Furthermore, the numbers of iterations as well as the time per iteration are very comparable.
A larger key difference can however is in the complexities. These give an indication of the memory overhead of the AMG hierarchy compared to the fine grid matrix. To this end, we introduce the operator complexity
where \(nz(A_l)\) is the number of non-zero elements of the matrix \(A_l\), the grid complexity
and, in addition, compare the average number of non-zero entries per row throughout the multigrid hierarchies.
Since the GFDM matrix has a lot of strong couplings, the coarsening is a lot faster than in the FD case. Note that we limit the number of neighbors for interior points to 40 and those are chosen based on their distance to the central point, preferring points that are closer to the central point. Because of the weights in the least squares problem, these points have quite strong couplings to the central point, resulting in a fast coarsening rate, as can be seen from the operator and grid complexities in Tables 1 and 2 For the 9-point stencil, the standard coarsening yields a coarsening rate of exactly 0.5 on the first level, whereas for the GFDM discretization it yields 0.06, which means in the latter case, the second level already has one order of magnitude less rows than in the FD case. Note however that the costs per cycle are the same in both cases because the FD matrices are a lot more sparse. This is not only true for the fine level matrix, but for the hierarchy of matrices as a whole as well: The average number of non-zero coefficients per matrix row across all levels is about a factor 4–6 higher in the FPM case. Still, AMG only needs very limited additional memory compared to the original matrix, especially in the case of aggressive coarsening on the first level. Hence, we employ this setting for all scalar problems considered in the following examples.
4.2 Coupled versus segregated approach
In order to give an example which clearly shows that the segregated approach is not always sufficient, we look at a simple pipe with an inflow at one end and an outflow on the other end. At the inflow we set a constant velocity boundary condition of \(v_0=1.0\) m/s and a Neumann boundary condition for the velocity at the outflow. With a Reynolds Number of \(10^{-3}\), the viscous forces are dominant in this laminar flow. Owing to the low Reynolds Number, the coupled approach should be used. For this problem we know that for any cross section of the pipe that is far enough away from the inflow, we expect the maximum velocity \(v_\text {max} = 2v_0\) to occur in the center of the pipe with a quadratic fall-off to the sides. After \(t=0.0002\) s, using the segregated approach, our simulation has already produced velocities of \(v \approx 100\) m/s and does not show the parabolic profile in the cross sections, see Fig. 1. With the coupled approach and a virtual time step size of \(\varDelta t_\text {virt} = 0.1\varDelta t\) though, we get \(v_\text {max}=2.0\) m/s both at \(t=0.0002\) s and \(t=0.1\) s, showing that the scheme reproduces the physical behavior over time. With this approach, the method shows the parabolic velocity distribution in the cross sections as well, see Fig. 2. In both cases, roughly 31,000 FPM points are used.
On the other hand, for larger Reynolds numbers, the segregated approach is usually faster. In Table 3, we give the number of BiCGStab(2) and AMG-preconditioned BiCGStab (or, in the case of the coupled system, GMRES(30)) iterations needed to solve the various linear systems for the same example but now we used a Reynolds number \(\approx 1\). As we have neglected the gravity in our model, we do not have to solve for the hydrostatic pressure component. We see that the iteration count coupled velocity-pressure system is significantly higher than for the segregated velocity system, which is due to the properties of the saddle point structure of the linear system in the coupled case. Note that while all linear systems for the different pressures have as many equations as there are points in the point cloud, the segregated velocity system has three equations for every point (x-, y- and z-velocity components) and the coupled velocity system even has four equations per point (x-, y- and z-velocity components plus one equation for the correction pressure). In addition, this system also has more entries per row as the additional couplings to the pressure are included. In the general case, we can expect that the total number of non-zero entries in the coupled matrix is \(\approx 16/9\) times the number of non-zeros in the velocity system. If there are no couplings between the different velocity components, this factor can even grow up to 10/3, hence the computational cost of every matrix-vector product also increases by this factor. AMG can be used to reduce the number of iterations needed, but still the coupled system is harder to solve than the segregated velocity system. Hence, the segregated method will be faster whenever it can be used. Moreover, in these situations the segregated velocity system typically can be solved efficiently using BiCGStab(2). On the other hand, this experiment shows that in situations with small Reynolds numbers the segregated approach cannot be used and the coupled approach is the only option giving realistic results. For a more detailed discussion on the advantages and disadvantages of the various approaches we refer to [18].
4.3 Scalability with problem size
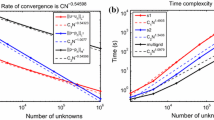
To evaluate the scalability of our method, we simulate a flow through a Kenics mixer. A Kenics mixer is a helical mixing element used for mixing fluids (see Fig. 3, [4]). We successively refine the point cloud by reducing the smoothing length h. Table 4 shows timings and iteration counts for both AMG and BiCGStab(2) running on one core solving the hydrostatic pressure system. We use the segregated approach in this experiment, however since the hydrostatic pressure system is identical in both approaches, the results are not different for the coupled approach.
AMG scales almost linearly with the number of points, whereas BiCGStab(2) does not. Even for the smallest model, AMG is significantly faster. In all cases, operator and grid complexities remained below 1.1. The convergence rates of AMG in these examples are around 0.25, keeping the number of iterations needed at 11 to 12. This is not the case for BiCGStab(2), which needs a growing number of iterations as we would expect from a classical one-level solver.
The table also shows the time needed to assemble the matrix. This predominantly includes solving the least-squares problem (15)–(16) at every point. When applying AMG, the assembly takes more computational effort than the linear solver, indicating that in this situation, improving the overall performance of the method is now a question of speeding up the assembly rather than the linear solver. With BiCGStab(2) on the other hand, the linear solver highly outweighs the assembly. These observations may vary depending on the model, of course. Also note that the numbers we are giving here refer to the assembly of the matrix only. In FPM, there are other task like managing the point cloud that also take some computational effort.
4.4 Parallel speed-up
In this section, we show the (MPI-)parallel strong scalability of SAMG for a bifurcating tube model with \(\approx 3.5\hbox {m}\) points and a high Reynolds number of 1000 (Fig. 4). In this case, we can again use the segregated approach and consider the correction pressure. (The hydrostatic pressure equals 0 as no external forces are modeled).
We employ local, per-processor coarsening on the first 3 levels. On higher levels, the splitting into coarse and fine grid points is carried out on a single processor, while the computation of the interpolation operators and the Galerkin operator is performed in parallel.
From the last column in Table 5 we see that the grid complexity increases as more processors are involved. In consequence, for 256 processors the coarsest grid becomes relatively large (\(\approx 4500\) points compared to \(\approx 3350\) points in the 128 core case). While this improves the convergence factor, it increases the costs for the iteration (see column \(t_{sol}\)) Therefore, the overall speed-up stagnates with 256 cores. On the other hand, we have good speed-ups up to 128 cores. Note that the 32 cores run needed 14 iterations rather than 13 due to a small change in the initial residual that is caused by the slightly different point cloud.
4.5 Two-phase sloshing with free surface
An example for a simulation with a free surface is a sloshing fluid. In this case, we simulated a two-phase sloshing experiment with two different fluids, see Fig. 5. The “upper” fluid has a density of \(500\, \mathrm {kg/m}^3\), while the “lower” fluid has a density of \(1000 \,\mathrm {kg/m}^3\). For both phases, the viscosity is set to \(\eta = 0.001\, \mathrm {kg/(m s)}\).
Rather than moving the surrounding box, the gravity affecting each point was varied over space and time. At the free surface, we impose different boundary conditions for the “upper” (light) and “lower” (heavy) phase: For the “upper” phase, the interface acts as a moving boundary with slip conditions. The “lower” phase has a free boundary condition at the interface, and the pressure of the “upper” phase boundary is added to the boundary conditions for the “lower” phase boundary. Neither a pressure jump nor an additional surface tension are modeled. The smoothing length \(h_{\text {upper}}\) for the upper phase is chosen as \(h_{\text {lower}}/2\). We consider the coupled approach to investigate how the AMG method introduced in Sect. 3.3 performs for the pressure-velocity-systems. Since the model uses \(\varDelta t_{\text {virt}} = 0.2\varDelta t\), it is sufficient to use the (diagonal blocks) of \(\mathbf {A}\) and D to coarsen the velocity and pressure components respectively. There is no need to assemble the Schur complement \(C \hat{\mathbf {A}}^{-1} B + D\). As in the case of the scalar systems, the operator complexities remain below 1.1 even though we employed standard (not aggressive) coarsening on the first level here. We obtain grid complexities of 1.34 for the smaller and 1.30 for the larger problem.
In this example, the detection of decoupled subsystems is important, since droplets of water leave the main water component frequently. The detection of these subsystems is realized in parallel by using a local-diffusion based algorithm as described in [3]. The cost for the detection and redistribution of these subsystems among the 128 respectively 256 cores used in this example is below \(7\%\) of the overall linear solver time. The convergence rate of our AMG algorithm stays below 0.7 for both problem sizes. In contrast, the BiCGStab(2) solver has high communication cost due to the increased number of iterations and cores especially in the 256 core case and hence cannot compete with AMG, see Table 6.
4.6 Small virtual time steps
In order to achieve a divergence-free velocity field, the virtual time step \(\varDelta t_{\text {virt}}\) in (26) must be chosen as small as possible. In this section, we investigate the effects of small virtual time steps on the robustness of the linear solvers. We compare the BiCGStab(2) solver to the saddle point AMG solvers introduced in section, which employ different techniques to set up the coarse grid and interpolation operator for the pressure, see 3.3.
-
1.
Using just the entries of the lower right block D,
-
2.
Using the Schur complement \(C \hat{\mathbf {A}}^{-1} B + D\),
-
3.
Like 2, but with additional interpolation stabilization (56)
We again look at the bifurcating tube example introduced in Sect. 4.4. This time though we change the viscosity of the fluid so that the small diameter of the tube leads to a low Reynolds number \((Re = 0.0001)\) and the coupled approach must be used. We consider a relatively small example (289,830 points, i.e. the coupled linear system has 1,159,320 rows and columns) and carry out a sequential computation only. As the viscosity is constant throughout the domain, we omitted the block scaling (49). For this example we set the strength threshold \(\alpha = 0.5\).
In Table 7 we give the iteration counts for four different virtual time steps (given as fractions of the time step). We see that with decreasing virtual time step, the iteration count of all methods increases. While BiCGStab(2) is still feasible for this small example (timings reached from 641 to 1424 s), pressure coarsening using D only is not sufficient for time step factors smaller than 0.01 (see column \(\hbox {AMG}(D)\)) , so the whole Schur complement \(C \hat{\mathbf {A}}^{-1} B + D\) must be used (column \(\hbox {AMG}(S)\)) . For even smaller virtual time steps, we also need to employ additional stabilization (column \(\hbox {AMG}(ST)\)) , which however increases the costs of setup and cycling (up to 3255 s were needed in the worst case). This is also reflected in the complexities given in Table 8: With stabilization, the operator complexity is almost twice as large as without stabilization. Here, further research efforts will be required. First, as results from [20] indicate, it is not always required to stabilize on all levels. Second, the diagonal scaling of the FPM discretization may be replaced by a more physical scaling such that the physical background of the B and C blocks (which represent in fact operators that are adjoint to each other!) can be better represented in the Schur complement. As for larger systems standalone BiCGStab(2) will become computationally expensive, a robust AMG method is also needed here.
5 Conclusions and future work
In conclusion, we have created different AMG methods for the linear systems arising in the FPM. Our method is especially efficient for large point clouds. For the segregated pressure systems, our method is very close to a standard Ruge–Stüben method and works well in our test cases. However due to the lack of symmetry and the M-matrix property, a theoretical framework for its convergence remains to be explored. To this end we should mention that the work by Seibold [14] shows how to enforce the M-matrix property in FPM and work by Notay et al. [10, 11] shows two-level convergence for such matrices that need not necessarily be symmetric. In contrast to our work, Notay et al. use aggregation-based AMG. One should keep in mind, that although the discretization we presented in Sect. 2.3 leads to non-symmetric matrices, the operators we are discretizing in the FPM are symmetric operators by nature. This observation could give rise to some theoretical considerations in future work. But also the idea of aggregation-based AMG algorithms deserves some more attention: In an aggregation-based AMG it would be easier to reuse the setup across more than one time step. This is difficult to achieve with classical AMG methods, as the point cloud organization might introduce and delete points from the point cloud. In an aggregation-based algorithm this could be accounted for by simply deleting points from aggregates or adding them. Next, [14] also gives rise to the question whether the idea of minimal stencils leads to a more effective coarsening algorithm in the classical sense. The criterion for the existence of minimal stencils could lead to a coarsening algorithm that uses a minimal number of C-points.
As already pointed out in 4.6, the case of small time virtual time steps requires further developments, as small virtual time steps are important for accurate divergence-freeness of the velocity field.
Last, there are a number of other methods, e.g. various implicit SPH methods [5, 6, 19], that use discretizations leading to matrices with similar properties like the ones we have seen here. A theoretical framework build for the matrices we investigated here could also be applied to those methods.
References
Bank, R.E., Chan, T.F., Coughran, W.M., Smith, R.K.: The alternate-block-factorization procedure for systems of partial differential equations. BIT Numer. Math. 29(4), 938–954 (1989). https://doi.org/10.1007/BF01932753
Clees, T.: AMG strategies for PDE systems with applications in industrial semiconductor simulation. Dissertation, Universität zu Köln (2004)
Donev, A.: Connected components of a graph. Website, Michigan State University (2000). http://computation.pa.msu.edu/NO/ConnCompPresentation.html. Accessed 28 March 17
Hobbs, D., Muzzio, F.: The Kenics static mixer: a three-dimensional chaotic flow. Chem. Eng. J. 67(3), 153–166 (1997)
Ihmsen, M., Cornelis, J., Solenthaler, B., Horvath, C., Teschner, M.: Implicit incompressible SPH. IEEE Trans. Vis. Comput. Graph. 20(3), 426–435 (2014)
Kim, K., Trask, N., Maxey, M., Perego, M., Parks, M., Yang, K., Xu, J.: Development of scalable parallel implicit SPH using LAMMPS and Trilinos. In: LAMMPS Users’ Workshop and Symposium (2015)
Kuhnert, J.: Meshfree numerical scheme for time dependent problems in fluid and continuum mechanics. In: Sundar, S. (ed.) Advances in PDE Modeling and Computation, pp. 119–136. Anne books, New Delhi (2014)
Lancaster, P., Salkauskas, K.: Surfaces generated by moving least squares methods. Math. Comput. 37(155), 141–158 (1981)
Metsch, B.: Algebraic multigrid (AMG) for saddle point systems. Dissertation, Institut für Numerische Simulation, Universität Bonn (2013)
Notay, Y.: A robust algebraic multilevel preconditioner for non-symmetric M-matrices. Numer. Linear Algebra Appl. 7(5), 243–267 (2000)
Notay, Y.: Algebraic analysis of two-grid methods: the nonsymmetric case. Numer. Linear Algebra Appl. 17(1), 73–96 (2010)
Ruge, J.: AMG for problems of elasticity. Appl. Math. Comput. 19, 293–309 (1986)
Schöberl, J., Zulehner, W.: On Schwarz-type smoothers for saddle point problems. Numer. Math. 95(2), 377–399 (2003)
Seibold, B.: Performance of algebraic multigrid methods for non-symmetric matrices arising in particle methods. Numer. Linear Algebra Appl. 17(2–3), 433–451 (2010)
Sleijpen, G.L.G., Fokkema, D.R.: Bicgstab(l) for linear equations involving unsymmetric matrices with complex spectrum. Electron. Trans. Numer. Anal. 1, 11–32 (1993)
Stüben, K.: An introduction to algebraic multigrid. In: Trottenberg, U., Oosterlee, C.W., Schüller, A. (eds.) Multigrid, pp. 413–532. Academic Press, New York (2000)
Suchde, P.: Conservation and accuracy in meshfree generalized finite difference methods. Ph.D. thesis, University of Kaiserslautern (2017)
Suchde, P., Kuhnert, J., Tiwari, S.: On Meshfree GFDM solvers for the incompressible Navier–Stokes equations. arXiv:1701.03427 (2017)
Takahashi, T., Dobashi, Y., Fujishiro, I., Nishita, T., Lin, M.C.: Implicit formulation for SPH-based viscous fluids. Comput. Graph. Forum 34(2), 493–502 (2015)
Webster, R.: Stabilisation of AMG solvers for saddle-point Stokes problems. Int. J. Numer. Methods Fluids 81(10), 640–653 (2016). https://doi.org/10.1002/fld.4199
Acknowledgements
Open Access funding provided by Projekt DEAL. The authors want to thank the Grid-Free methods group at Fraunhofer ITWM. Furthermore, we want to thank John Ruge from FRSC for many helpful hints and advice.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Gabriel Wittum.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the Fraunhofer WISA “MESHFREE”.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Metsch, B., Nick, F. & Kuhnert, J. Algebraic multigrid for the finite pointset method. Comput. Visual Sci. 23, 3 (2020). https://doi.org/10.1007/s00791-020-00324-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00791-020-00324-3