Adaptive large eddy simulation

Abstract

Several a posteriori indicators in the framework of local grid adaptation and large eddy simulation (LES) are evaluated. In LES indicators must be capable to bound not only the discretisation error, but also the modeling error. Moreover, the numerical method must be able to adapt the computational grid dynamically, as the regions requiring different resolution are not static. The performance of different indicators is evaluated in two flow configurations. It turns out that the classic residual based error indicator and the newly introduced heuristic indicator perform best.

Appendix 1: error analysis

In LES one principally distinguishes between the disretisation and the modeling error. The discretisation error is determined by the discretisation scheme and is guided by the discretisation parameter h. The modeling error is caused by the shortcomings of the underlying LES model, which in turn depends on the filterwidth $\Delta$. Although both error types can be further sub-classified, the two error components mentioned are assumed to be the most prevailing [33]. Suppose the discretisation scheme and LES model are both convergent, the discretisation error ed and modeling error em behave like

$$\begin{aligned} \lim _{h\rightarrow 0}ed=0 \end{aligned}$$

and

$$\begin{aligned} \lim _{\Delta \rightarrow 0}em=0. \end{aligned}$$

(7)

Although (7) might not be valid for special scale similarity models [34], we presume convergent models here. Closely following the approach and notation of Geurts in [34], we denote $x_{LES}(\Delta ,h)$ as the LES computation with an appropriate grid and filter resolution with a discretisation and modeling error. A computation for substantially smaller h, whereas $\Delta$ is kept constant, is named a fine LES, which is denoted by $x_{LES}(\Delta ,0)$, reduces the discretisation error only, while the modeling error remains constant. Subtracting the fine LES solution from the standard LES solution, the discretisation error can be determined by

$$\begin{aligned} ed(x):=x_{LES}\left( \Delta ,h\right) -x_{LES}\left( \Delta ,0\right) , \end{aligned}$$

where x may stand for the velocity or any other reasonable quantity. In order to determine the modeling error, a direct numerical simulation (DNS), which exhibits no modeling error, is filtered explicitly with the filter operator $G(\Delta )$:

$$\begin{aligned} x_{\overline{DNS}}=x_{DNS}\circ G\left( \Delta \right) . \end{aligned}$$

Subtracting the explicitly filtered DNS from the fine LES, we obtain the modeling error:

$$\begin{aligned} em(x):=x_{LES}\left( \Delta ,0\right) -x_{\overline{DNS}}\left( \Delta \right) . \end{aligned}$$

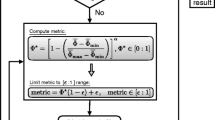
It should be noted that we do not deal with the real discretisation or modeling error. Rather, we express the influence of both error types on x. However, we assume a correlation between the real errors and this influence expressed by ed(x) and em(x) respectively. As the ratio between the two error types is of interest, we introduce

$$\begin{aligned} q:=ed{/}em. \end{aligned}$$

(8)

As we consider sequences of solutions with different finite grid size and filterwidth resolutions, they all exhibit a discretisation and modeling error to a larger or smaller extent.