1 Introduction

This paper addresses the problem of finding optimal allocations of risk among finitely many agents, i.e., solutions of the problem to

$$ \text{minimise $\sum _{i\in{ I}}\rho _{i}(X_{i})$ subject to $\sum _{i\in{ I}}X_{i}=X$.}$$
(1.1)

The agents under consideration form a finite set \(I\). Each agent \(i\in{ I}\) measures the risk of net losses \(Y\) in a space \(\mathcal {X}\) with a risk measure \(\rho _{i}\). Given the total loss \(X\) collected in the system, an allocation attributes a portion \(X_{i}\in \mathcal {X}\) to each agent, i.e., the condition \(\sum _{i\in{ I}}X_{i}=X\) holds. We do not impose any restriction on the notion of an allocation, i.e., every vector whose coordinates sum up to \(X\) is feasible. An allocation of \(X\) is optimal if it minimises the aggregated risk \(\sum _{i\in{ I}}\rho _{i}(X_{i})\) in the system. A fortiori, every optimal allocation is Pareto-optimal, i.e., no alternative allocation decreases the risk of one agent without increasing the risk burden of some other agent. The risk-sharing problem (1.1) is of fundamental importance for the theory of risk measures, for capital allocations in capital adequacy contexts, and in the design and discussion of regulatory frameworks; see Filipović and Kupper [26], Tsanakas [53] and Weber [55].

Often, the space of net losses appearing in (1.1) is an infinite-dimensional space of random variables, which complicates finding optima. Individual risk measures are often assumed to be convex and monetary, which are standard axioms in the theory of risk measures since Föllmer and Schied [29] and Frittelli and Rosazza Gianin [32]. Likewise, in the closely related field of utility assessment via variational preferences, concavity assumptions are common; see Maccheroni et al. [46]. Convexity (or concavity) alone is not sufficient though. A powerful solution theory has so far mostly been established under the additional assumption of law-invariance, meaning that the risk of a random variable \(X\) on a probability space \((\Omega ,\mathcal {F},\mathbb{P})\) merely depends on its distribution under the reference measure ℙ. A rich strand of literature has studied the wide-ranging analytic consequences of law-invariance in conjunction with convexity; see e.g. Bellini et al. [10], Chen et al. [18], Filipović and Svindland [28], Jouini et al. [36], Leung and Tantrawan [39], Liebrich and Svindland [41], Svindland [51, 52], and the references therein. Studies of the risk-sharing problem for convex monetary risk measures (or, equivalently, concave monetary utility functions) are Acciaio [1], Barrieu and El Karoui [9], Burgert and Rüschendorf [13], Filipović and Svindland [27], and Jouini et al. [37]. We also refer to Rüschendorf [50, Chaps. 10 and 11]. Risk-sharing problems with special law-invariant, but not necessarily convex functionals are considered in Embrechts et al. [25] and Liu et al. [44].

Abstractly speaking, the solution theory in the law-invariant case can be split in two steps. Step 1 is to reduce the set of optimisation-relevant allocations to comonotonic allocations. This reduction is driven by the fact that convexity and (semi)continuity properties in conjunction with law-invariance usually imply monotonicity of the involved functionals in the so-called convex order. Therefore, the comonotonic improvement results of Carlier et al. [15], Filipović and Svindland [27], Landsberger and Meilijson [38] and Ludkovski and Rüschendorf [45] can be used. In Step 2, one finds suitable bounds which prove that relevant comonotonic allocations form a compact set. This enables approximation procedures and the selection of converging optimising sequences. Under cash-additivity of the involved functionals, Step 2 poses no problem and can be achieved by a simple exchange of cash among the involved agents; see e.g. [27]. Steps 1 and 2 of the previous arguments are separated explicitly in e.g. Liebrich and Svindland [41], where also numerous economic optimisation problems are analysed according to that scheme.

The two steps rely fundamentally on the existence of a single “objective” reference probability measure which is common to all agents in \({ I}\). A more recent and quickly growing strand of literature in finance, insurance and economics, however, dispenses with this paradigm. Two economic considerations motivate these heterogeneous reference probability measures. First, different agents may have access to different sources of information, resulting in information asymmetry and different subjective beliefs. Secondly, agents may entertain heterogeneous probabilistic subjective beliefs as a result of their preferences or their use of different internal models.

Applying heterogeneous (probabilistic) beliefs in risk sharing and related problems, Amarante et al. [6] explores the demand for insurance when the insurer exhibits ambiguity, whereas the insured is an expected-utility agent. Under heterogeneous reference probabilities for insurer and insured, Boonen [11] provides optimal reinsurance designs, and Chi [20] and Ghossoub [34] generalise Arrow’s “theorem of the deductible”. Boonen and Ghossoub [12] study bilateral risk sharing with exposure constraints and admit a very general relation between the two involved reference probabilities. Asimit et al. [7, Sect. 6] consider optimal risk sharing under heterogeneous reference probabilities affected by exogenous triggering events, while Dana and Le Van [21] study the existence of Pareto optima and equilibria in a finite-dimensional setting when optimality of allocations is assessed relative to individual and potentially heterogeneous sets of probabilistic priors. Embrechts et al. [24] study risk sharing for value-at-risk and expected shortfall agents endowed with heterogeneous reference probability measures, and provide explicit formulae for the shape of optimal allocations. Liu [43] makes similar contributions to weighted risk sharing with distortion risk measures under heterogeneous beliefs. Finally, an important point of reference is Acciaio and Svindland [3]. In that paper, two agents with heterogeneous reference probability models try to share risks optimally, and each of them measures individual risk with a law-invariant concave monetary utility function. However, the risk-sharing problem is constrained to random variables over a finite \(\sigma \)-algebra, which reduces the optimisation problem to a finite-dimensional space; one of the two reference probabilities involved only takes rational values on the finite \(\sigma \)-algebra in question; and the mathematical techniques are quite different from those used here.

Against the outlined backdrop of the existing literature, several key features of our results stand out. First, whereas dealing with heterogeneous reference probability has sometimes been facilitated by restriction to a finite-dimensional setting, we consider problem (1.1) for the space \(\mathcal {X}\) of all bounded random variables over an atomless probability space \((\Omega ,\mathcal {F},\mathbb{P})\), a bona fide infinite-dimensional space.

Second, we generalise many existing results. As already stated, we consider a finite set \({ I}\) of agents, each measuring risk with a functional \(\rho _{i}\colon L^{\infty}\to \mathbb{R}\) which is law-invariant with respect to a probability measure \(\mathbb{Q}_{i}\) equivalent to ℙ. The latter only plays the role of a gauge and we are free to assume \(\mathbb{P}=\mathbb{Q}_{i_{0}}\) for some \(i_{0}\in{ I}\). Our main result in Sect. 4 provides mild sufficient conditions for the existence of optimal risk allocations without a rationality condition on involved probabilities as in [3]. Mathematically, a key to our strategy is to adapt the two-step procedure of comonotonic improvement outlined above to the case of heterogeneous reference probabilities. This is mostly achieved in Appendix B. However, the simplification of Step 2 in that procedure via “rebalancing cash” is not an option anymore under heterogeneity. Instead, finding suitable bounds for optimisation-relevant allocations becomes crucial. While optimal allocations will usually not be comonotonic in the heterogeneous case, our procedure nevertheless unifies various existence results under a single reference probability measure and extends them to the case of multiple reference measures.

Third, we do not assume convexity (or concavity) of the involved functionals. Instead, we work with three axiomatic properties of risk measures introduced and studied in the recent literature as alternatives to (quasi)convexity. While this trend is in large parts motivated by the lacking convexity of many distortion risk measures such as value-at-risk, Amarante [5, Sect. 1.2] presents further critical remarks on subadditivity.

A requirement we impose throughout our study is the assumption that individual risk measures be consistent, a property recently axiomatised by Mao and Wang [47]. While many desirable characterisations are shown to be equivalent, their eponymous feature is monotonicity with respect to second-order stochastic dominance. Each law-invariant and convex monetary risk measure is consistent (up to an affine transformation), but the converse implication does not hold.

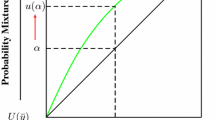
Another ingredient – which is mostly of technical relevance and makes the assumptions in the main results particularly satisfiable – is star-shapedness. Star-shaped risk measures have recently been studied systematically in Castagnoli et al. [16]. They are motivated for instance by the observation that subadditive risk measures intertwine the measurement of concentration and liquidity effects – by curves \(\mathbb{R}_{+}\ni t\mapsto \rho (tX)\) – with diversification benefits from merging portfolios. The latter is translated by (quasi)convexity of the risk measures in question. Star-shaped risk measures are more agnostic and replace (quasi)convexity by the demand that decreasing exposure to an acceptable loss profile (having at most neutral risk) does not lead to a loss of acceptability: For all \(X\in \mathcal {X}\) and all \(\lambda \in [0,1]\),

ρ(X)≤0⟹ρ(λX)≤0.

Further economic motivation is discussed in [16, Sect. 2].

Moreover, we require a certain compatibility of probabilistic beliefs and assume the existence of a finite measurable partition \(\pi \) of \(\Omega \) such that the agents agree on the associated conditional distributions. This is akin to and generalises the (much more specific) setting of Marshall [48], one of the earliest contributions on heterogeneous reference measures. While Sect. 3 reveals all necessary details and sheds more light on this assumption, we anticipate here the consequence that individual risk measures fall in the class of scenario-based risk measures recently introduced in Wang and Ziegel [54]. A desirable aspect of the latter perspective is that scenario-basedness is preserved under the infimal convolution operation (see Corollary 4.7), while the individual law-invariance is lost in the general heterogeneous case.

The paper unfolds as follows. Section 1.1 collects preliminaries. Consistent and star-shaped risk measures and their admissibility for our main results as introduced in Definition 2.1 are studied at length in Sect. 2. In Sect. 3, we carefully introduce our setting of heterogeneous reference probability measures and motivate the key assumption from different angles. The main result, Theorem 4.1, is stated in Sect. 4 and presents a sufficient condition under which heterogeneous agents endowed with consistent risk measures can find optimal allocations. The remainder of Sect. 4 is devoted to developing a profound understanding of these assumptions and to the formulation of related results. All proofs, mathematical details and auxiliary results can be found in Appendices A–E.

1.1 Preliminaries

We first outline terminology, notation and conventions adopted throughout the paper.

– The effective domain of a function \(f\colon S\to [-\infty ,\infty ]\) defined on a nonempty set \(S\) is \(\mbox{dom}(f):=\{s\in S: f(s)\in \mathbb{R}\}\). For an arbitrary natural number \(K\in \mathbb{N}\), we denote the set \(\{1,\ldots ,K\}\) by \([K]\).

– The absolute continuity relation between two probability measures ℚ and ℙ on a measurable space \((\Omega ,\mathcal {F})\) is denoted by \(\mathbb{Q}\ll \mathbb{P}\), and equivalence of probability measures by \(\mathbb{Q}\approx \mathbb{P}\).

– Fix a probability space \((\Omega ,\mathcal {F},\mathbb{P})\). Then \(L^{0}\) denotes the space of equivalence classes up to ℙ-almost sure (ℙ-a.s.) equality of real-valued random variables over \((\Omega ,\mathcal {F},\mathbb{P})\). The subspaces of equivalence classes of bounded and ℙ-integrable random variables are denoted by \(L^{\infty}\) and \(L^{1}\), respectively. All these spaces are canonically equipped with the ℙ-a.s. order ≤, and all appearing (in)equalities between random variables are understood in this sense. We denote the respective positive cones by \(L^{\infty}_{+}\) and \(L^{1}_{+}\), and the supremum norm on \(L^{\infty}\) by \(\|\cdot \|_{\infty}\). If we consider the spaces \(L^{\infty}\) and \(L^{1}\) with respect to a probability measure \(\mathbb{Q}\neq \mathbb{P}\) on \((\Omega ,\mathcal {F})\), we write \(L^{\infty}_{\mathbb{Q}}\) and \(L^{1}_{\mathbb{Q}}\).

– (Conditional) expectations (given a sub-\(\sigma \)-algebra \(\mathcal {G}\subseteq \mathcal {F}\)) computed with respect to a measure ℚ are denoted by \(\mathbb{E}_{\mathbb{Q}}[\,\cdot \,]\) (\(\mathbb{E}_{\mathbb{Q}}[\,\cdot \,|\mathcal {G}]\), respectively).

– As usual, we identify the dual space of \(L^{\infty}\), comprising all bounded linear functionals on that space, via the Dunford–Schwartz integral with the space \(\mathrm{ba}\) of all finitely additive set functions \(\mu \) with bounded total variation that are absolutely continuous with respect to ℙ, i.e., \(\mu (N)=0\) whenever \(\mathbb{P}[N]=0\). Often, the subspace of countably additive signed measures in \(\mathrm{ba}\) will be identified with \(L^{1}\). Note that every positive \(\mu \in \mathrm{ba}\) – i.e., \(\mu (A)\ge 0\) holds for all \(A\in \mathcal {F}\) – has a unique Yosida–Hewitt decomposition as the sum of a countably additive measure \(\zeta \ll \mathbb{P}\) and a positive pure charge \(\tau \), i.e., for a suitable vanishing sequence of events \((B_{n})\subseteq \mathcal {F}\), we have \(\tau (B_{n}^{c})=0\) for all \(n\in \mathbb{N}\). We write \(\mu =\zeta \oplus \tau \) or \(\mu =R\oplus \tau \), where \(R:=\frac{{\mathrm{d}}\zeta}{{\mathrm{d}}\mathbb{P}}\) is the ℙ-density of \(\zeta \). Note that we abuse notation slightly and denote integrals with respect to finitely additive \(\mu \in \mathrm{ba}\) by \(\mathbb{E}_{\mu}[\,\cdot \,]\).

– We assume throughout the paper that the underlying fixed probability space \((\Omega ,\mathcal {F},\mathbb{P})\) is atomless, i.e., we can define a random variable on it whose cumulative distribution function under ℙ is continuous. In particular, ℙ has convex range, i.e., for all \(A\in \mathcal {F}\) and all \(p\in [0,\mathbb{P}[A] ]\), we find \(B\in \mathcal {F}\) with the properties \(B\subseteq A\) and \(\mathbb{P}[B]=p\). Each probability measure \(\mathbb{Q}\ll \mathbb{P}\) is also atomless.

– \(\Pi \) denotes the set of finite measurable partitions \(\pi \subseteq \mathcal {F}\) of \(\Omega \) satisfying \(\mathbb{P}[B]>0\) for all \(B\in \pi \).

– For a probability measure ℚ on \((\Omega ,\mathcal {F})\) and an event \(B\in \mathcal {F}\) with \(\mathbb{Q}[B]>0\), we define the conditional probability measure \(\mathbb{Q}^{B}\colon \mathcal {F}\to [0,1]\) by \(\mathbb{Q}^{B}[A]:=\frac{\mathbb{Q}[A\cap B]}{\mathbb{Q}[B]}\).

– If for two elements \(X,Y\in L^{0}\) and a probability measure \(\mathbb{Q}\ll \mathbb{P}\), the distribution \(\mathbb{Q}\circ Y^{-1}\) of \(Y\) under ℚ agrees with the distribution \(\mathbb{Q}\circ X^{-1}\) of \(X\) under ℚ, we write \(X\sim _{\mathbb{Q}}Y\). A subset \(\mathcal {A}\subseteq L^{0}\) is law-invariant with respect to a probability measure \(\mathbb{Q}\ll \mathbb{P}\) (or ℚ-law-invariant) if

$$ X\in \mathcal {A}\text{ and } X\sim _{\mathbb{Q}}Y\quad \implies \quad Y \in \mathcal {A}.$$

Given nonempty sets \(\mathcal {A}\subseteq L^{0}\) and \(S\), a function \(f\colon \mathcal {A}\to S\) is law-invariant with respect to a probability measure \(\mathbb{Q}\ll \mathbb{P}\) if

$$ X,Y\in \mathcal {A}\text{ and } X\sim _{\mathbb{Q}}Y\quad \implies \quad f(X)=f(Y).$$

– Given \(X\in L^{0}\) and a probability measure \(\mathbb{Q}\ll \mathbb{P}\), \(q_{X}^{\mathbb{Q}}\) denotes the quantile function of \(X\) under ℚ, defined by

$$ q_{X}^{\mathbb{Q}}(s):=\inf \{x\in \mathbb{R}:\mathbb{Q}[X\le x]\ge s \},\qquad s\in (0,1). $$

– Unif\((0,1)\) denotes the uniform distribution over the interval \((0,1)\).

– A monetary risk measure \(\rho \colon L^{\infty}\to \mathbb{R}\) is a map that is

(a) monotonic, i.e., for \(X,Y\in L^{\infty}\) with \(X\le Y\), we have \(\rho (X)\le \rho (Y)\);

(b) cash-additive, i.e., for \(X\in L^{\infty}\) and \(m\in \mathbb{R}\),

$$ \rho (X+m)=\rho (X)+m. $$

As mentioned in the introduction and reflected by the preceding definition, risk measures are applied to losses net of gains in this manuscript, not gains net of losses. In particular, nonnegative random variables correspond to pure losses. A monetary risk measure \(\rho \colon L^{\infty}\to \mathbb{R}\) is normalised if \(\rho (0)=0\).

– The acceptance set \(\mathcal {A}_{\rho}:=\{X\in {L}^{\infty}: \rho (X)\le 0\}\) of a monetary risk measure \(\rho \) collects all loss profiles that bear neutral risk. By monotonicity and cash-additivity, \(\rho \) is a norm-continuous function and the acceptance set \(\mathcal {A}_{\rho}\) is closed. The risk measure \(\rho \) can also be recovered from \(\mathcal {A}_{\rho}\) via the formula

$$ \rho (X)=\inf \{m\in \mathbb{R}: X-m\in \mathcal {A}_{\rho}\},\qquad X \in L^{\infty}. $$

The asymptotic cone of the acceptance set \(\mathcal {A}_{\rho}\) of a risk measure \(\rho \) is the set \(\mathcal {A}_{\rho}^{\infty}\) of all \(U\in L^{\infty}\) that can be represented as \(U=\lim _{k\to \infty}s_{k}Y_{k}\) for a null sequence \((s_{k})\subseteq (0,\infty )\) and a sequence \((Y_{k})\subseteq \mathcal {A}_{\rho}\). More information on asymptotic cones in a finite-dimensional setting can be found in Auslender and Teboulle [8, Chap. 2].

– Two prominent normalised risk measures appear recurrently throughout the paper:

(a) The entropic risk measure with parameter \(\beta >0\) under \(\mathbb{Q}\ll \mathbb{P}\) is

$$ \mbox{Entr}^{\mathbb{Q}}_{\beta}(X):=\frac {1}{\beta}\log \mathbb{E}_{\mathbb{Q}}[e^{\beta X}],\qquad X\in L^{\infty}. $$

(b) The expected shortfall at level \(p\in [0,1]\) under \(\mathbb{Q}\ll \mathbb{P}\) is, for \(X\in L^{\infty}\),

$$ {\mathrm{ES}}_{p}^{\mathbb{Q}}(X):= \textstyle\begin{cases} \frac {1}{1-p}\int _{p}^{1}q^{\mathbb{Q}}_{X}(s)\,{\mathrm{d}}s&\quad \text{for }p\in [0,1), \\ \sup _{s\in (0,1)}q_{X}^{\mathbb{Q}}(s)&\quad \text{for }p=1. \end{cases} $$

– Consider an arbitrary function \(f\colon L^{\infty}\to [-\infty ,\infty ]\). We define the convex conjugate of \(f\) on \(\mathrm{ba}\) as

$$ f^{*}(\mu )=\sup \bigg\{ \int X\,{\mathrm{d}}\mu -f(X): X\in L^{\infty} \bigg\} ,\qquad \mu \in \mathrm{ba}. $$

2 Admissible risk measures

2.1 Consistent and star-shaped risk measures

This paper proves the existence of optimal risk-sharing schemes for consistent risk measures as introduced in Mao and Wang [47]. Consistency means that the risk assessment respects the second-order stochastic dominance relation between arguments. Given random variables \(X,Y\in L^{\infty}\) and a probability measure \(\mathbb{Q}\ll \mathbb{P}\), recall that \(Y\) dominates \(X\) in the ℚ-second-order stochastic dominance (ℚ-ssd) relation if \(\mathbb{E}_{\mathbb{Q}}[v(X)]\le \mathbb{E}_{\mathbb{Q}}[v(Y)]\) for all convex and nondecreasing functions \(v\colon \mathbb{R}\to \mathbb{R}\). A normalised monetary risk measure \(\rho \colon L^{\infty}\to \mathbb{R}\) is a ℚ-consistent risk measure (see [47]) if whenever \(Y\in L^{\infty}\) dominates \(X\in L^{\infty}\) in the ℚ-ssd relation, then also \(\rho (X)\le \rho (Y)\).

Each normalised, convex and ℚ-law-invariant monetary risk measure is ℚ-consistent. The pointwise infimum of a family of such risk measures also is if it is a risk measure itself (see [47, Proposition 3.2]). More precisely, by [47, Theorem 3.3], for each consistent risk measure \(\rho \), there is a set \(\mathcal {T}\) of ℚ-law-invariant and convex monetary risk measures \(\tau \) such that for all \(X\in L^{\infty}\), we have \(\rho (X)=\min _{\tau \in \mathcal {T}}\tau (X)\). A direct consequence of this representation is the formula for the convex conjugate \(\rho ^{*}\) of \(\rho \) given by

$$ \rho ^{*}(\,\cdot \,)=\sup _{\tau \in \mathcal {T}}\tau ^{*}(\,\cdot \,). $$
(2.1)

For every ℚ-consistent risk measure \(\rho \), one has \(\rho (\,\cdot \,)\ge \mathbb{E}_{\mathbb{Q}}[\,\cdot \,]\) and \(\rho ^{*}(\frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}})=0\). Indeed, each \(X\in L^{\infty}\) admits the estimate

$$ \rho (X)\ge \rho (\mathbb{E}_{\mathbb{Q}}[X])=\mathbb{E}_{\mathbb{Q}}[X]= \mathbb{E}_{\mathbb{P}}\bigg[ \frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}X\bigg]. $$

A normalised monetary risk measure \(\rho \colon L^{\infty}\to \mathbb{R}\) is star-shaped (see Castagnoli et al. [16]) if the acceptance set \(\mathcal {A}_{\rho}\) is a star-shaped set, i.e., \(sY\in \mathcal {A}_{\rho}\) holds for all pairs \((s,Y)\in [0,1]\times \mathcal {A}_{\rho}\). Star-shaped risk measures have recently been studied in detail in [16], and our definition implicitly invokes a characterisation provided in [16, Proposition 2]. Each normalised convex monetary risk measure is star-shaped; like consistency, star-shapedness is a weaker property than convexity. We also remark that the class of star-shaped consistent risk measures is discussed in [16, Theorem 4]. While they mostly play a technical role in our study, further background on them is provided in Lemma A.4.

2.2 Admissibility of consistent risk measures

Given \(\mathbb{Q}\ll \mathbb{P}\), we now isolate which ℚ-consistent risk measures \(\rho \) are admissible for our main results. As preparation, the conjunction of cash-additivity and monotonicity implies that a set function \(\mu \in \mathrm{ba}\) satisfies \(\rho ^{*}(\mu )<\infty \) only if \(\mu \) is a finitely additive probability, i.e., \(\mu (A)\ge 0\) holds for all \(A\in \mathcal {F}\) and the total mass is normalised to \(\mu (\Omega )=1\). We also recall that we identify countably additive elements in \(\mathrm{ba}\) with \(L^{1}\) via \(D\mapsto \mu _{D}\), \(\mu _{D}\colon \mathcal {F}\to \mathbb{R}\) being defined by \(\mu _{D}(A)=\mathbb{E}_{\mathbb{P}}[D\mathbf{1}_{A}]\). Note that the reference probability under which we integrate is always ℙ, even though we may consider a ℚ-consistent risk measure with \(\mathbb{Q}\neq \mathbb{P}\). Hence \(D\in L^{1}\) lies in \(\mbox{dom}(\rho ^{*})\) only if \(D\in L^{1}_{+}\) and \(\mathbb{E}_{\mathbb{P}}[D]=1\); so these elements are probability densities.

Definition 2.1

A ℚ-consistent risk measure \(\rho \colon L^{\infty}\to \mathbb{R}\) is admissible if there is a probability density \(D\in L^{1}_{+}\) with the following two properties:

  1. (a)

    \(\rho ^{*}(D)<\infty \).

  2. (b)

    If \(U\in \mathcal {A}^{\infty}_{\rho}\) satisfies \(\mathbb{E}_{\mathbb{P}}[DU]=0\), then \(U=0\).

We denote by \(C(\rho )\) the set of all compatible \(D\), i.e., \(D\) has properties (a)–(b) above.

Definition 2.1 is best illustrated in the special case where \(\rho \) is convex. Convexity entails that the asymptotic cone \(\mathcal {A}_{\rho}^{\infty}\) collects acceptable net losses \(U\) of particular quality: arbitrary quantities \(tU\) thereof with \(t>0\) are still acceptable. If \(\mathbb{E}_{\mathbb{P}}[DU]=0\) for a strictly positive probability density \(D\in L^{1}_{+}\) and \(U\) is not constant, then \(U\) must take negative and positive values, thus triggering net gains and net losses. If \(D\) is compatible, then \(\rho \) is too risk-averse to accept large gains compensating large losses obtaining in different states, and such a \(U\) cannot be acceptable in arbitrary volumes.

It is well possible that not every density in \(\mbox{dom}(\rho ^{*})\cap L^{1}\) is compatible with \(\rho \). For instance, the entropic risk measure \(\rho =\mbox{Entr}_{1}^{\mathbb{P}}\) satisfies \(\mathcal {A}_{\rho}^{\infty}=-L^{\infty}_{+}\) and \(\mbox{dom}(\rho ^{*})=\{D\in L^{1}_{+}: \mathbb{E}_{\mathbb{P}}[D]=1 \}\). In particular, a probability density \(D\in L^{1}_{+}\) lies in \(C(\mbox{Entr}_{1}^{\mathbb{P}})\) if and only if \(D>0\) ℙ-a.s.

Lemma 2.2

Suppose \(\mathbb{Q}\ll \mathbb{P}\) and \(\rho \) is an admissible ℚ-consistent risk measure. Then the following assertions hold:

1) \(\mathbb{Q}\approx \mathbb{P}\).

2) Each \(D\in C(\rho )\) satisfies \(\mathbb{P}[D>0]=1\).

3) For all \(Z\in \mbox{dom}(\rho ^{*})\cap L^{1}\), \(D\in C(\rho )\) and \(\lambda \in (0,1]\), we have

$$ \lambda D+(1-\lambda )Z\in C(\rho ).$$
(2.2)

The notions of admissibility and compatibility are of central importance for the second step in the quest for optimal allocations outlined in the introduction: extracting a convergent optimising sequence. They thus appear prominently in Theorem 4.1 below. The next proposition presents an exhaustive description of admissible risk measures.

Proposition 2.3

Suppose \(\mathbb{Q}\approx \mathbb{P}\) and \(\rho \) is a ℚ-consistent risk measure. Then the following are equivalent:

1) \(\rho \) is admissible.

2) \(\frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}\in C(\rho )\).

3) \(\mbox{dom}(\rho ^{*})\) contains at least two elements.

4) \(\mbox{dom}(\rho ^{*})\cap L^{1}\) contains at least two elements.

5) There is a finitely additive probability \(\nu \in \mbox{dom}(\rho ^{*})\) such that whenever \(U\in \mathcal {A}_{\rho}^{\infty}\) satisfies \(\mathbb{E}_{\nu}[U]=0\), then also \(U=0\).

Moreover, statements 1)–5) all imply

6) There is no constant \(\beta >0\) such that \(\rho (\,\cdot \,) \le \mathbb{E}_{\mathbb{Q}}[\,\cdot \,]+\beta \).

Note that point 6) in Proposition 2.3 means that an admissible consistent risk measure is locally more conservative than determining the expected loss under the reference measure ℚ and adding a safety margin. While disproving 6) therefore serves as an easy check against admissibility, verification of 6) does not suffice to verify admissibility.

Example 2.4

Define a risk measure \(\tau \colon L^{\infty}\to \mathbb{R}\) by

$$ \tau (X):=\inf \big\{ {\mathrm{ES}}^{\mathbb{P}}_{1/n}(X)+n: n\in \mathbb{N}\setminus \{1\} \big\} $$

and consider the ℙ-consistent risk measure \(\rho :=\min \{{\mathrm{ES}}_{1}^{\mathbb{P}},\tau \}\). Then \(\rho \) is not star-shaped (and therefore also not convex). Next we observe that assertion 6) in Proposition 2.3 applies. To see this, nonatomicity of \((\Omega ,\mathcal {F},\mathbb{P})\) yields a sequence \((X_{k})\subseteq L^{\infty}\) satisfying \(\mathbb{P}[X_{k}=-k^{2}]=1-\mathbb{P}[X_{k}=0]=\frac {1}{k}\), \(k\in \mathbb{N}\). For \(k\ge 2\),

$$ {\mathrm{ES}}_{1/n}^{\mathbb{P}}(X_{k})= \textstyle\begin{cases} 0&\quad \text{for $k\le n$}, \\ \frac{-k(n-k)}{n-1}&\quad \text{for $k>n$}.\end{cases} $$

A direct computation therefore gives \(\rho (X_{k})=0\) for all \(k\ge 2\), while \(\mathbb{E}_{\mathbb{P}}[X_{k}]=-k\). Nevertheless, \(C(\rho )=\emptyset \). Indeed, for \(n\ge 2\),

$$ \mbox{dom}\big(({\mathrm{ES}}_{1/n}^{\mathbb{P}})^{*}\big)=\bigg\{ D \in L^{\infty}_{+}\colon \mathbb{E}_{\mathbb{P}}[D]=1, D\le \frac{n}{n-1}\bigg\} . $$

By (2.1), a probability density \(D\in L^{1}_{+}\) lies in \(\mbox{dom}(\rho ^{*})\) only if \(D\le \frac {n}{n-1}\) for all \(n\ge 2\), i.e., only if \(D=1\). Hence \(C(\rho )=\emptyset \) follows with the equivalence between points 1) and 3) in Proposition 2.3.

An even simpler positive condition guaranteeing admissibility is available if \(\rho \) is additionally star-shaped. Admissibility then boils down to \(\rho \) not agreeing with the expectation under ℚ. The assumptions of Theorem 4.1 are therefore particularly mild for star-shaped consistent risk measures.

Proposition 2.5

Let \(\mathbb{Q}\approx \mathbb{P}\) and \(\rho \) be a ℚ-consistent and star-shaped risk measure. Then \(\rho \) is admissible if and only if \(\rho (\,\cdot \,)\neq \mathbb{E}_{\mathbb{Q}}[\,\cdot \,]\).

Note that Example 2.4 also shows that Proposition 2.5 fails without the assumption of star-shapedness.

We close this section with a few more technical remarks.

Remark 2.6

1) If \(\rho \) is admissible, then \(C(\rho )\) contains uncountably many different densities and is dense in \(\mbox{dom}(\rho ^{*})\cap L^{1}\). This follows from (2.2) together with points 2) and 4) of Proposition 2.3.

2) From Propositions 2.3 and 2.5, one can conclude that a ℚ-consistent risk measure \(\rho \) is admissible if and only if its biconjugate \(\rho ^{**}\colon L^{\infty}\to \mathbb{R}\) defined by

$$ \rho ^{**}(X)=\sup \{\mathbb{E}_{\mu}[X]-\rho ^{*}(\mu ):\mu \in \mbox{dom}(\rho ^{*}) \} $$

satisfies \(\rho ^{**}(\,\cdot \,)\neq \mathbb{E}_{\mathbb{Q}}[\,\cdot \,]\). This is due to \(\rho ^{**}\) being the “convexification” of \(\rho \), i.e., the largest convex ℚ-consistent risk measure dominated by \(\rho \) (see Liebrich and Munari [40, proof of Lemma F.3]).

3) The spirit of Definition 2.1 and more specifically the equivalence in Proposition 2.5 establishes a link to the realm of “collapse to the mean” results. The latter subsumes incompatibility results between law-invariance of a functional and the existence of “directions of linearity”. The asymptotic cone of the acceptance set of a consistent risk measure can be understood to collect such directions. In the theory of risk measures, “collapse to the mean results” go back at least to Frittelli and Rosazza Gianin [33]. For more details, we refer to the discussion in Liebrich and Munari [40].

3 Reference probabilities

Throughout the remainder of the paper, we consider \(n\ge 2\) agents identified by integers \(i\in [n]\). With each of them is associated a probability measure \(\mathbb{Q}_{i}\ll \mathbb{P}\), and \(i\) measures risks of net losses with a \(\mathbb{Q}_{i}\)-consistent risk measure \(\rho _{i}\colon L^{\infty}\to \mathbb{R}\). Note that for different agents \(i\neq j\), both \(\mathbb{Q}_{i}=\mathbb{Q}_{j}\) and \(\mathbb{Q}_{i}\neq \mathbb{Q}_{j}\) are possible. The next crucial structural assumption concerns the vector \((\mathbb{Q}_{1},\ldots ,\mathbb{Q}_{n})\) of reference probability measures on \((\Omega ,\mathcal {F})\).

Assumption 3.1

For each \(i\in [n]\), \(\mathbb{Q}_{i}\) is equivalent to ℙ and \(\frac{{\mathrm{d}}\mathbb{Q}_{i}}{{\mathrm{d}}\mathbb{P}}\) is a simple function. That is, there is a partition \(\pi \in \Pi \) such that

$$ \mathbb{Q}_{i}[E]=\sum _{B\in \pi}\mathbb{Q}_{i}[B]\mathbb{P}^{B}[E], \qquad E\in \mathcal {F}.$$
(3.1)

The main results in Sect. 4 make heavy use of Assumption 3.1. It injects a sufficient degree of finite-dimensionality into the problem to adapt the procedure of comonotonic improvement to the present heterogeneous setting. This is discussed in detail in Remark B.4. In view of its prominence, we discuss Assumption 3.1 at length from four conceivable angles.

Consider the finite set \(\mathcal {P}:=\{\mathbb{P}^{B}: B\in \pi \}\) of mutually singular probability measures. Each random variable \(X\in L^{\infty}\) induces a finite set \(\{\mathbb{P}^{B}\circ X^{-1}: B\in \pi \}\) of loss distributions, depending on the particular reference event \(B\) that obtains. These loss distributions are “objective” and recognised by all agents. In contrast, the likelihoods \(\mathbb{Q}_{i}[B]\) of the occurrence of the reference events \(B\in \pi \) are subjective and subject to potential disagreement. Consequently, if two random variables \(X,Y\in L^{\infty}\) agree in distribution under each \(\mathbb{P}^{B}\in \mathcal {P}\), (3.1) implies that \(X\sim _{\mathbb{Q}_{i}} Y\) for \(i\in [n]\). Hence \(\rho _{1},\ldots ,\rho _{n}\) are \(\mathcal {P}\)-based risk measures, a notion recently introduced in Wang and Ziegel [54]. Whenever two random variables \(X,Y\in L^{\infty}\) satisfy \(X\sim _{\mathbb{P}^{B}}Y\) for all \(\mathbb{P}^{B}\in \mathcal {P}\), then \(\rho _{i}(X)=\rho _{i}(Y)\) for \(i\in [n]\). The present case of mutually singular measures in \(\mathcal {P}\) enjoys particular prominence in [54].

Second, it seems immediate to ask how Assumption 3.1 is reflected by the \(\mathbb{Q}_{i}\)-consistent risk measures \(\rho _{i}\) used by the agents in the risk-sharing problem. A complete answer is provided by Theorem 3.2, the main result of this section. It translates Assumption 3.1 as a relaxed notion of dilatation-monotonicity common to all \(\rho _{i}\). We call a function \(\varphi \colon L^{\infty}\to \mathbb{R}\) ℙ-dilatation-monotonic if for every \(X\in L^{\infty}\) and every sub-\(\sigma \)-algebra \(\mathcal {G}\subseteq \mathcal {F}\), we have

$$ \varphi (\mathbb{E}_{\mathbb{P}}[X|\mathcal {G}])\le \varphi (X).$$
(3.2)

We say that \(\varphi \) is ℙ-dilatation-monotonic above a sub-\(\sigma \)-algebra \(\mathcal {H}\subseteq \mathcal {F}\) if (3.2) holds for all \(X\in L^{\infty}\) and all sub-\(\sigma \)-algebras \(\mathcal {G}\supseteq \mathcal {H}\). While the former notion of dilatation-monotonicity is standard in the literature (see e.g. Cherny and Grigoriev [19], Rahsepar and Xanthos [49] and the references therein for more information), dilatation-monotonicity above a threshold sub-\(\sigma \)-algebra seems to be less common.

Theorem 3.2

Suppose that for each \(i\in [n]\), \(\mathbb{Q}_{i}\approx \mathbb{P}\) and \(\rho _{i}\) is a \(\mathbb{Q}_{i}\)-consistent risk measure. Then the following are equivalent:

1) The probability measures \((\mathbb{Q}_{1},\ldots ,\mathbb{Q}_{n})\) can be chosen to satisfy Assumption 3.1.

2) Each \(\rho _{i}\) is ℙ-dilatation-monotonic above a common finite \(\sigma \)-algebra \(\mathcal {H}\subseteq \mathcal {F}\).

If \(\mathcal {G}\) is coarser than ℱ, the conditional expectation \(\mathbb{E}_{\mathbb{P}}[X|\mathcal {G}]\) displays less variability than the initial random variable \(X\). In this sense, \(\mathcal {G}\) can be seen as a gain of information while \(\mathbb{E}_{\mathbb{P}}[X|\mathcal {G}]\) is usually interpreted as the “best approximation” of \(X\) under the probability measure ℙ using the information provided by \(\mathcal {G}\). Dilatation-monotonicity of a risk measure now rewards decreased variability by not increasing the measured risk. Item 2) in Theorem 3.2 retains this intuition provided that the information is sufficient to decide which one of a set \(\mathcal {H}\subseteq \mathcal {G}\) of reference events occurs. In that case, each \(\rho _{i}\) rewards replacing \(X\) by its best approximation \(\mathbb{E}_{\mathbb{P}}[X|\mathcal {G}]\) under the universally shared probability model ℙ. Otherwise, the information is deemed too coarse, and agents withdraw to their potentially heterogeneous models \(\mathbb{Q}_{i}\).

Third, each event \(B\) in the finite measurable partition \(\pi \) from Assumption 3.1 can be understood as the occurrence of an exogenous shock or a test event used in a backtesting procedure. Asimit et al. [7] for instance speak about “exogenous environments”. In our setting, while agents disagree about the likelihood of those shocks, their respective relevance or conditional distributional implications are consensus. This is very similar to Marshall [48] who studies optimal insurance contracts under belief heterogeneity. A random loss there is modelled by a random variable \(X\ge 0\), the decision maker expresses probabilistic beliefs with a probability measure ℙ, and the insurer with a probability measure ℚ. One of the case studies in that paper, see [48, Sect. 2], assumes in our terminology that

$$ \mathbb{Q}[X=0]< \mathbb{P}[X=0] \qquad \text{and} \qquad \mathbb{P}^{ \{X>0\}}\circ X^{-1}=\mathbb{Q}^{\{X>0\}}\circ X^{-1}. $$
(3.3)

Equation (3.3) means that the decision maker is more optimistic about the absence of losses than the insurer. Comparing this to (3.1), one sees that the events \(\{X=0\}\) and \(\{X>0\}\) could play the role of shocks whose occurrence decision maker and insurer have potentially diverging opinions about, but whose consequences for the conditional distribution of \(X\) are acknowledged by both agents. In a backtesting context, Cambou and Filipović [14] impose Assumption 3.1 verbatim in their study of scenario aggregation. The latter problem is faced by a financial company validating (or rejecting) their internal probabilistic model on the basis of evaluating selected adverse test events sufficiently conservatively; see [14, Sect. 5]. Last but not least, [54] motivate scenario-based risk measures in the same vein.

Fourth and last, Assumption 3.1 can be phrased in the language of statistics. Recall that a sub-\(\sigma \)-algebra \(\mathcal {H}\subseteq \mathcal {F}\) is sufficient for \(\{\mathbb{Q}_{1},\ldots ,\mathbb{Q}_{n}\}\) if all bounded random variables \(f\colon \Omega \to \mathbb{R}\) admit a common version of the conditional expectation \(\mathbb{E}_{\mathbb{Q}_{i}}[f|\mathcal {H}]\) for \(i\in [n]\). Interpretationally, this condition expresses that complexity reduction in statistical experiments is feasible without implicitly requiring information about an unknown parameter (whose estimation usually is the goal).

Proposition 3.3

A vector \((\mathbb{Q}_{1},\dots ,\mathbb{Q}_{n})\) of equivalent probability measures on \((\Omega ,\mathcal {F})\) satisfies Assumption 3.1under \(\mathbb{P}=\mathbb{Q}_{1}\) if and only if there is a finite sub-\(\sigma \)-algebra \(\mathcal {H}\subseteq \mathcal {F}\) which is sufficient for \(\{\mathbb{Q}_{1},\dots ,\mathbb{Q}_{n}\}\).

For a thorough discussion of the relation between statistics, decision making and risk analysis, we refer to Cerreia-Vioglio et al. [17].

In view of Proposition 3.3, it should be clear that under Assumption 3.1, ℙ only plays the role of a weak gauge, determining with its nullsets the equivalence class of nonatomic probability measures within which all \(\mathbb{Q}_{i}\), \(i\in [n]\), are located. In fact, ℙ can always be chosen among the \(\mathbb{Q}_{i}\). For our analysis, it therefore serves as a somewhat arbitrary point of reference.

The equivalence of appearing reference probabilities is crucial though. If all risk measures involved in the risk-sharing procedure are admissible, this has already been motivated by Lemma 2.2, 1). However, Theorem 4.1 does not impose this assumption, so that a more intrinsic reason for the equivalence assumption among all the \(\mathbb{Q}_{i}\) is warranted. Indeed, in a risk-sharing scheme where equivalence fails, an agent could take on arbitrarily bad outcomes on a nullset from their own perspective that is a relevant ground for improvement for other involved agents. Intuitively, the existence of such splitting procedures should preclude the existence of optimal risk-sharing schemes. This phenomenon is illustrated in the following example.

Example 3.4

Suppose ℙ, ℚ are atomless probability measures on \((\Omega ,\mathcal {F})\) for which we can find \(0< p<1\) and disjoint events \(N_{\mathbb{P}}\), \(N_{\mathbb{Q}}\) in ℱ such that \(\mathbb{P}[N_{\mathbb{P}}]=\mathbb{Q}[N_{\mathbb{Q}}]=0\) and \(\mathbb{Q}[N_{\mathbb{P}}],\mathbb{P}[N_{\mathbb{Q}}]>p\). Consider \(\rho _{1}={\mathrm{ES}}_{p}^{\mathbb{P}}\) and \(\rho _{2}={\mathrm{ES}}_{p}^{\mathbb{Q}}\). A direct computation shows that \(\rho _{1}(-\mathbf{1}_{N_{\mathbb{Q}}}+\mathbf{1}_{N_{\mathbb{P}}})<0\) and \(\rho _{2}(\mathbf{1}_{N_{\mathbb{Q}}}-\mathbf{1}_{N_{\mathbb{P}}})<0\). Hence

$$ \inf _{(X_{1},X_{2})\in \mathbb{A}_{0}}\! \big(\rho _{1}(X_{1})+\rho _{2}(X_{2}) \big)\le \inf _{n\in \mathbb{N}} \big(\rho _{1}(-n\mathbf{1}_{N_{ \mathbb{Q}}}+n\mathbf{1}_{N_{\mathbb{P}}})+\rho _{2}(n\mathbf{1}_{N_{ \mathbb{Q}}}-n\mathbf{1}_{N_{\mathbb{P}}}) \big)=-\infty . $$

Thus no optimal allocation of \(X=0\) can exist.

4 The main result

For \(X\in L^{\infty}\), we denote by

$$ \mathbb{A}_{X}:=\{\mathbf {X}\in (L^{\infty})^{n}: X_{1}+\cdots +X_{n}=X \} $$

the set of all allocations of \(X\). Our problem of interest concerns \(\mathbb{Q}_{i}\)-consistent risk measures \(\rho _{i}\) on \(L^{\infty}\), where \(\mathbb{Q}_{i}\approx \mathbb{P}\) is some probability measure for \(i\in [n]\). For \(X\in L^{\infty }\), we aim to solve the problem

$$ \sum _{i=1}^{n}\rho _{i}(X_{i})\longrightarrow \min ! \qquad \text{subject to }\mathbf {X}\in \mathbb{A}_{X}.$$
(4.1)

The associated infimal convolution \(\rho :=\Box _{i\in [n]}\rho _{i}\) gives precisely the optimal value of (4.1). The functional \(\rho \) is known to be cash-additive and monotonic, i.e., \(\rho \) is a monetary risk measure if \(\mbox{dom}(\rho )\) is nonempty. An allocation \(\mathbf {X}\in \mathbb{A}_{X}\), \(X\in L^{\infty}\), is optimal if \(\mathbf {X}\) solves problem (4.1), i.e.,

If an optimal allocation of \(X\) exists, we say that \(\rho \) is exact at \(X\).

Theorem 4.1

Suppose that

(i) the probability measures \(\mathbb{Q}_{1},\ldots ,\mathbb{Q}_{n}\) satisfy Assumption 3.1;

(ii) for each \(i\in [n]\), \(\rho _{i}\) is a \(\mathbb{Q}_{i}\)-consistent risk measure;

(iii) the risk measures \(\rho _{1},\ldots ,\rho _{n-1}\) are admissible, and for all \(i\in [n-1]\), there is \(D_{i}\in C(\rho _{i})\) such that \(\rho _{k}^{*}(D_{i})<\infty \) for all \(k\in [n]\).

Then for each \(X\in L^{\infty}\), there is an optimal allocation \(\mathbf {X}\in \mathbb{A}_{X}\).

4.1 Discussion of assumption (iii)

Assumptions (i) and (ii) of Theorem 4.1 have been discussed in detail in Sects. 2–3. We therefore turn directly to assumption (iii) and discuss three aspects thereof.

First, assume for the moment that all risk measures \(\rho _{1},\ldots ,\rho _{n}\) are admissible. Then (iii) is implied by the simpler condition

$$ \rho ^{*}_{k}\bigg(\frac{{\mathrm{d}}\mathbb{Q}_{i}}{{\mathrm{d}}\mathbb{P}} \bigg)< \infty , \qquad \forall i\in [n-1], \forall k\in [n]. $$
(4.2)

Incidentally, in case \(n=2\), this is essentially the key Assumption 2.1 of Acciaio and Svindland [3]. This requirement has a clear interpretation if all the \(\rho _{i}\) are classical convex risk measures, in which case the probability densities in \(\mbox{dom}(\rho _{i}^{*})\cap L^{1}\) are “plausible probabilistic models that are taken more or less seriously” (see Föllmer and Weber [31]) by agent \(i\) depending on the size of \(\rho ^{*}_{i}\). Each reference model \(\frac{{\mathrm{d}}\mathbb{Q}_{i}}{{\mathrm{d}}\mathbb{P}}\) plays a fundamental role for agent \(i\), which is underscored by the fact that \(\rho _{i}^{*}(\frac{{\mathrm{d}}\mathbb{Q}_{i}}{{\mathrm{d}}\mathbb{P}})=0\), i.e., \(\frac{{\mathrm{d}}\mathbb{Q}_{i}}{{\mathrm{d}}\mathbb{P}}\) enjoys maximal plausibility from the point of view of \(i\). Equation (4.2) then means that \(\frac{{\mathrm{d}}\mathbb{Q}_{i}}{{\mathrm{d}}\mathbb{P}}\) is also deemed somewhat plausible by the other agents. We can adopt this reasoning in the more general consistent case, in which formula (2.1) holds for \(\rho _{i}^{*}\). However, two admissible risk measures \(\rho _{1}\) and \(\rho _{2}\) can satisfy all assumptions of Theorem 4.1, but fail (4.2).

Example 4.2

Fix an event \(A\in \mathcal {F}\) with \(\mathbb{P}[A]=\frac {1}{2}\) and consider the probability measure \(\mathbb{Q}\approx \mathbb{P}\) defined by \(\frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}=\frac {2}{3}\mathbf{1}_{A}+ \frac {4}{3}\mathbf{1}_{A^{c}}\). We set \(\rho _{1}:={\mathrm{ES}}_{1/5}^{\mathbb{P}}\) and \(\rho _{2}:={\mathrm{ES}}_{1/6}^{\mathbb{Q}}\). One then identifies

$$\begin{aligned} \mbox{dom}(\rho _{1}^{*})&=\{D\in L^{\infty}_{+}: \mathbb{E}_{ \mathbb{P}}[D]=1, D\le 1.25\}, \\ \mbox{dom}(\rho _{2}^{*})&=\{D\in L^{\infty}_{+}: \mathbb{E}_{ \mathbb{P}}[D]=1, D\le 0.8 \,\mathbf{1}_{A}+1.6\,\mathbf{1}_{A^{c}}\}. \end{aligned}$$

It is obvious that \(\rho _{1}^{*}(\frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}})=\rho ^{*}_{2}(1)= \infty \). However, Lemma 2.2, 3) shows that

$$\begin{aligned} 0.76 \,\mathbf{1}_{A}+1.24 \,\mathbf{1}_{A^{c}}=0.3\frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}+0.7(0.8 \,\mathbf{1}A+1.2 \,\mathbf{1}_{A^{c}})\in \mathrm{dom}(\rho_{1}^{*})\cap C(\rho_{2}). \end{aligned}$$

While (4.2) is too restrictive, its perspective can inform the interpretation of assumption (iii) itself. Given \(i\in [n-1]\) and the admissible risk measure \(\rho _{i}\), its compatible densities \(C(\rho _{i})\) are dense in \(\mbox{dom}(\rho _{i}^{*})\cap L^{1}\), but more plausible in the sense of being less extreme than models outside \(C(\rho _{i})\). Assumption (iii) means that within this set, we find a density \(D_{i}\) that enjoys a certain degree of confidence by all agents involved.

As a second remark, note that assumption (iii) is stronger than the requirement

$$ \bigcap _{i=1}^{n}\mbox{dom}(\rho _{i}^{*})\neq \emptyset .$$
(4.3)

On its own, (4.3) is insufficient to guarantee the existence of optimal allocations (see Example 4.5), and it is weaker than assumption (iii) (see Example 4.3). However, it is an “almost necessary” requirement in the following sense: whenever \(\rho_{1} ,\dots , \rho_{n}\) are convex risk measures whose infimal convolution \(\rho =\Box _{i\in [n]}\rho _{i}\) takes only finite values, (4.3) must be satisfied.

Example 4.3

Let \(\pi =\{B_{1},B_{2},B_{3}\}\in \Pi \) be a partition of \(\Omega \) such that \(\mathbb{P}[B_{i}]=\frac {1}{3}\) for \(i\in [3]\). Consider ℚ defined by the ℙ-density \(Q:=\frac {1}{3}\mathbf{1}_{A_{1}}+\mathbf{1}_{A_{2}}+\frac {5}{3} \mathbf{1}_{A_{3}}\). We define law-invariant coherent risk measures \(\rho _{1}\) and \(\rho _{2}\) on \(L^{\infty}\) by

$$\begin{aligned} \rho _{1}(X)&=\sup \bigg\{ \mathbb{E}_{\mathbb{P}}[DX]: \|D-1\|_{ \infty}\le \frac {1}{3}\bigg\} , \\ \rho _{2}(X)&=\sup \bigg\{ \mathbb{E}_{\mathbb{P}}[DX]: \frac {4}{5}Q \le D\le 2Q\bigg\} , \end{aligned}$$

and prove that \(\mbox{dom}(\rho _{1}^{*})\cap \mbox{dom}(\rho _{2}^{*})\) contains no density that is compatible with \(\rho _{1}\) or \(\rho _{2}\). Indeed, one first observes that a probability density \(D\) lies in \(\mbox{dom}(\rho _{1}^{*})\cap \mbox{dom}(\rho _{2}^{*})\) only if

$$ D\mathbf{1}_{A_{1}}=\frac {2}{3}\qquad \mbox{and} \qquad D \mathbf{1}_{A_{3}}=\frac {4}{3}.$$
(4.4)

Concerning \(\rho _{1}\), set \(U:=5\,\mathbf{1}_{A_{3}}-4\,\mathbf{1}_{A_{1}\cup A_{2}}\) and note that for every \(D\in \mbox{dom}(\rho _{1}^{*})\),

$$ \mathbb{E}_{\mathbb{P}}[DU]=9\mathbb{E}_{\mathbb{P}}[D\mathbf{1}_{A_{3}}]-4 \le 9\times \frac {4}{9}-4=0, $$

i.e., \(U\in \mathcal {A}_{\rho _{1}}^{\infty}\). As every \(D\) satisfying (4.4) leads to \(\mathbb{E}_{\mathbb{P}}[DU]=0\), we infer that no density in \(\mbox{dom}(\rho _{1}^{*})\cap \mbox{dom}(\rho _{2}^{*})\) is compatible with \(\rho _{1}\).

Similarly for \(\rho _{2}\), consider \(V=7\, \mathbf{1}_{A_{1}}-2\,\mathbf{1}_{A_{2}\cup A_{3}}\). For all \(D\in \mbox{dom}(\rho _{2}^{*})\), we have \(D\mathbf{1}_{A_{1}} \le \frac {2}{3}\mathbf{1}_{A_{1}}\), whence

$$ \mathbb{E}_{\mathbb{P}}[DV]=9\mathbb{E}_{\mathbb{P}}[D\mathbf{1}_{A_{1}}]-2 \le 9\times \frac {2}{9}-2=0, $$

and \(V\in \mathcal {A}_{\rho _{2}}^{\infty}\) follows. As every \(D\in \mbox{dom}(\rho _{1}^{*})\cap \mbox{dom}(\rho _{2}^{*})\) leads to \(\mathbb{E}_{\mathbb{P}}[DV]=0\), no such density is compatible with \(\rho _{2}\).

A third noteworthy aspect anticipates the role that assumption (iii) plays in the proof of Theorem 4.1. Inspecting its mechanics, one notes that it suffices to demand the existence of finitely additive probabilities \(\nu _{1},\ldots ,\nu _{n-1}\in \bigcap _{i=1}^{n}\mbox{dom}( \rho _{i}^{*})\) such that for all \(k\in[n-1]\),

$$ U\in \mathcal {A}_{\rho _{k}}^{\infty} \text{ and } \mathbb{E}_{\nu _{k}}[U]=0 \qquad \implies\qquad U=0.$$
(4.5)

However, as one might suspect on the basis of Proposition 2.3, 5), this does not increase generality.

Lemma 4.4

Suppose that assumptions (i) and (ii) in Theorem 4.1hold. Then assumption (iii) there is satisfied if and only if (4.5) holds.

Finally, we re-emphasise that Theorem 4.1 only assumes the admissibility of the risk measures \(\rho _{1},\ldots ,\rho _{n-1}\). This permits to include for instance expected loss assessments that price risk linearly, i.e., the \(\mathbb{Q}_{n}\)-consistent, but not admissible risk measure \(\rho _{n} (\,\cdot \,)=\mathbb{E}_{\mathbb{Q}_{n}}[\,\cdot \,]\). If \(\rho _{n}\) is not admissible, Proposition 2.3, 3) simplifies assumption (iii) substantially to the requirement that

$$ \frac{{\mathrm{d}}\mathbb{Q}_{n}}{{\mathrm{d}}\mathbb{P}}\in \bigcap _{i=1}^{n-1}C( \rho _{i}).$$
(4.6)

Moreover, condition (4.2) is precluded unless we are in a homogeneous situation. We can nevertheless also solve the optimal allocation problem if more than one agent measures risk with a non-admissible risk measure. The procedure starts by partitioning \([n]\) into two subsets \(\mathfrak {A}\) (which collects all admissible agents) and \(\mathfrak {B}\) (which collects all non-admissible agents). If there is to be a chance that optimal allocations exist, we must have \(\mathbb{Q}_{j}=\mathbb{Q}_{k}\) for all \(j,k\in \mathfrak {B}\). Define \(\rho _{0}:=\Box _{j\in \mathfrak {B}}\rho _{j}\). For arbitrary \(k\in \mathfrak {B}\), \(\rho _{0}\) is a \(\mathbb{Q}_{k}\)-consistent risk measure (see Mao and Wang [47, Theorem 4.1]). Next, we assume that for this \(k\), we have \(\frac{{\mathrm{d}}\mathbb{Q}_{k}}{{\mathrm{d}}\mathbb{P}}\in \bigcap _{i\in \mathfrak {A}}C(\rho _{i})\). The latter is the correct adaptation of (4.6) and allows applying Theorem 4.1 to allocate \(X\in L^{\infty}\) optimally in the new collective \(\mathfrak {A}\cup \{0\}\). This optimal allocation can then be used to construct an optimal allocation for the initial collective by sharing the portion attributed to agent 0 optimally in the collective \(\mathfrak {B}\). This can be done according to [47, Theorem 4.1].

4.2 Necessity of assumptions

We continue our discussion of Theorem 4.1 by shedding more light on the necessity of the individual assumptions. For the sake of transparency, we consider throughout the case of two agents, i.e., \(n=2\).

Example 4.5

1) Law invariance alone or combined with star-shapedness is not sufficient: It is noteworthy that this can already be illustrated in the homogeneous case in which all reference probability measures agree. Consider constants \(\alpha ,\beta >0\) with \(\alpha +\beta >1\). Let \(\rho _{i}\colon L^{\infty}\to \mathbb{R}\), \(i=1,2\), be defined by

$$\begin{aligned} \rho _{1}(X)&:=\inf \{x\in \mathbb{R}: \mathbb{P}[X\le x]>\alpha \}, \\ \rho _{2}(X)&:={\mathrm{ES}}^{\mathbb{P}}_{\beta}(X). \end{aligned}$$

Both functionals are ℙ-law-invariant risk measures that are positively homogeneous and thus star-shaped. However, \(\rho _{2}\) is a consistent risk measure, while \(\rho _{1}\) is not consistent. Finally, no \(X\in L^{\infty}\) with continuous distribution can be allocated optimally among the two agents (see Liu et al. [42, Proposition 1]).

2) All appearing reference probability measures must be equivalent: This is illustrated already in Example 3.4.

3) Equivalence of reference probability measures alone is not enough: To illustrate this, consider the convex monetary risk measures \(\rho _{1}:=\mbox{Entr}_{1}^{\mathbb{P}}\) and \(\rho _{2}(\,\cdot \,):=\mathbb{E}_{\mathbb{Q}}[\,\cdot \,]\), and assume \(\mathbb{Q}\approx \mathbb{P}\). If \(\rho _{1}\Box \rho _{2}\) were exact at each \(X\in L^{\infty }\), one could reason as in Jouini et al. [37, Example 6.1] and conclude that if \(\rho _{1}\Box \rho _{2}(X)=\rho _{1}(X_{1})+ \rho _{2}(X_{2})\) for some allocation \(\mathbf {X}\in \mathbb{A}_{X}\), then \(\frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}\) would have to be a subgradient of \(\rho _{1}\) at \(X_{1}\), i.e., \(\rho _{1}(X_{1})=\mathbb{E}_{\mathbb{P}}[ \frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}X_{1}]-\rho _{1}^{*}( \frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}})\). By Svindland [52, Lemma 6.1], the identity

$$ \frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}= \frac{\exp (X_{1})}{\mathbb{E}_{\mathbb{P}}[\exp (X_{1})]} $$

must hold. As \(X_{1}\in L^{\infty }\), \(\log \frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}\) must be bounded from above and below, i.e., there must be constants \(0< s< S\) such that \(\mathbb{P}[s\le \frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}\le S]=1\). Clearly, this is not satisfied for all \(\mathbb{Q}\approx \mathbb{P}\).

4) Assumption (iii) cannot be dropped, even if Assumption 3.1holds: Here we use Acciaio and Svindland [3, Example 4.3]. Consider a probability measure \(\mathbb{Q}\approx \mathbb{P}\) with

$$ \mathbb{P}\bigg[\frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}= \frac {1}{2}\bigg]=\mathbb{P}\bigg[ \frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}=\frac {3}{2}\bigg]= \frac {1}{2}$$

and the convex risk measures \(\rho _{1} (\,\cdot \,):=\frac {1}{2}(\mathbb{E}_{\mathbb{P}}[\, \cdot \,]+\mbox{Entr}_{1}^{\mathbb{P}}(\,\cdot \,))\) and \(\rho _{2} (\,\cdot \,) :=\mathbb{E}_{\mathbb{Q}}[\,\cdot \,]\). By [3, Example 4.3], \(\rho _{1}\Box \rho _{2}\) is not exact at all \(X\in L^{\infty}\). Next, we verify that assumption (iii) in Theorem 4.1 fails. As \(\mbox{dom}(\rho _{2})\) is a singleton, we need to check that \(\frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}\notin C(\rho _{1})\). Indeed, setting \(A=\{\frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}=\frac {1}{2}\}\), we consider \(U:=-3\,\mathbf{1}_{A}+\mathbf{1}_{A^{c}}\) and show by a direct computation that \(U\in \mathcal {A}_{\rho _{1}}^{\infty}\). As, however, \(\mathbb{E}_{\mathbb{Q}}[U]=0\), \(\frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}\) cannot be compatible for \(\rho _{1}\).

5) Assumption (iii) without Assumption 3.1is not enough: Let \(\rho _{1}:=\mbox{Entr}_{1}^{\mathbb{P}}\) and assume that \(Q:=\frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}\) is positive ℙ-a.s., but

$$ \mathbb{P}[Q\le \varepsilon ]>0,\qquad \forall \varepsilon >0.$$

Consequently Assumption 3.1 fails. Set

$$\begin{aligned} \rho _{2}(X)&:=\sup \bigg\{ \mathbb{E}_{\mathbb{P}}[DX]: \frac {1}{2}Q \le D\le \frac {3}{2}Q, \mathbb{E}_{\mathbb{P}}[D]=1\bigg\} \\ & \hphantom{:} =\sup \bigg\{ \mathbb{E}_{\mathbb{Q}}[ZX]: \frac {1}{2} \le Z\le \frac {3}{2}, \mathbb{E}_{\mathbb{Q}}[Z]=1\bigg\} \end{aligned}$$

and observe that \(\rho _{2}\) is an admissible ℚ-consistent risk measure with the property that \(Q\in C(\rho _{1})\cap C(\rho _{2})\). If \(\rho _{1}\Box \rho _{2}\) were exact at some \(X\in L^{\infty }\) with optimal allocation \((X_{1},X_{2})\in A_{X}\), the same argument already employed in 3) would lead to a subgradient \(D\in \mbox{dom}(\rho _{2}^{*})\) of \(\rho _{1}\) at \(X_{1}\). Again, we could find \(s>0\) such that \(D\ge s\) ℙ-a.s. However, we should also need that \(\frac {D}{Q}\in [\frac {1}{2},\frac {3}{2}]\) ℙ-a.s., meaning that \(D\le \frac {3}{2} Q\). These two constraints on \(D\) are irreconcilable.

4.3 A comparison to interior-point conditions

In this subsection, we address the question whether there is a valid mathematical approach to establishing the existence of optimal allocations among heterogeneous agents that could serve as an alternative to Theorem 4.1. At least in the convex case, interior-point conditions come to mind that are studied in Rüschendorf [50, Chap. 11.4.3] for convex risk functionals and that originate in the abstract study of infimal convolutions in convex analysis. For the sake of clarity, we consider \(n=2\) agents and look at the first two sufficient conditions in [50, Proposition 11.41]. These are

$$ \mbox{dom}(\rho _{1}^{*})\cap \mbox{int}\big( \mbox{dom}(\rho _{2}^{*})\big)\neq \emptyset ,$$
(4.7)
$$ \textstyle\begin{array}{c} \text{for each }\mu \in \mathrm{ba}\text{ and function }g_{\mu}\colon \mathbb{R}\ni t\mapsto t\mu , \\ 0\mbox{ is an interior point of }g_{\mu}^{-1}\big( \mbox{dom}(\rho _{1}^{*})-\mbox{dom}(\rho _{2}^{*})\big).\end{array} $$
(4.8)

Unfortunately, (4.7) and (4.8) are never satisfied by cash-additive risk measures. More promising is a condition inspired and implied by equation (11.124) in [50, Proposition 11.41]; this reads

$$ \textstyle\begin{array}{c} \text{for all }(\mu _{1},\mu _{2})\in \mbox{dom}(\rho _{1}^{*}) \times \mbox{dom}(\rho _{2}^{*}), \\ 0\mbox{ is an interior point of }g_{\mu _{1}-\mu _{2}}^{-1} \big(\mbox{dom}(\rho _{1}^{*})-\mbox{dom}(\rho _{2}^{*}) \big).\end{array} $$
(4.9)

If Assumption 3.1 holds and assumption (iii) in Theorem 4.1 is replaced by (4.9), a similar proof delivers the existence of optimal allocations. However, in addition to potential difficulties in verifying that (4.9) holds true, its value is extremely limited already in a homogeneous situation.

Proposition 4.6

Suppose \(n=2\) and \(\rho _{i}\) is a \(\mathbb{Q}_{i}\)-consistent risk measure for \(i=1,2\). Then:

1) If (4.9) is satisfied and \(\rho _{2}\) is not admissible, then also assumption (iii) from Theorem 4.1holds.

2) Suppose that

$$ \mbox{dom}(\rho _{1}^{*})\not \subset L^{\infty},\qquad \mbox{dom}(\rho _{2}^{*})\cap L^{1}\subseteq L^{\infty}, \qquad \frac{{\mathrm{d}}\mathbb{P}}{{\mathrm{d}}\mathbb{Q}_{1}}, \frac{{\mathrm{d}}\mathbb{Q}_{2}}{{\mathrm{d}}\mathbb{P}}\in L^{\infty}. $$

Then (4.9) fails.

Proposition 4.6, 2) reveals a wide array of situations in which assumption (iii) holds, but (4.9) fails; for instance, we can take \(\rho _{1}=\mbox{Entr}^{\mathbb{P}}_{\beta}\) and \(\rho _{2}={\mathrm{ES}}_{p}^{\mathbb{P}}\) for \((\beta ,p)\in (0, \infty )\times [0,1)\).

4.4 Shape of optimal allocations

One of the key findings in many (monetary) risk-sharing situations under a single homogeneous reference measures is that comonotonic optimal risk allocations can be found. Let ℭ denote the set of all functions \(f\colon \mathbb{R}\to \mathbb{R}^{n}\) for which each coordinate \(f_{i}\) is nondecreasing and which satisfy \(\sum _{i=1}^{n}f_{i}={\mathrm{id}}_{\mathbb{R}}\). In particular, each coordinate \(f_{i}\) of \(f\in \mathfrak {C}\) is 1-Lipschitz-continuous. We call the elements of ℭ comonotonic functions. For \(f\in \mathfrak {C}\), we abbreviate by \(\widetilde{f}\) the normalised function \(f-f(0)\). Given \(X\in L^{\infty}\), an allocation \(\mathbf {X}\in \mathbb{A}_{X}\) is called comonotonic if \(\mathbf {X}=f(X)\) for some \(f\in \mathfrak {C}\), i.e., the allocation is obtained by applying a comonotonic function to the aggregated quantity \(X\).

The proofs in Appendix E demonstrate that optimal allocations are usually not comonotonic under heterogeneous reference measures, marking a substantial difference between the heterogeneous and the homogeneous case. As an illustration, consider an arbitrary \(\mathbb{Q}\approx \mathbb{P}\), positive constants \(\beta _{1},\beta _{2}>0\) and the convex risk measures \(\rho _{1}={\mathrm{ES}}_{\beta _{1}}^{\mathbb{P}}\) and \(\rho _{2}:={\mathrm{ES}}_{\beta _{2}}^{\mathbb{Q}}\). Then \(\rho _{1}\Box \rho _{2}\) is exact at each \(X\in L^{\infty }\), and the unique optimal risk allocation \((X_{1},X_{2})\) is given by

$$\begin{aligned} X_{1}&=\frac{\beta _{2}}{\beta _{1}+\beta _{2}}X+ \frac{1}{\beta _{1}+\beta _{2}}\log \frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}, \\ X_{2}&=\frac{\beta _{1}}{\beta _{1}+\beta _{2}}X- \frac{1}{\beta _{1}+\beta _{2}}\log \frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}. \end{aligned}$$

The dependence on the density \(\frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}\) typically precludes comonotonicity unless \(\frac{{\mathrm{d}}\mathbb{Q}}{{\mathrm{d}}\mathbb{P}}= 1\), which is the case if and only if \(\mathbb{Q}=\mathbb{P}\).

In order to justify the desirability of comonotonic allocations, let us decompose each risk portion \(f_{i}(X)\) of a comonotonic allocation \(f(X)\) into two parts: \(f_{i}(0)\), a deterministic cost imposed on, or capital injected into the position of, agent \(i\); and the remainder \(\widetilde{f}_{i}(X)\). In actuarial terminology, the \(\widetilde{f}_{i}\) are indemnity functions that satisfy the no-sabotage principle, and each \(\widetilde{f}_{i}(X)\) reflects minimal rationality and fairness considerations of the agents involved in the risk-sharing scheme. If \(X>0\), i.e., a loss is produced at the system level, then \(0\le \widetilde{f}_{i}(X)\le X\), i.e., no agent \(i\in [n]\) makes a gain via \(\widetilde{f}_{i}(X)\) and the portions \(\widetilde{f}_{i}(X)\) never exceed the total net loss \(X\). Symmetrically, if \(X<0\) and a gain is obtained at a cumulated level, then \(X\le \widetilde{f}_{i}(X)\le 0\) and no agent incurs a loss via \(\widetilde{f}_{i}(X)\). Moreover, in the tradition of Huberman et al. [35], the nondecreasing nature of \(\widetilde{f}_{i}\) is interpreted as the absence of ex post moral hazard potentially incentivising agents to misreport their losses. By definition, the deterministic cash transfers \((f_{i}(0))_{i\in [n]}\in \mathbb{R}^{n}\) satisfy \(\sum _{i=1}^{n}f_{i}(0)=0\). Given that individual risk measures are cash-additive, deterministic capital transfers among agents – which could be perceived as unfair – can be eliminated without losing optimality, leading to the new optimal allocation \(\widetilde{f}(X)\) of \(X\). This “rebalancing of cash” can alternatively be justified by solving a second optimisation problem and selecting an optimal comonotonic function \(g\in \mathfrak {C}\) whose cash transfers \(g(0)\) are closest to a uniform distribution among agents; in other words, one additionally minimises the function \(\Xi \colon \mathfrak {C}\to \mathbb{R}\) defined by

$$ \Xi (f):=\min \bigg\{ \sum _{i=1}^{n}|f_{i}(0)-x|^{2}: x\in \mathbb{R} \bigg\} =\sum _{i=1}^{n}\bigg(f_{i}(0)-\frac {1}{n}\sum _{j=1}^{n}f_{j}(0) \bigg)^{2} $$

among all \(f\in \mathfrak {C}\) defining an optimal allocation.

In the heterogeneous case and under Assumption 3.1, the optimal allocations whose existence is verified in Theorem 4.1 are only locally comonotonic; see Appendix B. More precisely, if \(\pi \in \Pi \) is as in (3.1), one finds an optimal family \((f^{B})_{B\in \pi}\subseteq \mathfrak {C}\) of comonotonic functions such that

$$ X_{i}:=\sum _{B\in \pi}f_{i}^{B}(X)\mathbf{1}_{B},\qquad i\in [n],$$

defines an optimal allocation. Two observations ensue: The potential loss of comonotonicity is a consequence of the heterogeneity of reference measures, not of other properties of the risk measures. Second, locally comonotonic allocations split into a \(\pi \)-dependent cash transfer \(\sum _{B\in \pi}f_{i}(0)\mathbf{1}_{B}\) reflecting the heterogeneity structure and \(B\)-dependent indemnity schedules \(\sum _{B\in \pi}\widetilde{f}_{i}(X)\mathbf{1}_{B}\) applied to the aggregated loss \(X\).

Note that by Liebrich and Munari [40, Theorem 5.7], the risk measures \(\rho _{i}\) for \(i\in [n]\) cannot behave additively on span \(\{\mathbf{1}_{B}: B\in \pi \}\). Hence rebalancing of cash and eliminating cash transfers among agents in the way described above becomes impossible. This important distinctive feature of the heterogeneous case has been emphasised multiple times in this paper already. As a workaround, one can take the alternative approach to rebalancing cash, select a quality criterion \(\Xi \) measuring “unfairness”, and try to minimise it among all optimal allocations.

4.5 Infimal convolution preserves \(\mathcal {P}\)-basedness

Let us once again consider the situation of a homogeneous reference measure ℙ in which comonotonic optimal allocations can be found. As an important consequence, the infimal convolution preserves ℙ-law-invariance, i.e., the optimal value in (4.1) depends only on the distribution of the aggregated loss \(X\) under ℙ. For a general study of infimal convolutions preserving law-invariance under a single reference measure, we refer to Liu et al. [44].

However, Theorem 4.1 also applies to heterogeneous reference measures, and the lack of comonotonicity of optimal allocations outlined in Sect. 4.4 shows that one cannot expect the infimal convolution to be law-invariant with respect to some reference measure. Instead, the next corollary records that the infimal convolution operation preserves \(\mathcal {P}\)-basedness of the individual risk measures discussed in Sect. 3. This is an important addendum to Wang and Ziegel [54].

Corollary 4.7

In the situation of Theorem 4.1, let \(\pi \in \Pi \) be a finite measurable partition as in (3.1). Consider the set \(\mathcal {P}:=\{\mathbb{P}^{B}: B\in \pi \}\) of conditional probability measures. Then the infimal convolution \(\rho =\Box _{i\in [n]}\rho _{i}\) is \(\mathcal {P}\)-based: If we have \(X\sim _{\mathbb{P}^{B}}Y\) for \(X,Y\in L^{\infty}\) and all \(B\in \pi \), then \(\rho (X)=\rho (Y)\).