Abstract
In this paper, we address the problem of optimal dividend payout strategies from a surplus process governed by Brownian motion with drift under a drawdown constraint, i.e., the dividend rate can never decrease below a given fraction \(a\) of its historical maximum. We solve the resulting two-dimensional optimal control problem and identify the value function as the unique viscosity solution of the corresponding Hamilton–Jacobi–Bellman equation. We then derive sufficient conditions under which a two-curve strategy is optimal, and we show how to determine its concrete form using calculus of variations. We establish a smooth-pasting principle and show how it can be used to prove the optimality of two-curve strategies for sufficiently large initial and maximum dividend rates. We also give a number of numerical illustrations in which the optimality of the two-curve strategy can be established for instances with smaller values of the maximum dividend rate and the concrete form of the curves can be determined. One observes that the resulting drawdown strategies nicely interpolate between the solution for the classical unconstrained dividend problem and that for a ratcheting constraint as recently studied in Albrecher et al. (SIAM J. Financial Math. 13:657–701, 2022). When the maximum allowed dividend rate tends to infinity, we show a surprisingly simple and somewhat intriguing limit result in terms of the parameter \(a\) for the surplus level above which, for a sufficiently large current dividend rate, a take-the-money-and-run strategy is optimal in the presence of the drawdown constraint.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and model
Assume that the surplus process of a company is given by a Brownian motion with drift,
where \(W\) is a standard Brownian motion, and \(\mu > 0\), \(\sigma >0\) are given constants. Let \((\Omega ,\mathcal{F}, ( \mathcal{F}_{t} ) _{t\geq 0},\mathbb{P})\) be the complete probability space generated by the Brownian motion \((W_{t})_{t\geq 0}\). Assume further that the company uses part of the surplus to pay dividends to the shareholders with rates in a set \([0,\overline{c}]\), where \(\overline{c}>0\) is the maximum dividend rate possible. Let \(D_{t}\) denote the rate at which the company pays dividends at time \(t\); then the controlled surplus process can be written as
We assume that the process \((D_{t})_{t\geq 0} \) is progressively measurable. Thus \(\int _{0}^{\cdot }D_{s}ds\) and correspondingly \(X^{D}\) are continuous adapted processes. Note that since \(\mathcal{F}_{t}=\mathcal{F}_{t{-}}\), any adapted process is predictable.
It is a classical problem in risk theory to find a dividend strategy \(D=\left ( D_{t}\right ) _{t\geq 0}\) that maximises the reward function given by the expected sum of discounted dividend payments,
over a set of admissible candidate strategies. Here \(q>0\) is a discount factor and \(\tau = \inf \{ t\geq 0:X_{t}^{D}<0 \} = \tau _{x}\) is the ruin time of the controlled process. De Finetti [15] was the first to consider a problem of this kind for a simple random walk, and Gerber [19, 20] considered extensions, including the diffusion setup (1.1) given above; see also Shreve et al. [29]. For a finite maximum dividend rate \(\overline{c}\), this problem was then further investigated by Jeanblanc and Shiryaev [23], Radner and Shepp [27], Asmussen and Taksar [7] and Gerber and Shiu [21]. Since then, a lot of variants of this problem for the process (1.1) and more general underlying risk processes have been considered; see e.g. the surveys Albrecher and Thonhauser [4] and Avanzi [8]. For the diffusion model (1.1), we recently studied in Albrecher et al. [1] this optimal dividend problem under a ratcheting constraint, i.e., under the assumption that the dividend rate can never be decreased over the lifetime of the process, which renders the respective control problem two-dimensional, where the first dimension is the current surplus and the second dimension is the currently employed dividend rate. One motivation to consider that constraint was that it may be psychologically preferable for shareholders to not experience a decrease of dividend payments, and it is interesting to see to what extent such a constraint leads to an overall performance loss.
In this paper, we go one step further and allow reductions of the dividend rate over time, but only up to a certain percentage \(a\) of the largest already exercised dividend rate (“drawdown”). More formally, a dividend drawdown strategy \(D= ( D_{t} ) _{t\geq 0}\) with drawdown constraint \(a\in [ 0,1]\) is one that satisfies \(D_{t}\in [ aR_{t},\overline{c}]\), where \(R_{t}\) is the running maximum of the dividend rate, that is,
here we denote the initial dividend rate by \(R_{0{-}}=c\). A dividend drawdown strategy is called admissible if it is progressive with respect to the filtration \(\left ( \mathcal{F}_{t}\right ) _{t\geq 0}\).
Define \(\Pi _{x,c,a}^{[0,\overline{c}]}\) as the set of all admissible dividend drawdown strategies with initial surplus \(x\geq 0\), initial running maximum dividend rate \(c\in [ 0,\overline{c}]\) and drawdown constraint \(a\in [ 0,1]\). Given \(D\in \Pi _{x,c,a}^{[0,\overline{c}]}\), the reward function of this strategy is given by (1.2). Hence, for any triple \((x,c,a)\), our aim in this paper is to maximise
Note that the limit case \(a=1\) corresponds to the ratcheting case (considered previously in Albrecher et al. [1]), and the limit case \(a=0\) corresponds to the optimisation of bounded dividend rates without any drawdown constraint.
Drawdown phenomena have been studied in various contexts in the literature. On the one hand, drawdown times and properties of uncontrolled stochastic processes were investigated in quite some generality (see for instance Landriault et al. [25] for the case of Lévy processes). In the context of control problems, drawdown constraints on the wealth have been considered in portfolio problems in the mathematical finance literature; see for instance Elie and Touzi [18], Chen et al. [14] and Kardaras et al. [24]. For a minimisation of drawdown times of a risk process through dynamic reinsurance, see Brinker [11] and Brinker and Schmidli [12]. Our context, however, is different, as we are interested in implementing a drawdown constraint on the payment structure of the dividend rates, i.e., as a constraint on the admissible dividend policies. In that sense, our approach is more closely related to problems of lifetime consumption in the mathematical finance literature; see Angoshtari et al. [5] who extend Dusenberry’s ratcheting problem of consumption studied by Dybvig [16] to drawdown constraints. However, the concrete model setup and embedding, and also the involved techniques there, are very different from dividend problems of the De Finetti type as studied in this paper.
After deriving some basic analytic properties of the value function \(V_{a}^{\overline{c}}(x,c)\) of our drawdown problem in Sect. 3, we derive a Hamilton–Jacobi–Bellman equation for \(V_{a}^{\overline{c}}(x,c)\) in Sect. 4 and show that \(V_{a}^{\overline{c}}(x,c)\) is its unique viscosity solution with suitable boundary conditions. We then, in Sect. 5, briefly study in more detail the value function when one already starts at the maximal dividend rate \(\overline{c}\), which serves as a crucial ingredient for the analysis of \(V_{a}^{\overline{c}}(x,c)\) in Sect. 6. Sufficient conditions are given under which the optimal strategy for bounded dividend rates is a two-curve strategy in the space \((0,\infty )\times [ 0,\overline{c}]\) for \((x,c)\), which is partitioned by two curves \(\gamma ^{\overline{c}}(c)\) and \(\zeta ^{\overline{c}}(c)\) with \(\gamma ^{\overline{c}}(c)<\zeta ^{\overline{c}}(c)\) for all \(c\in [ 0,\overline{c}]\). If for a given \(c\), we have \(x<\gamma ^{\overline{c}}(c)\), then dividends are paid at rate \(ac\); if \(\gamma ^{\overline{c}}(c)\leq x\leq \zeta ^{\overline{c}}(c)\), then dividends are paid at rate \(c\); finally, if \(x>\zeta ^{\overline{c}}(c)\), then the dividend rate \(c\) is increased immediately until \(x=\zeta ^{\overline{c}}(c_{1})\) for some \(c_{1}\in (c,\overline{c})\) (or \(c=\overline{c}\), whichever happens first) is reached. We furthermore establish a smooth-pasting principle for these optimal curves. In Sect. 7, it is shown that the limits of \(\gamma ^{\overline{c}}(\overline{c})\) and \(\zeta ^{\overline{c}}(\overline{c})\) as \(\overline{c}\rightarrow \infty \) are finite and given by the surprisingly explicit formulas
This nicely extends the respective limit \(2\mu /q\) of the ratcheting curve that was identified for pure ratcheting (\(a=1\)) in [1, Lemma 5.21]. In Sect. 8, we then look further into the limiting case and show that for sufficiently large \(\overline{c}\), one has \(\gamma ^{\overline{c}}(c)\nearrow \gamma ^{\overline{c}}( \overline{c})\) and \(\zeta ^{\overline{c}}(c)\searrow \zeta ^{\overline{c}}(\overline{c})\) as \(c\rightarrow \overline{c}\). This enables us to establish the general optimality of two-curve strategies whenever the current dividend rate \(c\) and the maximal dividend rate \(\overline{c}\) are sufficiently large. At the same time, the negative derivative of \(\zeta ^{\overline{c}}(c)\) close to (sufficiently large) \(\overline{c}\) is notably different from the pure ratcheting case (\(a=1\)), for which it was shown in [1] that the corresponding derivative is positive for all \(c\) close to \(\overline{c}\) (and indeed the leading term in the asymptotics of \(0< a<1\) breaks down for \(a=1\) so that some sort of phase transition happens). The simplicity of the right-hand limit in (1.4) and in particular the appearance of the square-root of the drawdown coefficient \(a\) in the right-hand limit are somewhat intriguing. In the absence of an upper limit for the dividend rate, it identifies the minimum surplus level \(x\) above which, for sufficiently large current dividend rate, it is preferable to pay out all the surplus \(x\) immediately and generate ruin by doing so (a so-called “take-the-money-and-run” strategy, see e.g. Loeffen and Renaud [26]), and that value does not depend on the size of the volatility \(\sigma \). Consequently, one can get some intuition on this result in the much simpler deterministic model with \(\sigma =0\), which we therefore consider in Sect. 2 before approaching the general case \(\sigma >0\) in the rest of the paper. We give numerical illustrations in Sect. 9, where we establish the optimality of two-curve strategies also for smaller magnitudes of \(c\) and \(\overline{c}\) by numerically showing that the sufficient conditions from Sect. 6 are satisfied. We obtain the optimal curves by calculus of variation techniques and discuss the properties of the value functions of the drawdown dividend problem and their comparison to classical and ratcheting solutions for various parameter combinations. Finally, Sect. 10 concludes. Appendix A contains the proofs of the results of Sect. 6 together with some auxiliary lemmas, and Appendix B collects some longer formulas appearing in Sects. 7 and 8 in compact form.
2 Some intuition from the deterministic case
Assume in this section for simplicity a completely deterministic model
with a positive drift \(\mu >0\) (for the study of such a model in another context in the dividend literature, see e.g. Eisenberg et al. [17]). Then a constant dividend rate \(\overline{c}=\mu \) throughout time keeps the surplus at level \(x\) for all \(t\geq 0\) and correspondingly
for any \(x>0\). Consequently, whenever the initial surplus \(x\) is larger than \(\mu /q\), paying out all the surplus at the beginning (causing immediate ruin) is preferable to any other dividend strategy subject to the constraint \(\overline{c}\leq \mu \). At the same time, if a constant dividend rate \(\overline{c}>\mu \) is applied, the controlled process leads to ruin at the time \(t= x/(\overline{c}-\mu )\) and we obtain instead
The latter shows that whenever \(x>2\mu /q\), if allowed to do so, paying out all the surplus \(x\) immediately (and causing immediate ruin) is preferable to any other constant dividend strategy with large \(\overline{c}\). In other words, the potential gain from later ruin and therefore more dividend income (by exploiting the positive drift, without any risk) is outweighed by the discounting of such later dividend payments. This can also be seen as an intuitive explanation of the limit \(2\mu /q\) in Albrecher et al. [1, Lemma 5.21].
Let us now proceed to the case with drawdown. Assume that we start with initial capital \(x>b\) for some \(b\) to be determined and that we pay dividends at rate \(\overline{c}>\mu \) until we reach that lower level \(b\) at time \(t=(x-b)/(\overline{c}-\mu )\), from which time on we reduce the dividend payments to level \(a \overline{c}\) according to our drawdown constraint. In the deterministic model of this section, this then leads to
Taking the derivative with respect to \(b\) and setting it to zero gives, after simple calculations, for large \(\overline{c}\) the optimal level
But if one substitutes that value of \(b\) into (2.1), an expansion at \(\overline{c}=\infty \) gives
The numerator in the second term is negative exactly when
so that in those cases, it is preferable to immediately pay \(x\) as a lump sum dividend and go to ruin immediately (if that is allowed) rather than following the above refracting strategy, as the value \(x\) cannot be realised at any later point in time in view of the discounting, despite the continuing deterministic income with drift \(\mu \). One may expect that the size of the volatility does not matter when \(\overline{c}\to \infty \), and indeed, as a by-product of the results of this paper, it is shown in Sect. 7 that the same result can be established for the general case \(\sigma >0\); cf. Proposition 7.3. Another way to state this is the following: If one defines \(x^{*}(\overline{c})\) as the surplus value for which, when already currently paying the maximum dividend rate \(\overline{c}\), one is indifferent whether to further increase \(\overline{c}\) or not, the above result establishes that \(\lim _{\overline{c}\to \infty}x^{*}(\overline{c})=\frac{\mu}{q}(1+{1}/ \sqrt{a})\), and it is in terms of that notation that the more general result is proved in Sect. 7.
3 Basic results
Recall the definition (1.3) of our value function \(V_{a}^{\overline{c}}(x,c)\) and denote by \(V_{a}^{\infty}(x,c)\) the corresponding function when there is no ceiling on dividend rates, i.e., \(\overline{c}=\infty \). It is immediate to see that \(V_{a}^{\overline{c}}(0,c)=0\) for all \(c\in [ 0,\overline{c}]\) and \(a\in [ 0,1]\).
Remark 3.1
As mentioned in the introduction, the dividend optimisation problem without drawdown constraint has a long history; see e.g. Schmidli [28, Sect. 2.4]. Unlike the drawdown optimisation problem, the problem without the drawdown constraint is one-dimensional. If we denote its value function by \(\overline {V}^{\overline{c}}(x)\), then clearly \(V_{0}^{\overline{c}}(x,c)=\overline {V}^{\overline{c}}(x)\) and \(V_{a}^{\overline{c}}(x,c)\leq \overline {V}^{\overline{c}}(x)\) for all \(x\geq 0\), \(a\in [ 0,1]\) and \(c\in [ 0,\overline{c}]\). The function \(\overline{V}^{\overline{c}}\) is increasing, concave, twice continuously differentiable with \(\overline {V}^{\overline{c}}(0)=0\) and \(\lim _{x\rightarrow \infty}\overline{V}^{\overline{c}}(x)=\overline{c}/q\); so it is Lipschitz with Lipschitz constant \(( \overline{V}^{\overline{c}} ) ^{\prime}(0)\).
Remark 3.2
The dividend optimisation problem without any constraint was addressed by Gerber and Shiu [21] and Schmidli [28, Sect. 2.4]. If \(\overline {V}(x)\) denotes its value function, we have \(\overline{V}(x)=V_{0}^{\infty}(x,c)\) for any \(c>0\). Clearly, \(V_{a}^{\infty}(x,c)\leq \overline{V}(x)\) for all \(a\in [ 0,1]\). The function \(\overline{V}\) is increasing, concave, twice continuously differentiable with \(\overline {V}(0)=0\) and \(x\leq \overline{V}(x)\leq x+\mu /q\); so it is Lipschitz with Lipschitz constant \(\overline {V}{}^{\prime }(0)\).
Proposition 3.3
It holds that \(V_{a}^{\overline{c}}(x,c)\nearrow V_{a}^{\infty}(x,c)\) as \(\overline{c}\rightarrow \infty \).
Proof
It is straightforward that for any \(\overline{c}_{1}\leq \) \(\overline{c}_{2}\), \(V_{a}^{\overline{c}_{1}}(x,c)\leq V_{a}^{\overline{c}_{2}}(x,c)\) \(\leq V_{a}^{\infty}(x,c)\) for \(0\leq c\leq \overline{c}_{1}\). For any \(\varepsilon >0\), take a strategy \(D=(D_{t})_{t\geq 0}\in \Pi _{x,c,a}^{[0,\infty )}\) with ruin time \(\tau \) such that \(V_{a}^{\infty}(x,c)\leq J(x;D)+\varepsilon \). For an increasing sequence \(c_{n}\rightarrow \infty \) with \(c_{1}>c\), consider \(D^{n}=(D_{t}\wedge c_{n})_{t\geq 0}\in \Pi _{x,c,a}^{[0,c_{n}]}\) and let \(\tau ^{n}\geq \tau \) be the ruin time of \(D^{n}\). Then by monotone convergence,
and so we have the result. □
We now state a straightforward result regarding the boundedness and monotonicity of the value functions.
Proposition 3.4
In the case \(\overline{c}<\infty \), the value function \(V_{a}^{\overline{c}}(x,c)\) is bounded by \(\overline {c}/q\) with \(\lim _{x\rightarrow \infty}V_{a}^{\overline{c}}(x)=\overline{c}/q\), nondecreasing in \(x\) and nonincreasing in \(c\).
Proof
By Remark 3.1 and Albrecher et al. [1, Theorem 3.3], we have
with \(\lim _{x\rightarrow \infty}V_{1}^{\overline{c}}(x,c)=\lim _{x \rightarrow \infty}\overline{V}^{\overline{c}}(x)=\overline{c}/q\). So \(V_{a}^{\overline {c}}\) is bounded by \(\overline{c}/q\) with \(\lim _{x\rightarrow \infty}V_{a}^{\overline{c}}(x,c)=\overline{c}/q\).
On the one hand, \(V_{a}^{\overline{c}}(x,c)\) is nonincreasing in \(c\) because given \(c_{1}< c_{2}\leq \overline{c}\), we have \(\Pi _{x,c_{2},a}^{[0,\overline {c}]}\subseteq \Pi _{x,c_{1,a}}^{[0, \overline{c}]}\) for any \(x\geq 0\). On the other hand, given \(0\leq x_{1}< x_{2}\) and an admissible strategy \(D_{1}\in \Pi _{x_{1},c,a}^{[0,\overline{c}]}\) for any \(c\in [ 0,\overline{c}]\), define \(D_{2}\in \Pi _{x_{2},c,a}^{[0,\overline{c}]}\) as \(D_{2,t}= D_{1.t}\) until the ruin time of the controlled process \(X^{D^{1}}\) with \(X_{0}^{D^{1}}=x_{1}\), and pay the maximum rate \(\overline{c}\) afterwards. Thus \(J(x_{1};D_{1})\leq J(x_{2};D_{2})\) and we have the result. □
Proposition 3.5
The function \(V_{a}^{\infty}(x,c)\) is nondecreasing in \(x\) and nonincreasing in \(c\). For the case \(a>0 \), we have \(\lim _{c\rightarrow \infty}V_{a}^{\infty}(x,c)=x\). Moreover, \(x\leq V_{a}^{\infty}(x,c)\leq x+ \mu /q\).
Proof
By Propositions 3.3 and 3.4, \(V_{a}^{\infty}(x,c)\) is nondecreasing in \(x\) and nonincreasing in \(c\). Let us now show that \(V_{a}^{\infty}(x,c)\geq x\). The function \(V_{a}^{\infty}(x,c)\) is bounded from below by the reward function resulting from the strategy of paying a constant rate \(n\) up to ruin. Defining \({\tau}_{n}=\inf \{t:x+(\mu -n)t+\sigma W_{t}=0\}\), one gets
where the last equality follows from Borodin and Salminen [10, Equation 2.0.1].
Finally, let us argue that \(\lim _{c\rightarrow \infty}V_{a}^{\infty}(x,c)\leq x\). For any \(\varepsilon >0\) and for each \(c\), take \(D^{c}=(D_{t}^{c})_{t\geq 0}\in \Pi _{x,c,a}^{[0,\infty )}\) such that
Then \(D^{c}\geq ac\) and the corresponding ruin time is given by
so that
hence
This yields for \(c>\mu /a\) that \(\tau ^{c}<\infty \) a.s. and \(\mathbb{E} [ \tau ^{c} ] \rightarrow 0\) as \(c\rightarrow \infty \). Therefore,
and so we have the result. □
The Lipschitz property of the function \(\overline{V}\) can now be used to prove a global Lipschitz result on the regularity of the value function.
Proposition 3.6
In both the restricted case \(\overline{c}<\infty \) and the unrestricted case \(\overline{c}=\infty \), we have
for all \(0\leq x_{1}\leq x_{2}\) and \(c_{1},c_{2}\in [ 0,\overline{c}]\) with \(c_{1}\leq c_{2}\), with \(K=\max \{\frac{e^{-1}}{q}a,1\} \overline {V}{}^{\prime }(0)\).
Proof
In the case \(\overline{c}<\infty \), by Proposition 3.4, we have
for all \(0\leq x_{1}\leq x_{2}\) and \(c_{1},c_{2}\in [ 0,\overline{c}]\) with \(c_{1}\leq c_{2}\). Let us now show that there exists \(K_{1}>0\) such that
for all \(0\leq x_{1}\leq x_{2}\). Take \(\varepsilon >0\) and \(D\in \Pi _{x_{2},c,a}^{[0,\overline{c}]}\) such that
The associated control process is given by
Let \(\tau \) be the ruin time of the process \(X^{D}\). Define \(\widetilde {D}\in \Pi _{x_{1},c,a}^{[0,\overline{c}]}\) as \(\widetilde{D}_{t}=D_{t}\) and the associated control process
Let \(\widetilde{\tau}\leq \tau \) be the ruin time of the process \(X^{\widetilde{D}}\); then \(X_{t}^{D}-X_{t}^{\widetilde{D}}=x_{2}-x_{1}\) for \(t\leq \widetilde{\tau}\). We can write
The last inequality of (3.3) involves a shift of stopping times and follows from Claisse et al. [13, Theorem 2]. Indeed, the assumptions of this theorem are satisfied because we can write our controlled process as
where \(b(s,x,d)=\mu -d\), \(\sigma (s,x,d)\equiv \sigma \) and \(W\) is a standard Brownian motion. Hence we have
So by Remark 3.2, we have (3.2) with \(K_{1}=\overline {V}{}^{\prime }(0)\).
Let us now show that given \(c_{1},c_{2}\in [ 0,\overline{c}]\) with \(c_{1}\leq c_{2}\), there exists \(K_{2}>0\) with
Take \(\varepsilon >0\) and \(D\in \Pi _{x,c_{1,a}}^{[0,\overline{c}]}\) such that
and denote by \(\tau \) the ruin time of the process \(X^{D}\). Let us consider \(\widetilde{D}\in \Pi _{x,c_{2},a}^{[0,\overline{c}]} \) as \(\widetilde{D}_{t}=\max \{D_{t},ac_{2}\}\), denote by \(X^{\widetilde{D}}\) the associated controlled surplus process and by \(\overline{\tau}\leq \tau \) the corresponding ruin time. We have \(\widetilde{D}_{s}-D_{s}\leq ac_{2}-ac_{1}\) and so \(X_{\overline{\tau}}^{D}= X_{\overline{\tau}}^{D}- X_{\overline{\tau}}^{\widetilde{D}}\leq a(c_{2}-c_{1}) \overline{\tau}\). By Remark 3.2, we have
As before, the last inequality involves a shift of stopping times and follows from Claisse et al. [13, Theorem 2]. Then
Hence we can write
So we get (3.4) with \(K_{2}=K_{1}\max _{t\geq 0}(e^{-qt}ta)=K_{1}\frac{e^{-1}}{q}a \), \(K=K_{1}\max \{\frac{e^{-1}}{q}a,1\}\). We conclude the result from (3.1), (3.2) and (3.4).
In the case \(\overline{c}=\infty \), the result follows from Proposition 3.3. □
The following lemma states the dynamic programming principle. Its proof is similar to the one of Azcue and Muler [9, Lemma 1.2].
Lemma 3.7
Given any stopping time \(\widetilde{\tau}\), we can write in both the restricted case \(\overline{c}<\infty \) and the unrestricted case \(\overline{c}=\infty \) that
We now show a Lipschitz property of \(h(a)=V_{a}^{\overline{c}}(x,c)\) in the drawdown constant \(a\in [ 0,1]\), for fixed \(x\), \(c\) and finite \(\overline{c}\).
Proposition 3.8
Given \(\overline{c}<\infty \) and \(a_{1},a_{2}\in [ 0,1]\) with \(a_{1}< a_{2}\), there exists \(K_{3}>0\) such that
with \(K_{3}=\overline {V}{}^{\prime }(0)\frac{e^{-1}}{q}\overline{c}\) only depending on \(\overline{c}\). In the case \(\overline{c}=\infty \), \(V_{a}^{\infty}(x,c)\) is continuous in \(a\in [ 0,1]\).
Proof
Consider first the case \(\overline{c}<\infty \). Take \(\varepsilon >0\) and \(D\in \Pi _{x,c,a_{1}}^{[0,\overline{c}]}\) such that
Consider \(\widetilde{D}\in \Pi _{x,c,a_{2}}^{[0,\overline{c}]} \) defined as \(\widetilde{D}_{t}=\max \{D_{t},a_{2}R_{t}\}\). Denote by \(X^{\widetilde{D}}\) the associated controlled surplus process and by \(\overline{\tau}\leq \tau \) the corresponding ruin time. We have \(0\leq \widetilde{D}_{s}-D_{s}\leq (a_{2}-a_{1})R_{s}\) and so
We can write
and we obtain the result with \(K_{3}=\overline {V}{}^{\prime }(0)\frac{e^{-1}}{q}\overline{c}\).
In the case \(\overline{c}=\infty \), we want to show that given \(\varepsilon >0\) and \(a_{1}\geq 0\), there exists \(\delta >0\) such that if \(0< a_{2}-a_{1}<\delta \), then \(V_{a_{1}}^{\infty}(x,c)-V_{a_{2}}^{\infty}(x,c)<\varepsilon \). Take \(\overline{c}_{0}\) large enough such that \(V_{a_{1}}^{\infty}(x,c)-V_{a_{1}}^{\overline{c}_{0}}(x,c)<\varepsilon /2\) and \(\delta =\varepsilon /(2\overline {V}{}^{\prime }(0)\frac{e^{-1}}{q}\overline{c}_{0})\). Given any \(a_{2}\in (a_{1},a_{1}+\delta )\), we have
□
Remark 3.9
For \(a=0\), Proposition 3.5 does not hold. Indeed, \(V_{0}^{\infty}(x,c)=\overline{V}(x)\) so that \(\lim _{c\rightarrow \infty}V_{0}^{\infty}(x,c)=\overline{V}(x)>x\). Although \(\lim _{c\rightarrow \infty }V_{a}^{\infty}(x,c)=x\) for \(a\in (0,1]\) and \(\lim _{a\rightarrow 0{+}}V_{a}^{\infty}(x,c)=V_{0}^{\infty}(x,c)\) by Proposition 3.8, the lack of the Lipschitz property of \(V_{a}^{\infty}(x,c)\) at \(a=0\) makes it possible that the iterated limits
do not coincide.
In the next result, we study the continuity of \(V_{a}^{\overline{c}}(x,c)\) with respect to \(\overline{c}\).
Proposition 3.10
Given \(\overline{c}_{1},\overline{c}_{2}\in [ 0,\infty )\) with \(\overline{c}_{1}<\overline{c}_{2}\), there exists \(K_{2}>0\) such that
for \(c\leq \overline{c}_{1}\).
Proof
Take \(\varepsilon >0\) and \(D\in \Pi _{x,c,a}^{[0,\overline{c}_{2}]}\) such that
and denote the ruin time of the process \(X^{D}\) by \(\tau \). Let us consider \(\widetilde{D}\in \Pi _{x,c,a}^{[0,\overline{c}_{1}]} \) as \(\widetilde{D}_{t}=\min \{D_{t},\overline{c}_{1}\}=\overline{c}_{1}I_{\{D_{t}> \overline{c}_{1}\}}+D_{t}I_{\{D_{t}\leq \overline{c}_{1}\}}\) for \(t\leq \tau \) and \(\widetilde{D}_{t}=\overline{c}_{1}\) for \(t>\tau \), denote by \(X^{\widetilde{D}}\) the associated controlled surplus process and by \(\overline{\tau}\geq \tau \) the corresponding ruin time. We then have \(D_{s}-\widetilde{D}_{s}\leq \overline {c}_{2}-\overline{c}_{1}\) and can deduce
□
4 The Hamilton–Jacobi–Bellman equation
In this section, we introduce the Hamilton–Jacobi–Bellman (HJB) equation for the drawdown problem. We show that the value function \(V\) defined in (1.3) is the unique viscosity solution of the corresponding HJB equation with suitable boundary conditions.
As stated in the previous section, the limit case \(a=0\) (no drawdown restriction) has been studied for both \(\overline{c}<\infty \) and \(\overline {c}=\infty \), and the case \(a=1\) (ratcheting) for \(\overline{c}< \infty \).
Define
The HJB equation associated to (1.3) for both \(\overline{c}<\infty \) and \(\overline{c}=\infty \) is given by
The inequality \(\max _{\kappa \in [ ac,c]}\mathcal{L}^{\kappa} (u)(x,c)\leq 0\) comes from the dynamic programming principle in Lemma 3.7, considering the strategies of paying dividends at a constant rate \(\kappa \in [ ac,c]\). For these strategies, the running maximum is \(c\). The inequality \(\partial _{c}u(x,c)\leq 0\) comes from the fact that the value function is nonincreasing in \(c\), and it takes into account the strategies of paying dividends at a constant rate \(\kappa \in (c,\overline{c}]\), where the running maximum increases instantaneously from \(c\) to \(\kappa \).
Note that because the operator \(\mathcal{L}^{k}\) is linear in \(k\), an alternative equivalent formulation of (4.1) is
For the ratcheting case \(a=1\), the HJB equation correspondingly simplifies to
Let us introduce the usual notion of viscosity solution for the HJB equation in both cases \(0<\overline{c}<\infty \) or \(\overline{c}=\infty \).
Definition 4.1
(a) A locally Lipschitz function \(\overline{u}:[0,\infty )\times [ 0,\overline{c})\rightarrow{ \mathbb{R}}\) is a viscosity supersolution of (4.2) at \((x,c)\in (0,\infty )\times [ 0,\overline{c})\) if any \((2,1)\)-differentiable function \(\varphi :[0,\infty )\times [ 0,\overline{c})\rightarrow{ \mathbb{R}} \) with \(\varphi (x,c)=\overline{u}(x,c)\) such that \(\overline{u}-\varphi \) reaches the minimum at \(\left ( x,c\right ) \) satisfies
The function \(\varphi \) is called a test function for a supersolution at \((x,c)\).
(b) Similarly, a locally Lipschitz function \(\underline{u}: [0,\infty )\times [ 0,\overline {c})\rightarrow{\mathbb{R}} \) is a viscosity subsolution of (4.2) at \((x,c)\in (0,\infty )\times [ 0,\overline{c})\) if any \((2,1)\)-differentiable function \(\psi :[0,\infty )\times [ 0,\overline {c}) \rightarrow{\mathbb{R}} \) with \(\psi (x,c)=\underline{u}(x,c)\) such that \(\underline{u}-\psi \) reaches the maximum at \(\left ( x,c\right ) \) satisfies
The function \(\psi \) is called a test function for a subsolution at \((x,c)\).
(c) A locally Lipschitz function \(u:[0,\infty )\times [ 0,\overline{c})\rightarrow {\mathbb{R}}\) is a viscosity solution of (4.2) at \((x,c) \in [ 0,\infty )\times [ 0,\overline{c})\) if it is both a supersolution and a subsolution at \((x,c)\).
4.1 HJB equation with bounded dividend rates
Given \(a\in (0,1]\) and \(\overline{c}<\infty \), we define in the sequel, for simplicity of exposition,
Here the state variables are the current surplus and the running maximum dividend rate. The results of this subsection for the case \(a=1\) (ratcheting dividend constraint) were already proved in Albrecher et al. [1].
The next result states that \(V\) is a viscosity solution of the HJB equation.
Proposition 4.2
The function \(V\) is a viscosity solution of (4.2) in \((0,\infty )\times [ 0,\overline{c})\).
Proof
Let us show first that \(V\) is a viscosity supersolution in \((0,\infty )\times [ 0,\overline{c})\). By Proposition 3.4, \(\partial _{c}V\leq 0\) in \((0,\infty )\times [ 0,\overline{c})\) in the viscosity sense.
Consider now \((x,c)\in (0,\infty )\times [ 0,\overline{c})\) and the admissible strategy \(D\in \Pi _{x,c}\) which pays dividends at a constant rate \(\kappa \in [ ac,c]\) up to the ruin time \(\tau \). Let \(X^{D}\) be the corresponding controlled surplus process and suppose that there exists a test function \(\varphi \) for a supersolution of (4.2) at \((x,c)\); then \(\varphi \leq V\) and \(\varphi (x,c)=V(x,c)\). We want to prove that \(\mathcal{L}^{\kappa}\mathcal{(}\varphi )(x,c)\leq 0\). For that purpose, we consider an auxiliary test function for the supersolution \(\tilde{\varphi}\) in such a way that \(\tilde{\varphi}\leq \varphi \leq V\) in \([0,\infty )\times [ 0,\overline{c}]\), \(\tilde{\varphi}=\varphi \) in \([0,2x]\) (so \(\mathcal{L}^{\kappa}\mathcal{(}\varphi )(x,c)=\mathcal{L}^{\kappa}\mathcal{(}\tilde{\varphi})(x,c)\)) and \(\mathcal{L}^{\kappa} \mathcal{(}{\tilde{\varphi}})(\,\cdot \,,c)\) is bounded in \([0,\infty )\). We introduce \(\tilde{\varphi}\) because \(\mathcal{L}^{\kappa}\mathcal{(}\varphi )( \,\cdot \,,c)\) may be unbounded in \([0,\infty )\). We construct \(\tilde{\varphi}\) as follows: take \(g:[0,\infty )\rightarrow [ 0,1]\) twice continuously differentiable with \(g=0\) in \([2x+1,\infty )\) and \(g=1\) in \([0,2x]\), and define \(\tilde {\varphi}(y,\kappa )=\) \(\varphi (y,\kappa )g(y)\). Using Lemma 3.7, we obtain for \(h>0\),
Hence using Itô’s formula gives
Since \(\tau >0\) a.s.,
and
We conclude via dominated convergence that \(\mathcal{L}^{\kappa } (\varphi )(x,c)=\mathcal{L}^{\kappa}( \tilde{\varphi })(x,c)\leq 0\) for any \(\kappa \in [ ac,c]\); so \(V\) is a viscosity supersolution at \((x,c)\).
We skip the proof that \(V\) is a viscosity subsolution in \((0,\infty )\times [ 0,\overline{c})\), because it is similar to that of [1, Proposition 3.1]. □
Let us consider the function
The next proposition gives a comparison result for the viscosity solutions of (4.2) for \(\overline{c}>0\). The proof is similar to that of [1, Lemma 3.2].
Lemma 4.3
Assume that
(i) \(\underline{u}\) is a viscosity subsolution and \(\overline{u}\) is a viscosity supersolution of the HJB equation (4.2) for all \(x>0\) and all \(c\in [ 0,\overline{c})\);
(ii) \(\underline{u}\) and \(\overline{u}\) are nondecreasing in the variable \(x\) and Lipschitz in \([0,\infty )\times [ 0,\overline{c}]\);
(iii) \(\underline{u}(0,c)=\overline{u}(0,c)=0\), \(\lim _{x\rightarrow \infty }\underline{u}(x,c)\leq \overline{c}/q \leq \lim _{x\rightarrow \infty}\overline {u}(x,c)\);
(iv) \(\underline{u}(x,\overline{c})\leq v^{\overline{c}}(x)\leq \overline{u}(x,\overline{c})\) for \(x\geq 0\).
Then \(\underline{u}\leq \overline{u}\) in \([0,\infty )\times [ 0,\overline{c})\).
The following characterisation theorem is a direct consequence of the previous lemma and Propositions 3.4 and 4.2.
Theorem 4.4
The value function \(V\) is the unique function which is nondecreasing in \(x\) and a viscosity solution of (4.2) in \((0,\infty )\times [ 0,\overline{c})\) with \(V(0,c)=0\), \(V(x, \overline{c})=v^{\overline{c}}(x)\) and \(\lim _{x\rightarrow \infty}\) \(V(x,c)=\overline{c}/q\) for \(c\in [ 0,\overline{c})\).
From Definition 1.3, Lemma 4.3 and Proposition 3.4 together with Proposition 4.2, we also get the following verification theorem.
Theorem 4.5
Let \(\{ C_{x,c}\in \Pi _{x,c}:(x,c)\in [ 0,\infty )\times [ 0, \overline{c}] \} \) be a family of strategies. If the function \(W(x,c):=J(x;C_{x,c})\) is a viscosity supersolution of the HJB equation (4.2) in \((0,\infty )\times [ 0,\overline{c})\) with \(\lim _{x\rightarrow \infty}W(x,c)=\) \(\overline{c}/q\), then \(W\) is the value function \(V\). Also, if for each \(k\geq 1\), there exists a family \(\{ C_{x,c}^{k}\in \Pi _{x,c}:(x,c)\in [ 0,\infty )\times [ 0,\overline{c}] \} \) of strategies such that \(W(x,c):=\lim _{k\rightarrow \infty}J(x;C_{x,c}^{k})\) is a viscosity supersolution of the HJB equation (4.2) in \((0,\infty )\times [ 0,\overline{c})\) with \(\lim _{x \rightarrow \infty}W(x,c)=\overline{c}/q\), then \(W\) is the value function \(V\).
4.2 HJB equation with unbounded dividend rates
Let us now consider the case \(\overline{c}=\infty \) with \(a\in (0,1]\). Since \(a\) is fixed, we denote \(V^{\infty}= V_{a}^{\infty}\). The proof of the following result is similar to that of the case with bounded dividend rate.
Proposition 4.6
The function \(V^{\infty}\) is a viscosity solution of (4.2) for any \((x,c)\in (0,\infty )\times [ 0,\infty )\).
We now state a comparison result for the unbounded case.
Lemma 4.7
Assume that
(i) \(\underline{u}\) is a viscosity subsolution and \(\overline{u}\) is a viscosity supersolution of the HJB equation (4.2) for all \(x>0\) and for all \(c\in [ 0,\infty )\);
(ii) \(\underline{u}\) and \(\overline{u}\) are nondecreasing in the variable \(x\) and Lipschitz in \([0,\infty )\times [ 0,\infty )\);
(iii) \(\underline{u}(0,c)=\overline{u}(0,c)=0\);
(iv) \(~\underline{u}(x,c)\leq x+{\mu}/{q}\), \(x\leq \overline{u}(x,c)\);
(v) \(\lim _{c\rightarrow \infty }\underline{u}(x,c)\leq x \leq \lim _{c\rightarrow \infty}\overline{u}(x,c)\) for \(x\geq 0\).
Then \(\underline{u}\leq \overline{u}\) in \([0,\infty )\times [ 0,\infty )\).
Proof
Suppose there is \((x_{0},c_{0})\in (0,\infty )\times (0,\infty )\) with \(\underline{u}(x_{0},c_{0})-\overline{u}(x_{0},c_{0})>0\). Let us define
for any \(s>1\). We have
for \(s\in (1,2)\).
Let us now show that \(\overline{u}^{s}\) is a strict supersolution. We have that \(\varphi \) is a test function for the supersolution \(\overline{u}\) at \((x,c)\) if and only if \(\varphi ^{s}:=s\,h(c)\,\varphi \) is a test function for the supersolution \(\overline{u}^{s}\) at \((x,c)\). Moreover,
for \(\kappa \in [ ac,c]\), and
since \(\varphi (x,c)=\overline{u}(x,c)\geq x>0\).
Take \(s_{0}>1\) such that \(\underline{u}(x_{0},c_{0})-\overline{u}^{s_{0}}(x_{0},c_{0})>0\). We define
Let us show that
for some positive \(b\) and \(c_{1}\). Since \(\underline{u}(x,c)\leq x+ \frac{\mu }{q}\) and \(x\leq \overline{u}(x,c)\),
for \(x\) large enough; so there exists \(b>x_{0}\) such that
Besides, the function
satisfies lim sup \(_{c\rightarrow \infty}\) \(g(c)\leq 0\) because \(\lim _{c\rightarrow \infty}\underline{u}(x,c)\leq x\leq \lim _{c \rightarrow \infty}\overline{u}(x,c)\) for \(x\geq 0\). So there exists \(c_{1}>0\) with \(g(c)\leq \frac{M}{2}\) for \(c\geq c_{1}\) and we deduce (4.5). Hence the maximum is attained in a bounded set, that is,
This yields a contradiction by following the arguments of the proof of [1, Lemma 3.2]. □
As for bounded dividend rates, the following result is a direct consequence of the previous lemma, Remark 3.5 and Proposition 4.6.
Theorem 4.8
The value function \(V^{\infty}\) is the unique function which is nondecreasing in \(x\) and a viscosity solution of (4.2) in \((0,\infty )\times [ 0,\infty )\) with \(V^{\infty}(0,c)=0\), \(V^{\infty}(x,\overline{c})-x \) bounded and \(\lim _{c\rightarrow \infty}\) \(V^{\infty}(x,c)=x\).
From Definition 1.3, Lemma 4.7 and Remark 3.5 together with Proposition 4.6, we also get the following verification theorem.
Theorem 4.9
Consider a family \(\{ C_{x,c}\in \Pi _{x,c}:(x,c)\in [ 0, \infty )\times [ 0,\infty ) \}\) of strategies. If the function \(W(x,c):=J(x;C_{x,c})\) is a viscosity supersolution of the HJB equation (4.2) in \((0,\infty )\times [ 0,\infty )\) with \(W(x,c)\geq x\), then \(W\) is the value function \(V^{\infty}\). Also, if for each \(k\geq 1\), there exists a family \(\{ C_{x,c}^{k}\in \Pi _{x,c}:(x,c)\in [ 0,\infty )\times [ 0,\infty )\}\) of strategies such that \(W(x,c):=\lim _{k\rightarrow \infty}J(x;C_{x,c}^{k})\) is a viscosity supersolution of the HJB equation (4.2) in \((0,\infty )\times [ 0,\infty )\) with \(W(x,c)\geq x\), then \(W\) is the value function \(V^{\infty}\).
5 Refracting dividend strategies and \(v^{\overline{c}}\)
In the case \(0<\overline{c}<\infty \) and \(a\in (0,1)\), we now want to investigate further the function \(v^{\overline{c}}\) (defined in (4.4)) of paying dividends with rates \(\kappa \in [ a\overline{c},\overline{c}]\) in an optimal way. The following characterisation is the one-dimensional version of Theorem 4.4.
Proposition 5.1
The function \(v^{\overline{c}}:[0,\infty )\rightarrow {\mathbb{R}}\) is the unique viscosity solution of
with boundary conditions \(W(0)=0\) and \(\lim _{x\rightarrow \infty}W(x)=\overline{c}/q\).
We present in this section a formula for \(v^{\overline{c}}\), which turns out to be the reward function of the optimal refracting strategy as derived in Albrecher et al. [3].
The functions \(W\) that satisfy \(\mathcal{L}^{\kappa}(W)=0\) are given by
where \(\theta _{1}(\kappa )>0\) and \(\theta _{2}(\kappa )<0\) are the roots of the characteristic equation
associated to the operator \(\mathcal{L}^{\kappa}\), that is,
Basic properties of \(\theta _{1}(\kappa )\) and \(\theta _{2}(\kappa )\) are that
-
1)
\(\theta _{1}(\kappa )=-\theta _{2}(\kappa )\) if \(\kappa =\mu \), and \(\theta _{1}^{2}(\kappa )\geq \theta _{2}^{2}( \kappa )\) if and only if \(\kappa -\mu \geq 0\);
-
2)
\(\theta _{1}^{\prime}(\kappa )=\frac{1}{\sigma ^{2}}(1+ \frac{\kappa -\mu }{\sqrt{(\kappa -\mu )^{2}+2q\sigma ^{2}}})\) and \(\theta _{2}^{\prime}(\kappa )=\frac{1}{\sigma ^{2}}(1- \frac{\kappa -\mu}{\sqrt{(\kappa -\mu )^{2}+2q\sigma ^{2}}})\) so that \(\theta _{1}^{\prime}(\kappa ),\theta _{2}^{\prime }(\kappa )\in (0, \frac{2}{\sigma ^{2}})\).
The solutions of \(\mathcal{L}^{\kappa}(W)=0\) with boundary condition \(W(0)=0\) are of the more specific form
Finally, the unique solution of \(\mathcal{L}^{\kappa}(W)=0\) with boundary conditions \(W(0)=0\) and \(\lim _{x\rightarrow \infty}\) \(W(x)=\kappa /q \) corresponds to \(A=0\), so that
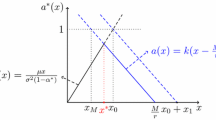
Note that this function is increasing and concave in \([0,\infty )\). In [3, Theorem 3.1], the reward function of a ‘refracting strategy’ that pays \(a\overline{c}\) when the current surplus is below a refracting threshold \(b\) and pays \(\overline{c}\) when the current surplus is above \(b\) was shown to be
where
The optimal threshold \(b^{\ast}(\overline{c})\) is given by
(note that since the underlying process \(X\) has no upward jumps, that value does not depend on \(x\)). In case (5.6) is positive, then by (5.4) the value of \(b\) satisfies
From [3], we know that the threshold can be characterised as the unique \(b\) such that \(v(x,\overline{c},b)\) is twice continuously differentiable in \(x=b\). Since \(v(x,\overline{c},b^{\ast}(\overline{c}))\) is twice continuously differentiable with \(v(0,\overline {c},b^{\ast}(\overline{c}))=0\), we therefore obtain \(\lim _{x\rightarrow \infty}v(x,\overline {c},b^{\ast}( \overline{c}))=\overline{c}/q\) and \(v(x,\overline{c},b^{*}(\overline{c}))\) is also a solution of
By Proposition 5.1, we have
that is, the strategy achieving \(v^{\overline{c}}\) has a ‘refracting’ threshold structure with optimal threshold \(b^{\ast}(\overline{c})\). Note also that since \(v^{\overline{c}}\) is twice continuously differentiable at \(b^{\ast}(\overline{c})\) and \(\mathcal{L}(v^{\overline{c}})(b^{\ast }(\overline{c}))=\mathcal{L}^{a \overline{c}}(v^{\overline{c}})(b^{\ast }(\overline{c}))=0\), we have \(\partial _{x}v^{\overline{c}}(b^{\ast}(\overline {c}))=1\). Also, since
we obtain
6 Curve strategies and the optimal two-curve strategy for bounded dividend rates
Using the formulas of the previous section, we can find the value function defined in (4.3). The proofs of all the results of this section together with the auxiliary lemmas used in these proofs are deferred to Appendix A. We also include in that appendix some explicit formulas.
Remark 6.1
Before proceeding, note that this optimisation problem is only interesting for \(\overline{c}>q\sigma ^{2}/(2\mu )\) as for smaller values of \(\overline{c}\), we know from Asmussen and Taksar [7, Eq. (1.8)] (translated to our notation) that even without a drawdown constraint, it is optimal to pay dividends at the maximal rate \(\overline{c}\) until the time of ruin. This is then also the optimal strategy in our situation, as the drawdown constraint does not affect its applicability. Indeed, and as a self-contained derivation of this result in the present context, the reward function of that strategy fulfils
for both \(\kappa =ac\) and \(\kappa =c\). So by Proposition 5.1, \(v^{\overline{c}}(x)=\frac{\overline{c}}{q} ( 1-e^{\theta _{2}(\overline{c})x} ) =: U(x,c) \) and \(b^{\ast}(\overline{c})=0\). By Theorem 4.4, it is then sufficient to prove that
for any \(c\in [ 0,\overline{c})\); but this follows from (6.1).
In the rest of this paper, we therefore assume that \(\overline{c}>\frac{q\sigma ^{2}}{2\mu}\).
Since \(V(x,c)\) solves the HJB equation (4.2), it satisfies either \(\mathcal{L}^{ac}(V)(x,c)=0\) or \(\mathcal{L}^{c}(V)(x,c)=0\) or \(\partial _{c}V(x,c)=0\). This suggests that the state space \([0,\infty )\times [ 0,\overline{c}]\) is partitioned into two regions: a non-change running maximum dividend region \(\mathcal{NC}^{ \ast}\) in which the running maximum dividend rate \(c\) does not change, and a change dividend region \(\mathcal{CH}^{\ast}\) in which the dividend rate exceeds \(c\) (so that the running maximum dividend rate increases). Moreover, the region \(\mathcal{NC}^{\ast}\) splits into two connected subregions: \(\mathcal{NC}_{ac}^{\ast}\) in which the dividends are paid at the constant rate \(ac\), and \(\mathcal{NC}_{c}^{\ast}\) in which the dividends are paid at the constant rate \(c\).
Roughly speaking, the interior of the region \(\mathcal{NC}_{ac}^{\ast}\) consists of the points \((x,c)\) in the state space where \(\mathcal{L}^{ac}(V)(x,c)=0\), \(\mathcal{L}^{c}(V)(x,c)<0\) and \(\partial _{c}V (x,c)<0\); the interior of the region \(\mathcal{NC}_{c}^{\ast}\) consists of the points where \(\mathcal{L}^{c}(V)(x,c)=0\), \(\mathcal{L}^{ac}(V)(x,c)<0\) and \(\partial _{c}V (x,c)<0\); and the interior of \(\mathcal{CH}^{\ast}\) consists of the points where \(\partial _{c}V (x,c)=0\), \(\mathcal{L}^{c}(V)(x,c)<0\) and \(\mathcal{L}^{ac}(V)(x,c)<0\). We introduce a family of two-curve strategies (or limits of two-curve strategies) where the different dividend payment regions are connected and are defined by two free boundary curves.
Consider a function \(\gamma :[0,\overline{c}]\rightarrow (0,\infty )\) which is continuously differentiable, and a function \(\zeta :[0,\overline{c}]\rightarrow (0,\infty )\) which is bounded, Riemann-integrable and càdlàg. Define the set
In the first part of this section, we define a function \(W^{\gamma ,\zeta}:[0,\infty )\times [ 0,\overline{c}] \rightarrow [ 0,\infty )\) for each \((\gamma ,\zeta )\in \) ℬ. We shall see that in some sense, \(W^{\gamma ,\zeta}(x,c)\) is the reward function of the two-curve strategy which pays dividends at the constant rate \(ac\) for the points to the left of the curve \(\mathcal{R}(\gamma )\), pays dividends at the constant rate \(c\) between the curves \(\mathcal{R}(\gamma )\) and \(\mathcal{R}(\zeta )\), and pays more than \(c\) as dividend rate otherwise, where
Hence the curves \(\mathcal{R}(\gamma )\) and \(\mathcal{R}(\zeta )\) split the state space \([0,\infty )\times [ 0,\overline{c})\) into three connected regions, namely
where dividends are paid with the constant rate \(ac\),
where dividends are paid with the constant rate \(c\), and
cf. Fig. 1. We set \(\mathcal{NC(\gamma},\mathcal{\zeta )=NC}_{ac}\mathcal{(\gamma}, \mathcal{\zeta )\cup NC}_{c}\mathcal{(\gamma },\mathcal{\zeta )}\).
In the second part of this section, we use calculus of variations to look for a pair \(( \mathcal{\gamma}^{0},\zeta ^{0} ) \in \mathcal{B}\) which maximises the reward function \(W^{\mathcal{\mathcal{\gamma}},\mathcal{\mathcal{\zeta}}}\) among all \(( \mathcal{\gamma},\zeta ) \in \) ℬ.
In order to define \(W^{\mathcal{\mathcal{\gamma}},\mathcal{\mathcal{\zeta}}}\) in the non-change regions \(\mathcal{NC}_{ac}\mathcal{(\gamma},\mathcal{\zeta )}\) and \(\mathcal{NC}_{c}\mathcal{(\mathcal{\mathcal{\gamma}}},\mathcal{\mathcal{\mathcal{\zeta}})}\), we need to introduce some auxiliary functions. Let us consider the set
and the functions \(b_{0}\), \(b_{1}:T\times [ 0,\infty )\times [ 0,\overline {c}] \rightarrow{\mathbb{R}}\) defined by
where the functions \(d\) and \(b_{00},b_{01},b_{10},b_{11}\) are defined in (A.1) and (A.2) below. In Lemma A.1 below, we show that the function \(d\) is positive so that \(b_{0}\) and \(b_{1}\) are well defined.
In the next result, we define and study the functions \(H^{\mathcal{\mathcal{\gamma}},\mathcal{\mathcal{\zeta}}}\) and \(A^{\mathcal{\mathcal{\gamma}},\mathcal{\mathcal{\zeta}}}\) that will be used to define \(W^{\gamma ,\zeta}\).
Proposition 6.2
For any given \((\gamma ,\mathcal{\mathcal{\zeta}})\in \mathcal{B}\), there exists a unique continuous function \(H^{\gamma ,\zeta}:[0, \infty )\times [ 0,\overline{c}]\rightarrow [ 0,\infty )\) with \(H^{\gamma ,\zeta}(\,\cdot \,,c)\) continuously differentiable which satisfies for any \(c\in [ 0,\overline{c})\) that
with the boundary conditions \(H^{\gamma ,\zeta}(0,c)=0\), \(H^{\gamma ,\zeta }(x,\overline{c})=v(x,\overline{c},\gamma ( \overline{c}))\) and \(\partial _{c}H^{\gamma ,\zeta}(\zeta (c),c)=0 \) at the points of continuity of \(\zeta \). It is given by
where \(f_{10}\), \(f_{11},f_{20},f_{21}\) are defined in (A.3)–(A.6) below,
and
where the function \(B\) is defined in (5.5) and the functions \(b_{0}\) and \(b_{1}\) are defined in (6.2). Moreover, \(A^{\mathcal{\mathcal{\gamma}},\mathcal{\mathcal{\zeta}}}\) is differentiable and satisfies
at the points where \(\zeta \) is continuous. Moreover, it satisfies the boundary condition (6.5).
Given \((\gamma ,\zeta )\in \mathcal{B}\), we define
where \(H^{\gamma ,\zeta}\) is defined in Proposition 6.2 and
for \(x\geq \zeta (c)\) and \(c\in [ 0,\overline{c})\); cf. Fig. 2.
In Appendix A, we show by using a Feynman–Kac argument that \(W^{\gamma ,\zeta}(x,c)\) is a uniform limit of reward functions of admissible strategies by constructing a sequence of step functions \(\zeta _{k}\) converging to \(\zeta \). See Definition A.2 and Lemmas A.3 and A.4.
Remark 6.3
Given a \((\gamma ,\zeta )\in \mathcal{B}\) where \(\zeta \) is not a step function, we say that \(W^{\gamma ,\zeta}\) is the reward function of the two-curve strategy \(\mathbf{\pi}^{(\gamma ,\zeta )}\) which starts with an initial surplus \(x\) and initial running maximum dividend rate \(c\). Then
(1) in the case \(0\leq x<\zeta (c)\), it follows the refracting strategy which pays \(ac\) when the current surplus is below a refracting threshold \(\gamma (c)\), and pays \(c\) when the current surplus is above \(\gamma (c)\), until either reaching the curve \(\mathcal{R(\zeta )}\) or ruin (whichever comes first);
(2) in the case \(x>\zeta (c)\), it increases immediately the dividend rate from \(c\) to \(\ell (x,c)\);
(3) in the case \(x=\zeta (c)\), it can be seen as the limit of admissible strategies \(\mathbf{\pi}_{x,c}^{(\gamma ,\zeta _{k})}\in \Pi _{x,c}\) arising from Lemma A.4 in Appendix A.
We now look for the maximum of \(W^{\gamma ,\zeta}\) among \((\gamma ,\zeta )\in \mathcal{B}\). Let us see that if there exists a pair \((\gamma _{0},\zeta _{0})\in \mathcal{B}\) such that
then \(W^{\gamma _{0},\zeta _{0}}(x,c)\geq W^{\gamma ,\zeta}(x,c)\) for all \((x,c)\in [ 0,\infty )\times [ 0,\overline{c}] \) and \((\gamma ,\zeta )\in \mathcal{B}\).
From Lemma A.1 and \(\theta _{2}>0>\theta _{1}\), we obtain that \(f_{11}\) and \(f_{21}\) defined in (A.4) and (A.6) are positive, and so by (6.3) and (6.6),
This implies that \(\operatorname*{arg\,max}_{(\gamma ,\zeta )\in \mathcal{B}}W^{\gamma ,\zeta }(x,c)\) does not depend on the initial capital \(x\). In addition, it also does not depend on the initial value \(c\); this follows from Lemma A.5, where we prove that the pair of functions \((\gamma _{0},\zeta _{0})\) which maximises (6.7) also maximises \(A^{\gamma ,\zeta}(c)\) for any \(c\in [ 0,\overline{c})\). Let us now find the implicit equation for the function \(A^{\gamma _{0},\zeta _{0}}\) for \((\gamma _{0},\zeta _{0})\) satisfying (6.7).
Proposition 6.4
If a pair \((\gamma _{0},\zeta _{0})\) as in (6.7) exists, then \(A^{\gamma _{0},\zeta _{0}}(c)\) satisfies
where for \(i=0,1\),
Moreover, \(\gamma _{0}(\overline{c})=b^{\ast}(\overline{c})\) is the optimal threshold defined in (5.6) and
Proposition 6.5
Consider the functions \(C_{0}\) and \(C_{ij}\) for \(i=1,2\) and \(j=0,1,2\) defined in (A.8)–(A.11). If \((\gamma _{0},\zeta _{0})\in \mathcal{B} \) defined in (6.7) satisfies that \(\zeta _{0}\) is continuous and
for \(c\in [ 0,\overline{c}]\), then \(\gamma _{0} \) and \(\zeta _{0}\) are infinitely differentiable and \((\gamma _{0},\zeta _{0})\) is a solution of the system of ODEs
with boundary conditions
where \(b^{\ast}(\overline{c})\) is the optimal threshold defined in (5.6).
Let us study the uniqueness of the solution of (6.12) with boundary condition (6.13). We know that if \(\left ( \gamma ,\zeta \right ) \in \mathcal{B}\) is a solution, then \(\gamma (\overline {c})=b^{\ast}(\overline{c})\), the optimal threshold defined in (5.6). In order to obtain \(\zeta (\overline{c})\), we have to find a zero of \(C_{0}(b^{\ast}(\overline{c}),\cdot ,\overline{c})\) in \((b^{\ast}(\overline{c}),\infty )\). Let us assume that there exists a unique zero \(z^{\ast}(\overline{c})\) of \(C_{0}(b^{\ast}(\overline{c}),\cdot ,\overline{c})\) in \((b^{\ast}(\overline{c}),\infty )\). In the next result, we show that under this assumption, the existence of a solution \(( \gamma ,\zeta ) \) of (6.12) implies its uniqueness.
In Sect. 7, we show that there is a unique zero \(z^{\ast}(\overline{c})\) of \(C_{0}(b^{\ast}(\overline{c}),\cdot ,\overline{c})\) in \((b^{\ast}(\overline{c}),\infty )\) for \(\overline{c}\) large enough. Also, we check this assumption in the numerical examples for each set of parameters.
Proposition 6.6
Assume that there exists a unique zero \(z^{\ast}(\overline{c})\) of \(C_{0}(b^{\ast}(\overline{c}),\cdot ,\overline{c})\) in \((b^{\ast}(\overline{c}),\infty )\). If \(( \gamma _{1},\zeta _{1} ) \in \mathcal{B} \) and \(( \gamma _{2},\zeta _{2} ) \in \mathcal{B}\) are two solutions of the system (6.12) of differential equations with boundary conditions (6.13), then \(( \gamma _{1},\zeta _{1} ) = ( \gamma _{2},\zeta _{2} ) \).
Let us now introduce a lower bound \(\underline{c}\) for the dividend rate (to be specified later), and denote by \(( \overline{\gamma},\overline{\zeta } ) \) a solution of (6.12) in \([\underline {c},\overline{c}]\) with boundary conditions (6.13).
Remark 6.7
Since the functions \(C_{ij}\) defined in (A.10) and (A.11) are infinitely differentiable, a recursive argument establishes that \(\overline{\gamma}\) and \(\overline{\zeta}\) are also infinitely differentiable.
The next result says that the reward function \(W^{\overline {\gamma},\overline{\zeta}}\) satisfies a smooth-pasting property on the two free-boundary curves. Note that this extends Albrecher et al. [1, Prop. 5.13] from the ratcheting case with one free boundary to our present drawdown case. For a general account on conditions for smooth-pasting when the value function is not necessarily smooth, see e.g. Guo and Tomecek [22].
Proposition 6.8
If a pair of infinitely differentiable functions \((\gamma ,\zeta )\in \mathcal{B}\) satisfies
then \((\gamma ,\zeta ) \) is a solution of both (6.8) and (6.9) in \([\underline{c},\overline{c}]\) with boundary conditions (6.13). Moreover, \(\partial _{x}(W^{\gamma ,\zeta})(\gamma (c),c)=1\) for \(c\in [ \underline{c} ,\overline{c}]\). Conversely, let \((\bar{\gamma},\bar{\zeta}) \) be a solution of (6.12) in \([\underline{c},\overline{c}]\) with boundary conditions (6.13). Then \(W^{\bar {\gamma},\bar{\zeta}}\) satisfies the smooth-pasting properties
The next result shows more regularity for \(W^{\overline{\gamma },\overline{\zeta}}\) if \(\overline{\zeta}\) is strictly monotone.
Proposition 6.9
If \((\overline{\gamma},\overline{\zeta}) \) is a solution of (6.12) in \([\underline{c},\overline{c}]\) with boundary conditions (6.13) and \(\overline {\zeta}{}^{\prime}(c)\neq 0\) in \([\underline{c},\overline{c}]\), then \(W^{\overline{\gamma},\overline{\zeta}}\) is \((2,1)\)-differentiable.
The next theorem is the main result of this section.
Theorem 6.10
Let \((\overline{\gamma},\overline{\zeta}) \) be a solution of (6.12) in \([\underline{c},\overline{c}]\) with boundary conditions (6.13) such that the function \(W^{\overline{\gamma},\overline{\zeta}}\) is \((2,1)\)-differentiable and satisfies
for \(c\in [ \underline{c},\overline{c})\). Then \(W^{\overline{\gamma},\bar{\zeta}}=V\).
Remark 6.11
We conjecture that there is always a unique zero \(z^{\ast}(\overline{c})\) of \(C_{0}(b^{\ast}(\overline{c}),\cdot ,\overline{c})\) in \((b^{\ast}(\overline{c}),\infty )\) for \(\overline {c}>\) \(q\sigma ^{2}/(2\mu )\), that there exists a solution \(( \overline{\gamma},\overline{\zeta} ) \in \mathcal{B}\) of the system of differential equations (6.12) satisfying the boundary conditions (6.13), and that the reward function \(W^{\overline{\gamma},\overline{\zeta}}\) is a viscosity supersolution of the HJB equation (4.2). If that holds, \((\overline{\gamma },\overline{\zeta})=(\gamma _{0},\zeta _{0})\) and \(W^{\overline{\gamma },\overline{\zeta}}\) is the value function \(V\). Moreover, the optimal strategy is then a two-curve strategy. In Sect. 8, we show that that this conjecture always holds in \([ \underline{c},\overline{c} ] \) for \(\overline{c}\) large enough and some suitable \(\underline{c}<\overline{c}\), and in Sect. 9, we also show numerically that it is true for further instances.
7 Asymptotic values as \(\overline{c}\rightarrow \infty \)
The symbolic computations of this section are highly involved; so we use the Wolfram Mathematica software to obtain Taylor expansions. Note that all results of this section are derived for \(0< a<1\), and the resulting expressions need not necessarily be applicable for the limit to \(a=1\), as dominant terms in the asymptotics may change.
Recall the boundary condition \(C_{0}(b^{\ast}(\overline{c}),\cdot ,\overline {c})=0\) of the differential equation (6.12); cf. (6.13). Note that for \(\overline{c}>\frac{q\sigma ^{2}}{2\mu}\), we have from Remark 6.1 that \(b^{\ast}(\overline{c})\) is the unique positive \(b\) satisfying (5.7). In this section, we show that there is a unique zero \(z^{\ast}(\overline{c})\) of \(C_{0}(b^{\ast}(\overline {c}),\cdot ,\overline{c})\) in \((b^{\ast}(\overline{c}),\infty )\) for \(\overline{c}\) large enough and that
We also show ↘-\(\lim _{\overline{c}\rightarrow \infty}V_{a}^{ \overline{c}}(x,\overline{c}) = x\) for \(0< x<\lim _{\overline{c}\rightarrow \infty }z^{\ast}(\overline{c})=\frac{\mu}{q}(1+\frac{1}{\sqrt{a}})\) and ↗-\(\lim _{\overline{c}\rightarrow \infty}V_{a}^{ \overline{c}}(x,\overline {c})= x\) for \(x>\lim _{\overline{c}\rightarrow \infty}z^{\ast}(\overline{c})=\frac{\mu}{q}(1+\frac{1}{\sqrt{a}})\).
In the rest of the section, we denote \(V_{a}^{\overline{c}}\) by \(V^{\overline {c}}\).
Proposition 7.1
It holds that \(\lim _{\overline {c}\rightarrow \infty}b^{\ast}(\overline{c})=\mu /q\). More precisely, the Taylor expansion of \(b^{\ast}(\overline{c})\) at \(\overline{c}=\infty \) is given by
Proof
We have from (5.6) that
But
where
Let us define \(F_{0}(\overline{c},b):=E(\overline{c},b)/e^{\theta _{1}(a \overline{c})b}\). The Taylor expansions of \(\theta _{1}(c)\) and \(\theta _{2}(c)\) in (5.2) at \(c=\infty \) are given by
Let us prove first that there is no sequence \(b^{\ast}(c_{n})\rightarrow \infty \) with \(c_{n}\rightarrow \infty \). Using (7.4), we obtain
First, let us assume that \(b^{\ast}(c_{n})=c_{n} \alpha _{n} \) with \(\alpha _{n}\rightarrow \overline{\alpha}\in (0,\infty )\). Then since \(1-e^{-\frac{q\overline{\alpha}}{a}} >0\) and \(a<1\),
which is a contradiction. Secondly, let us assume that \(b^{\ast}(c_{n})=c_{n} \alpha _{n} \) with \(\alpha _{n}\rightarrow \infty \). Then since \(e^{-\frac{qb^{\ast}(c_{n})}{ac_{n}}}\rightarrow 0\), we have \(0=\lim _{n\rightarrow \infty}F_{0}(c_{n},b^{\ast}(c_{n}))=-\infty \) which is also a contradiction. Finally, let us assume that \(b^{\ast}(c_{n})=c_{n} \alpha _{n} \) with \(\alpha _{n}\rightarrow 0{+}\). Then
gives again a contradiction. Hence \(\lim \sup _{\overline{c}\rightarrow \infty}b^{\ast}(\overline{c})< \infty \).
Let us define the function \(H_{0}:[0,\infty )\times (0,\infty )\rightarrow \mathbb{R}\) as
Then \(H_{0}(u,b)\) is infinitely continuously differentiable because it is infinitely continuously differentiable for \(u>0\) and \(\lim _{u\rightarrow 0{+}}F_{0}(\frac{1}{u},b)=4(a-1)aq(qb-\mu )/\sigma ^{4}<\infty \). Moreover, its first-order Taylor expansion at \(u = 0\) is given by
From (7.2), we obtain \(H_{0}(u,b^{\ast}(1/u))=0~\) for \(u>0\). Let us show that we have \(\lim _{u\rightarrow 0{+}}b^{ \ast}(1/u)=\mu /q\). We have already seen that \(b^{\ast}(1/u) \) is bounded for \(u\) \(\in [ 0,\varepsilon )\) for some \(\varepsilon >0\). Take any sequence \(u_{n}\rightarrow 0{+}\) with \(\lim _{n\rightarrow \infty}b^{\ast}(1/u_{n})=b_{0}<\infty \); then
and so \(b_{0}=\mu /q\). Using that \(\partial _{b}H_{0}(0,b)=\frac{4(a-1)aq^{2}}{\sigma ^{4}}\neq 0\), we conclude by the implicit function theorem that the function \(h:[0,\infty )\rightarrow \mathbb{R}\) defined as \(h(0)=\frac{\mu}{q}\) and \(h(u)= b^{\ast}(\frac{1}{u})\) for \(u>0\) is infinitely continuously differentiable, and the result follows. □
Proposition 7.2
There exists a unique zero \(z^{\ast }(\overline{c})\) of \(C_{0}(b^{\ast}(\overline{c}),\cdot ,\overline{c})\) in \((b^{\ast}(\overline{c}),\infty )\) for \(\overline{c}\) large enough with \(\lim _{\overline{c}\rightarrow \infty}z^{\ast}(\overline{c})= \frac{\mu}{q}(1+\frac{1}{\sqrt{a}})\). More precisely, \(z^{\ast}(\overline{c})\) is infinitely continuously differentiable for \(\overline{c}\) large enough, and its first-order Taylor expansion at \(\overline{c}=\infty \) is given by
Proof
Considering the functions \(C_{0}(y,z,c)\) defined in (A.8) and \(E(c,y)\) defined in (7.3), we define
Since \(E(\overline{c},b^{\ast}(\overline{c}))=0\), \(\theta _{2}(c)- \theta _{1}(c)<0\) and \(d(y,z,c)>0\), we see that the property \(C_{0}(b^{ \ast}(\overline {c}),z^{\ast}(\overline{c}),\overline{c})=0\) is equivalent to \(\tilde{C}_{0}(b^{\ast}(\overline{c}),z^{\ast}(\overline{c}),\overline{c})=0\). We can write
where the \(m_{i}(y,z,c)\) are of the form
and \(m_{i0}(y,c)\), \(m_{i1}(y,c)\) are polynomials in \(\theta _{1}(c)\), \(\theta _{2}(c)\), \(\theta _{1}(ac)\), \(\theta _{2}(ac)\), \(\theta _{1}^{\prime}(c)\), \(\theta _{2}^{\prime}(c)\), \(\theta _{1}^{\prime}(ac)\), \(\theta _{2}^{\prime}(ac)\), \(y\), \(c\), \(a\). The functions \(g_{i}(y,z,c)\) in (7.6) are positive linear combinations of \((z-y)\theta _{1}(c)\), \((z-y)\theta _{2}(c)\), \(y\theta _{1}(ac)\) and \(y\theta _{2}(ac)\), with the concrete form given in Appendix B. Define
Let us show first that there is no sequence \((z_{n},c_{n})\) with \(z_{n}>b^{\ast}(c_{n})\) such that \(C_{0}(b^{\ast}(c_{n}),z_{n},c_{n})=0\), \(c_{n}\rightarrow \infty \) and \(z_{n}\rightarrow \infty \). From the definitions of the exponents \(g_{i}\) given in Appendix B and the expressions (7.4), we have that
because the other terms are negligible. We can write
and
If \(z_{n}\rightarrow \infty \), \(c_{n}\rightarrow \infty \) with \(b^{\ast}(c_{n})\rightarrow \frac{\mu}{q}\), we deduce that
First, assume that \(z_{n}=c_{n} \alpha _{n} \) with \(\alpha _{n}\rightarrow \overline{\alpha}\in (0,\infty )\). Then \(e^{-q \overline {\alpha}}(e^{q\overline{\alpha}}-1-q\overline{\alpha})>0\) and \(a<1\) yield
which is a contradiction. Secondly, assume that \(z_{n}=c_{n}\alpha _{n} \) with \(\alpha _{n}\rightarrow \infty \). Then since
we have
which is also a contradiction. Finally, assume that \(z_{n}=c_{n}\alpha _{n} \) with \(\alpha _{n}\rightarrow 0{+}\). Then
which is also a contradiction. Hence there is no such sequence \((z_{n},c_{n})\).
Using the Taylor expansions of \(\theta _{1}(\overline{c})\), \(\theta _{2}(\overline{c}) \) and \(b^{\ast}(\overline{c})\) at \(\overline{c}=\infty \) given in (7.4) and Proposition 7.1, we find that the function
is infinitely continuously differentiable, because it is infinitely continuously differentiable for \(u>0\) and
Moreover, its first-order power series expansion is given by
Since the only zero of \(H_{1}(z,0)\) in \([\frac{\mu}{q},\infty )\) is \(\frac {\mu}{q}(1+\frac{1}{\sqrt{a}})\) and
for \(z\geq \frac{\mu}{q}\), we conclude by the implicit function theorem that there exist \(\varepsilon >0\) and a unique infinitely continuously differentiable function \(g:[0,\varepsilon )\rightarrow \mathbb{R}\) with \(g(0)= \frac{\mu}{q}(1+\frac{1}{\sqrt{a}})\) and \(H_{1}(g(u),u)=0\) for \(u\in [ 0,\varepsilon )\). In addition, \(g(u)\) is the unique zero of \(H_{1}(\,\cdot \,,u)\) in a neighbourhood \(U\) of \((\frac{\mu}{q}(1+\frac{1}{\sqrt{a}}),0)\). Moreover, the first-order Taylor expansion of \(g\) at \(u=0\) is given by
Let us now show that \(g(u)\) is the only zero of \(H_{1}(\,\cdot \,,u)\) in \((b^{\ast }(1/u),\infty )\) for \(u\) small enough. If this were not the case, there would be a sequence \((z_{n},u_{n})_{n\geq 1}\) with \(z_{n}>b^{\ast}(1/u_{n})\), \(z_{n}\neq g(u_{n})\) such that \(u_{n}\searrow 0\) and \(H_{1}(z_{n},u_{n})=0\). If there exists a convergent subsequence \((z_{n_{k}})\) with \(z_{n_{k}}\rightarrow z_{0}\in [ \frac{\mu}{q},\infty )\), then \(H_{1}(z_{0},0)=0\) by continuity and so \(z_{0}=g(0)=\frac{\mu}{q}(1+\frac{1}{\sqrt{a}})\) which is a contradiction because \((z_{n_{k}},u_{n_{k}})\notin U\) for \(k\) large enough. So \(z_{n}\rightarrow \infty \) and this is also a contradiction. So from (7.7), we get the result. □
Proposition 7.3
There exists a unique zero \(x^{\ast} (\overline{c})\) of \(\partial _{\overline{c}}V^{\overline{c}}(x,\overline{c})\) in \((0,\infty )\) for \(\overline{c}\) large enough with \(x^{\ast}(\overline {c})>b^{\ast}(\overline{c})\) and \(\lim _{\overline{c}\rightarrow \infty}x^{\ast }(\overline{c})= \frac{\mu}{q}(1+\frac{1}{\sqrt{a}})\). More precisely, \(x^{\ast}(\overline{c})\) is infinitely continuously differentiable for \(\overline{c}\) large enough and its first-order Taylor expansion at \(\overline{c}=\infty \) is given by
Moreover, we have
Proof
From (5.4), we have that
and from Proposition 7.1, we know that ↗-\(\lim _{\overline{c}\rightarrow \infty}b^{\ast}( \overline{c}) = \mu /q\).
Take \(x<\mu /q\). Then \(x< b^{\ast}(\overline{c})\) for \(\overline{c}\) large enough; so we have
and so
where
and
Here \(\ell _{i}(x,b,c)\) are polynomials in \(\theta _{1}(c)\), \(\theta _{2}(c)\), \(\theta _{1}(ac)\), \(\theta _{2}(ac)\), \(\theta _{1}^{\prime}(c)\), \(\theta _{2}^{\prime}(c)\), \(\theta _{1}^{\prime}(ac)\), \(\theta _{2}^{\prime}(ac)\), \(x\), \(b\), \(c\), \(a\), and \(h_{i}(x,b,c)\), \(i=1,\dots ,11\), are positive linear combinations of \(b\theta _{1}(ac)\), \(x\theta _{1}(ac)\), \(b\theta _{2}(ac)\) and \(x\theta _{2}(ac)\) stated in detail in Appendix B. Since \(\lim _{\overline{c}\rightarrow \infty}b^{\ast}(\overline{c})=\mu /q\), the Taylor expansion of \(F_{2}(x,\overline{c})/\overline{c}^{2}\) at \(\overline {c}=\infty \) is given by
Since \(xq-2\mu <\) 0, we have \(\partial _{\overline{c}}V^{\overline{c}}(x,\overline{c})<0\) for \(\overline{c}\) large enough, and so we obtain \(\lim _{\overline{c}\rightarrow \infty}V^{\overline{c}}(x, \overline{c})=x^{+}\) for \(x<\frac{\mu}{q}\).
Take now \(x\geq \mu /q>b^{\ast}(\overline{c})\). Then
and so
where
\(\ell _{0}(b,\overline{c})\) is defined in (7.9), \(\bar{\ell}_{i}(x,b,c)\) are polynomials in \(\theta _{1}(c)\), \(\theta _{2}(c)\), \(\theta _{1}(ac)\), \(\theta _{2}(ac)\), \(\theta _{1}^{\prime}(c)\), \(\theta _{2}^{\prime}(c)\), \(\theta _{1}^{\prime}(ac)\), \(\theta _{2}^{\prime}(ac)\), \(x\), \(b\), \(c\), \(a\), and \(k_{i}(x,b,c)\), \(i=1,\dots ,8\), are positive linear combinations of \(b\theta _{1}(ac)\), \(b\theta _{2}(ac)\) and \((x-b)\theta _{2}(c)\) as detailed in Appendix B. Since \(\lim _{\overline{c}\rightarrow \infty }b^{\ast}(\overline{c})=\mu /q\), the Taylor expansion of \(F_{3}(x,\overline {c})/\) \(\overline{c}^{2}\) at \(\overline{c}=\infty \) is given by
So \(F_{3}(x^{\ast}(\overline{c}),\overline{c})=0\) yields that the Taylor expansion of \(x^{\ast}(\overline{c})\) is given by (7.8).
Finally, for \(\overline{c}\) large enough, we get \(\partial _{\overline{c}}V^{\overline{c}}(x,\overline{c})<0\) for \(x\in [ \frac{\mu }{q},\frac{\mu}{q}(1+\frac{1}{\sqrt{a}}))\) and \(\partial _{\overline{c}}V^{\overline{c}}(x,\overline{c})>0\) for \(x>\frac{\mu}{q}(1+\frac{1}{\sqrt{a}})\). So the result follows. □
Remark 7.4
Note that
So \(z^{\ast}(\overline{c})>x^{\ast}(\overline{c})\) for \(\overline{c}\) large enough, and we have asymptotic equivalence for these two quantities when \(\overline {c}\to \infty \). At the same time, the inequality \(z^{\ast}(\overline{c})\geq x^{\ast}(\overline{c})\) can easily be seen to hold for any \(\overline{c}\) from the following argument: We have
since \(V^{\overline{c}}(x,c)\) is nondecreasing in \(\overline{c}\) by Proposition 3.10. Dividing by \(h\) and taking the limit as \(h\) goes to zero, we get
Hence \(\partial _{\overline{c}}V^{\overline{c}}(z^{\ast}(\overline {c}), \overline{c})\geq V_{c}^{\overline{c}}(z^{\ast}(\overline {c}),c) \big\vert _{c=\overline{c}}=0\), and then the value \(x^{\ast}(\overline{c})\) where \(\partial _{\overline{c}}V^{\overline{c}}(\,\cdot \, ,\overline{c})\) changes from negative to positive satisfies \(x^{\ast }(\overline{c})\leq z^{\ast}(\overline{c})\).
Remark 7.5
One observes from (7.5) that for very small values of \(a\), the coefficient of \(1/\overline{c}\) in the asymptotic expansion is positive so that the limit \(\mu (1+1/\sqrt{a})/q\) is approached from the right, whereas for larger values of \(a\), that coefficient is negative and the limit is approached from the left as \(\overline{c}\) becomes large; see also the numerical illustrations in Sect. 9. It may also be instructive to derive the higher-order limiting behaviour of \(x^{\ast}(\overline{c})\) established in Proposition 7.3 in a direct way for the deterministic case discussed in Sect. 2. Concretely, including one more term in the expansion (2.2) gives
and substituting \(x=\frac{\mu}{q}(1+\frac{1}{\sqrt{a}})+\frac{a_{0}}{\overline{c}}\) (for an \(a_{0}\in{\mathbb{R}}\) to be identified) into this expression gives
This fraction equals zero for \(a_{0}=\frac{(1-2\sqrt{a}-3a)\mu ^{2}}{3\sqrt{a^{3}}q}\) so that we obtain
which exactly corresponds to (7.8) for \(\sigma =0\). This formula shows that in the deterministic case, indeed the limit \(\mu (1+1/\sqrt{a})/q\) is approached from the right for \(a<1/9\) and from the left for \(a>1/9\) as \(\overline{c}\rightarrow \infty \).
8 Optimal strategies for \(\overline{c}\) large
In the next result, we show that for \(\overline{c}\) large enough, there exists a unique solution of (6.12) with boundary conditions (6.13) and that \(\overline{\zeta }{}^{\prime}<0\) and \(\overline{\gamma}{}^{\prime}>0\) in a neighbourhood of \(\overline{c}\). We emphasise again that for all results in this section, we assume \(a<1\).
Proposition 8.1
For \(\overline{c}\) large enough, we can find \(\underline{c}\in [ 0,\overline{c})\) such that there exists a unique solution \((\overline{\gamma}(c),\overline{\zeta}(c))\) of (6.12) with boundary conditions (6.13) in \([\underline{c},\overline{c}]\), and \(\overline{\gamma}\) is strictly increasing and \(\overline{\zeta}\) is strictly decreasing in \([\underline{c},\overline{c}]\), respectively.
Proof
In order to prove that there exists a unique solution \((\overline{\gamma}(c),\overline{\zeta}(c))\) of (6.12) in \([\underline{c},\overline{c}]\) for some \(\underline{c}<\overline{c}\), it suffices to show that
for \(\overline{c}\) large enough. Combining (7.1) and (7.5) with the formulas of \(C_{11}(y,z,c)\) and \(C_{22}(y,z,c)\) given in (A.9) and (A.11), we obtain that
and so
for \(\overline{c}\) large enough.
In order to prove that \(\overline{\gamma}(c)\) is increasing and \(\overline {\zeta}(c)\) is decreasing in \([\underline{c},\overline{c}]\) for \(\overline{c}\) large enough and some \(\underline{c}<\overline{c}\), we use the differential equations (6.12) at \(c=\overline{c}\) and the power series expansion of \(C_{ij}\) to show that
for \(\overline{c}\) large enough; so we have the result. □
In the following result, we show that the reward function \(W^{\overline{\gamma},\overline{\zeta}}\) of the two-curve strategy given by the solutions of \((\overline{\gamma},\overline{\zeta})\) of (6.12) with boundary conditions (6.13) is the value function in \([0,\infty )\times [ \underline{c},\overline{c}]\) for \(\overline{c}\) large enough and some \(\underline{c}<\overline{c}\). So the optimal strategy is a two-curve strategy.
Theorem 8.2
There exist a large \(\overline{c}> q\sigma ^{2}/(2\mu )\) and some \(\underline{c}<\overline{c}\) such that \(W^{\overline{\gamma},\overline{\zeta}}=V\) in \([0,\infty )\times [ \underline{c},\overline{c}]\).
Proof
By Proposition 8.1, there exist \(\overline{c}\) large enough and some \(\underline{c}<\overline{c}\) such that \(\overline{\zeta}{}^{\prime}(c)\neq 0\), and so by Proposition 6.9, \(W^{\overline{\gamma},\overline{\zeta}}\) is \((2,1)\)-differentiable in \([0,\infty )\times [ \underline{c},\overline{c}]\). Using Theorem 6.10, in order to prove the result, it is sufficient to show that
for \(c\in [ \underline{c},\overline{c})\). We have from Proposition 6.8 that \(\partial _{x}(W^{\overline{\gamma},\overline{\zeta}})( \overline{\gamma}(c),c)=1\) for \(c\in [ \underline{c},\overline{c}]\), and the Taylor expansion of \(\partial _{xx}v^{\overline{c}}(x)\) at \(\overline{c}=\infty \) is given by
which is negative so that \(\partial _{xx}v^{\overline{c}}(x)<0\) for \(\overline{c}\) large enough. Since \(\partial _{xx}(W^{\overline{\gamma},\overline{\zeta}})(x,c)\) is continuous, there exists \(\underline{c}<\overline{c}\) such that \(\partial _{xx}(W^{\overline{\gamma},\overline{\zeta}})(x,c)<0\) in \((x,c)\) for \(c\in [ \underline{c},\overline{c}]\) and \(x\in [ 0,\overline{\zeta }(c)]\). We conclude that (8.1) holds for \(c\in [ \underline{c},\overline{c}]\) and \(\overline{c}\) large enough.
Let us show that for \(\overline{c}\) large enough and some \(\underline{c}<\) \(\overline{c}\), we have \(\partial _{c}W^{ \overline{\gamma},\overline {\zeta}}(x,c)\leq 0\) for \(c\in [ \underline{c},\overline{c}]\) and \(0\leq x\leq \overline{\zeta}(c)\). We prove first that \(\partial _{c}W^{\overline {\gamma},\overline{\zeta}}(x,c)\leq 0\) for \(x\in [ \overline{\gamma }(c),\overline{\zeta}(c)]\). We have
and by Lemma A.1, \(f_{21}(y,x,c)>0\) for \(x>y\). So we should prove that
for \(x\in [ \overline{\gamma}(c),\overline{\zeta}(c)]\). By Proposition 6.8, \(0=\partial _{c}H^{\overline{\gamma}, \overline{\zeta}}(x,\overline{c})=\partial _{cx}H^{\overline{\gamma}, \overline{\zeta}}(x,\overline{c})\), and so we have \(G(\overline{\zeta}(\overline {c}),\overline{c})=\partial _{x}G( \overline{\zeta}(\overline{c}),\overline {c})=0\). Then it is sufficient to prove that \(\partial _{xx}G(x,c)<0\) for \(x\in [ \overline{\gamma}(c),\overline{\zeta}(c)]\). We first show that \(\partial _{xx}G(x,\overline{c})<0\) for \(x\in [ \overline{\gamma }(\overline{c}),\overline{\zeta}( \overline{c})] \) for \(\overline{c}\) large enough, and then the result follows for \(c\in [ \underline{c},\overline {c}]\) for some \(\underline{c}<\overline{c}\) by continuity arguments in a compact set. Using \(\overline{\gamma}(\overline{c})=b^{\ast}(\overline {c}),~\overline{\zeta}(\overline{c})=z^{\ast}(\overline{c})\), (7.1) and (7.5), we obtain that the Taylor expansion at \(\overline{c}=\infty \) of
is given by
and the Taylor expansion of \(h(z^{\ast}(\overline{c}),\overline{c})\) at \(\overline{c}=\infty \) is given by
Since
is positive and \(h(z^{\ast}(\overline{c}),\overline{c})<0\) for \(\overline{c}\) large enough, we conclude that \(\partial _{xx}G(x,\overline{c})<0 \) for \(x\in [ \overline{\gamma}(\overline{c}),\overline{\zeta}( \overline{c})]\). Let us show that for \(\overline{c}\) large enough and some \(\underline{c}<\) \(\overline{c}\), it holds that \(\partial _{c}W^{\overline{\gamma},\overline {\zeta}}(x,c)\leq 0\) for \(x\in [ 0,\overline{\gamma}(c)]\) and \(c\in [ \underline{c},\overline{c}]\). We can write
where \(f_{11}(x,c)>0\); so we should prove that
for \(x\in [ 0,\overline{\gamma}(c)]\). We have shown that \(\partial _{c}W^{\overline{\gamma},\overline{\zeta}}( \overline{\gamma}(c),c)<0\) so that \(G_{1}(\overline{\gamma}(c), \overline{c})<0\); then it suffices to prove that \(\partial _{x}G_{1}(x,c)>0\) for \(x\in [ 0,\overline{\gamma}(c)]\). We show first that \(\partial _{x}G_{1}(x,\overline{c})>0\) for \(x\in [ 0,\overline{\gamma}(\overline{c})] \) for \(\overline{c}\) large enough; then the result follows for \(c\in [ \underline{c},\overline{c}]\) with some \(\underline{c}<\overline{c}\) by continuity arguments in a compact set. Using \(\overline{\gamma}(\overline{c})=b^{\ast}(\overline{c})\), (7.1) and (7.5), we obtain that the Taylor expansion at \(\overline{c}=\infty \) of
is given by
which is positive for \(\overline{c}\) large enough and \(x\leq b^{\ast }(\overline{c})<\frac{\mu}{q}<\frac{2\mu}{q}\). □
9 Numerical examples
In this section, we consider some numerical illustrations for the case \(q=0.1\), \(\mu =4\) and \(\sigma =2\).
9.1 Bounded case
Let us first consider the case with an upper bound \(\overline{c}=3\) for the dividend rate. In this case, we are able to derive the value function and the optimal strategies for the problem with drawdown constraints \(a=0.2\), \(a=0.5\) and \(a=0.8\). Indeed, they are of two-curve type as conjectured in Remark 6.11. The obtained reward function and optimal dividend strategies then also allow us to compare them with those for the (already previously known) extreme cases \(a=0\) (classical dividend problem without any constraint) and \(a=1\) (dividend problem with ratcheting constraint). To obtain the value functions \(V_{a}^{\overline{c}}\) for each set of parameters, we proceed as follows:
-
1)
We check that there exists a unique zero \(z^{\ast}(\overline{c})\) of \(C_{0}(b^{\ast}(\overline{c}),\cdot \,,\overline{c})\) in \((b^{\ast}(\overline {c}),\infty )\).
-
2)
We obtain the curves \(\overline{\gamma}\) and \(\overline{\zeta}\) by solving numerically, by the Euler method, the system (6.12) of ordinary differential equations with boundary conditions (6.13).
-
3)
We check numerically that the pair \((\overline{\gamma},\overline{\zeta })\) satisfies (6.11) for \(c\in [ 0,\overline{c}]\). So by Proposition 6.6, we are approximating the unique solution \((\overline{\gamma},\overline{\zeta})\). We also verify that \(\overline{\zeta}\) is nondecreasing.
-
4)
We check that the function \(W^{\overline{\gamma},\overline{\zeta}}\) defined in (6.6) satisfies the conditions of Theorem 4.4. Hence \(W^{\overline{\gamma},\overline{\zeta}}\) is the value function \(V_{a}^{\overline{c}}\), and the optimal strategy is indeed a two-curve strategy given by \((\overline{\gamma},\overline{\zeta} )\in \mathcal{B}\).
Figure 3 depicts the graphs of \(V_{a}^{\overline{c}}(x,0)\) with \(\overline{c}=3\) for \(a=0\) (no restrictions, gray solid), \(a=0.5\) (dashed) and \(a=1\) (ratcheting, black solid) as a function of \(x\). One can nicely see how the drawdown case is – in terms of performance – a compromise between the unconstrained case and the stronger constraint of ratcheting.
In order to see the impact of the drawdown restriction more clearly, we plot in Fig. 4 the difference between \(V_{0}^{\overline{c}}(x)\) (the unconstrained value function) and \(V_{a}^{\overline{c}}(x,0)\) as a function of \(x\) for increasingly restrictive drawdown levels \(a=0.2\) (dotted), \(a=0.5\) (dashed), \(a=0.8\) (dotted–dashed) and finally \(a=1\) (ratcheting, solid). One observes that in particular for smaller values of \(x\), the relaxation of ratcheting towards the drawdown constraint improves the performance of the resulting strategy quite a bit, although the relative gap between the performance of the ratcheting and the unconstrained cases is anyway not so big (cf. Fig. 3). The latter speaks in favour of the consideration of such strategies, as ratcheting and drawdown may be important for shareholders from a psychological point of view, and the efficiency loss when introducing these constraints is quite minor. In particular, if for a given initial surplus level \(x\), one has a target efficiency loss one is willing to accept, results like Fig. 4 can help to identify the corresponding drawdown coefficient \(a\) that can still guarantee such a performance.
In terms of the nature of the optimal strategy (which indeed turns out to be of two-curve type), Fig. 5 shows the optimal drawdown curves \((\overline{\gamma}(c),c)\) (dotted) and \((\overline{\zeta}(c),c) \) (dashed) for \(a=0.2\), \(a=0.5\) and \(a=0.8\), respectively. In all plots, we also depict the optimal threshold of the unconstrained dividend problem \(a=0\) (solid gray) and the optimal ratcheting curve \(( \overline{\xi}(c),c ) \) for \(a=1\) (solid black). To that end, recall from Asmussen and Taksar [7] that the optimal threshold for \(a=0\) is given by
whereas the optimal strategy in the ratcheting case is given by a one-curve strategy which is obtained numerically according to the results in Albrecher et al. [1]. One can nicely see how the two curves \((\overline{\gamma}(c),c)\) and \((\overline{\zeta}(c),c)\) move towards the right as \(a\) increases, interpolating between the unconstrained and the ratcheting cases. Note that the resulting two-curve shapes are somewhat reminiscent of some figures obtained in Guo and Tomecek [22] for other types of singular control problems, where also a smooth-fit principle was established.
Notice also that the location of these curves can vary considerably as the maximally allowed dividend rate \(\overline{c}\) changes. Figure 6 depicts \(\overline{\gamma}^{\overline{c}}(c)\) and \(\overline {\zeta}^{\overline{c}}(c)\) for \(a=0.5\) for \(\overline{c}\) growing from 2 to 5. In particular, when \(\overline{c}\) is larger, the necessary surplus level \(x\) to switch to higher dividend rates is larger as well. Figure 7 shows the corresponding value functions for these increasing values of \(\overline{c}\) (\(a=0.5\)). Recall that while the drawdown constraint is not a major efficiency loss when compared to the unconstrained case for the same \(\overline{c}\) (cf. Fig. 3 for the case \(\overline{c}=3\)), the size of \(\overline{c}\) itself naturally has a considerable impact on the size of the value function.
9.2 Boundary conditions
Let us now investigate the situation when the maximally allowed dividend rate \(\overline{c}\) becomes large. In addition to \(a=0.5\) and \(a=0.8\), we now also consider a smaller drawdown level \(a=0.07\) (in order to illustrate the different monotonicity for small values of \(a\), cf. Remark 7.5). One finds numerically that there exists a unique zero \(z^{\ast}(\overline{c})\) of \(C_{0}(b^{\ast}(\overline{c}),\cdot \,,\overline{c})\) in \((b^{\ast}(\overline {c}),\infty )\) for any \(\overline{c}\geq 0\). We have also found that there exists a unique zero \(x^{\ast}(\overline{c})\) in \((0,\infty )\) of \(\partial _{\overline{c}}V^{\overline{c}}(\,\cdot \,,\overline{c})\) for \(\overline{c}\geq 5.17\) for \(a=0.07\), for \(\overline{c}\geq 3.45\) for \(a=0.5\), and for \(\overline{c}\geq 2.52\) for \(a=0.8\). Recall that we have proved in Propositions 7.1–7.3 that \(\lim _{\overline{c}\rightarrow \infty}z^{\ast}(\overline{c})=\lim _{ \overline {c}\rightarrow \infty}x^{\ast}(\overline{c})=\mu (1+1/\sqrt{a})/q\) and \(\lim _{\overline{c}\rightarrow \infty}b^{\ast}(\overline{c})=\mu /q\).
Figure 8 shows the curves of the boundary conditions \((b^{\ast }(\overline{c}),\overline{c})\), \((z^{\ast}(\overline{c}),\overline{c})\) and \((x^{\ast}(\overline{c}),\overline{c})\) for \(a=0.07\), \(a=0.5\) and \(a=0.8\), respectively. In the case \(a=0.07\), one sees how the limit \(\mu (1+1/\sqrt {a})/q=191.2\) (vertical dotted line) is indeed approached from the right as \(\overline{c}\rightarrow \infty \), whereas for \(a=0.5\) and \(a=0.8\), the respective limits 96.57 and 84.72 (vertical dotted line) are approached from the left; cf. Remark 7.5. It is important to keep in mind that these plots only depict the boundary value for each choice of \(\overline{c}\), and are not to be confused with the optimal drawdown curves in Fig. 5. Note that \(x^{\ast}(\overline{c})\) and \(z^{\ast}(\overline {c})\) are – already for moderate values of \(\overline{c}\) – almost identical, with \(z^{\ast}(\overline{c})>x^{\ast}(\overline{c})\); see Fig. 9 for a graph of the difference \(z^{\ast}(\overline{c})- x^{\ast}(\overline{c})\) for \(a=0.07\), \(a=0.5\) and \(a=0.8\), respectively. From the latter, one nicely sees \(z^{\ast}(\overline{c})>x^{\ast}(\overline{c})\) (cf. Remark 7.4) as well as the asymptotic equivalence (7.10) of the two quantities.
In Fig. 5, we saw that the curve \(\overline{\zeta}^{\overline {c}}(c)\) is to the left of the ratcheting curve \(\overline{\xi}^{\overline{c}}(c)\). At the same time, for large values of \(\overline{c}\), we know that \(\overline{\zeta}^{\overline{c}}(c)\) must be to the right of \(\overline{\xi }^{\overline{c}}(c)\), as
It is therefore of interest to see when this crossing for the limiting value takes place. Figure 10 depicts \(z^{\ast}(\overline{c})\) (solid) and \(\overline{\xi}^{\overline{c}}(\overline{c})\) (dotted) for \(a=0.07\), \(a=0.5\) and \(a=0.8\), respectively. We see that indeed \(z^{\ast}(\overline{c})<\overline{\xi}^{\overline{c}}(\overline{c})\) for \(\overline{c}\) small, and \(z^{\ast}(\overline{c})>\overline{\xi}^{\overline{c}}(\overline{c})\) for \(\overline{c}\) large. Moreover, we obtain numerically that the intersection point of the curves \(z^{\ast}(\overline{c}) \) and \(\overline{\xi}^{\overline{c}}(\overline{c})\) occurs at \(\overline{c}=39.70\) for \(a=0.07\), at \(\overline {c}=9.74\) for \(a=0.5\), and at \(\overline{c}=8.37\) for \(a=0.8\) for the given set of parameters. That is, if \(\overline{c}\) exceeds that threshold, the possibility of the drawdown increases the level of the surplus above which one starts to pay the maximal dividend rate, when compared to pure ratcheting, and it is intuitive that the difference is less pronounced as \(a\) increases.
10 Conclusions
In this paper, we have addressed the problem of optimal dividends under a drawdown constraint. We have shown that the value function can be expressed as the unique viscosity solution of a two-dimensional Hamilton–Jacobi–Bellman equation and have derived conditions under which the optimal strategy is of a two-curve form. We conjecture that these conditions are in fact always fulfilled and – using a smooth-fit principle – have proved this for large values of current and maximal dividend rate \(c\) and \(\overline{c}\), respectively. For concrete numerical examples, we have also proved the optimality of two-curve strategies numerically for small values of \(c\) and \(\overline{c}\), and have shown how to identify the resulting optimal curves. This turns out to be a very challenging and technical task, involving the numerical solution of a highly involved system of ordinary differential equations and its boundary conditions. We have illustrated how this can be concretely implemented for a moderate size of \(\overline{c}\); for high values of \(\overline{c}\), this is numerically difficult because the formulas involve algebraic sums with terms with exponentials with very large exponents and the computations require very high numerical precision. We furthermore have shown that when \(\overline{c}\) tends to infinity, the curves converge to a finite limit, the size of which follows a surprisingly simple and intriguing formula in terms of the square-root of the drawdown percentage \(a\) for any volatility parameter \(\sigma \). The latter fact also allows getting some intuition on the nature of this limit from the deterministic limit case \(\sigma =0\). Altogether, this paper is the first to explicitly address a drawdown constraint for a control problem in this context, and it has turned out that the resulting strategies smoothly interpolate between the unconstrained problem and the situation with ratcheting constraints, allowing to get some quantitative insight in the efficiency gain when relaxing the ratcheting. It will be interesting to see whether other dividend – and more generally control – problems can be extended in a similar way. In particular, extending the results from the Brownian risk model to a compound Poisson surplus process may be an interesting endeavour, which would lead to a relaxation of the ratcheting problem studied in Albrecher et al. [2]. Another future direction of research may be to extend the approach of the present paper to incorporate constraints on the dividend rate in terms of an average of its previous values, for instance along the lines of Angoshtari et al. [6].
References
Albrecher, H., Azcue, P., Muler, N.: Optimal ratcheting of dividends in a Brownian model. SIAM J. Financ. Math. 13, 657–701 (2022)
Albrecher, H., Azcue, P., Muler, N.: Optimal ratcheting of dividends in insurance. SIAM J. Control Optim. 58, 1822–1845 (2020)
Albrecher, H., Bäuerle, N., Bladt, M.: Dividends: from refracting to ratcheting. Insur. Math. Econ. 83, 47–58 (2018)
Albrecher, H., Thonhauser, S.: Optimality results for dividend problems in insurance. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 103, 295–320 (2009)
Angoshtari, B., Bayraktar, E., Young, V.R.: Optimal dividend distribution under drawdown and ratcheting constraints on dividend rates. SIAM J. Financ. Math. 10, 547–577 (2019)
Angoshtari, B., Bayraktar, E., Young, V.R.: Optimal consumption under a habit-formation constraint. SIAM J. Financ. Math. 13, 321–352 (2020)
Asmussen, S., Taksar, M.: Controlled diffusion models for optimal dividend pay-out. Insur. Math. Econ. 20, 1–15 (1997)
Avanzi, B.: Strategies for dividend distribution: a review. N. Am. Actuar. J. 13, 217–251 (2009)
Azcue, P., Muler, N.: Stochastic Optimization in Insurance: A Dynamic Programming Approach. Springer Briefs in Quantitative Finance. Springer, Berlin (2014)
Borodin, A.N., Salminen, P.: Handbook of Brownian Motion—Facts and Formulae, 2nd edn. Birkhäuser, Basel (2002)
Brinker, L.V.: Stochastic optimisation of drawdowns via dynamic reinsurance controls. Doctoral Dissertation, Universität zu Köln (2021). Available online at https://kups.ub.uni-koeln.de/54963/1/LVBrinkerOptStochContDrawdown.pdf
Brinker, L.V., Schmidli, H.: Optimal discounted drawdowns in a diffusion approximation under proportional reinsurance. J. Appl. Probab. 59, 527–540 (2022)
Claisse, J., Talay, D., Tan, X.: A pseudo-Markov property for controlled diffusion processes. SIAM J. Control Optim. 54, 1017–1029 (2016)
Chen, X., Landriault, D., Li, B., Li, D.: On minimizing drawdown risks of lifetime investments. Insur. Math. Econ. 65, 46–54 (2015)
De Finetti, B.: Su un’impostazione alternativa della teoria collettiva del rischio. In: Transactions of the 15th Int. Congress of Actuaries, pp. 433–443 (1957)
Dybvig, P.H.: Dusenberry’s ratcheting of consumption: optimal dynamic consumption and investment given intolerance for any decline in standard of living. Rev. Econ. Stud. 62, 287–313 (1995)
Eisenberg, J., Grandits, P., Thonhauser, S.: Optimal consumption under deterministic income. J. Optim. Theory Appl. 160, 255–279 (2014)
Elie, R., Touzi, N.: Optimal lifetime consumption and investment under a drawdown constraint. Finance Stoch. 12, 299–330 (2008)
Gerber, H.U.: Entscheidungskriterien für den zusammengesetzten Poisson-Prozess. Schweiz. Aktuarver. Mitt. (1969) 185–227 (1969)
Gerber, H.U.: Games of economic survival with discrete-and continuous-income processes. Oper. Res. 20, 37–45 (1972)
Gerber, H.U., Shiu, E.S.W.: Optimal dividends: analysis with Brownian motion. N. Am. Actuar. J. 8, 1–20 (2004)
Guo, X., Tomecek, P.: A class of singular control problems and the smooth fit principle. SIAM J. Control Optim. 47, 3076–3099 (2009)
Jeanblanc-Picqué, M., Shiryaev, A.: Optimization of the flow of dividends. Usp. Mat. Nauk 50, 25–46 (1995)
Kardaras, C., Obloj, J., Platen, E.: The numéraire property and long-term growth optimality for drawdown-constrained investments. Math. Finance 27, 68–95 (2017)
Landriault, D., Li, B., Zhang, H.: On magnitude, asymptotics and duration of drawdowns for Lévy models. Bernoulli 23, 432–458 (2017)
Loeffen, R.L., Renaud, J.F.: De Finetti’s optimal dividends problem with an affine penalty function at ruin. Insur. Math. Econ. 46, 98–108 (2010)
Radner, R., Shepp, L.: Risk vs. profit potential: a model for corporate strategy. J. Econ. Dyn. Control 20, 1373–1393 (1996)
Schmidli, H.: Stochastic Control in Insurance. Springer, New York (2008)
Shreve, S.E., Lehoczky, J.P., Gaver, D.P.: Optimal consumption for general diffusions with absorbing and reflecting barriers. SIAM J. Control Optim. 22, 55–75 (1984)
Funding
Open access funding provided by University of Lausanne. H. Albrecher acknowledges financial support from the Swiss National Science Foundation Project 200021_191984.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Results and proofs for Sect. 6
We first state some definitions and formulas used to define the functions \(b_{0}\) and \(b_{1}\) introduced in (6.2). We set
Lemma A.1
The function \(d(y,z,c)\) defined in (A.1) is positive in \(T\times [ 0,\overline{c}]\), and so \(b_{0}\) and \(b_{1}\) introduced in (6.2) are well defined.
Proof
Using \(\theta _{1}>0>\theta _{2}\) and \(\theta _{1}^{\prime },\theta _{2}^{\prime}>0\), define \(g(y,h,c)=d(y,y+h,c)/e^{h \theta _{2}(c)}\). Then
for \(y>0\) and
for \(y\geq 0\). So the result holds. □
To prove Proposition 6.2, we introduce some auxiliary formulas. Set
Proof of Proposition 6.2
As the function \(H^{\gamma ,\zeta}(\,\cdot \,,c)\) is continuously differentiable at \(x=\gamma (c)\) and satisfies \(H^{\gamma ,\zeta}(0,c)=0\), \(\mathcal{L}^{ac}(H^{\gamma ,\zeta})(x,c)=0\) for \(0\leq x<\gamma (c)\) and \(\mathcal{L}^{c}(H^{\gamma ,\zeta})(x,c)=0\) for \(\gamma (c)\leq x\), there exists by (5.1) and (5.3) a function \(A(c)\) with
Let us find a formula for the function \(A(c)\). Since
we obtain by (5.4) that
Using that \(\partial _{c}H^{\gamma ,\zeta}(x,c)\vert _{x=\zeta (c)}=0\) for all \(c\in [ 0,\overline{c}]\) and that \(\zeta (c)>\gamma (c)\), we get
and \(f_{21}(y,x,c)= \frac {d(y,x,c)}{\theta _{1}(c)-\theta _{2}(c)}>0\) for \(x>y\) by Lemma A.1. So we obtain
at the points where \(\zeta \) is continuous, with \(b_{0}\) and \(b_{1}\) defined in (6.2). Since \(\zeta \) is Riemann-integrable, it is differentiable almost everywhere. Note that the function \(A\) is the unique solution of this ODE. Since the function \(A\) depends on \(\gamma \) and \(\zeta \), we call it \(A^{\mathcal{\mathcal{\gamma}},\mathcal{\mathcal{\zeta}}}\). Hence we have the result. □
Definition A.2
Let \(\zeta :[0,\overline{c}]\rightarrow [ 0,\infty )\) be a step function, that is,
with \(0=c_{1}< c_{2}<\cdots <c_{n}=\overline{c}\) and \(z_{i}>0\). Then the two-curve strategy defined at the beginning of Sect. 6 and described in Fig. 1, starting with an initial surplus \(x\) and initial running maximum dividend rate \(c\), is given as follows:
(1) If \(0\leq x<\zeta (c)\), that is, \((x,c)\in \mathcal{NC(\mathcal{\mathcal{\gamma}}},\mathcal{\mathcal{\mathcal{\zeta}})}\), follow the refracting strategy which pays at the rate \(ac\) when the current surplus is below a refracting threshold \(\gamma (c)\) and at \(c\) when the current surplus is above \(\gamma (c)\), until either reaching the curve \(\mathcal{R(\zeta )}\) or ruin (whichever comes first).
(2) If \(x\geq \zeta (c)\), that is, \((x,c)\in \mathcal{CH(\mathcal{\mathcal{\gamma}}},\mathcal{\mathcal{\mathcal{\zeta}})}\), increase immediately the dividend rate to \(\ell (x,c)\in \{c_{2},\dots ,c_{n}\}\); note that
where \(h(c):=\min \{h:c_{h}\geq c\}\). We denote this two-curve strategy by \(\mathbf{\pi}^{(\gamma ,\zeta )}\).
In the next result, we show by using a Feynman–Kac argument that if \(\zeta \) is a step function, then \(W^{\gamma ,\zeta}\) is the reward function of a two-curve strategy. In the lemma that follows, we show that in the general case \((\gamma ,\zeta )\in \mathcal{B}\), \(W^{\gamma ,\zeta}\) is the limit of reward functions of two-curve strategies.
Lemma A.3
Consider \((\gamma ,\zeta )\in \mathcal{B,}\) with \(\zeta \) being a step function. Let \(D^{x,c}\in \Pi _{x,c}^{[0,\overline {c}]}\) be the admissible strategy corresponding to the two-curve strategy \(\mathbf{\pi}^{(\gamma ,\zeta )}\) starting in \((x,c)\). Calling \(j(x,c):=J(x;D^{x,c})\), we obtain that \(j\) is continuous in \([0,\infty )\times [ 0,\overline{c}]\) and \(j(x,c)=W^{\gamma ,\zeta}(x,c)\).
Proof
We prove inductively that \(j(x,c_{i}) \) is continuous in \(x\) for \(i=1,\ldots ,n\). First, \(j(\,\cdot \,,c_{i})\) is differentiable in \([0,z_{i})\) because it corresponds to the reward function of a refracting dividend strategy at \(x=\gamma (c_{i})\) with a given boundary condition at \(x=z_{i}\) (see for instance Albrecher et al. [3, Theorem 3.1]). In the case \(i=n\), \(j(x,c_{n})=v(x,c,\gamma (\overline{c}))\) which is continuous in \(x\); in the case \(i< n\), \(j(x,c_{i}) \) is continuous in \(x\) for \(x\leq z_{i}\) because
for some constant \(A_{i}\), and \(j(x,c_{i})=j(x,c_{i+1})\) for \(x\geq z_{i}\). As \(j(x,c)=j(x,c_{i+1})\) for \(c\in (c_{i},c_{i+1})\), we conclude that \(j\) is continuous in \([0,\infty )\times [ 0,\overline{c}]\).
Let us now show that \(j(x,c)\) satisfies the assumptions of Proposition 6.2 and so \(j(x,c)=H^{\gamma ,\zeta }(x,c)=W^{\gamma ,\zeta}(x,c)\) for \(0\leq x\leq \zeta (c)\). Indeed, it is straightforward that \(j(\, \cdot \,,\overline{c}) =H^{\gamma ,\zeta}(\,\cdot \,,\overline{c})= v(\,\cdot \,,c,\gamma (\overline{c}))\), \(j(\,\cdot \,,c)\) is continuously differentiable for any \(c\in [ 0,\overline{c})\), \(\mathcal{L}^{ac}(j)(x,c)=0\) for \(0\leq x<\gamma (c)\), \(\mathcal{L}^{c}(j)(x,c)=0\) for \(\gamma (c)\leq x\leq \zeta (c)\) and \(j(0,c)=0\). Also \(\partial _{c}j(\zeta (c),c)=0\) at the points of continuity of \(\zeta \) because \(j(x,c)=j(x,c_{i+1}{)}\) for \(x\geq \zeta (c)=z_{{i}}\) in the case \(c\in (c_{i},c_{i+1})\).
From the definition of \(\mathbf{\pi}^{(\gamma ,\zeta )}\), it is straightforward that \(j(x,c)=H^{\gamma ,\zeta}(x,\ell (x,c))\) if \(x\geq \zeta (c)\); so we get the result. □
In the next result, we show that for any \((\gamma ,\zeta )\in \mathcal{B}\), the function \(W^{\gamma ,\zeta}\) is the uniform limit of reward functions of curve strategies, where the \(\zeta _{k}\) are step functions with \(\zeta _{k}\rightarrow \zeta \).
Lemma A.4
Given \((\gamma ,\zeta )\in \mathcal{B}\), there exists a sequence of right-continuous step functions \(\zeta _{k}:[0,\overline {c}]\rightarrow [ 0,\infty )\) such that \(W^{\gamma ,\zeta _{k}}(x,c)\) converges uniformly to \(W^{\gamma ,\zeta}(x,c)\).
Proof
Since \(\zeta \) is a Riemann-integrable càdlàg function, we can approximate it uniformly by right-continuous step functions. Namely, take a sequence of finite sets \(\mathcal{S}^{k}=\{c_{1}^{k},c_{2}^{k},\dots ,c_{n_{k}}^{k}\}\) with \(0=c_{1}^{k}< c_{2}^{k}<\cdots <c_{n_{k}}^{k}=\overline{c}\) and consider the right-continuous step functions
with \(\delta (\mathcal{S}^{k})=\max _{i=1,\dots ,n_{k}-1}(c_{i+1}^{k}-c_{i}^{k})\rightarrow 0\). We have that \(\zeta _{k}\rightarrow \zeta \) uniformly, and so both \(A^{\gamma ,\zeta _{k}}\rightarrow A^{\gamma ,\zeta}\) and \(W^{\gamma ,\zeta _{k}}\) → \(W^{\gamma ,\zeta}\) uniformly. □
Lemma A.5
For a given \(c\in [ 0,\overline{c})\), consider \(\gamma :[c,\overline{c}]\rightarrow (0,\infty )\) which is continuously differentiable and \(\zeta :[c,\overline{c}]\rightarrow (0,\infty )\) which is bounded, Riemann-integrable and càdlàg. Define the set
If \((\gamma _{0},\zeta _{0})\in \mathcal{B}\) satisfies (6.7), then for any \(c\in [ 0,\overline{c})\),
Proof
Given \((\gamma ,\zeta ) \in \mathcal{B}\), we can write
Note that the pair \(( \gamma _{0} \vert _{[c,\overline{c})}, \zeta _{0} \vert _{[c,\overline{c})} )\) is in \(\mathcal{B}_{c}\). Indeed, given any \((\gamma ,\zeta ) \in \mathcal{B}_{c}\) and any function \(\chi :[0,\overline{c}]\rightarrow [ 0,1]\) which is continuously differentiable with \(\chi =0\) in \([0,c]\), we define the two functions \(\gamma _{1}(s)=\gamma _{0}(s)I_{\{0\leq s< c\}}+\gamma (s)\chi (s) I_{ \{c\leq s\leq \overline{c}\}}\) and \(\zeta _{1}(s)= \zeta _{0}(s)I_{\{0\leq s< c\}}+\zeta (s)\chi (s)I_{\{c\leq s\leq \overline{c}\}}\). Then \((\gamma _{1}, \zeta _{1}) \in \mathcal{B}\). Moreover,
Hence
and so we have \(\sup _{(\gamma ,\zeta )\in \mathcal{B}_{c}}A^{{{ \gamma}},\zeta}(c)=A^{\mathcal{\mathcal{\gamma}}_{0},\zeta _{0}}(c)\). □
Proof of Proposition 6.4
Consider any function \((\gamma _{1},\zeta _{1})\in \mathcal{B}\) with \(\gamma _{1}(\overline{c})=\zeta _{1}(\overline{c})=0\). Then
Taking the derivative with respect to \(\varepsilon \) at \(\eta =\varepsilon =0\), we get
Using integration by parts, we obtain
and so
Since this holds for any \(\zeta _{1}\) with \(\zeta _{1}(\overline{c})=0\), we get using (6.4) that for any \(c\in [ 0,\overline{c})\),
and so we deduce (6.8).
Taking the derivative with respect to \(\eta \) at \(\eta =\varepsilon =0\), we get
Using integration by parts, we obtain
Using that \(\gamma _{1}(\overline{c})=0\) and (6.4), we get
Since this holds for any \(\gamma _{1}\) with \(\gamma _{1}(\overline{c})=0\), we obtain
for all \(c\in [ 0,\overline{c}]\) and
By Lemma A.5, taking the derivative \(0= \partial _{\eta}A^{\gamma _{0}+\eta \gamma _{1},\zeta _{0}+\varepsilon \zeta _{1}}(c) \big\vert _{\eta =0,\varepsilon =0}\), we also obtain that (6.9) holds. Note that with (6.9), we have
and so, from (A.7)
from which we deduce (6.10). □
To prove Proposition 6.5, we next introduce some auxiliary formulas. Set
Proof of Proposition 6.5
From (6.2), we can write
which does not depend on \(w\). So we conclude that
Moreover, from Proposition 6.4, we get (6.13). From (6.9) and (6.10), we have
and we can write from (6.2) that
So since \(C_{11}(\gamma _{0}(c),\zeta _{0}(c),c)\neq 0\), we get the first equation of (6.12). Taking the derivative of (A.12) with respect to \(c\) and using that \(\zeta _{0}\) is continuous, \(\gamma _{0}\) is continuously differentiable and \(C_{22}(\gamma _{0}(c),\zeta _{0}(c),c)\neq 0\), we obtain that \(\zeta _{0}\) is continuously differentiable and
Using the first equation of (6.12), we get the second equation of (6.12). By a recursive argument, we finally obtain that \(\gamma _{0}\) and \(\zeta _{0}\) are infinitely differentiable. □
Proof of Proposition 6.6
Consider
Let us call
and \(F(y,z,c)=F_{1}(y.z,c)/F_{2}(y.z,c)\). Note that \(F_{1}, F_{2}\) and \(F\) are infinitely differentiable,
and \(( \gamma _{i}(c_{m}),\zeta _{i}(c_{m}) ) = ( \gamma _{i}(c_{m}), \zeta _{i}(c_{m}) ) \) for \(i=1,2 \) and
If \(c_{m}=0\), we have the result. On the other hand, for \(c_{m}>0\), using the Picard–Lindelöf theorem, there exists a unique solution of (6.12) with boundary condition \(\zeta (c_{m})=\zeta _{1}(c_{m})\) in \([\max \{c_{m}-\delta ,0\},c_{m}]\) for some \(\delta >0\), which is a contradiction. □
Proof of Proposition 6.8
Take a pair of infinitely differentiable functions \((\gamma ,\zeta )\in \mathcal{B}\) and consider the function \(H^{\gamma ,\zeta}(x,c)\) introduced in Proposition 6.2. First note that \(H^{\gamma ,\zeta }\) satisfies \(\mathcal{L}^{ac}(H^{\gamma ,\zeta})(x,c)=0\) for \(0\leq x\leq \gamma (c)\), \(\mathcal{L}^{c}(H^{\gamma ,\zeta})(x,c)=0\) for \(x\geq \gamma (c)\), \(H^{\gamma ,\zeta}(0,c)=0\), \(\partial _{c}H^{\gamma ,\zeta }(x,c) \vert _{x=\zeta (c)}=0\) and \(H^{\gamma ,\zeta}(x,\overline {c})=v\left ( x,\overline{c},\gamma ( \overline{c})\right ) \). So we have for \(x>\gamma (c)\) that
Since \(f_{21}(y,x,c)=d(y,x,c)/(\theta _{1}(c)-\theta _{2}(c))>0\) for \(x>y\) by Lemma A.1, we obtain that \(\partial _{cx}H^{\gamma ,\zeta}(x,c) \big\vert _{x=\zeta (c)}=0\) if and only if (6.8) holds for \((\gamma ,\zeta )\) in \([\underline {c},\overline{c}]\). As \(W^{\gamma ,\zeta}(x,c)=H^{\gamma ,\zeta}(x,c)\) for \(x<\zeta (c)\) and \(W^{\gamma ,\zeta}(x,c)=H^{\gamma ,\zeta}(x,C(x,c))\) for \(x\geq \zeta (c)\), we get \(\partial _{c}W^{\gamma ,\zeta}(x,c)=0\) for \(x\geq \zeta (c)\) and hence \(\partial _{cx}W^{\gamma ,\zeta}(\zeta (c),c)=0\). Moreover, \(\partial _{c}H^{\gamma ,\zeta}(\zeta (c),c)=0\) for \(c\in [ \underline{c},\overline{c}]\), and so
In all, since \(W^{\gamma ,\zeta}(x,c)=H^{\gamma ,\zeta}(x,C(x,c))\) if \(x\geq \zeta (c)\), we get \(\partial _{cc}W^{\gamma ,\zeta}(x,c)=0\) if \(x\geq \zeta (c)\) and so \(\partial _{cc}W^{\gamma ,\zeta}(\zeta (c),c)=0\).
Secondly, we have that \(\partial _{y}f_{11}(y,c)\neq 0\), \(b_{11}(y,z,c)>0\) and
So
and then
if and only if (6.9) holds for \((\gamma ,\zeta )\) in \([\underline{c},\overline{c}]\). Note that since
and \(\partial _{x}(W^{\gamma ,\zeta})(\gamma (c),c)=1\), we obtain
Therefore, when \((\bar{\gamma},\bar{\zeta}) \) is a solution of (6.12), it satisfies (6.8) and (6.9), and so
□
Proof of Proposition 6.9
It holds that
By Proposition 6.8, \(W_{xx}^{\overline{\gamma},\overline {\zeta}}(x,c)\) is continuous at \(x=\) \(\overline{\gamma}(c)\), and so \(W^{\overline{\gamma},\overline{\zeta}}\) is \((2,1)\)-differentiable for \(x\) \(<\overline{\zeta}(c)\).
If \(\overline{\zeta}{}^{\prime}(c)>0\) in \([\underline{c},\overline{c}]\), the inverse \(\overline{\zeta}^{-1}\) exists and \(\ell (x,c)\) can be written as
In order to show that \(W^{\overline{\gamma},\overline{\zeta}}\) is \((2,1)\)-differentiable, it is enough to prove that
for \(\overline{\zeta}(c)\leq x<\overline{\zeta}(\overline{c})\). We have by Proposition 6.8 that
Consequently,
If \(\overline{\zeta}{}^{\prime}(c)<0\) in \([\underline{c},\overline{c}]\), we have \(\ell (x,c)=\overline{c}\) for \(x\geq \overline{\zeta}(c)\). To show that \(W^{\overline{\gamma},\overline{\zeta}}\) is \((2,1)\)-differentiable, it is sufficient to prove that \(\partial _{xx}W^{\overline{\zeta}}(x^{+},c)= \partial _{xx}W^{\overline{\zeta}}(x^{-},c)\) for \(x=\overline{\zeta}(c)\). Since \(\ell (x,c)=\overline{c}\),
so that
Since \(H_{c}^{\overline{\gamma},\overline{\zeta}}(\overline{\zeta}(c),c)=W_{c}^{\overline{\gamma},\overline{\zeta}} (\overline{\zeta}(c),c )=0\) and \(\overline{\zeta}{}^{\prime}(c)<0\), we get
so that \(H_{x}^{\overline{\gamma},\overline{\zeta}}(\overline{\zeta }(c),c)=(v^{ \overline{c}})^{\prime}(\overline{\zeta}(c))\). Hence, taking the derivative one more time with respect to \(c\), we obtain
By Proposition 6.8, \(H_{xc}^{\overline{\gamma },\overline{\zeta}}(\overline{\zeta}(c),c)=H_{cx}^{ \overline{\gamma},\overline{\zeta}}(\overline{\zeta}(c),c)=0\) and \(\overline{\zeta}{}^{\prime }(c)<0\), and we get
□
Proof of Theorem 6.10
As \(\overline{\zeta}\) is continuous in \([\underline{c},\overline{c}]\), there exists \(M=\max _{c\in [ \underline{c},\overline{c}]}\overline{\zeta}(c)\). By definition, if \(x\geq M\), then \(\ell (x,c)=\overline{c}~\) and \(W^{\overline{\gamma},\overline{\zeta}}(x,c)=v^{\overline{c}}(x)\), and therefore \(\lim _{x\rightarrow \infty }W^{\overline{\gamma},\overline{\zeta}}(x,c)= \lim _{x\rightarrow \infty }v^{\overline{c}}(x)=\overline{c}/q\).
By (5.8), we have that
Since
we get \(\mathcal{L}^{ac}(W^{\overline{\gamma},\overline{\zeta}})(x,c)\leq \mathcal{L}^{c}(W^{\overline{\gamma},\overline{\zeta}})(x,c)=0\) for \(x\in [ \overline{\gamma}(c),\overline{\zeta}(c)]\) and
for \(x\in [ 0,\overline{\gamma}(c)]\).
By Theorem 4.4, it remains to prove that we have \(\mathcal{L}^{ac}W^{\overline{\gamma},\overline{\zeta}}(x,c)\leq 0\) and \(\mathcal{L}^{c}W^{\overline{\gamma},\overline{\zeta}}(x,c)\leq 0\) for \(x\geq \overline{\zeta}(c)\), \(c\in [ \underline{c},\overline{c})\). But
satisfies \(\ell (x,c)\geq c\), and also either \(\ell (x,c)=\overline{c}\) or \(\overline{\zeta}(\ell (x,c))=x\). So we obtain \(\mathcal{L}^{\alpha }W^{\overline{\gamma},\overline{\zeta}}(x, \alpha ) \big\vert _{\alpha =\ell (x,c)}=0\) and then
because (A.13) and \(\partial _{x}W^{\overline{\gamma},\overline{\zeta}}(\overline{\zeta}(c),c) \leq 1\) for \(c\in [ \underline{c},\overline{c}]\) imply \(\partial _{x}W^{\overline {\gamma},\overline{\zeta}}(x,\ell (x,c)) \leq 1\). Also,
for \(x\geq \overline{\zeta}(c)\), \(c\in [ \underline{c},\overline{c})\). □
Appendix B: Some formulas of Sects. 7 and 8
In the following, we state in a compact way some formulas referred to in Sects. 7 and 8.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Albrecher, H., Azcue, P. & Muler, N. Optimal dividends under a drawdown constraint and a curious square-root rule. Finance Stoch 27, 341–400 (2023). https://doi.org/10.1007/s00780-023-00500-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00780-023-00500-6