Abstract
This paper revisits the optimal capital structure model with endogenous bankruptcy, first studied by Leland (J. Finance 49:1213–1252, 1994) and Leland and Toft (J. Finance 51:987–1019, 1996). Unlike in the standard case where shareholders continuously observe the asset value and bankruptcy is executed instantaneously without delay, the information of the asset value is assumed to be updated periodically at the jump times of an independent Poisson process. Under a spectrally negative Lévy model, we obtain the optimal bankruptcy strategy and the corresponding capital structure. A series of numerical studies provide an analysis of the sensitivity, with respect to the observation frequency, of the optimal strategies, optimal leverage and credit spreads.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The study of capital structures dates back to the seminal work by Modigliani and Miller [45] which shows that in a frictionless economy, the value of a firm is invariant to the choice of capital structures. While the Modigliani–Miller (MM) theory is regarded as an effective starting point for research on capital structures and has provided valuable insights in the field, it is not directly applicable to businesses. In reality, the selection of capital structures is not perfectly random. Instead, it depends significantly on factors such as industry type, country and corporate law. In the field of corporate finance, various approaches have been taken to explain how much debt a firm should issue. A reasonable conclusion can be obtained only after challenging some of the assumptions of the classical MM theory.
The trade-off theory is one well-known approach for the study of capital structures. While various frictions may affect a firm’s decisions, bankruptcy costs and tax benefits are believed to be the most important factors. By issuing debt, bankruptcy costs increase, while at the same time the firm can enjoy tax shields for coupon payments to the bondholders. The trade-off theory states that firms issue the appropriate debt to solve the trade-off between minimising bankruptcy costs and maximising tax benefits. To formulate this optimisation problem, one needs an efficient and realistic way of modelling not only bankruptcy, but also tax benefits, which depend heavily on the dynamics of the firm’s asset value. For more details on the trade-off theory and its review, see e.g. Frank and Goyal [27], Ju et al. [30] and Kraus and Litzenberger [32].
Classically, there are two models of bankruptcy in credit risk: the structural approach and the reduced-form approach (see Bielecki and Rutkowski [12, Sects. 1.4, 3.3, 3.6 and Part III]). The former, first proposed by Black and Cox [14], models the bankruptcy time as the first time the asset value goes below a fixed barrier. The latter models it as the first jump epoch of a doubly stochastic process (known hereafter as a Cox process) where the jump rate is driven by another stochastic process. Both approaches were developed extensively in the 2000s and are now commonly used throughout the asset pricing and credit risk literature. An extension of the structural approach, which we call the excursion (Parisian) approach, models the bankruptcy time as the first instance in which the amount of time the asset value stays continuously below a threshold exceeds a given grace period. Motivated by the Parisian option, this is sometimes called the Parisian ruin (see Chesney et al. [20]). In the corporate finance literature, the approach has been used to model the reorganisation process (Chap. 11), as in Broadie et al. [16] or François and Morellec [26]. Here, reorganisation is undertaken whenever the asset value is below a threshold; although there is a chance of recovering to return above the threshold, if the reorganisation time exceeds the grace period, the firm is liquidated. For more information, see the literature review in Sect. 1.3.
1.1 A new model of bankruptcy
This paper considers the scenario where asset value information is updated only at epochs \((T_{n}^{\lambda })_{n \geq 1}\) given by the jump times of a Poisson process \((N^{\lambda }_{t})_{t \geq 0}\) with fixed rate \(\lambda \). Given a bankruptcy barrier \(V_{B}\) chosen by the equity holders, bankruptcy is triggered at the first update time where the asset process \((V_{t})_{t \geq 0}\) is below \(V_{B}\), i.e., at
This can also be written as the classical bankruptcy time
of the asset value if the latter is only updated at \((T_{n}^{\lambda })_{n \geq 1}\), i.e., for
Here \(T^{\lambda }_{N^{\lambda }_{t}}\) is the most recent update time before \(t\). In Fig. 1, we plot sample paths of \((V_{t})_{t \geq 0}\), \((V_{t}^{\lambda })_{t \geq 0}\), \((T_{n}^{\lambda })_{n \geq 1}\) and the corresponding bankruptcy time.
Sample paths of the asset value \((V_{t})_{t \geq 0}\) (black lines) and \((V_{t}^{\lambda })_{t \geq 0}\) (horizontal blue lines) along with the Poisson arrival times \((T_{n}^{\lambda })_{n \geq 1}\) (indicated by dotted vertical lines labelled \(T_{i}\) on the \(x\)-axis). The red zone \((0, V_{B})\) is given by the rectangle colored in red. The asset values at bankruptcy and other observation times are indicated by the red circle and blue triangles, respectively. Here, the bankruptcy time corresponds to \(T_{1}^{\lambda }\), but the asset value has crossed \(V_{B}\) before and then recovered back before \(T_{1}^{\lambda }\). Note that \((V_{t}^{\lambda })_{t \geq 0}\) has a positive jump at \(T_{6}^{\lambda }\)
The bankruptcy model (1.1) is closely related to the reduced-form and excursion approaches reviewed above:
1) The bankruptcy time (1.1) is equivalent to the Parisian ruin with the (constant) grace period replaced with an exponential time clock, the first epoch being the time spent continuously below \(V_{B}\) for more than an independent exponential time. For more details, see Appendix A.
2) It is also equivalent to the bankruptcy time in a reduced-form credit risk model where the bankruptcy time is the first jump time of a Cox process with hazard rate given by \(h_{t} := \lambda \mathbf{1}_{\{V_{t} < V_{B} \}}\), \(t \geq 0\). As in Fig. 1, the region \((0, V_{B})\) can be seen as the “red zone”; here, bankruptcy is triggered at rate \(\lambda \), whereas in the “healthy zone” \((V_{B}, \infty )\), this probability is negligible.
There are several motivations for considering the bankruptcy strategy (1.1) for the study of capital structures.
First, in reality, it is not possible to continuously observe the accurate status of a firm and make bankruptcy decisions instantaneously. In addition, unlike in the case of American option pricing for which computer programs can be set up to exercise automatically, in our case, information is acquired by humans. As observed in the literature of rational inattention (Sims [52]), the amount of information a decision maker can capture and handle is limited, and instead they rationally decide to stay with imperfect information. Taking a bankruptcy decision requires complex information, and it is more realistic to assume that the information for the decision makers is updated only at random discrete times. While they are expected to respond promptly, delays are inevitable and possibly have a significant impact on bankruptcy costs.
Second, the majority of the existing literature assumes continuous observation using a continuous asset value process; in this case, the asset value at bankruptcy is in any event precisely \(V_{B}\). Unfortunately, it is unreasonable to assume that one can precisely predict the asset value at bankruptcy, which is in reality random. The randomness can be realised by adding negative jumps to the process. We underline that in our model, this randomness can also be achieved by any choice (continuous or càdlàg) of the underlying process. See Fig. 6 in Sect. 6.
Third, this model generalises the classical model and allows more flexibility by having one more parameter \(\lambda \). The classical structural model (with instantaneous liquidation upon downcrossing the barrier) corresponds to the case \(\lambda = \infty \), and the no-bankruptcy model to the case \(\lambda = 0\). With careful calibration of \(\lambda \), the model can potentially estimate the bankruptcy costs and tax benefits more precisely. Typically, for calibration, credit spread data is used. As shown in the numerical results (see Fig. 8), a variety of term structures can be achieved by choosing the value of \(\lambda \).
Finally, thanks to the equivalence of our bankruptcy time with the classical bankruptcy time (1.2) of the process \((V^{\lambda }_{t})_{t \geq 0}\), this research can be considered a contribution to the classical structural approach. Existing results featuring asset value processes with two-sided jumps are rather limited. However, we provide a new analytically tractable case for \((V^{\lambda }_{t})_{t \geq 0}\), containing two-sided jumps even when \((V_{t})_{t \geq 0}\) does not have positive jumps (see Fig. 1). By appropriately selecting the driving process \((V_{t})_{t \geq 0}\) as well as \(\lambda \), it is possible to construct a wide range of stochastic processes with two-sided jumps.
1.2 Contributions of the paper
Our model is built based on the seminal paper by Leland and Toft [39], with a feature of endogenous default. While Leland’s [38] framework is used more frequently and certainly more mathematically tractable, its extension [39] more accurately captures the flow of debt financing by avoiding the use of perpetual bonds assumed in [38].
In addition, while the majority of papers in financial economics assume a geometric Brownian motion for the asset value \((V_{t})_{t \geq 0}\), we follow the works of Hilberink and Rogers [28], Kyprianou and Surya [37] and Surya and Yamazaki [54] and consider an exponential Lévy process with arbitrary negative jumps (i.e., a spectrally negative Lévy process). Although it is more desirable to also allow positive jumps as in Chen and Kou [19], as discussed in [28], negative jumps occur more frequently and effectively model the downward risks. With the spectrally negative assumption, semi-explicit expressions of the equity value as well as the optimal bankruptcy threshold are elicited, without focusing on a particular set of jump measures. Again, see the discussion above on how our model is capable of modelling the two-sided jump case in the classical structural approach, even when a spectrally negative Lévy process is used for \((V_{t})_{t \geq 0}\). For a more general study of financial models using Lévy processes, the reader should refer to Cont and Tankov [21, Chaps. II and III].
To solve our problem, recent developments of the fluctuation theory of Lévy processes are utilised. First, the firm/debt/equity values are expressed in terms of the so-called scale functions, which exist for a general spectrally negative Lévy process. These permit direct computation of the optimal bankruptcy barrier and the corresponding firm/debt/equity values.
With these analytical results, a sequence of numerical experiments can be conducted. Here, to easily comprehend the impacts of the parameters describing the problem, we use a (spectrally negative) hyperexponential jump diffusion (a mixture of Brownian motion and i.i.d. hyperexponentially distributed jumps), for which the scale function can be written as a sum of exponential functions. The equity/debt/firm values can be written explicitly and the optimal bankruptcy barrier can be computed instantaneously by a classical bisection method. The optimal capital structure is obtained by solving the two-stage optimisation problem as proposed in [39]. In addition, with numerical Laplace inversion, we also obtain the term structures of credit spreads and the density/distribution of the bankruptcy time and the corresponding asset value. Because various numerical experiments have already been conducted in other papers, we focus here on analysing the impacts of the frequency of observation \(\lambda \). We verify the convergence to the classical case of [28, 37] and also observe monotonicity, with respect to \(\lambda \), of the bankruptcy barrier, the firm value under the optimal capital structure, the optimal leverage and the credit spread.
1.3 Related literature
Before concluding this section, we review several relevant papers motivating our problem.
The most relevant paper, to the best of our knowledge, is François and Morellec [26] in which the authors model the reorganisation process (Chap. 11) using the excursion approach with a deterministic grace period as described above. Broadie et al. [16] consider a similar model with an additional barrier for immediate liquidation upon crossing, whereas Moraux [46] considers a variant of [26] using the occupation time approach, in which distress level accumulates without being reset each time the asset process recovers to a healthy state. These papers are based on Leland [38], with perpetual bonds and asset values driven by geometric Brownian motions for mathematical tractability. However, computation of the solutions is significantly more challenging than the classical structural approach and hence most papers rely on numerical approaches. In the present paper, on the other hand, semi-analytical solutions for a more general asset value process with jumps are obtained as a result of the use of Poisson arrival times for the update times.
This paper is also motivated by Duffie and Lando [22] who model the asymmetry of information between firms and bond investors. The authors assume that bond investors cannot observe the firm’s assets directly and instead receive only periodic and imperfect accounting reports on the firm’s status. Under these assumptions, the authors successfully explain the non-zero credit spread limit.
Regarding the study of Lévy processes observed at Poisson arrival times, there has been substantial progress in the last few years. Recently, Albrecher and Ivanovs [1] investigated close links between Lévy processes observed continuously and periodically. In results similar to those for the classical hitting time at a barrier, they found that the exit identities under periodic observation can be obtained if the Wiener–Hopf factorisation is known. In particular, when focusing on the spectrally one-sided case, these can be written in terms of the scale function. For the results of our paper, we use the joint Laplace transform of the bankruptcy time (1.1) and the asset value at that time, which is obtained in [2, 1]. In addition, we obtain the resolvent measure killed at the first Poisson downward passage time (1.1) for the computation of tax benefits.
Regarding the optimal stopping problems under Poisson observations, perpetual American options have been studied by Dupuis and Wang [23] for the geometric Brownian motion case. This has recently been generalised to the Lévy case by Pérez and Yamazaki [49]. Several key studies have been performed on the application of scale functions in optimal stopping in a continuous observation setting (see e.g. Alili and Kyprianou [3], Avram et al. [7], Long and Zhang [43], Rodosthenous and Zhang [51] and Surya [53, Chap. 6]). The periodic observation model is more frequently used in the insurance community, in particular in the optimal dividend problem (see Avanzi et al. [5, 6] and Noba et al. [47]).
To the best of our knowledge, this is the first attempt to introduce Poisson observations in the problem of capital structures. We believe the techniques used in this paper can be used similarly in related problems described above when a Poisson observation scheme is introduced.
1.4 Organisation of the paper
The organisation of this paper is as follows. In Sect. 2, we present formally the main problem that we work on in this article. In Sect. 3, we compute the equity value using the scale function, and in Sect. 4, we identify the optimal barrier. Section 5 considers the two-stage problem to obtain the optimal capital structure. Section 6 deals with numerical examples confirming the theoretical results. Section 7 concludes the paper. Long proofs are deferred to Appendices B and C.
2 Problem formulation
Let \((\Omega , \mathcal{F}, \mathbb{P})\) be a complete probability space hosting a Lévy process \(X=(X_{t})_{t\ge 0}\). The value of the firm’s asset is assumed to evolve according to an exponential Lévy process given, for the initial value \(V > 0\), by
Let \(r > 0\) be the positive risk-free interest rate and \(0 \leq \delta < r\) the total dividend rate to the firm’s investors. We assume that the process \((e^{-(r-\delta ) t} V_{t})_{t \geq 0}\) is a ℙ-martingale.
The firm is partly financed by debt with a constant debt profile: it issues, for some given constants \(p, m > 0\), new debt at a constant rate \(p\) with maturity profile \(\varphi (s) := m e^{-ms}\). In other words, the face value of the debt issued in the small time interval \((t, t+\mathrm{d}t)\) that matures in the small time interval \((t+s, t+s+\mathrm{d}s)\) is approximately given by \(p \varphi (s) \mathrm{d}t \mathrm{d}s\). Assuming an infinite past, the face value of debt held at time 0 that matures in \((s, s+ \mathrm{d}s)\) becomes
and the face value of all debt is a constant value, given by
For more details, see Hilberink and Rogers [28] and Kyprianou and Surya [37].
Let \((N^{\lambda }_{t})_{t \geq 0}\) be an independent Poisson process with rate \(\lambda > 0\) and \(\mathcal{T} := (T_{n}^{\lambda })_{n \geq 1}\) its jump times. Suppose the bankruptcy is triggered at the first time of \(\mathcal{T}\) the asset value process \((V_{t})_{t \geq 0}\) goes below a given level \(V_{B} > 0\), i.e., at
with the convention \(\inf \emptyset =\infty \). In our model, it is more natural to assume that the bankruptcy decision can be made at time zero. Hence, we modify the above and consider the random time
(i) Suppose first that \(V \geq V_{B}\) so that \(\overline{T}_{V_{B}}^{-} = T_{V_{B}}^{-}\). The debt pays a constant coupon flow at a fixed rate \(\rho > 0\), and a constant fraction \(0 <\alpha < 1\)of the asset value is lost at the bankruptcy time \(T_{V_{B}}^{-}\). In this setting, the value of the debt with a unit face value and maturity \(t>0\) becomes
Here, the first term is the total value of the coupon payments accumulated until maturity or bankruptcy whichever comes first; the second term is the value of the principal payment; the last term corresponds to the \(1/P\) fraction of the remaining asset value that is distributed, in the event of bankruptcy, to the bondholder of a unit face value. Integrating this, the total value of debt becomes, by (2.1) and Fubini’s theorem,
Regarding the value of the firm, it is assumed that there is a corporate tax rate \(\kappa > 0\) and its (full) rebate on coupon payments is gained if and only if \(V_{t} \geq V_{T}\) for some given cut-off level \(V_{T} \geq 0\) (for the case \(V_{T} = 0\), it enjoys the benefit at all times). Based on the trade-off theory (see e.g. Brealey and Myers [15, Chap. 9]), the firm value becomes the sum of the asset value and total value of tax benefits less the value of loss at bankruptcy and is given by
(ii) Suppose now \(V< V_{B}\) so that \(\overline{T}_{V_{B}}^{-} = 0\). Then by setting \(T_{V_{B}}^{-}=0\) in the computations in (i), we obtain
The problem is to find an optimal bankruptcy level \(V_{B} \geq 0\) that maximises the equity value
subject to the limited liability constraint
if such a level exists. Here, \(V_{B} = 0\) means that it is never optimal to go bankrupt with the limited liability constraint satisfied for all \(V >0\). Note that when \(V < V_{B}\), then (2.3) gives \(\mathcal{E}(V;V_{B}) = 0\).
3 Computation of the equity value
Suppose from now on that \((X_{t})_{t \geq 0}\)is a spectrally negative Lévy process, that is, a Lévy process without positive jumps. We denote by
its Laplace exponent with the right inverse
3.1 Scale functions
The starting point of the whole analysis is introducing the so-called \(q\)-scale function \(W^{(q)}(x)\), with \(q\geq 0\) and \(x\in \mathbb{R}\). It features invariably in almost all known fluctuation identities of spectrally negative Lévy processes; see Zolotarev [56] and Takács [55, Part 4] for the origin of this function. See also Kuznetsov et al. [35] and Kyprianou and Surya [37] for a detailed review.
Fix \(q \geq 0\). The \(q\)-scale function \(W^{({q})}\) is the mapping from ℝ to \([0, \infty )\) that takes value zero on the negative half-line, while on the positive half-line it is a continuous and strictly increasing function with the Laplace transform
Define also the second scale function
In particular, for \(x \in \mathbb{R}\), we let \(Z^{(q)}(x) :=Z^{(q)}(x; 0)\), and for \(\lambda > 0\),
In the next section, we shall see that the equity value (2.4) can be written in terms of the scale functions \(W^{(q)}\) and \(Z^{(q)}\).
3.2 Related fluctuation identities
For \(y \in \mathbb{R}\), let \(\mathbb{P}_{y}\) be the conditional probability under which the initial value of the spectrally negative Lévy process is \(X_{0} = y\).
Following equation (4.5) in [37] (see also Emery [25] and Avram et al. [8, Eq. (3.19)]), the joint Laplace transform of the first passage time
and \(X_{\tau _{0}^{-}}\) is given by the identity
where \(y\in \mathbb{R}\), \(\theta \geq 0\) and \(q \geq 0\). Similar results have been obtained for the Poisson observation case. Recall that \(\mathcal{T} :=(T_{n}^{\lambda })_{n \geq 1}\) is the set of jump times of an independent Poisson process. We define
By equation (14) of Theorem 3.1 in Albrecher et al. [2], for \(\theta \geq 0\) and \(y \in \mathbb{R}\),
Remark 3.1
1) We have
where the positivity holds by the probabilistic expression of \(J^{(q,\lambda )}\) as in (3.7).
2) We have
To see this, by the memoryless property of the exponential distribution, we can write, for some independent exponential random variable \(\mathbf{e}_{\lambda }\), the first observation time at which \(X\) is below zero as \(\tau _{0}^{-} + \mathbf{e}_{\lambda }\), and hence \(\tilde{T}_{0}^{-}\) is bounded from below by an exponential random variable. In addition, we must have \(X_{\tilde{T}_{0}^{-}} \leq 0\)\(\mathbb{P}_{y}\)-a.s. and hence we have (3.8).
In order to write the equity value, we obtain an expression for
In Appendix B, we obtain the resolvent measure killed at \(\tilde{T}_{z}^{-}\) and the following result as a corollary.
Proposition 3.2
Fix \(y, z \in \mathbb{R}\). For \(V_{T} > 0\), we have
where \(\overline{W}^{(q)}(y) := \int _{0}^{y} W^{(q)}(u) \mathrm{d}u\)for all \(q > 0\)and \(y \in \mathbb{R}\). For \(V_{T} = 0\), we have \(\Lambda ^{(r,\lambda )}(y,z)=(1-J^{(r,\lambda )}(y-z;0))/r\).
3.3 Expression for the equity value in terms of the scale function
Using the identities in Sect. 3.2, the equity value (2.4) can be written as follows. Here, we focus on the case \(V_{B} > 0\). The case \(V_{B} = 0\) (for which, as we shall see, only the case \(V_{T} = 0\) needs to be considered) is given later in (4.4).
First, (3.7) gives, for \(q = r\) and \(q = r+m\),
In addition, by (3.9),
Hence we can write
and therefore, by taking their difference, the equity value is
4 Optimal barrier
Having identified the equity value \(\mathcal{E}(V;V_{B})\) in (3.11), we are ready to find the optimal barrier \(V_{B}^{*}\) that maximises it. Our objective in this paper is to show that the optimal barrier is \(V_{B}^{*}\) such that
if it exists, where by (3.11) and Remark 3.1, 1), for \(V_{B} > 0\),
4.1 Existence
We first exhibit a condition for the existence of \(V_{B}^{*}\) satisfying (4.1). To this end, we show the following result; the proof is given in Appendix C.1.
Lemma 4.1
The mapping \(z \mapsto \Lambda ^{(r,\lambda )}(z,z)\)is nondecreasing on ℝ with the limit
This lemma leads to the following proposition. For numerical illustration, see Fig. 2.
Plots of \(V_{B} \mapsto \mathcal{E}(V_{B};V_{B})\) for \(V_{T} = 0,10,20,\ldots , 100\). Solid lines are for the case \(V_{T}=0\) and dotted lines for the other cases. The points at \(V_{B}^{*}\) are indicated by circles. The left plot is based on the parameter set in Case B in Sect. 6 (except \(V_{T}\)), and achieves \(V_{B}^{*} > 0\) for all cases. The right plot is based on the same parameters except that we set \(\kappa = 0.9999\), \(m = 10\), \(\rho = 0.2\) and \(\lambda = 0.1\) to achieve \(V_{B}^{*} = 0\) when \(V_{T} = 0\)
Proposition 4.2
The mapping \(V_{B} \mapsto \mathcal{E}(V_{B};V_{B})\) is strictly increasing on \((0, \infty )\) with the limits
Proof
From Remark 3.1, 2), we have \(1 - \alpha J^{(r, \lambda )}(0; 1) - (1-\alpha ) J^{(r+m, \lambda )}(0; 1) > 0\). By this, Lemma 4.1 and because \(z \mapsto \Lambda ^{(r,\lambda )}(z,z)\) is nondecreasing and bounded, the claim is immediate in view of the second equality in (4.2). □
Now by Proposition 4.2, we define the candidate optimal threshold \(V_{B}^{*}\) formally as follows:
1) If \(V_{T} > 0\) or if \(V_{T}= 0\) with \(\frac{P \kappa \rho }{\lambda +r} \frac{\Phi (r+\lambda )}{\Phi (r)}- \frac{P \rho + p}{\lambda +r+m} \frac{\Phi (r+m+\lambda )}{\Phi (r+m)} < 0\), we set \(V_{B}^{*}>0\) such that \(\mathcal{E}(V_{B}^{*}; V_{B}^{*}) = 0\), whose existence and uniqueness hold by Proposition 4.2.
2) If \(V_{T}= 0\) with
we set \(V_{B}^{*} =0\).
The debt/firm/equity values for the case \(V_{B}^{*} >0\) can be computed by (3.10) and (3.11). For the case \(V_{B}^{*} =0\) where necessarily \(V_{T}=0\), we have, for all \(V > 0\),
and therefore
4.2 Optimality
In the rest of this section, we show the following one of our main results.
Theorem 4.3
The barrier \(V_{B}^{*}\)is optimal for the problem of maximising (2.4) subject to (2.5).
To prove the optimality, it is sufficient to show the following:
1) If \(V_{B}^{*} > 0\), then every threshold \(V_{B} < V_{B}^{*}\) violates the limited liability constraint (2.5).
2) \(V_{B}^{*}\) attains a higher equity value than any \(V_{B} > V_{B}^{*}\) does.
3) \(V_{B}^{*}\) is feasible.
Proposition 4.4
Suppose \(V_{B}^{*} > 0\). For \(V_{B} < V_{B}^{*}\), the limited liability constraint (2.5) is not satisfied.
Proof
By the (strict) monotonicity in Proposition 4.2 and because \(\mathcal{E}(V_{B}^{*}; V_{B}^{*}) =0\) (given that \(V_{B}^{*} > 0\)), we have \(\mathcal{E}(V_{B} ;V_{B}) < 0\) for \(V_{B} < V_{B}^{*}\). □
The proof of the following result is given in Appendix C.2.
Proposition 4.5
For \(V > V_{B} > 0\), we have
where \(H^{(r+m)}\)is as in (3.5) and for \(x,z \in \mathbb{R}\),
The proofs of the following results are given in Appendices C.3 and C.4.
Proposition 4.6
Suppose \(V_{B} > V_{B}^{*} \geq 0\). We have \(\frac{\partial }{\partial V_{B}} \mathcal{E}(V;V_{B}) < 0\)for \(V > V_{B}\). Hence \(\mathcal{E}(V; V_{B}) < \mathcal{E}(V; V_{B}^{*})\)for all \(V > V_{B}\).
Proposition 4.7
For \(V > V_{B} > 0\), we have
where \(R^{(r,\lambda )}\)is the resolvent density given in (B.2).
Proposition 4.8
We have \(\mathcal{E}(V;V_{B}^{*})\geq 0\)for all \(V\geq V_{B}^{*}\)when \(V_{B}^{*} > 0\), and for all \(V > 0\)when \(V_{B}^{*} = 0\). In other words, \(V_{B}^{*}\)is feasible.
Proof
Suppose first that \(V_{B}^{*}>0\). Because \(R^{(r,\lambda )}\) is the resolvent density, it is nonnegative. By this together with Propositions 4.6 and 4.7, for \(V> V_{B}^{*}>0\),
where the second inequality holds by Remark 3.1, 2). Applying this and the fact that \(\mathcal{E}(V_{B}^{*};V_{B}^{*})= 0\) when \(V_{B}^{*} > 0\), the claim is immediate.
For the case \(V_{B}^{*}=0\), recall that necessarily \(V_{T}=0\), and hence (4.4) gives
Moreover, by Remark 3.1, 1) and because \(q \mapsto J^{(q, \lambda )}(0;0)\) is nonincreasing in view of its probabilistic expression, for \(m>0\),
By this and recalling (4.3), we have that
Hence \(\frac{P \kappa \rho }{r}-\frac{P \rho + p}{r+m} \geq 0\) and therefore
Using (4.6) together with (4.7) completes the proof. □
Proof of Theorem 4.3
By Propositions 4.4, 4.6 and 4.8, the proof is complete. □
Remark 4.9
Intuitively, as \(\lambda \rightarrow \infty \), the optimal barrier is expected to converge to that in the classical case as in Kyprianou and Surya [37]. In order to confirm this assertion, we provide the following result; its proof is deferred to Appendix C.5.
Lemma 4.10
Suppose \(V_{T} > 0\)and let \(V_{B}\geq 0\)be fixed. We have
This is consistent with the identity (3.26) in [37], where the optimal bankruptcy level is such that the right-hand side of (4.8) vanishes.
5 Two-stage problem
We now obtain the optimal leverage by solving the two-stage problem as studied by Chen and Kou [19], Leland [38] and Leland and Toft [39], where the final goal is to choose \(P\) that maximises the firm’s value \(\mathcal{V}\). For fixed \(V > 0\), the problem is formulated as
where we emphasise the dependence of \(\mathcal{V}\) and \(V_{B}^{*}\) on \(P\).
In this two-stage problem, it is worth investigating the shape of \(\mathcal{V}(V; V_{B}^{*}(P), P)\) with respect to \(P\) to confirm whether it has a unique maximiser. Chen and Kou [19] verified the concavity in the continuous observation case with a double jump-diffusion as the underlying model and the assumption that \(V_{T}=0\).
In this section, we show in the periodic observation setting the concavity for the case when \(V_{T}=0\) and the following assumption is satisfied.
Assumption 5.1
The Lévy measure \(\overline{\Pi }\)of the dual process \(-X\)has a completely monotone density, i.e., \(\overline{\Pi }\)has a density \(\pi \)whose \(n\)th derivative \(\pi ^{(n)}\)exists for all \(n \geq 1\)and satisfies
Important examples satisfying Assumption 5.1 include (the spectrally negative versions of) the hyperexponential jump-diffusion (as a generalisation of [19]), the variance gamma process (Madan and Seneta [44]), the CGMY process (Carr et al. [18]), as well as meromorphic Lévy processes (Kuznetsov et al. [34]).
To show this claim, we first show the following property.
Lemma 5.2
Under Assumption 5.1, the mapping \(x\mapsto H^{(r)}(x;\Phi (r+\lambda ))\)is decreasing.
Proof
For the completely monotone case, it is known from Loeffen [41, Theorem 2] that the scale function admits the form
for some finite measure \(\mu ^{(r)}\). Substituting this and using Fubini’s theorem, we get
Now substituting the above expressions in (3.5), we have
where
Because \(\lim _{x\to \infty }H^{(r)}(x; \Phi (r+\lambda ) ) =0\) in view of the probabilistic expression (3.5) and \(\lim _{x \rightarrow \infty } B(x) = 0\) by monotone convergence, we must have \(A = 0\). Hence \(H^{(r)}(x; \Phi (r+\lambda ) ) = B(x)\) and its derivative becomes
where the negativity holds because \(\Phi (r+\lambda ) > \Phi (r) > 0\) and hence the integrand is always positive. This shows the claim. □
Now suppose \(V_{T}=0\) so that
By Proposition 3.2 and (4.2), the optimal barrier \(V_{B}^{*}(P)\) is given by the root of \(\mathcal{E}(V_{B};V_{B}, P) = 0\) for the case \(V_{B}^{*}(P) > 0\), where
Recall that by (4.3) and due to \(p = mP\),
which does not depend on the value of \(P\). Hence the criterion for \(V_{B}^{*}(P) = 0\) is irrelevant to the selection of \(P\).
1) First consider the case \(\frac{\kappa \rho }{\lambda +r} \frac{\Phi (r+\lambda )}{\Phi (r)}- \frac{\rho + m}{\lambda +r+m} \frac{\Phi (r+m+\lambda )}{\Phi (r+m)} \geq 0\) so that \(V_{B}^{*}(P) = 0\) for any choice of \(P > 0\). In this case,
which is linear (and hence concave) in \(P\).
2) Suppose \(\frac{\kappa \rho }{\lambda +r} \frac{\Phi (r+\lambda )}{\Phi (r)}- \frac{\rho + m}{\lambda +r+m} \frac{\Phi (r+m+\lambda )}{\Phi (r+m)} < 0\) so that \(V_{B}^{*}(P) > 0\) is irrelevant to the selection of \(P\). Because \(p=Pm\), solving \(\mathcal{E}(V_{B};V_{B}, P) = 0\) with (5.2) gives
where
Now as in (3.10) and Proposition 3.2, the firm’s value is given by
Differentiating the above expression and using Lemmas C.1 and C.2 (in Appendix C), we have
Here the coefficient \(\frac{\psi (1)-r}{\lambda +r-\psi (1)} \frac{\Phi (r+\lambda )-\Phi (r)}{1-\Phi (r)}(\Phi (r+\lambda )-1)\) is positive by the convexity of \(\psi \) on \([0,\infty )\).
The mapping \(x \mapsto J^{(r, \lambda )}(x;0)=\mathbb{E}_{x} [ e^{-r\tilde{T}_{0}^{-}} \mathbf{1}_{\{\tilde{T}_{0}^{-}<\infty \}} ] = \mathbb{E}[ e^{-r \tilde{T}_{-x}^{-}}\mathbf{1}_{\{\tilde{T}_{-x}^{-}<\infty \}} ]\) is decreasing because \(\tilde{T}_{-x}^{-}\) is increasing in \(x\). On the other hand, Lemma 5.2 shows that the mapping \(x\mapsto H^{(r)}(x;\Phi (r+\lambda ))\) is decreasing as well.
Using these facts together with (5.3), we can conclude that \(\frac{\partial }{\partial P}\mathcal{V}(V;V_{B}^{*}(P),P)\) is decreasing in \(P\), and therefore that the firm’s value \(\mathcal{V}(V;V_{B}^{*}(P),P)\) is a concave function of \(P\). In summary, we have the following result.
Theorem 5.3
Suppose \(V_{T} = 0\)and Assumption 5.1is satisfied.
(1) If \(\frac{\kappa \rho }{\lambda +r} \frac{\Phi (r+\lambda )}{\Phi (r)}- \frac{\rho + m}{\lambda +r+m} \frac{\Phi (r+m+\lambda )}{\Phi (r+m)} \geq 0\), then \(V_{B}^{*}(P) = 0\)for all \(P > 0\)and we have \(\mathcal{V}(V; V_{B}^{*}(P),P) = V + \frac{P \kappa \rho }{r}\).
(2) Otherwise, \(V_{B}^{*}(P)=\varepsilon P > 0\)for all \(P > 0\)and \(\mathcal{V}(V; V_{B}^{*}(P),P)\)is concave in \(P\)for any \(V > 0\).
6 Numerical examples
In this section, we confirm the analytical results obtained in the previous sections through a sequence of numerical examples. In addition, we study numerically the impact of the rate of observation \(\lambda \) on the solutions, obtain the optimal leverage by considering the two-stage problem considered in (5.1), and analyse the behaviours of credit spreads.
Throughout this section, we use \(r=7.5\%\), \(\delta =7\%\), \(\kappa = 35\%\), \(\alpha =50\%\) for the parameters of the problem as used in [28, 37, 38, 39]. Additionally, unless stated otherwise, we set \(\rho = 8.162\%\) and \(m=0.2\), which were used in [19], \(P=50\) and \(\lambda = 4\) (on average four times per year). For the tax threshold, we set
as used in [37] and also suggested by [28, 39]. By the choice (6.1), necessarily \(V_{T} > 0\) and hence \(V_{B}^{*} > 0\) as discussed in Sect. 4.1.
For the process \((X_{t})_{t \geq 0}\), we use a mixture of Brownian motion and a compound Poisson process with i.i.d. hyperexponential jumps, \(X_{t}=\mu t +\sigma B_{t} -\sum _{k=1}^{N_{t}}U_{k}\), \(t \geq 0\), where \((B_{t})_{t \geq 0}\) is a standard Brownian motion, \((N_{t})_{t \geq 0}\) is a Poisson process with intensity \(\gamma \) and each \(U_{k}\) takes an exponential random variable with rate \(\beta _{i} > 0\) with probability \(p_{i}\) for \(1 \leq i \leq m\) such that \(\sum _{i=1}^{m} p_{i} = 1\). Note that this process satisfies the complete monotonicity condition in Assumption 5.1. The corresponding Laplace exponent (3.1) becomes
This is a special case of a phase-type Lévy process (Asmussen et al. [4]), and its scale function has an explicit expression written as a sum of exponential functions; see e.g. Egami and Yamazaki [24] or Kuznetsov et al. [35]. In particular, we consider the following two parameter sets:
Case A (without jumps): \(\sigma = 0.2\), \(\mu = -0.015\), \(\gamma = 0\);
Case B (with jumps): \(\sigma = 0.2\), \(\mu = 0.055\), \(\gamma = 0.5\), \((p_{1}, p_{2}) = (0.9,0.1)\) and \((\beta _{1}, \beta _{2}) = (9,1)\).
Here \(\mu \) is chosen such that the martingale property \(\psi (1)=r-\delta = 0.005\) is satisfied. In Case B, the jump size \(U\) models both small and large jumps (with parameters 9 and 1) that occur with probabilities 0.9 and 0.1, respectively.
6.1 Optimality
For the above parameter settings, we first confirm the optimality of the suggested barrier \(V_{B}^{*}\) that satisfies \(\mathcal{E}(V_{B}^{*};V_{B}^{*}) = 0\). Because the mapping \(V_{B} \mapsto \mathcal{E}(V_{B};V_{B})\) (given in (4.2)) is monotonically increasing (see Proposition 4.2), the value of \(V_{B}^{*}\) can be computed by classical bisection methods. The corresponding capital structure is then computed by (3.10) and (3.11).
At the top of Fig. 3, for Cases A and B, we plot \(V \mapsto \mathcal{E}(V; V_{B}^{*})\) along with \(V \mapsto \mathcal{E}(V; V_{B})\) for \(V_{B} \neq V_{B}^{*}\). Here, we confirm Theorem 4.3: the level \(V_{B}^{*}\) satisfies the limited liability constraint (2.5), and any level \(V_{B}\) lower than \(V_{B}^{*}\) violates (2.5), while for \(V_{B}\) larger than \(V_{B}^{*}\), \(\mathcal{E}(V; V_{B})\) is dominated by \(\mathcal{E}(V; V_{B}^{*})\). The corresponding debt and firm values are also plotted in Fig. 3.
The equity/debt/firm values as functions of \(V\) on \((V_{B}, \infty )\) for \(V_{B}=V_{B}^{*}\) (solid) along with \(V_{B} = V_{B}^{*} \exp (\epsilon )\) (dotted) for \(\epsilon = -0.5,-0.4, \ldots , -0.1, 0.1, 0.2, \ldots , 0.5\). The values at \(V = V_{B}\) are indicated by circles for \(V_{B} = V_{B}^{*}\), whereas those for \(V_{B} < V_{B}^{*}\) (resp. \(V_{B} > V_{B}^{*}\)) are indicated by up- (resp. down-) pointing triangles
6.2 Sensitivity with respect to \(\lambda \) of the equity value
We now proceed to study the sensitivity of the optimal bankruptcy barrier and the equity value with respect to the rate of observation \(\lambda \). In the left plot of Fig. 4, we show the equity value \(\mathcal{E}(\, \cdot \, ; V_{B}^{*})\) for various values of \(\lambda \) along with the classical (continuous-observation) case as obtained in [28, 37]. We see that the optimal barrier \(V_{B}^{*}\) is decreasing in \(\lambda \) and converges to the optimal barrier, say \(\tilde{V}_{B}\), of the classical case. This confirms Remark 4.9.
(Top) The equity values \(\mathcal{E}(V; V_{B}^{*})\) (dotted) for \(\lambda = 1,2,4,6,12,52,365\) along with the classical case \(\tilde{\mathcal{E}}(V; \tilde{V}_{B})\) (solid). The corresponding values at \(V = V_{B}^{*}\) are indicated by circles. (Bottom) The difference \(\mathcal{E}(V; V_{B}^{*}) - \tilde{\mathcal{E}}(V; \tilde{V}_{B})\) for the same set of \(\lambda \)-values
We also confirm the convergence of \(\mathcal{E}(V;V_{B}^{*})\) to the classical case, say \(\tilde{\mathcal{E}}(V;\tilde{V}_{B})\), for each starting value \(V\). On the other hand, monotonicity of \(\mathcal{E}(V;V_{B}^{*})\) with respect to \(\lambda \) fails. When \(V\) is small, the equity value tends to be higher for small values of \(\lambda \), but it is not necessarily so for higher values of \(V\). In order to investigate this, we show in the bottom plots of Fig. 4 the difference \(\mathcal{E}(V;V_{B}^{*})- \tilde{\mathcal{E}}(V;\tilde{V}_{B})\). We observe also the differences between Cases A and B — in Case A, a lower value of \(\lambda \) clearly achieves higher equity value when \(V\) is large whereas this is not clear in Case B.
6.3 Analysis of the bankruptcy time and the asset value at bankruptcy
While it was confirmed that the barrier level \(V_{B}^{*}\) is monotone in \(\lambda \), it is not clear how the distributions of \((T^{-}_{V_{B}^{*}}, V_{T^{-}_{V_{B}^{*}}})\) change in \(\lambda \). Here, by taking advantage of the joint Laplace transform \((q, \theta ) \mapsto J^{(q, \lambda )} (\, \cdot \, ; \theta )\) as in (3.7), we compute numerically the density and distribution of the random variables \(T^{-}_{V_{B}^{*}}\) and \(V_{T^{-}_{V_{B}^{*}}}\) for each \(\lambda \). We also obtain those in the classical case by inverting \((q, \theta ) \mapsto H^{(q)} (\, \cdot \, ; \theta )\) as in (3.5).
For Laplace inversion, we adopt the Gaver–Stehfest algorithm, whose use was suggested in Kou and Wang [31] (see also Kuznetsov [33] for its convergence results). The algorithm is easy to implement and only requires real values. While a major challenge is to handle the cases involving large numbers, our case can be handled without difficulty in the standard Matlab environment with double precision.
In our case, the scale function \(W^{(q)}\) is written in terms of a linear sum of \(e^{\Phi (q)x}\) and \(e^{-\xi _{i,q}x}\), \(1 \leq i \leq n\) (\(n=1\) in Case A and \(n=3\) in Case B), where \(\Phi (q)\) is as in (3.2) and \(-\xi _{i,q}\) are the negative roots of \(\psi (\, \cdot \,) = q\). As in the proof of Lemma 5.2, the terms for \(e^{\Phi (q) x}\) all cancel out in the Laplace transforms \(J^{(q, \lambda )}(\, \cdot \, ; \theta )\) and \(H^{(q)}( \, \cdot \, ; \theta )\). Hence the algorithm runs without the need of handling large numbers even for high values of \(q\). The same can be said about the parameter \(\theta \).
For the initial value \(V = 100\), we plot in Fig. 5 the density and distribution functions of \(T^{-}_{V_{B}^{*}}\) and in Fig. 6 those for \(V_{T^{-}_{V_{B}^{*}}}\) for the same parameter sets as used for Fig. 4 (note that the value of \(V_{B}^{*}\) depends on \(\lambda \)). For comparison, those in the classical case (computed by inverting \((q, \theta )\mapsto H^{(q)}(\log V; \theta )\)) are also plotted. It is noted that in Fig. 6, the distribution is not purely diffusive and instead the probability of the event \(V_{T^{-}_{V_{B}^{*}}}=V_{B}^{*}\) is strictly positive. In particular, for Case A, \(V_{T^{-}_{V_{B}^{*}}}=V_{B}^{*}\) a.s. At least in our examples, the distribution functions for \(T^{-}_{V_{B}^{*}}\) appear to be monotone in \(\lambda \), while they are not for \(V_{T^{-}_{V_{B}^{*}}}\).
Density \(\mathbb{P}[T_{V_{B}^{*}}^{-} \in {\mathrm{d}}t]/ {\mathrm{d}}t\) and distribution \(\mathbb{P}[T_{V_{B}^{*}}^{-} \leq t]\) (indicated by dotted lines) for \(\lambda = 1,2,4,6,12,52,365\), the initial value \(V = 100\) and \(V_{B}^{*}\) determined as in Fig. 4. The classical cases are also shown by solid lines. These values are plotted against the logarithm of time
Density \(\mathbb{P}[V_{T_{V_{B}^{*}}^{-}} \in {\mathrm{d}}v]/ {\mathrm{d}}v\) and distribution \(\mathbb{P}[V_{T_{V_{B}^{*}}^{-}} \leq v]\) (indicated by dotted lines) for \(\lambda = 1,2,4,6,12,52,365\), the initial value \(V = 100\) and \(V_{B}^{*}\) determined as in Fig. 4. The classical cases are also shown by solid lines, in which the distribution of the value at bankruptcy has a positive mass at the bankruptcy level
6.4 Two-stage problem
Now we consider the two-stage problem (5.1). Recall, as confirmed in Theorem 5.3, that the firm value \(\mathcal{V}(V;V_{B}^{*}(P), P)\) is concave in \(P\) for the case \(V_{T} = 0\). Here, in order to see if the concavity holds when \(V_{T} > 0\), we continue to use the tax cutoff level \(V_{T}\) from (6.1) as a function of \(P\).
For our numerical results, we set \(V = 100\) and obtain \(V_{B}^{*}\) for \(P\) running from 0 to 100 (leverage \(P/V\) running from 0 to 1). The corresponding firm and debt values are computed for each \(P\) and \(V_{B}^{*} = V_{B}^{*}(P)\), and shown in Fig. 7. For comparison, analogous results on the classical case are also plotted. Here, the concavity with respect to \(P\) is confirmed in all considered cases.
The firm values (top) and debt values (bottom) as functions of the leverage \(P/V\) for the two-stage problem for \(V = 100\). The periodic cases with \(\lambda = 1,2,4,6,12,52,365\) (dotted) are indicated by dotted lines, and the classical case corresponds to the solid lines. The points at \(P^{*}/V\) are indicated by circles
Regarding the analysis with respect to \(\lambda \), at least in these examples, we observe that the firm and debt values for each \(P\) are monotone in \(\lambda \) and converge to those in the classical case. In addition, we see that the optimal face value \(P^{*}\) decreases in \(\lambda \) and converges to that in the classical case.
6.5 The term structure of credit spreads
We now move on to the analysis of the credit spread. Let \(V_{B} > 0\) be a fixed bankruptcy level. The credit spread is defined as the excess of the amount of coupon over the risk-free interest rate required to induce the investor to lend one dollar to the firm until the maturity time \(t\). To be more precise, by finding the coupon rate \(\rho ^{*}\) that makes the value of the debt \(d(V;V_{B},t)\) defined in (2.2) of unit face value equal to one, the credit spread \(\rho ^{*}-r\) is given after some rearrangement of (2.2) by
Before showing numerical results, we prove the following analytical limits. The proofs are deferred to Appendices C.6 and C.7.
Proposition 6.1
For \(V\neq V_{B}\), we have \(\lim _{t \downarrow 0} \mathrm{CS}_{\lambda }(t)=\frac{\lambda }{P} ( P-(1- \alpha )V ) \mathbf{1}_{\{V< V_{B}\}}\).
Let \(\mathrm{CS}(t)\) denote the credit spread in the classical case as described in Hilberink and Rogers [28].
Proposition 6.2
For \(V_{B} > 0\), \(V\neq V_{B}\)and \(t > 0\), we have \(\lim _{\lambda \to \infty }\mathrm{CS}_{\lambda }(t)=\mathrm{CS}(t)\).
Remark 6.3
While theoretically the credit spread converges to zero as the maturity \(t\) decreases to zero as in Proposition 6.1 when \(V > V_{B}\), we shall see below that the rate of convergence can be controlled by the selection of \(X\) and \(\lambda \) and can be made very slow as shown in Fig. 8 below.
To compute credit spreads, we follow the procedures for Fig. 6 of Hilberink and Rogers [28] (given in their Appendix B).
Fix \(V\) and \(m\). The first step is to choose, for fixed leverage \(0 \leq L \leq 1\), the face value of debt \(\hat{P} := \hat{P}(L)\) and \(\hat{\rho } = \hat{\rho }(L)\) satisfying \(\mathcal{D}(V; \hat{V}_{B}) := \mathcal{D}(V; \hat{V}_{B}; \hat{P}, \hat{\rho }) = \hat{P}\) and \(L = \hat{P}/\mathcal{V}(V; \hat{V}_{B}) := \hat{P}/\mathcal{V}(V; \hat{V}_{B}; \hat{P}, \hat{\rho })\), where \(\hat{V}_{B}\) is the optimal bankruptcy level when \(\rho = \hat{\rho }\) and \(P = \hat{P}\). For this computation, at least in our numerical experiments, the mapping \(P \mapsto P/\mathcal{V}(V; \hat{V}_{B}; P, \rho )\), for fixed \(\rho \), is monotonically increasing and hence the root \(\hat{P}(\rho )\) solving \(L = \hat{P}(\rho )/\mathcal{V}(V; \hat{V}_{B}; \hat{P}(\rho ), \rho )\) was obtained by classical bisection. In addition, \(\rho \mapsto \mathcal{D}(V; \hat{V}_{B}; \hat{P}(\rho ), \rho ) - \hat{P}(\rho )\) was also monotone and hence the desired \(\hat{P}\) and \(\hat{\rho }\) were obtained by (nested) bisection methods.
For each leverage \(L\), after \(\hat{P}\) and \(\hat{\rho }\) are computed, the second step is to obtain for each maturity \(t > 0\) the root \(\rho ^{*} = \rho ^{*}(t)\) with \(1 = d(V; \hat{V}_{B}, t) := d(V; \hat{V}_{B}, t; \rho ^{*})\), where
The spread is given by \(\rho ^{*} - r\) (for each maturity \(t\)). The expectations on the right-hand side can be computed again by the Gaver–Stehfest algorithm, by inverting \(q \mapsto J^{(q, \lambda )}(\, \cdot \, ; \theta )\) as in (3.7) for \(\theta = 0, 1\). Those for the classical case can be computed by inverting \(q \mapsto H^{(q)}(\, \cdot \, ; \theta )\).
Here, we consider leverages \(L = 50,75\) again for Cases A and B. In Table 1, the computed values of \(\hat{P}\), \(\hat{\rho }\) and \(\hat{V}_{B}\) are listed for each \(\lambda = 1,2,4,6,12,52,365\) along with those for the classical case. In Fig. 8, we plot the credit spread with respect to the log maturity for each \(\lambda \). For comparison, we also plot those in the classical case. The spread appears to be monotone in \(\lambda \) and converges to that in the classical case for each maturity.
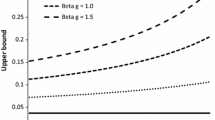
Regarding the credit spread limit, while the convergence to zero has been confirmed in Proposition 6.1 for the periodic case, the rate of convergence depends significantly on the selection of \(\lambda \) and the underlying asset value process. In Case A (without negative jumps), the credit spread converges to zero quickly as the maturity decreases. On the other hand, in Case B (where the credit spread does not converge to zero as the maturity goes to zero in the continuous-observation case), the convergence to zero of the credit spread is very slow for large values of \(\lambda \), as can be seen in Fig. 8. In view of these observations, with a selection of asset values with negative jumps and the observation rate \(\lambda \), realistic short-maturity credit spread behaviours can be achieved.
7 Concluding remarks
We have studied an extension of the Leland–Toft optimal capital structure model where the information on the asset value is updated only at the jump times of an independent Poisson process. In settings where the asset value follows an exponential Lévy process with negative jumps, we have obtained explicitly an optimal bankruptcy strategy and the corresponding equity/debt/firm values. These analytical results have enabled us to efficiently conduct numerical experiments and further analysis of the impact of the observation rate on the optimal leverages and credit spreads.
There are various venues for future research. First, it is a natural direction to consider the case in which the asset value process contains both positive and negative jumps. Because positive jumps do not have a direct influence on the model of the default, similar results are expected, and for example the optimal barrier is likely to be given by \(V_{B}\) such that \(\mathcal{E}(V_{B};V_{B}) = 0\). While the techniques using the scale function employed in this paper cannot be directly applied to two-sided jump cases, there are several potential alternative approaches. One approach would be to add phase-type upward jumps to a spectrally negative Lévy process via fluid embedding and construct a Lévy process with two-sided jumps in terms of a Markov additive process. To do this, the phase-type jumps of the Lévy process can be substituted by linear stretches of unit slope. This procedure requires though adding a supplementary background Markov chain; see e.g. Ivanovs [29, Sect. 2.7] for details. Another approach would be to focus on a Lévy process with two-sided phase-type distributed jumps and use them to approximate a general case. This may be possible by combining the results of Asmussen et al. [4] and Albrecher et al. [2].
Second, it is important to consider the constant grace period case described in 1) of Sect. 1.1. As discussed, this paper’s results, featuring exponential grace periods, may be used to approximate the constant case when the grace period is short. However, an alternative approach is required when it is long. One potential approach would be to use Carr’s [17] randomisation method to approximate the constant period in terms of an Erlang random variable, or the sum of i.i.d. exponential random variables. As in Leung et al. [40], a recursive algorithm may be constructed to compute the required fluctuation identities.
References
Albrecher, H., Ivanovs, J.: Strikingly simple identities relating exit problems for Lévy processes under continuous and Poisson observations. Stoch. Process. Appl. 127, 643–656 (2017)
Albrecher, H., Ivanovs, J., Zhou, X.: Exit identities for Lévy processes observed at Poisson arrival times. Bernoulli 22, 1364–1382 (2016)
Alili, L., Kyprianou, A.E.: Some remarks on first passage of Lévy processes, the American put and pasting principles. Ann. Appl. Probab. 15, 2062–2080 (2005)
Asmussen, S., Avram, F., Pistorius, M.R.: Russian and American put options under exponential phase-type Lévy models. Stoch. Process. Appl. 109, 79–111 (2004)
Avanzi, B., Cheung, E.C., Wong, B., Woo, J.K.: On a periodic dividend barrier strategy in the dual model with continuous monitoring of solvency. Insur. Math. Econ. 52, 98–113 (2013)
Avanzi, B., Tu, V., Wong, B.: On optimal periodic dividend strategies in the dual model with diffusion. Insur. Math. Econ. 55, 210–224 (2014)
Avram, F., Kyprianou, A.E., Pistorius, M.R.: Exit problems for spectrally negative Lévy processes and applications to (Canadized) Russian options. Ann. Appl. Probab. 14, 215–238 (2004)
Avram, F., Palmowski, Z., Pistorius, M.: On the optimal dividend problem for a spectrally negative Lévy process. Ann. Appl. Probab. 17, 156–180 (2007)
Avram, F., Pérez, J.L., Yamazaki, K.: Spectrally negative Lévy processes with Parisian reflection below and classical reflection above. Stoch. Process. Appl. 128, 255–290 (2018)
Baurdoux, E.J., Pardo, J.C., Pérez, J.L., Renaud, J.F.: Gerber–Shiu distribution at Parisian ruin for Lévy insurance risk processes. J. Appl. Probab. 53, 572–584 (2016)
Bertoin, J.: Lévy Processes. Cambridge University Press, Cambridge (1996)
Bielecki, T.R., Rutkowski, M.: Credit Risk: Modeling, Valuation and Hedging. Springer, Berlin (2013)
Billingsley, P.: Convergence of Probability Measures, 2nd edn. Wiley, New York (1999)
Black, F., Cox, J.: Valuing corporate securities: some effects of bond indenture provisions. J. Finance 31, 351–367 (1976)
Brealey, R.A., Myers, S.C.: Principles of Corporate Finance. McGraw-Hill, New York (2001)
Broadie, M., Chernov, M., Sundaresan, S.: Optimal debt and equity values in the presence of Chap. 7 and Chap. 11. J. Finance 62, 1341–1377 (2007)
Carr, P.: Randomization and the American put. Rev. Financ. Stud. 11, 597–626 (1998)
Carr, P., Geman, H., Madan, D.B., Yor, M.: The fine structure of asset returns: an empirical investigation. J. Bus. 75, 305–332 (2002)
Chen, N., Kou, S.G.: Credit spreads, optimal capital structure, and implied volatility with endogenous default and jump risk. Math. Finance 19, 343–378 (2009)
Chesney, M., Jeanblanc-Picqué, M., Yor, M.: Brownian excursions and Parisian barrier options. Adv. Appl. Probab. 29, 165–184 (1997)
Cont, R., Tankov, P.: Financial Modelling with Jump Processes. Chapman & Hall, London (2003)
Duffie, D., Lando, D.: Term structure of credit spreads with incomplete accounting information. Econometrica 69, 633–664 (2001)
Dupuis, P., Wang, H.: Optimal stopping with random intervention times. Adv. Appl. Probab. 34, 141–157 (2002)
Egami, M., Yamazaki, K.: Phase-type fitting of scale functions for spectrally negative Lévy processes. J. Comput. Appl. Math. 264, 1–22 (2014)
Emery, D.J.: Exit problem for a spectrally positive Lévy process. Adv. Appl. Probab. 5, 498–520 (1973)
François, P., Morellec, E.: Capital structure and asset prices: some effects of bankruptcy procedures. J. Bus. 77, 387–411 (2004)
Frank, M.Z., Goyal, V.K.: Trade-off and pecking order theories of debt. In: Eckbo, B.E. (ed.) Handbook of Empirical Corporate Finance, pp. 135–202. Elsevier, Amsterdam (2008)
Hilberink, B., Rogers, L.C.G.: Optimal capital structure and endogenous default. Finance Stoch. 6, 237–263 (2002)
Ivanovs, J.: One-Sided Markov Additive Processes and Related Exit Problems. PhD Dissertation, University of Amsterdam (2011). Available online at https://dare.uva.nl/search?identifier=8a595e5d-db0c-4f15-bd24-5fd7767a9b2d
Ju, N., Parrino, R., Poteshman, A.M., Weisbach, M.S.: Horses and rabbits? Trade-off theory and optimal capital structure. J. Financ. Quant. Anal. 40, 259–281 (2005)
Kou, S.G., Wang, H.: First passage times of a jump diffusion process. Adv. Appl. Probab. 35, 504–531 (2003)
Kraus, A., Litzenberger, R.H.: A state-preference model of optimal financial leverage. J. Finance 28, 911–922 (1973)
Kuznetsov, A.: On the convergence of the Gaver–Stehfest algorithm. SIAM J. Numer. Anal. 51, 2984–2998 (2013)
Kuznetsov, A., Kyprianou, A.E., Pardo, J.C.: Meromorphic Lévy processes and their fluctuation identities. Ann. Appl. Probab. 22, 1101–1135 (2012)
Kuznetsov, A., Kyprianou, A.E., Rivero, V.: The theory of scale functions for spectrally negative Lévy processes. In: Barndorff-Nielsen, O.E., et al. (eds.) Lévy Matters II. Springer Lecture Notes in Mathematics, vol. 2061, pp. 97–186 (2013)
Kyprianou, A.E.: Fluctuations of Lévy Processes with Applications. Springer, Heidelberg (2014)
Kyprianou, A.E., Surya, B.A.: Principles of smooth and continuous fit in the determination of endogenous bankruptcy levels. Finance Stoch. 11, 131–152 (2007)
Leland, H.E.: Corporate debt value, bond covenants, and optimal capital structure. J. Finance 49, 1213–1252 (1994)
Leland, H.E., Toft, K.B.: Optimal capital structure, endogenous bankruptcy, and the term structure of credit spreads. J. Finance 51, 987–1019 (1996)
Leung, T., Yamazaki, K., Zhang, H.: An analytic recursive method for optimal multiple stopping: Canadization and phase-type fitting. Int. J. Theor. Appl. Finance 18, 1550032-1–1550032-31 (2015)
Loeffen, R.L.: An optimal dividends problem with a terminal value for spectrally negative Lévy processes with a completely monotone jump density. J. Appl. Probab. 46, 85–98 (2009)
Loeffen, R.L., Renaud, J.F., Zhou, X.: Occupation times of intervals until first passage times for spectrally negative Lévy processes with applications. Stoch. Process. Appl. 124, 1408–1435 (2014)
Long, M., Zhang, H.: On the optimality of threshold type strategies in single and recursive optimal stopping under Lévy models. Stoch. Process. Appl. 129, 2821–2849 (2019)
Madan, D.B., Seneta, E.: The variance gamma (VG) model for share market returns. J. Bus. 63, 511–524 (1990)
Modigliani, F., Miller, M.: The cost of capital, corporation finance and the theory of investment. Am. Econ. Rev. 48, 267–297 (1958)
Moraux, F.: Valuing corporate liabilities when the default threshold is not an absorbing barrier. EFMA 2002 London Meetings. Available online at https://ssrn.com/abstract=314404
Noba, K., Pérez, J.L., Yamazaki, K., Yano, K.: On optimal periodic dividend strategies for Lévy risk processes. Insur. Math. Econ. 80, 29–44 (2018)
Pardo, J.C., Pérez, J.L., Rivero, V.M.: The excursion measure away from zero for spectrally negative Lévy processes. Ann. Inst. Henri Poincaré Probab. Stat. 54, 75–99 (2018)
Pérez, J.L., Yamazaki, K.: American options under periodic exercise opportunities. Stat. Probab. Lett. 135, 92–101 (2018)
Pérez, J.L., Yamazaki, K., Bensoussan, A.: Optimal periodic replenishment policies for spectrally positive Lévy processes. Preprint (2018). Available online at https://arxiv.org/abs/1806.09216
Rodosthenous, N., Zhang, H.: Beating the omega clock: an optimal stopping problem with random time-horizon under spectrally negative Lévy models. Ann. Appl. Probab. 28, 2105–2140 (2018)
Sims, C.A.: Implications of rational inattention. J. Monet. Econ. 50, 665–690 (2003)
Surya, B.A.: Optimal Stopping of Lévy Processes and Pasting Principles. PhD dissertation, University of Utrecht (2007). Available online at https://dspace.library.uu.nl/bitstream/handle/1874/19086/full.pdf
Surya, B.A., Yamazaki, K.: Optimal capital structure with scale effects under spectrally negative Lévy models. Int. J. Theor. Appl. Finance 17, 1450013-1–1450013-31 (2014)
Takács, L.: Combinatorial Methods in the Theory of Stochastic Processes. Wiley, New York (1966)
Zolotarev, V.M.: The first passage time of a level and the behavior at infinity for a class of processes with independent increments. Theory Probab. Appl. 9, 653–664 (1964)
Acknowledgements
The authors thank the anonymous referees and Co-Editor for careful reading of the paper and constructive comments and suggestions. They also thank Nan Chen, Sebastian Gryglewicz, and Tak-Yuen Wong for helpful comments and discussions. This paper was supported by the National Science Centre under the grant 2016/23/B/HS4/00566 (2017-2020) and by MEXT KAKENHI grant no. 17K05377, 19H01791 and 20K03758. Part of the work was completed while Z. Palmowski was visiting Kansai University and Kyoto University at the invitation of K. Yamazaki. Z. Palmowski is very grateful for the hospitality provided by Kazutoshi Yamazaki, Kouji Yano and Takashi Kumagai.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Relation between the bankruptcy model (1.1) and Parisian ruin
Let \(G\) denote the set of starting points of the negative excursions of the shifted process \((V_{t}-V_{B})_{t \geq 0}\) and consider a set of mutually independent exponential random variables \(\{\mathbf{e}_{\lambda }^{g}:g\in G\}\), independent of \((V_{t})_{t \geq 0}\) as well. Let \(g_{t} :=\sup \{s\leq t:V_{s} \geq V_{B} \}\) be the last time before \(t\) the asset value was at or above \(V_{B}\) (i.e., the starting point of the excursion). Then the Parisian ruin with exponential grace periods is defined as
The equivalence with (1.1) can be easily verified. In each negative excursion with starting time \(g\) for the shifted process \((V_{t}-V_{B})_{t\geq 0}\) between two Poisson observation times, say \(T_{i(g)}\) and \(T_{i(g)+1}\) for some \(i(g) \geq 0\), we consider the waiting time \(T_{i(g)+1}-g\) until the next observation. Due to the lack of memory property of the exponential distribution and the strong Markov property, these waiting times are equal in distribution to a set of mutually independent exponentially distributed random variables. Consequently, (1.1) can be written as (A.1) with \(\mathbf{e}_{\lambda }^{g_{t}}\) replaced by these independent exponential random variables. In fact, it has been shown in Baurdoux et al. [10, Remark 1.1] that the joint distribution of the bankruptcy time (1.1) and the corresponding position of \(X\) is the same as that of (A.1) and the corresponding position of \(X\) (refer to Avram et al. [9] and Pardo et al. [48] for related literature).
It is worth investigating which impact the randomness of the grace period has on the asset values at bankruptcy. To this end, we compare in Table 2 the expected discounted asset values at bankruptcy for the cases when the grace periods are constant or exponentially distributed (with the common mean \(\lambda ^{-1}\)). When \(\lambda \) is low, the random (exponential) case tends to overestimate the asset value, but as \(\lambda \) becomes larger (i.e., observation is more frequent), the differences become smaller. This implies that when the observation is frequent, our model can approximate the constant grace period case reasonably well.
Appendix B: Proof of Proposition 3.2
For brevity, throughout this appendix, we use the notation
We first obtain the \(q\)-resolvent measure of the spectrally negative Lévy process \((X_{t})_{t \geq 0}\) killed at the stopping time (3.6) in terms of the function \(H^{(q+\lambda )}(\, \cdot \, ; \theta )\) as in (3.5) and
The proof of the following result is given in Appendix D.
Theorem B.1
For any bounded measurable function \(h:\mathbb{R}\to \mathbb{R}\)with compact support,
where
Using Theorem B.1, we show Proposition 3.2. The case \(V_{T} = 0\) is trivial, and hence we assume \(V_{T} > 0\) for the rest of this proof. By integrating the density in Theorem B.1 and using (B.1), we can write (3.9) as
where we define
which are shown to be finite immediately below. The rest of the proof of Proposition 3.2 is devoted to the simplification of the integrals ℋ and ℐ.
Lemma B.2
We have \(\overline{W}^{(r+\lambda )}(y) -\lambda \int _{0}^{y}W^{(r)}(y-z) \overline{W}^{(r+\lambda )}(z) \mathrm{d}z= \overline{W}^{(r)}(y)\)for all \(y \in \mathbb{R}\).
Proof
We have
where the last equality holds by Loeffen et al. [42, identity (6)]. Integrating this and because \(\overline{W}^{(r+\lambda )}(0) = \overline{W}^{(r)}(0) = 0\), the proof is complete. □
Lemma B.3
We have for \(x,z \in \mathbb{R}\) that
Proof
For \(z_{T}> 0\), we have
where we used \(x-z+z_{T} = x - \log V_{T}\) (see (B.1)) in the second equality and Lemma B.2 in the last one. On the other hand, as in Pérez et al. [50, Remark 4.3(ii)], we have
and therefore
Now the result is immediate by adding the two integrals and using (again see (B.1))
□
We note that (B.3) together with Lemma B.3 implies that
Lemma B.4
For \(z \in \mathbb{R}\), we have
Proof
First, by (3.5), we have
where in particular \(H^{(r+\lambda )}(y;\Phi (r)) = e^{\Phi (r)y}\) for \(y < 0\). For \(z_{T}>0\),
and hence
On the other hand, for \(z_{T}\in \mathbb{R}\),
By adding up the integrals, we obtain (B.7). □
Now applying Lemmas B.3 and B.4 in (B.3), we get Proposition 3.2. □
Appendix C: Other proofs
3.1 C.1 Proof of Lemma 4.1
For the case \(V_{T} > 0\),
is clearly nondecreasing in \(z\), and by bounded convergence, \(\lim _{z \downarrow -\infty }\Lambda ^{(r,\lambda )}(z,z) =0\).
On the other hand, if \(V_{T}=0\), then Proposition 3.2 and Remark 3.1, 1) yield \(\Lambda ^{(r,\lambda )}(z,z) =\frac{1}{r}(1-J^{(r, \lambda )}(0;0))= \frac{1}{\lambda +r} \frac{\Phi (r+\lambda )}{\Phi (r)}\). □
3.2 C.2 Proof of Proposition 4.5
We start from several key introductory identities. Fix \(q > 0\). Because
we have for \(x \neq z\) that
In particular,
Moreover, we have for \(x \neq z\) that
By setting \(\theta = 0\), we obtain the following result.
Lemma C.1
We have for \(x \neq z\) and \(q > 0\) that
Noting that \(\frac{\partial }{\partial z} ( e^{z} J^{(q, \lambda )}(x-z;1) ) = e^{z} J^{(q, \lambda )}(x-z;1) - e^{z} \frac{\partial }{\partial x} J^{(q, \lambda )}(x-z;1)\) and using (C.2) with \(\theta =1\), we have the following result.
Lemma C.2
We have for \(x \neq z\) and \(q > 0\) that
We also need the following observation.
Lemma C.3
We have for \(z_{T}\neq0\) and \(x > z\) that
Proof
By differentiating the identity in Lemma B.3, for \(z_{T}\neq0\), by (C.1),
By (3.5) and (C.1), we can write
Using (B.4), we have for \(x > z\) and \(z_{T}\neq0\) that
By (B.7) and (C.4), this equals
Furthermore, by (B.7),
In sum, we have
By applying (C.3) and (C.6) in (B.3), the proof is complete. □
We now prove Proposition 4.5. Differentiating (3.11) and using Lemmas C.1–C.3 gives
which reduces to (4.5) after simplification using Remark 3.1, 1). □
3.3 C.3 Proof of Proposition 4.6
In view of the probabilistic expression (3.5), \(q \mapsto H^{(q)}(x-z; \Phi (q+\lambda ))\) is nonincreasing for \(x,z\in \mathbb{R}\), and hence
On the other hand, because \(\psi \) is strictly convex and strictly increasing on \([\Phi (0), \infty )\), its right inverse \(\Phi \) is strictly concave, that is, \(\Phi '(r+\lambda +x)-\Phi '(r+x)<0\) for \(x, \lambda > 0\). Therefore
Combining these, we obtain
By Remark 3.1, 2) and because (3.5) implies that \(H^{(r+\lambda )}\) is nonnegative on ℝ, we have
Combining this with (B.6), (C.7) and (4.2) gives
In addition, because \(V_{B} \geq V_{B}^{*}\), the monotonicity in Proposition 4.2 implies that \(\mathcal{E}(V_{B};V_{B}) \geq 0\). Note when \(V_{B}^{*} = 0\) that \(\mathcal{E}(V_{B};V_{B}) \geq 0\) for all \(V_{B} > 0\) by Proposition 4.2.
Now by Proposition 4.5 and recalling that \(H^{(r+m)}\) is positive,
□
3.4 C.4 Proof of Proposition 4.7
Using Lemma B.3 together with (C.1) and (C.3), for \(x\neq\log V_{T}\) and \(z \in \mathbb{R}\) such that \(z_{T} \neq 0\), we have
where we used (B.5) for the case \(z_{T} <0\). Hence using (C.5) and (C.8) in (B.3), and by (B.2),
Now we write (3.11) as
where
Differentiating this with respect to \(x\) and \(z\), we get
and hence
Finally, using (C.9) and (C.11) in (C.10), we obtain
which reduces to the desired expression by noting that (C.10) gives
□
3.5 C.5 Proof of Lemma 4.10
First we note by Bertoin [11, Theorem VII.4] that for \(q\geq 0\),
On the other hand, (B.6) implies for \(V_{B}> 0\) that
where we used \(H^{(r+\lambda )}(y;\Phi (r)) = \exp (\Phi (r)y)\) for \(y \leq 0\). In addition, by the probabilistic expression of \(H^{(r+\lambda )}\) given in (3.5) and using dominated convergence, we have
This together with (C.12) gives
From Remark 3.1, 1) and (C.12), we can conclude that for \(q\geq 0\),
Combining these and (4.2), we obtain (4.8). □
3.6 C.6 Proof of Proposition 6.1
Fix \(t > 0\). Let us define the event
where \(S := T^{\lambda }_{2} - T^{\lambda }_{1}\) has an exponential distribution with parameter \(\lambda \). Note that
We start by analysing the numerator of (6.2). We decompose it as
where
Here, by (C.13) and because \(S\) is an independent exponential random variable with parameter \(\lambda \),
and \(|f_{2}(t)| \leq (|P|+(1-\alpha )V_{B}) \mathbb{P} [ N_{t}^{\lambda }\geq 2] =o(t)\) as \(t \downarrow 0\). Summing \(f_{1}(t)\) and \(f_{2}(t)\),
On the other hand, we transform the denominator of (6.2) as
where
Similarly to the computation for \(f_{1}(t)\) and \(f_{2}(t)\), by (C.13),
and \(g_{2}(t) \leq \mathbb{P} [N_{t}^{\lambda }\geq 2] = o(t)\). Hence putting all the pieces together, we get that
Now from (C.14), (C.15) and the mean value theorem,
By dividing the first by the second limit, we have the claim. □
3.7 C.7 Proof of Proposition 6.2
By (3.5) and (3.7), we can write for any \(\theta \geq 0\) and \(q \geq 0\) that
For \(y\neq0\), we now note the following:
1) For the cases (i) \(y < 0\) or (ii) \(y > 0\) and \(X\) does not have a diffusion component, we have that \(H^{(q)}(y;\Phi (q+\lambda )) \xrightarrow{\lambda \uparrow \infty } 0 \) (because the process does not creep downward as in Kyprianou [36, Exercise 7.6]) and \(\frac{\Phi (q+\lambda )-\Phi (q)}{\lambda }\) is bounded for \(\lambda \ge \delta >0\) (which can be verified by the convexity of \(\psi \)).
2) For the case where \(y > 0\) and \(X\) has a diffusion component,
and \(\frac{\Phi (q+\lambda )-\Phi (q)}{\lambda } \xrightarrow{\lambda \uparrow \infty } 0\) (because \(\psi (\theta ) \sim \frac{1}{2} \sigma ^{2} \theta ^{2}\) as \(\theta \rightarrow \infty \), where \(\sigma \) is the diffusion coefficient of \(X\)). Hence the previous arguments imply that for \(y \neq 0\),
Given that \(J^{(q, \lambda )}(y;\theta )\) is the Laplace transform of the random vector \((\tilde{T}_{0}^{-} (\lambda ) ,X_{\tilde{T}_{0}^{-}(\lambda )})\) (where we put \((\lambda )\) to spell out the dependence on \(\lambda \)), Lévy’s continuity theorem implies that \((\tilde{T}_{0}^{-} (\lambda ) ,X_{\tilde{T}_{0}^{-}}(\lambda ))\) converges in distribution to \((\tau _{0}^{-},X_{\tau _{0}^{-}})\). Hence using Skorohod’s representation theorem (see Billingsley [13, Theorem 6.7]) as well as dominated convergence, we obtain for \(V \neq V_{B}\) that
□
Appendix D: Proof of Theorem B.1
From Kuznetsov et al. [35, Theorem 2.7], for any Borel set \(A\) in \([0, \infty )\), in ℝ and in \((-\infty ,0]\), respectively, we have
where \(\tau _{0}^{-}\) is defined in (3.4) and \(\tau _{0}^{+}:=\inf \{t\geq 0: X_{t}>0\}\).
We prove the result for \(z=0\) and compute
The general case follows because the spatial homogeneity of the Lévy process implies that \(\mathbb{E}_{x} [ \int _{0}^{\tilde{T}_{z}^{-} } e^{-qt} h(X_{t}) { \mathrm{d}}t ] =\mathbb{E}_{x-z} [ \int _{0}^{\tilde{T}_{0}^{-}} e^{-qt} h (X_{t}+z) \mathrm{d}t ]\) for \(x,z\in \mathbb{R}\).
For \(x \in \mathbb{R}\), by the strong Markov property,
In particular, for \(x < 0\), again by the strong Markov property,
where for \(x \leq 0\),
Here the first equality for \(A(x)\) holds by the fact that \(T_{1}^{\lambda }\) is an independent exponential random variable with parameter \(\lambda \) and Kyprianou [36, Theorem 3.12]. The equality for \(B(x)\) is a consequence of (D.3).
Now by (3.5),
for the function \(H^{(q)}\) defined in (3.5). In addition, by Pérez et al. [50, proof of Theorem 4.1], we have
Substituting these in (D.4) and then applying (D.1) and [50, Remark 4.3], we obtain for all \(x \in \mathbb{R}\) that
On the other hand, by the strong Markov property, we can also write
where
We compute \(\gamma _{1}\) and \(\gamma _{2}\) below. First observe that
For \(\gamma _{2}\), by (D.2), we can write
which we compute by using the expression of \(g\) in (D.5). First, by [50, identity (A.8)], we have
while (3.3) gives \(\int _{0}^{\infty }e^{-\Phi (q+\lambda ) y} W^{(q)}(y) \mathrm{d}y = \lambda ^{-1}\), and therefore
Again by [50, proof of Theorem 4.1], we have
Substituting these in (D.7) and with the help of (D.5),
Now substituting the computed values of \(\gamma _{1}\) and \(\gamma _{2}\) in (D.6), we obtain
and hence solving for \(g(0)\), we obtain
Substituting this back in (D.5), we have
Hence the resolvent density is given by (B.2), as claimed. □
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Palmowski, Z., Pérez, J.L., Surya, B.A. et al. The Leland–Toft optimal capital structure model under Poisson observations. Finance Stoch 24, 1035–1082 (2020). https://doi.org/10.1007/s00780-020-00431-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00780-020-00431-6
Keywords
- Credit risk
- Endogenous bankruptcy
- Optimal capital structure
- Spectrally negative Lévy processes
- Term structure of credit spreads