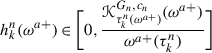1 Introduction

This paper belongs to the area of game-theoretic probability (see e.g. [9]). The advantage of game-theoretic probability for mathematical finance over the dominant approach of measure-theoretic probability is that it allows us to state and prove results free of any statistical assumptions even in situations where such assumptions are often regarded as essential (see e.g. the probability-free Dubins–Schwarz theorem in [11] and the probability-free theory of stochastic integration in [7]). In this paper, we consider the framework of an idealized financial market with one tradable security and assume for simplicity a zero interest rate.

The necessity of a non-trivial requirement of measurability (such as Borel-, Lebesgue-, or universal) is well known in measure theory (without measurability, we have counter-intuitive results such as the Banach–Tarski paradox [12]), and it is inherited by measure-theoretic probability. In game-theoretic probability, measurability is usually not needed in discrete time (and is never assumed in e.g. [9]); the present paper, however, shows that in continuous time, imposing some regularity conditions (such as Borel- or universal measurability) is essential even in the foundations of game-theoretic probability. If such conditions are not imposed, the basic definitions of game-theoretic probability become uninteresting, or even degenerate; e.g. in the case of continuous price paths, the upper probability of sets can take only two values, namely 1 (if the set contains a constant price path) or 0 (if not).

This paper constructs explicit trading strategies for enriching the trader given a well-order of the space of all possible price paths; however, such a well-order exists only under the axiom of choice (which is, despite some anomalous corollaries, universally accepted). Since we cannot construct such well-orders, our strategies cannot be regarded as genuinely constructive. Therefore, they cannot be regarded as practical get-rich-quick schemes. Moreover, they do not affect the existing results of continuous-time game-theoretic probability, which always explicitly assume measurability (to the best of my knowledge).

Our trading strategies will be very simple and based on Hardin and Taylor’s work on hat puzzles. These authors show in [4] (see also [5, Sect. 7.4]) that the axiom of choice provides us with an Occam-type strategy able to predict the short-term future (usually albeit not always), which makes it easy to get rich when allowed to trade in a security whose price changes in a non-trivial manner.

Section 2 is devoted to continuous price paths. The assumption of continuity allows us to use leverage and stop-loss strategies, and the trader can profit greatly and quickly whenever the price path is not constant. (We only consider trading strategies that never risk bankruptcy. It is clear that profiting from a constant price path is impossible.)

In Sect. 3, we assume instead of continuity that the price path is càdlàg. To make trading possible, we further assume that the price path is positive. It is impossible for the trader to become infinitely rich if the log-price path has finite variation. If the variation is infinite, there will be either points in time such that the variation of the log-price is infinite in any of their left neighbourhoods or points in time such that the variation of the log-price is infinite in any of their right neighbourhoods. Becoming infinitely rich is possible after points of the latter type. Standard stochastic models of financial markets postulate price paths that have such points almost surely.

In the short Sect. 4, we only assume that the price path is positive; the theory in this case is almost identical to the theory for positive càdlàg price paths.

The proofs of all our main results are collected in a separate section, Sect. 5; they are based on Hardin and Taylor’s results. Appendix A provides a more general picture of predicting the short-term future using the axiom of choice. It answers several very natural questions (and at the end asks 256 more questions answering just one of them).

Our definitions of the basic notions of continuous-time probability (such as stopping times) will be Galmarino-type (see e.g. [2, Theorems 1.2 and 1.4]) and modelled on the ones in the technical report [11] (the journal version uses slightly different definitions), except that the requirements of measurability will be dropped. By “positive” I mean “nonnegative”, adding “strictly” when necessary. The restriction \(f|_{C}\) of a function \(f:A\to B\) to a set \(C\) is defined as \(f|_{A\cap C}\); this notation will be used even when \(C\not\subseteq A\).

2 Continuous price paths

Let \(\Omega\) be the set \(C[0,1]\) of all continuous functions \(\omega:[0,1]\to\mathbb{R}\) (intuitively, these are the potential price paths over the time interval \([0,1]\)). An adapted process \(\mathfrak{S}\) is a family of functions \(\mathfrak{S}_{t}:\Omega\to[-\infty,\infty]\), \(t\in[0,1]\), such that for all \(\omega,\omega'\in\Omega\) and all \(t\in[0,1]\),

$$ \omega|_{[0,t]} = \omega'|_{[0,t]} \quad \Longrightarrow \quad \mathfrak{S}_{t}(\omega)=\mathfrak{S}_{t}(\omega'). $$

The intuition is that \(\mathfrak{S}_{t}(\omega)\) depends on \(\omega\) only via \(\omega|_{[0,t]}\): if \(\omega\) changes over \((t,1]\), \(\mathfrak{S}_{t}(\omega)\) is not affected. A stopping time is a function \(\tau:\Omega\to[0,1]\) such that for all \(\omega,\omega'\in\Omega\),

$$ \omega|_{[0,\tau(\omega)]} = \omega'|_{[0,\tau(\omega)]} \quad \Longrightarrow \quad \tau(\omega)=\tau(\omega'). $$
(2.1)

The intuition is that \(\tau(\omega)\) is not affected if \(\omega\) changes over \((\tau(\omega),1]\). For any stopping time \(\tau\), a function \(X:\Omega\to\mathbb{R}\) is said to be determined by time \(\tau\) if for all \(\omega,\omega'\in\Omega\),

$$ \omega|_{[0,\tau(\omega)]} = \omega'|_{[0,\tau(\omega)]} \quad \Longrightarrow \quad X(\omega)=X(\omega'). $$
(2.2)

The intuition is that \(X(\omega)\) depends on \(\omega\) only via \(\omega|_{[0,\tau(\omega)]}\). We often simplify \(\omega(\tau(\omega))\) to \(\omega(\tau)\) (occasionally, the argument \(\omega\) will be omitted in other cases as well).

The class of allowed trading strategies is defined in two steps. First, a simple trading strategy \(G\) consists of an increasing sequence of stopping times \(\tau_{1}\le\tau_{2}\le\cdots\) and, for each \(k=1,2,\ldots\), a bounded function \(h_{k}\) that is determined by time \(\tau_{k}\). It is required that for each \(\omega\in\Omega\), \(\tau_{k}(\omega)=1\) from some \(k\) on. To such \(G\) and an initial capital \(c\in\mathbb{R}\) corresponds the simple capital process

(2.3)

(with the zero terms in the sum ignored, which makes the sum finite); the value \(h_{k}(\omega)\) is called the bet at time \(\tau_{k}(\omega)\), and is referred to as the capital at time \(t\).

Second, a positive capital process is any adapted process \(\mathfrak{S}\) that can be represented in the form

(2.4)

where the simple capital processes are required to be positive for all \(t\) and \(\omega\), and the positive series \(\sum_{n=1}^{\infty}c_{n}\) is required to converge in ℝ. The sum (2.4) is always positive but allowed to take the value \(\infty\). Since does not depend on \(\omega\), \(\mathfrak{S}_{0}(\omega)\) also does not depend on \(\omega\) and is sometimes abbreviated to \(\mathfrak{S}_{0}\).

The upper probability of a set \(E\subseteq\Omega\) is defined as

$$ \overline {\mathbb {P}}(E) := \inf \{ \mathfrak{S}_{0} : \forall\omega\in\Omega, \mathfrak{S}_{1}(\omega) \ge \boldsymbol {1}_{E}(\omega) \}, $$
(2.5)

where \(\mathfrak{S}\) ranges over the positive capital processes and \(\boldsymbol {1}_{E}\) stands for the indicator function of \(E\). We say that a set \(E\subseteq\Omega\) is null if \(\overline {\mathbb {P}}(E)=0\).

Remark 2.1

The intuition behind a simple trading strategy is that the trader is allowed to take positions \(h_{k}\), either long or short, in a security whose price at time \(t\in[0,1]\) is denoted \(\omega(t)\). The positions can change only at a discrete sequence of times \(\tau_{1},\tau_{2},\ldots\), which makes the definition (2.3) of the trader’s capital at time \(t\) uncontroversial. To obtain more useful trading strategies, we allow the trader to split his initial capital into a countable number of accounts and to run a separate simple trading strategy for each account; none of the component simple trading strategies is allowed to go into debt. The resulting total capital at time \(t\) is given by (2.4). The upper probability \(\overline {\mathbb {P}}(E)\) defined by (2.5) is the smallest initial capital sufficient for superhedging the binary option on \(E\).

The following theorem is proved in Sect. 5.

Theorem 2.2

The set of all non-constant \(\omega\in\Omega\) is null. Moreover, there is a positive capital process \(\mathfrak{S}\) with \(\mathfrak{S}_{0}=1\) that becomes infinite as soon as \(\omega\) ceases to be constant: for all \(t\in[0,1]\),

$$ \exists t_{1},t_{2}\in[0,t)\ \textit{ with }\ \omega(t_{1})\ne\omega(t_{2}) \quad \Longrightarrow \quad \mathfrak{S}_{t}(\omega)=\infty. $$
(2.6)

Remark 2.3

A more popular version of our definition (2.5) was given by Perkowski and Prömel [7]. Perkowski and Prömel’s definition is more permissive [7, Sect. 2.3], and so the first statement of Theorem 2.2 continues to hold for it as well if we allow non-measurable (but still non-anticipative) trading strategies. Like all papers (that I am aware of) on continuous-time game-theoretic probability, the definitions given in [7] assume the measurability of all strategies.

Remark 2.4

The definitions of this section assume that the trader is permitted to short the security (which allows \(h_{k}(\omega)<0\)) and borrow money (which allows leverage, \(H_{k}(\omega)>1\) in the notation of Remark 3.4 below). If shorting and borrowing are not permitted (in the notation of Remark 3.4, if the \(H_{k}\) are only permitted to take values in \([0,1]\)), Theorem 2.2 ceases to be true, but Theorem 3.3 is still applicable.

3 Positive càdlàg price paths

In this section, we prove an analogue of Theorem 2.2 for positive càdlàg price paths \(\omega\); the picture now becomes more complicated. Intuitively, \(\omega:[0,1]\to[0,\infty)\) is a price path of a financial security whose price is known always to stay positive (such as a stock, and from now on it will be referred to as stock). For simplicity, in the bulk of this section, we consider the price paths \(\omega\) satisfying \(\inf\omega>0\); the case of general positive \(\omega\) is considered in Remark 3.8 at the end of the section. Therefore, we redefine \(\Omega\) as the set of all \(\omega:[0,1]\to[0,\infty)\) such that \(\inf\omega>0\). The definitions of adapted processes, stopping times, etc., stay literally as before (but with the new definition of \(\Omega\)). Our goal is to determine the sign of \(\overline {\mathbb {P}}(E)\) (i.e., to determine whether \(\overline {\mathbb {P}}(E)>0\)) for a wide family of sets \(E\subseteq\Omega\).

For each function \(f:[a,b]\to\mathbb{R}\), where \([a,b]\subseteq[0,1]\), its variation \(\operatorname {var}f\) is defined as

$$ \operatorname {var}(f) := \sup \sum_{i=1}^{n} \left| f(t_{i}) - f(t_{i-1}) \right| \in [0,\infty], $$
(3.1)

where the sup is taken over all \(n=1,2,\ldots\) and all partitions

$$a=t_{0}< t_{1}< \cdots< t_{n}=b; $$

this definition is usually used for \([a,b]=[0,1]\). As noticed in [10], we have that \(\overline {\mathbb {P}}(\{\omega\})>0\) for each price path \(\omega\in\Omega\) with \(\operatorname {var}(\log\omega)<\infty\). Namely, we have the following simple result (to be proved in Sect. 5.2).

Theorem 3.1

For any \(\omega\in\Omega\),

$$ \overline {\mathbb {P}}(\{\omega\}) = \sqrt{\frac{\omega(0)}{\omega(1)}e^{-\operatorname {var}(\log\omega)}}. $$
(3.2)

We can see that \(\overline {\mathbb {P}}(E)>0\) whenever \(E\) contains \(\omega\) with \(\operatorname {var}(\log\omega)<\infty\). Therefore, in the rest of this section, we concentrate on \(\omega\in\Omega\) with \(\operatorname {var}(\log\omega)=\infty\). We start from a classification of such \(\omega\).

For any \(f:[0,1]\to\mathbb{R}\) and \(t\in[0,1]\), set

$$\begin{aligned} \operatorname {var}(f,t-) &:= \inf_{t'\in[0,t)} \operatorname {var}\left( f|_{[t',t]} \right), \end{aligned}$$
(3.3)
$$\begin{aligned} \operatorname {var}(f,t+) &:= \inf_{t'\in(t,1]} \operatorname {var}\left( f|_{[t,t']} \right); \end{aligned}$$
(3.4)

the cases \(\operatorname {var}(f,0-):=0\) and \(\operatorname {var}(f,1+):=0\) are treated separately. Notice that \(\operatorname {var}(f,t-)\) and \(\operatorname {var}(f,t+)\) always take values in the two-element sets \(\{\lvert\Delta f(t)\rvert,\infty\}\) and \(\{0,\infty\}\), respectively (where \(\Delta f(t):=f(t)-f(t-)\) is the jump of \(f\) at \(t\)). Furthermore, for each \(\omega\in\Omega\), set

$$\begin{aligned} I^{-}_{\omega} &:= \left\{ t\in[0,1] :\operatorname {var}(\log\omega,t-) = \infty \right\} \subseteq (0,1], \end{aligned}$$
(3.5)
$$\begin{aligned} I^{+}_{\omega} &:= \left\{ t\in[0,1] :\operatorname {var}(\log\omega,t+) = \infty \right\} \subseteq [0,1). \end{aligned}$$
(3.6)

The next lemma shows that the set of all \(\omega\in\Omega\) with infinite variation of their logarithm can be represented as

$$ \{\omega\in\Omega : \operatorname {var}(\log\omega)=\infty\} = \{\omega\in\Omega :I^{-}_{\omega}\ne\emptyset\} \cup \{\omega\in\Omega :I^{+}_{\omega}\ne\emptyset\}. $$
(3.7)

Lemma 3.2

For any \(f:[0,1]\to\mathbb{R}\),

$$ \operatorname {var}(f)=\infty \quad \Longleftrightarrow \quad \exists t\in[0,1] \ \textit{with}\ \operatorname {var}(f,t+)=\infty\ \textit{or}\ \operatorname {var}(f,t-)=\infty . $$

Proof

The implication “⇐” is obvious, and so we only check “⇒”. Suppose that \(\operatorname {var}(f,t+)<\infty\) and \(\operatorname {var}(f,t-)<\infty\) for all \(t\in[0,1]\). Fix a neighbourhood \(O_{t}=(a_{t},b_{t})\) of each \(t\) such that \(\operatorname {var}(f|_{O_{t}})<\infty\). These neighbourhoods form a cover of \([0,1]\). The existence of a finite subcover immediately implies that \(\operatorname {var}(f)<\infty\). □

The following theorem (proved in Sect. 5) tackles the second term of the union in (3.7).

Theorem 3.3

The set of all \(\omega\in\Omega\) such that \(I^{+}_{\omega}\ne\emptyset\) is null. Moreover, there is a positive capital process \(\mathfrak{S}\) with \(\mathfrak{S}_{0}=1\) that becomes infinite immediately after the time \(\inf I^{+}_{\omega}\) if \(I^{+}_{\omega}\ne\emptyset\): For all \(t\in[0,1]\) and \(\omega\in\Omega\),

$$ \exists t'\in[0,t)\ \textit{with}\ \operatorname {var}(\log\omega,t'+)=\infty \quad \Longrightarrow \quad \mathfrak{S}_{t}(\omega)=\infty. $$
(3.8)

Remark 3.4

A stopping time \(\tau\) is said to be predictable if (2.1) holds with the two entries of \([0,\tau(\omega)]\) replaced by \([0,\tau(\omega))\) (cf. [3, Theorem IV.99(a)]). Similarly, a function \(X:\Omega\to\mathbb{R}\) is determined before a stopping time \(\tau\) if (2.2) holds with the two entries of \([0,\tau(\omega)]\) replaced by \([0,\tau(\omega))\) (cf. [3, Theorem IV.99(b)]). We shall impose this requirement on the relative bets

involved in a simple capital process (2.3); intuitively, \(H_{k}(\omega)\) is the fraction of the trader’s capital invested in the stock at time \(\tau_{k}\). In terms of the relative bets, the simple capital process (2.3) can be rewritten as

Notice that this simple capital process is positive if and only if the relative bets \(H_{k}\) are always in the range \([0,1]\) (since the stock price can shoot up or drop nearly to 0 at any time). A positive capital process (2.4) is predictable if the component simple capital processes involve only predictable stopping times \(\tau_{k}\) and relative bets \(H_{k}\) determined before \(\tau_{k}\). Theorem 3.3 can be strengthened by requiring the positive capital process \(\mathfrak{S}\) to be in addition predictable. (Notice that predictability was automatic in the continuous case of Sect. 2.) This observation can be strengthened further. Let us say that a stopping time \(\tau\) is strongly predictable if for every \(\omega\in\Omega\), there exists \(t<\tau(\omega)\) such that for every \(\omega'\in\Omega\),

$$ \omega|_{[0,t]} = \omega'|_{[0,t]} \quad \Longrightarrow \quad \tau(\omega)=\tau(\omega'). $$

A function \(X:\Omega\to\mathbb{R}\) is said to be determined strictly before a stopping time \(\tau\) if for every \(\omega\in\Omega\), there exists \(t<\tau(\omega)\) such that for every \(\omega'\in\Omega\),

$$ \omega|_{[0,t]} = \omega'|_{[0,t]} \quad \Longrightarrow \quad X(\omega) = X(\omega'). $$

A positive capital process (2.4) is strongly predictable if the component simple capital processes involve only strongly predictable stopping times \(\tau_{k}\) and relative bets \(H_{k}\) determined strictly before \(\tau_{k}\). Theorem 3.3 can be further strengthened by requiring the positive capital process \(\mathfrak{S}\) to be strongly predictable. A simple modification of the proof of Theorem 3.3 demonstrating this fact is given in Remark 5.3.

Remark 3.5

In the context of the previous remark, imposing the requirement of being determined before \(\tau_{k}\) on the bets \(h_{k}\) rather than relative bets \(H_{k}\) would lead to a useless notion of a predictable positive capital process: all such processes would be constant. Indeed, suppose there is a predictable positive capital process that is not constant (where “predictable” is defined in terms of \(h_{k}\) rather than \(H_{k}\)). Let \(\omega\in\Omega\) be a path on which is not constant. Fix such an \(\omega\) and let \(k\) be the smallest integer such that \(\tau_{k}(\omega)<\tau_{k+1}(\omega)\) and \(h_{k}(\omega)\ne 0\) (such a \(k\) exists since the process is not constant on \(\omega\)). Let us consider the more difficult (since it is safer for the trader) case \(h_{k}(\omega)>0\). Define \(\omega'\) as \(\omega\) over the time interval \([0,\tau_{k}(\omega))\), as a sufficiently large positive number at the time \(\tau_{k}(\omega)\) (namely, it should be such that the product of \(h_{k}(\omega)=h_{k}(\omega')\) and \(\omega'(\tau_{k}(\omega))-1\) exceeds the current capital ), and as a linear function over the time interval \([\tau_{k}(\omega),1]\) decreasing from \(\omega'(\tau_{k}(\omega))\) at the left endpoint to 1 at the right endpoint. If \(\tau_{k+1}(\omega')=1\), we have , a contradiction. Since \(\tau_{k+1}(\omega')=\tau_{k}(\omega')\) is impossible by our assumption \(\tau_{k+1}(\omega)>\tau_{k}(\omega)\) and the predictability of \(\tau_{k}\) and \(\tau_{k+1}\), we can assume \(\tau_{k}(\omega')<\tau_{k+1}(\omega')<1\). Defining \(\omega''\) as \(\omega'\) over the time interval \([0,\tau_{k+1}(\omega'))\) and as 1 over the complementary time interval \([\tau_{k+1}(\omega'),1]\), we obtain , again a contradiction.

In the continuous case of Sect. 2 (where \(\omega\) is not required to be positive), the notion of a predictable positive capital process is equivalent to that of a positive capital process, but the notion of a strongly predictable positive capital process, even as given in the previous remark, is useless: again, any such process is a constant.

Theorems 3.1 and 3.3 show that the only non-trivial part of \(\Omega\) (as far as the sign of \(\overline {\mathbb {P}}\) is concerned) is

$$ \Omega^{\rm nt} := \{ \omega\in\Omega :I^{-}_{\omega} \ne \emptyset, I^{+}_{\omega} = \emptyset \}. $$

Namely,

$$ \overline {\mathbb {P}}(E) \textstyle\begin{cases} {}> 0 & \quad \text{if $\exists\omega\in E$ with $\operatorname {var}(\log\omega)< \infty$,}\\ {}= \overline {\mathbb {P}}(E\cap\Omega^{\rm nt}) &\quad \text{otherwise}. \end{cases} $$

Theorem 3.1 and the following result (also to be proved in Sect. 5) show that this part is really non-trivial: it has subsets of upper probability one and non-empty subsets (such as any singleton) of upper probability zero.

Theorem 3.6

The set \(\Omega^{\rm nt}\) has upper probability one. Moreover,

$$ \overline {\mathbb {P}}\big(\big\{ \omega\in\Omega :I^{-}_{\omega}=\{t\}, I^{+}_{\omega}=\emptyset \big\} \big) = 1 $$
(3.9)

for each \(t\in(0,1]\).

Remark 3.7

The following modification of variation (3.1) is often useful: define

$$ \operatorname {var}^{+}(f) := \sup \sum_{i=1}^{n} \big( f(t_{i}) - f(t_{i-1}) \big)^{+}, $$
(3.10)

where \(u^{+}:=u\vee 0\); we allow \(f:[0,1]\to[-\infty,\infty)\). Using this definition, (3.2) can be simplified (cf. [?, end of Sect. 2]) to

$$ \overline {\mathbb {P}}(\{\omega\}) = e^{-\operatorname {var}^{+}(\log\omega)}, $$
(3.11)

and in this form the equality becomes true for any positive càdlàg \(\omega\) (with \(\inf\omega=0\) allowed). The modified versions of (3.3)–(3.6) are

$$\begin{aligned} \operatorname {var}^{+}(f,t-) &:= \inf_{t'\in[0,t)} \operatorname {var}^{+} \left( f|_{[t',t]} \right), \end{aligned}$$
(3.12)
$$\begin{aligned} \operatorname {var}^{+}(f,t+) &:= \inf_{t'\in(t,1]} \operatorname {var}^{+} \left( f|_{[t,t']} \right), \end{aligned}$$
(3.13)
$$\begin{aligned} J^{-}_{\omega} &:= \{ t\in[0,1] :\operatorname {var}^{+}(\log\omega,t-) = \infty \} \subseteq (0,1], \end{aligned}$$
(3.14)
$$\begin{aligned} J^{+}_{\omega} &:= \{ t\in[0,1] :\operatorname {var}^{+}(\log\omega,t+) = \infty \} \subseteq [0,1). \end{aligned}$$
(3.15)

Lemma 3.2 and Theorems 3.3 and 3.6 continue to hold if we replace all entries of \(\operatorname {var}\) by \(\operatorname {var}^{+}\) and all entries of \(I\) by \(J\).

Remark 3.8

In this remark, we allow the price path \(\omega\) to take the value zero. Redefine \(\Omega\) as the set of all positive càdlàg functions \(\omega:[0,1]\to[0,\infty)\), and consider the partition of \(\Omega\) into the three subsets

$$\begin{aligned} A &:= \{\omega\in\Omega :\inf\omega>0\},\\ B &:= \{\omega\in\Omega :\exists t\in[0,1]\ \textrm{with}\ \operatorname {sign}\omega=\boldsymbol {1}_{[0,t)}\},\\ C &:= \Omega\setminus(A\cup B), \end{aligned}$$

where

$$ \operatorname {sign}u := \textstyle\begin{cases} 1 & \quad \text{if $u>0$,}\\ 0 &\quad \text{if $u=0$,}\\ -1 &\quad \text{if $u< 0$}. \end{cases} $$

In other words, \(A\) is the old \(\Omega\) as defined in the main part of this section, \(B\) is the set of all \(\omega\in\Omega\) that become zero at some point \(t\) in time and then never recover, and \(C\) is the set of all \(\omega\in\Omega\) such that \(\omega(t_{1}-)\wedge\omega(t_{1})=0\) and \(\omega(t_{2})>0\) for some \(t_{1}< t_{2}\). Theorems 3.3 and 3.6, as stated originally or as modified in the previous remark, describe the sign of \(\overline {\mathbb {P}}\) for subsets of \(A\). We can ignore the price paths in \(C\) because \(\overline {\mathbb {P}}(C)=0\) and therefore, for any \(E\subseteq\Omega\),

$$ \overline {\mathbb {P}}(E) = \overline {\mathbb {P}}\big(E\cap(A\cup B)\big). $$

In the rest of this remark, we allow not only \(f:[0,1]\to[-\infty,\infty)\) in (3.10), (3.12) and (3.13), but also any \(\omega\in\Omega\) (for the new definition of \(\Omega\)) in (3.14) and (3.15). Theorem 3.3 continues to hold for \(\omega\in A\cup B\) if we replace \(\operatorname {var}\) by \(\operatorname {var}^{+}\) and \(I\) by \(J\) (as shown by the same argument, given in Sect. 5). Equation (3.9) in Theorem 3.6 can be rewritten as

$$ \overline {\mathbb {P}}\big(\big\{ \omega\in A :J^{-}_{\omega}=\{t\}, J^{+}_{\omega}=\emptyset \big\} \big) = 1. $$

4 Positive price paths

Let us now redefine \(\Omega\) to be the set of all positive functions \(\omega:[0,1]\to[0,\infty)\) satisfying \(\inf\omega>0\) (without any continuity requirements). The definitions of adapted processes, stopping times, etc., again stay as in Sect. 2. Theorems 3.3 and 3.6 still hold, as shown by the same arguments in the next section. Remark 3.4 still holds with the same definitions of predictable and strongly predictable positive capital processes. Remark 3.8 still holds for \(\Omega\) being the set of all positive functions \(\omega:[0,1]\to[0,\infty)\).

5 Proofs of the theorems

The next result (Lemma 5.1) is applicable to all \(\Omega\) considered in Sects. 2–4. Fix a well-order ⪯ of \(\Omega\), which exists by the Zermelo theorem (one of the alternative forms of the axiom of choice; see e.g. [6, Theorem 5.1]). Let \(\omega^{a}\), where \(\omega\in\Omega\) and \(a\in[0,1]\), be the ⪯-smallest element of \(\Omega\) such that \(\omega^{a}|_{[0,a]}=\omega|_{[0,a]}\). Intuitively, using \(\omega^{a}\) as the prediction at time \(a\) for \(\omega\) is an instance of Occam’s razor: out of all hypotheses compatible with the available data \(\omega|_{[0,a]}\), we choose the simplest one, where simplicity is measured by the chosen well-order.

For any \(\omega\in\Omega\), set

$$\begin{aligned} W_{\omega} &:= \{ t\in[0,1] :\forall t'\in(t,1], \omega^{t'}\ne\omega^{t} \} \\ &\phantom{:}= \{ t\in[0,1] :\forall t'\in(t,1], \omega^{t'}\succ\omega^{t} \} \\ &\phantom{:}= \{ t\in[0,1] :\forall t'\in(t,1], \omega^{t}|_{[0,t']}\ne\omega|_{[0,t']} \} \end{aligned}$$
(5.1)

(in particular, \(1\in W_{\omega}\)). The following lemma says, intuitively, that short-term prediction of the future is usually possible.

Lemma 5.1

  1. 1.

    The set \(W_{\omega}\) is well-ordered by ≤. (Therefore, each of its points is isolated on the right, which implies that \(W_{\omega}\) is countable and nowhere dense.)

  2. 2.

    If \(t\in[0,1]\setminus W_{\omega}\), there exists \(t'>t\) such that \(\omega^{t}|_{[t,t']}=\omega|_{[t,t']}\).

  3. 3.

    If \(t\in[0,1)\), there exists \(t'>t\) such that \(\omega^{s}|_{[t,t']}=\omega|_{[t,t']}\) for all \(s\in(t,t')\).

Part 1 of Lemma 5.1 says, informally, that the set \(W_{\omega}\) is small. Part 2 says that at each time point \(t\) outside the small set \(W_{\omega}\), the Occam prediction system that outputs \(\omega^{t}\) as its prediction is correct (over some non-trivial time interval). Part 3 says that even at time points \(t\) in \(W_{\omega}\), the Occam prediction system becomes correct (in the same weak sense) immediately after time \(t\).

Proof of Lemma 5.1

Let us first check that \(W_{\omega}\) is well-ordered by ≤. Suppose there is an infinite strictly decreasing chain \(t_{1}>t_{2}>\cdots\) of elements of \(W_{\omega}\). Then we have \(\omega^{t_{1}}\succ\omega^{t_{2}}\succ\cdots\), which contradicts ⪯ being a well-order.

Each point \(t\in W_{\omega}\setminus\{1\}\) is isolated on the right since \(W_{\omega}\cap(t,t')=\emptyset\), where \(t'\) is the successor in \(W_{\omega}\) of \(t\). Therefore, \(W_{\omega}\) is nowhere dense. To check that \(W_{\omega}\) is countable, map each \(t\in W_{\omega}\setminus\{1\}\) to a rational number in the interval \((t,t')\), where \(t'\) is the successor in \(W_{\omega}\) of \(t\); this mapping is an injection.

As part 2 is obvious (and essentially asserted in (5.1)), let us check part 3. Suppose \(t\in[0,1)\). The set of all \(\omega^{s}\), \(s\in(t,1]\), has a smallest element \(\omega^{t'}\), where \(t'\in(t,1]\). It remains to notice that \(\omega^{s}=\omega^{t'}\) for all \(s\in(t,t')\). □

Remark 5.2

It might be tempting to conjecture that for any \(t\in W_{\omega}\setminus\{1\}\), the function \(s\mapsto\omega^{s}\) does not depend on \(s\in(t,t')\), where \(t'\) is the successor in \(W_{\omega}\) of \(t\). While this statement is true for \(\Omega=C[0,1]\), simple examples show that it is wrong in general; see Lemma A.3 in Appendix A.

5.1 Proof of Theorem 2.2

For each pair \((a,b)\) of rational numbers such that \(0< a< b<1\), fix a strictly positive weight \(w_{a,b}>0\) such that \(\sum_{a,b} w_{a,b} = 1\), the sum being over all such pairs. For each such pair \((a,b)\), we define a positive capital process such that and when \(\omega|_{[a,b]}=\omega^{a}|_{[a,b]}\) and \(\omega|_{[a,b]}\) is not constant. Let us check that the process

(5.2)

will then achieve our goal (2.6).

Let \(\omega\in\Omega\) and let \(c\) be the largest \(t\in[0,1]\) such that \(\omega|_{[0,t]}\) is constant (the supremum is attained by the continuity of \(\omega\)). Assuming that \(\omega\) is not constant, we have \(c<1\). Set \(\omega^{c+}:=\omega^{t}\) for \(t\in(c,c+\epsilon)\) for a sufficiently small \(\epsilon>0\) (namely, such that \(t\mapsto\omega^{t}\) is constant over the interval \((c,c+\epsilon)\); such an \(\epsilon\) exists by Lemma 5.1). Choose \(d\in(c,1)\) such that \(\omega^{d}=\omega^{c+}\) (and therefore \(\omega|_{(c,d]}=\omega^{c+}|_{(c,d]}\) and \(\omega^{t}=\omega^{c+}\) for all \(t\in(c,d]\)). Take rational \(a,b\in(c,d)\) such that \(a< b\) and \(\omega|_{[a,b]}\) is not constant; since , (5.2) gives \(\mathfrak{S}_{b}(\omega)=\infty\); and since \(b\) can be arbitrarily close to \(c\), we obtain (2.6).

It remains to construct such a positive capital process for fixed \(a,b\). For the rest of this proof, \(\omega\) is a generic element of \(\Omega\). For each \(n\in\{1,2,\ldots\}\), let \(\mathbb{D}_{n}:=\{k2^{-n}:k\in\mathbb{Z}\}\) be the dyadic rationals of order \(n\) and define a sequence of stopping times \(T^{n}_{k}\), \(k=-1,0,1,2,\ldots\), inductively by \(T^{n}_{-1}:=a\),

$$\begin{aligned} T^{n}_{0}(\omega) &:= \inf \left\{ t\in[a,b] :\omega(t)\in\mathbb{D}_{n} \right\},\\ T^{n}_{k}(\omega) &:= \inf \{ t\in[T^{n}_{k-1}(\omega),b] :\omega(t)\in\mathbb{D}_{n} \ \textrm{and} \ \omega(t)\ne\omega(T^{n}_{k-1}) \}, \enspace k=1,2,\ldots, \end{aligned}$$

where we set \(\inf\emptyset:=b\). For each \(n=1,2,\ldots\), define a simple capital process as the capital process of the simple trading strategy with the stopping times

$$ \omega\in\Omega\mapsto\tau^{n}_{k}(\omega):=T^{n}_{k}(\omega)\wedge T^{n}_{k}(\omega^{a}), \quad k=0,1,\ldots, $$

the corresponding bets \(h^{n}_{k}\) that are defined as

$$ h^{n}_{k}(\omega) := \textstyle\begin{cases} 2^{2n} (\omega^{a}(\tau^{n}_{k+1}(\omega^{a}))-\omega(\tau^{n}_{k})) & \quad \text{if $\omega^{\tau^{n}_{k}(\omega)}=\omega^{a}$ and $\tau^{n}_{k}(\omega)< b$,}\\ 0 &\quad \text{otherwise}, \end{cases} $$

and an initial capital of 1. Since the increments of this simple capital process never exceed 1 in absolute value (and trading stops as soon as the prediction \(\omega^{a}\) is falsified), its initial capital of 1 ensures that it always stays positive. The final value satisfies unless \(\omega|_{[a,b]}\ne\omega^{a}|_{[a,b]}\) or \(\omega|_{[a,b]}\) is constant. If we now set

we obtain and unless \(\omega|_{[a,b]}\ne\omega^{a}|_{[a,b]}\) or \(\omega|_{[a,b]}\) is constant. This completes the proof of Theorem 2.2.  □

5.2 Proof of Theorem 3.1

We follow the proof of Proposition 2 in [?] (that proposition considers measurable strategies, but the assumption of measurability is not essential there). Let us check the equivalent statement (3.11). If \(c<\operatorname {var}^{+}(\log\omega)\), we can find a partition \(0=t_{0}< t_{1}<\cdots<t_{n}=1\) of \([0,1]\) such that

$$ \sup \sum_{i=1}^{n} \big( \log\omega(t_{i}) - \log\omega(t_{i-1}) \big)^{+} > c $$

(cf. (3.10)). By investing all the available capital into \(\omega\) at time \(t_{i-1}\) whenever we have \(( \log\omega(t_{i}) - \log\omega(t_{i-1}) )^{+} > 0 \) (i.e., whenever \(\omega(t_{i})>\omega(t_{i-1})\)), the trader can turn 1 into at least \(e^{c}\). This proves the inequality “≤” in (3.11). And it is clear that this is the best the trader can do without risking bankruptcy.

For further (obvious) details, see the proof of Proposition 2 in [10].  □

5.3 Proof of Theorem 3.3

The proof uses the fact that \(\inf I^{+}_{\omega}\in I^{+}_{\omega}\) when \(I^{+}_{\omega}\ne\emptyset\). Notice that \(I^{+}_{\omega}=J^{+}_{\omega}\), where \(J^{+}_{\omega}\) is defined in Remark 3.7.

In this section, we construct a positive capital process \(\mathfrak{S}\) such that \(\mathfrak{S}_{0}<\infty\) and \(\mathfrak{S}_{1}=\infty\) whenever \(I^{+}_{\omega}\ne\emptyset\); moreover, it satisfies (3.8). Namely, we define \(\mathfrak{S}\) via its representation (2.4) with the components , where \(\omega\) is a generic element of \(\Omega\), defined as follows:

  • \(c_{n}=1/n^{2}\) (which ensures that the total initial capital \(\sum_{n} 1/n^{2}\) is finite); \(G_{n}\) will consist of stopping times denoted as \(\tau^{n}_{1},\tau^{n}_{2},\ldots\) and bets denoted as \(h^{n}_{1},h^{n}_{2},\ldots\);

  • if \(I^{+}_{\omega}=\emptyset\), set \(\tau^{n}_{1}(\omega)=\tau^{n}_{2}(\omega)=\cdots=1\) and \(h^{n}_{1}(\omega)=h^{n}_{2}(\omega)=\cdots=0\) (intuitively, \(G_{n}\) never bets, which makes this part of the definition non-anticipatory); in the rest of this definition we will assume that \(I^{+}_{\omega}\ne\emptyset\) and, therefore, \(\inf I^{+}_{\omega}<1\);

  • set \(a:=\inf I^{+}_{\omega}\); we know that \(a\in I^{+}_{\omega}\) and \(a<1\);

  • in view of Lemma 5.1, set \(\omega^{a+}:=\omega^{t}\) for \(t\in(a,a+\epsilon)\) for a sufficiently small \(\epsilon\) (such that \(t\mapsto\omega^{t}\) does not depend on \(t\in(a,a+\epsilon)\));

  • define

    $$ c := \inf \big\{ t \in \big(a,(a+2^{-n})\wedge 1\big] :\operatorname {var}^{+}\big(\log\omega^{a+}|_{[t,t+2^{-n}]}\big) \le n \big\} $$

    (with \(\inf\emptyset:=(a+2^{-n})\wedge 1\));

  • set \(d:=(a+c)/2\) and define

    $$ \tau^{n}_{k}(\omega^{a+})\in[d,(d+2^{-n})\wedge1]\cup\{1\} $$
    (5.3)

    and \(h^{n}_{k}(\omega^{a+})\), \(k=1,2,\ldots\), in such a way that

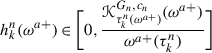    (5.4)

    (which is required implicitly by the definition of the positivity of \(\mathfrak{S}\) and is equivalent to the relative bets being in the range \([0,1]\)) and

    (5.5)

    the latter can be done because of

    $$ \operatorname {var}^{+} \big( \log\omega^{a+}|_{[d,d+2^{-n}]} \big) > n $$

    and the fact that (3.11) remains true if only positive simple capital processes are used as \(\mathfrak{S}\) in the definition (2.5) of \(\overline {\mathbb {P}}\) (as can be seen from the proof in Sect. 5.2);

  • set

    $$ \tau^{n}_{k}(\omega) := \textstyle\begin{cases} \tau^{n}_{k}(\omega^{a+}) &\quad \text{if $\omega|_{[0,\tau^{n}_{k}(\omega^{a+})]}=\omega^{a+}|_{[0,\tau^{n}_{k}(\omega^{a+})]}$,}\\ 1 &\quad \text{otherwise,} \end{cases} $$
    (5.6)

    and

    $$ h^{n}_{k}(\omega) := \textstyle\begin{cases} h^{n}_{k}(\omega^{a+}) & \quad \text{if $\omega|_{[0,\tau^{n}_{k}(\omega^{a+})]}=\omega^{a+}|_{[0,\tau^{n}_{k}(\omega^{a+})]}$,}\\ 0 &\quad \text{otherwise}. \end{cases} $$

Let us check (3.8). Suppose the premise part of (3.8) holds for given \(t\in[0,1]\) and \(\omega\in\Omega\). Using the notation introduced in the previous paragraph (and suppressing the dependence on \(\omega\) and \(n\), as before), we can see that \(t>a\). From some \(n\) on, we have \(d+2^{-n}< t\) and \(\omega^{s}=\omega^{a+}\) for all \(s\in(a,d+2^{-n})\), and so the divergence of the series \(\sum_{n} e^{n}/n^{2}\) implies that \(\mathfrak{S}_{t}(\omega)=\infty\).  □

Remark 5.3

Let us check that the proof of Theorem 3.3 can be modified to prove the stronger statement in Remark 3.4. Notice that without loss of generality, we can replace the interval \([0,\ldots]\) in (5.4) by the two-element set \(\{0,\ldots\}\) consisting of its end-points (see the proof in Sect. 5.2); this ensures that the relative bets always satisfy \(H^{n}_{k}(\omega)\in\{0,1\}\). In addition to the stopping times (5.3) and bets (5.4), define stopping times \(\sigma^{n}_{k}\) in such a way that

  • \(\sigma^{n}_{k}(\omega^{a+})\in[\tau^{n}_{k}(\omega^{a+}),\tau^{n}_{k+1}(\omega^{a+})]\) and \(\sigma^{n}_{k}(\omega^{a+})\in(\tau^{n}_{k}(\omega^{a+}),\tau^{n}_{k+1}(\omega^{a+}))\) when \(\tau^{n}_{k}(\omega^{a+})<\tau^{n}_{k+1}(\omega^{a+})\);

  • \(\sigma^{n}_{k}(\omega^{a+})\) are so close to \(\tau^{n}_{k}(\omega^{a+})\) that (5.5) still holds when we replace the stopping times \(\tau^{n}_{k}\) by \(\sigma^{n}_{k}\) in the definition of \(G_{n}\) (with the relative bets corresponding to (5.4) unchanged);

  • for an arbitrary \(\omega\in\Omega\),

    $$ \sigma^{n}_{k}(\omega) := \textstyle\begin{cases} \sigma^{n}_{k}(\omega^{a+}) & \quad \text{if $\omega|_{[0,\tau^{n}_{k}(\omega^{a+})]}=\omega^{a+}|_{[0,\tau^{n}_{k}(\omega^{a+})]}$,}\\ 1 & \quad \text{otherwise} \end{cases} $$

    (cf. (5.6)).

After changing all the \(G_{n}\) in this way, we obtain a positive capital process that is strongly predictable and still satisfies (3.8).

5.4 Proof of Theorem 3.6

We prove (3.9) for a fixed \(t\in(0,1]\). Fix a strictly increasing sequence \(t_{1},t_{2},\ldots\) of numbers in the interval \((0,1)\) that converge to \(t\), \(t_{i}\uparrow t\) as \(i\to\infty\); set \(t_{0}:=0\). Let \(\Xi:=\{-1,1\}^{\infty}\). For each sequence \(\xi=(\xi_{1},\xi_{2},\ldots)\in\Xi\), define \(\omega_{\xi}\) as the càdlàg function on \([0,t)\) that is constant on each of the intervals \([t_{i-1},t_{i})\), \(i=1,2,\ldots\), and satisfies \(\omega_{\xi}(0):=1\) and

$$ \omega_{\xi}(t_{i}) := \omega_{\xi}(t_{i-1}) \bigg( 1 + \frac{\xi_{i}}{i+1} \bigg), \quad i=1,2,\ldots $$
(5.7)

We are particularly interested in \(\omega_{\xi}\) such that \(\lim_{i\to\infty}\omega_{\xi}(t_{i})\) exists in \((0,\infty)\); we can then extend \(\omega_{\xi}\) to an element \(\omega_{\xi\to}\) of \(\Omega\) that is constant over \([t,1]\). We call such \(\omega_{\xi}\) extendable; for them \(\omega_{\xi\to}\) exists and is an element of the set \(\{ \omega\in\Omega :I^{-}_{\omega}=\{t\}, I^{+}_{\omega}=\emptyset\}\) in (3.9).

Let us check that no positive capital process \(\mathfrak{S}\) grows by a factor of at least \(1+\epsilon\), where \(\epsilon>0\) is a given constant, on each extendable \(\omega_{\xi}\). Suppose, on the contrary, that a given \(\mathfrak{S}\) satisfies \(\mathfrak{S}_{0}=1\) and

$$ \mathfrak{S}_{t}(\omega_{\xi\to})\ge1+\epsilon $$
(5.8)

for all extendable \(\omega_{\xi}\). Consider any representation of \(\mathfrak{S}\) in the form (2.4).

This proof uses methods of measure-theoretic probability; our probability space is \(\Xi\) equipped with the canonical filtration \((\mathcal{F}_{i})\) and the power of the uniform probability measure on \(\{-1,1\}\); \(\mathcal{F}_{i}\) consists of all subsets of \(\Xi\) that are unions of cylinders \(\{(\xi_{1},\xi_{2},\ldots)\in\Xi :\xi_{1}=c_{1},\ldots,\xi_{i}=c_{i}\}\), and the measure of each such cylinder is \(2^{-i}\). This is a discrete probability space without any measurability issues (the simple idea of using such a “poor” probability space was used earlier in e.g. [9, Sect. 4.3]).

To simplify formulas, we use the notation \(\omega_{i}:=\omega_{\xi}(t_{i})\) and \(K_{i}:=\mathfrak{S}_{t_{i}}(\omega)\) for any \(\omega\in\Omega\) that agrees with \(\omega_{\xi}\) over the interval \([0,t_{i}]\) (there is no dependence on such \(\omega\), and the dependence on \(\xi\) is suppressed, as usual in measure-theoretic probability). According to (5.7), \(\omega_{i}\) is a martingale. Let us check that

$$ K_{i} = K_{i-1} + b_{i}(\omega_{i}-\omega_{i-1}), $$
(5.9)

where \(b_{i}\) is the total bet of all the \(G_{n}\) immediately before time \(t_{i}\) after observing \(\omega_{\xi}|_{[0,t_{i})}\) (the only issue in this check is convergence). Formally,

$$ b_{i} := \sum_{n=1}^{\infty} h^{n}_{k(n,i)}, $$
(5.10)

where

$$ k(n,i) := \max\{k:\tau^{n}_{k}< t_{i}\} $$

and \((\tau^{n}_{k})\) and \((h^{n}_{k})\) are the stopping times and bets of \(G_{n}\). The series (5.10) converges in \([0,\infty]\) as its terms are positive (to ensure the positivity of each ). Since the capital process \(\mathfrak{S}\) is positive and \(\omega\) can drop almost to 0 at any time, we have \(b_{i}\in[0,K_{i-1}/\omega_{i-1}]\) (this follows from the analogous inclusions for the component simple capital processes). We can see that (5.9) is indeed true. Let us define \(\alpha_{i}\in[0,1]\) by the condition

$$ b_{i}=\alpha_{i}K_{i-1}/\omega_{i-1}. $$
(5.11)

Being a martingale transform of \(\omega_{i}\), \(K_{i}\) is also a martingale. Combining (5.7), (5.9) and (5.11), we can see that the recurrences for the two martingales are

$$\begin{aligned} \omega_{i} &= \omega_{i-1} \left( 1 + \frac{\xi_{i}}{i+1} \right),\\ K_{i} &= K_{i-1} \left( 1 + \alpha_{i} \frac{\xi_{i}}{i+1} \right), \quad i=1,2,\ldots \end{aligned}$$

Let us check that \(\log\omega_{i}\) converges in ℝ for almost all \(\xi\) as \(i\to\infty\). This follows from Taylor’s formula

$$ \log\omega_{i} - \log\omega_{i-1} = \frac{\xi_{i}}{i+1} - \frac{1}{2} \frac{1}{(1+\theta_{i}\xi_{i}/(i+1))^{2}} \frac{1}{(i+1)^{2}} $$

(where \(\theta_{i}\in[0,1]\)), the almost sure convergence of \(\sum_{i} \xi_{i}/(i+1)\) (which follows from Kolmogorov’s two series theorem), and the convergence of \(\sum_{i} (i+1)^{-2}\). We can see that \(\omega_{\xi}\) is almost surely extendable. In the same way, we can demonstrate the convergence of \(\log K_{i}\) in ℝ, but we do not need it.

By Fatou’s lemma, we have, for any \(\xi\in\Xi\) with extendable \(\omega_{\xi}\),

Another application of Fatou’s lemma and the fact that almost all \(\omega_{\xi}\) are extendable show that the chain

$$ \mathbb {E}[\mathfrak{S}_{t} (\omega_{\xi\to})] \le \mathbb {E}\Big[\liminf_{i\to\infty} K_{i}\Big] \le \liminf_{i\to\infty} \mathbb {E}[ K_{i}] = 1 $$

is well defined and correct. This contradicts our assumption (5.8).  □

6 Conclusion

This paper shows that some assumptions of regularity (apart from being non-anticipative, such as universal measurability) should be imposed on continuous-time trading strategies even in game-theoretic probability. This is not a serious problem in applications since only computable trading strategies can be of practical interest, and computable trading strategies will be measurable under any reasonable computational model.

There are many interesting directions of further research, such as:

  • Is it possible to extend Theorems 2.2, 3.3 and 3.6 to the case where only the most recent past is known to the trader, as in [5, p. vii and Sect. 7.3] and [4, Sect. 5]?

  • Is it possible to extend Theorems 2.2, 3.3 and 3.6 to the case of the trader without a synchronized watch (see [5, Sect. 7.7] or [1])?

  • The construction in Sect. 5.4 produces a set \(E\subseteq\Omega\) (consisting of all \(\omega_{\xi\to}\) for \(\xi\in\Xi\) with extendable \(\omega_{\xi}\)) that satisfies both \(\overline {\mathbb {P}}(E)=1\) and \(\operatorname {var}(\log\omega)=\infty\) for all \(\omega\in E\). However, \(\operatorname {vi}(\log\omega)=1\) for all \(\omega\in E\) (see e.g. [?, Sect. 4.2] for the definition of the variation index \(\operatorname {vi}\)). Do \(E\subseteq\Omega\) with \(\overline {\mathbb {P}}(E)=1\) and \(\inf_{\omega\in E}\operatorname {vi}(\log\omega)>1\) exist?