Static hedging under maturity mismatch

Abstract

Can shorter maturity European options be statically hedged with longer maturity plain vanilla options? This problem appears, for example, when analysing options on forwards in relation to liquid options on the spot underlying. Under mild assumptions on the underlying security price process and the option’s payoff function, we show that approximate static hedges exist and we provide a recipe for constructing them. Examples illustrate the power of the hedge and its sensitivity to modelling assumptions. The results can be extended to formulating semi-static hedging strategies for discretely monitored path-dependent contingent claims.

Appendices

Appendix A: Application of the Nyquist–Shannon theorem

We apply the Nyquist–Shannon theorem (Whittaker–Shannon theorem, sampling theorem) to derive an approximate hedging strategy for a call option; see e.g. Sect. 2.2 of Bertero and Boccacci [9] for the theorem.

Theorem A.1

(Nyquist–Shannon theorem)

Let f be a bandlimited and square-integrable function with band interior to the interval [−Ω,Ω]. Then

$$ f(x) = \sum_{n=-\infty}^\infty f\left(n\frac{\pi}{\varOmega}\right) \operatorname{sinc}\left(\frac{\varOmega}{\pi} \left(x-n\frac{\pi }{\varOmega}\right)\right), $$

(A.1)

where $\operatorname{sinc} x= \frac{\sin(\pi x)}{\pi x}$.

In the following, we set τ:=π/Ω.

Let us first assume that $\tilde{p}$ satisfies the conditions of Lemma 3.1. Then, assuming that $\tilde{p}$ has bandwidth Ω and using the decomposition (A.1), we obtain, using that the Fourier transform (FT) is a linear transform,

$$\begin{aligned} \tilde{g} &= \mathfrak {F}^{-1}\bigg(\frac{\mathfrak {F}(\tilde{p})}{\mathfrak {F}(\gamma)}\bigg) = \mathfrak {F}^{-1}\bigg(\frac{\mathfrak {F}(\sum_{n=-\infty}^\infty\tilde{p}(n \tau) \operatorname{sinc}\left(1/\tau(x-n\tau)\right))}{\mathfrak {F}(\gamma)}\bigg)\\ &= \sum_{n=-\infty}^\infty \mathfrak {F}^{-1}\bigg(\frac{\tilde{p}(n\tau) \mathfrak {F}(\operatorname{sinc}\left(1/\tau (x-n\tau)\right))}{\mathfrak {F}(\gamma)}\bigg)\\ &= \sum_{n=-\infty}^\infty\tilde{p}(n\tau) \mathfrak {F}^{-1}\bigg(\frac{\mathfrak {F}(\operatorname{sinc}\left(1/\tau (x-n\tau)\right))}{\mathfrak {F}(\gamma)}\bigg). \end{aligned}$$

The FT of the sinc function is given by

$$ \mathfrak {F}(\operatorname{sinc})(\omega) = \mathbf{1}_{\{-\pi,\pi\}}(\omega). $$

By using that the FT has the properties

$$\begin{aligned} \mathfrak {F}\big(f(x-x_0)\big)(\omega) =& \mathrm{e}^{i\omega x_0} \mathfrak {F}(f)(\omega ), \quad x_0\in\mathbb{R},\\ \mathfrak {F}\big(f(a x)\big)(\omega) =& \frac{1}{a} \mathfrak {F}(f)\left(\frac{\omega}{a}\right), \quad a\neq0, \end{aligned}$$

we obtain

$$\begin{aligned} \mathfrak {F}\Big(\operatorname{sinc}\big(1/\tau(x-n\tau)\big)\Big)(\omega) =& \tau \mathfrak {F}\big(\operatorname{sinc}(x-n\tau)\big)\left(\omega\tau\right) \\ = &\tau\mathrm{e}^{i\omega\mathrm{n}\tau} \mathfrak {F}(\operatorname {sinc})(\omega\tau)\\ =& \tau\mathrm{e}^{i\omega n\tau} \mathbf{1}_{\{-\pi/\tau,\pi/\tau\} }(\omega). \end{aligned}$$

Continuing above, we have

$$\begin{aligned} \tilde{g}(x) =& \sum_{n=-\infty}^\infty\tilde{p}(n\tau) \mathfrak {F}^{-1}\bigg(\frac{\tau\mathrm{e}^{-i\omega n\tau \mathbf{1}_{\{-\pi/\tau,\pi/\tau\}}(\omega)}}{\mathfrak {F}(\gamma)(\omega )}\bigg)(x)\\ =& \sum_{n=-\infty}^\infty\tilde{p}(n\tau) \frac{1}{2\pi} \int_{-\pi/\tau}^{\pi/\tau} \frac{\tau\mathrm {e}^{i\omega n \tau} }{\mathfrak {F}(\gamma)(\omega)} \mathrm{e}^{-i\omega x}\, \mathrm {d}\omega, \end{aligned}$$

which can be calculated numerically, using (2.3) and (2.4) to calculate $\mathfrak {F}(\gamma)$.

If the payoff function $\tilde{p}$ is not bandlimited, one can approximate the hedging strategy by forcing $\tilde{p}$ to be bandlimited through an appropriate choice of Ω.

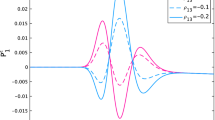
The example in Fig. 1 is parameterised as follows. The payoff to be hedged (resp., replicated) is a call option with strike K=0.9 maturing at 0.5, that is, the payoff is $p(x)=\left(\mathrm{e}^{x}-0.9\right)^{+}$, and $\tilde{p}(x)=\mathrm {e}^{-(1+\alpha) x} (\mathrm{e}^{x}-0.9)^{+}$. We choose α=1. The hedging instruments are call options maturing at time 1. We assume a BSM model for the underlying asset price process, with volatility σ=0.16836.

In order to apply the Nyquist–Shannon theorem, we choose Ω=16 so that τ=π/16, and furthermore, we let the sum in (A.1) range from −30 to 30.

Appendix B: Market data

Table 4 Implied volatilities of options on the S&P 500 index on 15 May 2013. Source, Bloomberg

Table 5 Call prices derived from implied volatilities, assuming S ₀=1 and r=q=0

Fig. 7

Calibration results. Circles are market implied volatilities of call options for several maturities and strikes, crosses are corresponding model implied volatilities. (Top) BSM; (middle) CGMY; (bottom) Heston