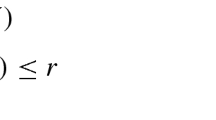Multi-portfolio time consistency for set-valued convex and coherent risk measures

Abstract

Equivalent characterizations of multi-portfolio time consistency are deduced for closed convex and coherent set-valued risk measures on $L^{p}({\varOmega,\mathcal{F},\mathbb{P}; \mathbb{R}^{d}})$ with image space in the power set of $L^{p}({\varOmega,\mathcal{F}_{t},\mathbb{P}; \mathbb{R}^{d}})$. In the convex case, multi-portfolio time consistency is equivalent to a cocycle condition on the sum of minimal penalty functions. In the coherent case, multi-portfolio time consistency is equivalent to a generalized version of stability of the dual variables. As examples, the set-valued entropic risk measure with constant risk aversion coefficient is shown to satisfy the cocycle condition for its minimal penalty functions; the set of superhedging portfolios is shown to have in markets with proportional transaction costs the stability property and to satisfy in markets with convex transaction costs the composed cocycle condition; and a multi-portfolio time-consistent version of the set-valued average value at risk, the composed AV@R, is given, and its dual representation deduced.

Appendices

Appendix A: On the relationship of dual variables at different times

In considering how closed convex (and coherent) risk measures relate through time, we must consider how the sets of dual variables relate. In the following lemma, we provide such a relationship between elements of $\mathcal{W}_{t}$ and elements of $\mathcal{W}_{s}$ for any times t,s with t≤s. In fact, we define a mapping on $\mathcal{W}_{t}$ that is equivalent (in the set-valued replacement for continuous linear functionals) in $\mathcal{W} _{s}$. In the scalar framework, this type of property is not needed since the set $\mathcal{W}_{t}$ can be simplified to any $\mathbb{Q}\ll \mathbb{P}$ for any time t (where $\mathbb{Q}= \mathbb{P}|_{\mathcal{F}_{t}}$).

Lemma A.1

For any choice of times t and s>t, it follows that

• (1) $\{(\mathbb{Q}^{s},w_{t}^{s}(\mathbb{Q},w)): (\mathbb{Q},w) \in \mathcal{W}_{t}\} \subseteq\mathcal{W}_{s}$.

• (2) For every $(\mathbb{R},v) \in\mathcal{W}_{s}$, there exists $(\mathbb{Q},w) \in\mathcal{W}_{t}$ with $F_{(\mathbb{R},v)}^{s} = F_{(\mathbb {Q}^{s},w_{t}^{s}(\mathbb{Q},w))}^{s}$.

Proof

(1) We have $\{(\mathbb{Q}^{s},w_{t}^{s}(\mathbb{Q},w)): (\mathbb{Q},w) \in\mathcal{W}_{t}\} \subseteq\mathcal{W}_{s}$ if and only if for every pair $(\mathbb {Q},w) \in\mathcal{W}_{t}$, it follows that $w_{t}^{s}(\mathbb{Q},w) \in M_{s,+}^{+} \backslash M_{s}^{\perp}$ and $w_{s}^{T}(\mathbb{Q}^{s},w_{t}^{s}(\mathbb{Q},w)) \in L^{q}_{+}$. So let $(\mathbb{Q} ,w) \in\mathcal{W}_{t}$. To show that $w_{t}^{s}(\mathbb{Q},w) \in M_{s,+}^{+} \backslash M_{s}^{\perp}$, let m _s ∈M _s,+. Then

$$\mathbb{E}[w_t^{s}(\mathbb{Q},w)^{\mathsf{T}} m_{s}] = \mathbb {E}\big[w^{\mathsf{T}} \mathbb{E}^{\mathbb{Q}}[m_{s} | \mathcal {F}_{t}]\big] \geq0 $$

since $\mathbb{E}^{\mathbb{Q}}[m_{s}|\mathcal{F}_{t}] \in M_{t,+}$ by $M_{t} \supseteq M_{s} \cap L^{p}_{t}$ and $M_{s} = L^{p}_{s}(M)$. Since $(\mathbb{Q},w) \in \mathcal{W}_{t}$, in particular, since $w\notin M_{t}^{\perp}$, there exists m _t ∈M _t ⊆M _s with $\mathbb{E}[w^{\mathsf{T}} m_{t}] \neq0$. Then

$$\mathbb{E}[w_t^{s}(\mathbb{Q},w)^{\mathsf{T}} m_t] = \mathbb{E}\big[w^{\mathsf{T}} \mathbb{E}^{\mathbb{Q}}[m_t | \mathcal{F}_{t}]\big] = \mathbb{E}[w^{\mathsf{T}} m_t] \neq0. $$

Finally, $w_{s}^{T}(\mathbb{Q}^{s},w_{t}^{s}(\mathbb{Q},w)) = w_{t}^{T}(\mathbb{Q},w) \in L^{q}_{+}$ by $(\mathbb{Q},w) \in\mathcal{W}_{t}$.

(2) By Lemma 4.5 in [17], for every $(\mathbb{R},v) \in \mathcal{W}_{s}$, there exists a $(Y,\bar{v})$ such that $Y \in L^{q}_{+}$ and $\bar{v} \in(\mathbb{E}[Y| \mathcal{F}_{s}] + M_{s}^{\perp}) \backslash M_{s}^{\perp}$ with $F_{(\mathbb{R},v)}^{s} = \tilde{F}_{(Y,\bar{v})}^{s}$. Moreover, for every $(Y,\bar{v})$ with $Y \in L^{q}_{+}$ and $\bar{v} \in(\mathbb{E}[Y| \mathcal{F}_{s}] + M_{s}^{\perp}) \backslash M_{s}^{\perp}$, there exists $(\hat{\mathbb{Q}},w_{s})\in\mathcal{W}_{s}$ with $\tilde{F}_{(Y,\bar{v})}^{s} = F_{(\hat{\mathbb{Q}},w_{s})}^{s}$ by setting $w_{s} = \mathbb{E}[Y | \mathcal{F}_{s}]$ and

$$\bar{\xi}_{r,s}^i[\omega] = \begin{cases}\frac{\mathbb{E}[Y_i | \mathcal{F}_{s}](\omega )}{\mathbb{E}[Y_i | \mathcal{F}_{r}](\omega)} &\text{if } \mathbb{E}[Y_i | \mathcal{F}_{r}](\omega) > 0\\ 1 &\text{else} \end{cases} $$

for every ω∈Ω, and $\frac{d\hat{\mathbb {Q}}_{i}}{d\mathbb{P}} = \bar{\xi }_{s,T}^{i}$. Define $\mathbb{Q} \in\mathcal{M}$ by $\frac{d\mathbb {Q}_{i}}{d\mathbb{P}}= \bar{\xi}_{t,T}^{i}$; thus, $\mathbb{Q}^{s} = \hat{\mathbb{Q}}$. Therefore, it remains to show that there exists a $w_{t} \in L^{q}_{t}$ such that $w_{s} = w_{t}^{s}(\mathbb {Q},w_{t})$ and $(\mathbb{Q} ,w_{t}) \in\mathcal{W}_{t}$. Let $w_{t} :=\mathbb{E}[w_{s}| \mathcal {F}_{t}] =\mathbb{E}[Y| \mathcal{F}_{t}]$.

We want to show $w_{s} = w_{t}^{s}(\mathbb{Q},w_{t})$, that is, $(w_{s})_{i}(\omega) = (w_{t})_{i}(\omega) \bar{\xi}_{t,s}^{i}(\omega)$ for every index i=1,…,d and almost every ω∈Ω. We know that if $\mathbb{E} [Y_{i} | \mathcal{F}_{t}] (\omega) = 0$, then (w _t ) _i (ω)=0 and (w _s ) _i (ω)=0, and thus $(w_{s})_{i}(\omega) = (w_{t}^{s}(\mathbb{Q} ,w_{t}))_{i}[\omega]$. If $\mathbb{E}[Y_{i}| \mathcal{F}_{t}] (\omega) > 0$, then

$$\begin{aligned} w_t^{s}(\mathbb{Q},w_t)_i[\omega] &= \mathbb{E}[Y_i | \mathcal {F}_{t}](\omega) \frac{\mathbb{E}[Y_i | \mathcal{F}_{s}](\omega )}{\mathbb{E}[Y_i | \mathcal{F}_{t}](\omega)}= \mathbb{E}[Y_i | \mathcal{F}_{s}](\omega) = (w_{s})_i(\omega). \end{aligned}$$

Now we show that $(\mathbb{Q},w_{t}) \in\mathcal{W}_{t}$. To show first that $w_{t} \in M_{t,+}^{+} \backslash M_{t}^{\perp}$, let m _t ∈M _t,+; then $\mathbb{E}[w_{t}^{\mathsf{T}} m_{t}] = \mathbb{E}[\mathbb {E}[w_{s}| \mathcal{F}_{t}] m_{t}^{\mathsf{T}}] = \mathbb {E}[w_{s}^{\mathsf{T}} m_{t}] \geq0$ due to the tower property, M _t,+⊆M _s,+ and $w_{s}\in M_{s,+}^{+}$. Since $(\mathbb{Q} ^{s},w_{s}) \in\mathcal{W}_{s}$, in particular, since $w_{s}\notin M_{s}^{\perp}$, there exists m _s ∈M _s with $\mathbb{E}[w_{s}^{\mathsf{T}} m_{s}] \neq0$. Then $\mathbb {E}^{\mathbb{Q}}[m_{s} | \mathcal{F}_{t}] \in M_{t}$ by $M_{t} \supseteq M_{s} \cap L^{p}_{t}$ and $M_{s} = L^{p}_{s}(M)$. Hence,

$$\mathbb{E}\big[w_t^{\mathsf{T}} \mathbb{E}^\mathbb{Q}[m_{s}| \mathcal{F}_t]\big] = \mathbb{E}[w_t^{s}(\mathbb{Q},w_t)^{\mathsf{T}} m_{s}] = \mathbb{E}[w_{s}^{\mathsf{T}} m_{s}] \neq0. $$

Finally, $w_{t}^{T}(\mathbb{Q},w_{t}) = w_{s}^{T}(\mathbb {Q}^{s},w_{t}^{s}(\mathbb{Q},w_{t})) = w_{s}^{T}(\hat{\mathbb{Q}},w_{s}) \in L^{q}_{+}$. □

The following corollary of Lemma A.1 uses the above result applied to penalty functions instead of the functionals F _(⋅,⋅)[⋅].

Corollary A.2

For any $(\mathbb{R},v) \in\mathcal{W}_{s}$, there exists $(\mathbb {Q},w) \in\mathcal{W}_{t}$ such that

$$-\beta_{s}^{\min}(\mathbb{R},v) = -\beta_{s}^{\min}\big(\mathbb {Q}^{s},w_t^{s}(\mathbb{Q},w)\big) $$

for any times 0≤t<s≤T.

Proof

We have

$$\begin{aligned} -\beta_{s}^{\min}(\mathbb{R},v) & = \operatorname{cl}\bigcup_{Z \in A_{s}}\!\! F_{(\mathbb{R} ,v)}^{s}[Z] \\ &= \operatorname{cl}\bigcup_{Z \in A_{s}}\!\! F_{(\mathbb {Q}^s,w_t^{s}(\mathbb{Q},w))}^{s}[Z] = -\beta_{s}^{\min}\big(\mathbb{Q}^{s},w_t^{s}(\mathbb{Q},w)\big), \end{aligned}$$

where the second equality is a result of Lemma A.1. □

Lemma A.1 and Corollary A.2 show that for any times t≤s and for a given penalty function $-\beta_{s}^{\min}$, the set of dual variables $\{(\mathbb{Q} ^{s},w_{t}^{s}(\mathbb{Q},w)): (\mathbb{Q},w) \in\mathcal{W}_{t}\}$ defines the same closed and convex risk measure at time s as the set of dual variables $\mathcal{W} _{s}$, that is,

$$\begin{aligned} R_{s}(X)& = \bigcap_{(\mathbb{Q},w) \in\mathcal{W}_t} \Big(-\beta _{s}^{\min}\big(\mathbb{Q} ^{s},w_t^{s}(\mathbb{Q},w)\big) + \mathbb{E}^{\mathbb{Q}}[-X | \mathcal{F}_{s}] + G_{s}\big(w_t^{s}(\mathbb{Q} ,w)\big)\Big) \cap M_{s}. \end{aligned}$$

The following lemma about the expectation of minimal penalty functions is an extension of Lemma 2.6 in [19]. As a set-valued operation, this theorem gives a set-valued version of when the conditional expectation of an infimum is equivalent to the infimum of the conditional expectation. The proof of the lemma is a simplified version of the proof of Lemma 2.6 in [19] since the sets $\{\mathbb {E}^{\mathbb{Q}}[X| \mathcal{F} _{t}] + G_{t}(w)\}$ are shifted half-spaces for any X∈A _t and a fixed $(\mathbb{Q},w) \in\mathcal{W}_{t}$ and thus are completely ordered, in contrast to the scalar case, where the points $\mathbb{E}^{\mathbb{Q}}[X| \mathcal{F}_{t}]$ under consideration are not completely ordered.

Lemma A.3

For any times 0≤t<s≤T and if R _t is a closed convex risk measure, then for any $(\mathbb{Q},w) \in\mathcal{W}_{t}$, it follows that

$$\mathbb{E}^\mathbb{Q}\big[-\beta_{s}^{\min}\big(\mathbb {Q}^{s},w_t^{s}(\mathbb{Q},w)\big)\big| \mathcal{F}_t\big]= \operatorname{cl}\bigcup_{X \in A_{s}} \big(\mathbb{E}^{\mathbb {Q}}[X | \mathcal{F}_{t}] + G_t(w)\big) \cap M_t. $$

Proof

Let $(\mathbb{Q},w) \in\mathcal{W}_{t}$. Then by Lemma A.1, $(\mathbb{Q} ^{s},w_{t}^{s}(\mathbb{Q},w))\in\mathcal{W}_{s}$. It holds

$$\begin{aligned} &-\beta_{s}^{\min} \big(\mathbb{Q}^{s},w_t^{s}(\mathbb{Q},w)\big) \\ &\quad= \operatorname{cl}\bigcup_{X \in A_{s}} \Big(\mathbb{E}^{\mathbb {Q}}[X | \mathcal{F}_{s}] + G_{s}\big(w_t^{s}(\mathbb{Q} ,w)\big)\Big) \cap M_{s} \\ &\quad= \operatorname{cl}\bigcup_{X \in A_{s}}\big\{ u \in M_{s}: \mathbb {E}\big[w_t^{s}(\mathbb{Q} ,w)^{\mathsf{T}} \mathbb{E}^{\mathbb {Q}}[X | \mathcal{F}_{s}]\big] \leq\mathbb{E}[w_t^{s}(\mathbb {Q},w)^{\mathsf{T}}u]\big\} \\ &\quad= \operatorname{cl}\bigcup_{X \in A_{s}} \big\{ u \in M_{s}: \mathbb {E}\big[w^{\mathsf{T}}\mathbb{E}^{\mathbb{Q}}[X | \mathcal {F}_{t}]\big] \leq\mathbb{E}\big[w^{\mathsf{T}}\mathbb {E}^{\mathbb{Q}}[u | \mathcal{F}_{t}]\big]\big\} \\ &\quad= \Big\{ u \in M_{s}: \inf_{X \in A_{s}} \mathbb{E}\big[w^{\mathsf {T}}\mathbb{E}^{\mathbb{Q}}[X | \mathcal{F}_{t}]\big] \leq\mathbb{E}\big[w^{\mathsf{T}}\mathbb{E}^{\mathbb{Q}}[u | \mathcal{F}_{t}]\big]\Big\} . \end{aligned}$$

Taking the conditional expectation on both sides yields

$$\begin{aligned} &\mathbb{E}^\mathbb{Q}\big[-\beta_{s}^{\min}\big(\mathbb {Q}^{s},w_t^{s}(\mathbb{Q},w)\big)\big|\mathcal{F}_t\big] \\ &\quad= \Big\{ \mathbb{E}^{\mathbb{Q}}[u | \mathcal{F}_{t}]: u \in M_{s},\inf_{X \in A_{s}} \mathbb{E}\big[w^{\mathsf{T}}\mathbb {E}^{\mathbb{Q}}[X | \mathcal{F}_{t}]\big] \leq\mathbb{E}\big[w^{\mathsf{T}}\mathbb{E}^{\mathbb{Q}}[u | \mathcal{F}_{t}]\big]\Big\} \\ &\quad=\Big\{ u \in M_t:\inf_{X \in A_{s}} \mathbb{E}\big[w^{\mathsf {T}}\mathbb{E}^{\mathbb{Q}}[X | \mathcal{F}_{t}]\big] \leq\mathbb{E}[w^{\mathsf{T}}u]\Big\} \\ &\quad= \operatorname{cl}\bigcup_{X \in A_{s}} \big(\mathbb{E}^{\mathbb {Q}}[X | \mathcal{F}_{t}] + G_t(w)\big) \cap M_t. \end{aligned}$$

 □

One can now show that the $\mathbb{Q}$-conditional expectation (at time t) of the positive half-space defined by $w_{t}^{s}(\mathbb{Q},w)$ is given by the positive half-space defined by w.

Corollary A.4

Let 0≤t<s≤T, $\mathbb{Q}\in\mathcal{M}$ where $\mathbb {Q}= \mathbb{P}|_{\mathcal{F}_{t}}$, and $w \in L^{q}_{t}$. Then

$$\mathbb{E}^{\mathbb{Q}}[G_{s}\big(w_t^{s}(\mathbb{Q},w)\big) | \mathcal{F}_{t}] = G_t(w). $$

Proof

This is a special case of Lemma A.3, obtained for $M = \mathbb{R}^{d}$ and $A_{s} = L^{p}_{+}$. □

We conclude our discussion on how dual variables across time are related by considering the conditional expectations of the $\alpha _{s}^{\min}$ and Γ _s functions used in the dual representation of conditionally convex risk measures (see Corollary 2.4).

Lemma A.5

For any times 0≤t<s≤T and if R _t is a closed conditionally convex risk measure, then for any $(\mathbb{Q},w) \in \mathcal{W}_{t}$ with $\mathbb{Q}\in\mathcal{M}^{e}$, it follows that

$$\operatorname{cl}\mathbb{E}^\mathbb{Q}\big[-\alpha_s^{\min}\big(\mathbb{Q}^s,w_t^s(\mathbb{Q},w)\big)\big|\mathcal{F}_t\big] = \operatorname{cl}\bigcup_{Z \in A_s} \big(\mathbb{E}^{\mathbb {Q}}[Z | \mathcal{F}_{t}] + \varGamma_t(w)\big) \cap M_t. $$

Proof

“⊆”: We have

$$\begin{aligned} &\mathbb{E}^\mathbb{Q}\big[-\alpha_s^{\min}\big(\mathbb {Q}^s,w_t^s(\mathbb{Q},w)\big)\big| \mathcal{F}_t\big] \\ &\quad =\Big\{ \mathbb{E}^{\mathbb{Q}}[u_s | \mathcal{F}_{t}]: u_s \in M_s, w_t^s(\mathbb{Q},w)^{\mathsf{T}}u_s \geq\mathop{\mathrm{ess\,inf}} _{Z \in A_s} w_t^s(\mathbb{Q},w)^{\mathsf{T}}\mathbb{E}^{\mathbb {Q}}[Z | \mathcal{F}_{s}] \ \mathbb{P}\text{-}\text{a.s.}\Big\} \\ &\quad \subseteq\Big\{ \mathbb{E}^{\mathbb{Q}}[u_s | \mathcal{F}_{t}]: u_s \in M_s, \mathbb{E}[w_t^s(\mathbb{Q} ,w)^{\mathsf {T}}u_s|\mathcal{F}_t] \\ &\phantom{\quad\subseteq\Big\{ \mathbb{E}^{\mathbb{Q}}[u_s | \mathcal {F}_{t}]: u_s \in M_s,} \geq\mathbb{E}\big[\mathop{\mathrm{ess\,inf}}_{Z \in A_s} w_t^s(\mathbb{Q},w)^{\mathsf {T}}\mathbb{E}^{\mathbb{Q}}[Z | \mathcal{F}_{s}]\big|\mathcal {F}_t\big] \ \mathbb{P}\text{-}\text{a.s.} \Big\} \\ &\quad =\Big\{ u_t \in M_t: w^{\mathsf{T}}u_t \geq\mathop{\mathrm{ess\, inf}}_{Z \in A_s} w^{\mathsf{T}}\mathbb{E}^{\mathbb{Q}}[Z | \mathcal {F}_{t}] \ \mathbb{P}\text{-}\text{a.s.}\Big\} \\ &\quad = \operatorname{cl}\bigcup_{Z \in A_s}\big(\mathbb{E}^{\mathbb {Q}}[Z | \mathcal{F}_{t}] + \varGamma_t(w)\big) \cap M_t, \end{aligned}$$

and since $\operatorname{cl}\bigcup_{Z \in A_{s}}(\mathbb{E}^{\mathbb{Q}}[ Z| \mathcal{F}_{t}] + \varGamma_{t}(w) \cap M_{t})$ is closed, this direction is shown.

“⊇”: Consider a point $u \in\operatorname{cl}\bigcup_{Z \in A_{s}} (\mathbb{E}^{\mathbb{Q}} [ Z| \mathcal{F}_{t}] + \varGamma_{t}(w)) \cap M_{t}$ and further assume that $u \notin \operatorname{cl}(\mathbb{E}^{\mathbb{Q}}[-\alpha_{s}^{\min}(\mathbb {Q}^{s},w_{t}^{s}(\mathbb{Q},w))|\mathcal{F}_{t}])$. Since the latter set is closed and convex, we can separate it from {u} by some $v \in L^{q}_{t}$, that is, let $v \in L^{q}_{t}$ be such that

$$\begin{aligned} \mathbb{E}[v^{\mathsf{T}}u] &< \inf_{z_t \in\operatorname {cl}\mathbb{E}^\mathbb{Q}[-\alpha_s^{\min}(\mathbb{Q} ^s,w_t^s(\mathbb{Q},w))| \mathcal{F}_t]}\mathbb{E}[v^{\mathsf {T}}z_t]\\ &= \inf_{z_s \in-\alpha_s^{\min}(\mathbb{Q}^s,w_t^s(\mathbb {Q},w))} \mathbb{E}[w_t^s(\mathbb{Q},v)^{\mathsf{T}}z_s]\\ &= \mathbb{E}\Big[\mathop{\mathrm{ess\,inf}}_{z_s \in-\alpha _s^{\min}(\mathbb{Q}^s,w_t^s(\mathbb{Q},w))} w_t^s(\mathbb {Q},v)^{\mathsf{T}}z_s\Big]. \end{aligned}$$

Note that in the last equality above, we can interchange the expectation and infimum since $-\alpha_{s}^{\min}(\mathbb {Q}^{s},w_{t}^{s}(\mathbb{Q},w))$ is decomposable. By construction,

$$\begin{aligned} \mathop{\mathrm{ess\,inf}}_{z_s \in-\alpha_s^{\min}(\mathbb {Q}^s,w_t^s(\mathbb{Q},w))} w_t^s(\mathbb{Q} ,v)^{\mathsf{T}}z_s = \begin{cases} \mathop{\mathrm{ess\,inf}}_{Z \in A_s} w_t^s(\mathbb {Q},v)^{\mathsf{T}}\mathbb{E}^{\mathbb{Q}}[Z | \mathcal{F}_{s}] & \text{on } D,\\ -\infty&\text{on } D^c, \end{cases} \end{aligned}$$

where $D = \{\omega\in\varOmega: G_{0}(w_{t}^{s}(\mathbb{Q},v)[\omega]) = G_{0}(w_{t}^{s}(\mathbb{Q},w)[\omega])\}$. Since $\mathbb{Q}\in\mathcal{M}^{e}$, we have $G_{0}(w_{t}^{s}(\mathbb {Q},v)[\omega]) = G_{0}(w_{t}^{s}(\mathbb{Q},w)[\omega])$ if and only if v(ω)=λ(ω)w(ω) for some $\lambda\in L^{0}_{t}(\mathbb{R}_{++})$ (with $\lambda w \in L^{q}_{t}$). So

$$\mathbb{E}\Big[\mathop{\mathrm{ess\,inf}}_{z_s \in-\alpha_s^{\min }(\mathbb{Q}^s,w_t^s(\mathbb{Q},w))} w_t^s(\mathbb{Q},v)^{\mathsf {T}}z_s\Big] > -\infty $$

if and only if

$$\begin{aligned} \mathbb{E}\Big[\mathop{\mathrm{ess\,inf}}_{z_s \in-\alpha_s^{\min }(\mathbb{Q}^s,w_t^s(\mathbb{Q},w))} w_t^s(\mathbb{Q},v)^{\mathsf {T}}z_s\Big] &=\mathbb{E}\Big[\lambda\mathop{\mathrm{ess\, inf}}_{z_s \in-\alpha_s^{\min }(\mathbb{Q}^s,w_t^s(\mathbb{Q},w))} w_t^s(\mathbb{Q},w)^{\mathsf {T}}z_s\Big]\\ &= \mathbb{E}\Big[\lambda\mathop{\mathrm{ess\,inf}}_{Z \in A_s} w^{\mathsf{T}}\mathbb{E}^{\mathbb{Q}}[Z | \mathcal{F}_{t}]\Big]. \end{aligned}$$

But this implies $\mathbb{E}[\lambda w^{\mathsf{T}}u] < \mathbb {E}[\lambda\mathop{\mathrm{ess\,inf}}_{Z \in A_{s}} w^{\mathsf{T}} \mathbb{E}^{\mathbb{Q}}[Z |\mathcal{F}_{t}]]$, which is a contradiction to $u \in\operatorname{cl}\bigcup_{Z \in A_{s}} (\mathbb{E}^{\mathbb{Q}}[Z | \mathcal{F}_{t}] + \varGamma_{t}(w)) \cap M_{t}$. □

Corollary A.6

Let 0≤t<s≤T, and $(\mathbb{Q},w) \in\mathcal{W}_{t}$ with $\mathbb{Q}\in\mathcal {M}^{e}$. It follows that

$$\operatorname{cl}\mathbb{E}^{\mathbb{Q}}[\varGamma_{s}\big(w_t^{s}(\mathbb{Q},w)\big) | \mathcal{F}_{t}] = \varGamma_t(w). $$

Proof

This is a special case of Lemma A.5, obtained for $M = \mathbb{R}^{d}$ and $A_{s} = L^{p}_{+}$. □

Appendix B: On the sum of closed acceptance sets and convex upper continuity

When considering multi-portfolio time consistency for closed risk measures, we need to guarantee that the composed risk measures are closed, or else the recursive form would fail to hold. In particular, this would be true if the sum of acceptance sets are themselves closed. We demonstrate the closedness of the sum of convex acceptance sets when the associated dynamic risk measure is convex upper continuous.

Recall that a function $F: X \to\mathcal{P}(Y;C)$ is convex upper continuous (c.u.c.) if F ⁻¹(D):={x∈X:F(x)∩D≠∅} is closed for any closed set $D \in\mathcal{G}(Y;-C)$.

Proposition B.1

Let $F: X \to\mathcal{P}(Y;C_{Y})$ and $G: Y \to\mathcal{P}(Z;C_{Z})$. If F,G are c.u.c. and G is convex and −C _Y -monotone, then $H: X \to \mathcal{P}(Z;C_{Z})$ defined by the composition H(x):=⋃ _y∈F(x) G(y) for any x∈X is c.u.c.

Proof

For any D∈2^Z, we have

$$\begin{aligned} H^{-1}(D) &= \left\{x \in X: H(x) \cap D \neq\emptyset\right\} = \bigg\{ x \in X: \bigcup_{y \in F(x)} G(y) \cap D \neq\emptyset\bigg\} \\ &= \left\{x \in X: \exists y \in F(x), G(y) \cap D \neq\emptyset \right\} =\{ x \in X: F(x) \cap G^{-1}(D) \neq\emptyset\}\\ &= F^{-1}\big(G^{-1}(D)\big). \end{aligned}$$

Additionally, if $D \in\mathcal{G}(Z;-C_{Z})$, then G ⁻¹(D) is closed; if x,y∈G ⁻¹(D) and λ∈[0,1], then G(λx+(1−λ)y)∩D≠∅; and if x,y∈Y are such that x−y∈C _Y with x∈G ⁻¹(D), then y∈G ⁻¹(D). This implies that $G^{-1}(D) \in\mathcal{G}(Y,-C_{Y})$, and thus F ⁻¹(G ⁻¹(D)) is closed for any $D \in\mathcal{G}(Z;-C_{Z})$. □

Lemma B.2

Let M _t (M _s ) be the set of eligible portfolios at time t (s) (a closed linear subspace of $L^{p}_{t}$ $(L^{p}_{s})$). Let R _t,s be a c.u.c. convex stepped risk measure from t to s, and R _s a c.u.c. risk measure at time s. Then A _t,s +A _s is closed.

Proof

By Lemma 3.6(i) in [17], $A_{t,s} + A_{s} = \{X \in L^{p}: 0 \in\bigcup_{Z \in R_{s}(X)} R_{t,s}(-Z)\}$. Indeed,

$$\begin{aligned} X\in A_{t,s} + A_{s} &\Longleftrightarrow-R_{s}(X)\cap A_t\neq \emptyset \\ &\Longleftrightarrow\exists Z\in R_{s}(X) \quad\mbox{with } -Z\in A_t \ (\mbox{i.e., } 0\in R_t(-Z) =R_{t,s}(-Z))\\ &\Longleftrightarrow0 \in\bigcup_{Z \in R_{s}(X)}R_{t,s}(-Z). \end{aligned}$$

Let $\tilde{R}_{t}(X) := \bigcup_{Z \in R_{s}(X)} R_{t,s}(-Z)$; then $A_{t,s} + A_{s} = \tilde{R}_{t}^{-1}(M_{t,-})$. By Proposition B.1, $\tilde {R}_{t}$ is c.u.c., and thus $\tilde{R}_{t}^{-1}(M_{t,-})$ is closed. □

Remark B.3

Let R _t be a conditional risk measure at time t, and $R_{t,s} := R_{t}|_{M_{s}}$ the stepped risk measure from t to s associated with R _t . If R _t is c.u.c., then trivially R _t,s is c.u.c.

When applying Lemma 3.1 to the proof of Theorem 3.2 and Corollary 3.3, we need not only the sum of closed convex acceptance sets to be closed, but also to be a (closed) convex acceptance set itself. This is given in the following lemma.

Lemma B.4

Let $(A_{t})_{t=0}^{T}$ be a sequence of closed convex normalized acceptance sets. Assume that A _t,t+1+A _t+1⊆A _t . Then A _t,t+1+A _t+1 is a convex acceptance set at time t. Furthermore, if $(A_{t})_{t=0}^{T}$ is c.u.c., then A _t,t+1+A _t+1 is closed.

Proof

Let us check the properties of acceptance sets (see Definition 2.2).

• (1) A _t,t+1+A _t+1⊆L ^p trivially.

• (2) M _t ∩(A _t,t+1+A _t+1)⊇M _t ∩M _t+1∩A _t ≠∅ since 0∈A _t+1 (since A _t+1 is closed and normalized), M _t ∩A _t ≠∅, and M _t ∩M _t+1=M _t .

• (3) M _t ∩(L ^p∖{A _t,t+1+A _t+1})⊇M _t ∩(L ^p∖A _t )≠∅ by A _t,t+1+A _t+1⊆A _t .

• (4) $A_{t,t+1} + A_{t+1} + L^{p}_{+} \subseteq A_{t,t+1} + A_{t+1}$ trivially.

Moreover, A _t,t+1+A _t+1 is convex since both A _t,t+1 and A _t+1 are convex, and A _t,t+1+A _t+1 is closed by Lemma B.2 if $(A_{t})_{t=0}^{T}$ is c.u.c. □

We finish this section by considering a class of risk measures that are point plus cone and show that these risk measures will be c.u.c. under p=+∞ and the weak* topology.

Proposition B.5

Consider the full eligible space $M_{t} = L^{\infty}_{t}$ and let p=+∞. Let $R_{t}(X) := \rho_{t}(X) + L^{\infty}_{t,+}$ for some vector ρ _t of scalar conditional risk measures, that is, ρ _t (X):=((ρ _t )₁(X ₁),…,(ρ _t ) _d (X _d ))^T. If ρ _t is (componentwise) lower semicontinuous and convex, then R _t is c.u.c.

Proof

Recall from the scalar literature that $\rho_{t}(X) \in L^{\infty}_{t}$ for any X∈L ^∞. Consider any set $D \in\mathcal{G}(L^{\infty }_{t};L^{\infty}_{t,-})$. It follows that

$$\begin{aligned} R_t^{-1}(D) &= \{X \in L^{\infty}: R_t(X) \cap D \neq\emptyset\}\\ &= \{X \in L^{\infty}: \exists\hat{d} \in D, \rho_t(X) \preceq \hat{d}\}\\ &= \{X \in L^{\infty}: \exists\hat{d} \in D, \rho_t(X) = \hat {d} \ \mathbb{P}\text{-}\text{a.s.}\}\\ &= \{X \in L^{\infty}: \rho_t(X) \in D\} = \rho_t^{-1}(D). \end{aligned}$$

Therefore, we wish to show that $\rho_{t}^{-1}(D)$ is weak* closed. From convexity of ρ _t it immediately follows that $\rho_{t}^{-1}(D)$ is convex; therefore, $\rho_{t}^{-1}(D)$ is weak* closed if and only if $\rho _{t}^{-1}(D) \cap\{Z \in L^{\infty}: \|Z\|_{\infty} \leq k\}$ is closed in probability for every k, by [34, Proposition 5.5.1]. Pick any k≥0 and consider

$$(Z_n)_{n \in\mathbb{N}} \subseteq\rho_t^{-1}(D) \cap\{Z \in L^{\infty}: \|Z\| _{\infty} \leq k\} $$

with $Z_{n} \to\bar{Z}$ in probability (and thus $\bar{Z} \in\{Z \in L^{\infty}: \|Z\|_{\infty} \leq k\}$). Note that convergence in probability implies that there exists a subsequence that converges almost surely; we denote this subsequence by $(Z_{n_{m}})_{m \in\mathbb {N}} \to \bar{Z}$. For any sequence of random vectors (Y _n )⊆L ^∞, define lim inf _n→∞ ρ _t (Y _n )=lim _n→∞inf _m≥n ρ _t (Y _m ), where

$$\inf_{m \geq n} \rho_t(Y_m) = \left( \begin{array}{c} \inf_{m \geq n} (\rho_t)_1((Y_m)_1) \\ \vdots\\ \inf _{m \geq n} (\rho_t)_d((Y_m)_d) \end{array} \right). $$

Since D is a lower set and $\inf_{\hat{m} \geq m} \rho _{t}(Z_{n_{\hat {m}}}) \preceq \rho_{t}(Z_{n_{m}})$ (and $\rho_{t}(Z_{n_{m}}) \in D$) for any $m \in \mathbb{N}$, it follows that $\inf_{\hat{m} \geq m} \rho _{t}(Z_{n_{\hat{m}}}) \in D$ for any $m \in\mathbb{N}$. Note that $\| \inf_{\hat {m} \geq m} \rho_{t}(Z_{n_{\hat{m}}})\|_{\infty} \leq\max(\|\rho _{t}(0)+k\| _{\infty},\|\rho_{t}(0)-k\|_{\infty}) =: \hat{k}$ due to $\| Z_{n_{\hat {m}}}\|_{\infty} \leq k$ for every $\hat{m} \in\mathbb{N}$. Since $D \cap \{u \in L^{\infty}_{t}: \|u\|_{\infty} \leq\hat{k}\}$ is closed in probability (by [34, Proposition 5.5.1]), it must contain all almost sure limit points; therefore, we have that $\liminf_{m \to \infty } \rho_{t}(Z_{n_{m}}) \in D \cap\{u \in L^{\infty}_{t}: \|u\|_{\infty} \leq\hat{k}\}$. Finally, from componentwise lower semicontinuity we have $\liminf_{m \to\infty} \rho_{t}(Z_{n_{m}}) \succeq\rho_{t}(Z)$; because D is a lower set, it hence follows that $\rho_{t}(\bar{Z}) \in D$, that is, $\bar{Z} \in\rho_{t}^{-1}(D)$. □

Appendix C: Stepped risk measures

In this section, we consider the dual representation of closed convex and coherent stepped risk measures $R_{t,s}: M_{s} \to\mathcal {P}(M_{t};M_{t,+})$. This is used in Sects. 3 and 4, as the stepped penalty functions and stepped sets of dual variables play a role when discussing equivalent characterizations of multi-portfolio time consistency. For the dual representation, we use set-valued duality defined in [25] analogously as for conditional risk measures in Sect. 4 of [17].

Given a risk measure $R_{t}: L^{p} \to\mathcal{P}(M_{t};M_{t,+})$, a stepped risk measure is the restriction of R _t to M _s , that is, $R_{t,s}=R_{t}|_{M_{s}}$. The primal representation can immediately be seen, that is, R _t,s (X):={u∈M _t :X+u∈A _t,s } for X∈M _s . Therefore, if R _t is closed convex (coherent), then R _t,s is closed convex (coherent). Furthermore, if R _t is $L^{p}_{+}$-monotone, then R _t,s is M _s,+-monotone.

Lemma C.1

Let R _t be a closed convex risk measure. The set of dual variables for $R_{t,s}: M_{s} \to\mathcal{P}(M_{t};M_{t,+})$ with t<s is given by

$$\mathcal{W}_{t,s} = \big\{ (\mathbb{Q},w) \in\mathcal{M} \times(M_{t,+}^+ \backslash M_t^{\perp}): w_t^{s}(\mathbb{Q},w) \in M_{s,+}^+, \mathbb {Q}= \mathbb{P}|_{\mathcal{F}_{t}}\big\} . $$

Proof

By the logic of Proposition 4.4 in [17], the set of (classical) stepped dual variables is given by $\{(Y,v): Y \in M_{s,+}^{+}, v \in(\mathbb{E}[Y | \mathcal{F}_{t}] + M_{t}^{\perp}) \backslash M_{t}^{\perp}\}$. Then it remains to show that for any dual pair (Y,v), there is a $(\mathbb{Q},w) \in\mathcal{W}_{t,s}$ with $\tilde {F}_{(Y,v)}^{t}[X] = F_{(\mathbb{Q},w)}^{t}[X]$ for any X∈M _s and vice versa, where $\tilde{F}_{(Y,v)}^{t}[X] := \{u \in M_{t}: \mathbb {E}[X^{\mathsf{T}}Y] \leq\mathbb{E}[v^{\mathsf{T}}u]\}$.

(1) Let $(\mathbb{Q},w) \in\mathcal{W}_{t,s}$. Then we show that there exists a dual pair

$$(Y,v) \in\{(Y,v): Y \in M_{s,+}^+, v \in(\mathbb{E}[Y | \mathcal {F}_{t}] + M_t^{\perp }) \backslash M_t^{\perp}\} $$

with $\tilde{F}_{(Y,v)}^{t}[X] = F_{(\mathbb{Q},w)}^{t}[X]$ for any X∈M _s . Let $Y = w_{t}^{s}(\mathbb{Q},w) \in M_{s,+}^{+}$ (by Remark C.2 and Lemma A.1(i)); thus,

$$\mathbb{E}[X^{\mathsf{T}}Y] = \mathbb{E}[w_t^{s}(\mathbb{Q},w)^{\mathsf{T}}X] = \mathbb{E}[w^{\mathsf{T}}\mathbb{E}^\mathbb{Q}[X|\mathcal{F}_t]] $$

and $\mathbb{E}[Y | \mathcal{F}_{t}]=w$. From $w \in M_{t,+}^{+} \backslash M_{t}^{\perp }$, we can rewrite $w = w_{M_{t,+}^{+}} + w_{M_{t}^{\perp}}$. Thus, $v = w_{M_{t,+}^{+}} = w - w_{M_{t}^{\perp}} \in\mathbb{E}[Y|\mathcal {F}_{t}] + M_{t}^{\perp }$. Finally, $w \notin M_{t}^{\perp}$ implies $v \notin M_{t}^{\perp}$, and $\mathbb{E}[w^{\mathsf{T}}u] = \mathbb{E}[v^{\mathsf{T}}u]$ for every u∈M _t since $w \in v + M_{t}^{\perp}$.

(2) Let $Y \in M_{s,+}^{+}$ and $v \in(\mathbb{E}[Y|\mathcal{F}_{t}] + M_{t}^{\perp}) \backslash M_{t}^{\perp}$. We want to show that there exists a $(\mathbb{Q}^{t},w) \in\mathcal {W}_{t,s}$ such that $\tilde{F}_{(Y,v)}^{t}[X] = F_{(\mathbb{Q},w)}^{t}[X]$ for any X∈M _s . First, we let $w \in\mathbb{E} [(Y + M_{s}^{\perp}) \cap L^{q}_{s,+}|\mathcal{F}_{t}]$ (which is nonempty), that is, $w = \mathbb{E}[Y + m^{\perp}|\mathcal{F}_{t}]$ for some $m^{\perp } \in M_{s}^{\perp }$ and $Y + m^{\perp} \in L^{q}_{s,+}$. Then it can easily be seen that $w \in v + M_{t}^{\perp}$ for $v \in(\mathbb{E}[Y|\mathcal{F}_{t}] + M_{t}^{\perp}) \backslash M_{t}^{\perp} \subseteq M_{t,+}^{+}$. Thus, $w \in M_{t,+}^{+} + M_{t}^{\perp}$, and with $v \notin M_{t}^{\perp}$, this implies $w \in M_{t,+}^{+} \backslash M_{t}^{\perp}$. From $w \in v + M_{t}^{\perp}$ it follows that $\mathbb{E}[w^{\mathsf{T}}u] = \mathbb {E}[v^{\mathsf{T}}u]$ for every u∈M _t .

Additionally, choose $\mathbb{Q}\in\mathcal{M}$ such that $\frac {d\mathbb{Q}_{i}}{d\mathbb{P}}= \bar{\xi }_{0,s}(\mathbb{Q}_{i})$, where

$$\bar{\xi}_{r,s}(\mathbb{Q}_i)[\omega] = \begin{cases}\frac{\mathbb{E}[Y_i + m_i^{\perp} | \mathcal {F}_{s}](\omega)}{\mathbb{E}[Y_i + m_i^{\perp} | \mathcal {F}_{r}](\omega)} &\text{if } \mathbb{E}[Y_i + m_i^{\perp } | \mathcal{F}_{r}](\omega) > 0\\ 1 &\text{else} \end{cases} $$

for any 0≤r≤s and almost every ω∈Ω. Define the measure $\mathbb{Q}^{t}\in\mathcal{M}$ by its density $\frac {d\mathbb{Q}^{t}_{i}}{d\mathbb{P}} = \bar{\xi}_{t,s}(\mathbb{Q}_{i})$. Then $w_{t}^{s}(\mathbb{Q}^{t},w) = w_{t}^{s}(\mathbb{Q},w) = Y + m^{\perp} \in M_{s,+}^{+} + M_{s}^{\perp} \subseteq M_{s,+}^{+}$. Therefore, $\mathbb{E}[w^{\mathsf{T}} \mathbb{E}[X|\mathcal{F}_{t}]] = \mathbb{E}[w_{t}^{s}(\mathbb{Q}^{t},w)^{\mathsf{T}}X] = \mathbb{E}[Y^{\mathsf{T}}X]$ for every X∈M _s . □

Remark C.2

For any choice of eligible portfolios M _t , it follows that $\mathcal{W} _{t,s} \supseteq\mathcal{W}_{t}$ for any t<s.

Remark C.3

If we consider the case where $M_{t} = L^{p}_{t}$ for all times t, then an inspection of the proof of Lemma 4.5 from [17] shows that $\mathcal{W}_{t,s} = \mathcal{W}_{t}$.

The next lemma gives a dual representation for closed convex stepped risk measures. In particular, it demonstrates that the minimal stepped penalty function as defined in (3.1) can be used in a dual representation to define a closed convex stepped risk measure.

Lemma C.4

The dual representation for any closed convex stepped risk measure $R_{t,s}: M_{s} \to\mathcal{G}(M_{t};M_{t,+})$ with t<s is given by

$$R_{t,s}(X) = \bigcap_{(\mathbb{Q},w) \in\mathcal{W}_{t,s}} \Big(-\beta_{t,s}^{\min}(\mathbb{Q} ,w) + \big(\mathbb{E}^{\mathbb{Q}}[-X | \mathcal{F}_{t}] + G_t(w)\big) \cap M_t\Big) $$

for any X∈M _s where

$$-\beta_{t,s}^{\min}(\mathbb{Q},w) = \operatorname{cl}\bigcup_{X \in A_{t,s}} \big(\mathbb{E}^{\mathbb{Q}}[X | \mathcal{F}_{t}] + G_t(w)\big) \cap M_t. $$

Proof

This is an adaptation of Theorem 2.3 to stepped risk measures, using Lemma C.1. □

We use the above results to give a dual representation for closed coherent stepped risk measures.

Corollary C.5

The dual representation for any closed coherent stepped risk measure $R_{t,s}: M_{s} \to\mathcal{G}(M_{t};M_{t,+})$ with t<s is given by

$$R_{t,s}(X) = \bigcap_{(\mathbb{Q},w) \in\mathcal{W}_{t,s}^{\max }}\big(\mathbb{E}^{\mathbb{Q}}[-X | \mathcal{F}_{t}] + G_t(w)\big) \cap M_t $$

for any X∈M _s , where

$$\mathcal{W}_{t,s}^{\max} = \{(\mathbb{Q},w) \in\mathcal{W}_{t,s}: w_t^{s}(\mathbb{Q},w) \in A_{t,s}^+\}. $$

Proof

Note that

$$-\beta_{t,s}^{\min}(\mathbb{Q},w) = \operatorname{cl}\bigcup_{X \in A_{t,s}} (\mathbb{E} ^\mathbb{Q}[X| \mathcal{F}_t] + G_t(w)) \cap M_t = G_t(w) \cap M_t $$

if and only if for every X∈A _t,s , we have

$$\mathbb{E}\big[w^{\mathsf{T}}\mathbb{E}^{\mathbb{Q}}[X | \mathcal {F}_{t}]\big] = \mathbb{E}\big[w_t^{s}(\mathbb{Q},w)^{\mathsf {T}}X\big] \geq0, $$

that is, $w_{t}^{s}(\mathbb{Q},w) \in A_{t,s}^{+}$. Thus, for an M _s,+-monotone closed coherent stepped risk measure R _t,s with 0≤t<s≤T, it holds that for any $(\mathbb {Q},w) \in \mathcal{W}_{t,s}$,

$$-\beta_{t,s}^{\min}(\mathbb{Q},w) = G_t(w) \cap M_t \quad\Longleftrightarrow\quad w_t^{s}(\mathbb{Q},w) \in A_{t,s}^+. $$

An application of Lemma C.1 provides the desired result. □

Finally, we use the above duality results to extend Corollary 2.4 to stepped risk measures.

Corollary C.6

The dual representation for any closed conditionally convex stepped risk measure $R_{t,s}: M_{s} \to\mathcal{G}(M_{t};M_{t,+})$ with t<s is given by

$$R_{t,s}(X) = \bigcap_{(\mathbb{Q},w) \in\mathcal{W}_{t,s}} \Big(-\alpha_{t,s}^{\min }(\mathbb{Q},w) + \big(\mathbb{E}^{\mathbb{Q}}[-X | \mathcal {F}_{t}] + \varGamma_t(w)\big)\cap M_t\Big) $$

for any X∈M _s , where

$$-\alpha_{t,s}^{\min}(\mathbb{Q},w) = \operatorname{cl}\bigcup_{X \in A_{t,s}} \big(\mathbb{E}^{\mathbb{Q}}[X | \mathcal{F}_{t}] + \varGamma_t(w)\big) \cap M_t. $$

If R _t,s is additionally conditionally coherent, then

$$R_{t,s}(X) = \bigcap_{(\mathbb{Q},w) \in\mathcal{W}_{t,s}^{\max}} \big(\mathbb{E}^{\mathbb{Q}}[-X | \mathcal{F}_{t}] + \varGamma_t(w)\big) \cap M_t. $$

Proof

This is an adaptation of Corollary 2.4 to stepped risk measures, using the results of Lemma C.4 and Corollary C.5. □