Activity discovery using Dirichlet multinomial mixture models from discrete sensor data in smart homes

Abstract

To develop smart home technology designed to analyze the activity of residents based on the logs of installed sensors, an activity model tailored to individuals must be constructed from less privacy-invasive sensors to avoid interference in daily life. Unsupervised machine learning techniques are desirable to automatically construct such models without costly data annotation, but their application has not yet been sufficiently successful. In this study, we show that an activity model can be effectively estimated without activity labels via the Dirichlet multinomial mixture (DMM) model. The DMM model assumes that sensor signals are generated according to a Dirichlet multinomial distribution conditioned on a single unobservable activity and can capture the burstiness of sensors, in which even sensors that rarely fire may fire repeatedly after being triggered. We demonstrate the burstiness phenomenon in real data using passive infrared ray motion sensors. For such data, the assumptions of the DMM model are more suitable than the assumptions employed in models used in previous studies. Moreover, we extend the DMM model so that each activity depends on the preceding activity to capture the Markov dependency of activities, and a Gibbs sampler used in the model estimation algorithm is also presented. An empirical study using publicly available data collected in real-life settings shows that the DMM models can discover activities more correctly than the other models and expected to be used as a primitive activity extraction tool in activity analysis.

1 Introduction

Data mining to identify behavioral patterns of residents of smart homes has attracted considerable attention [1,2,3]. For the elderly in particular, such an approach is considered to be effective for assisting in their health care and contributing to their independence [2, 4, 5]. In this study, we propose a modeling method for behavioral patterns of aged persons living alone to monitor their activities of daily living (ADLs).

To develop the behavior model, ADL classifiers based on hand-crafted rules [6] can be used. While specification-based methods can be used to easily describe high-level activities, Describing low-level activities based on sensor signals is difficult. In contrast, learning-based methods have been used to build models from sensor data [1,2,3].

Most learning-based methods employed to date use sensor data annotated with activity labels to construct a classifier of activities through supervised learning, which is known as activity recognition. Because the cost of an annotation is generally high, preparing annotated data for each resident is cost-prohibitive, and the cost is warranted only if a model trained for a particular resident is applicable to other residents. However, sharing activity models between residents is difficult, particularly when only unobtrusive binary sensors, e.g., passive infrared ray (PIR) motion sensors, are allowed [6, 7]. More informative sensors such as video, audio, or wearable sensors are unacceptable in monitoring activities conducted over extended periods owing to intrusiveness, and potential to interfere with daily life [2, 5]. The identification of activities with motion sensors depends not only on detecting motion but also on the layout of the sensors. The location where a sensor is installed can be a strong indicator for certain activities (e.g., using the bathroom), or a sequence of reactions of adjacent sensors can identify other activities (e.g., moving toward an entrance). Because the living environment and the sensor layout of each resident is unique, sharing an activity model is difficult, and the model should therefore be individually tailored to each resident. To keep the modeling cost within reasonable bounds, unsupervised learning techniques have been identified as a promising approach [3], which is known as activity discovery [4, 8].

Among unsupervised learning techniques for activity discovery, this study focuses on generative models [9] of sensor signals. These are probabilistic models describing sensor signals generated from unobservable activities. After fitting a model to a sequence of sensor signals, trained model can be used to estimate an activity that is most likely to have generated a new set of sensor signals. In previous research, topic models such as latent Dirichlet allocation (LDA) models [10] and hierarchical Dirichlet processes mixture (DPM) models [11] have been applied to activity discovery [12,13,14,15]. In this study, we investigate the use of Dirichlet multinomial mixture (DMM) models [16, 17].

The DMM model, which is a uni-topic version of the LDA model, assumes that sensor signals are generated from a single activity that occurs among unobservable activities. Because DMM models have been successfully applied to the modeling for short documents [17], which tend to concern a single topic, they can also be effective for modeling sensor signals within a short time period, which are reasonably hypothesized as being generated from a single activity rather than from multiple activities.

Another advantage of the DMM model is that it can capture burstiness in sensor data: once a sensor fires, there is a high probability that it will continue to fire, even if it fires only rarely. The burstiness stems from the fact that the distribution of sensor signals follows the power law, which is also observed in a wide variety of natural and social phenomena [18]. As discussed in a subsequent section, burstiness is indeed observed in motion sensor data, and the DMM model can fit a model to such data more accurately and robustly than alternative methods.

However, applying the DMM model to activity discovery involves the drawback that it cannot model the Markov dependency of the activities. Because the sensor data are time-series data, a particular activity naturally depends on previous activities. To cope with this dependency, hidden Markov models (HMMs) have been extensively used to perform activity recognition [19, 20]. As with HMMs, the DMM models can be extended to take into account the Markov dependency on activities by applying their bigram statistics. To fit the extended DMM model to the data, a Gibbs sampler used in the Markov chain Monte Carlo (MCMC) method [9] is also presented.

We evaluate the applicability of the DMM model to activity discovery by an empirical study using publicly available datasets collected by experiments in real-life settings, one of which used reed switch sensors and does not exhibit burstiness, whereas the other used PIR motion sensors and does exhibit burstiness. Activity discovery is typically used in human-in-the-loop analysis with the help of visualization tools [21]. Activity patterns to be discovered have various levels of granularity, ranging from gestures, ambulation, and ADL to social interaction [1]. An evaluation that takes all of these into account is beyond the scope of this study. Rather, we focus on evaluating the performance of clustering primitive patterns in sequences of binary sensor signals under as few assumptions as possible, because the basic clustering performance is an important first step in a complex activity analysis. Also, clustering can be directly used to evaluate the quantity and quality of primitive activities, such as the restlessness behavior of patients with Alzheimer’s disease [22]. To this end, we evaluated the performance of clustering activities corresponding to short time periods using various generative models for sensor signals as well as the k-means method, a typical clustering method, and frequent sequence mining [8] previously used in activity discovery other than generative models.

Reminder of this work is organized as follows. After briefly reviewing previously studied activity discovery techniques in Section 2 and particularly the use of probabilistic generative models in Section 3, the DMM model and its extension are presented together with Gibbs samplers in Section 4. Then, in Section 5, we describe our empirical investigation of the DMM model and the DMM model with activity bigrams together with other clustering methods for activity discovery. Finally, the last sections conclude with a summary of the results and areas of future study.

2 Related works

Activity recognition, which identifies known activities, has been studied extensively. In contrast activity discovery, which discovers unknown activities latent in data, has not been studied to the same extent [1,2,3]. Research on activity discovery conducted to date has included the use of background knowledge regarding activities and sensors [23] and the clustering of sensor data based on heuristics of daily behaviors [5]. In [24], frequent itemset mining [25] together with heuristics of daily behavior is applied for activty discovery.

Because the sensor data comprise time-series, subsequences of sensor signals are extracted from data and are used to form patterns of activities in [4, 8, 21, 24]. In [8], frequent patterns of activities can be extracted by using frequent sequence mining. These are then used to partially define “other activities” that do not correspond to the predefined activities and thus can contribute to improving the accuracy of activity recognition. In [21], subsequences of sensor signals are processed further by using business process mining techniques, and the frequent patterns of activities are extracted as graphs with subsequences as nodes. Though the process is not fully unsupervised, users of the visualization tool can analyze the behavior of residents using activity patterns extracted semi-automatically from a massive number of subsequences. However, the susceptibility of such sequence mining to noise is a clear weakness. Noise occurs frequently in data from PIR motion sensors; for example, it occurs due to false detection of nonhuman heat sources or by incorrectly triggering adjacent sensors due to movement in slightly anomalous locations. If noise is treated as a gap in sequences of data, the computational complexity of sequence mining becomes intractable in general [26].

Methods that use probabilistic models are robust to noise. In [27], the Gaussian mixture model for time spent in each room is learned based on which mixture components specify the distribution of time required for certain activities. Other studies assume models in which unobservable activities generate raw sensor signals or low-level discriminative features. For example, the LDA model, which is a topic model that defines a process to generate words depending on topics in documents, is used to model the process of generating low-level discriminative features depending on daily routines [12]. In [13], an LDA model is also used to discover human actions in video from spatio-temporal codebooks extracted from a video sequence. To relax the need to specify the number of activities, hierarchical DPM models are used in [14, 15]. In these methods, after the parameters of the models are estimated through unsupervised learning, an activity that generates new observations is estimated using the posterior probability of the model.

In this study, we focus on activity discovery using generative models of binary sensor signals generated from latent activities. In addition to the LDA and the DPM models, we also consider the use of the HMM for activity discovery. Although the HMM has been extensively used to perform activity recognition under supervised learning settings, it can be trained without activity labels under an unsupervised learning setting. Moreover, in this study, we consider the DMM model, which has favorable properties for modeling motion sensor signals. When no supervised signal is available, the joint probability distribution of the observations is used as a clue to fit the model to the data. We consider that the key to improving activity models is to ensure that the model’s assumptions about the generation of the observations capture the essence of the real data generation process.

3 Generative models for activity discovery

Generative models [9] are probabilistic models describing the generation of observations depending on states. After fitting a model to data, the trained model can be used to estimate a state that would have generated new observations.

For activity discovery, the observations are sensor signals and the states are unobservable activities that remain to be discovered. In this section, we review the generative models that have been used in activity discovery in more detail, along with the related key concepts such as the burstiness of sensor signals, modeling latent activities, and Markov dependency on activities.

3.1 Modeling burstiness of sensor signals

Perhaps the simplest generative model of binary sensors would include the naive Bayes assumption: given an activity, each sensor signal is generated independently of other signals within that activity. When each signal $w_{n} \in \{1,\ldots ,V\}$ ($1 \le n \le N$) is assumed to be distributed according to a categorical distribution with parameter $\varvec{\phi } = \phi _{1},\ldots ,\phi _{V}$ (${{\sum }_{v}^{V}} \phi _{v} = 1$), the probability of generating an observation $\mathbf {w} = w_{1},\ldots ,w_{N}$ vector can be written as follows:

$$\begin{aligned} P(\mathbf {w} \mid \varvec{\phi }) = {\prod \limits _{n}^{N}} \prod \limits _{v}^{V}\phi _{v}^{[w_{n} = v]} = \prod \limits _{v}^{V} \phi _{v}^{x_{v}}, \end{aligned}$$

where $x_{v} = {\sum }_{n}^{N} [w_{n} = v]$ and $[\cdot ]$ is Iverson bracket, i.e., $[P] = 1$ if P is true and $[P] = 0$ otherwise.

For any count vector $\mathbf {x} = (x_{1},\ldots ,x_{V})$, $\mathbf {x}$ is then distributed according to a multinomial distribution with parameters $\varvec{\phi }$:

$$\begin{aligned} {Mul}\left( \mathbf {x} \mid \varvec{\phi }\right) = N! {\prod \limits _{v}^{V}} \frac{\phi _{v}^{x_{v}}}{x_{v}!}, \end{aligned}$$

where $N = {\sum }_{v}^{V} x_{v}$.

Fig. 1

Power law of count probabilities of motion sensors in a dataset. The probabilities of firing exactly x times within every activity were averaged for 3 groups, the 6 most frequently fired sensors, 11 sensors with an average frequency, and 15 rarely fired sensors

However, modeling sensor signals with a multinomial distribution overlooks an important property, i.e., their burstiness. Figure 1 shows count probabilities of PIR motion sensors in a dataset described in a subsequent section. All 32 sensors are divided into three groups according to their frequency of occurrence: the 6 most frequently occurred sensors, 11 sensors with average frequency of occurrence, and 15 rarely occurred sensors. For each sensor, the probability of firing exactly x times within an activity is calculated and averaged for each group. If x is distributed according to a multinomial distribution, the probability of firing exactly x times decays exponentially and exhibited a straight descending line in the semi-logarithmic graph. In reality, the count probabilities of all three groups of sensors follow the power law. This may be attributed to their burstiness, i.e., once a sensor fires during an activity, it fires multiple times within that activity even if its overall frequency is low.

Because burstiness also appears in text modeling, in [28], the authors address word burstiness using a Dirichlet multinomial (DM) distribution. A DM distribution is obtained as a compound distribution averaging across all possible multinomial distributions. As a conjugate prior of the multinomial distribution $Mul\left( \mathbf {x} \mid \varvec{\phi }\right)$, the Dirichlet distribution $Dir\left( \varvec{\phi } \mid \varvec{\beta }\right)$ is used.

$$\begin{aligned} DM\left( \mathbf {x} \mid \varvec{\beta }\right)= & {} \int _{{\varvec{\phi }}} {Dir}\left( {\varvec{\phi }} \mid \varvec{\beta }\right) Mul\left( \mathbf {x} \mid \varvec{\phi }\right) d \varvec{\phi } \nonumber \\= & {} \int _{\varvec{\phi }} \left( \frac{\Gamma \left( \beta _{\cdot }\right) }{\prod_{v} \Gamma \left( \beta_{v}\right)} \prod \limits _{v}^{V} \phi _{v}^{\beta _{v} - 1}\right) \left( N! \prod \limits _{v}^{V} \frac{\phi _{v}^{x_{v}}}{x_{v}!}\right) d {\varvec{\phi }} \nonumber \\= & {} \int _{\varvec{\phi }} \frac{\Gamma \left( N+1\right) \Gamma \left( \beta _{\cdot }\right) }{\prod _{v} \Gamma \left( x_{v} + 1\right) \Gamma \left( \beta _{v}\right) } {\prod \limits _{v}^{V}} \phi _{v}^{x_{v} + \beta _{v} - 1} d \varvec{\phi } \nonumber \\= & {} \frac{\Gamma \left( N+1\right) \Gamma \left( \beta _{\cdot }\right) }{\Gamma \left( \beta _{\cdot }+N\right) } {\prod \limits _{v}^{V}} \frac{\Gamma \left( x_{v} + \beta _{v}\right) }{\Gamma \left( x_{v} + 1\right) \Gamma \left( \beta _{v}\right) }, \end{aligned}$$

(1)

where $\beta _{\cdot } = {\sum _{v}^{V}} \beta _{v}$, and the last equation is based on $\int _{{\varvec{\phi }}} {Dir}\left( {\varvec{\phi }} \mid \varvec{\beta } + \mathbf {x}\right) d {\varvec{\phi }} = 1$.

By fixing $x_{u} (u \not = v)$ as constants, Eq. 1 is written as $P(x_{v}) = C \frac{\Gamma \left( x_{v} + N^{\prime } + 1\right) \Gamma \left( x_{v} + \beta _{v}\right) }{\Gamma \left( x_{v} + N^{\prime } + \beta _{\cdot }\right) \Gamma \left( x_{v} + 1\right) }$, where $N^{\prime } = N - x_{v}$ and C is a constant. Using Stirling’s approximation $\Gamma \left( x\right) \sim \sqrt{\frac{2\pi }{e}} (\frac{x}{e})^{x-\frac{1}{2}}$, $P(x_{v})$ is approximated as follows with a constant $C^{\prime }$.

$$\begin{aligned} P(x_{v})\sim & {} C^{\prime } \frac{(x_{v} + N^{\prime } + 1)^{x_{v} + N^{\prime } + \frac{1}{2}} (x_{v} + \beta _{v})^{x_{v} + \beta _{v} - \frac{1}{2}}}{(x_{v} + N^{\prime } + \beta _{\cdot } )^{x_{v} + N^{\prime } + \beta _{\cdot } - \frac{1}{2}} (x_{v} + 1)^{x_{v} + \frac{1}{2}}} \\= & {} C^{\prime } \left( \frac{x_{v} + N^{\prime } + 1}{x_{v} + N^{\prime } + \beta _{\cdot }}\right) ^{x_{v}} \left( \frac{x_{v} + \beta _{v}}{x_{v} + 1}\right) ^{x_{v}} \frac{(x_{v} + N^{\prime } + 1)^{N^{\prime } + \frac{1}{2}} (x_{v} + \beta _{v})^{\beta _{v} - \frac{1}{2}}}{(x_{v} + N^{\prime } + \beta _{\cdot } )^{N^{\prime } + \beta _{\cdot } - \frac{1}{2}} (x_{v} + 1)^{\frac{1}{2}}} .\end{aligned}$$

Based on the fact that $\left( \frac{x + a}{x + b}\right) ^{x}$ converges to a constant $e^{a - b}$ in the limit $x \rightarrow \infty$, the power law of the count probability, that is, $p(x_{v}) = O(x_{v}^{\beta _{v} - \beta _{\cdot }})$, may be observed. In Eq. 10 presented in Section 4, the burstiness is explained by placing greater emphasis on sensors that fire multiple times. This can be viewed as a Pólya urn model [29]: after a sensor v is drawn from the urn, it is then returned to the urn and an additional sensor v is added. This rich-get-richer process causes burstiness in sensor signals.

For any observation vector $\mathbf {w}$, the DM distribution is written as follows.

$$\begin{aligned} DM\left( \mathbf {w} \mid \varvec{\beta }\right) = \frac{\Gamma \left( \beta _{\cdot }\right) }{\Gamma \left( \beta _{\cdot }+N\right) } {\prod \limits _{v}^{V}} \frac{\Gamma \left( x_{v} + \beta _{v}\right) }{\Gamma \left( \beta _{v}\right) } = \frac{B\left( \mathbf {x} + \varvec{\beta }\right) }{B\left( \varvec{\beta }\right) }, \end{aligned}$$

(2)

where $B(\cdot )$ is the multi-valiate beta function $B(\varvec{\beta }) = \frac{{\prod _{v}^{V}} \Gamma \left( \beta _{v}\right) }{\Gamma \left( \beta _{\cdot }\right) }$.

3.2 Modeling latent activities

The generative models of sensor signals introduced above can be naturally extended to a mixture model with latent activities.

$$\begin{aligned} P(\mathbf {w})= & {} {\sum \limits _{k}^{K}} P(z = k) P(\mathbf {w} \mid z = k), \end{aligned}$$

where z is a random variable for latent K activities. Nigam et al. [16] assumes that the mixture weight $P(z = k)$ is distributed according to a categorical distribution with parameter ${\varvec{\theta }}$, and ${\varvec{\theta }}$ is distributed according to a Dirichlet distribution with parameter $\varvec{\alpha } = (\alpha _{1},\ldots ,\alpha _{K})$, as given below.

$$\begin{aligned} P(\mathbf {w} \mid \varvec{\alpha },\varvec{\beta }) = \int _{{\varvec{\theta }}} Dir\left( {\varvec{\theta }} \mid \varvec{\alpha }\right) \ {\sum \limits _{k}^{K}} P(z = k \mid {\varvec{\theta }}) DM\left( \mathbf {w} \mid z = k, \varvec{\beta }_{k}\right) d {\varvec{\theta }}. \end{aligned}$$

This mixture model is called the DMM model [17].

The LDA model [10] is perhaps a more well-known mixture model with latent activities. It assumes a more complex generation process: an activity is assigned to each sensor output rather than to all outputs, as follows.

$$\begin{aligned} P(\mathbf {w} \mid \varvec{\alpha },\varvec{\beta }) = \int _{{\varvec{\theta }}} Dir \left( {\varvec{\theta }} \mid \varvec{\alpha }\right) \left( {\prod \limits _{n}^{N}} {\sum \limits _{k}^{K}} P(z = k \mid {\varvec{\theta }}) DM\left( w_{n} \mid z = k, \varvec{\beta }_{k}\right) \right) d {\varvec{\theta }}. \end{aligned}$$

Fig. 2

Graphical models for DMM and LDA models

Figure 2 shows the DMM and LDA models for M segments, i.e., for $\mathbf {w}_{1},\ldots ,\mathbf {w}_{M}$. Again, the activity z to which is assigned is a notable difference between DMM and LDA models. In the DMM model, z is assigned to each $\mathbf {w}_{m}$, whereas in the LDA model, z is assigned to each $w_{m,n} \in \mathbf {w}_{m}$. To express the multi-topic nature of a document, the LDA model assigns multiple topics to a document. The hierarchical DPM model has the same generation process of words though the number of topics is determined by data. In contrast, the DMM model is used to model short documents [17], given that short documents tend to discuss a single topic. The current research hypothesizes that considering that a single activity generates sensor signals within a short period is more effective than considering a mixture of multiple activities. As discussed in [1], there are many types of home activities with different levels of complexity. An activity with a higher complexity may have sub-activities, and the LDA model can be a suitable approach to describing a complex activity. However, in activity discovery, a stream of sensor signals is often structured in a bottom-up manner, being divided into fixed-length short segments, and a sequence of activities generating the segments is estimated during the first step. The DMM model is expected to be effective in modeling each short segment generated by a single activity.

Burstiness is another advantage of the DMM model over the LDA model. Although both models use a DM distribution, an LDA model cannot capture burstiness as DMM models do. Note that, with an LDA model, each sensor signal in a segment is obtained using a single draw from a DM distribution conditioned on an activity. Although a single drawing of a sensor v from an urn increases the number of sensors v in the urn, a burst of such sensors is suppressed because the next v may not necessarily be drawn from the same urn. In contrast, in the DMM model, because all sensor signals in a segment are drawn from the same urn, the more sensors v that are chosen from the urn, the more likely a specific v will be chosen.

3.3 Modeling Markov dependency on activities

As a drawback of the LDA and DMM models, neither can capture the dependencies on the activities. Because any activity naturally depends on previous activities, a generative model that can capture these dependencies is expected to be effective. For this reason, the HMM is used to perform activity recognition. The HMM assumes that a transition into another state depends on the current state which is defined by the transition probability of such states. Then, each sensor signal is assumed to be emitted from a state according to the emission probability. In activity recognition, because the transition of states, i.e., activities, can be observed along with the sensor signals, the transition probability can be estimated using the maximum likelihood method directly from the observations. In activity discovery, the transition of activities cannot be observed. In this case, using the Baum-Welch algorithm [30], the parameters of the HMM can be estimated solely from the sensor signals.

In the HMM, sensor signals in a segment are generated from multiple activities, similar to the LDA model, because an activity generates a single sensor signal. Although, in this respect, the DMM model is expected to be advantageous for modeling the burst signal generation within a short time period, it requires the ability to describe dependencies between the activities. In the following section, we extend the DMM model to capture the dependency on activities using activity bigrams.

4 DMM models

In [17], the DMM model is applied to the clustering of short texts, and a Gibbs sampler used to estimate the parameters of the model is presented. In the present work, we present an extension of the DMM model with activity bigrams and another Gibbs sampler for the extended model. To introduce the extension, we revisit the derivation of the original Gibbs sampler.

4.1 Gibbs sampler for DMM model

Although activities $\mathbf {Z} = z_{1},\ldots ,z_{M}$ are unobservable in a real setting, we start by showing the joint distribution of activities $\mathbf {Z}$ and sensors data $\mathbf {W} = \mathbf {w}_{1},\ldots ,\mathbf {w}_{M}$, where $\mathbf {w}_{m} = w_{m,1},\ldots ,w_{m,N_{m}}$ ($1 \le m \le M$) are sensor outputs in the m-th segment with length $N_{m}$. The joint probability is composed of two factors, which comprise the following.

$$\begin{aligned} P(\mathbf {W}, \mathbf {Z} \mid \varvec{\beta }, \varvec{\alpha }) = P(\mathbf {Z} \mid \varvec{\alpha }) P(\mathbf {W} \mid \mathbf {Z}, \varvec{\beta }, \varvec{\alpha }). \end{aligned}$$

The first factor is

$$\begin{aligned} P(\mathbf {Z} \mid \varvec{\alpha })= & {} \int _{\varvec{\theta }} Dir \left( {\varvec{\theta }} \mid \varvec{\alpha }\right) {\prod \limits _{k}^{K}} (\theta _{k})^{\tau _{k}}\ d {\varvec{\theta }} \nonumber \\= & {} \int _{{\varvec{\theta }}} \left( \frac{1}{B\left( \varvec{\alpha }\right) } \prod \limits _{k} (\theta _{k})^{\alpha _{k} - 1}\right) {\prod \limits _{k}^{K}} (\theta _{k})^{\tau _{k}} d {\varvec{\theta }} \nonumber \\= & {} \frac{B\left( \varvec{\tau } + \varvec{\alpha }\right) }{B\left( \varvec{\alpha }\right) }, \end{aligned}$$

(3)

where $\varvec{\tau } = (\tau _{1},\ldots ,\tau _{K})$ are counters for each activity, i.e., $\tau _{k} = {\sum }_{m}^{M} [z_{m} = k]$ for each k ($1 \le k \le K$). The second factor is

$$\begin{aligned} P(\mathbf {W} \mid \mathbf {Z}, \varvec{\beta }, \varvec{\alpha })= & {} {\prod \limits _{k}^{K}} \int _{{\varvec{\phi }}_{k}} Dir \left( {\varvec{\phi }}_{k} \mid \varvec{\beta }_{k}\right) {\prod \limits _{v}^{V}} \phi _{k,v}^{\omega _{k, v}}\ d {\varvec{\phi }}_{k} \nonumber \\= & {} {\prod \limits _{k}^{K}} \int _{{\varvec{\phi }}_{k}} \left( \frac{1}{B\left( \varvec{\beta }_{k}\right) } {\prod \limits _{v}^{V}} (\phi _{k,v})^{\beta _{k,v} - 1}\right) {\prod \limits _{v}^{V}} (\phi _{k,v})^{\omega _{k,v}}\ d\varvec{\phi }_{k} \nonumber \\= & {} {\prod \limits _{k}^{K}} \frac{B\left( \varvec{\omega }_{k} + \varvec{\beta }_{k}\right) }{B\left( \varvec{\beta }_{k}\right) }, \end{aligned}$$

(4)

where $\varvec{\omega }_{k} = (\omega _{k,1},\ldots ,\omega _{k,V})$ are counters for each sensor, that is, $\omega _{k,v} = {{\sum }_{m}^{M}} {\sum }_{n}^{N_{m}} [z_{m} = k\ \text {and}\ w_{m,n} = v]$ for each k ($1 \le k \le K$) and v ($1 \le v \le V$).

To estimate unobservable $\boldsymbol{Z}$ using the MCMC method, a Gibbs sampler randomly samples each activity $z_{m}$ according to the following conditional probability.

$$\begin{aligned} P(z_{m}= & {} k \mid \mathbf {Z}^{\backslash m}, \mathbf {W}, \varvec{\alpha }, \varvec{\beta }) = \frac{P(\mathbf {Z}, \mathbf {W} \mid \varvec{\alpha }, \varvec{\beta })}{P(\mathbf {Z}^{\backslash m}, \mathbf {W} \mid \varvec{\alpha }, \varvec{\beta })}\end{aligned}$$

(5)

$$\begin{aligned}= & {} \frac{P(\mathbf {Z} \mid \varvec{\alpha }) P(\mathbf {W} \mid \mathbf {Z}, \varvec{\beta })}{P(\mathbf {Z}^{\backslash m} \mid \varvec{\alpha }) P(\mathbf {w}_{m} \mathbf {W}^{\backslash m} \mid \mathbf {Z}^{\backslash m}, \varvec{\beta })} \end{aligned}$$

(6)

$$\begin{aligned}= & {} \frac{P(\mathbf {Z} \mid \varvec{\alpha }) P(\mathbf {W} \mid \mathbf {Z}, \varvec{\beta })}{P(\mathbf {Z}^{\backslash m} \mid \varvec{\alpha }) P(\mathbf {W}^{\backslash m} \mid \mathbf {Z}^{\backslash m}, \varvec{\beta })P(\mathbf {w}_{m} \mid \mathbf {Z}^{\backslash m}, \varvec{\beta })} \end{aligned}$$

(7)

$$\begin{aligned}\propto & {} \frac{P(\mathbf {Z} \mid \varvec{\alpha })}{P(\mathbf {Z}^{\backslash m} \mid \varvec{\alpha })} \frac{P(\mathbf {W} \mid \mathbf {Z}, \varvec{\beta })}{P(\mathbf {W}^{\backslash m} \mid \mathbf {Z}^{\backslash m}, \varvec{\beta })}, \end{aligned}$$

(8)

where $\mathbf {Z}^{\backslash m} = z_{1},\ldots ,z_{m-1},z_{m+1},\ldots ,z_{M}$, and

$\mathbf {W}^{\backslash m} = \mathbf {w}_{1},\ldots ,\mathbf {w}_{m-1},\mathbf {w}_{m+1},\ldots ,\mathbf {w}_{M}$.

From Eq. 3, the factor for activities in Eq. 8, which is equivalent to

$P(Z_{m} = k \mid \mathbf {Z}^{\backslash m}, \varvec{\alpha })$, is obtained as follows.

$$\begin{aligned} \frac{P(\mathbf {Z} \mid \varvec{\alpha })}{P(\mathbf {Z}^{\backslash m} \mid \varvec{\alpha })}= & {} \frac{B\left( \varvec{\tau } + \varvec{\alpha }\right) }{B\left( \varvec{\tau }^{\backslash m} + \varvec{\alpha }\right) } \nonumber \\= & {} \frac{\Gamma \left( \tau _{k} + \alpha _{k}\right) }{\Gamma \left( \tau _{k}^{\backslash m} + \alpha _{k}\right) } \frac{\Gamma \left( M - 1 + \alpha _{\cdot }\right) }{\Gamma \left( M + \alpha _{\cdot }\right) } \nonumber \\= & {} \frac{\tau _{k}^{\backslash m} + \alpha _{k}}{M - 1 + \alpha _{\cdot }}, \end{aligned}$$

(9)

where $\alpha _{\cdot } = {\sum _{k}^{K}} \alpha _{k}$, $\tau _{k}^{\backslash m} = \tau _{k} - [z_{m} = k]$, and $\varvec{\tau }^{\backslash m} = (\tau _{1}^{\backslash m},\ldots ,\tau _{K}^{\backslash m})$. The last equation is obtained by noting $\tau _{k} = \tau _{k}^{\backslash m} + 1$ and $\Gamma \left( x + 1\right) = x\, \Gamma \left( x\right)$.

From Eq. 4, the factor for sensors in Eq. 8, which is equivalent to

$P(\mathbf {w}_{m} \mid \mathbf {Z}, \mathbf {W}^{\backslash m}, \varvec{\beta })$, is obtained as follows.

$$\begin{aligned} \frac{P(\mathbf {W} \mid \mathbf {Z}, \varvec{\beta })}{P(\mathbf {W}^{\backslash m} \mid \mathbf {Z}^{\backslash m}, \varvec{\beta })}= & {} {\prod \limits _{k}^{K}} \frac{B\left( \varvec{\omega }_{k} + \varvec{\beta }_{k}\right) }{B\left( \varvec{\omega }_{k}^{\backslash m} + \varvec{\beta }_{k}\right) } \nonumber \\= & {} \frac{\Gamma \left( \omega _{k,\cdot }^{\backslash m} + \beta _{k,\cdot }\right) }{\Gamma \left( \omega _{k,\cdot } +\beta _{k,\cdot }\right) } {\prod \limits _{v}^{V}} \frac{\Gamma \left( \omega _{k,v} + \beta _{k,v}\right) }{\Gamma \left( \omega _{k,v}^{\backslash m} + \beta _{k,v}\right) } \nonumber \\= & {} \frac{{\prod }_{v}^{V} {\prod }_{\ell =1}^{N_{m}^{v}} (\omega _{k,v}^{\backslash m} + \beta _{k,v} + \ell - 1)}{{\prod }_{n=1}^{N_{m}} (\omega _{k,\cdot }^{\backslash m} + \beta _{k,\cdot } + n - 1)}, \end{aligned}$$

(10)

where $\beta _{k,\cdot } = {\sum }_{v}^{V} \beta _{k,v}$, $\omega _{k,\cdot } = {\sum }_{v}^{V} \omega _{k,v}$, $N_{m}^{v} = \sum _{n}^{N_{m}} [w_{m,n} = v]$,

$\omega _{k,v}^{\backslash m} = \omega _{k,v} - N_{m}^{v}$, $\varvec{\omega }^{\backslash m} = (\omega _{1}^{\backslash m},\ldots ,\omega _{V}^{\backslash m})$, and $\omega _{k,\cdot }^{\backslash m} = {\sum _{v}^{V}} \omega _{k,v}^{\backslash m}$. The last equation is obtained by noting $\omega _{k,v} = \omega _{k,v}^{\backslash m} + N_{m}^{v}$ and $\omega _{k,\cdot } = \omega _{k,\cdot }^{\backslash m} + N_{m}$, and by using $\Gamma \left( x + 1\right) = x\, \Gamma \left( x\right)$ multiple times for $\Gamma \left( \omega _{k,v} + \beta _{k,v}\right)$ and $\Gamma \left( \omega _{k,\cdot } +\beta _{k,\cdot }\right)$. We can see that it describes a Pólya urn model; after the $\ell$-th drawing of v from $\omega _{k,v}^{\backslash m} + \beta _{k,v} + \ell - 1$ sensors of v in the urn, it is then returned to the urn and an additional v is added. Therefore, before the ($\ell +1$)-th drawing of v, there exist $\omega _{k,v}^{\backslash m} + \beta _{k,v} + \ell$ sensors of v in the urn, and the larger the number of sensors v that are drawn from the urn, the more likely v will be chosen. This rich-get-richer process causes burstiness of the sensor outputs.

Combining Eqs. 9 and 10, we obtain the conditional probability for the Gibbs sampler.

$$\begin{aligned} P(z_{m} = k \mid \mathbf {Z}^{\backslash m}, \mathbf {W}, \varvec{\alpha }, \varvec{\beta }) \propto \frac{\tau _{k}^{\backslash m} + \alpha _{k}}{M - 1 + \alpha _{\cdot }}\ \frac{{\prod _{v}^{V}} {\prod }_{n=1}^{N_{m}^{v}} (\omega _{k,v}^{\backslash m} + \beta _{k,v} + n - 1)}{\prod _{n=1}^{N_{m}} (\omega _{k,\cdot }^{\backslash m} + \beta _{k,\cdot } + n - 1)}. \end{aligned}$$

(11)

4.2 DMM model with activity bigrams

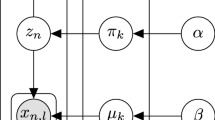
To capture the Markov dependency on the activities, we assume that $z_{m}$ depends on $z_{m-1}$. Because $z_{m}$ is drawn from a categorical distribution ${\varvec{\theta }}$, ${\varvec{\theta }}$ should also be conditioned on $z_{m-1}$. Let us assume that a distribution ${\varvec{\theta }}_{q}$ depends on the previous activity q, and is drawn from a Dirichlet distribution with hyper parameters ${\varvec{\alpha }}_{q} = (\alpha _{q,1},\ldots ,\alpha _{q,K})$. Figure 3 shows an extended DMM model with activity bigrams.

Fig. 3

DMM model with Markov dependency on the activities

For the DMM models, although the dynamical change in topic distributions is introduced in [31], we consider a static correlation between topics of adjacent documents employing topic bigrams.

For the extended model, whereas the factor for the sensor outputs in a joint distribution is the same as Eq. 4, the factor for the activities in a joint distribution differs from Eq. 3 as follows.

$$\begin{aligned} P(\mathbf {Z} \mid \varvec{\alpha })= & {} {\prod \limits _{q}^{K}} \int _{{\varvec{\theta }}_{q}} {Dir}\left( {\varvec{\theta }}_{q} \mid \varvec{\alpha }_{q}\right) {\prod \limits _{r}^{K}} (\theta _{q,r})^{\tau _{q,r}}\ d{\varvec{\theta }}_{q} \nonumber \\= & {} {\prod \limits _{q}^{K}} \int _{{\varvec{\theta }}_{q}} \left( \frac{1}{B\left( \varvec{\alpha }_{q}\right) } {\prod \limits _{r}^{K}} (\theta _{q,r})^{\alpha _{q,r} - 1}\right) {\prod \limits _{r}^{K}} (\theta _{q,r})^{\tau _{q,r}} d\varvec{\theta }_{q} \nonumber \\= & {} {\prod \limits _{q}^{K}} \frac{B\left( \varvec{\tau }_{q} + \varvec{\alpha }_{q}\right) }{B\left( \varvec{\alpha }_{q}\right) }, \end{aligned}$$

(12)

where $\varvec{\alpha } = \varvec{\alpha }_{1},\ldots ,\varvec{\alpha }_{K}$, $\tau _{q,r} = {\sum }_{m}^{M} [z_{m-1} = q\ \text {and}\ z_{m} = r]$,

$\varvec{\tau }_{q} = (\tau _{q,1},\ldots ,\tau _{q,K})$.

To obtain a Gibbs sampler for the extended DMM model, we can again use Eq. 8 because $\mathbf {w}_{m}$ and $\mathbf {w}_{m^{\prime }}$ ($m^{\prime } \not = m$) are independent given $z_{m^{\prime }}$ even when dependency on $\mathbf {Z}$ exists, and thus Eq. 7 remains equals to Eq. 6. However, the factor for the activities differs from Eq. 9 and is obtained from Eq. 12 as follows.

$$\begin{aligned} P(z_{m} = k \mid \mathbf {Z}^{\backslash m}, \varvec{\alpha })= & {} \frac{P(\mathbf {Z} \mid \varvec{\alpha })}{P(\mathbf {Z}^{\backslash m} \mid \varvec{\alpha })} \nonumber \\= & {} \prod \limits _{q}^{K} \frac{B\left( \varvec{\tau }_{q} + \varvec{\alpha }_{q}\right) }{B\left( \varvec{\tau }_{q}^{\backslash m} + \varvec{\alpha }_{q}\right) } \nonumber \\= & {} \prod \limits _{q}^{K} \frac{\Gamma \left( \tau _{q,\cdot }^{\backslash m} + \alpha _{q,\cdot }\right) }{\Gamma \left( \tau _{q,\cdot } + \alpha _{q,\cdot }\right) } \ \prod \limits _{r}^{K} \frac{\Gamma \left( \tau _{q,r} + \alpha _{q,r}\right) }{\Gamma \left( \tau _{q,r}^{\backslash m} + \alpha _{q,r}\right) }. \end{aligned}$$

Here, recall that $z_{m}$ depends not only on $z_{m-1}$ but also on $z_{m+1}$¹, and thus $z_{m}$ affects $\varvec{\tau }_{z_{m-1}}$ and $\varvec{\tau }_{z_{m}}$. Let us assume that $z_{m-1} = j$ and $z_{m+1} = \ell$, and consider the following three cases.

For $j \not = k$, we can see that $\tau _{j,\cdot } = \tau _{j,\cdot }^{\backslash m} + 1$ and $\tau _{k,\cdot } = \tau _{k,\cdot }^{\backslash m} + 1$, and for the other cases $q \not = j,k$, $\tau _{q,\cdot } = \tau _{q,\cdot }^{\backslash m}$ hold. It may be observed that $\tau _{j,k} = \tau _{j,k}^{\backslash m} + 1$ and $\tau _{k,\ell } = \tau _{k,\ell }^{\backslash m} + 1$ hold, as does $\tau _{q,r} = \tau _{q,r}^{\backslash m}$ for the other cases. We thus obtain the following.

$$\begin{aligned} P(z_{m} = k \mid \mathbf {Z}^{\backslash m}, \varvec{\alpha })= & {} \prod \limits _{q\not =j,k}^{K} \frac{\Gamma \left( \tau _{q,\cdot }^{\backslash m} + \alpha _{q,\cdot }\right) }{\Gamma \left( \tau _{q,\cdot } + \alpha _{q,\cdot }\right) } {\prod \limits _{r}^{K}} \frac{\Gamma \left( \tau _{q,r} + \alpha _{q,r}\right) }{\Gamma \left( \tau _{q,r}^{\backslash m} + \alpha _{q,r}\right) } \\&\frac{\Gamma \left( \tau _{j,\cdot }^{\backslash m} + \alpha _{j,\cdot }\right) }{\Gamma \left( \tau _{j,\cdot } + \alpha _{j,\cdot }\right) } \frac{\Gamma \left( \tau _{j,k} + \alpha _{j,k}\right) }{\Gamma \left( \tau _{j,k}^{\backslash m} + \alpha _{j,k}\right) } \prod \limits _{r\not =k}^{K} \frac{\Gamma {(\tau _{j,r} + \alpha _{j,r}})}{\Gamma \left( \tau _{j,r}^{\backslash m} + \alpha _{q,r}\right) } \nonumber \\&\frac{\Gamma \left( \tau _{k,\cdot }^{\backslash m} + \alpha _{k,\cdot }\right) }{\Gamma \left( \tau _{k,\cdot } + \alpha _{k,\cdot }\right) } \frac{\Gamma \left( \tau _{k,\ell } + \alpha _{k,\ell }\right) }{\Gamma \left( \tau _{k,\ell }^{\backslash m} + \alpha _{k,\ell }\right) } \prod \limits _{r\not =\ell }^{K} \frac{\Gamma {(\tau _{k,r} + \alpha _{k,r}})}{\Gamma \left( \tau _{k,r}^{\backslash m} + \alpha _{k,r}\right) } \nonumber \\= & {} \frac{\Gamma \left( \tau _{j,\cdot }^{\backslash m} + \alpha _{j,\cdot }\right) }{\Gamma \left( \tau _{j,\cdot }^{\backslash m} + \alpha _{j,\cdot } + 1\right) } \frac{\Gamma \left( \tau _{j,k}^{\backslash m} + \alpha _{j,k} + 1\right) }{\Gamma \left( \tau _{j,k}^{\backslash m} + \alpha _{j,k}\right) }\\&\frac{\Gamma \left( \tau _{k,\cdot }^{\backslash m} + \alpha _{k,\cdot }\right) }{\Gamma \left( \tau _{k,\cdot }^{\backslash m} + \alpha _{k,\cdot } + 1\right) } \frac{\Gamma \left( \tau _{k,\ell }^{\backslash m} + \alpha _{k,\ell } + 1\right) }{\Gamma \left( \tau _{k,\ell }^{\backslash m} + \alpha _{k,\ell }\right) }\\= & {} \frac{\tau _{j,k}^{\backslash m} + \alpha _{j,k}}{\tau _{j,\cdot }^{\backslash m} + \alpha _{j,\cdot }} \ \frac{\tau _{k,\ell }^{\backslash m} + \alpha _{k,\ell }}{\tau _{k,\cdot }^{\backslash m} + \alpha _{k,\cdot }}, \end{aligned}$$

where the last equation is obtained by using $\Gamma \left( x+1\right) = x\, \Gamma \left( x\right)$.

For $j = k$ and $\ell \not = k$, we can see that $\tau _{k,\cdot } = \tau _{k,\cdot }^{\backslash m} + 2$ and for the other case $q \not = k$, $\tau _{q,\cdot } = \tau _{q,\cdot }^{\backslash m}$ hold. We can also note that $\tau _{k,k} = \tau _{k,k}^{\backslash m} + 1$ and $\tau _{k,\ell } = \tau _{k,\ell }^{\backslash m} + 1$ hold, as does $\tau _{q,r} = \tau _{q,r}^{\backslash m}$ for the other cases. We thus have the following.

$$\begin{aligned} P(z_{m}= & {} k \mid \mathbf {Z}^{\backslash m}, \varvec{\alpha }) \\= & {} \frac{\Gamma \left( \tau _{k,\cdot }^{\backslash m} + \alpha _{k,\cdot }\right) }{\Gamma \left( \tau _{k,\cdot }^{\backslash m} + \alpha _{k,\cdot } + 2\right) } \frac{\Gamma \left( \tau _{k,k}^{\backslash m} + \alpha _{k,k} + 1\right) }{\Gamma \left( \tau _{k,k}^{\backslash m} + \alpha _{k,k}\right) } \ \frac{\Gamma \left( \tau _{k,\ell }^{\backslash m} + \alpha _{k,\ell } + 1\right) }{\Gamma \left( \tau _{k,\ell }^{\backslash m} + \alpha _{k,\ell }\right) }\nonumber \\= & {} \frac{\tau _{k,k}^{\backslash m} + \alpha _{k,k}}{\tau _{k,\cdot }^{\backslash m} + \alpha _{k,\cdot }} \ \frac{\tau _{k,\ell }^{\backslash m} + \alpha _{k,\ell }}{\tau _{k,\cdot }^{\backslash m} + \alpha _{k,\cdot } + 1}. \end{aligned}$$

For $j = k$ and $\ell = k$, we can see that $\tau _{k,\cdot } = \tau _{k,\cdot }^{\backslash m} + 2$ and for the other case $q \not = k$, $\tau _{q,\cdot } = \tau _{q,\cdot }^{\backslash m}$ hold. Moreover we can also note that $\tau _{k,k} = \tau _{k,k}^{\backslash m} + 2$ hold, as does $\tau _{q,r} = \tau _{q,r}^{\backslash m}$ for the other cases. We thus have the following.

$$\begin{aligned} P(z_{m} = k \mid \mathbf {Z}^{\backslash m}, \varvec{\alpha })= & {} \frac{\Gamma \left( \tau _{k,\cdot }^{\backslash m} + \alpha _{k,\cdot }\right) }{\Gamma \left( \tau _{k,\cdot }^{\backslash m} + \alpha _{j,\cdot } + 2\right) } \frac{\Gamma \left( \tau _{k,k}^{\backslash m} + \alpha _{k,k} + 2\right) }{\Gamma \left( \tau _{k,k}^{\backslash m} + \alpha _{k,k}\right) } \nonumber \\= & {} \frac{\tau _{k,k}^{\backslash m} + \alpha _{k,k}}{\tau _{k,\cdot }^{\backslash m} + \alpha _{k,\cdot }} \ \frac{\tau _{k,k}^{\backslash m} + \alpha _{k,k} + 1}{\tau _{k,\cdot }^{\backslash m} + \alpha _{k,\cdot } + 1}. \end{aligned}$$

To summarize, for $Z_{m-1} = j$ and $Z_{m+1} = \ell$,

$$\begin{aligned} P(z_{m}=k\mid \mathbf {Z}^{\backslash m},\varvec{\alpha }) = {\left\{ \begin{array}{ll} \frac{\tau _{j,k}^{\backslash m} + \alpha _{j,k}}{\tau _{j,\cdot }^{\backslash m} + \alpha _{j,\cdot }} \frac{\tau _{k,\ell }^{\backslash m} + \alpha _{k,\ell }}{\tau _{k,\cdot }^{\backslash m} + \alpha _{k,\cdot }} &{} j \not = k\\ \frac{\tau _{k,k}^{\backslash m} + \alpha _{k,k}}{\tau _{k,\cdot }^{\backslash m} + \alpha _{k,\cdot }} \frac{\tau _{k,\ell }^{\backslash m} + \alpha _{k,\ell }}{\tau _{k,\cdot }^{\backslash m} + \alpha _{k,\cdot } + 1} &{} j = k \text { and } \ell \not = k \\ \frac{\tau _{k,k}^{\backslash m} + \alpha _{k,k}}{\tau _{k,\cdot }^{\backslash m} + \alpha _{k,\cdot }} \frac{\tau _{k,k}^{\backslash m} + \alpha _{k,k} + 1}{\tau _{k,\cdot }^{\backslash m} + \alpha _{k,\cdot } + 1} &{} j = k \text { and } \ell = k .\end{array}\right. } \end{aligned}$$

(13)

Because the factor for the sensor outputs is the same as Eq. 10, we obtain the following conditional probability for a Gibbs sampling to estimate the parameters of the DMM model with activity bigrams.

$$\begin{aligned} P(z_{m}= & {} k \mid \mathbf {Z}^{\backslash m}, \mathbf {W}, \varvec{\alpha }, \varvec{\beta }) \nonumber \\\propto & {} P(z_{m} = k \mid \mathbf {Z}^{\backslash m}, \varvec{\alpha }) \frac{{\prod _{v}^{V}} \prod _{n=1}^{N_{m}^{v}} (\omega _{k,v}^{\backslash m} + \beta _{k,v} + n - 1)}{\prod _{n=1}^{N_{m}} (\omega _{k,\cdot }^{\backslash m} + \beta _{k,\cdot } + n - 1)}. \end{aligned}$$

(14)

By using Gibbs samplers described above, we obtain the learning algorithm for the DMM models, which is listed in the Appendix 1.

5 Experiments

In this study, we examine the effectiveness of DMM models in activity discovery using two publicly available datasets obtained from real-life environments. In particular, we aim to gain insight into the following research questions.

• 1. Are DMM models, which are known to be effective in clustering short texts, also effective in activity discovery? We compared the DMM models with other generative models, HMMs, LDA models and hierarchical DPM models as well as the k-means clustering method and the sequence mining method to answer this question.

• 2. Are the bigrams of activities in DMM models effective?

• 3. How does the number of clusters pre-fed to a model affect the performance? In particular, we would like to know how much overfitting to the data occurs if we apply a larger number of clusters than is strictly necessary.

• 4. How much do the hyper parameters $\alpha$ and $\beta$ affect the results? In particular, we would like to know whether it is appropriate to give initial values $\alpha _{k} = 1$ $(1 \le k \le K)$ and $\beta _{v} = 1$ $(1 \le v \le V)$, which seems reasonable in the absence of prior knowledge.

• 5. How does the length of the analysis window affect the result? Though the use of the DMM model for short time interval seems to be effective, we would like to know the extent to which its performance degrades as the length increases.

• 6. How the data representation affect the result? Especially, we are interested in how to deal with the time intervals that have no sensor signals.

The target sensor stream is divided into segments with a constant time width, and their clusters are predicted as possible activities using the generative models trained from training data without actual activity labels. Because the actual labels also give clusters of segments, that is, clusters of segments with the same activity label, the agreement of these two sets of clusters is evaluated by commonly used clustering metrics.

However, in the actual use of activity discovery algorithms, discovered clusters are examined by the users and assigned appropriate activity labels. A cluster can be more specific than an activity assumed by the users. To examine the correspondence between discovered clusters and activities given by the annotators, we calculate a mapping from the clusters to the activity labels based on the activity labels given to the training data. The mapping can also be used to compute activity labels for any segments in the evaluation data, and more straightforward evaluation metrics such as the accuracy, and F1 score are calculated. These metrics allow us to compare the results of activity discovery algorithms with those of previously studied activity recognition algorithms.

5.1 Datasets

We use two publicly available datasets for which activity discovery has been studied.

The first dataset is the house A testbed used in [19]. The data were collected from a 26-year-old man living in a three-room apartment for 25 days. A total of 14 sensors were installed in three rooms, including reed switch sensors to detect the opening and closing of doors, cupboards, microwave ovens, refrigerators, and washing machines, and a flush sensor to detect toilets flushing. In addition, 10 activities, including leaving the residence, using the toilet, showering, brushing one's teeth, sleeping, preparing breakfast and dinner, snacking, drinking water, and others, were annotated. In the literature [24], frequent itemset mining was applied together with various assumptions regarding activities to obtain a result comparable to supervised classification. We refer to this dataset as the Kasteren dataset.

The Kasteren dataset is a benchmark that has been cited in previous studies. However, because reed switch sensors requires significant time and effort to install, PIR motion sensors, which are battery-powered and easy to install, are often used to monitor and analyze the daily activities of the elderly [6, 7]. For this study, we used the Aruba testbed data from the WSU CASAS dataset [20]. This dataset contains data from motion sensors, door switch sensors, and temperature sensors, which were placed in the home of an elderly female volunteer. Although it contains data for a period of approximately 7 months, we only use the data from the first 30 days. This is because living environment and daily activity patterns are highly likely to change during a lengthy period, and we want to remove such data drift in the evaluation of the ability of the generative model to fit the data. Furthermore, we ignore the data from the temperature sensors and the wide-range motion sensors covering an entire room. A total of 26 motion sensors and 3 door opening-sensors are used. For the motion sensors, we ignore “off” signals because they are not directly related to activities, and reach an “off” state when a certain time has passed since the sensor stopped detecting people. The dataset is annotated with 11 activities: meal preparation, relaxing, eating, working, sleeping, washing dishes, using the toilet, entering the home, leaving the home, housekeeping, and using a medical device. During the experiments described below, we merge the periods between leaving and entering the residence into a single period and label them as “going out” because we are interested only in the fact that the resident is not present in the house. In addition, we assigned the activity label “others” to a time interval in which no activity label is given. As a result, a total of 11 activity labels were assigned. We refer to such data as the Aruba dataset. The literature [21] shows that, for the Aruba dataset, activity patterns corresponding to the predefined activities can be extracted semi-automatically.

Both datasets were divided into day-by-day data for the evaluation using leave-one-day-out cross-validation. As in a previous study [19], we divided the data at 3:00 a.m., which is the probable end time of the day’s activities. As a result, the Kasteren dataset was divided into 25 days, and the Aruba dataset was divided into 30 days.

5.2 Data representation

Because the time intervals of the activities were not known in advance, the time series of the sensor data were divided into analysis windows for which the activities were estimated. Previous studies have used analysis windows defined by a fixed time width or a fixed number of sensor events. The larger the analysis window used, the more error there will be based on the boundary discrepancies between activities and windows. In contrast, if the analysis window is reduced, less information is used for analysis and the prediction error increases. Therefore, the size of the analysis window is directly related to the performance of the activity recognition and the activity discovery. In [19], various fixed time lengths were examined, and finally analysis windows with a 1-min length were adopted. In this paper, we use the same 1-min analysis windows for the Kasteren dataset. For the Aruba dataset, we examined the different lengths of windows: from 30 seconds to 10 minutes.

In [19], each analysis window is represented with a multi-hot vector whose dimensions are the same as the number of sensors and in which three different representations were considered. The first representation was referred to as “raw representation,” where any component corresponding to the sensor turned on in the analysis window is set to a value of 1. The second is “change representation,” which sets 1 to those components corresponding to sensors whose values have changed by turning on and off in the analysis window. The third is “last representation,” which sets a value of 1 to the component corresponding to the last sensor that changed its value before the end of the analysis window. According to the results of the experiment described in [19], the raw representation exhibited a poor activity classification performance. This is partly because a switch sensor is not necessarily turned off when the resident stops using the corresponding object. For example, doors are often left open by mistake, and the switch sensor attached to the door always remains on even if the resident is out of the house. The change representation and the last representation are not affected by such noise.

However, as a drawback of the change representation, the values of all components in a feature vector will be 0 when the state of all sensors is not changed. For example, for 10 minutes while the dishwasher is running, no sensor signal is obtained for most of the segments within 10 min except for the firs t and last segments. Models that do not consider a context including the first and the last segment, e.g., the LDA model and the DMM model without activity bigrams, have no information to predict activities for the segments with no sensor signal. In this situation, the last representation is helpful, that is, the power on signal of the dishwasher is given to the segments that have no signal. The last representation assumes that the resident stays in the same situation when no sensor information is available because if a situation of the resident changes, it is highly likely that another sensor will be activated in the new situation. This assumption has an unexpectedly positive side effect for the going-out activity, which occupies a large amount of time in the data. During time periods in which the resident is out, for segments that have no sensor signal, the bits corresponding to the front door are set to 1. Although this is simply a heuristic, in fact, the resident is not in the house during the activity, it seems to have been effective, at least for the Kasteren dataset. As shown later, it was also effective for the Aruba dataset, especially for models that cannot describe the context of activities. However, for models capable of taking into account the context of the activities, it is not necessarily needed, which is discussed in Section 5.6.3.

As a drawback of the last representation, when the values of multiple sensors change within a certain analysis window, all information other than the last changed sensor is ignored. Therefore, in this study, we combine the change representation with the last representation. That is, sensors whose values have changed within a certain window were added to the corresponding observation vector, and if no such sensor existed, the last sensor outputting a changed value is then added to the observation vector.

As mentioned above, if the sensor does not change for a long period of time, for example, when the resident is out of the house, a series of analysis windows that include only the last changed sensor are considered. To ensure that such windows are included in a consistent cluster, and to improve the computational efficiency by reducing the number of analysis windows, we merge the consecutive windows in which no sensor changes. We refer to an analysis window or merged windows as a segment.

5.3 Generative models and hyper parameters

We investigated five different generative models with latent activities, i.e., the HHM, the LDA model, the hierarchical DPM model, the DMM model, and the DMM model using activity bigrams as well as the k-means clustering method and an activity discovery algorithm using frequent sequence mining.

For the HMM, we used the class hmmlearn.hmm.MultinomialHMM in the hmmlearn toolbox². The maximum number of iterations was set to 3000, and different values of the the possible number K of hidden states were attempted. Default values were used for all other parameters. Because multiple states were estimated for a segment, the state with the highest frequency was considered as the state of the segment.

For the LDA models, we used the class models.ldamodel in the Gensim toolbox [36]. For the number K of topics, namely, latent activities, different values were attempted. We used the option in which the hyperparameters ${\varvec{\alpha }}$ and ${\varvec{\beta }}$ were learned as asymmetric values from the data. All other parameters were set to the default values. After obtaining the proportion of topics for each segment, the topic with the maximum weight is assigned to the segment.

For the hierarchical DPM models, we used the class models.hdpmodel in the Gensim toolbox [36].

For the DMM model, we used Algorithms 1 and 2 with $B=0$, and Eq. 11 as a Gibbs sampler. For the DMM model using activity bigrams, we use Algorithms 1 and 2 with $B=1$, and Eq. 14 as a Gibbs sampler. The numbers of iterations $I_{t}$ and $I_{e}$ were set to 3000 and 1000, respectively. All hyperparameters $\alpha _{k}$ ($1 \le k \le K$) and $\beta _{v}$ ($1 \le v \le V$) are set to 1. These symmetric and flat parameters are reasonable when no assumption about the prior probabilities is known because they give the same probability mass on the ($K-1$)-simplex of the activities and the ($V-1$)-simplex of the sensors. Different values of the number K of allowable clusters were attempted.

Other than these generative models, a typical clustering algorithm, the k-means method, was applied. We used the class sklearn.cluster.KMeans in the Scikit-lean [35] toolbox. Each segment was represented by a vector whose elements were the probabilities of occurrence of each sensor. Different values of the number K of clusters were attempted.

A frequent sequence mining algorithm, called the AD algorithm, presented in [8] was also applied. We used the code downloadable from CASAS repository [20]. This algorithm loops a specified number of times to extract sequential patterns from sensor signals labeled as the activity “others” and then performs clustering to extract frequent sequence patterns that can compress the data well. In the following experiment, all labels for predefined activities were converted into “others,” and then K loops were run to extract the frequent sequence patterns. While the code can extract frequent patterns in a training dataset, it cannot extract the same patterns in a test dataset. Therefore, we applied the code for the entire dataset and extracted frequent patterns and evaluated the extracted patterns with leave-one-day-out cross-validation. This means the evaluation was not completely fair and is advantageous to this method: patterns were extracted not only from training splits but also from a test split.

5.4 Evaluation metrics

To compare the performance of activity discovery algorithms that predict clusters of segments, we use commonly used evaluation metrics of clustering that measures how much discovered clusters agree with annotated activities. In addition, to analyze the correspondence between the clusters and the activities, mappings from cluster labels to activity labels are computed from the activity labels assigned to the training data. With this mapping, we can assign activity labels to the clusters of the evaluation data, and evaluate discovered clusters using more straightforward metrics, i.e., the accuracy, precision, recall, and F1 score. These metrics were computed for all analysis windows in the evaluation data. When consecutive analysis windows were merged into a single segment, the cluster label assigned to the segment was copied to the merged analysis windows. After the evaluation metrics for all analysis windows in an evaluation day were calculated, the computed metrics were then averaged across all evaluation days through leave-one-day-out cross-validation.

To compare the results of experiments using different lengths of the analysis window, we equalized the length of windows prior to the above evaluation. When the length of the analysis window was longer than 60 seconds, then each window was divided into windows of length 60 seconds, and the cluster label of the original window was assigned to the divided windows. If the length of the analysis window was shorter than 60 seconds, shorter windows were merged into a window of length 60 seconds and the cluster label that appeared most frequently in the shorter windows was assigned to the merged window.

The first clustering metric is the adjusted mutual information (AMI) [32], which is an information theoretic measure and quantifies the amount of common information between two partitions of data. The upper bound of AMI is 1, which indicates that the two partitions are equal up to the permutation. For a random partition, the AMI score reaches close to 0.

Another clustering metric, the adjusted Rand index (ARI) [33], is also used. The Rand index [34] counts the number of pairs with matched label assignments, that is, both are assigned to the same cluster label and the same activity label, or both are assigned to different cluster labels and different activity labels. The ARI score is the normalized version of the Rand index; and thus, it is adjusted to close to 0 for random label assignments. For a cluster label assignment equal with the class labels up to the permutation, the ARI score is 1.

To compute both metrics, we used the code in the Scikit-learn [35] toolbox.

When applying an activity discovery to real-world problems, the discovered clusters are examined by humans and are assigned appropriate activity labels. To simulate this process, we used the activity labels assigned to the training data to calculate the mapping $act\left( \cdot \right)$ from the cluster labels to the activity labels, which is simply defined as a majority vote. More precisely,

$$\begin{aligned} act\left( c\right) = \underset{a}{\text {arg} \max } \mid \{t \in T \mid C\left( t\right) = c\ \text {and}\ A\left( t\right) = a\}\mid , \end{aligned}$$

where T is the set of analysis windows in the training data, $C\left( t\right)$ is the cluster label of t, and $A\left( t\right)$ is the activity label of t. If $act\left( \cdot \right)$ is not undefined for c, which is the case that c is discovered only in the evaluation data, then we assume c is mapp ed to the activity “others”. Assuming the mapping $act\left( \cdot \right)$, the accuracy, precision, and recall for the evaluation data are computed as usual. In the literature [19], the precision and recall are macro-averaged across the activity labels, and the F1 score is computed from the macro-averaged precision and recall. More precisely, they are computed as follows.

$$\begin{aligned} Accuracy (E)= & {} \frac{\sum _{a \in AC\left( E\right) } \mid TP_{a}\left( E\right) \mid }{\mid E\mid } \\ pre (E)= & {} \frac{1}{\mid A\left( E\right) \cup AC\left( E\right) \mid } \sum \limits _{a \in AC\left( E\right) } \ \frac{\mid TP_{a}\left( E\right) \mid }{\mid \{e \in E \mid act\left( C\left( e\right) \right) = a\}\mid } \\ rec (E)= & {} \frac{1}{\mid A\left( E\right) \mid } \sum \limits _{a \in A\left( E\right) } \frac{\mid TP_{a}\left( E\right) \mid }{\mid \{e \in E \mid A\left( e\right) = a\}\mid }\\ F1(E)= & {} {\left\{ \begin{array}{ll} \frac{2 pre(E) rec(E)}{pre(E) + rec(E)} &{} pre(E) + rec(E) > 0\\ 0 &{} pre(E) + rec(E) = 0 ,\end{array}\right. } \end{aligned}$$

where E is the set of analysis windows in the evaluation data, $TP_{a}\left( E\right) = \{e \in E \mid act\left( C\left( e\right) \right) = A\left( e\right) = a\}$, $A\left( E\right) = \{A\left( e\right) \mid e \in E\}$, and $AC\left( E\right) = \{act\left( C\left( e\right) \right) \mid e \in E\}$. To compare the results in [19], we use the same definition above.

As described above, these metrics are calculated for all analysis widows with the same length. Therefore, the accuracy is evaluated by placing more weight on the activities that occupy a greater amount of time. In contrast, the precision, recall, and F1 score are obtained by averaging the scores calculated for each activity; and thus, activities occupying a small amount of time are evaluated with equal weight.

It is also important to note that the accuracy, precision, recall, and F1 score tend to become higher as the number of discovered clusters increases. As an extreme case, if we consider the case in which each cluster consists of only a single element, these evaluation metrics takes a value of 1 under a mapping of each cluster label into the activity label given to the single element. Therefore, although such metrics can be used to compare the results obtained with a similar number of clusters, they should not be used to compare the results with significantly different numbers of clusters. In this regard, the AMI and ARI score can be used to compare the results obtained with different numbers of clusters because the effect of the number of clusters is adjusted for both scores.

Table 1 shows the numbers of discovered clusters for the Kasteren dataset and the Aruba dataset, where HMM, DMM2, DMM, DPM, SeqM and KM denote the HMM, the DMM model with activity bigrams, the DMM model, the hie rarchical DPM model, the frequent sequence mining algorithm and the k-means clustering method respectively. It may be observed that the DMM model maintains a small number of discovered clusters even when K is large. In terms of dataset differences, it is also worth noting that more clusters have been found in the Aruba dataset than in the Kasteren dataset.

Table 1 The numbers of discovered clusters for (a) Kasteren dataset and (b) Aruba dataset: the numbers are listed for different models with different K starting from the numbers of annotated activities, 10 for Kasteren dataset and 11 for Aruba dataset. For each model, the first row shows the arithmetic means (AMs) of the number of clusters obtained through leave-one-day-out cross-validation. The second row shows their standard deviations (SDs)

5.5 Results for the Kasteren dataset

Table 2 shows the AMI and ARI scores of different clustering methods applied to the Kasteren dataset. We also show the results of an activity classifier, denoted by supHMM, using the HMM trained with supervised learning with activity labels. Although the classifier may be considered impractical owing to the limited availability of labeled data, we expected it to exhibit better performance than unsupervised clustering methods. It also shows the results of the DMM model with $\alpha =100$, denoted by DMM$\alpha$, and the DMM model using activity bigrams with $\alpha =100$, denoted by DMM2$\alpha$. These extreme settings were motivated by the unexpected highest performance of the k-means clustering, which only uses the similarity between distributions of sensor signals. A large $\alpha$ approximates the factor of the acti vities, Eq. 9 or 13, as constants and is equivalent to assuming that activities are determined almost solely by sensor signals, without the help of the distribution of activities. Under the assumption, DMM$\alpha$ performed better than DMM significantly, DMM2$\alpha$ performed better than DMM2 significantly, and there exists no significant difference between DMM2$\alpha$ and DMM$\alpha$.

Table 2 Kasteren dataset: clustering scores (a) AMI and (b) ARI for different models with different numbers K of clusters starting from 10, which is the number of annotated activities. For each model, the first row shows the arithmetic means (AMs) of scores obtained through leave-one-day-out cross-validation. The second row shows their standard deviations (SDs). Each p-value in the third row was obtained from paired t-test against DMM2$\alpha$ with the same K

Table 3 Kasteren dataset: classification scores (a) accuracy and (b) F1 score for different models with different numbers K of clusters

Moreover, DMM2$\alpha$ performed comparably with KM and DPM, and it performed slightly, though not significantly, worse than supHMM. The sequence mining, SeqM, performed significantly worse than DMM2$\alpha$ except at $K=30,50$. The fully unsupervised clustering using the HMM, denoted by HMM, performed worse than DMM2$\alpha$ as K increased and exhibited overfitting as the capacity of the model increased. The LDA model performed comparably or worse than DMM2$\alpha$ at $K=30, 50$.

Table 3 shows the accuracy and F1 scores of of different models. As explained in Section 5.4, both scores were computed after discovered clusters were transformed into activity labels by a mapping defined by the activity labels given to the training data. For both scores, similar results were observed as well as the AMI and ARI scores. Again the k-means clustering method, KM, performed best, and the sequence mining, SeqM, performed worst especially at a small K. The DMM model using activity bigrams with $\alpha =100$, DMM2$\alpha$, performed slightly worse than KM, and comparable with DMM$\alpha$ and DPM, and performed better than HMM and LDA.

Of note, the accuracy of the classifier supHMM was worse than other clustering methods; in particular it was worse than HMM employing the same type of the HMM model. A more detailed analysis shows that supHMM exhibited a poor recall rate for the activity labeled “others.” This is because the activity “others” includes a variety of different activities, and a single multinomial distribution of sensor signals cannot represent the class of multiple activities. The HMM model trained through unsupervised learning was able to assign different clusters for activities corresponding to the activity “others” and thus obtained better accuracy. In contrast, for the F1 score, supHMM performed better than clustering methods because clustering methods failed to assign clusters for activities occupying a small amount of time and the F1 score evaluates such minor activities with equal weight.

In general, activities in the Kasteren dataset seems to be strongly correlated with specific sensor signals; thus, predicting activities based on the sensor signals is relatively easy.

Table 4 Aruba dataset: clustering scores (a) AMI and (b) ARI for different models with different numbers K of clusters

5.6 Results for the Aruba dataset

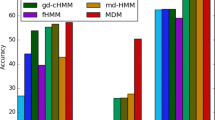
Table 4 shows the AMI and ARI scores of different models applied to the Aruba dataset.

We can see that the DMM model and the DMM models with activity bigrams performed better than the other methods. In particular, the DMM model with activity bigrams scored significantly higher than the HMM, the LDA model, the hierchical DPM model, the sequence mining algorithm, and k-means clustering method at all Ks, and also scored significantly higher than the DMM model at $K=11, 15$. As another observation, both the DMM models showed consistently high scores even when K increased, whereas the LDA model and the HMM degraded as K increased.

Table 5 Aruba dataset: classification scores (a) accuracy and (b) F1 score

Table 5 shows the accuracy and F1 scores of different models applied to the Aruba dataset. It may be observed that the DMM model and the DMM model with activity bigrams performed better at a small K. Even in comparison with the classifier, supHMM, trained through supervised learning, the DMM model with activity bigrams showed a comparable performance. As we stated above for the Kasteren dataset, the lower performance of supHMM stems from a lower recall rate for the activity “others”.

As K increases, the difference against other methods becomes small. However, overly specific clusters make subsequent analysis difficult. In this regard, for HMM, DPM, and KM, the large number discovered clusters shown in Table 1 might be undesirable.

5.6.1 Influence of the initial hyper parameters

Table 6 shows the effects of the initial parameters $\mathbf {\varvec{\alpha }}$ and $\mathbf {\varvec{\beta }}$ on the AMI scores at $K=11$ for the Aruba dataset. Here, we assume the parameters of Dirichlet distributions are symmetric, that is, $\alpha _{k} = \alpha$ ($1 \le k \le K$) and $\beta _{v} = \beta$ ($1 \le v \le V$). We can see that for both the DMM model and the DMM model with activity bigrams, $\alpha$ did not seem to have any significant effect on the AMI score. For parameter $\beta$, it made a significant difference in the results, but for the DMM model, $\beta =1$ yielded the best score, whereas for the DMM model with activity bigrams, $\beta =4$ provided the highest AMI score. In any case, there was no large difference from the case of $\beta =1$. Therefore, for this dataset, learning with the initial values of $\alpha =1$ and $\beta =1$, which is reasonable in the absence of prior knowledge, is not an unsuitable option.

Table 6 Aruba dataset: comparing the AMI score of (a) the DMM model and (b) the DMM model with activity bigrams at $K=11$ for different initial parameters of Dirichlet distributions. Each p-value in the third row was obtained from paired t-test against the setting $\alpha =1$ and $\beta =1$

5.6.2 Influence of the length of the analysis window

Tables 7, 8, and 9 show the AMI and ARI scores of different models applied to the Aruba dataset represented with the analysis window of length 30, 300, and 600 s respectively. Figure 4 shows the change in both scores versus the length of the analysis window at $K=11$. As the length of the analysis window increases, the performance of the LDA model and the hierarchical DPM model, which generates sensor signals according to a mixture distribution of multiple activities, are expected to improve. However, for the lengths studied here, the performance of the DMM models was consistently better.

Fig. 4

Aruba dataset: clustering scores (a) AMI and (b) ARI for data represented with the analysis window with lengths of 30, 60, 300, and 600 seconds at $K=11$

Table 7 Aruba dataset: clustering scores (a) AMI and (b) ARI for data represented with analysis windows of length 30 seconds

Table 8 Aruba dataset: clustering scores (a) AMI and (b) ARI for data represented with analysis windows of length 300 seconds

Table 9 Aruba dataset: clustering scores (a) AMI and (b) ARI for data represented with analysis windows of length 600 seconds

5.6.3 Influence of the use of the last representation

Table 10 shows the AMI and ARI scores of different models applied to the Aruba dataset represented without the last representation. For any segment where there was no sensor signal, a special symbol, referred to as the null symbol, was inserted into the null segment.

Table 10 Aruba dataset: clustering scores (a) AMI and (b) ARI for data represented without use of the last representation

Models other than HMM and DMM2 showed significant degradation in performance. This is because they cannot distinguish activities such as “sleeping,” “going out,” and “relaxing,” in which the null segments frequently appear. Since there is no information to distinguish the null segments other than context information, they cannot identify activities to which the null segments belong. On the other hand, for a model capable of taking into account the Markov property on activities, it is possible to estimate which activity generated the null segment depending on the previous and next activity.

Another interesting observation is that the performance of supHMM is worse than that of HMM and DMM2. For activities “sleeping” and “going out,” the probability of the occurrence of the null signal is relatively high since the frequency of sensor signals other than the null signal is low in these activities. In contrast, for the activity “relaxing,” there exist many sensor signals other than the null signal occurring in this activity; and thus, the probability of the occurrence of the null signal is relatively low in this activity. Therefore, it is difficult to predict the activity “relaxing” for the null segment even if contextual information of previous and next activities is available. For the HMM and the DMM model with activity bigrams trained through unsupervised learning, a specific cluster can be assigned to the null segments during the activity “relaxing”; and thus, their performance does not degrade. If the data is described by the last representation, sensor signals that frequently appear in the activity “relaxing” will be inserted in the null segment, so supHMM can predict the null segment correctly; and thus, its performance degradation can be avoided.

As shown above, the last representation was a useful heuristics for the Aruba dataset as well as for the Kasteren dataset though it is not necessarily useful for other datasets. Without the use of the last representation, the HMM model and the DMM model with activity bigrams trained through unsupervised learning showed good performance. Especially, the DMM model with activity bigrams showed consistently better performance even when its model capacity became large in contrast with the HMM model, which overfitted as K increased.

5.7 Discussion

As may be seen above, in the Kasteren dataset, there is no significant performance difference between different activity discovery methods investigated in this study. However, the HMM degrades at a large number K of activities, and K should be carefully chosen for the sequence mining method. Also for the DMM models, by setting the hyperparameter $\alpha$ to an extremely large value, the factor of the distribution of activities should be canceled out. Then activities were estimated only from the distribution of sensor signals; and thus, good performance is obtained. Together with the highest performance of the k-means clustering methods that use only the similarity between the distribution of sensor signals, activities in this dataset can be easily predicted directly from sensor signals. It is also consistent with the result shown in [24] that the frequent itemset mining is applied to the dataset and yields a comparable performance to the classifier using the HMM trained through supervised learning. We could not find much merit in applying the DMM models to the dataset although the models achieve comparable performance by adapting to the extreme condition.

In contrast, for the Aruba dataset, the DMM models perform better than the other activity discovery methods above. One of the differences between the two datasets is the burstiness. In the Kasteren dataset, after a sensor is turned on, it is unlikely that the sensor will continue to be turned on, for example, it is unlikely that a toilet flushing sensor will be turned on multiple times. In contrast, in the case of the Aruba dataset, when a sensor detects a motion, it likely fires more than once owing to the same motion, and it makes sense that we would observe the burstiness shown in Fig. 1. The results of the experiment in which the DMM models perform well in the Aruba dataset support the hypothesis that the DMM models are advantageous for data that show burstiness. One might think that the burstiness can be artificially removed by filtering out sensor signals that fire repeatedly. However, it is not obvious that burstiness can be removed because the firing of a signal is not necessarily repeated consecutively, but is interrupted by the firing of other signals and noise. Moreover, artificially manipulating the sensor signal has a high risk of distorting the true distribution. Rather, the burstiness should be used as a hint for estimating the true distribution. For example, if some sensor signals are not inherently associated with activities and do not exhibit burstiness, then we can reduce the effect of the noisy signals by capturing burstiness of sensors generated from the activities. Thus, a more noise-robust and accurate activity model is expected to be estimated from the data.

As can be seen in Table 4, the number K of possible clusters does not affect the AMI and ARI scores of the DMM model. In contrast, the HMM and the LDA model degrade significantly when a large K is given, which means that both models require a method for determining the appropriate K depending on the data. Hierchical DPM model is a topic model similar to the LDA model, but it determines the number of clusters from the data. The DMM model performs consistently better than the DPM model , regardless of the value of K. Especially, the DMM model with activity bigrams performs significantly better than the original DMM model at $K=11,15$, and slightly superior at $K=100$. Infomation on the context of activities seems to be effective even when data are described by using the last representation, but it is more vital when the last representation is not used as shown in Table 10.

Compared with the activity classifier supHMM using the HMM trained through supervised learning, the DMM model with activity bigrams performs significantly worse for the AMI and ARI scores. In terms of accuracy, it performs comparable or slightly better than the classifier. As stated before, the performance gain is because different clusters can be assigned to the various activities included in the activiy labeled as “others”. The improvement is consistent with a result in the literature [8], in which a newly discovered activity that does not correspond to the predefined activities can contribute to improving the accuracy of activity recognition. Data collected in a real-life setting contains many activities other than predetermined activities, and accurate modeling is possible by finding the latent activities through activity discovery. This is another advantage of activity discovery other than lower annotation cost.

For the F1 score, the DMM model with activity bigrams performs comparable or slightly worse than supHMM. This is due to the poor prediction of some activities, such as “using the toilet,” “washing dishes,” “housekeeping,” and “using medical device.” This is partly because of the lack of data to estimate clusters corresponding to the activities. However, another reason stems from the mapping of the activity label for discovered clusters based on the majority voting. For a cluster of segments, the activity label for the cluster is determined as the most frequent label among labels assigned to the segments. Now, if we consider a case in which one discovered cluster is a common sub-activity of multiple activities, the label of this cluster will be mapped to the label of the most frequent activity. As a result, the precision, recall, and F1 scores for less frequent activities will deteriorate significantly, whereas the accuracy, which depends heavily on the frequent activities, does not deteriorate much. Even if a common sub-activity is correctly identified, it will not be utilized if it is converted into an activity label defined by the majority vote. It is thus necessary to have a mechanism to assign a new and different label as a common sub-activity or to assign different sub-activity labels depending on which activity it belongs to.

A clear drawback of the DMM model is the simplistic assumption that sensor signals are generated from a single activity. This contrasts with the LDA and hierarchical DPM models, which assume that the sensor signals are generated from a mixture of multiple activities. It seems reasonable to assume that sensor signals within short time intervals are generated by one specific activity, not multiple activities. However, the more the length of the analysis window, the more likely multiple activities are involved in the process of the generation of sensor signals. To see the influence of the length of the analysis window, we conducted experiments using the analysis window with different lengths: 30, 60, 300, and 600 seconds. The experiments show that the DMM model consistently performed well in all cases. Therefore, the DMM model seems to be effective in discovering activities that correspond to the time granularity considered here.

6 Limitations and future work

In the experiments discussed above, to automatically calculate the accuracy and F1 scores, the mapping from clusters to activity labels is calculated using the activity labels assigned to the training data. However, the actual use of an activity discovery algorithm requires interacting with users to determine the activity labels of the discovered clusters. To this end, it is important to have a means to efficiently determine the correspondence between clusters and activities with as few questions for the users as possible.

For example, a cluster may need to be identified as different activities depending on the day of the week or the time of the day. In other cases, when a common sub-activity of different activities is extracted as a single cluster, it may be desirable to distinguish the cluster depending on which activity it belongs to. Alternatively, it may be necessary to hierarchize different clusters to form a common activity. Though we cannot discuss the problem of transforming discovered clusters into activity labels understandable for users, it is an important future research topic.

The proposed method can also be improved by incorporating various assumptions used in the activity analysis. For example, if the possible activities differ depending on the day of the week or the time of the day, it would be effective to divide up data by the day of the week or the time of the day and then to train separate models. In addition, the proposed method does not model the duration of activities. Although it clusters segments with a fixed time interval and identifies successive identical clusters as a single activity a posteriori, it may be possible to improve the clustering performance by explicitly modeling the duration.

Finally, data drift needs to be addressed in an actual deployment of the proposed method. The manner in which activities are conducted can change over even a short period of time owing to changes in the physical or psychological capabilities of the residents, or owing to changes in the living environment such as the layout of furniture or equipment. Since the proposed method uses unsupervised learning, it has the advantage that a new model can be built without data annotation cost if it is retrained with the most recent data. However, there are many unresolved issues, such as when to relearn and how to maintain the consistency of the discovered activities before and after relearning.

7 Conclusion

We have applied the DMM model to the activity discovery problem. The DMM model assumes that a latent activity generates sensor outputs, and employs the DM distribution as a probability distribution for the generation of sensor outputs. We empirically confirmed the effectiveness of the DMM model over other generative models such as the HMM, the LDA model, and the hierarchical DPM model, as well as the k-means method and frequent sequence mining. In particular, based on the DM distribution, the DMM model can more accurately model the data generation process in a dataset using PIR motion sensors, which exhibit burstiness, where the distribution of sensors follows the power law and even sensors that rarely fire may fire repeatedly after being triggered. To cope with the Markov dependency on activities, the DMM model was extended so that each activity depends on the preceding activity. To estimate the parameters of the extended model, we have presented a Gibbs sampler used in the MCMC algorithm. It was also shown empirically that the extended DMM model can discover a latent structure of activities in the dataset more accurately than the original DMM model. The activity discovery method discussed in this paper can be used as a primitive activity extraction tool in a more advanced human-in-the-loop activity analysis system. It is also expected that the DMM model can be useful to model other data with burstiness generated from latent states with the Markov property.

Appendix 1: Activity discovery algorithm using the DMM models