Out of sight: a toolkit for tracking occluded human joint positions
- 2.1k Downloads
- 3 Citations
Abstract
Real-time identification and tracking of the joint positions of people can be achieved with off-the-shelf sensing technologies such as the Microsoft Kinect, or other camera-based systems with computer vision. However, tracking is constrained by the system’s field of view of people. When a person is occluded from the camera view, their position can no longer be followed. Out of Sight addresses the occlusion problem in depth-sensing tracking systems. Our new tracking infrastructure provides human skeleton joint positions during occlusion, by combining the field of view of multiple Kinects using geometric calibration and affine transformation. We verified the technique’s accuracy through a system evaluation consisting of 20 participants in stationary position and in motion, with two Kinects positioned parallel, \(45^{\circ }\), and \(90^{\circ }\) apart. Results show that our skeleton matching is accurate to within 16.1 cm (s.d. = 5.8 cm), which is within a person’s personal space. In a realistic scenario study, groups of two people quickly occlude each other, and occlusion is resolved for \(85\%\) of the participants. A RESTful API was developed to allow distributed access of occlusion-free skeleton joint positions. As a further contribution, we provide the system as open source.
Keywords
Kinect Occlusion Toolkit1 Introduction
Examples of where occlusion arises in a single-camera system, showing (a) almost complete occlusion and (b) partial occlusion. In such scenarios, the person in the foreground has their skeleton detected, while the person being occluded is ignored
1.1 Problem
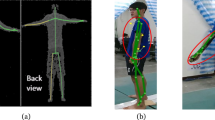
Interactive systems which depend on people and body feature detection can suffer when the tracked target is occluded by other people or objects from the system’s field of view. In particular, the occlusion problem (demonstrated in Fig. 1) is common in real deployment of single, front-view camera systems. During occlusion, the system cannot locate a users’ body joint positions. Out of Sight resolves this problem. For HCI, resolving the occlusion problem will enable interactive systems to consistently track spatial (e.g., position) or physiological (e.g., facial features) information of the users in spaces, thus improving user interactions which rely on, for example, face tracking or gesture recognition. Without knowledge of the users’ position over time, when occlusions occur naturally from interaction, depth-sensing systems currently have the following limitations: unrealistic contrived scenarios in applications, limited natural movements imposed by users’ knowledge of the system limits, and short duration of interaction before interruption due to occlusion.
1.2 Out of sight toolkit
Out of Sight is a toolkit that resolves the occlusion problem in depth-sensing systems. Specifically, it extends the existing Kinect tracking infrastructure by providing users’ joint positions during occlusion. Leveraging the larger, extended field of view comprised of multiple Kinects, the system can sense the tracking area from different angles, hence fills any missing data during occlusion from the additional Kinects. The toolkit provides occlusion-free skeleton positions from any Kinect’s field of view. Our approach builds on Wei et al.’s [5] work on the calibration of a single skeleton in a two-Kinect system. We adapt the technique to track multiple people, by transforming the skeletons in different fields of view closer to their respective camera (a common coordinate system), then matching the skeletons in this new coordinate system across cameras. This approach can be applied to other depth-sensing infrastructure which provides human skeleton joint data, as the technique only relies on geometric transformations of the joint positions. Wei et al. did not consider the occlusion problem, and in this paper, we also extend their evaluation and provide a web-based API for the real-time occlusion-free skeleton stream.
There are several Kinect-based interactive systems and interaction techniques that could be extended with the Out of Sight API. Further research can use the API to track the positions of multiple people in an occluded environment, thus resolving existing system constraints and enabling new capabilities. Research in kinesics is currently limited to two-person interactions where users are strictly standing next to each other [6]. Location-aware wearable haptics [7] require the system to robustly track users’ positions; therefore, occlusion can cause interruptions to the interaction. Sound localization [8] can also be affected by occlusion, but the use of auxiliary Kinects could enable new types of Kinect-based sound localization solutions. In collaborative environments, such as the attention- and proximity-aware multiuser interface developed by Dostal et al. [9], our occlusion-free joint data could help the system recognize otherwise absent gestures. Moreover, the API could improve ad hoc proxemic [10] and cross-device interactions [11], where interactions would no longer be limited to within the visible field of view of a single camera. In addition, the API would resolve much of the occlusion which occurs during daily human activities, for example gesturing, moving, or dancing in multiplayer gaming scenarios.
1.3 Contributions
- 1.
A toolkit (using a web-based API) for tracking multiple people’s joint positions in an interaction space with occlusion.
- 2.
A system evaluation validating the accuracy of both current and previous work on tracking human joint positions with multiple depth-sensing cameras. Our evaluation also includes new occlusion scenarios (e.g., in one’s personal space [12]).
- 3.
The tested toolkit and API are open sourced, enabling future researchers to develop tools or interaction techniques that are unaffected by occlusion.
2 Related work
Human detection in images is a widely studied area in the field of computer vision, where many challenging datasets have been created [13, 14, 15, 16, 17]. The state-of-the art approaches can reliably detect pedestrians in different poses and appearances given good imaging conditions [17], where common features are derived from gradient orientations and color channels, along with discrete cosine transforms [18]. The best results are achieved with one of the three machine learning algorithms: deformable part models, convolutional neural networks, and decision forests [18]. However, accuracy degrades with decreasing size of input images and the presence of occlusion [17].
Previous research shows that individuals can be reliably tracked in complex environments including occlusion, but current systems do not provide spatial information about people lost in occlusion, as they are blocked from the camera’s line of sight. Tang et al. [19] train a deformable parts model detector to recognize patterns of partial occlusion for pairs of people. Liu et al. [20] and Luber et al. [21] track positions of people before and after occlusion, although not during occlusion, using point ensemble images and a person detector combined with an online-learned model, respectively, from RGB-D data. Luber et al. also used multiple Kinects with an extended field of view. These systems do not track body joint positions during occlusion, as shown here. Our approach to the occlusion problem is inspired by the idea of extending the field of view with multiple depth-sensing cameras, i.e., multiple Kinect sensors. The use of multiple cameras for tracking people has been demonstrated in previous research with overlapping [22, 23, 24] and non-overlapping [25, 26] fields of view. A similar work is [27] in which multiple Kinect depth streams are combined, whereas we merge the skeleton streams while accounting for occlusion, arguably more useful for rapid design and prototyping of HCI systems.
Kinect skeleton tracking has been used in many interactive systems [9, 10, 11, 28, 29], but the occlusion problem remains unresolved. These systems require most of the user to remain unobstructed from the only camera’s field of view, hence limiting the type of interactions that would otherwise normally occur. Systems such as [4, 30] reduce occlusion by employing a top–down Kinect. However, recognizing complex gestures and interaction patterns from a top–down Kinect is difficult, because self-occlusion increases the challenge of joint localization. Furthermore, commodity depth-sensing cameras, such as the Kinect, do not provide the skeleton stream when placed in a top–down position. None of these systems provide the skeleton view of people during occlusion.
Combined view of a person’s skeleton from two different Kinects (right), and the transformed skeletons in the field of view of the front (left) and \(45^{\circ }\) (middle) Kinect. In particular, the averaged skeleton is colored in white
Out of Sight merges two Kinects’ fields of view (left and right) and provides persistent tracking of the occluded person’s joint positions in the initially limited field of view (center). In the central image, the toolkit visualizes two people’s skeleton (one occluded and the other one unoccluded), by accessing the merged skeleton stream via the RESTful API
3 Methodology
The Out of Sight toolkit locates occlusion-free body joint positions in three stages: (1) a sensing application, (2) a calibration procedure, and (3) a tracking module. Firstly, the sensing application processes incoming skeleton streams from the Kinects. Then, the application initializes calibration. For each skeleton in each field of view, it calculates their initial center position as well as the angle between their body and the camera. After calibration, the skeleton joints from every field of view are transformed to a common world coordinate system, allowing for a comparison between the skeletons. The world coordinate system is the same as the Kinect camera space, except that the skeletons during calibration are pulled closer to the camera.
The skeletons of a person from different fields of view are matched by their spatial proximity, and then tracked, in this coordinate system. Lastly, the system transforms the joint positions of the matched, averaged skeleton to the selected field of view by reversing the transformation. Figure 2 shows an example where a person’s skeleton appears in multiple depth-sensing cameras’ field of view, but we can transform their skeletons from multiple views to a single field of view, thus enabling a new occlusion-aware tracking system, in particular when the view (i.e., visibility) of the person is occluded in one camera (Fig. 3).
Out of Sight system architecture
3.1 Calibration
We briefly describe the calibration and transformation procedure presented by Wei et al. [5] (The complete mathematical formulas are presented in their paper). The system assumes that all users are visible from all Kinects during calibration. The first 120 frames are used in calibration. For every detected skeleton in each field of view, their initial center position and relative body angle to the Kinect are calculated. The skeleton’s center position is defined as the average of all 3D joint positions over all calibration frames. The angle between the skeleton and the Kinect is defined as the average angle of rotation between two vectors: the vector connecting the left and right shoulders and the perpendicular vector from the origin of the camera.
3.2 Transformation
After obtaining its initial center position and rotation angle, we can translate and rotate the skeleton to the world coordinate system, where the new coordinate system is calibrated to the origin of the Kinect device. Firstly, the joint positions are translated by the initial body center position to the origin of the camera. Secondly, the new joint coordinates are rotated about the y-axis by the initial body angle. After calibration and the initial transformation, the skeleton is parallel to the Kinect in the world coordinate system. The transformation process is applied to every skeleton in each field of view. These calculations require only the 3D body joint positions as input; hence, the approach is applicable to any depth-sensing tracking infrastructure (i.e., other than the Kinect) with human pose estimation (joint data).
3.3 Tracking
The initial tracking result contains the spatial information (i.e., the original Kinect coordinates and the world coordinates) of all currently tracked people, where each person is represented by skeletons from all fields of view. The tracking module matches skeletons across all fields of view by their spatial proximity in the world coordinate system. This extends the methodology initially proposed by Wei et al., as only one person was tracked [5]. The average skeleton (calculated using only the tracked joints) in the world coordinate system is the view-dependent representation of a person. Assuming that all people were visible to all cameras during calibration, we can reverse the Kinect-to-world coordinate transformation (i.e., inversely rotating by the initial body angle and then translating by the body center position) to obtain joint positions back in the Kinect coordinate system. The inverse transformation enables real-time tracking of people’s position through occlusion in different Kinects’ field of view. A person’s body joint positions are updated in both coordinate systems, either calculated from the skeleton feeds or through transformation. During occlusion, the tracking module provides the joint data using only cameras that have clear sight of them.
3.4 Out of sight API
Occlusion-free skeleton joint positions data sample
Participant movements instructions in the system evaluation (from left to right) of stationary, stepping, walking, obstacle, and occlusion. The number(s) in yellow circles is the order of a sub-action in a task
4 System evaluation
We designed a system evaluation to verify the accuracy of our approach. We are interested in whether such accuracy would be acceptable for HCI research and development, in both normal and occlusion settings. We define accuracy as the average Euclidean distance, with respect to the 3D joint positions, between the skeletons of a person from different fields of view. During tracking, Out of Sight extracts multiple skeletons of a person, including a skeleton from the current field of view (zero transformation) and skeletons from other fields of view (some transformation following our approach). We argue that the smaller the difference between the skeleton positions, the more accurate our approach. During the evaluation, the system logged each participant’s joint positions after transforming the skeletons to the same (front) field of view.
Our participants were required to perform five different tasks: standing, stepping, walking, going around an obstacle, and occluding another participant, as shown in Fig. 6. In each individual experiment, there were 20 multinational University students and staff, and whose age ranges from 18 to 35 years old. We included participants with a wide range of heights, weights, and of different genders. The two Kinects were placed at one of three pre-defined locations, either they were parallel, \(45^{\circ }\) or \(90^{\circ }\) apart. One Kinect was always placed at the front position. The location of the devices and participant movements were labeled clearly on the tracking area throughout the evaluation. Participant movements were restricted to a space of 192.5 cm in width and 187 cm in length. Our evaluation captures the error in skeleton joint transformation using a richer set of scenarios than previously studied [5].
4.1 Stationary
In the first study, participants were required to remain stationary for ten seconds in the center of the tracking area (Fig. 6a). The study was done with all three Kinect configurations (parallel, \(45^{\circ }\) apart and \(90^{\circ }\) apart).
4.2 Stepping
To allow for comparison with the results of Wei et al., the second study required the participants to move in the same way. This included basic movements such as moving forward, backward, left, and right (Fig. 6b). The study was done with all three Kinect configurations.
4.3 Walking
The third study required the participants to walk around the perimeter of the tracking area, and then walk diagonally to each of the four corners (Fig. 6c). As with the previous two tasks, the walking task was performed with all three Kinect configurations. This more complex scenario (tracking and transformation could be less accurate) enabled a more realistic testing of the method than seen previously.
4.4 Obstacle
Participants also walked around a large obstacle, which in our case was a \(0.82\,\mathrm{m} \times 2.10\,\mathrm{m}\) freestanding poster. The obstacle separated the fields of view of two Kinects at \(90^{\circ }\) apart (Fig. 6d). The participant started on one side of the obstacle where they were visible to both Kinects. As the participant walked around the obstacle from behind, the Kinect that was initially looking from the side of the participant slowly loses sight of the person. When the participant was on the other side of the obstacle, only the front-facing Kinect was able to see the person. If Out of Sight worked as intended, the study should demonstrate that the system could still track the person despite one of the Kinects, either temporarily or permanently, loses sight of the person.
4.5 Occlusion
Our proposed approach was also tested against an occlusion scenario, with two Kinects at \(45^{\circ }\) apart. The developed toolkit and API were validated by running a user study involving 10 participants, with two participants tested at once. The participants stood next to each other, the calibration process was initiated, the matched average skeletons were tracked and displayed, and then one person obstructed the other in one field of view (Fig. 6e). It was visually noted if the occluded skeleton was successfully located and tracked, and then this experiment was repeated for the other participant.
4.6 Accuracy
Overall system evaluation results, including the average \({\Delta } x\), \({\Delta } y\), \({\Delta } z\) and \({\Delta } d\), or accuracy, where appropriate. All values are rounded up to two decimal places
| Kinects and evaluation | \(\bar{{\Delta } x}\) (cm) | \(\bar{{\Delta } y}\) (cm) | \(\bar{{\Delta } z}\) (cm) | \(\bar{{\Delta } d}\) (cm) |
|---|---|---|---|---|
| Parallel, stationary | \(1.84 \pm 1.03\) | \(1.28 \pm 0.49\) | 2.08 ± 0.89 | 3.52 ± 1.33 |
| Parallel, stepping | \(4.48 \pm 0.53\) | \(2.13 \pm 0.32\) | 3.58 ± 0.95 | 6.87 ± 0.90 |
| Parallel, walking | \(5.76 \pm 0.97\) | \(3.17 \pm 0.57\) | 6.04 ± 0.95 | 10.17 ± 1.64 |
| \(45^{\circ }\), stationary | \(3.38 \pm 1.52\) | \(3.59 \pm 1.50\) | 3.17 ± 1.45 | 6.95 ± 2.67 |
| \(45^{\circ }\), stepping | \(8.18 \pm 0.70\) | \(4.11 \pm 0.85\) | 6.47 ± 1.77 | 12.80 ± 1.92 |
| \(45^{\circ }\), walking | \(10.18 \pm 1.16\) | \(5.78 \pm 0.70\) | 9.94 ± 1.69 | 17.67 ± 2.37 |
| \(90^{\circ }\), stationary | \(7.30 \pm 2.94\) | \(4.35 \pm 2.15\) | 5.19 ± 1.84 | 11.39 ± 4.45 |
| \(90^{\circ }\), stepping | \(16.67 \pm 1.69\) | \(5.20 \pm 2.07\) | 13.83 ± 1.95 | 25.13 ± 3.46 |
| \(90^{\circ }\), walking | \(21.02 \pm 1.73\) | \(5.47 \pm 0.96\) | 19.03 ± 2.07 | 32.38 ± 3.38 |
| \(90^{\circ }\), obstacle | \(100\%\) accuracy | |||
| Occlusion | \(85\%\) accuracy | |||
5 Results
5.1 Skeleton mapping
The overall results are summarized in Table 1 and visualized in Fig. 7a. The best accuracy, or the smallest average distance between skeletons, is found with parallel Kinects in the stationary scenario (\(\bar{{\Delta } d}\) = 3.52 cm, s.d. = 0.84 cm). The worst accuracy is found with Kinects placed at \(90^{\circ }\) from each other in the walking scenario (\(\bar{{\Delta } d}\) = 32.38 cm, s.d. = 13.87 cm). In addition, the smallest and largest skeleton joint distances are found with HipRight (\(\bar{{\Delta } d}\) = 13.45 cm, s.d. = 5.77 cm) and ThumbLeft (\(\bar{{\Delta } d}\) = 20.00 cm, s.d. = 5.95 cm), respectively (Fig. 7b).
Figure 8a shows the effect of task complexity on the average skeleton distance, in each of the stationary, stepping, and walking tasks. The values are averaged across all three Kinect positions. The average skeleton distance is smallest in the stationary task (\(\bar{{\Delta } d}\) = 6.75 cm, s.d. = 2.27 cm) and largest in the walking task (\(\bar{{\Delta } d}\) = 19.27 cm, s.d. = 7.32 cm). The average skeleton distance in these three scenarios is 16.08 cm (s.d. = 5.84 cm).
Figure 8b shows the effect of Kinect placement on the average skeleton distance. The values are averaged over the stationary, stepping, and walking tasks. The average skeleton distance is smallest in the parallel Kinect position (\(\bar{{\Delta } d}\) = 8.13 cm, s.d. = 2.58 cm) and largest in the \(90^{\circ }\) position (\(\bar{{\Delta } d}\) = 27.76 cm, s.d. = 12.44 cm).
5.2 One-person obstacle
The system is able to consistently track the person when they walk around an obstacle (Fig. 6d), successfully tracking them in 100% of cases while the person disappears from the field of view of one of the Kinects.
5.3 Two-person occlusion
When testing the API and the toolkit with 10 participants for tracking occluded people, the skeletons were tracked correctly when there is no occlusion, and in 17 out of 20 (\(85\%\) accuracy) occlusion cases, the skeletons were tracked consistently. An example of a person tracked during occlusion is shown in Fig. 3.
6 Discussion
For each of the primary tasks (stationary, stepping, and walking), this discussion addresses how the average skeleton and joint distances change with different Kinect positions. It is worth noting that Wei et al. [5] only studied stationary and stepping tasks, with near parallel and 45\(^{\circ }\) apart Kinects. We compare results with those in Wei et al.’s study where appropriate.
6.1 Stationary
The stationary task shows the best results when the Kinects are parallel to each other and worst when they are at furthest (90\(^{\circ }\)) apart. All measures of distances follow the same trend, from \({\Delta } x\) to \({\Delta } z\) and \({\Delta } d\) (Table 1). Skeleton distances in the stationary task increase with increasing angle between the Kinects.
The \({\Delta } y\) values are the smallest both when the Kinects are parallel to each other and when they are 90\(^{\circ }\) apart. The \({\Delta } y\) value in the stepping task is only slightly higher than its \({\Delta } x\) and \({\Delta } z\) values (0.21 cm and 0.42 higher, respectively). We observe that in general the skeleton transformation makes the least errors in the coordinate transformation of the y-axis, since we rotate the skeletons around the y-axis. Furthermore, the heights of both Kinects in the evaluation were fixed, and the participants did not move along the y-axis.
a The average skeleton joint distance in each evaluation scenario. b The distance per joint across the stationary, stepping, and walking tasks, for parallel, \(45^{\circ }\) and \(90^{\circ }\) Kinects
a The average skeleton distance with respect to the stationary, stepping, and walking tasks. b The average skeleton distance with respect to parallel, \(45^{\circ }\) and \(90^{\circ }\) apart Kinects, across all three tasks
6.2 Stepping
Overall, the skeleton distances in the stepping task are higher compared to those in the stationary task; for every Kinect position tested, see comparison of averages in Fig. 8a. The increase in skeleton distances is expected, because the task requires the participants to take steps both closer and away from the Kinect sensor, which causes the tracking system to produce larger differences between the skeletons because of transformation. Similarly to the stationary task, the stepping task also shows best results when the Kinects are parallel to each other and worst when they are 90\(^{\circ }\) apart. All measures of distances follow the same trend, from \({\Delta } x\) to \({\Delta } z\) and \({\Delta } d\) (Table 1). For all Kinect positions, the \({\Delta } x\) values are the highest, then \({\Delta } z\) and \({\Delta } y\). The skeleton distances also increase with increasing angle between Kinects. This shows that the tracking accuracy of Out of Sight is affected by both increasing angles between Kinects and increasing complex human activities.
Wei et al. [5] also reported lower values. In their stepping task (average difference after movement) with parallel (\(4.25^{\circ }\) apart) Kinects, the skeleton distances in the \({\Delta } x\), \({\Delta } y\), and \({\Delta } z\) were 2.00, 1.28, and 3.78 cm, respectively. The calculated \({\Delta } d\) was 4.46 cm which is lower than the 6.87 cm (Table 1) found in the current study. In their same task with \(45^{\circ }\) (\(44.37^{\circ }\)) apart Kinects, the skeleton distances in the \({\Delta } x\), \({\Delta } y\), and \({\Delta } z\) were 4.28, 1.64, and 5.28 cm, respectively. The calculated \({\Delta } d\) was 6.99 cm which is lower than the 12.80 cm found in the current work but in accordance with the differences reported.
6.3 Walking
The skeleton distances in the walking task are also higher compared to those in the stationary and stepping tasks; for every type of Kinect configuration, see Table 1 and the averages in Fig. 8a. Since walking movements are even larger than stepping and stationary movements, the error in the walking task will be higher compared to the other two tasks. On the other hand, the skeleton transformation also works best with parallel Kinects, and the average skeleton joint distance from different fields of view increases with larger angles (Table 1). Likewise, when the Kinects are \(45^{\circ }\) and \(90^{\circ }\) apart, the \({\Delta } x\) values are still the highest, followed by \({\Delta } z\) and \({\Delta } y\).
The average and standard deviation of \({\Delta } y\) are almost invariant to changes from the stationary to the walking task (Fig. 7a and Fig. 8a, b). The standard deviation of \({\Delta } y\) is the lowest compared to that of \({\Delta } x\) or \({\Delta } z\) in all the tasks discussed so far (stationary, stepping, and walking), with all different Kinect positions (parallel, \(45^{\circ }\), and \(90^{\circ }\) apart Kinects), except in the stationary task with \(45^{\circ }\) and \(90^{\circ }\) apart Kinects. The average skeleton distance over all tasks and Kinect positions is smallest in the \({\Delta } y\) component (4.11 cm, s.d. = 1.36 cm), compared to both \({\Delta } x\) (10.04 cm, s.d. = 4.12 cm) and \({\Delta } z\) (9.01 cm, s.d. = 3.35 cm). This finding supports the aforementioned argument that \({\Delta } y\) is steady throughout the tracking process, regardless of tasks and Kinect positions.
Wei et al. [5] did not run their experiments with a walking task as described in the current work. There is not other similar work in the literature. These results show new accuracy measurements for multi-Kinect tracking systems in a more realistic scenario.
6.4 Scenario and position comparison
The stationary, stepping, and walking tasks can be ordered on a spectrum of complexity, where the former requires zero movement, and the latter requires continuous movement. The evaluation so far shows that skeleton distances increase with increasing task complexity (Fig. 8a). The correlation can be attributed to increasing joint movements and turning of the shoulders. There is little variation in the accuracy of the technique between the distance dimensions across different joints, as shown in Fig. 7b. Therefore, skeleton transformation can be applied to all joints with the same confidence of joint positioning.
When testing the correlation of the angle to distance accuracy, a high correlation for \({\Delta } d\) of 0.985 shows that the larger the angle, the larger the distance between estimated skeletons, which is also visible in Fig. 8b. The angle between Kinects is related to the degree of rotation used in the transformation of multiple skeletons. A larger angle between the Kinects means that the skeletons will be rotated more, hence producing larger coordinate differences.
When varying only either the task complexity or the angle between the Kinects, the results show similar trends (Fig. 8a, b). In short, the distance between two computed skeleton joints increases with either a more complex task or a larger angle between multiple Kinects. The average distance \({\Delta } d\) is smallest in the stationary task with parallel Kinects (3.52 cm), and it is largest in the walking task with 90\(^{\circ }\) apart Kinects (32.38 cm). The overall average across all cases of task complexity and Kinect placement is 16.08 cm (s.d. = 5.84 cm). We believe interactive systems can make use of our Out of Sight tracking infrastructure within this error. This important finding shows the limits of how close people can be and still be distinct from one another when using this technique with multiple Kinects, both to extend coverage and to overcome occlusion.
The least accurate positioning of the Kinect was when the Kinects are \(90^{\circ }\) apart, where the average overall scenario was shown to have a \({\Delta } d\) mean distance of 27.76 cm (Fig. 8b). This boundary is still within the personal space, or the space where only one person is most likely to occupy, where close personal space can be defined as within 45 cm from the person; for a discussion of personal space, see [12]. The results therefore show preliminary success in tracking people using transformed 3D skeleton joint positions.
6.5 Tracking behind an obstacle
The obstacle task demonstrates that the tracking system can acquire, as complete as possible, joint coordinates for the same person from multiple Kinects when the person is occluded in one of the fields of view. Specifically, Out of Sight constructs an average skeleton from detected skeletons in all available fields of view. This has implications in scenarios where only one of multiple depth-sensing cameras has a clear view of the target. A use case would be a two-player interactive game, where the players are provided with feedback based on the other player’s position behind an obstacle, such as a wall. Another example would be a group of robots collectively searching for a person with particular appearance features in a large, occluded environment. The current system shows that this approach can reconstruct a person’s average skeleton when they are occluded and when they reappear from occlusion.
6.6 Tracking during occlusion
The Out of Sight RESTful API was validated with a toolkit usage scenario of two users standing side by side and then one user obstructing another, and vice versa. The API was shown to provide the matched skeletons for both scenarios when the participants were visible to both Kinects, and it also worked in 85% of the binary tests where one person obstructed the other person in one field of view. An example of the toolkit is shown in Fig. 3. This shows that the API can be used to track people behind obstructing objects, allowing future integration of occlusion-free skeleton stream into custom applications.
7 Limitations and future work
The tracking accuracy was tested with Kinects placed at the same height and tilting angle. Further evaluation could investigate whether the results are still within a person’s personal space with more varied heights and tilting angles. Furthermore, evaluation could also be carried out in more realistic, cluttered settings such as office spaces. We only used two Kinects and invited at most two participants at once. However, real-world environments are usually more chaotic, often consisting of groups of more than two people. The tracking system should demonstrate the same accuracy and speed with more people. Current work also lacks insights about how additional Kinects would affect performance. In theory, our approach is applicable to other depth-sensing systems with support for human joint data, but it is not tested with other alternatives to the Kinect. An important future work would be a comparison of various techniques of tracking people during occlusion using multiple depth-sensing cameras, for example a comparison of speed and accuracy trade-offs or limitations. Other techniques could include an alternative calibration method using triangulation of static objects or features in environments, a combination of depth fusion and human pose estimation, or a system using top–down (bird’s-eye view) cameras. Different techniques could have different usage scenarios such as ad hoc (calibration-free) tracking of people. In addition, we ignored the cost of running multiple Kinects in interactive spaces. A practical extension would be to derive a cost function which finds an optimal placement of depth-sensing cameras in a known environment, in which the effective size of the field of view is maximized. Given the constraint of the Kinect v2 SDK, the current system can only track up to six people, whereas previous research had demonstrated that it is possible to track more than six people with a single [32] and multiple [21] Kinects.
8 Conclusion
We have presented Out of Sight, an occlusion-aware skeleton tracking system using multiple Kinects. During calibration, it transforms each detected skeleton into a common coordinate system by translating and rotating the joints toward the corresponding Kinect sensor. Skeletons of the same person from different fields of view are matched by their spatial proximity in the new coordinate system, and their joint positions are subsequently updated during tracking. The system can also perform reverse transformation to estimate the person’s joint positions in a particular field of view. Furthermore, it resolves occlusion in one depth-sensing camera, for example when users are obstructed by others or objects, by averaging joint positions from other cameras.
A system evaluation measured the tracking accuracy as the average distance between multiple skeletons of a person from different fields of view after transformation, discussed in terms of the \({\Delta } x\), \({\Delta } y\), \({\Delta } z\), and \({\Delta } d\) values (in centimeters). Results show that the average skeleton (and joint) distance increases with both the complexity of the task (from standing to walking) and the angle between Kinects (from parallel to \(90^{\circ }\)). Even though we found lower accuracy in similar scenarios compared to previous work, our average skeleton distance of 16.08 cm is still within the region of personal space. It was also demonstrated that the current system can track the joint positions of multiple people during obstruction and occlusion.
Tracking people through occlusion enables interactive systems to leverage otherwise hidden information and to deliver purposeful actions, for example showing users information that is currently obstructed in their (and camera’s) line of sight. Our work creates opportunities for custom applications to leverage occlusion-free human joint positions using a multi-Kinect tracking infrastructure. To make it easier for future developers, we also open sourced the toolkit and API.
Footnotes
- 1.
The Kinect for Windows 2.0 SDK provides 25 tracked joints of up to six people: https://msdn.microsoft.com/en-us/library/windowspreview.kinect.jointtype.aspx.
- 2.
There is currently a maximum of one Kinect per computer when using the Microsoft Kinect v2 SDK.
- 3.
A definition of REST is given in Fielding and Taylor [31].
Notes
Acknowledgements
We would like to thank St Andrews Human Computer Interaction group (SACHI), especially Michael Mauderer for help with statistics and Johannes Lang for anonymizing the image shown in Fig. 1.
References
- 1.Seer S, Brändle N, Ratti C (2014) Kinects and human kinetics: a new approach for studying pedestrian behavior. Trans Res Part C Emerg Technol 48:212–228CrossRefGoogle Scholar
- 2.Munaro M, Menegatti E (2014) Fast rgb-d people tracking for service robots. Auton Robots 37(3):227–242CrossRefGoogle Scholar
- 3.Preis J, Kessel M, Werner M, Linnhoff-Popien C (2012) Gait recognition with kinect. In: 1st international workshop on kinect in pervasive computing. New Castle, UK, pp P1–P4Google Scholar
- 4.Marquardt N, Hinckley K, Greenberg S (2012) Cross-device interaction via micro-mobility and f-formations. In: Proceedings of the 25th annual ACM symposium on User interface software and technology. ACM, pp 13–22Google Scholar
- 5.Wei T, Qiao Y, Lee B (2014) Kinect skeleton coordinate calibration for remote physical training. In: Proceedings of the International Conference on Advances in Multimedia (MMEDIA), pp 23–27Google Scholar
- 6.Avola D, Cinque L, Levialdi S, Placidi G (2013) Human body language analysis: a preliminary study based on kinect skeleton tracking. In: New trends in image analysis and processing–ICIAP 2013. Springer, pp 465–473Google Scholar
- 7.Frati V, Prattichizzo D (2011) Using kinect for hand tracking and rendering in wearable haptics. In: World haptics conference (WHC), 2011 IEEE. IEEE, pp 317–321Google Scholar
- 8.Seewald LA, Gonzaga L, Veronez MR, Minotto VP, Jung CR (2014) Combining srp-phat and two kinects for 3d sound source localization. Expert Syst Appl 41(16):7106–7113CrossRefGoogle Scholar
- 9.Dostal J, Hinrichs U, Kristensson PO, Quigley A (2014) Spidereyes: designing attention-and proximity-aware collaborative interfaces for wall-sized displays. In: Proceedings of the 19th international conference on intelligent user interfaces. ACM, pp 143–152Google Scholar
- 10.Ballendat T, Marquardt N, Greenberg S (2010) Proxemic interaction: designing for a proximity and orientation-aware environment. In: ACM international conference on interactive tabletops and surfaces. ACM, pp 121–130Google Scholar
- 11.Nebeling M, Teunissen E, Husmann M, Norrie MC (2014) Xdkinect: development framework for cross-device interaction using kinect. In: Proceedings of the 2014 ACM SIGCHI symposium on engineering interactive computing systems. ACM, pp 65–74Google Scholar
- 12.Hall ET, Birdwhistell RL, Bock B, Bohannan P, Diebold Jr, AR, Durbin M, Edmonson MS, Fischer JL, Hymes D, Kimball ST et al (1968) Proxemics [and comments and replies]. Current anthropology, pp 83–108Google Scholar
- 13.Dalal N, Triggs B (2005) Histograms of oriented gradients for human detection. In: IEEE computer society conference on computer vision and pattern recognition, 2005 (CVPR 2005), vol 1. IEEE, pp 886–893Google Scholar
- 14.Ess A, Leibe B, Schindler K, Gool LV (2008) A mobile vision system for robust multi-person tracking. In: IEEE conference on computer vision and pattern recognition, 2008 (CVPR 2008). IEEE, pp 1–8Google Scholar
- 15.Wojek C, Walk S, Schiele B (2009) Multi-cue onboard pedestrian detection. In: IEEE Conference on computer vision and pattern recognition, 2009 (CVPR 2009). IEEE, pp 794–801Google Scholar
- 16.Enzweiler M, Gavrila DM (2009) Monocular pedestrian detection: survey and experiments. Pattern Analy Mach Intell IEEE Trans 31(12):2179–2195CrossRefGoogle Scholar
- 17.Dollar P, Wojek C, Schiele B, Perona P (2012) Pedestrian detection: an evaluation of the state of the art. Pattern Anal Mach Intell IEEE Trans 34(4):743–761CrossRefGoogle Scholar
- 18.Benenson R, Omran M, Hosang J, Schiele B (2014) Ten years of pedestrian detection, what have we learned? In: Computer vision-ECCV 2014 Workshops. Springer, pp 613–627Google Scholar
- 19.Tang S, Andriluka M, Schiele B (2014) Detection and tracking of occluded people. Int J Comput Vis 110(1):58–69CrossRefGoogle Scholar
- 20.Liu J, Liu Y, Zhang G, Zhu P, Chen YQ (2015) Detecting and tracking people in real time with rgb-d camera. Pattern Recognit Lett 53:16–23CrossRefGoogle Scholar
- 21.Luber M, Spinello L, Arras KO (2011) People tracking in rgb-d data with on-line boosted target models. In: 2011 IEEE/RSJ international conference on Intelligent Robots and Systems (IROS). IEEE, pp 3844–3849Google Scholar
- 22.Chu C-T, Hwang J-N, Lan K-M, Wang S-Z (2011) Tracking across multiple cameras with overlapping views based on brightness and tangent transfer functions. In: 2011 fifth ACM/IEEE international conference on distributed smart cameras (ICDSC). IEEE, pp 1–6Google Scholar
- 23.Yildiz A, Akgul YS (2010) A fast method for tracking people with multiple cameras. In: Trends and topics in computer vision. Springer, pp 128–138Google Scholar
- 24.Yamashita A, Ito Y, Kaneko T, Asama H (2011) Human tracking with multiple cameras based on face detection and mean shift. In: 2011 IEEE international conference on robotics and biomimetics (ROBIO). IEEE, pp 1664–1671Google Scholar
- 25.Cai Y, Medioni G (2014) Exploring context information for inter-camera multiple target tracking. In: 2014 IEEE winter conference on applications of computer vision (WACV). IEEE, pp 761–768Google Scholar
- 26.Javed Omar, Rasheed Zeeshan, Shafique Khurram, Shah Mubarak (2003) Tracking across multiple cameras with disjoint views. In: Proceedings Ninth IEEE international conference on computer vision, 2003. IEEE, pp 952–957Google Scholar
- 27.Zhang L, Sturm J, Cremers D, Lee D (2012) Real-time human motion tracking using multiple depth cameras. In: 2012 IEEE/RSJ international conference on intelligent robots and systems (IROS). IEEE, pp 2389–2395Google Scholar
- 28.Caon M, Yue Y, Tscherrig J, Mugellini E, Khaled OA (2011) Context-aware 3d gesture interaction based on multiple kinects. In: Proceedings of the first international conference on ambient computing, applications, services and technologies, AMBIENTGoogle Scholar
- 29.Li H , Zhang P, Al Moubayed S, Patel SN, Sample AP (2016) Id-match: a hybrid computer vision and rfid system for recognizing individuals in groups. In: Proceedings of the 2016 CHI conference extended abstracts on human factors in computing systems. ACM, pp 7–7Google Scholar
- 30.Hu G, Reilly D, Alnusayri M, Swinden B, Gao Q (2014) Dt-dt: top-down human activity analysis for interactive surface applications. In: Proceedings of the ninth ACM international conference on interactive tabletops and surfaces. ACM, pp 167–176Google Scholar
- 31.Fielding RT, Taylor RN (2002) Principled design of the modern web architecture. ACM Trans Internet Technol (TOIT) 2(2):115–150CrossRefGoogle Scholar
- 32.Munaro M, Basso F, Menegatti E (2012) Tracking people within groups with rgb-d data. In: 2012 IEEE/RSJ international conference on intelligent Robots and Systems (IROS). IEEE, pp 2101–2107Google Scholar
Copyright information
Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.