Abstract
The automated detection of sequential anomalies in time series is an essential task for many applications, such as the monitoring of technical systems, fraud detection in high-frequency trading, or the early detection of disease symptoms. All these applications require the detection to find all sequential anomalies possibly fast on potentially very large time series. In other words, the detection needs to be effective, efficient and scalable w.r.t. the input size. Series2Graph is an effective solution based on graph embeddings that are robust against re-occurring anomalies and can discover sequential anomalies of arbitrary length and works without training data. Yet, Series2Graph is no t scalable due to its single-threaded approach; it cannot, in particular, process arbitrarily large sequences due to the memory constraints of a single machine. In this paper, we propose our distributed anomaly detection system, short DADS, which is an efficient and scalable adaptation of Series2Graph. Based on the actor programming model, DADS distributes the input time sequence, intermediate state and the computation to all processors of a cluster in a way that minimizes communication costs and synchronization barriers. Our evaluation shows that DADS is orders of magnitude faster than S2G, scales almost linearly with the number of processors in the cluster and can process much larger input sequences due to its scale-out property.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Sequential anomaly detection
Time series analysis is a multi-disciplinary field with use cases in astrophysics [12], neurosciences [37], environmental monitoring [35], Internet of things [14], finance [46], asset tracking [29], aviation engineering [7] and many further disciplines. Most of these analyses are about the discovery of special events as well as frequent and rare time series patterns. Due to the valuable knowledge that is lying within time series datasets, much research has been conducted on efficient and effective time series mining techniques [36].
Univariate time series are ordered sequences of one-dimensional, real-valued records [3, 16, 24, 42, 52]. The ordering is usually time-related—hence the name—but sometimes also follows other continuous measures, such as size, distance or speed. Anomalies in time series denote subsequences with significant, i.e., particularly infrequent values or patterns. In general, we distinguish between point anomalies a.k.a. outliers and sequential anomalies a.k.a. collective anomalies [13]. Because point anomalies are sequential anomalies of size one, sequential anomalies cover point anomalies. For example, a temperature reading of \(50\,^\circ \)C in an ordinary room is a point anomaly; a sudden temperature increase of \(10\,^\circ \)C directly followed by a drastic drop of \(15\,^\circ \)C is a sequential anomaly, if common temperature changes are slow.
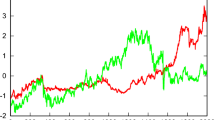
Anomalies often indicate meaningful events in time series and are, therefore, important for various applications. Examples for such applications range from intrusion detection in digital networks [23, 39], over finding unexpected phenomenons in astrophysical measurements [51], to medical studies of disease cases [18]. Figure 1 shows another example from aircraft engineering: We see a time series T of engine measurements with various regular spikes and one anomalously lean spike. None of the records in the anomaly is an outlier, but its shape is clearly different from other patterns that we find in the sequence. An anomaly score, which is depicted in red in Fig. 1, is a proper indicator of this anomaly. In this paper, we propose a scalable algorithm that efficiently calculates such anomaly scores.
Sequential anomalies are hard to detect, because they often differ in length, vary in degree of anomaly and might even re-occur a few times; moreover, the input time series can be very long (often millions to billions of records), and the input might be comprised of different but normal subsequence patterns. For this reason, automatic anomaly detection has been a research topic for more than 30 years [48], which led to the invention of various anomaly detection algorithms [13]. But although we find effective, efficient and scalable detection approaches for sequential anomalies, none of the approaches covers all three properties.
An effective sequential anomaly detection algorithm automatically marks all anomalous, i.e., infrequent subsequences in a time series; thereby the algorithm is robust against re-occurring anomalies, can discover sequential anomalies of arbitrary length and works without training data. Being able to detect re-occurring patterns as anomalous is important, because many anomalous events, such as earth quakes in seismological recordings, engine misfires in vehicle monitoring or heartbeat dropouts in cardiography, can repeat several times while still being rare events overall. Considering different anomaly lengths is important as well, not only because the duration of certain events and, hence, the length of their recordings is usually unpredictable, it might also differ in one and the same time series. Storms in climate data or load fluctuation in online systems, for example, can both be short and long-lasting events. An effective anomaly detection system, finally, cannot rely on labeled training data, because it does not exist (in sufficient quantity) in many cases, such as when monitoring aircraft engines for failures or astrophysical scans for surprising events.
The Series2Graph (S2G) algorithm [10] is a sequential anomaly detection approach that meets all the discussed effectiveness properties. The algorithm is based on a novel subsequence embedding technique that is used to map univariate time series to cyclic, directed, and weighted graphs, which—once constructed—can be traversed to find anomalies of different lengths. The graph also enables the detection of re-occurring sequential anomalies and assigns anomaly scores based on statistical re-occurrence frequencies and subsequence similarity, which is without a need for training data. Series2Graph is also an efficient algorithm considering state-of-the-art competitor algorithms: The authors demonstrate that S2G outperforms DAD [51], LSTM [33], Lof [11], GrammarViz [43], Isolation Forest [31] and STOMP [52] in both runtime and detection accuracy while also being more robust against imprecise parameters. Nevertheless, we found that S2G’s calculation time can be improved significantly by the use of more efficient data structures and parallelization.
The real limiting aspect of S2G is its lack of scalability. The algorithm is a single-threaded approach that works on only one machine. Because the algorithm needs to keep the input time series and certain intermediate data structures in main memory, the available memory is a hard constraint for the algorithm’s applicability. Typical time series of terabyte to petabyte size, such as those that often appear in domains like bioinformatics [20] or astrophysics [51], are hardly computable with the current version of S2G.
For this reason, we introduce our Distributed Anomaly Detection System (DADS). DADS is a parallelized and distributed adaptation of Series2Graph that overcomes the main memory restrictions of a single computer by combining the computed resources of multiple machines in a cluster. Our system follows exactly the same conceptual transformation steps as proposed by S2G, but translates them into a more efficient and scalable execution model. Via reactive, actor-based programming, DADS distributes the input time sequence, intermediate state and the computation to arbitrary many machines in a way that minimizes communication costs and synchronization barriers.
In this paper, we first discuss related work (Sect. 2) and the formal foundations for the discovery of sequential anomalies (Sect. 3). We then describe the processing steps of the S2G algorithm and our approaches for their parallelization and distribution (Sect. 4). Afterward, we make the following S2G-based contributions:
-
1.
Distributed S2G System. We decompose the transformation process into eight reactive protocols; for these protocols, we design an asynchronous communication scheme that orchestrates protocol executions and data sharing (Sect. 5).
-
2.
Distributed S2G Sequence Embedding. We partition the input data and intermediate state so that communication costs are minimized; we also propose a more compact data structure for the embedding space matrix (Sect. 6).
-
3.
Distributed S2G Node Extraction. We distribute the node extraction in a way that exploits data locality, maximizes the parallelization potential and makes use of peer-to-peer data exchange to relieve the master node (Sect. 7).
-
4.
Distributed S2G Edge Extraction. We distribute the edge extraction analogously to the node extraction and assemble the final graph from the nodes and edges with an event-based broadcast mechanism (Sect. 8).
-
5.
Distributed S2G Subsequence Scoring. We re-use the distribution of already calculated intermediate results to distribute the scoring process (Sect. 9).
In Sect. 10, we evaluate DADS’ runtime, CPU, memory and network utilization on differently sized input time series and with different cluster sizes. The comparison with S2G shows that DADS is orders of magnitude faster even on a single processor and scales almost linearly with the number of processors in the cluster; on 12 processors, DADS could process 50 times longer sequences than S2G in less than 16% of the time.
2 Related work
The survey of Chandola et al. [13] defines three general classes of anomaly detection approaches: supervised, semi-supervised and unsupervised detection algorithms. Although supervised and semi-supervised approaches are able to deliver competitive results in specific applications [17, 32, 50], they require labeled training data that are for many time series not or in not sufficient quantity available. For this reason, we focus on an unsupervised anomaly detection approach in this work.
Anomaly detection systems are also divided into point and sequence anomalies. If some use case is interested in only point anomalies, more efficient detection approaches exist. In this section, we cover both types of anomalies and discuss distributed approaches for their detection.
2.1 Point anomaly detection
Basic point anomaly detection algorithms classify points as outliers mostly based on statistical methods [6, 28, 41, 49]. A popular approach is to form clusters in some embedding space. All records with the largest distance (e.g. Euclidean distance) to these clusters are then recognized as outliers. Such approaches usually do not consider the order of the input records for the outlier detection. Many publications on outlier detection also study multi-dimensional data [15, 26, 40]. Their contributions are different optimizations and pruning strategies to deal with the quadratic runtime complexity of the problem.
Point anomaly detection is a particularly important tool for the analysis of sensor networks. For this special purpose, several time series mining algorithms have been introduced [35]. To identify distance- or density-based outliers, algorithms, such as [44], propose to estimate the data distribution of the underlying time series across the network of sensors and, then, calculate local outliers to these estimates. The algorithms can often handle multi-dimensional data but are restricted to point anomalies.
The use of machine learning is another popular strategy for finding outliers [3, 4, 27]. In this context, unsupervised approaches, such as the work of Ahmed et al. [3], are particularly interesting, because they demonstrate that no training data are needed to achieve reliable results. Deriving appropriate anomaly parameters is, however, still an issue for these approaches. For a more comprehensive summary of outlier detection methodologies and a technical overview of various detection methods, we refer the interested reader to [22].
Outlier detection is also a recurring task in mining streaming data. An extensive comparison of different algorithms can be found in [45].
2.2 Sequence anomaly detection
The Series2Graph (S2G) algorithm by Boniol et al. [10] is the most recent publication on unsupervised sequential anomaly detection. In their work, the authors introduce a novel approach that represents time series of real-valued records as graphs. With this graph, subsequences of arbitrary size can efficiently be scored and, in this way, classified as normal or anomalous. The authors show that their approach outperforms state-of-the-art competitors, such as DAD [51], LSTM [33], Lof [11], GrammarViz [43], Isolation Forest [31] and STOMP [52], under almost all circumstances and w.r.t. both detection accuracy and efficiency; the algorithm is also able to detect repeated anomalies. S2G is, however, a single-threaded, non-scalable algorithm whose applicability is bound to the available memory of its host machine. Our DADS algorithm overcomes this limitation.
Other than S2G, all competing state-of-the-art approaches for sequential anomaly detection, i.e., DAD [51], LSTM [33], Lof [11], GrammarViz [43], Isolation Forest [31] and STOMP [52], are based on the discord definition. Hereby, abnormal subsequences are defined by their spatial distance to all other subsequences. In other words, the subsequences with the largest distances to their nearest neighbors are assumed to have the least commonalities with the remaining data and, therefore, must be anomalous. An advantage of the discord definition is its simplicity; a major drawback is, however, that repeated or similar anomalies cannot be detected, because they are spatially close together and, hence, also close to their nearest neighbor.
One algorithm that circumvents this issue is the Disk Aware Discord Discovery (DAD) of Yankov et al. [51]. To deal with repeated anomalies, the authors propose \(m^{th}\) discords. Inspired by the definition of distance-based outliers [26], m th discords are isolated sequences that have the largest distance to their m nearest neighbors. In this way, similar or repeated anomalies can be detected if the parameter m is chosen correctly. The DAD algorithm is also an interesting competitor for our work, because it is able to process very large datasets due to the usage of external memory, i.e., disk, and it can be distributed. However, we did not include a comparative evaluation in this work, because Boniol et al. have already shown in [10] that DAD is significantly slower than other approaches that operate on sequences in main memory, that it is very sensitive to a correct choice of m (high risk of false-positive or false-negative results), and that it offers the across many experiments on average worst detection accuracy (sometimes as low as 1%).
Another special approach in related work is the Long Short-Term Memory Network (LSTM) algorithm [33] by Malhotra et al., because it is the only semi-supervised detection method for sequential anomalies. Despite being able to use domain-specific training data, LSTMs do not produce more accurate sequential anomaly results than S2G w.r.t. average detection rate.
The recently published anomaly detection algorithm VALMOD [30] discovers and ranks motifs and discords in time series by systematically calculating the Euclidean distance of certain subsequences to all other subsequences of the same length. To improve its performance, VALMOD re-uses already calculated Euclidean distances of shorter subsequence pairs for subsequent comparisons. Similar to S2G, VALMOD can discover anomalies of different lengths, but a qualitative comparison between the two approaches is still missing. In this paper, we focus on S2G, because memory and runtime limitations seem more problematic for this approach than for VALMOD.
The NorM [8] algorithm is another recent sequence anomaly discovery approach for time series. It constructs a model that represents the normal character of the time series to find subsequences that deviate from this character. Like most anomaly discovery algorithm, NorM fixes the length of the target anomalies prior to the discovery process. VALMOD, in contrast, searches for all anomalies in a given range, and S2G uses a query length only in the final scoring step once the anomaly graph has already been calculated.
Many of the above-discussed algorithms are implemented in the SAD anomaly detection tool [9]. SAD allows data scientists to interactively discover anomalies in time series and compare the results of different algorithms.
2.3 Distributed anomaly detection
Besides the distributed DAD algorithm [51], which we already discussed in Sect. 2.2, we find only two other distributed anomaly detection approaches. The first is a distributed, unsupervised detection algorithm for point anomalies proposed by Rajasegarar et al. [39]. The proposed algorithm pre-clusters records distributedly before sending a description of these clusters to a central agent, which then performs a spatial distance-based analysis. Like other related works, the algorithm cannot find re-occurring or similar anomalies and it focuses on only point anomalies.
Another distributed anomaly detection algorithm that finds contextual collective anomalies within a collection of data streams was published by Jiang et al. [24]. To find anomalously behaving streams, this algorithm simultaneously processes multiple data streams that provide context information to one another. Because multiple streams are necessary for this approach to provide context information and because it detects a completely different class of anomalies, it is not applicable to sequential anomaly detection in basic time series.
2.4 Distributed principal component analysis
One step in the S2G algorithm uses Principal Component Analysis(PCA) for dimensionality reduction. In our version of S2G, we need to distribute this step, because it is computationally expensive and , if the projected time series does not fit into one processor’s main memory, the input for the PCA can be too large for one processor alone. In other words, our DADS algorithm needs to calculate the PCA of arbitrarily large, distributed embedding spaces that result from the embeddings of numerous subsequences. For this purpose, we use the work of Bai et al. [5]. Their distributed PCA algorithm overcomes the issue of large network transfers by performing QR decompositions on the local data parts and sharing only the relatively small R portion of the results. This step needs to be repeated \(\lceil \log _2 n \rceil \) times, where n is the total number of partition locations. Section 6.2 explains the algorithm in more detail. A major advantage of the approach is that it produces exact results, where earlier approaches, such as [38], rely on approximation techniques to reduce network transfer volumes.
3 Foundations
Throughout the paper, we use the symbols and notation listed in Table 1. The notation mostly follows the conventions of [10]. In this section, we first provide the theoretical background for the anomaly detection with the S2G algorithm and, then, provide some foundations for the distribution of the algorithm.
3.1 Anomaly detection
In this work, we focus on anomalies in time series data, which is formally defined as follows:
Definition 1
(Time Series) A time series T with \(T = \{T_0, T_1, ..., T_{n-1}\} \in {\mathbb {R}}^n\) is a chronologically ordered (univariate) sequence of real-valued records \(T_i \in {\mathbb {R}}\) with length \(|T| = n\) where \(T_i\) is the value at the \(i^{th}\) position in T with \(0 \le i < n\).
We sometimes also refer to time series as (record) sequences or simply (data) series, because time is not the only possible ordering criterion. Within the time series, we are interested in finding subsequences that are shaped anomalously, which is differently from the vast majority of the other subsequences. Thereby, a subsequence is defined as follows:
Definition 2
(Subsequence) A (time series) subsequence \(T_{[From, To)} \in {\mathbb {R}}^{To - From}\) with \(T_{[From, To)} = \{\,T_{From}, T_{From+1}, ...,\) \(T_{To-1}\,\}\) is a chronologically ordered series of consecutive records from T so that \(0 \le From < To \le |T|\).
The idea of the S2G algorithm is to extract all subsequences of a specific length l from a given time series in order to convert, i.e., embed these subsequences into a weighted graph \(G_l(N, {\mathscr {E}})\) where N is the set of nodes and \({\mathscr {E}}\) is the set of directed edges between these nodes. We describe this conversion process in Sect. 4. Intuitively, a node represents a certain value pattern of length l that corresponds to one or more subsequences \(T_{[From, To)}\) and an edge represents pattern changes. In the graph, node degrees and edge weights correspond to the frequency of subsequences, i.e., similar subsequences are mapped to the same nodes so that paths in the graph over heavy edges and strongly connected nodes represent frequent, normal subsequences and, vice versa, paths over light edges and weakly connected nodes represent infrequent, anomalous subsequences. A path is formally defined as follows [10]:
Definition 3
(Path) Let \(N_{From} \in N\) be the node that represents the subsequence \(T_{[From, To)}\) of series T. Then, a path P in the embedding graph \(G_l(N, {\mathscr {E}})\) of time series T is an ordered sequence of nodes \(P = \{\,N_{From_0}, N_{From_1}, \ldots , N_{From_m}\,\}\) such that \(\forall N_{From_i},\) \(N_{From_{i+1}} \in P: From_i + 1 = From_{i+1}\).
According to this definition, it needs to be true that \((N_{From_i} \rightarrow N_{From_{i+1}}) \in {\mathscr {E}}\). If two subsequences map to the same node, it can be that \(N_{From_i} = N_{From_{i+1}}\). For better readability, we write \(P = \{\,N_0, N_1, \ldots , N_m\,\}\) implicitly assuming that \(N_0\) to \(N_m\) represent successive subsequences in T.
We can use the paths in the weighted graph to define a normality value for the subsequences and their changes in T as follows [10]:
Definition 4
(Normality Value) The normality of a path P and, hence, the pattern changes in the respective subsequences of a time series T is defined as \(Norm(P) = \sum \nolimits _{k=0}^{|P|-1} \frac{weight(N_{k} \rightarrow N_{k+1}) \cdot (degree(N_k) - 1)}{|P|}\) where \(weight(N_{k} \rightarrow N_{k+1})\) is the weight of the directed edge between the nodes \(N_k\) and \(N_{k+1}\) and \(degree(N_k)\) is the node degree of node \(N_k\).
Because we are interested in anomalies rather than normal patterns, we define a continuous anomaly score, such as the one depicted in Fig. 1, as follows [10]:
Definition 5
(Anomality Score) The anomality of a path P in the embedding graph \(G_l\) of a time series T is defined as \(Anomaly(P) = 1 - \frac{Norm(P) - norm_{min}}{norm_{max} - norm_{min}}\) where \(norm_{min}\) and \(norm_{max}\) are the smallest and largest measured normality values, respectively, for all paths of length |P|.
In other words, the anomaly score normalizes the normality values to the range [0, 1] and inverts them. The length of P, i.e., |P|, depends on the expected anomaly length: Only long enough paths can cover long anomalies, but short paths assign higher weights to short anomalies and can, therefore, detect them better. With the graph representation of T, an application can efficiently, i.e., in linear time, test various anomaly lengths—for this reason, the algorithm is considered capable of detecting anomalies of different lengths.
In summary, the anomaly score serves to rank the anomality of subsequences; it can be calculated for subsequences of different lengths with the same graph representation of the time series.
3.2 Distributed computing
To distinguish between graph nodes and compute nodes, i.e., the nodes in the graph representation of our time series and the nodes of the computer cluster used to distribute the graph construction, we refer to graph nodes simply as nodes (N) and to compute nodes as processors or (cluster) participants.
For the distribution of the anomaly detection process, we use the actor programming model [2] that encapsulates program state and behavior in special actor objects. Actors communicate asynchronously via messaging, run their individual tasks in parallel and protect their private state from concurrent access. This design and the fact that messages can transparently be exchanged over the network makes the actor programming model ideal for the development of highly parallel, distributed systems.
Technically, we use the AkkaFootnote 1 actor programming toolkit. Because Akka runs on the Java virtual machine, it enables easy cross-platform deployment and execution. For complex mathematical calculations, such as the matrix calculations, we use the highly optimized oj!AlgoFootnote 2 library.
4 Series2Graph algorithm overview
The Series2Graph (S2G) algorithm scores subsequences of time series by their anomality w.r.t. all other subsequences of same length using a graph-based approach. In this section, we give a fundamental overview of the steps involved in this process and the intuition on how we approach their parallelization and distribution.
Figure 2 summarizes the four-step workflow and visualizes how data are transformed along the way: S2G first embeds all subsequences of a certain length in a low-dimensional space; from this time series embedding, it extracts graph nodes and, then, graph edges; the graph representation is in the end used to score arbitrary subsequences of the time series (see subsect. 3.1). In the following, we discuss these steps in more detail.
\({\underline{Left:}}\) Systematical overview of the S2G workflow and its four main steps including the most important subroutines within each step. Additionally, inputs and outputs of individual steps and subroutines are shown as labels on the arrows that indicate the overall flow of the process. \({\underline{Right:}}\) Symbolic sketches of what the data transformation along the process looks like. Image sources from top to bottom: Collective Anomaly (first) [13]; SProj (second) and path score (fifth) [10]
4.1 Subsequence embedding
The first step of the algorithm extracts subsequences \(T_{[From, To)}\) of a certain length l from the sequence T and maps them to the two-dimensional embedding space \(SProj(T, l, \lambda )\), which represents shape-related spatial commonalities and differences between subsequences of T. Thereby, besides the actual sequence T, the parameters \(\lambda \), which is the size of the local convolution, and l, which specifies the length of extracted subsequences, are decisive for the resulting embedding. Both l and \(\lambda \) are user-specified parameters. Boniol et al. use \(\lambda = \frac{l}{3}\) for all of their experiments, because results do not significantly differ for \(\lambda \) between \(\frac{l}{10}\) and \(\frac{l}{2}\).
The subsequence embedding is achieved through a three-stage process of (I) projection creation, (II) PCA calculation and (III) dimension reduction. The general idea is to first extract and embed subsequences in a high-dimensional space \(Proj(T, l, \lambda )\); via PCA, S2G then finds and uses the most significant principal components to reduce the dimensionality of the embedding space down to three; the three-dimensional embedding space \(RProj(T, l, \lambda )\) is, finally, rotated along what is identified to be the time axis so that only shape-related information is preserved, which yields SProj as a result.
For our distribution, the general idea is to distribute the global sequence T, which is initially stored on disk on the cluster leader (master), to all cluster processors. To keep the ordering of T intact, the master processor creates consecutive slices of T, i.e., one slice for each processor in the cluster, and sends them to the respective processors so that each compute node owns one sequence slice \(T_{[From, To)}\) for the rest of the computation.
Projection Creation The projection creation of S2G extracts subsequences from T using a sliding windows of length l. Each subsequence \(T_{[i, i + l)}\) is transformed into a vector \(V_{[i, i + l)} \in {\mathbb {R}}^n\) where \(n = l - \lambda \) is the number of components of the vector. This is done through local convolution in the following way:
All of these vectors (embedded subsequences) are combined to build the embedding space \(Proj(T, \lambda , l) \in {\mathbb {R}}^{m \times n}\) with \(m = |T|-l+1\) being the number of subsequences of length l that can be extracted from T:
With T being already distributed, each processor can perform the projection creation locally. In other words, each processor creates a local slice of the embedding space \(Proj_{[From, To)}\) from its \(T_{[From, To)}\) subsequence of T. As a result, the global embedding space is distributed within our cluster exactly like the global time series. The necessary parameters l and \(\lambda \) for this step are provided by the master processor.
PCA Calculation The dimensionality of the embedding space Proj depends on the length l of the subsequence. Via PCA, S2G reduces the dimensionality of Proj to the three most significant dimensions that capture the shape of the sequences. For this purpose, S2G first determines Proj’s principal components to, then, select the three most significant ones.
Calculating the principal components via PCA is a straight-forward operation, but it is not trivial to distribute. In our DADS algorithm, we propose an actor-based PCA implementation of the distributed approach of Bai et al. [5]. The general idea is to perform a series of QR decompositions on each local slice of the embedding space while sending only the (small) R portion of the result to the next processor. This procedure ends after \(\lceil \log _2 n \rceil \) steps with the master processor calculating and, then, broadcasting the final principal components.
Dimension Reduction The last stage of the sequence embedding uses the principal components to transform \(Proj(T, l, \lambda )\) into \(SProj(T, l, \lambda ) \in {\mathbb {R}}^{m \times 2}\). This is done by first calculating the reduced embedding space \(RProj(T, l, \lambda ) \in {\mathbb {R}}^{m \times 3}\) using \(Proj(T, l, \lambda )\) and \(PCA_3\). After that, S2G rotates RProj to extract the most important shape-related information. To do so, the authors define a reference vector as \(\mathbf {v}_{ref} = \overrightarrow{O_{mn}O_{mx}}\), where \(O_{mn} = PCA_3(min(T) * \lambda * \mathbf {1}_{l-\lambda })\) and \(O_{mx} = PCA(max(T) * \lambda * \mathbf {1}_{l-\lambda })\). \(\mathbf {v}_{ref}\) naturally describes the time dimension of value changes. Hereby, the function PCA(x) reduces the dimensionality of x down to three using the principal components from earlier. The reference vector is used to calculate the angles \(\varPhi _x = \angle \mathbf {u}_x\mathbf {v}_{ref}, \varPhi _y= \angle \mathbf {u}_y\mathbf {v}_{ref}, \varPhi _z = \angle \mathbf {u}_z\mathbf {v}_{ref}\) between itself and the unit vectors \(\mathbf {u}_x, \mathbf {u}_y, \mathbf {u}_z\) that represent the axes of RProj. Finally, the reduced embedding space is rotated using the rotation matrices \(R_{u_x}(\varPhi _x), R_{u_y}(\varPhi _y), R_{u_z}(\varPhi _z)\) so that \(SProj = R_{u_x}(\varPhi _x) R_{u_y}(\varPhi _y) R_{u_z}(\varPhi _z) RProj^T\).
For the distribution of this stage, the master first calculates min(T) and max(T), which are the global minimum and maximum of T, from the local minimum and maximum values \(min(T_{[From, To)})\) and \(max(T_{[From, To)})\) of each processor. The master then broadcasts min(T) and max(T) so that every processor can calculate the reference vector \(\mathbf {v}_{ref}\). After calculating \(\mathbf {v}_{ref}\), all processors transform their local \(Proj_{[From, To)}\) to \(SProj_{[From, To)}\) independently. This is possible, because every processor receives the same min(T), max(T) and \(PCA_3\); hence, the reduced embedding spaces represented by \(\mathbf {u}_x, \mathbf {u}_y, \mathbf {u}_z\) as well as the rotations \(R_{u_x}(\varPhi _x) R_{u_y}(\varPhi _y) R_{u_z}(\varPhi _z)\) are the same for all processors without further synchronization.
4.2 Node extraction
The node extraction is the second step in S2G and the first of two steps to extract the embedding graph \(G_l(N, E)\) from the two-dimensional embedding space \(SProj(T, l, \lambda )\) that is the result of the subsequence embedding (Sect. 4.1). During this step, S2G extracts the nodes N by measuring the density of the embedding space within different segments. Figure 3 illustrates the node creation that consists of the three subroutines: (I) intersection calculation, (II) density estimation and (III) node creation. As a prerequisite, S2G partitions the two-dimensional embedding space SProj with a series of vectors of the form \(\mathbf {u}_\psi = \cos (\psi )\mathbf {r}_y + \sin (\psi )\mathbf {r}_z\). Thereby, \(\mathbf {r}_y\) and \(\mathbf {r}_z\) are the axes’ unit vectors of SProj and \(\psi \in \varPsi = (i * \frac{2\pi }{r})_{i \in [0,r]}\) with \(r \in {\mathbb {N}}\) being the user-defined number of samples. The intersections of the vectors \(\mathbf {u}_\psi \) with the embedded subsequences later form the nodes N of \(G_l\) whereby dense intersections are grouped into same nodes.
Intersection Calculation The intersection calculation partitions the two-dimensional embedding space SProj with a series of vectors of the form \(\mathbf {u}_\psi = \cos (\psi )\mathbf {r}_y + \sin (\psi )\mathbf {r}_z\). Thereby, \(\mathbf {r}_y\) and \(\mathbf {r}_z\) are the axes’ unit vectors of SProj, and \(\psi \in \varPsi = (i * \frac{2\pi }{r})_{i \in [0,r]}\) with \(r \in {\mathbb {N}}\) is the user-defined number of samples. The intersections of the vectors \(\mathbf {u}_\psi \) with the embedded subsequences form the nodes N of \(G_l\) whereby dense intersections are grouped into same nodes. Each vector angle \(\psi \in \varPsi \) leads to the creation of an intersection segment \(I_\psi \) that is defined through the vector \(\mathbf {u}_\psi = \cos (\psi )\mathbf {r}_y + \sin (\psi )\mathbf {r}_z\). These intersection segments are used to calculate the intersections \(I^\psi = \{x\,|(\mathbf {u}_\psi \times \mathbf {x} = \mathbf {0}) \wedge (\overrightarrow{x_{i-1} x} \times \overrightarrow{x_{i-1} x_i} = \mathbf {0})\}\) with \(x_{i-1}\) and \(x_i\) are two consecutive rows in SProj and \(\times \) is the cross-product. S2G hands these intersections (and the radius sets) to the next subroutine.
In our distributed system, we build upon the already distributed slices of the reduced embedding space SProj that is stored on the individual processors. With the user-defined parameter r, which is also broadcasted by the master processor, all processors autonomously calculate the intersection segments and the corresponding intersections in their local slice. Every processor needs to create every intersection segment, but we can aggressively parallelize the segment calculation. After the intersection calculations, S2G needs to re-partition the intersections so that all segments with the same angle can be aggregated on the same processor.
Density Estimation Based on the intersections, S2G performs a density estimation on every aggregated intersection segment; local maxima in the densities, i.e., estimated probability function, then, represent the graph nodes for their near embedded subsequences. The density estimation uses a Gaussian distribution of the intersection distances, such as \(|\mathbf {I^\psi _x}|\) where \(I^\psi _x \in I^\psi \). This leads to the creation of multiple estimated Gaussian probability functions—one function as visualized in Fig. 4 for each intersection segment. S2G then samples these functions using a fixed number of equally distributed points, which results in the creation of a set of density probabilities \(D^\psi \) that are needed to extract the set of nodes \(N^\psi \).
Sketch of the probability distribution (blue) estimated from the calculated intersections (red) using a Gaussian kernel on one specific intersection segment \(I_\psi \) with the node set \(N^\psi = \{N^\psi _0 , N^\psi _1\}\) extracted from the local maxima (yellow) of the distribution, which are determined by sampling the distribution with a fixed number of equally distributed points (gray and yellow, not all shown)
To estimate the distribution functions in the distributed setup, all intersection segments with the same angle need to be aggregated on one processor. For this purpose, the master processor assigns responsibilities for individual segments to each cluster participant. In this way, every processor knows already while performing the calculation where to send its calculated intersections. Processors send empty messages for segments with no intersections so that a processor knows when all intersections have been received and the density estimation can start. For each intersection vector \(\mathbf {I^\psi _x}\), S2G sends only its distance to the origin, because nothing else is needed to estimate the Gaussian distribution along the intersection vector \(\mathbf {u}_\psi = \cos (\psi )\mathbf {r}_y + \sin (\psi )\mathbf {r}_z\). Once the estimation is done, each processor samples the distribution as if it had calculated all the intersections itself.
Node Creation Given the sampled density probabilities \(D^\psi \), S2G extracts a graph node \(N_i^\psi \) for each local maximum in \(D^\psi \). S2G does this for every intersection segment, i.e., every angle \(\psi \). This process yields the set of nodes \(N = \bigcup \limits _{i=0}^{r} N^{\psi _i}\), which is then passed to the edge extraction step.
In DADS, the sampled density probabilities are already partitioned by their intersection segments so that every owner of such a segment \(I_\psi \) can create the nodes \(N^\psi \) independently of all other nodes. In this process, N is assembled from the \(N^\psi \)’s by letting every processor broadcast its local \(N^\psi \). In the end, every processor knows all the nodes N of \(G_l\), which is necessary for the edge extraction.
4.3 Edge extraction
The edge extraction step of S2G completes the graph extraction by calculating the weighted edges \({\mathscr {E}}\) of \(G_l(N, {\mathscr {E}})\). For this purpose, S2G iterates the entire embedding space SProj to find for each subsequence the corresponding intersection point and, from that, its corresponding graph node \(N_x\). With these nodes, S2G constructs the sequence \((N_0, N_1, \ldots , N_n)\) that corresponds to the sequence of embedded subsequences \((SProj(T, l, \lambda )_0, SProj(T, l, \lambda )_1, \ldots , SProj(T, l, \lambda )_n)\). This sequence of nodes includes every node of \(G_l\) at least once. Each consecutive pair \((N_i, N_{i+1})\) represents an edge of \({\mathscr {E}}\). In this process, the edge weights are calculated by counting the number of appearances of each specific node pair. The node sequence \((N_0, N_1, N_2, N_0, N_1)\), for example, corresponds to the node pairs \([(N_0, N_1), (N_1, N_2), (N_2, N_0), (N_0, N_1)]\), which are transformed into the weighted edges \({\mathscr {E}} = [(N_0 \xrightarrow []{2} N_1), (N_1 \xrightarrow []{1} N_2), (N_2 \xrightarrow []{1} N_0)]\). With \({\mathscr {E}}\), the entire graph \(G_l(N, {\mathscr {E}})\) is assembled.
In the distributed setting, every processor creates the node sequence and, hence, the edges for its local subsequence \(T_{[From, To)}\). A processor that finishes the edge creation locally, sends the results to the master processor that combines the partial results into one global graph \(G_l(N, {\mathscr {E}})\). For the scoring step, the global graph is then again broadcasted to all cluster participants.
4.4 Subsequence scoring
We covered much of the subsequence scoring already in subsection 3.1 and focused on the more technical details here. In summary, we use the previously constructed graph \(G_l(N, {\mathscr {E}})\) to create relative anomaly scores for paths in \(G_l\) with length \(l_q\) that correspond to subsequences of T (see Definition 5). The path lengths \(l_q\) are a user-defined query parameter, and it is important to note that, although we show it as the last processing step, the subsequence scoring is rather a separate process that uses the outcome of the S2G transformation process, i.e., the constructed graph \(G_l\), to score anomalies w.r.t. potentially multiple values of \(l_q\). In other words, the scoring process can be repeated arbitrarily often, without running all of the previous steps, to find anomalies of different lengths. Overall, the subsequence scoring step is divided into two subroutines: (I) path scoring and (II) score normalization. The first subroutine calculates the absolute normality values (see Definition 4); the second calculates the final anomality score (see Definition 5).
Path Scoring The path scoring extracts all paths \(P_{From}\) of length \(l_q\) from the graph \(G_l\) to calculate \(Norm(P_{From})\) for every \(P_{From}\). A path \(P_{From}\) starts with the subsequence \(T_{[From,To)}\) and ends with the subsequence \(T_{[From + l_q,To + l_q)}\). The normality values, hence, describe the ranges \([From,To + l_q)\). To make the retrieval of paths from \(G_l\) efficient, S2G stores which subsequences \(T_{[From,To)}\) correspond to which nodes in \(G_l\). In this way, the algorithm can iterate the input time series T and efficiently retrieve the corresponding graph nodes on the way. A window of size \(l_q\) thereby generates the paths \(P_{From}\).
In our distributed system, we re-use the already distributed time series T and the replicated graph \(G_l\). In this way, every processor can calculate the normality value of paths corresponding to its local subsequences. Just like the base S2G algorithm, DADS also stores, which subsequences produced which nodes and edges of \(G_l\) during the edge extraction step—technically, we simply store the edge order during their creation, which corresponds to the order of subsequences in T. With the global graph \(G_l\) and the edge creation orders, every processor can autonomously calculate the normality value for all of its local subsequences in \(T_{[From, To)}\).
Score Normalization The score normalization first calculates \(norm_{min}\) and \(norm_{max}\) over all normality values and, then, simply applies Definition 5 to all normality values. This inverts and normalizes the values into anomaly scores. We can plot these anomaly scores with their time series T to generate visuals, such as Fig. 1, or rank the subsequences by this score to detect anomalies.
To calculate the anomaly scores distributedly, DADS also needs to find the global minimum and maximum normality values. For this purpose, all processors find their local minimum and maximum values and share it with the rest of the cluster. Thus, every processor knows the global normality value range after it has received the local values from every other processor. At that point, the processor normalizes its local normality values and sends the results to the master processor, which persists them on disk.
5 Distributed anomaly detection system
DADS is our distributed implementation of the S2G algorithm. For the design of DADS, we leverage the capabilities of actor programming to devise reactive, highly scalable protocols for the distributed computation of the S2G transformation steps. In this section, we first introduce our protocol concept that is used for the reactive modularization of DADS. Afterward, we describe the architecture of our system and how the system is started.
5.1 DADS protocols
Protocols in DADS are self-contained, loosely coupled, distributed modules. This means that protocols communicate asynchronously via events and messages and that they span over multiple processors, i.e., actors that are placed on different machines. A protocol solves a specific task and exposes a public “interface” that consists of a set of accepted messages while hiding internal structures and logic, such as actor hierarchies and internal messages. Protocols can fire events that can be intercepted by any protocol, i.e., actor in the system. Events allow us to trigger the execution of protocols and to exchange calculation results. Protocols may consider the role of the processor that starts them so that they alter their behavior depending on whether they need to lead or follow in their execution. We later design our system as a sequence of such protocols.
Every protocol contains at least two mandatory actors: an EventDispatcher and a RootActor. The EventDispatcher allows the actors of this and other protocols to subscribe to the events emitted by this protocol; the EventDispatcher then sends the events created by actors of the local protocol to all subscribers. The RootActor of a protocol, which is not to be confused with Akka’s Root actor, is responsible for the creation of the protocol’s worker actors that implement the protocol logic; it is also the central contact point for external actors in other protocols that need to address actors in this protocol. By writing protocol X receives message Y/publishes event Z, we implicitly mean that either the RootActor receives and forwards a message or a worker actor of the protocol creates and publishes an event using the EventDispatcher.
A central protocol in DADS is the actor pool protocol, because it implements a cross-cutting concern. The actor pool protocol is used to control the parallel execution of different calculations. Its RootActor accepts generic types of work packages and dispatches them to its internal worker actors that simply complete whatever calculation they receive. The number of workers (parameter workers) in this protocol can be used to control the degree of parallelism for calculations so that they interfere less with system-related tasks, such as message passing or cluster heartbeats. The RootActor of the actor pool protocols also maintains a work queue for not yet dispatched messages and, hence, serves as a load balancer and buffer. The protocol also accepts WorkFactories, which are larger tasks that procedurally generate smaller work packages; these WorkFactories serve to save memory, and we mark them with  annotations in sequence diagrams.
annotations in sequence diagrams.
5.2 DADS architecture
DADS is a distributed algorithm with a master/slave architecture: Every setup has one master processor and arbitrary many slave processors. The master is a special slave that takes some additional responsibility for I/O, cluster supervision and algorithm orchestration. All slave processors (including the master processor) process their share of the global time series T. In contrast to batch processing, slaves communicate among each other, which relieves pressure from the master and adds peer-to-peer characteristics to the system.
The architecture of DADS is a sequence of eight protocols that implement the S2G transformation workflow as illustrated in Fig. 5. In the following, we give a brief overview over the protocols and their event-based interaction.
-
1.
Processor Registration: The processor registration initializes the DADS cluster and the local protocol instances. It also connects all processors so that they can exchange peer-to-peer and peer-to-master messages. (see Sect. 5.3)
-
2.
Sequence Slice Distribution: Once a certain number of processors have successfully registered, the sequence slice distribution step distributes T to the cluster participants, which transform them into slices of the embedding space \(Proj(T, l, \lambda )\). (Sect. 6.1)
-
3.
Principal Component Analysis: The principal component analysis step requires the projections Proj to then distributedly calculate the exact principal components of Proj. (Section 6.2)
-
4.
Dimension Reduction: Both Proj and its principal components are consumed by the dimension reduction step that calculates the two-dimensional embedding space SProj. (Section 6.3)
-
5.
Node Creation: From the embedding space SProj, the node creation step extracts the nodes N for the graph \(G_l(N,{\mathscr {E}})\) and, then, shares these nodes among all processors. (Section 7)
-
6.
Edge Creation: In the edge creation step, every processor extracts its local part of edges with the intersections and nodes given from the previous step. This step also adopts the processor responsibilities from the node creation step. (Section 8.1)
-
7.
Graph Merging: The graph merging step is triggered by the completion of all certain graph partitions. It collects and combines the edge partitions and, then, replicates the resulting graph \(G_l\) to all processors. (Section 8.2)
-
8.
Scoring: The scoring can be executed for different lengths \(l_q\) once \(G_l\) is received by all processors. It creates the anomaly scores to rank the subsequences accordingly. (Section 9)
5.3 Processor registration
The processor registration protocol consists of a single worker actor, which is the ProcessorRegistry actor. Once a slave system is started, this actor runs the following initialization steps:
-
1.
Protocol instantiation: The ProcessorRegistry creates all local protocols, i.e., their RootActors and EventDispatchers, which then spawn and initialize their protocol-specific worker actors.
-
2.
Local event subscription: The ProcessorRegistry wires all local protocols up by sending a SetupProtocolMessage with references to all previously instantiated protocols to all these protocols. Actors within the protocols then decide to which events they need to subscribe.
-
3.
Registration: The ProcessorRegistry periodically sends a ProcessorRegistrationMessage with a list of all local protocols to the master’s ProcessorRegistry until the master acknowledges the registration with a list of all other protocols in the cluster.
-
4.
Remote event subscription: The ProcessorRegistry shares the remote protocols with all local protocols so that they can subscribe to their events as well. This concludes the wiring process and triggers the sequence slice distribution protocol.
6 Distributed subsequence embedding
To distribute the subsequence embedding, we propose three protocols: sequence slice distribution, principle component analysis and dimensionality reduction. In this section, we discuss the three protocols in detail.
6.1 Sequence slice distribution
The sequence slice distribution protocol consists of two worker actors: the SequenceSliceDistributor and its counterpart the SequenceSliceReceiver. The protocol starts on the master processor with the SequenceSliceDistributor reading, slicing and then distributing the global sequence T. We divide T into p consecutive, evenly sized partitions, i.e., subsequences \(T_{[From,To)}\) with \(0 \le From < To \le |T|\). Each of the p processors in the cluster receives one of these slices of T via its SequenceSliceReceiver.
Because every processor gets an equal share of the input time series T, the slice length \(s = |T_{[From, To)}| = To - From\) is defined by the length of the input series |T| and the number of processors in the cluster p. We also need to consider an overlap of \(l - 1\) records between adjacent slices so that every embedding subsequence of length l falls completely into one slice. Hence, s is actually defined as \(\frac{|T|}{p} + (l - 1)\). At this point, we emphasize that DADS handles three different kinds of subsequences: (I) the slices of T of length s that are owned by the different processors, (II) the embedded subsequences of T of length l that are created for the embedding and (III) the anomaly scoring subsequences of length \(l_q + l - 1\).
To send large messages, such as the slices in this protocol, over the network, we use a dedicated channel, work pulling and reliable proxy actors. This prevents system-relevant control messages, such as heartbeats, to be blocked or critically delayed. In diagrams, we indicate the transmission of large messages with the  annotation.
annotation.
After receiving the local sequence slice, the SequenceSliceReceiver calculates the first local and then global minimum (min(T)) and maximum (max(T)) record values. These serve to create \(\mathbf {v}_{ref}\) and then rotate the projection space accordingly (see Sect. 4.1). The SequenceSliceReceiver signals that the local embedding slice \(Proj_{[From_i,To_i - (l - 1)]}\) is fully calculated, by issuing a ProjectionCreatedEvent.
Matrix Compaction. The embedding space \(Proj(T, l, \lambda )\) is technically a matrix of \(n \times m\) double (8 bytes) values where \(n = |T| - (l - 1)\) is the number of rows (embedded subsequences) that each consists of \(m = l - \lambda \) components (columns). This makes Proj the largest data structure in the transformation process. It effectively prevents the S2G algorithm from calculating larger time series T that consume multiple gigabytes or even terabytes [20, 51] of memory, because Proj needs to be kept in memory. For example, the MIT-BIH Supraventricular Arrhythmia Database [18, 34] (MBA) dataset of patient 14046 contains roughly \(10 \times 10^6\) records, which consume mere 80 megabytes of disk storage. Representing the embedding space \(Proj(T, l, \lambda )\) with \(l = 100\) and \(\lambda = \lfloor \frac{l}{3} \rfloor = 33\), as proposed in the S2G publication [10], takes more than 5 gigabytes of main memory already. Scaling this example up to a sequence of 10 gigabytes size, the matrix would consume more than 660 gigabytes of memory for the sequence embedding alone. Although we slice and distribute Proj, this memory limits the applicability of the algorithm.
To mitigate this issue, we propose a sequence matrix data structure for storing Proj that reduces the memory consumption from \({\mathscr {O}}(n \times m)\) down to \({\mathscr {O}}(n + m)\) exploiting the fact that large parts of the matrix store redundant data. The redundancies are the result of the local convolutions that are applied to subsequences of T, as illustrated in Fig. 6.
The sequence matrix is a floating point array that stores only physical cells, i.e., non-replicated cells. All virtual cells, i.e., cell with redundant values, are not stored explicitly, but inferred from the physical cells via pointer arithmetic. Figure 7 illustrates the mapping of virtual cells to physical cells in the sequence matrix. The sequence matrix calculates the mapping transparently and exposes the same interface (e.g. getValue(row, column)) as a fully materialized matrix.
Altogether, the sequence matrix structure stores only the first embedded subsequence of length m plus one additional record for every following subsequence, consequentially reducing the required space to \(m + (n - 1) = |T| - \lambda \) values, which is even less than the input time series T. In Sect. 10, we demonstrate the significant memory savings of this compression.
6.2 Principal component analysis
The principal component analysis protocol calculates the PCA for the global embedding space Proj on its distributed slices. It is an actor-based implementation of the PCA algorithm by Bai et al. [5] and consists of two actors: the PCACoordinator and the PCACalculator. The PCACoordinator is created only on the master processor and is responsible for assigning unique identifiers, i.e., indices to all processors; afterward, it is directly terminated. The PCACalculator on every processor is the actor that implements the PCA calculation on the local Proj slice. Figure 8 gives an overview of the protocol.
Distributed PCA calculation using Bai et al.’s algorithm [5], which is concluded by firing the PrincipalComponentsCreatedEvent
The PCA algorithm of Bai et al. assumes that the global data matrix \(X \in {\mathbb {R}}^{n \times p}\) (\(n \gg p\)), which is our embedding space Proj, is distributed among s different processors, i.e., \(X = [X_0, X_1, ... X_{s-1}]^T\) . Hereby, X is horizontally, i.e., row-based partitioned into chunks \(X_i \in {\mathbb {R}}^{n_i \times p}\), where each processor i (\(0 \le i < s\)) stores one of these partitions so that \(n = \sum _{i=0}^{s-1}n_i\). With \(X = Proj\) and \(X_i = Proj_{[From_i, To_i)}\), this directly maps to our situation.
At first, every PCACalculator calculates the column means \({\bar{x}}^T_i \in {\mathbb {R}}^{1 \times p} = \frac{1}{n_i} e^T_{n_i} X_i\) and the column-centered data matrix \({\bar{X}}_i \in {\mathbb {R}}^{n_i \times p} = X_i - e_{n_i} {\bar{x}}^T_i = Q^{(0)}_i R^{(0)}_i\) of their local data slice where \(e_l \in {\mathbb {R}}^{l \times 1} = (1, 1, \ldots , 1)\) is a column vector of length l that contains all 1s. Hereby, \(R^{(0)}_i \in {\mathbb {R}}^{p \times p}\) is an upper triangular matrix that results from applying the QR decomposition [19] to \({\bar{X}}_i\), which is required for the further calculation; at this point, \(Q^{(0)}_i\) is no longer required and can be dropped. Afterward, every PCACalculator transfers its local column means \({\bar{x}}^T_i\) and the number of rows \(n_i\) to the processor with index 0 (which is always the master processor in DADS). This processor is responsible for finalizing the PCA computation at the end of the algorithm. Additionally, processors with an index \(i \ge \frac{s}{2}\) send their local \(R^{(0)}_i\) to the processor with index \(i - \frac{s}{2}\). To address the correct processor, the PCACalculators need to know the processor indices; thanks to the PCACoordinator, these indices have already been broadcasted via InitializePCACalculationMessages.
The sending of the \(R^{(0)}_i\) matrices concludes the initialization step. In the \(c \in [1, \lceil \log _2 s \rceil ]\) following steps, the results are successively aggregated: In each step c, the processors with indices \(0 \le i < \frac{s}{2^{c}}\) calculate the following QR decomposition:
Again, \(R^{(c)}_i \in {\mathbb {R}}^{p \times p}\) is an upper triangular matrix, which is transferred to the processor with index \(i - \frac{s}{2^{c+1}}\) if \(i \ge \frac{s}{2^{c+1}}\). This procedure repeats until the master processor at index \(i = 0\) calculates the final matrix. Figure 9 shows an example of this process with eight processors.
Exemplary procedure of the distributed PCA computation of Bai et al. [5] with 8 involved processors
The master then calculates the last required QR decomposition using the previously transferred column means \({\bar{x}}_i\), the row counts \(n_i\), and \({\bar{x}} = \frac{1}{n}\sum \limits _{i=0}^{s-1}n_i{\bar{x}}_i\):
From the result, the master calculates the PCA via singular value decomposition. It then ends by issuing a PrincipalComponentsCreatedEvent with the three most significant components \(PCA_3\).
6.3 Dimension reduction
After receiving \(PCA_3\) from the principal component analysis and the min(T) and max(T) values from the sequence slice distribution, the dimension reduction protocol transforms the global embedding space \(Proj(T, l, \lambda )\) into the global reduced embedding space \(SProj(T, l, \lambda )\). For this, we use two worker actors: DimensionReductionDistributor and DimensionReductionReceiver.
The DimensionReductionDistributor exists only on the master. It calculates the rotation matrices \(R_{u_x}(\varPsi _x)\) \(R_{u_y}(\varPsi _y)\) \(R_{u_z}(\varPsi _z)\) and sends the results to all processors. For optimal bandwidth utilization, the protocol sends the matrices to all target processors simultaneously.
The DimensionReductionReceiver is created once on every processor. It uses \(PCA_3\) to reduce its local slice of the embedding space \(Proj_{[From, To)}\) to \(RProj_{[From, To)}\). Then, it uses the rotation matrices to transform \(RProj_{[From, To)}\) into \(SProj_{[From, To)}\). It finally ends the subsequence embedding by issuing a ReducedProjectionCreatedEvent; at this point, the two-dimensional embedding space SProj is, like Proj, horizontally partitioned—each processor stores one slice.
7 Distributed node extraction
The node creation step of the Series2Graph transformation process consists of three subroutines, which are intersection calculation, density estimation and node extraction (see subsection 4.2). Although these subroutines could be implemented in three protocols, we put them into one, because the calculation process is particularly coherent in that it requires the master only once and then uses peer-to-peer communication throughout the three subroutines. The task of the protocol is to extract the nodes of the graph \(G_l(N, E)\) from the reduced projection SProj. For this, it creates three worker actors: NodeCreationCoordinator, NodeCreator, DensityEstimator.
The NodeCreationCoordinator is a master-only actor that assigns in an initial setup phase each processor to a range of intersection segments. Afterward, the NodeCreators can find each other directly so that the NodeCreationCoordinator can be terminated. The NodeCreator actor orchestrates the local node extraction workflow, which covers all three subroutines. It creates for each intersection segment one DensityEstimator as a child actor. Each DensityEstimator is responsible for the calculation of the probability function of its segment, the sampling of density probabilities \(D^\psi \) and the extraction of the node set \(N^\psi \). For optimal local parallelization, the NodeCreator and the DensityEstimator dispatch intersection calculation tasks and density estimation tasks, respectively, to local worker actors of the actor pool protocol. Figure 10 illustrates the entire node extraction protocol and its phases. In the following, we describe these steps in more detail.
Setup Once a local reduced embedding slice \(SProj_{[From, To)}\) has been received, its NodeCreator signals its readiness via NodeCreatorReadyMessage, which contains the local sequence slice indices From and To, to the NodeCreationCoordinator. Once all NodeCreators are ready, the NodeCreationCoordinator splits the range of intersection segments [0, r] into equal partitions and distributes them among the available processors. It then sends these responsibilities, and sequence slice ranges \([From_i, To_i)\) of the individual processors via InitializeNodeCreationMessage to all NodeCreators. Afterward, the NodeCreationCoordinator terminates.
Each NodeCreator determines whether it has a successor, i.e., a processor responsible for the subsequent sequence slice, and/or a predecessor, i.e., a processor with a preceding sequence. For example, if the global time series T is distributed among three processors A, B and C so that A is responsible for \(SProj_{[0, To_A)}\), B is responsible for \(SProj_{[To_A, To_B)}\), and C is responsible for \(SProj_{[To_B, |T|)}\) (we ignore the subsequence overlap of \(l-1\) here), then A and B have successors B and C, respectively, and B and C have predecessors A and B, respectively. Because intersections are calculated between the segments \(\mathbf {u}_{\psi \in \varPsi }\) and vectors \(\overrightarrow{x_{i-1} x_i}\) defined by two consecutive rows \(x_{i-1}\) and \(x_i\) of SProj, we need to make sure that all pairs of consecutive rows coincide on one NodeCreator. For this reason, every NodeCreator sends its last embedded subsequence, which is a single-, two-dimensional point, to its successor and receives a new first embedded subsequence from its predecessor, if a successor and/or predecessor exists.
Intersection Calculation Once a processor receives the last embedded subsequence from its predecessor or if the processor does not have a predecessor, it immediately starts the local intersection calculation. The intersection calculations work exactly as described in subsection 4.2) but only on the local reduced embedding slice \(SProj_{[From, To)}\). For parallelization, the protocol exploits that each pair of consecutive rows \(x_{i-1}\) and \(x_i\) of SProj can be processed independently. It therefore divides \(SProj_{[From, To)}\), which might be preceded by the last reduced subsequence from a predecessor, into horizontal partitions that overlap by one subsequence each. Then, it sends a WorkFactory (see Sect. 5.1), which creates individual CalculateIntersectionsMessage tasks that contain the overlapping chunks and the parameter r, to the local actor pool protocol. The worker actors in the actor pool calculate the intersections \(I^\psi \) for all \(\psi \in \varPsi \) and send them to the NodeCreator. Note that each pair of consecutive rows \(x_{i-1}\) and \(x_i\) can create between 0 and \(\frac{r}{2}\) intersections depending on how many intersection segments their connection crosses. Once an intersection is calculated, the algorithm stores not only the intersection point but also a mapping to the embedded sequence \(x_{i-1}\). This mapping helps during edge creation and path scoring to quickly relate an intersection (or graph node) back to its (embedded) subsequence of T. After collecting the last result, the NodeCreator emits an IntersectionsCalculatedEvent containing all locally calculated intersections \(I_{[From,To)}\).
Density Estimation The first step in the density estimation phase is a shuffle operation: Each processor groups its local intersections I by their intersection segment \(\psi \) (note that for each point \(x \in I^\psi \) only its distance to the root, i.e., \(||\mathbf {x}||\) is needed, which reduces the size of \(I^\psi \)). The resulting groups are then transferred to the processors that are responsible for specific segments. In this way, the following density estimations each take as input one complete intersection segment \(I^\psi \). Once all intersections of a segment \(I^\psi \) are collected, a NodeCreator immediately spawns a new DensityEstimator for \(I^\psi \) that performs the density estimation and node extraction for intersection segment \(\psi \), as we will detail next.
After receiving the intersections \(I^\psi \), the DensityEstimator needs to estimate the density for a fixed number of equidistant evaluation points. These points are taken from the range [0, max(I)], where max(I) is the largest distance of any sequence embedding to the root. Following the implementation of Series2Graph, we take 250 of these evaluation points per intersection segment. For the density estimation, each DensityEstimator re-implements the kernel density estimation (kde) algorithm of python’s scipyFootnote 3 library; more specifically, kde.pyFootnote 4. This algorithm, which was also used in the implementation of S2G, takes \(I^\psi \) and calculates a density estimate \(d \in D^\psi \) for every estimation point. For the calculations, kde proposes to either loop over the intersection points or the evaluation points depending on which point set is larger—we adopt this strategy. Regardless of which point set is used, we divide it into small chunks for parallelization. Each chunk can be processed independently by the worker actors of the local actor pool protocols, which improves the calculation efficiency significantly. If we parallelized over the intersection points, the DensityEstimator needs to concatenate all results; if we parallelized over the evaluation points, the DensityEstimator aggregates the results. Either way, the results are the density estimations \(D^\psi \) for the segment \(I^\psi \).
Node Extraction The node extraction continues in the DensityEstimators. From the density estimations \(D^\psi \), it selects all local maxima \(D_i^\psi \), which are estimates with \(D_i^\psi > D_{(i-1)}^\psi \) and \(D_i^\psi > D_{(i+1)}^\psi \), as nodes \(N_i^\psi \). The DensityEstimators finally broadcast their nodes via NodesCreated events so that the complete node set \(N = \bigcup \nolimits _{i=0}^{r} N^{\psi _i}\) is known to all processors. After receiving a NodeCollectionCreated message from all local DensityEstimators, the NodeCreator ends the protocol.
8 Distributed edge extraction
The edge extraction step extracts the weighted graph edges \({\mathscr {E}}\) from the intersections I and nodes N and assembles the final graph \(G_l(N,{\mathscr {E}})\). It uses two protocols: edge creation and graph merging.
8.1 Edge creation
The edge creation protocol consists of a single worker actor, which is the EdgeCreator. As detailed in Fig. 11, this EdgeCreator initially waits for three events:
-
The ResponsibilitiesReceived event with the intersection segment and sequence slice responsibilities of all processors tells whether this processor has a successor/predecessor w.r.t. the sequence slices.
-
The IntersectionsCalculated event with the local intersections \(I_{[From,To)}\) and the mapping from intersections to embedded subsequences defines how the intersections need to be sorted.
-
All NodesCreated events with the nodes \(N^\psi \) together deliver the node set N that needs to be connected via edges.
As soon as all these events are received, the EdgeCreator extracts the edges as described in subsection 4.3: Because the intersections in \(I_{[From,To)}\) arrive grouped by their intersection segment angles \(\psi \), the EdgeCreator at first sorts the local intersections \(I_{[From,To)}\) by the order of their corresponding subsequences in the time series T. For the sorting, we use the mapping of intersections to their subsequence that comes with the IntersectionsCalculated event.
Once the intersections are sorted, the EdgeCreator can iterate the intersections to retrieve for each intersection its nearest node. These nodes are put into a sequence \((N_0, N_1,\ldots , N_{From - To})\), from which we can extract the weighted edges \({\mathscr {E}}\). However, because we calculate the edges distributedly on time series slices [From, To), the edges between two consecutive slices cannot be created by either of the corresponding processors. This is because the intersection sets are distinct, i.e., partitioned without overlap. Although DADS exchanged the last embedded subsequence during node creation (see Sect. 7), the intersections, which are formed by pairs of embedded subsequences, are known in one slice [From, To) only. Hence, the local node sequences \((N_0, N_1,\ldots , N_{From - To})\) are overlap-free as well. To create the edges between consecutive node sequences, every EdgeCreator i sends its last node \(N_{From_i - To_i}\) to its successor EdgeCreator \(i+1\), if the ResponsibilitiesReceived event indicates that a successor exists.
It turns out that finding the nearest node for an intersection point and extracting the edges from the node sequence are expensive, but parallelizable operations. For this reason, the EdgeCreator calculates only the last node from the sorted intersection sequence itself (because it needs to send this node to its successor); all further node calculations and edge extractions are parallelized by splitting the sorted intersection sequence \(I_{[From,To)} = (I_0, I_1,\ldots , I_{From - To})\) into smaller partitions. Note that these partitions need to overlap by one intersection as well to create the partition-linking edges. Each partition is then given to and processed by a worker actor of the actor pool protocol. For this purpose, the EdgeCreator sends a WorkFactory to the local actor pool protocol. This factory produces CreateGraphPartitionMessages that contain equidistant, overlapping partitions of \(I_{[From,To)}\) and the starting node (if there is any). To complete a CreateGraphPartitionMessage, each worker first creates the corresponding node sequence. Each pair of subsequent nodes in the sequence, then, becomes an edge, and if an edge exists already, the worker increases its weight by one (see subsect. 4.3). The resulting edge sets \({\mathscr {E}}_i\) are send back to the EdgeCreator via GraphPartitionChunk message. The EdgeCreator merges these edges into the local edge set \({\mathscr {E}}_{[From,To)} = \bigcup {\mathscr {E}}_i\), which it then sends via GraphPartitionCreated event to all cluster participants.
8.2 Graph merging
The graph merging assembles and distributes the final graph \(G_l(N,{\mathscr {E}})\). The protocol starts when all local graph partitions \(G_{l,[From,To)}(N,{\mathscr {E}}_{[From,To)})\) have been created. It consists of four actors: GraphSliceSender, GraphSliceReceiver, GraphMerger and GraphReceiver. While the first and last actors exist on all processors, the other two are started on only the master.
Because the nodes N have already been broadcasted to all processors, the GraphSliceSenders start by sending only the local edges \({\mathscr {E}}_{[From,To)}\) to the master’s GraphSliceReceiver via large message channel. Edges are represented by compact triples \((id(N_{from})\), weight, \(id(N_{to}))\) where \(id(N_x)\) returns a 4 bytes integer that points to node \(N_x\) and weight is an 8 bytes long. The GraphSliceReceiver accepts the incoming edges and forwards them directly to the GraphMerger. GraphSliceReceiver and GraphMerger are two actors on the master so that edges can be received and merged in parallel for latency hiding. The GraphMerger incrementally calculates \({\mathscr {E}} = \bigcup {\mathscr {E}}_{[From_i,To_i)}\) by merging every received edge e into the edge set \({\mathscr {E}}\): If e does not already exist, it simply adds e to \({\mathscr {E}}\); otherwise, it increases the weight of e by the incoming weight. Once all edges are received, \(G_l(N,{\mathscr {E}})\) is the complete graph. The GraphMerger, then, sends \({\mathscr {E}}\) via large message channel to all GraphReceivers, which publish GraphReceived events upon completion.
9 Distributed scoring
The scoring protocol calculates the anomaly scores of paths in \(G_l\) as already discussed in subsect. 4.4. In this section, we discuss the protocol’s actors and message flow in more detail. Figure 12 visualizes the scoring procedure. It involves two worker actors, which are the ScoreCalculator on all processors and a ScoreReceiver on the master. The ScoreCalculators perform the entire scoring process, and the ScoreReceiver persists the results. Because the time series T is already appropriately partitioned across the processors, the ScoreCalculators simply infer their responsibilities from their local slices.
The protocol requires three events to start: the ResponsibilitiesReceived event with the sequence slice ranges of all processors to find a successor/predecessor w.r.t. the local sequence slice [From, To), the GraphPartitionCreated event with the different edge creation orders to determine which paths belong to which embedded subsequences, and the GraphReceived event with the weighted edges. In addition to these events, the ScoreCalculators also receive the query length \(l_q\) via ScoringParameter messages from the master.
Our approach of distributing the scoring procedure is that we score all the different paths w.r.t. T in parallel; each path, however, should be scored on one local partition. To match each path of length \(l_q\) entirely to one ScoreCalculator, their edge sets need to overlap by \(l_q - 1\) edges. Because every ScoreCalculator initially owns only those edges that correspond to its local slice of T, the ScoreCalculators first exchange their \(l_q - 1\) last edges with their successors. Afterward, they score all local paths of length \(l_q\) by adding up their edge weights. In a second synchronization step, the ScoreCalculators exchange their local minimum \(norm_{min,[From, To)}\) and maximum \(norm_{max,[From, To)}\) scores to determine the global extrema \(norm_{min}\) and \(norm_{max}\). To calculate the running mean, DADS needs to slide a window of length \(l_q\) over the sequence of path scores, which again requires the exchange of overlapping path scores between subsequent processors. After the score exchange, each processor normalizes its local path scores and transfers them to the ScoreReceiver.
To not exhaust the memory of the master, the ScoreReceiver stores all received path scores immediately, but only temporarily in individual files on disk. It thereby remembers the corresponding sequence slice ranges so that it can later, once all path scores are completely transferred, merge the scores in the correct order into a single result file. In this way, the scores in the result file are aligned with their subsequences in the time series T. The ScoreReceiver finally ends the scoring for \(l_q\) with a ReadyForTermination event.
10 Evaluation
In this section, we evaluate DADSFootnote 5 w.r.t. computation quality, memory consumption on a single processor and runtime scalability depending on both cluster size and input data size. Hereby, we compare the results of our system with results produced by the original implementation of S2GFootnote 6 and an improved implementation \(S2G^{+}\). In the improved implementation, we applied a major algorithmic optimization that we also used in the implementation of DADS: The original S2G code calculates the intersections twice, once for generating the vertices and once for generating the edges; in \(S2G^{+}\), we reuse the already calculated intersections and, hence, save a lot of computations.
Hardware We ran the experiments on a cluster of up to 12 processors each equipped with an Intel Xeon E5-2630 v4 CPU (10 cores at 2.2 GHz), Ethernet network of 1 GiBit/s bandwidth and 31 GiB RAM.
Time Series Data Our experiments use the real-world and synthetic datasets that have also been used in the evaluation of the S2G algorithm. The 26 evaluation datasets are listed in Table 2 and cover various domains.
Configuration Unless stated differently, our experiments use the same parameters as the evaluation of S2G in [10], which are \(l = 50\), \(\lambda = 16\), \(r = 50\) and \(l_q = 75\). We assume that the global time series T is initially stored on only the master processor and that also the results need to be transferred back to the master, which writes them into a single-output file. This means that all absolute execution times for DADS include the initial data distribution time and the final score collection time. We also included the time for reading and writing data from/to disk for all algorithms.
10.1 Anomaly detection quality
The DADS algorithm aims to improve the S2G algorithm in terms of efficiency and scalability. The majority of experiments in this section therefore focuses on these two aspects. In a first set of experiments, however, we validate that the distribution does not affect the quality of the discovered anomalies. For this, we measure the area under the ROC curve (ROC-AUC) [21] for different results on the MBA [18, 34] dataset and the synthetic SRW [10] datasets. Besides S2G and DADS, we also considered the STOMP [52] algorithm (with a window size of 75) in this experiment as another state-of-the-art reference algorithm.
The measurements, which are shown in Table 3, show three interesting performance properties: First, both S2G and DADS yield the same ROC-AUC scores; it is therefore shown that the distribution does not impact the effectiveness of the approach. Second, both S2G and DADS produce better results than STOMP, which confirms the experimental results of [10] on the SRW and MBA datasets. Third, the result quality of DADS (and S2G) is relatively stable when the input dataset is concatenated multiple times with itself. This can be explained by the fact that the algorithm identifies anomalous subsequences by their relatively low occurrence frequency; by concatenating a sequence with itself, the frequencies of all subsequence patterns in the series are multiplied proportionally so that anomalous sequences remain anomalous. The reason for the small performance changes is the subsequences at the concatenation points, which are not present in the original time series. Because the concatenation works well for S2G and DADS, we will use the same construction to generate longer time series in other experiments as wellFootnote 7.
Although both DADS and S2G achieve almost identical ROC-AUC scores, the results are slightly different. We therefore compared the results of both algorithms in a systematic way: For each of the 26 datasets, we conducted four experiments, each with different parameter configuration. For each parameter configuration, we measured the maximum and average result differences throughout the 26 datasets. Table 4 lists the outcome of the experiment.
The measurements show an average difference of mere \(4 \times 10^{-12}\), which is practically insignificant. These differences stem from floating point rounding behavior that happens unavoidably in the various calculations of, for example, the subsequence embedding or principal component calculations. Rounding inaccuracies happen in both implementations, which is pretty normal in this type of application. Hence, we consider both results as correct and essentially the same. We also observe that the differences become slightly smaller when we increase the subsequence length l and query length \(l_q\). This is because rounding issues may happen in either direction and summing up more values, as in the calculation of longer paths, compensates for some of these issues.
10.2 Scaling in memory capacity
We now evaluate DADS’ scalability w.r.t. the main memory capacity of a single machine. The experiment emphasizes the impact of our sequence matrix data structure by showing DADS peek memory consumption with and without this optimized data structure. For increasing amounts of main memory, the experiments find the longest processable time series for both DADS and S2G. The time series in this experiment is a snippet/concatenation taken from the MBA (ECG) database. Figure 13 plots the results.
\({\underline{Left}}\): Absolute runtimes of the different processing steps (relative times in Fig. 14). \({\underline{Right}}\): Total runtime of DADS using X Processors with 20 Threads each (blue) in comparison with the ideal time for linear scalability (green) and the ideal time for linear scalability when considering the result storing costs as constant time (red)
We observe that S2G and DADS without our sequence matrix have very similar limits. The small advantage of DADS (without sequence matrix) over S2G is the result of a few small memory optimizations. The reference implementation, for example, calculates and stores intersections twice, once for the node extraction and once again for the edge extraction; DADS calculates them only once and passes the results over. We added such small improvements in the \(S2G^{+}\) variant. Both implementations do scale linearly w.r.t. the maximum processable time series length depending on the upper main memory limit.
The experiment also shows that our sequence matrix optimization significantly reduces DADS’ main memory consumption. More specifically, the matrix size reduces by a factor of \(l - \lambda \), which more than halves the overall memory consumption for executions on one processor.
10.3 Scaling in cluster size
In this section, we evaluate DADS’ scalability w.r.t. the number of processors in the cluster. For this purpose, we measured the runtime of DADS while gradually increasing the number of processors from 1 to 12. All experiments in this evaluation were conducted on a concatenated variant of the MBA dataset with a total of 50 million records.
Effectiveness of Parallelization First, we investigate how effective DADS parallelizes the graph transformation steps by measuring the steps’ relative (see Fig. 14) and absolute (see Fig. 15) runtimes depending on the number of processors. The three most time-consuming steps in DADS are the PCA (Sect. 6.2), the node creation (Sect. 7) and the result storing, which is a subroutine of the scoring protocol (Sect. 9).
The measurements in Fig. 14 and 15 (left) show that all parts of the algorithm except the result storing, which is executed in about the same time in all experiments, scale well with the cluster size, which is, they require proportionally less execution time with an increasing number of processors. Because DADS does not parallelize the result storing, this behavior is expected. So, when increasing the number of processors, the result storing takes an increasing portion of the relative runtimes.
Figure 15 (right) plots DADS’ total execution time and two ideal curves that mark perfect linear scaling times with and without a scaling result storing step. The curves show that DADS scales almost perfectly linear with an increasing number of processors when ignoring the constant result storing. Hence, all our distribution and parallelization protocols for S2G scale well.
CPU Utilization Figure 16 plots the average and maximum CPU statistics of the cluster during an execution of DADS. Here, we observe that DADS uses the entire cluster, i.e., all of the available 240 threads, for the most part of the intersection calculation [29,32], the node creation [32,65] and the edge creation [65,67]. For almost the entire period [29,67], at least one processor is always fully utilized, because these steps are mostly CPU bound. The drop in average cluster utilization in [52,65] is caused by the synchronization barrier between the node creation and edge creation protocol and the fact that some processors need to extract nodes from more intersections than others—by chance, their intersection segments produced relatively many intersections.
For the remaining execution time, especially for the PCA and result storing routines, we observe a rather low CPU utilization: about 7% during PCA and only about 2% on average during result storing. These relatively low numbers are to be expected, because the steps are not CPU bound. The distributed PCA algorithm of Bai et al. [5] is designed to run single-threaded on each processor, which theoretically corresponds to exactly 5% CPU utilization on our processors (1 out of 20 available threads). Because the processors exchange messages during PCA, the average utilization is slightly higher. For the result storing, we basically measure only messaging overhead, because the writing happens solely on the master and is, therefore, bound by the master’s disk speed.
Network Utilization Figure 17 visualizes the amount of data transferred via large message channel over the network during a distributed DADS execution. Hereby, 99% of total traffic are the sequence slices (see Sect. 6.1), the intersections (see Sect. 7) and the anomaly scores (see Sect. 9). The remaining transfers, such as the graph distribution (see Sect. 8.2), use less than 5 MiB in total. Both the sequence slice and the anomaly score transfers are smaller than the initial time series T, because one slice of each transfer stays on the master, while only 11 out of 12 need to be transferred. The amount of transferred intersection data, however, exceeds even the size of T, because on average every pair of consecutive subsequences produces more than one intersection (each pair can produce between 0 and \(\frac{r}{2}\) intersections); in our experiment, DADS produces more than 58 million intersections from the initial 50 million records. By distributing the intersection calculation, however, DADS greatly benefits from the cluster resources as shown in Fig. 16 [28,32]; the transfer also serves to keep the remaining data transfers as small as they are.
Besides the transfer volumes, Fig. 17 also annotates the average transfer rates in GiBit/s. We see that the transfer of intersections utilizes about the entire bandwidth of our cluster, which is 1 GiBit/s. The work-pulling mechanism of our large data transfers artificially reduces the bandwidth in the other two transfers, because the data recipients cannot process the data fast enough and, therefore, apply backpressure: For the sequence slices, the receiving processor directly constructs the (high-dimensional) embedding space and, for the anomaly scores, the master directly persists the data to disk. The latter shows that the result storing is actually disk and not network bound.
10.4 Scaling in data size
We now evaluate the runtime scalability of DADS w.r.t. the input data size by conducting a series of experiments with different configurations of DADS, the single-threaded reference implementation S2G and the slightly improved implementation \(S2G^{+}\) to compare their execution times. For DADS, we used three configurations: (I) one processor with one thread, which is the same S2G and S2G+ can use; (II) one processor with 20 threads, which shows the parallelization effects; and (III) 12 processors with each 20 threads, which shows the distribution effects. The experiments use snippets/concatenations of the MBA dataset of patient 14046 with lengths varying between \(10 \times 10^3\) and \(500 \times 10^6\) records. The results are listed in Table 5 and visualized in Fig. 18. Note that Fig. 18 uses two axes, a logarithmic scale left to compare all runtimes and a linear scale right to emphasize DADS’ linear scaling w.r.t. the length of the input time series T—the green and the blue line represent the same configuration on different scales. The measurements show the best of three execution times, where execution time deviations were practically negligible, i.e., within around 1%.
The measurements show that all configurations could process the entire original time series, which consists of roughly 10 million records. On this relatively short sequence, all configurations of DADS already outperform the reference implementations by a factor of 6.5/3.4 (DADS-1P-1T vs. S2G/\(S2G^{+}\)), 40.7/21.1 (DADS-1P-20T), up to 226.8/118.3 (DADS-12P-20T). S2G then exceeds the time limit of 8 hours when increasing the input time series length to 50 million records. On the 100 million records time series, all non-distributed configurations run out of memory, because the intermediate state exceeds the available 58 GiB main memory. DADS successfully solves this limitation by distributing the computation to (in our setup) 12 processors. In this way, it processes a time series of 500 million records in less than 17 minutes using a combined amount of 336 GiB main memory. Comparing the execution times for the largest processed inputs, this is a still 6 times faster than S2G while processing a 50 times longer input.
11 Conclusion
In this paper, we presented DADS, an efficient, distributed and scalable adaptation of the S2G algorithm. With DADS we can detect anomalously shaped subsequences of different lengths in huge univariate time series. Via reactive programming concepts, DADS makes best use of the available resources, i.e., memory, CPU and network. The algorithm is orders of magnitude faster than S2G, and because its memory consumption can be distributed over multiple machines, it could process 50 times longer sequences than S2G on our 12 processor cluster. We achieve these improvements through the parallelization and distribution of the algorithm’s processing steps, the minimization of communication requirements and the optimization of intermediate data structures.
Notes
https://akka.io/ (26.05.2020).
https://www.ojalgo.org/ (25.05.2020).
https://www.scipy.org/ (21.05.2020).
Please note that the concatenation trick does not work for anomaly detection algorithms that cannot deal with repeated anomalies.
References
Abdul-Aziz, Ali, Woike, Mark R., Oza, Nikunj C., Matthews, Bryan L., lekki, John D.: Rotor health monitoring combining spin tests and data-driven anomaly detection methods. Structural Health Monitoring 2012, 3–12 (2012)
Agha, Gul, Hewitt, Carl: Actors: A conceptual foundation for concurrent object-oriented programming. Research directions in object-oriented programming. 49–74 (1987)
Ahmed, Tarem, Oreshkin, Boris, Coates, Mark: Machine learning approaches to network anomaly detection. Proceedings of the Workshop on Tackling Computer Systems Problems with Machine Learning Techniques (TCSPMLT). 1–6 (2007)
Arning, Andreas, Agrawal, Rakesh, Raghavan, Prabhakar: A Linear Method for Deviation Detection in Large Databases. Proceedings of the International Conference on Knowledge discovery and data mining (SIGKDD). 972–981 (1996)
Bai, Zheng-Jian., Chan, Raymond H., Luk, Franklin T.: Principal Component Analysis for Distributed Data Sets with Updating. Advanced Parallel Processing Technologies. 471–483 (2005)
Barnett, Vic, Lewis, Toby: Outliers in Statistical Data, 3rd Edition (1994)
Basora, Luis, Olive, Xavier, Dubot, Thomas: 2019. Recent Advances in Anomaly Detection Methods Applied to Aviation. Aerospace 6, 11 (2019)
Boniol, Paul, Linardi, Michele, Roncallo, Federico, Palpanas, Themis: Automated Anomaly Detection in Large Sequences. In 2020 IEEE 36th International Conference on Data Engineering (ICDE). IEEE, 1834–1837 (2020)
Boniol, Paul, Linardi, Michele, Roncallo, Federico, Palpanas, Themis: SAD: An Unsupervised System for Subsequence Anomaly Detection. In 2020 IEEE 36th International Conference on Data Engineering (ICDE). IEEE, 1778–1781 (2020)
Boniol, Paul, Palpanas, Themis: Series2Graph: Graph-based Subsequence Anomaly Detection for Time Series. In Proceedings of the VLDB Endowment, Vol. 13 (2020)
Breunig, Markus M., Kriegel, Hans-Peter, Ng, Raymond T., Sander, Jörg: LOF: identifying density-based local outliers. In Proceedings of the International Conference on Management of Data (SIGMOD). 93–104 (2000)
de Miranda Cardoso, José Vinícius, Hedges, Christina, Gully-Santiago, Michael, Saunders, Nicholas, Cody, Ann Marie, Barclay, Thomas, Hall, Oliver, Sagear, Sheila, Turtelboom, Emma, Zhang, Johnny, Tzanidakis, Andy, Mighell, Ken, Coughlin, Jeff, Bell, Keaton, Berta-Thompson, Zach, Williams, Peter, Dotson, Jessie, Barentsen, Geert: 2018. Lightkurve: Kepler and TESS time series analysis in Python. Astrophysics Source Code Library ascl-1812, 013 (2018)
Chandola, Varun, Banerjee, Arindam, Kumar, Vipin: Anomaly Detection: A Survey. Comput. Surveys 2009, 1–72 (2009)
Cook, A.A., Mısırlı, G., Fan, Z.: Anomaly Detection for IoT Time-Series Data: A Survey. IEEE Internet of Things Journal 7 7(2020), 6481–6494 (2020)
Ester, Martin, Kriegel, Hans-Peter., Sander, Jörg., Xiaowei, Xu.: A density-based algorithm for discovering clusters in large spatial databases with noise. Proceedings of the International Conference on Knowledge discovery and data mining (SIGKDD). 226–231 (1996)
Jiang, Fan, Wu, Ying, Katsaggelos, A.K.: Detecting contextual anomalies of crowd motion in surveillance video. In Proceedings of the International Conference on Image Processing (ICIP). 1117–1120 (2009)
Gaddam, Shekhar R., Phoha, Vir V., Balagani, Kiran S.: K-Means+ID3: A Novel Method for Supervised Anomaly Detection by Cascading K-Means Clustering and ID3 Decision Tree Learning Methods. IEEE Transactions on Knowledge and Data Engineering (TKDE) 2007, 345–354 (2007)
Goldberger, Ary L., Amaral, Luis A.N., Glass, Leon, Hausdorff, Jeffrey M., Ivanov, Plamen Ch., Mark, Roger G., Mietus, Joseph E., Moody, George B., Peng, Chung-Kang, Stanley, H.Eugene: PhysioBank, PhysioToolkit, and PhysioNet: components of a new research resource for complex physiologic signals. Circulation 2000, 215–220 (2000)
Golub, Gene H., Van Loan, Charles F.: Matrix computations (2012)
Greene, Casey S., Tan, Jie, Ung, Matthew, Moore, Jason H., Cheng, Chao: Big data bioinformatics. Journal of cellular physiology 2014, 1896–1900 (2014)
Hanley, James A., McNeil, Barbara J.: The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 143 1(1982), 29–36 (1982)
Hodge, Victoria, Austin, Jim: A survey of outlier detection methodologies. Artificial Intelligence Review 2004, 85–126 (2004)
Hofmeyr, Steven A., Forrest, Stephanie, Somayaji, Anil: Intrusion detection using sequences of system calls. Journal of Computer Security 1998, 151–180 (1998)
Jiang, Yexi, Zeng, Chunqiu, Jian, Xu., Li, Tao: Real time contextual collective anomaly detection over multiple data streams. Proceedings of the Workshop on Outlier Detection and Description (ODD). 23–30 (2014)
Keogh, Eamonn, Lin, Jessica, Fu, Ada: Hot sax: Efficiently finding the most unusual time series subsequence. In Proceedings of the International Conference on Data Mining (ICDM). 8 (2005)
Knox, Edwin M., Ng, Raymond T.: Algorithms for mining distancebased outliers in large datasets. In Proceedings of the VLDB Endowment. 392–403 (1998)
Kohonen, Teuvo: Self-Organizing Maps (1997)
Laurikkala, Jorma, Juhola, Martti, Kentala, Erna, Lavrac, N., Miksch, S., Kavsek, B.: Informal identification of outliers in medical data. In International Workshop on Intelligent Data Analysis in Medicine and Pharmacology (IDAMAP). 20–24 (2000)
Lee, C.K.M., Palaniappan, S.: Effective asset management for hospitals with RFID. In 2014 IEEE International Technology Management Conference. 1–4 (2014)
Linardi, Michele, Zhu, Yan, Palpanas, Themis, Keogh, Eamonn: 2020. Matrix profile goes MAD: variable-length motif and discord discovery in data series. DATA MINING AND KNOWLEDGE DISCOVERY (2020)
Liu, Fei Tony, Ting, Kai Ming, Zhou, Zhi-Hua: Isolation forest. In Proceedings of the International Conference on Data Mining (ICDM). 413–422 (2008)
Ma, Jiangang, Sun, Le, Wang, Hua, Zhang, Yanchun, Aickelin, Uwe: Supervised anomaly detection in uncertain pseudoperiodic data streams. ACM Transactions on Internet Technology 2016, 1–20 (2016)
Malhotra, Pankaj, Vig, Lovekesh, Shroff, Gautam, Agarwal, Puneet: Long short term memory networks for anomaly detection in time series. In European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESANN) (2015)
Moody, George B., Mark, Roger G.: The impact of the MIT-BIH arrhythmia database. IEEE Engineering in Medicine and Biology Magazine (EMB) 2001, 45–50 (2001)
Palpanas, Themis: Real-time data analytics in sensor networks. Managing and Mining Sensor Data. Springer 173–210 (2013)
Palpanas, Themis, Beckmann, Volker: 2019. Report on the first and second interdisciplinary time series analysis workshop (itisa). ACM SIGMOD Record 48, 3, 36–40 (2019)
Pourahmadi, Mohsen, Noorbaloochi, Siamak: Multivariate time series analysis of neuroscience data: some challenges and opportunities. Current Opinion in Neurobiology 37(2016), 12–15 (2016)
Qu, Yongming, Ostrouchov, George, Samatova, Nagiza, Geist, Al: Principal component analysis for dimension reduction in massive distributed data sets. In Proceedings of the International Conference on Data Mining (ICDM) (2002)
Rajasegarar, Sutharshan, Leckie, Christopher, Palaniswami, Marimuthu, Bezdek, James: Distributed Anomaly Detection in Wireless Sensor Networks. International Conference on Communication Systems (ICCS). 1–5 (2006)
Ramaswamy, Sridhar, Rastogi, Rajeev, Shim, Kyuseok: Efficient algorithms for mining outliers from large data sets. Proceedings of the International Conference on Management of Data (SIGMOD). 427–438 (2000)
Rousseeuw, Peter J., Leroy, Annick M.: Robust regression and outlier detection (1996)
Senin, Pavel, Lin, Jessica, Wang, Xing, Oates, Tim, Gandhi, Sunil, Boedihardjo, Arnold P., Chen, Crystal, Frankenstein, Susan: Time series anomaly discovery with grammar-based compression.. In Proceedings of the International Conference on Extending Database Technology (EDBT). 481–492 (2015)
Senin, Pavel, Lin, Jessica, Wang, Xing, Oates, Tim, Gandhi, Sunil, Boedihardjo, Arnold P., Chen, Crystal, Frankenstein, Susan: Time series anomaly discovery with grammar-based compression. In Proceedings of the International Conference on Extending Database Technology (EDBT) (2015)
Subramaniam, Sharmila, Palpanas, Themis, Papadopoulos, Dimitris, Kalogeraki, Vana, Gunopulos, Dimitrios: Online outlier detection in sensor data using non-parametric models. In Proceedings of the 32nd international conference on Very large data bases. 187–198 (2006)
Tran, Luan, Fan, Liyue, Shahabi, Cyrus: 2016. Distance-based outlier detection in data streams. Proceedings of the VLDB Endowment 9, 12 (2016), 1089–1100
Tsay, Ruey S.: Analysis of Financial Time Series, 3rd Edition (2010)
Van Wijk, Jarke J., Van Selow, Edward R.: Cluster and calendar based visualization of time series data. In Proceedings of the IEEE Symposium on Information Visualization (InfoVis). 4–9 (1999)
Vigna, G., Kemmerer, R.A.: Intrusion Detection: A Brief History and Overview. IEEE Computer Magazine 2002, 27–30 (2002)
Wettschereck, Dietrich: titleA study of distance-based machine learning algorithms. thesistypePh.D. Dissertation (1994)
Wulsin, D., Blanco, J., Mani, R., Litt, B.: Semi-Supervised Anomaly Detection for EEG Waveforms Using Deep Belief Nets. Proceedings of the International Conference on Machine Learning and Applications (ICMLA). 436–441 (2010)
Yankov, Dragomir, Keogh, Eamonn, Rebbapragada, Umaa: Disk aware discord discovery: Finding unusual time series in terabyte sized datasets. Knowledge and Information Systems 2008, 241–262 (2008)
Yeh, Chin-Chia Michael, Zhu, Yan, Ulanova, Liudmila, Begum, Nurjahan, Ding, Yifei, Dau, Hoang Anh, Silva, Diego Furtado, Mueen, Abdullah, Keogh, Eamonn: Matrix profile I: all pairs similarity joins for time series: a unifying view that includes motifs, discords and shapelets. In Proceedings of the International Conference on Data Mining (ICDM). 1317–1322 (2016)
Acknowledgements
The work was funded by the German government as part of the LuFo VI call I program (Luftfahrtforschungsprogramm) under the grant number 20D1915. The management of Rolls-Royce Deutschland Ltd. & Co. KG is gratefully acknowledged for supporting the work and permitting the presentation of results.
We thank Paul Boniol and Themis Palpanas for their valuable feedback on our research project and their help with the Sequence2Graph algorithm.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schneider, J., Wenig, P. & Papenbrock, T. Distributed detection of sequential anomalies in univariate time series. The VLDB Journal 30, 579–602 (2021). https://doi.org/10.1007/s00778-021-00657-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00778-021-00657-6